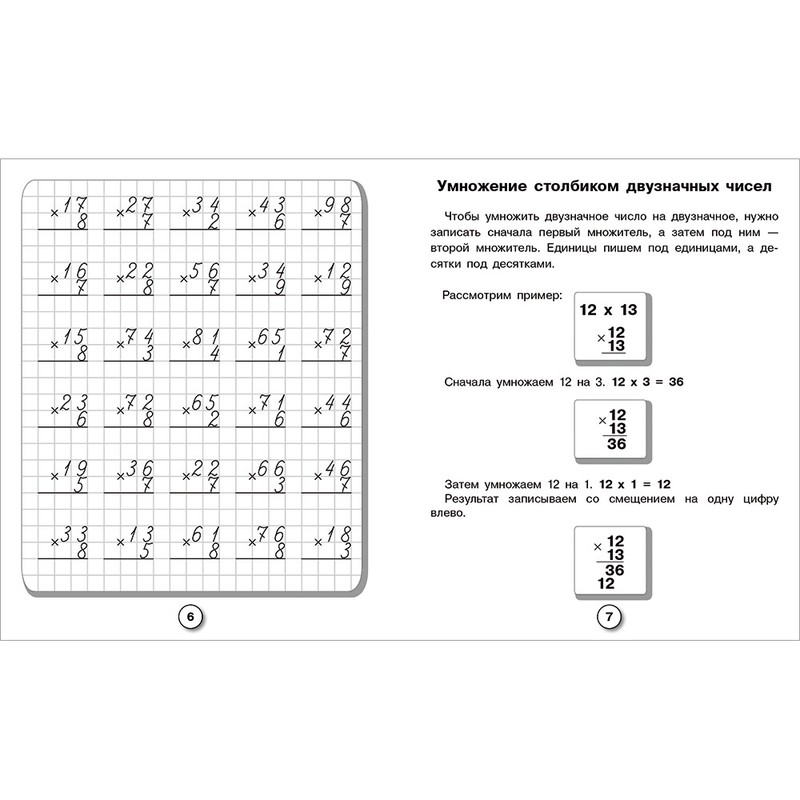
Решить пример в столбик на умножение: Онлайн калькулятор. Умножение столбиком

Содержание

Умножение столбиком многозначных натуральных чисел

Автор Ольга Андрющенко На чтение 6 мин. Просмотров 540 Опубликовано 29 октября 2022

Рассмотрим в этой статье как умножать столбиком различные числа — двузначные, трехзначные и другие — большие и маленькие. Если умножать большие числа, то умножать их столбиком, конечно, быстрее и проще всего. Маленькие числа можно умножить и в уме. Рассмотрим умножение столбиком на примере. Умножать в столбик умеет уже и 3, и 4 класс. Начинают вводить такой способ умножения уже в 3 классе, и закрепляют в 4 классе. То есть четвероклассник должен уметь это делать легко и быстро, а для этого надо хорошо знать таблицу умножения. А в 5 классе это уже отработанный навык. В этой статье мы дадим вам алгоритм умножения больших (начиная с двузначных) натуральных чисел и объясним как научить ребенка умножению, как правильно объяснить как считать в столбик.

В статье вы рассмотрите подробное решение примеров столбиком на умножение, повторите таблицу умножения и вспомните как решается любой пример на умножение больших чисел. Мы приведем примеры умножения в столбик натуральных чисел.

Содержание

Умножение двузначных чисел столбиком

Умножим два числа: 25 и 44. Когда мы записываем числа столбиком, важно записать их друг под другом так, чтобы десятки были под десятками, единицы под единицами. Вот так считать в столбик:

Правильная запись умножения столбиком

Теперь начинаем последовательно умножать сначала число 25 на первую четверку (число единиц), получим:

Умножение столбиком двузначных чисел 1 часть — умножили число 25 на число единиц (на 4) — получили 100.

Обратите внимание — число 100 записывается в процессе умножения справа налево — то есть, идем от единиц к десяткам, умножаем сначала 5 на 4, получаем 20, записываем 0 под числом единиц, а число 2 держим в уме. Теперь умножаем 2 на 4, получаем 8, но так как у нас в уме еще 2, то складываем 2 и 8, получаем 10, записываем 10, причем так как мы сейчас умножаем число десятков на число единиц второго числа — на 4, то и число 10 записываем, начиная с числа десятков — 0 под десятками и 1 слева. В итоге получаем 100.

Мы умножили число 25 на число единиц 4 второго числа 44. Теперь сделаем умножение числа 25 на число десятков 4 числа 44. Результат умножения столбиком начнем писать справа налево, то есть начнем писать его под числом десятков, получим:

Умножение в столбик двухзначных чисел

Итак, мы выполнили умножение числа 25 сначала на число единиц — 4 — второго числа 44, а потом на число десятков — 4 — второго числа 44. Следующим шагом будет сложение этих последовательных результатов умножения. Получим:

Умножение в столбик двузначных чисел результат

Обратите внимание — мы складываем не 100+100, а последовательно числа по разрядам, то есть сначала числа, стоящие на местах единиц (у нас тут один ноль), потом числа стоящие на местах десятков (0+0), числа, стоящие на позиции сотен (1+0) и числа, стоящие на месте тысяч (1). Если число только одно, то мы его просто сносим вниз, мысленно складывая с нулем.

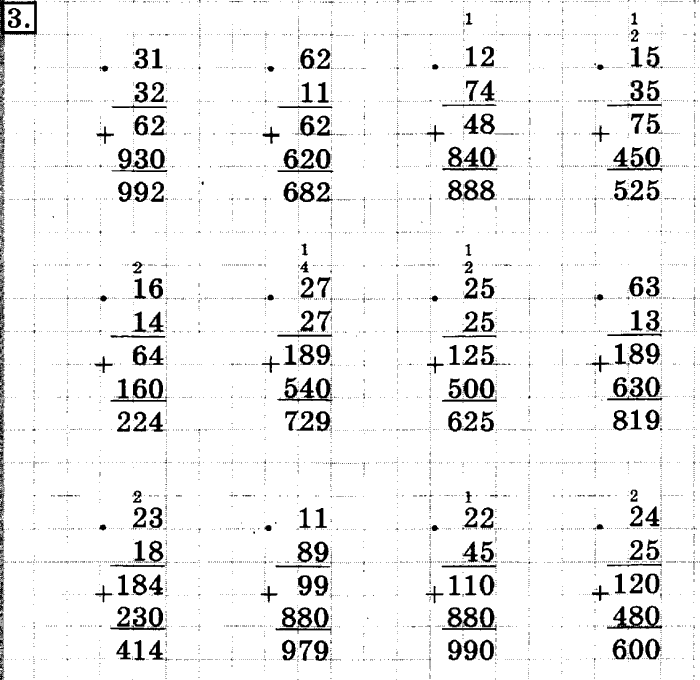
Примеры умножения двузначных чисел

Чтобы лучше разобраться в умножении двузначных чисел столбиком, рассмотрим следующие примеры решения столбиком. Вы сможете рассмотрев каждый пример подробно научиться решать такие примеры:

Пример 1

Умножим число 15 на число 37. Пошаговый алгоритм умножения столбиком:

Умножение двузначных чисел в столбик

Пример 2

Умножим число 23 на число 79. Пошаговый алгоритм умножения столбиком:

Умножение столбиком 23 и 79

Умножение столбиком трехзначных чисел

Для того, чтобы умножать столбиком трехзначные числа — все действия выполняем также, алгоритм не меняется. Только у нас появляется умножение первого (верхнего) числа на число сотен второго (нижнего) числа.

Давайте рассмотрим пример умножения столбиком трёхзначного числа на трехзначное число. Пусть нам нужно умножить 345 на 726. Вот что получится — пошаговый алгоритм:

Умножение столбиком трехзначных чисел

Таким образом, общий принцип ясен и можно перемножать в столбик числа с любым количеством знаков.

Умножение столбиком многозначных натуральных чисел

Правильная поразрядная запись умножения столбиком

Теперь рассмотрим, как надо умножать круглые числа. Тут есть небольшая хитрость для удобства умножения.

Умножение столбиком круглых чисел

Когда мы умножаем в уме круглые числа, мы не обращаем при умножении сначала внимания на ноль, например, нам нужно умножить 50 на 30. Мы в уме перемножаем 5 на 3 и просто приписываем два нуля, памятуя о том, что 10 на 10 дают 100.

Значит, если мы будем умножать, скажем 50 на 35, то эти числа в столбик нам удобнее записать не так:

Запись умножения в столбик круглого числа 1

А так:

Умножение в столбик круглого числа

Тогда нам нужно будет просто умножить число 35 на 5 и приписать 0. Здесь мы использовали следующее свойство умножения: от перемены мест множителей произведение не меняется. Поэтому вместо верхнего числа 50, мы записали нижнее число 35 — поменяли их местами.

Итак, мы рассмотрели как умножать в столбик двузначные, трехзначные и любые многозначные натуральные числа, рассмотрели алгоритм умножения в столбик, привели примеры такого умножения.

Home -Photomath

Математика еще никогда не была такой увлекательной

Наши пошаговые объяснения помогут вам освоить многие разделы математики, от арифметики и до анализа, благодаря чему вы станете увереннее в своих силах.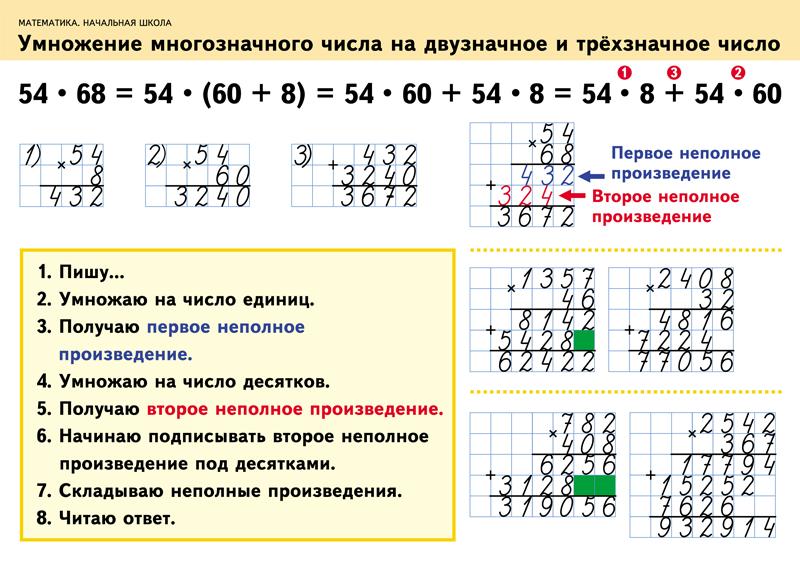

С чем мы можем помочь?

Математический анализ
Деление в столбик
Алгебра
Геометрия
Сложение и вычитание
Функции
Тригонометрия
Умножение
Дроби
Пределы и интегралы
Текстовые задачи
Элементарная математика
Статистика
и многое другое!

Начать обучение

Решение задач с основ

Один отец хотел помочь своим детям с домашней работой по математике. Теперь его творение помогает уже миллионам учеников по всему миру.

Родителям

Damir Sabol

основатель

Нечто большее, чем приложение

Один школьный учитель должен уделять внимание многим ученикам. В приложении Photomath, напротив, одному ученику предоставляется множество учителей.

Photomath для обучения

Более 220 млн

скачиваний

4.

Рейтинг приложения

ОБОЖАЮ это приложение. Каждый раз, когда я использую его в классе, мы с учениками поражаемся его способностям. Приложение демонстрирует несколько вариантов решения тех или иных уравнений, что дает ученикам благоприятные возможности для обучения, которые порой отсутствуют на обычном уроке.

Прекрасное приложение для решения математических задач, часто выручает в самый нужный момент!

Благодаря Photomath моего 8-летнего сына будто бы осенило: он понял, как в его случае получается правильный ответ.

Большое спасибо! Я в математическом классе, и мне это очень полезно, спасибо!

О нас пишут

4.

Умножение матриц

Важно: Мы можем перемножать матрицы, только если количество столбцов в первой матрице совпадает с количеством строк во второй матрице.

Пример 1

а) Умножение матрицы 2 × 3 на матрицу 3 × 4 возможно и дает в качестве ответа матрицу 2 × 4.

b) Умножение матрицы 7 × 1 на матрицу 1 × 2 допустимо; это дает матрицу 7 × 2

c) Матрица 4 × 3, умноженная на матрицу 2 × 3, НЕвозможна.

Как умножить 2 матрицы

Сначала мы используем буквы, чтобы понять, что происходит. После этого мы увидим пример с числами.

В качестве примера возьмем обычную матрицу 2 × 3, умноженную на матрицу 3 × 2.

`[(a,b,c),(d,e,f)][(u,v),(w,x),(y,z)]`

Ответом будет матрица 2 × 2.

Умножаем и складываем элементы следующим образом. Мы работаем через 1-й строки первой матрицы, умножая на 1-й столбец второй матрицы, элемент за элементом. Мы добавить полученных продуктов. Наш ответ занимает позицию a ₁₁ (вверху слева) матрицы ответов.

Проделываем аналогичный процесс для 1-й строки первой матрицы

и 2-го столбца второй матрицы. Результат помещается в позицию a ₁₂ .

Теперь о 2-й -й строке первой матрицы и 1-м -м столбце второй матрицы. Результат помещается в позицию а ₂₁ .

Наконец, делаем 2-ю строку первой матрицы и 2-й столбец второй матрицы. Результат помещается в позицию a ₂₂ .

Таким образом, результат умножения двух наших матриц выглядит следующим образом:

`[(a,b,c),(d,e,f)][(u,v),(w,x),(y,z)]` `=[(au+bw+cy,av +bx+cz),(du+ew+fy,dv+ex+fz)]`

Теперь давайте рассмотрим числовой пример.

Пользователи телефона

ПРИМЕЧАНИЕ. Если вы разговариваете по телефону, вы можете прокручивать любые широкие матрицы на этой странице вправо или влево, чтобы увидеть все выражение.

Пример 2

Умножить:

`((0,-1,2),(4,11,2))((3,-1),(1,2),(6,1))`

Ответить

Это 2×3 умножить на 3×2, что даст нам 2×2 отвечать.

`((0,-1,2),(4,11,2)) ((3,-1),(1,2),(6,1))`

`=((0xx3+ — 1xx1 + 2xx6,0xx-1+ -1xx2 + 2xx1), (4xx3+11xx1+2xx6,4xx -1 + 11xx2 + 2xx1))`

` = ((0-1+12,0-2+2), (12+11+12,-4+22+2))`

` = ((11,0),(35,20)) `

Наш ответ — матрица 2×2.

Умножение матриц 2 × 2

Процесс одинаков для матрицы любого размера. Мы умножаем на строк первой матрицы и на столбцов второй матрицы, элемент за элементом. Затем мы добавляем продукты:

`((a,b),(c,d))((e,f),(g,h))` `=((ae+bg,af+bh),(ce+dg,cf+dh ))`

В этом случае мы умножаем матрицу 2 × 2 на матрицу 2 × 2 и в результате получаем матрицу 2 × 2.

Пример 3

Умножить:

`((8,9),(5,-1))((-2,3),(4,0))`

Ответить

` ((8,9),(5,-1))((-2,3),(4,0)) `

`= ((8 xx -2+9xx4,8xx3+9xx0),( 5xx-2+ -1xx4,5xx3 + -1xx0))`

` = ((-16+36,24+0),(-10+ -4,15 + 0)) `

` = ((20 ,24),(-14,15)) `

Матрицы и системы одновременных линейных уравнений

Теперь мы видим, как написать систему линейных уравнений, используя матричное умножение.

Пример 4

Система уравнений

−3 х + y = 1
6 х — 3 у = -4

можно записать как:

`((-3,1),(6,-3))((x),(y))=((1),(-4))`

Матрицы идеально подходят для компьютерного решения задач, потому что компьютеры легко формируют массивы . Мы можем опустить алгебраические символы. Компьютеру для решения системы требуются только первая и последняя матрицы, как мы увидим в разделе «Матрицы и линейные уравнения».

Примечание 1 — Обозначение

Уход с

записью умножение матриц.

Следующие выражения имеют различных значения:

AB это умножение матриц
A × B является произведением перекрестного , которое возвращает вектор
A * B используется в компьютерной записи, но не на бумаге

А • B Произведение точек , которое возвращает скаляр .

[Дополнительную информацию о векторных и скалярных величинах см. в главе «Вектор».]

Примечание 2. Коммутативность умножения матриц

`AB = BA`?

Давайте посмотрим, так ли это на примере.

Пример 5

Если

`А=((0,-1,2),(4,11,2))`

`В=((3,-1),(1,2),(6,1))`

найти AB и ВА.

Ответить

Мы выполнили AB выше, и ответ был:

`AB = ((0,-1,2),(4,11,2)) ((3,-1),(1,2), (6,1))`

` = ( (11,0),(35,20) )`

Теперь BA равно (3 × 2)(2 × 3), что даст 3 × 3:

`BA= ((3,-1),(1,2),(6,1))((0,-1,2),(4,11,2))`

`= ((0 -4,-3-11,6-2),(0+8,-1+22,2+4),(0+4,-6+11,12+2))`

` = (( -4,-14,4),(8,21,6),(4,5,14)) `

Итак, в этом случае AB НЕ равно BA.

На самом деле, для большинства матриц нельзя изменить порядок умножения и получить тот же результат.

В общем случае при перемножении матриц перестановочный закон не выполняется, т.е. AB ≠ BA . Есть два общих исключения из этого:

Матрица идентичности: IA = AI = A .
обратная матрица: A ^-1 А
= АА ^-1 = I.

В следующем разделе мы узнаем, как найти обратную матрицу.

Пример 6. Умножение на матрицу идентичности

Учитывая, что

`А=((-3,1,6),(3,-1,0),(4,2,5))`

найти AI .

Ответить

`AI = ((-3,1,6),(3,-1,0),(4,2,5)) ((1,0,0),(0,1,0),(0 ,0,1))`

`=((-3+0+0,0+1+0,0+0+6),(3+0+0,0+ -1+0,0+0 +0),(4+0+0,0+2+0,0+0+5))`

`=((-3,1,6),(3,-1,0),(4,2,5))`

`=A`

Мы видим, что умножение на единичную матрицу не изменить значение исходной матрицы.

То есть

АИ = А

Упражнения

1. Если возможно, найдите BA и AB .

`А=((-2,1,7),(3,-1,0),(0,2,-1))`

`В=(4\\-1\\\5)`

Ответить

`BA=(4\ \ -1\ \ \ 5)((-2,1,7),(3,-1,0),(0,2,-1))`

`=(-8+(-3)+0\ \ \ 4+1+10\ \ \ 28+0+(-5))`

`=(-11\ \ 15\ \ 23)`

AB невозможно. (3 × 3) × (1 × 3).

2. Определить, если B = A ^-1, учитывая:

`А=((3,-4),(5,-7))`
`В=((7,4),(5,3))`

Ответить

Если B = A ^-1 , то `AB = I`.

`AB=((3,-4),(5,-7))((7,4),(5,3))`

`=((21-20,12-12),( 35-35,20-21))`

`=((1,0),(0,-1))`

` !=I`

Итак, B НЕ является обратным A.

3. При изучении движения электронов, одна из спиновых матриц Паули равна

`s=((0,-j),(j,0))`

где

`j=sqrt(-1)`

Покажите, что с ² = I.

[Если вы никогда раньше не видели j , перейдите в раздел, посвященный комплексным числам].

92+0))`

`= ((1,0),(0,1))`

`=I`

4. Оцените следующее матричное умножение, которое используется при управлении движением роботизированного механизма .

`( (cos\ 60° ,-sin\ 60° ,0),(sin\ 60°, cos\ 60°,0),(0,0,1))((2),(4),( 0))`

Ответить

`( (cos\ 60° ,-sin\ 60° ,0),(sin\ 60°, cos\ 60°,0),(0,0,1))((2),(4),( 0))`

`=((2(0,5)-4(0,866)+0),(2(0,866)+4(0,5)+0),(0+0+0))`

`= ((-2.464),(3.732),(0))`

Интерпретация этого заключается в том, что рука робота перемещается из позиции (2, 4, 0) в позицию (-2,46, 3,73, 0). То есть это движется в x-y плоскость, но ее высота остается равной z = 0 . Матрица 3 × 3, содержащая sin и Значения cos говорят ему, на сколько градусов двигаться.

Интерактивы Matrix Multiplication

Другие примеры умножения матриц
Интерактивные операции с матрицами

Как умножать матрицы? С Примерами

Умножение матриц является одной из фундаментальных, но продвинутых концепций матриц. Вы должны быть осторожны при умножении матриц. Это не так просто, как кажется. Вы должны хорошо знать все основные понятия, такие как, что такое матрица, строки и столбцы в матрице, как представлять матрицу и как умножать матрицы.

Снова в школу: Матрицы — это группы чисел, переменных, символов или выражений в прямоугольной таблице с различным количеством строк и столбцов. Это прямоугольные массивы с различными операциями, такими как сложение, умножение и транспонирование. Элементами матрицы являются числа или элементы, составляющие матрицу. Горизонтальные элементы матриц — это строки, а вертикальные — столбцы.

Количество строк и столбцов можно изобразить с помощью переменных. Например, пусть количество строк в матрице K равно «m», а количество столбцов — «n». Таким образом, мы можем представить матрицу K как [K] _{м х п} . Матрица представлена в квадратных скобках «[]» с произведением ее строк и столбцов в нижнем индексе.

До 1812 года человечеству не было известно умножение матриц. Филипп Мари Бине, французский математик, изобрел умножение матриц в 1812 году для описания линейных карт с матрицами. Он обнаружил, что умножение матриц является бинарной операцией. Две матрицы перемножаются, образуя одну матрицу.

Далее в этой статье вы узнаете правила и основные принципы умножения матриц.

Matrix Multiplication Formula

Example of Matrix Formula

Take A and B are two matrices,

A=[A11 A12 ⋯A1n

A21 A22 ⋯A2n

………….

AM1 AM2 ⋯ AMN],

B = [B11 B12 ⋯ B1N

B21 B22 ⋯ B2N

………….

Bm1 Bm2 ⋯Bmn]

Матрица C = AB обозначается

C = [C11C12 …… .C1C

C21C22 …… .C2C

……………

CA1CA2… — произведение матрицы A X B.

Элемент матрицы C, где C — произведение матрицы A X B. и y= 1…….c

Правила умножения матриц
Если количество столбцов в A равно количеству строк в B, то произведение A и B определено.
Нет необходимости определять BA, если определен AB.
И AB, и BA определены, если A и B — квадратные матрицы одного порядка.
Не требуется, чтобы AB равнялся BA, если определены AB и BA.
Не требуется, чтобы одна из матриц была нулевой матрицей, если произведение двух матриц является нулевой матрицей.
Характеристики умножения матриц
В математике операция умножения матриц имеет некоторые специфические характеристики. Эти характеристики перечислены ниже.
Некоммутативность: когда две матрицы A и B перемножаются, AB BA означает, что умножение матриц некоммутативно.
Распределяемость: если A, B и C совместимы, свойство распределения можно использовать при умножении матриц, т. е. A (B + C) = AB + BC.
Произведение со скаляром: Если перемножить матрицы A и B, результатом будет AB, тогда c(AB) = (cA)B = A(Bc), где c — скаляр.
Транспонирование: Формула (AB)T = BTAT, где T означает транспонирование, может использоваться для выражения транспонирования произведения матриц A и B.
Комплексное сопряжение: (AB)* = B *A*, если A и B являются сложными элементами.
Умножение матриц ассоциативно. Если произведения (AB)C и A(BC) трех матриц A, B и C определены, то (AB)C = A. (BC).
Определитель: Сумма определителей каждой отдельной матрицы равна определителю произведения матриц. Например, Det (AB) = Det A Det B.
Умножение матриц с примерами
Во введении к этой статье вы прочитали, что умножение матриц — это бинарная операция. Это означает, что всякий раз, когда вы находите произведение двух или более матриц, ответом является единственная матрица, следующая за исходными матрицами. Для перемножения двух матриц проверяется их совместимость. Это означает, что две матрицы должны следовать набору правил для умножения.
Эти параметры совместимости описаны ниже:
Значение количества столбцов в матрице один должно быть равно значению количества строк в матрице 2.
Если вышеуказанное условие не удовлетворяет, матрицы нельзя умножать.
Если матрицы являются квадратными матрицами одного порядка, их можно умножать друг на друга.
Квадратную матрицу 2 x 2 нельзя умножить на квадратную матрицу 3 x 3. Ее можно умножить на другую квадратную матрицу 2 x 2.
Давайте рассмотрим пример, чтобы лучше понять это:
Пример 1: Предположим, у нас есть две матрицы, K и L. Порядок матриц задан как m x n и n x o соответственно. Выяснить, можно ли перемножать матрицы?
Решение: Дано
Матрица 1 = [ K ] _{m x n}
Матрица 2 = [ L ] _{n x o}
Мы видим, что количество столбцов в матрицах равно количеству строк K матрица L. Следовательно, две матрицы можно перемножить.
Результирующая матрица: Матрица, полученная путем умножения двух матриц, является результирующей матрицей. Эта матрица может быть представлена как:
Название матрицы в квадратных скобках
Произведение количества строк матрицы 1 на количество столбцов матрицы два в порядке.
Снова обратимся к приведенному выше примеру:
Мы знаем, что K и L совместимы с умножением. Таким образом, результирующая матрица, скажем, D, будет = [D] _{m x o}, где m = количество строк матрицы один и o = количество столбцов матрицы 2.
Пример 2: Матрица [ K ] _{2 x 4} умножается на матрицу [ X ] _{4 х 2} . Если [ Y ] результирующая матрица, то каков порядок Y.
Решение: Нам дано
Матрица 1 = [ K ] _{2 x 4}
Матрица 2 = [ X ] _{4 x 2}
Поскольку количество столбцов матрицы K равно количеству строк матрицы X, K и X можно перемножить. Следовательно,
Матрица Y = [ Y ] _{2 x 2}
Порядок матрицы Y равен 2 x 2. Y – квадратная матрица.
Ориентация двух матриц также является решающим фактором для определения произведения матриц. Если есть две матрицы, K и L, то чтобы найти произведение K и L, вы должны сначала написать матрицу K, а затем написать матрицу L. Если вы запишете матрицу L перед матрицей K, вы получите совершенно другую матрицу . Коммутативный закон не применяется при умножении матриц. Это означает, что KL ≠ LK.
Теперь, когда мы разобрались с правилами умножения двух матриц, давайте научимся умножать матрицы.
Как умножать матрицы?
Давайте изучим пошаговую процедуру умножения двух матриц. Поначалу это может показаться вам запутанным, но когда вы освоитесь, перемножать матрицы так же просто, как намазать маслом свой тост.
Шаг 1: Проверьте совместимость предоставленных матриц. Если они несовместимы, оставьте умножение.
Шаг 2: Возьмите первую строку матрицы 1 и умножьте ее на первый столбец матрицы 2. Затем умножьте первую строку матрицы 1 на 2-й столбец матрицы 2. Теперь умножьте первую строку матрицы 1 на 3-й столбец матрицы 2 и так далее. Полученные из них значения заполнят первую строку матрицы продукта.
Шаг 3: Теперь возьмите вторую строку матрицы 1 и умножьте ее на первый столбец матрицы 2 и выполните те же шаги, что и для 2. Это заполнит вторую строку матрицы произведения.
Шаг 4: Продолжайте эти шаги, выполняя каждую строку, пока не будет получена матрица произведения.
Под умножением строк и столбцов мы подразумеваем, что элементы, присутствующие в этих строках и столбцах, будут умножены. Не забудьте умножить соответствующие элементы, а затем добавить продукты, чтобы найти элемент матрицы продукта.
Если вы не уверены в шагах, посмотрите на пример пошагового решения ниже:
Пример: Найдите произведение матриц, приведенных ниже:
K = и L =
Решение:
Шаг 1: Матрица K имеет порядок 1 x 4, а матрица L имеет порядок 4 x 2. Поскольку количество столбцов матрицы K соответствует количеству строк матрицы L, поэтому матрицы совместимы для умножения. Полученная матрица имеет порядок 1 x 2.
Шаг 2: Поскольку K имеет только 1 строку, умножьте ее на первый столбец матрицы L следующим образом: (2 x 4) + (4 x 5) + (1 x 4) + (7 x 3) = 51. Обратите внимание, как 1-й элемент строки умножается на 1-й элемент столбца 1, аналогично 2-му, 3-му и 4-му. Затем они складываются вместе, чтобы получить результирующий матричный элемент.
Шаг 3: Теперь аналогичным образом умножьте 1-ю строку на второй столбец матрицы L. Результат будет (2 x 3) + (4 x 2) + (1 x 9) + (7 x 6) = 65. .
Шаг 4: Разместите результат в матрице продуктов. Предположим, что [ X ] — результирующая матрица; следовательно, X = [51 65].
Мы только что научились перемножать две матрицы. В следующем разделе вы узнаете, как решить квадратную матрицу (2 x 2).
Мы только что научились перемножать две матрицы. В следующем разделе вы узнаете, как решить квадратную матрицу (2 x 2).
Как умножить матрицу 2 x 2
Для умножения матриц 2 x 2 вы должны хорошо знать шаги, описанные в предыдущем разделе. Поскольку мы перемножаем 2 квадратные матрицы одного порядка, нам не нужно проверять совместимость в этом случае. Помните, что матрица произведения также будет иметь тот же порядок, что и квадратная матрица. Давайте решим пример, чтобы понять, как умножить матрицу 2 x 2.
Пример: Умножить квадратную матрицу на
A = и B =
Шаг 1: Умножая первую строку матрицы A на первый столбец матрицы B. Получаем (2 x 1) + (9 x 3) = 29. Теперь умножаем первую строку матрицы A со вторым столбцом матрицы B. Получаем (2 x -4) + (9 x 7) = -8 + 63 = 55.
Шаг 2: Повторим шаг 1, но изменим строку матрица A. Первый и второй столбцы матрицы B будут умножены на строку 2 матрицы A. Результатом будет
(3 x 1) + (-7 x 3) = 3 – 21 = -18, и (3 x -4) + (-7 х 7) = -12 – 49= -61
Шаг 3: Разместите результаты правильно
.
Следовательно, результирующая матрица C =
Точно так же вы можете решать квадратные матрицы, такие как 3 x 3, 4 x 4 и так далее.
Часто задаваемые вопросы
Q1.
Что такое умножение матриц?
Ответ: Процесс умножения двух матриц для получения результата в виде одной матрицы известен как умножение матриц. Используется такой вид бинарной операции.
Q2. Как умножить две заданные матрицы?
Ответ: Чтобы перемножить две матрицы, мы должны сначала определить, совпадают ли количество строк в первой матрице и количество столбцов во второй матрице. Элементы столбца и строк первой матрицы теперь должны быть умножены друг на друга и сложены. Здесь мы должны сделать скалярное произведение столбцов и строк.
Q3. Что получится в результате умножения матрицы (2×3) на матрицу (3×3)?
Ответ: Единственная матрица, полученная путем умножения матриц (2×3) и (33), — это матрица (2×3).
Q4. Как умножить матрицу 3×3?
Ответ: Первый элемент получается сложением всех строк и столбцов первой и второй матриц. Аналогичным образом умножьте и сложите компоненты двух матриц по столбцам и по строкам, чтобы получить элементы произведения двух матриц 3 × 3.