Тренажер на умножение столбиком — «Семья и Школа»
Содержание
Как научиться делению столбиком, 3 класс,4 класс. Деление столбиком 3 двухзначных чисел. Деление столбиком 4 трёхзначных чисел. Пример деления столбиком без остатка, с остатком
Итак, тема сложения и вычитания усвоена, есть четкое представление о математических операциях умножения и деления, можно приступать к делению чисел столбиком. Не каждый школьник с первого урока поймет смысл данной темы, особенно в случаях деления многозначных чисел и чисел с остатком. И здесь ему потребуется всяческая поддержка родителей. Чтобы помочь ребен ;:ку справиться с делением уголком, воспользуйтесь нашими теоретическими подсказками. Статья имеет подробное пояснение хода решения примеров, а также доступные наглядные иллюстрации.
Содержание статьи
- Как научиться делить столбиком 3 класс
- Как научиться делить столбиком 4 класс
- Как научиться делить столбиком на двузначное
- Видео как научиться делить в столбик
- Как научиться делить в столбик с остатком
- Как научиться делить столбиком трехзначные числа
- Как научиться делить в столбик многозначные числа
Как научиться делить столбиком 3 класс
Арифметические расчеты в 3 классе базируются на таблице умножения от 1 до 10 в пределах чисел до 100.
На этом этапе ребенок должен понимать сам процесс деления и безошибочно определять категории «делителя», «делимого» и «частного». Конечно, деление многозначных чисел проще всего проводить столбиком. Школьник меньше путается и не теряет цифры. Таким образом, вырабатывается мысленная логическая схема. Суть метода нельзя уловить без знания таблицы умножения и способа «обратного» деления.
Алгоритм деления в столбик:
Например, 98 необходимо разделить в столбик на 7.
В нашем примере 98 – делимое, 7 – делитель, результат деления, который получится в итоге – частное. Его и необходимо найти.
Делимое и делитель запишем рядом, разделив их вертикальной линией с уголком. Теперь необходимо определить, сколько семерок поместится в девятке – одна. Цифру «1» запишем под линией в правом нижнем углу.
Под девяткой запишем семерку, подчеркнем линией, отнимем и запишем разницу — 2. Если в двойке не помещается ни одной семерки, значит решение верно.
Если в двойке не помещается ни одной семерки, значит решение верно.
Снесем к двойке верхнюю восьмерку. Получим — 28. Проанализируем, сколько семерок может поместиться в цифре «28» – 4. Полученный ответ запишем рядом с «1».
От 28 отнимем цифру «28» и получим «0» — значит, деление произвели правильно. Если в итоге деления не получается ноль, возможна в подсчетах арифметическая ошибка или деление без остатка невозможно. В итоге частное получилось «14».
Правильность деление можно проверить, если при умножении 14 на 7 получается 98 — подсчеты верны.
Главная проблема, с которой сталкиваются третьеклассники на уроках математики – это отсутствие умения производить быстрые арифметические действия. А ведь вся школьная программа начальной школы базируется на этой основе, особенно действия на деление.
Как научиться делить столбиком 4 класс
Программа 4 класса, по сравнению с прошлым учебным годом, усложняется в сторону увеличения расчетных чисел. Четвероклассники проводят деление многозначных чисел больше 100. Они учатся делить уголком числа с двух и трехзначным делителем, а также решать примеры с остатком.
Четвероклассники проводят деление многозначных чисел больше 100. Они учатся делить уголком числа с двух и трехзначным делителем, а также решать примеры с остатком.
Алгоритм решения деления уголком аналогичен алгоритму, изучаемому в третьем классе.
Давайте, в качестве примера 1072 разделим на 8. Сразу необходимо определиться с категориями деления, 1072 — делимое, 8 – делитель. Результат, полученный в качестве действия, — частное.
Числа запишем с двух сторон уголка.
Сразу определимся с числом, которое больше самого делителя. 1<8, поэтому начинают действие с 10. В данном числе может содержаться лишь одна 8. Запишем результат в правой колонке.
Делитель 8 умножим на 1 и получим — 8. Результат подпишем под делимым 1072 и вычтем. Полученное число 2<8, поэтому его увеличим за счет следующего неиспользованного числа делимого — 7. В итоге получится цифра «27».
Затем действуют по алгоритму. Проанализируем, сколько восьмерок содержит число «27». В нем заключено 3 х 8=24. Цифру «3» допишем в правой колонке рядом с частным 1. На данный момент частное – 13.
В нем заключено 3 х 8=24. Цифру «3» допишем в правой колонке рядом с частным 1. На данный момент частное – 13.
Слева от 27 – 24 = 3.
Последним числом частного будет цифра «32», за счет неиспользованного делителя.
Проанализировав число, запишем результат: 32 : 8 = 4. Полученную 4 присоединим к частному — 134. Осталось лишь проверить результат: 134 х 8 =1072.
Как научиться делить столбиком на двузначное
В 4 классе ученик должен уметь делить уголком многозначные значения на двух- и трехзначное число. Полученный навык необходим для дальнейшего курса математики вплоть до 11 класса.
Для примера выполним действие: 144 : 24
Как и в случае однозначного деления, определим число большее самого делителя: 14<24, т.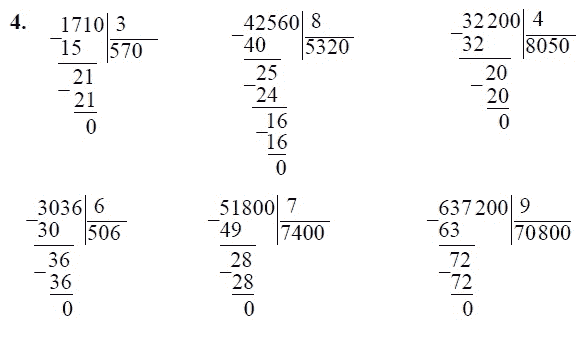 е. будем делить сразу все число — 144. Прикинем 144 : 20, получим примерно 7. Пробную цифру пока не пишут в колонке. Проверим, 7 х 24 = 168, что значительно больше нашего делимого. Возьмем по 6 х 24 = 144 – это наше число. Подпишем его под делимым и получим ответ – 6.
е. будем делить сразу все число — 144. Прикинем 144 : 20, получим примерно 7. Пробную цифру пока не пишут в колонке. Проверим, 7 х 24 = 168, что значительно больше нашего делимого. Возьмем по 6 х 24 = 144 – это наше число. Подпишем его под делимым и получим ответ – 6.
После постепенного освоения простых примеров, можно перейти к более сложным.
Разделим 1035 на 23.
Определив первую цифру, 103 >23, делим ее на 23. 20 х 5 = 100, но у нас в примере 23 х 5 = 115, что больше 103. Возьмем по 4: 23 х 4 = 92. Запишем ответ в правой колонке под чертой.
От 103 – 92 = 11. Данные запишем под делимым. 11<23, т.е. расчеты сделаны верно.
К 11 снесем 5 и получим цифру «115». Методом подбора определим результат: 23 х 5 = 115.
Цифру «5» запишем рядом с 4 в ответ – 45.
Проверим: 45 х 23 = 1035, результат верен.
Аналогично выполняют деление на любые многозначные числа (трехзначные, четырехзначные и т. п.).
п.).
Видео как научиться делить в столбик
Как научиться делить в столбик с остатком
Деление с остатком – следующий этап обучения. Во время таких действий делимое невозможно ровно разделить на части. Ответ примера будет иметь неделимый кусок, меньший делителя. Чтобы школьник быстрее понял смысл математических действий, тему объясняют на доступных примерах.
На подносе находится 34 конфеты, которые нужно разделить на 8 детей. Когда каждый ребенок получит по 4 конфеты, на столе останется еще 2 штуки. Это и будет остаток. Вычисления выглядят следующим образом:
34 : 8= 4 ост (2). Откуда взялась цифра «2»? 8 х 4= 32, 34 — 32= 2.
Принцип деления уголком с остатком аналогичен классическому, с одной разницей – наличием остатка.
Для примера разделим 235 на 14.
235 — делимое, расположим слева, делитель (14) напишем правее. Оба значения между собой разделим уголком. Приступим к поиску целого. 23>14, в данном числе помещается 1 делитель. Единицу запишем внизу под уголком. 23 — 14 = 9.
Оба значения между собой разделим уголком. Приступим к поиску целого. 23>14, в данном числе помещается 1 делитель. Единицу запишем внизу под уголком. 23 — 14 = 9.
К 9 снесем 5 — цифру единиц делимого и в итоге получим второе неполное делимое – 95.
Попробуем 14 х 8= 112. 112>95, поэтому возьмем на единицу меньше: 7 х 14= 98, что также больше 96 на две единицы. Теперь уже точно известно, что нужная цифра 6: 6 х 14= 84
95 — 84= 11, т.е. 11 — это остаток.
Во время решения примеров с остатком, ответ может быть записан двумя способами:
- в виде дроби, когда в числителе размещают остаток, а в знаменатель записывают делитель:11/16,
- но чаще всего ответ записывают словами: 6 целых и 11 в остатке.
Как научиться делить столбиком трехзначные числа
Когда в делителе стоит трехзначное число, действие лучше всего выполнять в столбик. Алгоритм математического решения аналогичен делению на двузначное число.
Алгоритм математического решения аналогичен делению на двузначное число.
Для примера рассмотрим следующие действия: 146676 : 719
146<719, поэтому сразу возьмем четырехзначное число «1466». В данном значении помещается 2 делителя: 719 х 2= 1438. Цифра «2» будет первым значением частного. Ее запишем справа под уголком.
1466 — 1438 = 28. Полученную разность запишем под чертой слева. Снесем к 28 цифру «7». 287<719, поэтому рядом с двойкой запишем «0».
Снесем последнюю цифру делимого «6», в итоге получится число «2876», которое разделим на 719. Возьмем по 3: 719 х 3 = 2157 — мало, можно взять по 4: 719 х 4 = 2876. Цифру «4» запишем рядом с «20», получим в ответе 204. От 2876 отнимем 2876 , получим разность 0.
Желательно в конце проверить правильность выполнения действий: 204 х 719 = 146676. Ответ верен.
Как научиться делить в столбик многозначные числа
Этапы деления в столбик многозначного числа аналогичны классическому делению многозначного числа на однозначное.
Математические действия на деление в столбик будут под силу школьнику, если он поймет основной алгоритм вычисления. Правильность решения всегда можно проверить умножением.
Конспект урока для 3 класса по теме: «Деление трёхзначного числа на однозначное»
Романова Мария Романовна
МОУ «Средняя общеобразовательная школа №5» г. Ивантеевка
Учитель начальных классов
Конспект по математике 3 класс, М.И. Башмакова, М.Г. Нефёдова
Тема: Деление трёхзначного числа на однозначное.
Цель: научить письменному делению трёхзначного числа на однозначное число в столбик.
Задачи:
Предметные: повторить поместное значение цифр, повторить умение анализировать трёхзначные числа, закрепить табличное умножение и не табличное умножение, сложение и вычитание в пределах тысячи, свойство сложения: деление суммы на число, умножение в пределах тысячи, повторить выполнение порядка действий, принцип деления с остатком
Метапредметные: развитие психических процессов, развитие устной речи, развитие умения анализировать, сравнивать, сопоставлять.
Личностные: активность, самостоятельность.
1.Орг. момент.
Здравствуйте дети, меня зовут Мария Романовна. Сегодня я буду вести у вас урок математики. Я вижу вашу готовность к уроку, молодцы.
2.Повторение изученного материала (устный счёт) и актуализация имеющихся знаний.
Что обозначает каждая цифра в числе: 66,92,695,781
Какое число состоит из 9 десятков и 7 единиц; 7 сотен, 3 десятков и 3 единиц; 5 сотен, 5 десятков и 7 единиц
Представьте число в виде суммы разрядных слагаемых: 863, 984, 436
Посмотрите на доску и найдите значение выражений:
7*9=_ ; 35:_=7; 6*_=48; 9*4=_
3. Изучение нового материала
Изучение нового материала
Давайте откроем учебник на странице 30 и посмотрим на задание под №1. Внимательно прочитайте задание. Внимательно посмотрите на пример 363:3=121. Каким способом здесь произвели действие деление?- делимое разложили на сумму разрядных слагаемых и поочередно разделили их на делитель, затем полученные результаты сложили. Вы абсолютно правы, ребята. А сейчас прочитайте задание, которое написано ниже.
Сейчас я вам предлагаю вам решить данные примеры, только мы с вами должны будем подумать, на какие слагаемые мы будем раскладывать делимое: на разрядные или удобные слагаемые. При делении двузначного и трехзначного чисел на однозначное число нужно делимое заменить суммой удобных слагаемых, при этом первое число должно содержать наибольшее число десятков, делящихся на делитель, затем вычтя это число из делимого найдем второе удобное слагаемое.
98:7=(70+28):7=70:7+28:7=10+4=14
85:5=(50+35):5=50:5+35:5=10+7=17
468:4=(400+40+28):4=400:4+40:4+28:4=100+10+7=117
678:6=(600+60+18):6=600:6+60:6+18:6=100+10+3=113
Молодцы ребята, вы хорошо справились с заданием. Но решать данные примеры можно и немного иным способом. Деление может производиться в столбик. На странице 30 давайте обратим внимание на то, что выделено в рамку и прочитаем то, что там написано. Давайте прочитаем вслух. Ребята деление можно записать в столбик и сейчас мы с вами научимся это делать. Я буду писать на доске, а вы сначала посмотрите, потом мы с вами всё запишем.
Но решать данные примеры можно и немного иным способом. Деление может производиться в столбик. На странице 30 давайте обратим внимание на то, что выделено в рамку и прочитаем то, что там написано. Давайте прочитаем вслух. Ребята деление можно записать в столбик и сейчас мы с вами научимся это делать. Я буду писать на доске, а вы сначала посмотрите, потом мы с вами всё запишем.
Сначала записываем в строчку делимое 98. Затем рядом рисуем прямой угол, горизонтальную линию проводим на две клетки вправо, а вертикальную можем немного продлить вниз. Внутри угла записываем делитель 7. Под углом мы с вами будем записывать цифры частного. Хочу обратить ваше внимание на то, что деление начинается с самого большого разряда.
____
А сейчас берите ручки, мы будем с вами записывать и проговаривать вслух, что мы делаем (повторяем алгоритм записи ещё раз). А сейчас мы вместе решим этот пример.
Берём 9 десятков, подбираем цифру в частном.7*1=7, поэтому записываем 9-7 и находим остаток 2. Списываем под линию следующую цифру делимого 8. Ищем цифру, а частном. 784=28, поэтому пишем 28-28 и находим остаток, единицы разделились полностью.
Списываем под линию следующую цифру делимого 8. Ищем цифру, а частном. 784=28, поэтому пишем 28-28 и находим остаток, единицы разделились полностью.
Ребята, а сейчас я хочу вам открыть ещё один секрет. Ещё не решая, мы с вами можем определить количество цифр в частном. Как же это делается?- если первое неполное делимое однозначное число, т. е. первая цифра в делимом обозначает число, которое больше или равно делителю, то в частном будет столько цифр, сколько в делимом и за каждую цифру, нужно поставить точку в частное. Но если первое неполное делимое двузначное число, а это может быть только тогда, когда первая цифра делимого обозначает число, которое меньше делителя, и поэтому необходимо начать действие деление с числа, записанного двумя первыми цифрами, то в частном будет на одну цифру меньше, чем в делимом.
Давайте обратимся к номеру 2.И вслух объясним все примеры, которые здесь решены. Затем проверим правильность выполнения деления действием умножением.
Следующее задание №3. Внимательно прочитайте задание. Давайте выполним его.
Внимательно прочитайте задание. Давайте выполним его.
1 пример- при делении двузначного числа на однозначное получается трёхзначное, может такое быть?- нет, не может. Тогда давайте исправим ошибки. Для начала определим количество цифр в частном. Первая цифра делимого больше делителя?- да больше. Значит, сколько цифр будет в частном?- 2 цифры.
А сейчас начинаем делить число 76 на 2.Первый разряд, который мы будем делить это десятки (т.к. я уже говорила, деление в столбик начинается с самого большого разряда). Поэтому первое неполное делимое у нас 7.7 десятков делим на 2.Это таблица умножения, какое число нужно умножить на 2, чтобы получить 7?такого числа нет, но мы можем подобрать максимально близкое число к 7- правильно число 6.Записываем 3 в частное и проверяем.3*2=6, всё правильно. Вычитаем 7-6=1, и находим остаток 1. Сносим следующую цифру делимого 6 и образуем второе неполное делимое 16. Какое число нужно умножить на 2, чтобы получить 16?- вы правы, это число 8. Пишем 8 в частное и проверяем 8*2=16 и вычитаем. Вычитаем из единиц единицы, они разделились без остатка. Ответ:38. И теперь нужно выполнить проверку 38*2=78- деление было выполнено верно.
Вычитаем из единиц единицы, они разделились без остатка. Ответ:38. И теперь нужно выполнить проверку 38*2=78- деление было выполнено верно.
Второй пример-91:7 и получаем 121-может такое быть? Почему? Тогда давайте определим, сколько цифр в частном должно быть и исправим ошибку. Первая цифра делимого больше или меньше делителя?- она больше. Что это обозначает?- что в значении частного будет 2 цифры. А сейчас начинаем делить число 91на 7.Первый разряд, который мы будем делить это десятки (т.к. я уже говорила, деление в столбик начинается с самого большого разряда). Поэтому первое неполное делимое у нас 9.9 десятков делим на 2.Это таблица умножения, какое число нужно умножить на 2, чтобы получить 9?такого числа нет, но мы можем подобрать максимально близкое число к 9- правильно число 7.Записываем 1 в частное и проверяем.7*1=7, всё правильно. Вычитаем 9-7=2, и находим остаток 2. Сносим следующую цифру делимого 7 и образуем второе неполное делимое 21. Какое число нужно умножить на 7, чтобы получить 21?- вы правы, это число 3. Пишем 3 в частное и проверяем 7*3=21 и вычитаем. Вычитаем из единиц единицы, они разделились без остатка. Ответ:13.Теперь давайте сделаем проверку 13*7=91. Деление выполнено, верно.
Пишем 3 в частное и проверяем 7*3=21 и вычитаем. Вычитаем из единиц единицы, они разделились без остатка. Ответ:13.Теперь давайте сделаем проверку 13*7=91. Деление выполнено, верно.
И последний пример- 87:3 и получаем трёхзначное число, потому что каждая точка в частном обозначает одну цифру частного. Может такое быть?- нет, не может. Тогда давайте исправим ошибку и найдём верный ответ.
А сейчас начинаем делить число 87 : 3.Первый разряд, который мы будем делить это десятки (т.к. я уже говорила, деление в столбик начинается с самого большого разряда). Поэтому первое неполное делимое у нас 8.8 десятков делим на 3.Это таблица умножения, какое число нужно умножить на 3, чтобы получить 8?такого числа нет, но мы можем подобрать максимально близкое число к 8- правильно число 6.Записываем 2 в частное и проверяем.2*3=6, всё правильно. Вычитаем 8-6=2, и находим остаток 2. Сносим следующую цифру делимого 7 и образуем второе неполное делимое 27. Какое число нужно умножить на 3, чтобы получить 27?- вы правы, это число 9. Пишем 3 в частное и проверяем 9*3=27 и вычитаем. Вычитаем из единиц единицы, они разделились без остатка. Ответ:29. И делаем проверку примера 3*29=87.
Пишем 3 в частное и проверяем 9*3=27 и вычитаем. Вычитаем из единиц единицы, они разделились без остатка. Ответ:29. И делаем проверку примера 3*29=87.
4. Первичное закрепление
Теперь выполняем упражнение №4.
В этом номере мы с вами будем выполнять деление с остатком. Давайте вспомним, что это обозначает на примере 56:9?Чтобы 56 :9 нужно подобрать такое число, чтобы при умножении на делитель получилось число, близкое к 56, но не больше него. Найти остаток и сравнить с делителем. Если остаток меньше делителя, то деление выполнено, верно. И как можно проверить правильность выполнения примера? 56:9=6(ост.2). молодцы ребята, вы хорошо справились, а теперь мы можем приступить к решению более сложного примера.
283 нужно разделить на 3. Чему будет равно первое неполное делимое?- 2 на 3 разделить нельзя, поэтому будем делить не одну первую цифру, а две, значит первое неполное делимое 28.Поэтому первая цифра в частном будет равна 9, записываем её в частное и проверяем. 3*9=27, и вычитаем 28-27=1, остаток равен 1. Списываем следующую цифру делимого и образуем второе неполное делимое 13. 13 на 3 разделить, поэтому ищем число, которое при умножении на 3, даёт число близкое к 13, 3*4=12. 4 записываем в частное и находим остаток 1. Деление закончено. Теперь нужно проверить правильно ли мы выполнили деление: 283:3=94(ост. 1) 3*94+1=283-деление выполнено верно.
3*9=27, и вычитаем 28-27=1, остаток равен 1. Списываем следующую цифру делимого и образуем второе неполное делимое 13. 13 на 3 разделить, поэтому ищем число, которое при умножении на 3, даёт число близкое к 13, 3*4=12. 4 записываем в частное и находим остаток 1. Деление закончено. Теперь нужно проверить правильно ли мы выполнили деление: 283:3=94(ост. 1) 3*94+1=283-деление выполнено верно.
Следующий №6- выполним деление не в столбик, а другим способом.
400:4-как мы будем выполнять деление? представим делимое в виде произведения слагаемых (4*100):4=4:4*100=100
816:4=(800+16):4=800:4+16:4=200+4=204
428:4=(400+28):4=400:4+28:4=100+7=107
5.Итог урока.
Что нового мы сегодня узнали?
Что делали на уроке?
6. Домашнее задание.
Упр. №6, все примеры которые остались в этом номере выполните дома
Матрицы – умножение, деление, сложение и вычитание
Перейти к содержимому
Умножение
Умножение
youtube.com/embed/PqobOjdYyBU» frameborder=»0″ allow=»accelerometer; autoplay; encrypted-media; gyroscope; picture-in-picture» allowfullscreen=»»>Деление
Матрица представляет собой массив чисел, в котором есть строки и столбцы, которые показывают размер или размеры матриц.
Умножить матрицу на одно число очень просто –
Вычисления выполняются по следующей формуле –
Все мы знаем, что число 2 в этом состоянии является скаляром, поэтому оно известно как скалярное умножение.
Умножение матрицы на другую матрицу
Но для умножения матрицы на другую матрицу нам нужно решить скалярное произведение строк и столбцов, и что это значит? Теперь давайте посмотрим на пример для выработки ответа или решения для строки 1 st и столбца 1 st .
Скалярный продукт — это умножение совпадающих членов и их суммирование —
(1, 2, 3). (7, 9, 10) = 1 * 7 + 2 * 9 + 3 * 10 = 7 + 11 + 30 = 48. 2 и членов, таких как 2 и 9, и 3 и членов, которые являются 3 и 10, а затем, наконец, суммируйте все это.
(7, 9, 10) = 1 * 7 + 2 * 9 + 3 * 10 = 7 + 11 + 30 = 48. 2 и членов, таких как 2 и 9, и 3 и членов, которые являются 3 и 10, а затем, наконец, суммируйте все это.
Хотите решить еще один пример? Тогда вот для 1-й строки и 2-го столбца —
(2, 3, 4). (7, 8 ,9) = 2 * 7 + 3 * 8 + 4 * 9 = 14 + 24 + 36 = 74
Теперь мы можем сделать то же самое для 2 -й -й ряд и 1-й столбец –
(1, 2, 1). (2, 3, 4) = 1 * 2 + 2 * 3 + 1 * 4 = 2 + 6 + 4 = 12
И тогда для 2 -й строки и 2-го столбца –
(3, 1, 2 ). (1, 2, 3) = 3 * 1 + 1 * 2 + 2 * 3 = 3 + 2 + 6 = 11
Тогда мы окончательно получим результат.
Надеюсь, теперь вы разобрались с методом и решениями?
Дивизия
А что такое деление? На самом деле мы не делим матрицы, так как делаем это таким образом.
X / Y = X * (1/Y) = X * B -1
Где B обратная означает обратную матрицу B. Поэтому здесь нам не нужно делить ее, а умножить на обратную матрицы. Есть несколько специальных способов узнать обратную матрицу.
Есть несколько специальных способов узнать обратную матрицу.
Для обратной матрицы вам нужно выписать матрицу и идентифицировать матрицу рядом, а также выполнить некоторые операции со строками, чтобы матрица B идентична матрице. Выполняя операции со строками, B затем станет единичной матрицей, а фактическая единичная матрица станет обратной матрице B, поскольку все операции будут выполняться в единичной матрице.
После получения обратной матрицы вам нужно умножить обратную матрицу B на A, что будет делением матриц.
Сложение и вычитание
Прежде всего, давайте выясним, что такое матрица. Матрица может быть добавлена или вычтена из другой матрицы только в том случае, если обе матрицы имеют одинаковые размеры. Для добавления двух матриц просто добавьте записи и получите сумму вместо полученной матрицы.
Давайте решим несколько примеров и разберемся в них глубже –
Пример – 1
[1 2] + [2 -3]
Во-первых, обратите внимание, что обе матрицы являются матрицами 1 * 1, затем мы можем добавить их.
[1 2] + [2 -3]
= [1+2 2+(-3)]
= [3 -1]
Вычитание также является очень простой процедурой с матрицами. Давайте посмотрим на некоторые примеры, чтобы мы могли иметь четкое представление о них.
Пример – 2
[4 5] – [2 1]
Сначала ясно видим, что обе матрицы имеют одинаковую размерность, а затем начинаем вычитать –
[4 5] – [2 1]
= [4-2 5-1]
= [2 4]
Сложение матрицы очень простое и выполняется с каждой записью.
Давайте решим несколько критических примеров, которые дадут лучшее понимание матриц:
Добавьте следующие матрицы
Теперь нам просто нужно добавить эту пару записей, а затем упростить окончательное решение.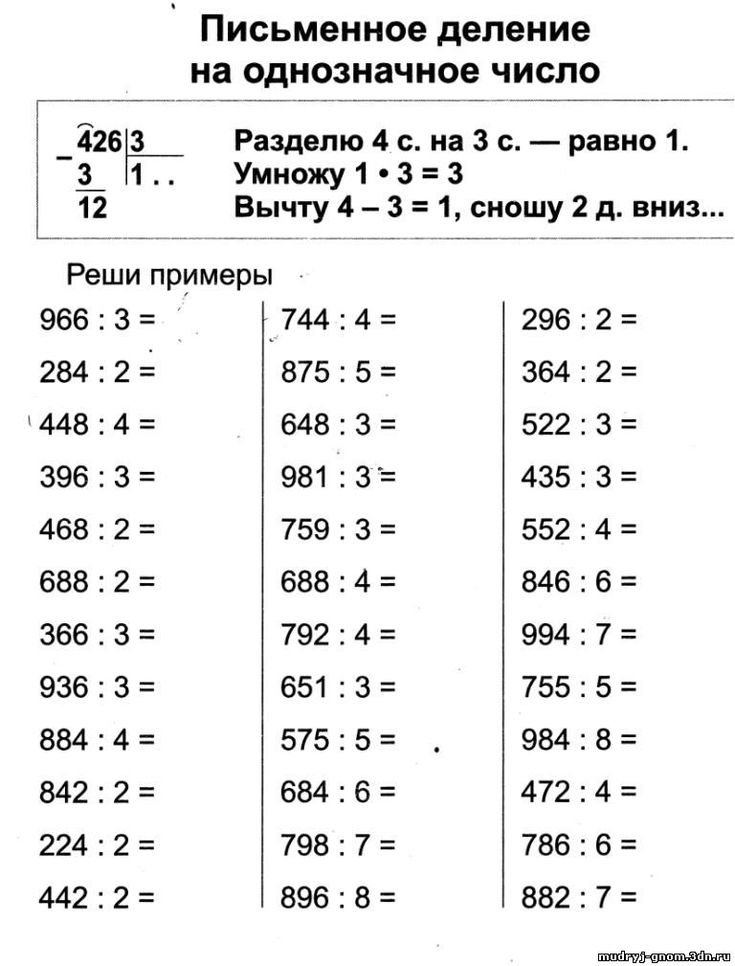
Итак, окончательный ответ —
До сих пор вы научились складывать две вещи в матрицах, такие как переменные, числа, уравнения и другие. Но сложение не всегда работает с матрицами.
Оцените приведенную ниже задачу или, если это невозможно, укажите причину.
Хотя матрицы добавляются при каждой записи, нам нужно сложить два числа, например 2 и 2, 1 и 8, затем 3 и 4, 4 и 6. Но что еще мы можем сделать при сложении чисел 6 и 7 и у которых нет прямых чисел в другой матрице? Итак, ответ –
Эти матрицы нельзя складывать, так как они не имеют одинаковых размеров и размеров.
Это всегда так при добавлении матриц, нужны обе матрицы одинакового размера. Если они не одинакового размера, то дополнение не применяется. В нем нет никакой математической логики для сложения неравных матриц.
Вычитание также работает с каждой записью и при тех же условиях. Вычитание матриц, как и сложение, невозможно выполнить, если матрицы имеют разную размерность или размеры. Это касается как сложения, так и вычитания матриц.
Это касается как сложения, так и вычитания матриц.
Найдите значения x и y для следующих уравнений –
Во-первых, вам нужно легко вычислить левую часть с помощью стороны и входа –
, Таким образом, при равенстве матрицы работает с вводом, мы сравниваем эти записи для создания простых уравнений, которые мы можем решить. В таких случаях
X + 6 = 7 и 2y -3 = -5
X = 7 – 6
X = 1
And
2y – 3 = -5
Y = -5 + 3 / 2
Y = -2 / 2
Д = -1
Перейти к началу
смешанных словесных задач для 3 класса
AlleBilderBücherVideosMapsNewsShopping
suchoptionen
Bilder
Alle anzeigen
Alle word Mixed
0005
www. k5learning.com › … › Словесные задачи
Математические задачи 3 класса на сложение, вычитание, умножение и деление. Проблемы короткие и простые; основная задача для …
Рабочие листы для 3-го класса по математике — K5 Learning
www. k5learning.com › Рабочие листы › Математика › 3 класс
k5learning.com › Рабочие листы › Математика › 3 класс
Смешанные текстовые задачи для 3-го класса. Следующие рабочие листы содержат набор задач на сложение, вычитание, умножение и деление для 3 класса. Смешивание математики …
[PDF] Рабочий лист смешанных математических и текстовых задач для 3 класса
www.mathinenglish.com › PWP › Grade3MixedBagI
3 класс. Смешанный пакет I. Словесные задачи … Сколько он сэкономит за 3 месяца? Вопрос 4. Цена гамбургера 3 доллара.
Рабочий лист по смешанным задачам третьего класса на сложение и …
www.math-only-math.com › рабочий лист на третьем классе…
Ответы к рабочему листу по смешанным задачам третьего класса сложение и вычитание приведены ниже, чтобы проверить точные ответы на вышеуказанные текстовые задачи.
Математические словесные задачи (смешанные навыки) — Рабочие листы Super Teacher
www.superteacherworksheets.com › Mixed-word-pr…
(Уровень C: Класс 3). Смешанная математика: C1 БЕСПЛАТНО. Смешанные задачи обзора на этой странице включают добавление, вычитание, подсчет денег.
Смешанная математика: C1 БЕСПЛАТНО. Смешанные задачи обзора на этой странице включают добавление, вычитание, подсчет денег.
Смешанные словесные задачи для 3-го года — Liveworksheets.com
www.liveworksheets.com › рабочие листы › Математика › Словесные_задачи › Смешанные…
Смешанные словесные задачи на сложение, вычитание, деление и умножение. ID: 1598857. Язык: английский Учебный предмет: Математика Класс/уровень: 3. Возраст: 8-10
Смешанные задачи со словами
www.dadsworksheets.com › … › Словарные задачи
Все операции со словами готовы для печати PDF-файлов. Без регистрации и входа! Отличная практика по прикладной математике для учащихся четвертого или пятого классов,
Word Problems Worksheets | Динамически созданный .
Таблица деления (математика для детей, 2, 3 класс)
На 1
1 ÷ 1 = 1
2 ÷ 1 = 2
3 ÷ 1 = 3
4 ÷ 1 = 4
5 ÷ 1 = 5
6 ÷ 1 = 6
7 ÷ 1 = 7
8 ÷ 1 = 8
9 ÷ 1 = 9
10 ÷ 1 = 10
На 2
2 ÷ 2 = 1
4 ÷ 2 = 2
6 ÷ 2 = 3
8 ÷ 2 = 4
10 ÷ 2 = 5
12 ÷ 2 = 6
14 ÷ 2 = 7
16 ÷ 2 = 8
18 ÷ 2 = 9
20 ÷ 2 = 10
На 3
3 ÷ 3 = 1
6 ÷ 3 = 2
9 ÷ 3 = 3
12 ÷ 3 = 4
15 ÷ 3 = 5
18 ÷ 3 = 6
21 ÷ 3 = 7
24 ÷ 3 = 8
27 ÷ 3 = 9
30 ÷ 3 = 10
На 4
4 ÷ 4 = 1
8 ÷ 4 = 2
12 ÷ 4 = 3
16 ÷ 4 = 4
20 ÷ 4 = 5
24 ÷ 4 = 6
28 ÷ 4 = 7
32 ÷ 4 = 8
36 ÷ 4 = 9
40 ÷ 4 = 10
На 5
5 ÷ 5 = 1
10 ÷ 5 = 2
15 ÷ 5 = 3
20 ÷ 5 = 4
25 ÷ 5 = 5
30 ÷ 5 = 6
35 ÷ 5 = 7
40 ÷ 5 = 8
45 ÷ 5 = 9
50 ÷ 5 = 10
На 6
6 ÷ 6 = 1
12 ÷ 6 = 2
18 ÷ 6 = 3
24 ÷ 6 = 4
30 ÷ 6 = 5
36 ÷ 6 = 6
42 ÷ 6 = 7
48 ÷ 6 = 8
54 ÷ 6 = 9
60 ÷ 6 = 10
На 7
7 ÷ 7 = 1
14 ÷ 7 = 2
21 ÷ 7 = 3
28 ÷ 7 = 4
35 ÷ 7 = 5
42 ÷ 7 = 6
49 ÷ 7 = 7
56 ÷ 7 = 8
63 ÷ 7 = 9
70 ÷ 7 = 10
На 8
8 ÷ 8 = 1
16 ÷ 8 = 2
24 ÷ 8 = 3
32 ÷ 8 = 4
40 ÷ 8 = 5
48 ÷ 8 = 6
56 ÷ 8 = 7
64 ÷ 8 = 8
72 ÷ 8 = 9
80 ÷ 8 = 10
На 9
9 ÷ 9 = 1
18 ÷ 9 = 2
27 ÷ 9 = 3
36 ÷ 9 = 4
45 ÷ 9 = 5
54 ÷ 9 = 6
63 ÷ 9 = 7
72 ÷ 9 = 8
81 ÷ 9 = 9
90 ÷ 9 = 10
На 10
10 ÷ 10 = 1
20 ÷ 10 = 2
30 ÷ 10 = 3
40 ÷ 10 = 4
50 ÷ 10 = 5
60 ÷ 10 = 6
70 ÷ 10 = 7
80 ÷ 10 = 8
90 ÷ 10 = 9
100 ÷ 10 = 10
(на 0 делить нельзя)
Учить таблицу деления — игра
Математическим действием, которое противоположно умножению, называется деление. Деление обозначается дробной чертой или знаком «:». Число, которое делится, называется «делимым». Делимое всегда находится в числителе дроби – над дробной чертой. Число, на которое делят, называется «делителем». Делитель всегда находится в знаменателе дроби – под дробной чертой. Результат деления называется «частным». Частное всегда положительно, если делятся положительные числа. Если одно из двух чисел, делимое или делитель, отрицательно, результат получается отрицательным – плюс на минус дает минус, минус на плюс дает минус. При делении отрицательного числа на отрицательное получается положительное число – минус на минус дает плюс. Из результатов деления получается таблица деления. Её можно представить правильными или десятичными дробями.
Деление обозначается дробной чертой или знаком «:». Число, которое делится, называется «делимым». Делимое всегда находится в числителе дроби – над дробной чертой. Число, на которое делят, называется «делителем». Делитель всегда находится в знаменателе дроби – под дробной чертой. Результат деления называется «частным». Частное всегда положительно, если делятся положительные числа. Если одно из двух чисел, делимое или делитель, отрицательно, результат получается отрицательным – плюс на минус дает минус, минус на плюс дает минус. При делении отрицательного числа на отрицательное получается положительное число – минус на минус дает плюс. Из результатов деления получается таблица деления. Её можно представить правильными или десятичными дробями.
Таблица деления в виде картинки
Чтобы распечатать, скопируйте картинку в любой редактор. Обычно таблицу деления дети проходят на математике в третьем классе.
Открыть в отдельном окне в полном размере
Деление онлайн
/Посмотрите также видео о делении в столбик.

Таблица деления для этого может пригодиться.
Всё для учебы » Математика в школе » Таблица деления (математика для детей, 2, 3 класс)
Если страница помогла, сохраните её и поделитесь ссылкой с друзьями:
Ссылка: https://uchim.org/matematika/tablica-deleniya
iLearn, Inc.
Данная тема является подготовкой к решению текстовых задач (прикладных задач) на умножение и деление. Учащиеся учатся представлять мультипликативное отношение в сетке, полученной на уроках по этой теме.
Таблицы умножения
Учащиеся учатся представлять повторяющееся умножение на то же число, что и таблица умножения, и как таблица связана с массивом, который использовался для иллюстрации умножения на предыдущих уроках. В таблице три строки. Нижняя строка показывает переменный фактор, который отличается в каждом столбце. В средней строке показан постоянный коэффициент, одинаковый для всех столбцов, а в верхней строке — произведение.
В средней строке показан постоянный коэффициент, одинаковый для всех столбцов, а в верхней строке — произведение.
Целью использования этой таблицы является использование ее в качестве основы для графического органайзера в качестве вспомогательного средства для обучения решению текстовых задач на последующих уроках. Когда структура таблицы объяснена, средняя строка удаляется, и учащийся узнает, что значение в верхней строке в первом столбце сообщает ему число, которое идет в каждом столбце средней строки, так что эта строка больше не является нужный.
В задачах этого урока ученику дается двухстрочная таблица умножения, в которой отсутствует одно значение. Учащийся должен использовать информацию в таблице, чтобы определить, что такое постоянный фактор, и использовать ее для определения отсутствующего продукта или отсутствующего фактора.
Семейства умножения: операторы умножения
В этом уроке двухстрочное умножение из предыдущего урока еще более сжато. В этом уроке все столбцы таблицы, кроме двух, удалены, в результате чего получается сетка с четырьмя прямоугольниками — по два в каждой строке и по два в каждом столбце. Числа в сетке определяются как семейство чисел умножения.
В этом уроке все столбцы таблицы, кроме двух, удалены, в результате чего получается сетка с четырьмя прямоугольниками — по два в каждой строке и по два в каждом столбце. Числа в сетке определяются как семейство чисел умножения.
В семействе чисел умножения, отображаемом в этой сетке, первый столбец указывает мультипликативное соотношение, поскольку нижний левый квадрат всегда равен 1, а верхний левый квадрат — это произведение 1 и некоторого числа. Имея эти два числа, можно определить отсутствующее число в правом столбце, когда задано другое число в этом столбце. Когда даны оба числа в правом столбце, а также 1 в нижнем левом поле (которое всегда присутствует), отношение этих двух чисел говорит о недостающем числе в верхней левой ячейке.
Это графический органайзер, который будет использоваться при решении текстовых задач на следующих уроках. В задачах этого урока учащимся дается семейство чисел умножения в сетке, в котором отсутствует одно из трех значений (кроме 1). Они используют информацию в сетке, чтобы написать предложение умножения, в котором отсутствует либо произведение, либо один из множителей.
Они используют информацию в сетке, чтобы написать предложение умножения, в котором отсутствует либо произведение, либо один из множителей.
Семейства умножения: отсутствует номер
На этом уроке учащиеся расширяют знания, полученные на предыдущих уроках, чтобы найти пропущенное число в семействе чисел умножения, представленном в графическом органайзере, который использовался на последнем уроке. Им дается сетка семейства чисел, в которой отсутствует одно из трех чисел, как и в предыдущем уроке, но на этом уроке они находят пропущенное число, не записывая предложение с числом умножения, и вводят число в сетку.
« Вернуться к темам по математике по классам
Сложение, вычитание, умножение и деление Повторение — 3-й класс математики
Начните с единицы справа (👉) и решайте столбец за столбцом.
Итак, каков ответ?
Верно! Это 7359.
Дополнение Пример 2
675 + 198 = ?
Запишите задачу в виде столбца.
На этот раз нам пришлось перегруппироваться!
Совет: Когда сумма в столбце больше 9, вам нужно перегруппировать !
Отлично!
Теперь приступим к вычитанию.
Обзор вычитания
Вычитание — это вычитание части числа.
Попробуем вычесть несколько чисел.
Пример вычитания 1
497 — 251 = ?
Давайте вычтем, используя столбец формы.
Как и в случае сложения, начните со столбца «Единицы».
Какая разница?
497 — 251 = 246
Отличная работа! 👏
Пример вычитания 2
7,301 — 6,361 = ?
Вычитаем! На этот раз нам нужно перегруппировать .
Какая тебе разница?
7 301 — 6 361 = 940
Вперед! 🤗
Давайте теперь рассмотрим умножение и деление.
Просмотр умножения
Добавление одинаковых групп снова и снова называется умножение.
Например, когда мы умножаем 2 круга 5 раза, получаем 10 кругов.
5 × 2 = 10
Уравнения умножения состоят из множителей и произведения.
Давайте рассмотрим несколько примеров умножения.
Пример умножения 1
9 × 8 = ?
Умножение — это быстрый способ многократного сложения .
Это означает добавить 9 до сам 8 раз, или добавить 8 к раз 3
2 9 раз9 × 8 =
9 + 9 + 9 + 9 + 9 + 9 + 9 + 9 = 72
Итак,
9 × 8 = 72
Пример умножения 2
3 256 ×
Давайте умножим эти большие числа, используя форму столбца .
Сначала мы умножаем цифру на Единицы место на 3.
Затем мы умножаем цифру Десятки место на 3 и добавляем перенос.
Получаем 16, так что надо переносить на сотни.
Наконец, мы умножаем цифру в разряде Сотни на 3 и добавляем перенос.
Отличная работа! 👏
Division Review
Division разбивает число на равные группы.
Например, когда мы разбиваем 10 круги на 5 равняем группы, получаем по 2 круга в каждой группе.
10 ÷ 5 = 2
A деление уравнение имеет делимое , делитель , символ деления (÷ или ⟌) и частное .
Давайте рассмотрим некоторые задачи на деление.
Раздел Пример 1
30 ÷ 6 = ?
Давайте решим это, используя повторяется вычитание.
✅ Мы начинаем с 30 и вычитаем 6 из и из , пока не достигнем 0. Количество раз, которое мы вычитаем, является нашим ответом.
Итак,
30 ÷ 6 = 5
Отлично!
Совет: Думайте о делении как о противоположности умножения. Если вы видите 30 ÷ 6 = ? только подумайте: какое число умножить на 6 будет 30?
6 х ? = 30
И вы получите тот же ответ: 5!
Раздел Пример 2
882 ÷ 7 = ?
Давайте решим этот вопрос, используя длинное деление .
Начнем с расстановки чисел в форме деления.
Теперь посмотрите на первую цифру, 8.
Можете ли вы сказать, сколько семерок поместится в 8?
Очень хорошо! 1.
Напишите 1 на сверху и напишите продукт из 1 и 7 3 9 8.
Теперь вычесть этот продукт из 8 , чтобы получить остаток.