Что делают первым умножение или деление: Какие правила порядка выполнения действий в выражениях со скобками тебе известны

Что будет первым умножение или деление? – Обзоры Вики

Порядок операций можно запомнить по аббревиатуре PEMDAS, которая означает: круглые скобки, показатели степени, умножение и деление слева направо, а сложение и вычитание слева направо. Здесь нет круглых скобок или показателей степени, поэтому начните с умножения и деления слева направо.

Итак, каков порядок операций в математике? Чтобы помочь учащимся в Соединенных Штатах запомнить этот порядок операций, учителя вставляют в них аббревиатуру PEMDAS: круглые скобки, показатели, умножение, деление, сложение, вычитание.

Имеет ли значение порядок умножения и деления? Умножение и деление можно делать вместе. Другими словами, не имеет значения, выполняете ли вы сначала деление или умножение, но они должны выполняться после круглых скобок и показателей степени, а также перед сложением и вычитанием.

Дополнительно Можно ли выполнять умножение и деление в любом порядке? заказ операций говорит вам сначала выполнить умножение и деление слева направо, прежде чем выполнять сложение и вычитание. Продолжайте выполнять умножение и деление слева направо. Далее складываем и вычитаем слева направо.

Можно ли выучить деление перед умножением? дети начинают учить умножение во втором классе, и деление в третьем классе.

Каковы 5 порядка операций?

Она выступает за Круглые скобки, экспоненты, умножение / деление, сложение / вычитание. В школах PEMDAS часто расширяется до мнемоники «Пожалуйста, извините, моя дорогая тетя Салли». Канада и Новая Зеландия используют BEDMAS, что означает скобки, экспоненты, деление/умножение, сложение/вычитание.

Почему вы делаете сначала умножение и деление? Учащиеся должны были своими словами ответить на вопрос, который передает концепцию: Умножение и деление делается до сложения и вычитания чтобы преобразовать группы элементов в промежуточные итоги похожих элементов, которые можно объединить для получения общей суммы.

Что такое правило MDAS в математике? MDAS означает Умножение, деление, сложение и вычитание.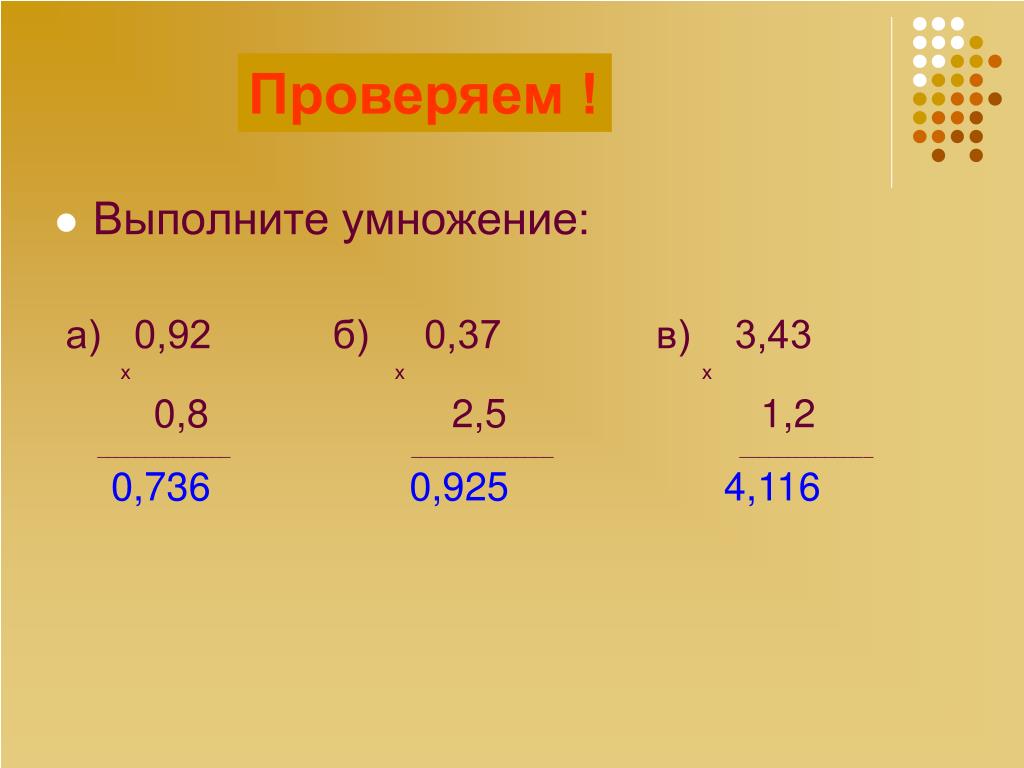 Это часть Порядка операций, набора правил, определяющих последовательность упрощения математических операций. Он используется, когда выражение или уравнение имеют более одной операции.

Имеет ли деление преимущество перед умножением?

Умножение имеет тот же приоритет, что и деление, но умножение и деление имеют более высокий приоритет, чем сложение и вычитание.

Также Каковы четыре правила математики? Четыре правила математики сложение, вычитание, умножение и деление. На следующих веб-страницах вы можете узнать, как это сделать вручную (без калькулятора), а также другую важную информацию о порядке приоритета этих операций.

Что такое правило DMAS?

правило DMAS следует, когда в данной задаче присутствует несколько арифметических операций, таких как сложение, вычитание, умножение и деление. В нем говорится, что они должны выполняться в порядке деления, умножения, сложения и вычитания.

Почему студенты борются с разделением? Ребенку, которому не хватает фундаментального навыка, будет трудно разделить потому что это связано с предыдущими концепциями. Деление — это повторное вычитание и противоположность умножения. Это связано со счетом, целым и частями и пропорциональным мышлением.

Верно ли правило Бодмаса?

Его буквы обозначают скобки, порядок (значение полномочий), деление, умножение, сложение, вычитание. … Он не содержит скобок, степеней, деления или умножения, поэтому мы будем следовать BODMAS и делать сложение с последующим вычитанием: это ошибочно. Правильное значение 3.

В Бодмасе деление предшествует умножению?

PEMDAS («круглые скобки, показатели степени…») и BEDMAS также используются в США и Австралии. Возвращаясь к приведенному выше примеру, правильным ответом будет первый ответ, поскольку он следует правилам BODMAS: деление можно сделать перед умножением и должно быть сделано до сложения, а умножение предшествует сложению.

Что правильно MDAS или DMAS? Это не MDAS. На самом деле это DMAS, что означает деление, умножение, сложение и вычитание. В математике это правило соблюдается, что означает, что в уравнении или задаче порядок упрощения будет в указанном выше формате.

Как решить порядок действий? Порядок операций сообщает нам порядок решения шагов в выражениях с более чем одной операцией. Первый, решаем любые операции внутри скобок или скобок. Во-вторых, решаем любые показатели. В-третьих, мы решаем все умножение и деление слева направо.

Как вы оцениваете MDAS?

Чем отличается деление умножения? Умножение и деление тесно связаны между собой, поскольку деление — это обратная операция умножения. Когда мы делим, мы пытаемся разделить на равные группы, в то время как умножение предполагает объединение равных групп. … Если мы разделим этот продукт на один из множителей, то в результате получим другой множитель.

Каковы 4 порядка операций?

Порядок операций — это правило, указывающее правильную последовательность шагов для вычисления математического выражения. Мы можем запомнить порядок с помощью PEMDAS: Круглые скобки, экспоненты, умножение и деление (слева направо), сложение и вычитание (слева направо). Создал Сал Хан.

Почему умножение и деление имеют одинаковый приоритет? Сказать, что умножение и деление имеют одинаковый приоритет, значит сказать, что в выражении без скобок они оба должны выполняться до операций с более низким приоритетом, такие как сложение и вычитание, и что они оба должны выполняться после операций более высокого приоритета, таких как возведение в степень.

Какую скобку вы решите в первую очередь?

Согласно правилу BODMAS, если выражение содержит скобки ((), {}, []) мы должны сначала решить или упростить скобку, за которой следует «порядок» (что означает степени и корни и т. д.), затем деление, умножение, сложение и вычитание слева направо.

Каковы основные математические формулы? Некоторые примеры основных математических формул:

• Периметр прямоугольника = 2 (длина + ширина)
• Площадь прямоугольника = длина × ширина.
• Периметр квадрата = 4 × длина стороны.
• Площадь квадрата = длина стороны × длина стороны.
• Объем прямоугольного параллелепипеда = длина × ширина × высота.
• Прибыль = Цена продажи – Себестоимость.

Чем сложение и вычитание отличаются от умножения и деления?

Хотя операций четыре, они влекут за собой только два действия: объединение или разделение. Сложение и умножение объединяют действия и вычитание и деление являются разделяющими действиями.

Может ли MDAS быть DMSA? Это в равной степени может быть DMAS, DMSA и MDAS.. Дело в том, что умножение и деление всегда имеют более высокий приоритет, чем сложение и вычитание, за исключением скобок.

В чем разница между правилом Пемдаса и Бодмаса?

PEMDAS и BODMAS абсолютно идентичны; это разные названия одного и того же набора правил. В BODMAS вы не всегда делаете «деление перед умножением», а в PEMDAS вы не всегда делаете «умножение перед делением».

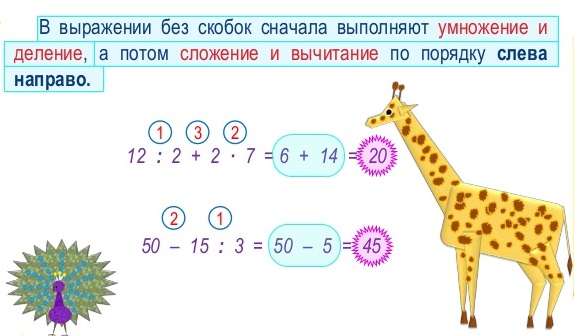
Порядок выполнения действий в выражениях без скобок

Цели:

• Предметные: организовать деятельность учащихся по изучению порядка действий в выражениях.
• Познавательные — развивать умение самостоятельно находить и извлекать нужную информацию, осуществлять для решения учебных задач операции анализа, синтеза, сравнения, классификации, устанавливать причинно-следственные связи, делать обобщения, выводы.
• Регулятивные — развивать умение планировать необходимые действия; контролировать процесс и результат деятельности, вносить необходимые коррективы; осознавать возникшие трудности, искать их причину и пути преодоления.
• Коммуникативные — развивать умение вступать в диалог с учителем, сверстниками, участвовать в беседе, соблюдая правила речевого поведения; формулировать собственные мысли, высказывать и обосновывать свою точку зрения, осуществлять совместную деятельность в парах с учетом конкретных учебно-познавательных задач.
• Личностные: формирование положительного отношения к познавательной деятельности, желание приобретать новые знания, проявлять интерес к предмету.

Тип занятия: учебное занятие по изучению и первичному закреплению нового материала

Оборудование:

• проектор, компьютер,
• для каждого ученика — учебник, учебные принадлежности, тетрадь, карточки с заданиями

Задачи:

• формировать способности к практическому использованию правила;
• развивать умение анализировать и обобщать;
• учить учебному сотрудничеству.

Ход урока

I. Организационный момент

II. Мотивация к учебной деятельности

— В природе есть солнце. Оно светит и греет.

А кого в нашем родном крае называют солнцем Осетии?

(Основоположника осетинской литературы Коста Левановича Хетагурова).

— Да, Коста-солнце Осетии…

Так пусть же сегодня каждый лучик солнца доберётся до вас и не только согреет своим теплом, но и придаст вам сил и уверенности в своих знаниях.

Это отрывок из стихотворения К.Хетагурова…

Учись, дружок, с охотой,
Чтоб мудрость всю познать,
И с радостью работай,
Чтоб человеком стать!

— Прочитайте на доске высказывание всемирно известного ученого, физика, математика, филолога Михаила Ломоносова.

(Высказывание)

«Математику уже затем учить следует, что она ум в порядок приводит».
М.Ломоносов

— Как вы понимаете это высказывание?

(Математика точная наука, она учит терпению, раскладывает всё по полочкам, дисциплинирует мозг)

— Да, математика, большая любительница порядка. Где в математике вы имели дело с порядком? (В числовой последовательности; порядок действий в выражениях…)

— Наш урок сегодня будет посвящен открытию нового знания

III. Актуализация и фиксирование индивидуального затруднения в пробном учебном действии

Цели:

• организовать актуализацию умений;
• организует выполнение учащимися пробного учебного действия;
• организовать фиксирования учащимися индивидуального затруднения;
• уточнить следующий шаг учебной деятельности.

— Посмотрите внимательно на выражения, разделите их на группы и запишите в 2 столбика

(Буквенные и числовые)

(a — b )+ с	(a — b )+ с	(6 ∙ 3) : 2= 9
(6 ∙ 3) : 2 =	(а : b) + c	40 : 5 ∙ 2 = 16?
40 : 5 ∙ 3 =
(а : b) + c

— Найдите значение числовых выражений.

IV. Выявление места и причины затруднения

Цели:

• выявить место (шаг, операция) затруднения;
• зафиксировать во внешней речи причину затруднения.

Учащиеся выявляют затруднение при определении порядка действий в выражении, содержащем скобки

Проверка.

— Кто справился без ошибок? У кого есть ошибки?

— В каком месте возникло затруднение? (В выражении без скобок)

— Почему возникло затруднение? (Из-за разного порядка действий)

Построение выхода из затруднения.

— Какую цель вы поставите перед собой? (Научиться решать выражения без скобок)

— Попробуйте сформулировать тему нашего урока. (Порядок выполнения действий в выражениях без скобок

)

— Посмотрите еще раз на данное выражение 40 : 5 ∙ 2 = 16 (На доске) и давайте составим план наших действий

Составление плана действий

1. Из каких арифметических действий составлено выражение ?

2. В каком направлении считать?

3. Какое действие выполнять первым?

4. Какое действие выполнять вторым?

5. Сделать вывод.

V. Реализация построенного проекта

— Предлагаю поработать в парах. 20: 4 ∙ 5 =25

Карточка № 1 и опорная картинка «Волк и Заяц»

— Исследуйте с помощью плана и опорной картинки «Волк и Заяц» последовательность выполнения действий в данном выражении и найдите значение выражения.

— Проверим

20: 4 ∙ 5 =25

— Как решали выражение? (1 ученик)

(Выражение не содержит скобок, из арифметических действий только умножение и деление, считали слева направо по порядку)

— Какой вывод сделали?

(Если выражение содержит только умножение и деление и нет скобок, то выполнять надо по порядку)

— Сравните вывод, который вы сделали с эталоном в учебнике с.107 (читает ученик)

VI. Первичное закрепление с проговариванием во внешней речи

— Можно ли сказать, что вы уже все сделали на уроке? (Нет)

— Какую цель вы поставите на оставшиеся этапы? (Научиться применять эталон)

— Что для этого надо сделать? (Потренироваться в использовании нового эталона)

с. 108 № 2 — с комментированием у доски

(Это выражение без скобок, содержит только деление, буду выполнять действия по порядку, ….)

16 : 4 : 2 = 2
72 : 9 ∙ 8 = 64
5 ∙1 ∙ 9 = 45
6 ∙ 4 : 8 : 3 = 1

ФИЗМИНУТКА

№ 3 с. 108 устно

— Какое правило нарушил Волк? (Правило порядка действий в примерах без скобок)

— Как нужно было решить? (Сначала выполнить деление 12:3, а затем умножение)

Каким правилом воспользоваться? Проговорите его. (Проговаривают правило и решают пример устно)

(Если выражение без скобок содержит из действий только умножение, только деление или умножение и деление, то принято выполнять их по порядку слева направо)

VII. Самостоятельная работа с самопроверкой по эталону

Цели:

• организовать выполнение учащимися самостоятельной работы на новое знание;
• организовать самопроверку по эталону;
• организовать выявление места и причины затруднений, работу над ошибками.

— Вы поработали вместе, в парах, а теперь необходимо поработать самостоятельно.

— Выполните задание самостоятельно, карточка №2

• 18 : 2 ∙ 3
• 7 ∙ 6 : 6
• 4 ∙ 2 ∙ 9
• 2 ∙ 9 : 3 : 2
• 56 : 7 : 4

10 СЛАЙД

— Проверьте решение по эталону для самопроверки.

Подробный образец	Эталон
18 : 2 ∙ 3 =27 7 ∙ 6 : 6 = 7 4 ∙ 2 ∙ 9 = 72 2 ∙ 9 : 3 : 2 = 3 56 : 7 : 4= 2	Выражение без скобок и содержит только умножение и деление. Выполняем действия по порядку слева направо

— У кого получился другой ответ — поставьте «?».

— В каком месте вы допустили ошибку.

— Почему у вас возникло затруднение? (В расстановке порядка действий (применение нового правила), знание таблицы умножения и деления)

— Что необходимо сделать, чтобы такие ошибки не допускать? (Проговаривают правило, необходимо повторить таблицу умножения и деления, порядок действий в выражениях)

— Кто справился с заданием без ошибок?

— Поставьте себе «+». Замечательно.

VIII. Рефлексия учебной деятельности на уроке (итог)

Цели:

• зафиксировать новое содержание, изученное на уроке;
• организовать рефлексию и самооценку учениками собственной учебной деятельности.
• соотнести ее цель и результаты, зафиксировать степень их соответствия, и наметить дальнейшие цели деятельности.

— Вернёмся к выражению, которое мы в начале урока на доске разбирали.

40 : 5 ∙ 2 = 16

— Почему были разные ответы? (Не знали порядок действий в выражениях на умножение и деление без скобок)

— Какие шаги выполняли? (Когда возникло затруднение, составили план, нашли решение и пришли к выводу)

— Какой сделали вывод? (Если выражение из скобок содержит из действий только умножение, только деление или умножение и деление, то принято выполнять их по порядку)

— Сегодня вы ещё на один шаг продвинулись в своём обучении.

Теперь я предлагаю вам оценить свою работу на уроке. Положите перед собой «лестницу успеха». Покажите, на какой ступеньке вы находитесь в конце урока. Если вы выполнили самостоятельную работу без ошибок, и у вас нет вопросов, то поставьте себя на верхнюю ступеньку. Если вы выполнили самостоятельную работу, но у вас остались вопросы, поставьте себя на среднюю ступеньку. Если вы ошиблись в самостоятельной работе, у вас остались вопросы, поставьте себя на нижнюю ступеньку.

IX. Домашнее задание

Р. т. стр. 53, № 187, 188.

— Спасибо за урок!

Почему учителям математики пора выбросить БОДМАС

SecondaryMaths

Практически каждый учащийся средней школы в Великобритании сталкивался с аббревиатурой порядка операций, но есть проблема; не всегда получается…

по Оуэн Элтон

Что означает БОДМАС?

Аббревиатура BODMAS означает скобки, порядок, деление, умножение, сложение, вычитание.

Иногда его называют BIDMAS (с «Индексами», используемыми вместо «Порядков»), или правилом PEMDAS в Америке (с «Скобками» и «Экспонентами»).

правило БОДМАС

Это математическое правило диктует правильный порядок операций, которым необходимо следовать, когда вы выполняете задание на математическое числовое предложение с различными операциями.

Первый шаг — сделать что-нибудь в скобках, затем порядки (например, квадратный корень или индексы). Деление и умножение находятся на одном уровне, что означает, что они имеют одинаковый приоритет и должны выполняться слева направо, а не все деление, а затем все умножение. Точно так же сложение и вычитание находятся на одном уровне и должны выполняться слева направо.

---

Я начал свою преподавательскую деятельность в школе Highgate. Молодой, неподготовленный и еще не лысеющий, я столкнулся с самой крутой кривой обучения в своей жизни.

Еженедельные встречи с моим начальником отдела были жизненно важны для обсуждения педагогики, и я верно следовал его инструкциям: «Никогда не сокращайте кумулятивную частоту», «Мы всегда подбрасываем монеты и выпадаем решкой, мы никогда не подбрасываем монеты и выпадаем орлом», и самое главное , «Мы никогда, никогда не используем BODMAS».

Не использовать BODMAS было не так просто, как вы можете себе представить. Студенты приехали хорошо разбирающиеся в его применении.

Нам пришлось и научить этому. Нам пришлось убедить комнаты, полные подростков, что они должны изменить фундаментальные принципы своей арифметической системы убеждений. Это было трудно, потому что подростки ненавидят перемены и ненавидят прозелитизм взрослых.

Так с какой стати нам беспокоиться? Что убедило весь отдел в том, что нужно направить столько усилий на такое, казалось бы, тривиальное дело?

БОДМАС неправильный. Это то что.

Неправильный ответ

Его буквы обозначают Скобки, Порядок (значение сил), Деление, Умножение, Сложение, Вычитание. Таким образом, предполагается, что в этой последовательности происходит упрощение любого заданного математического выражения.

Например, чтобы вычислить  3 + (3 + 3) ³ ÷ 3 – 3 x 3  действуем в порядке, указанном выше:

Это был бы действительно полезный алгоритм, если бы он работал в любой ситуации, но рассмотрим гораздо более простое выражение 1 – 2 + 4 . Он не содержит скобок, степеней, деления или умножения, поэтому мы будем следовать BODMAS и делать сложение с последующим вычитанием:

Это ошибка. Правильное значение — 3. BODMAS подвел нас. Позор BODMAS!

Математические задачи

У нас не может быть волшебной мнемоники, которая не работает все время; предположим, что он решил не работать в важный момент. Представьте, что вы пытаетесь объяснить своему ученику, что причина, по которой он потерял оценку на экзамене, заключалась в том, что то, о чем вы говорили ему, всегда работает, на самом деле не работает во всех случаях, и на самом деле один из таких случаев произошел в эта бумага GCSE.

Это не новая проблема. Я не первый, кто об этом пишет. Даже Википедия решает эту проблему и предлагает некоторые альтернативы. Студенты любят Википедию! Так почему же BODMAS все еще актуален?

В Хайгейте это было окружено таким клеймом, что некоторые стороны высмеивали меня более десяти лет после того, как мой коллега пережил обмен в классе, который проходил примерно так:

Учитель: Как нам упростить это выражение? Студент: БОДМАС, сэр. Учитель: Мы не используем здесь BODMAS. Студент: Но именно этому нас научил мистер Элтон в прошлом году, сэр.

После этого мне несправедливо присвоили прозвище «БОДМАС», которое преследовало меня повсюду. У меня не было защиты; платный студент сделал заявление, так что это должно быть правдой. По крайней мере, один человек (он знает, кто он такой) до сих пор называет меня БОДМАСом чаще, чем использует мое настоящее имя.

Несмотря на то, что я абсолютно не виновен в том, что оскверняю умы невинных учеников, я чувствую себя обязанным загладить свою вину, поэтому я использую эту платформу. Думайте об этом как о общественной работе.

Правильный ответ

Однако нет смысла ругать BODMAS, не предлагая альтернативы. Ошибка, показанная выше, вызвана тем фактом, что сложение и вычитание не обязательно должны происходить в указанном порядке. Если у нас есть строка из этих двух операций, она называется суммой, и мы должны работать слева направо:

.

Точно так же деление не более важно, чем умножение. Если у нас есть строка из этих двух операций, она называется произведением, и мы снова будем работать слева направо:

Теперь у нас следующий порядок: Скобки, Порядок, Произведения, Суммы.

Это дает нам BOPS, который на целый слог короче, чем BODMAS, и имеет значительное преимущество в том, что он надежен.

Уверен, что если бы кто-то предложил БОПС до БОДМАСа, то последний был бы предан забвению. Даже сейчас еще не поздно избавиться от двусложных арифметических сокращений.

Я призываю своих коллег по всему миру запретить BIDMAS и очистить PEMDAS. Не оставляй от них следов. Пусть БОПС нанесет везде победный удар юным математикам.

Оуэн Элтон — учитель математики, сочинитель/исполнитель глупых песенок и автор математических минут. Вы можете следить за его новостями в Твиттере @owenelton.

Когда дети изучают умножение и деление

Из всех математических операций умножение и деление могут быть самыми трудными для изучения детьми. Овладение этими навыками — логичный следующий шаг после сложения и вычитания. Но на самом деле это скорее скачок для большинства детей. Узнайте, когда дети учатся умножать и делить.

Когда дети обычно изучают умножение

Учиться умножать можно уже во втором классе. Дети обычно начинают со сложения равных групп (3 + 3 + 3 = 9, что равносильно 3 × 3 = 9). Это называется повторным добавлением.

Вот как и когда дети учатся умножать:

• Во втором классе дети учатся визуализировать повторяющееся сложение. (Это похоже на рисование квадрата с пятью строками и пятью столбцами для представления 5 × 5 = 25.)
• В третьем классе дети начинают понимать связь между умножением и делением. (Это как знать, что 3 × 4 = 12, а 12 ÷ 4 = 3.)
• В четвертом классе детей начинают умножать двузначные числа на двузначные числа.

Чтобы научиться умножению, дети используют практические материалы и наглядные модели, чтобы разбить числа и построить концепцию.

К концу пятого класса большинство детей знают, как использовать распространенную процедуру умножения больших чисел. Некоторым нужно немного больше времени и практики, чтобы полностью понять концепцию.

Когда дети обычно изучают деление

Деление обычно является самым сложным математическим понятием для детей. Уравнение деления состоит из трех частей:

• Делимое — это число, которое делится (первое число в задаче).
• Делитель — это число, на которое делится делимое (второе число в задаче).

Обучение делению начинается в третьем классе. Дети знакомятся с понятием, выполняя многократное вычитание. (Например, 20 – 5, затем еще 5, и еще 5, и еще одно 5. Это то же самое, что 20 ÷ 4.)

Вот как и когда дети учатся делить:

• В третьем классе детей начинают деление повторным вычитанием. Они учатся делить две цифры на однозначные числа с решениями больше 10.
• В четвертом классе дети начинают учиться делить четырехзначные числа на однозначные числа. (Например, 4000 ÷ 2.)
• В пятом классе детей начинают делить четырехзначные числа на четырехзначные числа. (Например, 8 000 ÷ 4 000.) Кроме того, большинство детей знакомятся с десятичными дробями в пятом классе.

Ожидается, что дети полностью поймут, как умножать и делить, прежде чем перейдут в среднюю школу. Но это не значит, что каждый ребенок это поймет. Некоторым детям нужно больше времени и практики.

Почему у некоторых детей возникают проблемы с умножением и делением

У детей нередко возникают проблемы с математикой, особенно с умножением и делением. Для этого есть много причин и много способов помочь. Поддержка, такая как отдельное обучение или обучение в небольшой группе, может со временем иметь большое значение.

Например, у некоторых детей возникают проблемы с пониманием основных математических понятий, известных как чувство числа. Проблемы с концентрацией внимания или памятью могут повлиять на изучение математики.