Что первое умножение или деление со скобками: Ошибка 403 — доступ запрещён

Как делить со скобками, что вперед: деление или умножение, как решить 36:3(8–6) дробь 6, правильный ответ на пример — 17 января 2023

Сможете решить правильно?

Иллюстрация: Юрий Орлов / NGS.RU

Поделиться

Минимум неделю в интернете миллионы людей ломают копья из-за простенького, на первый взгляд, примера. NGS.RU решил задачку вместе с кандидатом физико-математических наук, доцентом и преподавателем Новосибирского государственного университета Ильей Марьясовым.

Вот этот пример: 36 : 3 (8 − 6) дробь 6.

Некоторые люди готовы спорить часами, как решить этот пример

Фото: Александра Бруня / NGS.RU

Поделиться

— Подвоха здесь особо никакого нет. У нас в математике есть соглашение о том, как у нас должны выполняться арифметические операции. Умножение и деление имеют более высокий приоритет, чем сложение и вычитание. Когда нужно изменить порядок вычисления, чтобы сложение и вычитание выполнялись раньше, то используются скобки. И еще один момент — когда появляются дроби, а дробная черта — это деление, то в этом случае оно выполняется в последнюю очередь, — объяснил Илья Марьясов

Разбираемся с числителем. По очереди идут деление, умножение, вычитание — при этом последняя операция идет в скобках. Начинаем решать слева направо.

— Поскольку деление и умножение равноправны. Сначала 36 делим на 3 и получаем 12. Потом мы должны выполнить умножение, но поскольку вычитание стоит в скобках, то сначала делаем его. Из 8 вычитаем 6 и получаем 2. Теперь делаем умножение. Мы 12 умножаем на 2 и получаем 24. Теперь делим числитель на знаменатель. То есть 24 делим на 6 и получаем 4, — объяснил специалист.

Правильный ответ — 4.

— Как изучают математику в школе. В начальном звене вводят операции — сложение, вычитание, умножение и деление. Примерно до 6-го класса дети не знают, что существуют рациональные числа, которые записываются в виде дробной черты. Когда они вводятся, то выясняется, что операцию деления можно записать не в виде двух точек. И до самого вуза очень часто все выражения записываются, как дробное число и отдельная операция деления через две точки редко используется. Так умножение у людей фиксируется как приоритетная операция, — объяснил Илья Марьясов.

В итоге это приводит к ошибке в вычислениях.

— У людей возникает соблазн 3 умножить на 8 минус 6 (то есть на 2) и получается у них 6. Потом 36 делят на 6, получая 6. И в итоге 6 делят на 6 и выходит 1. Это неверный ответ в данном случае, — отметил математик.

Ранее в Высшей школе экономики подсчитали, что средний проходной балл ЕГЭ для поступления в вузы снизился впервые за 10 лет. Предлагаем вам ответить на несколько вопросов (разных лет) из того самого итогового среза знаний.

По теме

• 20 января 2023, 16:00

  Один и тот же пример в разных странах решают по-разному. Как это получается?

• 18 декабря 2022, 15:30

  «Любите ли вы сплетничать?» Журналист попытался обмануть детектор лжи, и вот что обнаружил полиграф

• 01 апреля 2023, 16:00

  Как по дате рождения определить количество разводов — простая формула расскажет о перспективах вашей пары

• 26 марта 2023, 16:00

  Эти 10 слов с одной и двумя «н» мы со школы запомнить не можем. А вы справитесь с нашим тестом?

• 18 декабря 2022, 14:00

  Русский не родной? 10 простейших слов, которые все пишут с ошибками

Александра Бруня

Корреспондент

МатематикаРешениеПримерРазбор

• ЛАЙК0
• СМЕХ0
• УДИВЛЕНИЕ0
• ГНЕВ0
• ПЕЧАЛЬ0

Увидели опечатку? Выделите фрагмент и нажмите Ctrl+Enter

КОММЕНТАРИИ0

Гость

Войти

Новости СМИ2

Новости СМИ2

Онлайн тест по Математике по теме Порядок действий

Математический тест «Порядок действий» составлен таким образом, чтобы учащиеся 4-го класса, изучающие тему сложения, вычитания, умножения и деления, могли проверить и закрепить полученные знания на практике. Как правило, решение простых примеров с двумя числами не вызывает у детей никаких сложностей, но, когда в одном выражении сочетается несколько видов математических действий, встает вопрос о том, в какой последовательности их необходимо выполнять.

В зависимости от того, как это сделать, результат ответа может получиться разным, но правильный вариант всего один. Поэтому важно четко представлять себе алгоритм вычислений в таких сложных выражениях. Чтобы хорошо пройти тест, нужно повторить, как выполняются действия в выражениях, где есть скобки (сначала то, что в скобках, потом последовательно все остальное) и без скобок (сначала умножение и деление, потом сложение и вычитание по порядку).

Задания в тесте подобраны по принципу постепенного усложнения. Правильно выполнив все задания, можно с уверенностью сказать о хорошем уровне подготовки ученика.

---

---

Пройти тест онлайн

1. Какое действие в выражении сделаешь первым 110 – ( 60 +40) :10 х 8 ?

сложение


деление


вычитание

2. Какое действие в выражении 110 – ( 60 +40) :10 х 8 сделаешь вторым?

вычитание


деление


умножение

3. Выбери правильный вариант ответа выражения 110 – ( 60 +40) :10 х 8:

800


8


30

4. Ответом на выражение 150 : ( 80 – 60 :2) х 3 будет:

9


45


1

5. В каком из выражений последнее действие умножение?

1001 :13 х (318 +466) :22


391 х 37 : 17 х (2248:8 – 162)


10000 – (5 х 9+56 х 7) х 2

6.

В каком из выражений первое действие вычитание?

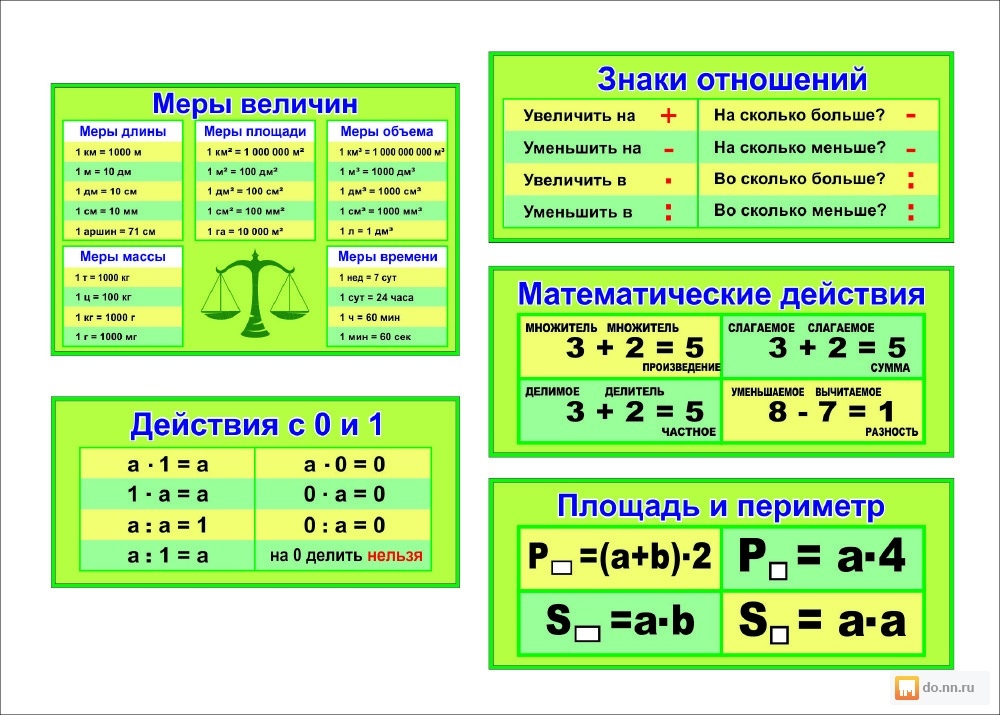
2025 :5 – (524 – 24 :6) х45


5870 + (90-50 +30) х8 -90


5400 :60 х (3600:90 -90)х5

7. Выбери верное высказывание: «В выражении без скобок действия выполняются:»

по порядку


сначала в скобках


сначала деление и умножение, затем по порядку

8. Выбери верное высказывание: «В выражении со скобками действия выполняются:»

сначала в скобках


по порядку записи


сначала деление и умножение, затем по порядку

9. Выбери верный ответ 90 – (50- 40:5)+ 30 :

78


92


36

10. Выбери верный ответ 100-(18:3+45)

100


49


55

---

---

Ещё никто не оставил комментария, вы будете первым.

Написать комментарий

Другие тесты

Некоторые недоразумения относительно порядка операций

В этой статье я опишу некоторые недоразумения относительно порядка операций и предложу лучший способ осмысления этой темы. Пожалуйста, добавляйте свои идеи в комментарии.

Порядок операций — это набор правил, которые мы используем для вычисления математических выражений. Правила следующие:

1. Выполнять все операции внутри круглых скобок.
2. Применить показатели.
3. Выполнить все операции умножения и деления слева направо.
4. Выполняйте все операции сложения и вычитания слева направо.

Мне нравится начинать тему, показывая своим ученикам два способа расчета и спрашивая их, какой из них правильный. Я также показываю им, что разные калькуляторы дадут разные ответы на одну и ту же задачу в зависимости от типа логики, которую они используют. Калькулятор с четырьмя функциями дает ответ 35, а научный калькулятор дает 23. На самом деле, калькулятор Windows дает оба ответа, в зависимости от режима (стандартный или научный).

Многие ученики и некоторые учителя неправильно понимают эти правила. Есть некоторые тонкости правил, которые опускаются во многих книгах, и эти упущения приводят к путанице. Вот некоторые из этих недоразумений.

1. Порядок операций указан в скобках.

Некоторые учащиеся знают, что сначала им следует упрощать в скобках, но они не понимают, что порядок операций также применяется при работе внутри скобок. Например, в выражении

ученик может не знать, что сначала нужно выполнить умножение.

2. Упрощение в круглых скобках не означает удаление круглых скобок.

Некоторые учителя описывают первый шаг как избавление от круглых скобок. Это вызывает путаницу, когда студентов просят упростить такие выражения, как или . В этих случаях выражения внутри круглых скобок уже были упрощены, но круглые скобки по-прежнему служат полезной цели.

3. Группировка иногда обозначается другими средствами, кроме скобок.

Круглые скобки часто используются для группировки, но мы также используем квадратные скобки [ ] или фигурные скобки { }. Столетие назад также было распространено использование vinculum, представляющего собой вертикальную черту, написанную над частью выражения. Винкулум сегодня редко используется, но он сохраняется в обозначении квадратных корней.

Иногда подразумевается группировка. Когда выражение записывается в виде вертикальной дроби, подразумевается, что члены в числителе сгруппированы вместе, как и члены в знаменателе. Например,

Выражения в показателе степени также содержат круглые скобки. Эти скобки необходимо вводить явно при использовании калькулятора.

4. Умножение и деление имеют одинаковый приоритет и должны выполняться слева направо. То же самое верно для сложения и вычитания.

Этот момент обсуждается в отличном блоге Дэвида Гинзбурга, поэтому я не буду обсуждать его в этом посте. Пожалуйста, прочитайте его пост!

5. Порядок операций является чрезмерным упрощением.

Если мы задумаемся над тем, как мы на самом деле упрощаем выражения, мы поймем, что не всегда строго следуем порядку операций. Иногда мы выполняем вычисления параллельно и можем даже сначала выполнить операцию с более низким приоритетом. Например:

Это нарушение правил операций, так как мы сначала выполнили сложение. И все же мы знаем, что это нарушение безобидно; ответ по-прежнему правильный. Есть ли хороший способ сформулировать правила порядка операций, чтобы обеспечить эту гибкость?

6.

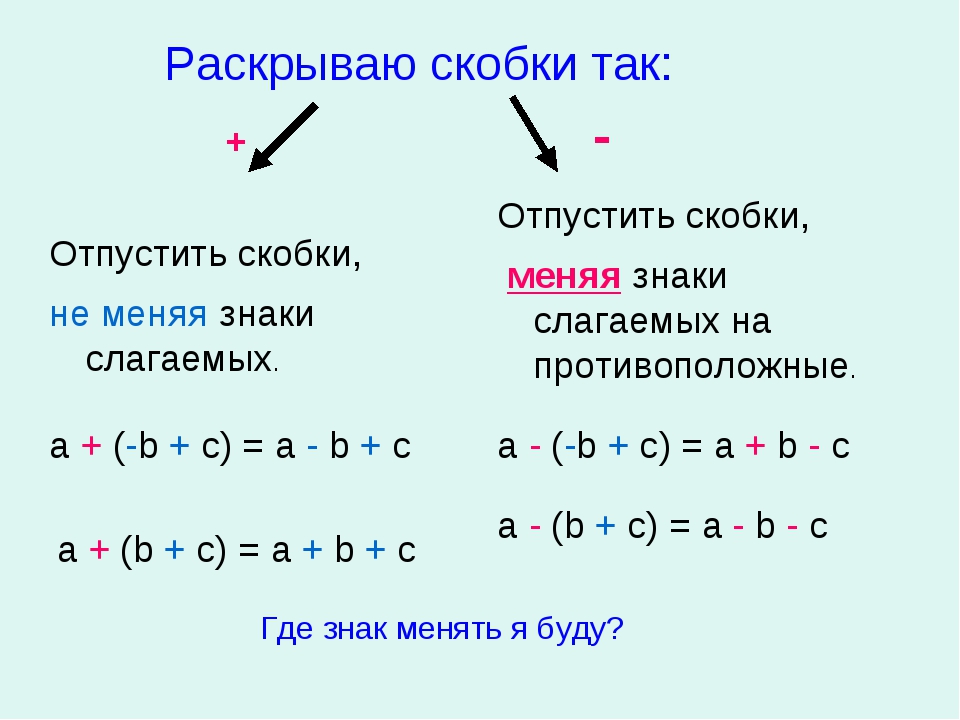Математические выражения рекурсивны.

Рекурсия — сложная тема, но она имеет решающее значение для понимания математических выражений. Наша нотация вынуждает нас записывать математические выражения в линейном порядке, но истинная структура лучше отражается деревом. Например, вот древовидная структура для .

Дерево выражений для 1 + 2 − 3 × 4.

Важно, чтобы учащиеся научились видеть эту рекурсивную структуру. Структуру можно показать и другими способами, например, обведя кружком 1+2 и 3×4.

7. Последняя операция является самой важной.

В начальной алгебре каждое выражение представляет собой либо одно число, либо сумму, либо разность, либо произведение, либо частное, либо степень. Тип выражения определяется последней выполняемой операцией. Эта операция находится в корневом узле дерева выражений.

Мы используем последнюю операцию, когда решаем линейное уравнение. Чтобы решить уравнение

, мы сначала вычтем 3 из обеих частей, потому что мы должны отменить последнюю операцию, которая заключалась в добавлении 3.

Последняя операция является ключом к применению правил для производных в исчислении. Если последней операцией является сложение, мы используем правило сумм, а если последней операцией является умножение, то используем правило произведения.

Нравится:

Нравится Загрузка…

обозначение — В чем причина текущего порядка операций? (ПЕМДАС)

спросил 7 лет, 8 месяцев назад

Изменено 2 года, 8 месяцев назад

Просмотрено 20 тысяч раз

$\begingroup$

Прочитав несколько других вопросов, я только что задал себе вопрос:

Как был определен порядок операций и почему именно этот порядок, а не другой?

Большинство из нас знает такие вещи, как умножение/деление перед сложением/вычитанием, сначала круглые скобки и т. д., но в чем истинная причина этого? Я, вероятно, предубежден, следуя этим правилам с детства, поэтому я не могу придумать другого пути.

2 + 2 x 2 = 6, а не 8

Но если изменить порядок, скажем, на «сложение/вычитание перед умножением/делением», будет ли этот порядок по-прежнему работать, если мы предположим, что математика будет основываться на это? Или есть какая-то странная математическая проблема, если бы мы использовали другой порядок?

Конечно, круглые скобки выполняют функцию группировки, поэтому они всегда должны стоять первыми — в основном я говорю о возведении в степень, умножении/делении, сложении/вычитании (и, возможно, о других операциях).

• обозначение

$\endgroup$

2

$\begingroup$

Как указал Зак Стоун, порядок операций — это просто соглашение, и если вы решите изменить порядок, все, что произойдет, — это вам нужно будет использовать круглые скобки в разных местах. Все будет хорошо, если вы сделаете правильные настройки. Это, как говорится, есть причина для конвенции. В некотором смысле умножение — это просто многократное сложение. Кроме того, возведение в степень — это просто повторное умножение (пока мы ограничиваемся целыми числами), поэтому имеет смысл сначала превратить все показатели степени в умножение, затем превратить все умножения в сложение, а затем решить задачу сложения. Таким образом, по крайней мере, что касается целых чисел, существует естественный порядок операций, основанный на их определении. Это становится более сложным, когда вы начинаете иметь дело со всеми действительными числами, но порядок наследуется от целочисленной арифметики.

$\endgroup$

10

$\begingroup$

Предположим, что умножение произошло после сложения. Попробуйте написать это без скобок: $$(а\раз б)+с$$ Вам будет очень тяжело. c$), поэтому показатель степени ставится перед умножением. Умножение распределяется над сложением (т. е. $(a+b)\times c=a\times c+b\times c$), поэтому умножение идет первым. С PEMDAS мы можем избавиться от круглых скобок, используя дистрибутивность. С другим заказом («PEASMD»?) мы не можем.

$\endgroup$

$\begingroup$

В сознании людей и демонов умножение является более важной операцией, чем сложение. Кроме того, люди разработали алгебраическую систему счисления из своего основного языка, который был латинским, когда я родился, но теперь стал английским.

Я до сих пор помню, как Линкольн назвал Геттисбергский адрес. «Четыре и семь лет назад…» Это 4 доллара умножить на 20 + 7 долларов лет. По-немецки он мог бы сказать: «Sieben und achtzig Jahre ſind verfloſſn, šeit unsere Väter auf dieſem Continent einer neue Nation…» Это 7 долларов + 8 х 10 долларов в год. Десятки, десятки, сотни, брутто — вот как вы обращаетесь со многими целыми числами, а затем корректируете их небольшими добавлениями или вычитаниями. 9{2n}}\right).$$

Посмотрите практически любую книгу о языке программирования или даже о языке сценариев, таком как Javascript, и одна из самых первых вещей, которые вы увидите, неизменно будет таблицей приоритета операций. . Компьютеру, в его славной тупости, нужно указывать, в каком порядке выполнять операции.

$\endgroup$

1

$\begingroup$

Полиномы важны сами по себе, независимо от обозначения. Мы остановились на обозначениях, которые облегчают их запись. Мы могли бы просто использовать круглые скобки между каждой операцией, но это было бы ужасно. Это просто соглашение для упрощения чтения и письма. Изменение соглашения ничего не сломает, нам просто нужно много скобок, чтобы выразить то, что мы хотим.

Одним из мест, где полиномы органично встречаются, являются расширения полей. На самом деле можно было бы немного поработать над теорией Галуа, даже не записывая полином в явном виде. Точно так же полиномы органично встречаются в линейной алгебре (можно использовать тензорные произведения, чтобы абстрагироваться от таких вещей, как характеристические полиномы). Это было бы сложнее, но не менее мощно. Но это помогает объяснить, почему мы заботимся о многочленах и почему мы можем захотеть их записать.

$\endgroup$

9

$\begingroup$

Это действительно лингвистический вопрос, поэтому ответ является типичным лингвистическим ответом: порядок операций такой, какой он есть, потому что это сделало общение более эффективным.

Мы меняем формат нашего обозначения в соответствии с нашими потребностями. В случае порядков операторов обычно было обнаружено, что формулы были более читабельными с порядком операций (вероятно, из-за уменьшения количества группирующих символов). 92)) + (vt) + x_0$ Можно ли так написать? Конечно, но это сложнее.

За прошедшие годы математики нашли текущий порядок операций чрезвычайно удобным, поэтому они придерживаются его.

Этот нечеткий процесс также является объяснением известной головоломки $6/2(3) = ?$. Некоторые считают, что это должно равняться 9, потому что это то же самое, что $6 / 2 \cdot 3$. Другие считают, что оно должно равняться 1, потому что умножение на круглые скобки связывает «плотнее», чем обычное деление: $\frac{6}{2\cdot3}$. У них есть на что опереться, потому что большинство из нас согласны с тем, что $6/xy == \frac{6}{xy}$, так что неясно, по какому пути идти. Реальный ответ состоит в том, что это лингвистическая двусмысленность, которая существует потому, что она не была достаточно важной, чтобы большая часть математиков согласилась с ней. Если бы это когда-нибудь действительно стало важным, мы бы так или иначе решили.

$\endgroup$

$\begingroup$

Хотя многие говорят, что (PEMDAS) — это всего лишь условность, мне нравится думать следующее: (Умножение и деление) — это краткие формы представления (сложения и вычитания), поэтому выполнение (MD) перед (AS) помещает все в одном и том же виде операции: т. е. (AS). Точно так же возведение в степень — это формы представления (умножения и деления), по крайней мере, для целых чисел степени … и, следовательно, (E) может быть преобразовано в (MD), которое, в свою очередь, может быть преобразовано в (AS). Скобки, с другой стороны, являются способом явного определения приоритета операции, поэтому она должна быть хорошо… расставлена ​​по приоритетам.

$\endgroup$

1

$\begingroup$

PEMDAS устарел, и мы никогда не должны на него полагаться. Всегда используйте () для устранения всей двусмысленности, если вы пишете уравнение или выражение.

Несмотря на то, что существующая конвенция имеет веские причины, больше нет оснований полагаться на то, что читатель запомнит ее и правильно интерпретирует уравнение или выражение, использующее ее. Единственная причина писать x = y + z * w вместо x = y + (z * w) состоит в том, чтобы сэкономить 2 символа ширины пробела или 2 байта памяти на компьютере. Когда все было на бумаге, это был разумный способ сэкономить место в текстах и, следовательно, деньги за счет сокращения расходов на бумагу и печать. Позже, когда у компьютеров был крошечный объем памяти, это тоже имело смысл. Я бы сказал, что любые время, сэкономленное при вводе или написании дополнительных символов, было бы более чем компенсировано ошибками и дополнительным временем, затраченным на его расшифровку без (). В настоящее время большинство вещей находятся в Интернете, и у нас достаточно памяти компьютера, поэтому больше нет оправдания вносить какую-либо двусмысленность, опуская ().

Тот факт, что в Интернете есть много страниц, посвященных конвенции PEMDAS, свидетельствует о том, что многие люди считают ее запутанной и часто приводят к ненужным ошибкам. Ошибки, которых можно было бы избежать, просто набрав несколько (), чтобы избежать двусмысленности и путаницы.

По возможности всегда следует избегать двусмысленности, особенно в математике и компьютерном коде.