Что сначала делают деление или умножение: Что выполняется первым умножение или деление если оно стоит первым

Порядок выполнения действий | Математика | 5 класс

На уроке вы узнаете о роли скобок в выражениях и о правилах, по которым выполняются действия. А также решите несколько интересных примеров.

 

Введение

В любом языке есть правила грамотной записи. Кроме самих слов, который несут основной смысл, мы используем знаки препинания. Они тоже крайне важны.

Вспомним всем известное «казнить нельзя помиловать». От того, где поставить запятую, смысл выражения меняется на противоположный (см. рис. 1).

Рис. 1. Как меняется смысл фразы от запятой

В этом предложении есть слова, которые несут смысл, а есть знак препинания – запятая, который очень сильно на этот смысл влияет.

В математическом языке тоже есть такой знак препинания, это скобки.

Пример 1

Если выполнять действия, как они записаны, то получаем 6: .

Но если поставить скобки вокруг суммы , то сразу смысл выражения меняется: .

Роль скобок. Порядок операций

В математике есть простые правила, указывающие, какие действия в каком порядке надо совершать. Скобки нужны, если мы хотим влиять на этот порядок действий. Зная эти правила, ошибиться в порядке действий практически невозможно. Их мы сейчас и обсудим.

Сложение и вычитание равноправны

В этом примере у нас есть и сложение, и вычитание. Эти действия равноправны. Мы делаем их все подряд слева направо. Расставим последовательность действий.

Умножение и деление тоже равноправны

Если у нас только умножение и деление, то мы опять делаем все действия подряд слева направо:

Сначала умножение и деление, потом сложение и вычитание

Если у нас разные действия в одном примере, то сначала нужно сделать все умножения и деления, слева направо, а потом все сложения и вычитания, тоже слева направо.

Действия в скобках раньше всего

Действия в скобках делаются в первую очередь. Сначала вспомним еще раз нашу задачку, с которой начали урок.

Умножение идет первым, поэтому сначала умножение, потом сложение.

Но если поставить сложение в скобки, то начинаем мы с него, а умножение делаем вторым.

Очень простая задача, но здесь видно, что последовательность действий важна, меняем последовательность, получаем разные ответы.

Пример 2

Сначала действия в скобках. Их две. Значит, расставляем последовательность действий над скобками слева направо. Потом идут умножение и деление слева направо, и последнее вычитание:

Порядок выполнения действий

• действия в скобках
• умножение и деление
• сложение и вычитание

Пример 3

Внутри скобок может оказаться несколько действий. Тогда они выполняются по обычным правилам: сначала действия в скобках – сначала умножение, потом вычитание. Остались снаружи от скобок деление и последнее сложение.

Пример 4

Внутри скобок могут оказаться еще скобки. Значит, смотрим на весь пример, сначала нужно сделать все действия внутри больших скобок, пользуясь правилом, то есть сначала действия в скобках, затем деление, затем сложение. Снаружи больших скобок сначала умножение, потом сложение.

Пример 5

Рассмотрим еще один прием вычислений, который иллюстрирует, как можно сократить количество действий.

Расставим последовательность действий.

Получилось восемь действий. Делая по одному действию, мы должны будем переписать этот пример восемь раз и только потом получим ответ. Это будет выглядеть так:

Запись можно сократить. Расставим последовательность действий. 1 и 2 действие не влияют на третье. Его можно сделать одновременно с первым. А то, что мы делаем в первых скобках, не влияет на то, что делаем во вторых. Действия в первых больших и последних скобках тоже можно делать одновременно.

За один раз выполнены три действия. Далее одновременно можно сделать по одному действию в первых и вторых скобках: деление и вычитание.

Заканчиваем решение:

Запись получилась короче.

Заключение

Этот прием одновременных вычислений требует тренировки. Навык сам появится, когда вы выполните достаточное количество примеров.

 

Список рекомендованной литературы

1. Математика. 5 класс. Зубарева И. И., Мордкович А. Г. 14-е изд., испр. и доп. — М.: 2013. – 270 с.
2. Математика. 5 класс. Виленкин Н. Я., Жохов В. И. и др. 24-е изд., испр. — М.: 2008. — 280 с.
3. Математика. 5 класс. Учебник в 2 ч. Дорофеев Г. В., Петерсон Л. Г. 2-е изд., перераб. — М.: 2011; Ч. 1 — 176 с, Ч. 2 — 240 с.

 

Рекомендованные ссылки на ресурсы сети Интернет

1. Интернет-портал «matematika-na.ru» (Источник)
2. Интернет-портал «school-assistant.ru» (Источник)
3. Интернет-портал «urokimatematiki.ru» (Источник)

 

Домашнее задание

Решите примеры:

Как делить со скобками, что вперед: деление или умножение, как решить 36:3(8–6) дробь 6, правильный ответ на пример — 17 января 2023

Все новости

Наказывать за дискредитацию Вооруженных сил будут еще строже: нарушителям грозит срок до 15 лет

Челябинск в середине марта завалило снегом. Когда ждать весны

В СК рассказали, в чем заподозрили управленца из челябинской «дочки» НОВАТЭКа

Назад никто не ломится, но едут. Правда ли, что из Грузии в Россию потянулись назад релоканты

Серые панельки ушли в историю: девелоперы назвали материал, из которого строить — быстро и красиво

Водитель Hyundai устроил аварию с тремя машинами под Челябинском. Есть пострадавшие

Александра Розенбаума госпитализировали с тромбом

«Я не на левые деньги покупал»: у южноуральца отжимают Land Cruiser из-за банкротства продавца машины

В Челябинске из-за снегопада пробки достигли 10 баллов

Челябинский аэропорт закрыли из-за снегопада

В России готовятся повысить призывной возраст: 30-летние отправятся служить уже в следующем году

На разрыв. Восьмилетняя девочка стала заложницей родителей — их война превратила ее жизнь в скитания и допросы

«Просидел в аэропорту 12 часов»: инвалида из Челябинска не пустили в самолет из-за электропривода на коляске

В Кремле рассказали, можно ли решить конфликт на Украине мирным путем: новости СВО за 13 марта

В Челябинске силовики пришли с обысками в «дочку» НОВАТЭКа

«Дети сидели под партами 40 минут»: экстренные службы приехали в школу в Копейске

«Ей предстояла операция»: 14-летняя девочка покончила с собой в Челябинской области

Время уже пришло: как вырастить арбуз в теплице — инструкция для ленивых садоводов

Мужчина, вытолкнувший школьницу из маршрутки в Челябинске, попал под статью

Избиение челябинского адвоката у подъезда его дома вылилось в уголовное дело

«Закружилась голова, бросило в жар»: как журналист 40 минут стояла на гвоздях — и почему это так популярно

В Госдуму внесли закон о повышении призывного возраста

В Челябинске задержали заключенного, сбежавшего из колонии в Тольятти

Восьмиклассник покончил с собой в Челябинской области

У сервисов «ВКонтакте» массовый сбой, пользователей «выкидывает» из аккаунтов

В Челябинской области массово эвакуируют школы и детские сады. Видео

На Челябинскую область надвигаются метели и мокрый снег

В Челябинской области продлили работу поезда до горнолыжного курорта

Запись в первые классы в Челябинске начнется раньше обычного

Улицы возле железнодорожного вокзала в Челябинске заволокло дымом из-за пожара

Наталья Котова отправила чиновников искать сосульки и наледь на крышах

«Чаще встречается у молодых женщин». Кардиолог — об инфаркте, который нельзя увидеть на обследовании

Дело о смертельной драке с участием следователей в центре Челябинска передали в суд

11 слов, которые докажут, что вам пора обратно за школьную парту (сложный и запутанный тест)

Семерка на максималках: за что китайский кроссовер Chery Tiggo 7 Pro получил приставку Max

Ушла в минус на первой же неделе. Как журналист жила на МРОТ и чуть не провалила эксперимент

Бывшие менеджеры и продавцы массово переучиваются на IT. С чем это связано и кто берет их на работу

«Обещают много и быстро»: юрист назвал признаки, по которым легко вычислить мошенника

На замену ушедшим брендам: в Челябинске стали продавать высококачественное моторное масло из ОАЭ

Все новости

Сможете решить правильно?

org/Person»>Иллюстрация: Юрий Орлов / NGS.RU

Поделиться

Минимум неделю в интернете миллионы людей ломают копья из-за простенького, на первый взгляд, примера. NGS.RU решил задачку вместе с кандидатом физико-математических наук, доцентом и преподавателем Новосибирского государственного университета Ильей Марьясовым.

Вот этот пример: 36 : 3 (8 − 6) дробь 6.

Некоторые люди готовы спорить часами, как решить этот пример

Фото: Александра Бруня / NGS.RU

Поделиться

— Подвоха здесь особо никакого нет. У нас в математике есть соглашение о том, как у нас должны выполняться арифметические операции. Умножение и деление имеют более высокий приоритет, чем сложение и вычитание. Когда нужно изменить порядок вычисления, чтобы сложение и вычитание выполнялись раньше, то используются скобки. И еще один момент — когда появляются дроби, а дробная черта — это деление, то в этом случае оно выполняется в последнюю очередь, — объяснил Илья Марьясов

Разбираемся с числителем.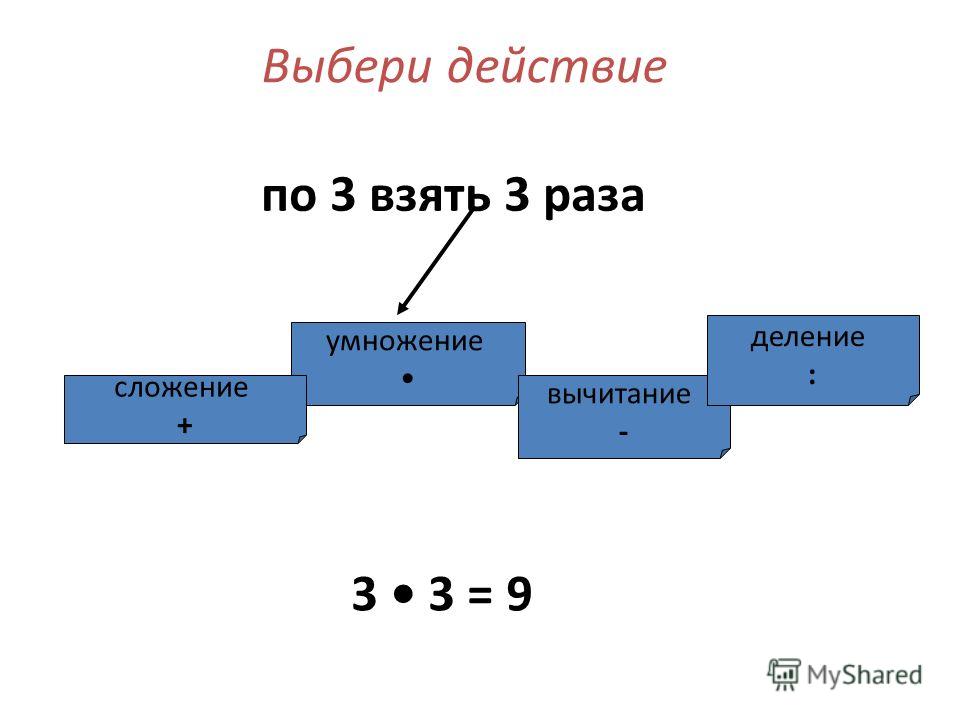 По очереди идут деление, умножение, вычитание — при этом последняя операция идет в скобках. Начинаем решать слева направо.

— Поскольку деление и умножение равноправны. Сначала 36 делим на 3 и получаем 12. Потом мы должны выполнить умножение, но поскольку вычитание стоит в скобках, то сначала делаем его. Из 8 вычитаем 6 и получаем 2. Теперь делаем умножение. Мы 12 умножаем на 2 и получаем 24. Теперь делим числитель на знаменатель. То есть 24 делим на 6 и получаем 4, — объяснил специалист.

Правильный ответ — 4.

— Как изучают математику в школе. В начальном звене вводят операции — сложение, вычитание, умножение и деление. Примерно до 6-го класса дети не знают, что существуют рациональные числа, которые записываются в виде дробной черты. Когда они вводятся, то выясняется, что операцию деления можно записать не в виде двух точек. И до самого вуза очень часто все выражения записываются, как дробное число и отдельная операция деления через две точки редко используется. Так умножение у людей фиксируется как приоритетная операция, — объяснил Илья Марьясов.

В итоге это приводит к ошибке в вычислениях.

— У людей возникает соблазн 3 умножить на 8 минус 6 (то есть на 2) и получается у них 6. Потом 36 делят на 6, получая 6. И в итоге 6 делят на 6 и выходит 1. Это неверный ответ в данном случае, — отметил математик.

Ранее в Высшей школе экономики подсчитали, что средний проходной балл ЕГЭ для поступления в вузы снизился впервые за 10 лет. Предлагаем вам ответить на несколько вопросов (разных лет) из того самого итогового среза знаний.

По теме

• 20 января 2023, 16:00

  Один и тот же пример в разных странах решают по-разному. Как это получается?

• 14 декабря 2022, 07:45

  Врем про губернатора: мы попытались обмануть детектор лжи, и вот что обнаружил полиграф

• 19 сентября 2022, 10:00

  Это точно русский? Проверьте, сможете ли вы написать правильно все эти слова

• 18 декабря 2022, 14:00

  Русский не родной? 10 простейших слов, которые все пишут с ошибками

• 23 февраля 2023, 17:00

  Зеркальная дата 23. 02.2023: что не стоит делать в этот день, чтобы не накликать беду, — советы нумеролога

Александра Бруня

Корреспондент

МатематикаРешениеПримерРазбор

• ЛАЙК8
• СМЕХ9
• УДИВЛЕНИЕ4
• ГНЕВ1
• ПЕЧАЛЬ2

Увидели опечатку? Выделите фрагмент и нажмите Ctrl+Enter

КОММЕНТАРИИ255

Читать все комментарии

Гость

Войти

Новости СМИ2

Новости СМИ2

Арифметика

— можете ли вы опровергнуть это правило PEDMSA? — (деление перед умножением, вычитание перед сложением)

Чтобы расширить ответ Losethegame

Losethegame ответил: «Я попал сюда, погуглив тот же вопрос, хотя я не уверен, что (m) любой из комментаторов ответил на него конкретно. Я думаю, вы правы в том, что ваше правило нельзя нарушать. Вероятно, это можно доказать алгебраически, потому что a * (b / c) = (a / c) * b и a + (b-c) =(а-в)+б…?»

Я согласен, что это, вероятно, может быть доказано алгебраически с помощью методов, подобных тому, который упоминает Losethegame (хотя пример с LoseGame может быть ошибочным, поскольку, как указывает пользователь 21280, Losethegame меняет операнды местами). Но развивая идею алгебраического доказательства (и без замены операндов!), я могу придумать какую-нибудь алгебру, которая могла бы это доказать. (Предоставленный пользователь 21280 считает, что мои примеры не учитывают все возможности. Его ответ с использованием логических формул мог бы).

Дано уравнение, в котором умножение предшествует делению, например. 3*4/2 неважно, что вы сделаете первым. Так что буквальный PEMDAS или PEDMAS подойдет. Принимая во внимание уравнение, в котором деление идет текстуально перед умножением, например. 6/2*3 тогда имеет значение, что вы сделаете первым. Традиционное прочтение PEMDAS или PEDMAS делает это правильно (потому что они сказали бы сначала сделать первое, а это деление), буквальное PEDMSA делает это правильно. Буквальное прочтение PEMDAS может привести к ошибкам.

Вычитание и деление разделяют это свойство. Допустим, мы составим небольшое уравнение из той части уравнения, в которой операторы конкурируют друг с другом. Если вычитание конкурирует со сложением, и вычитание происходит первым (текстуально, в уравнении), оно должно быть выполнено первым. Если деление конкурирует с умножением, а деление идет первым, деление должно быть выполнено первым. В то время как если бы сложение конкурировало с вычитанием, то независимо от того, происходит ли оно первым текстуально или нет, не имеет значения, выполняется ли сначала сложение или вычитание. Точно так же, если умножение конкурирует с делением, если умножение идет первым текстуально, то не имеет значения, выполняется ли сначала деление или умножение. Таким образом, литерал PEDMSA всегда работает (т.е. строго выполняет деление перед умножением, вычитание перед сложением). Как и традиционное/правильное прочтение PEMDAS/PEDMAS, то есть чтение, в котором говорится, что умножение и деление имеют одинаковый приоритет и сначала выполняют первое, аналогично сложению и вычитанию.

Так, например.

Взятие 1*2/3 , так что a*b/c
Следование PEDMSA буквально дает 1*(2/3) , так a(b/c) Следуя PEDMSA, мы традиционно получаем (1*2)/3 , поэтому (ab)/c

И мы знаем алгебраически, что a(b/c) = (ab)/c

 1*2/ 3 а* б/к
"="
1*2/3 сб/с
 

Принимая 1/2*3 так a/b*c Это оценивается одинаково независимо от того, следуете ли вы строго упорядоченному PEDMSA или традиционному PEMDAS, т. Е. Делаете ли вы сначала деление, как правило, или сначала вы выполняете первое из умножения и деления, это (a/b)*c в обоих случаях так явно одно и то же.

 1/2*3 (а/б)*в
"="
1/2*3 (а/б)*в
 

С 1+2-3 , если мы делаем a+ b-c , который заказан PEDMSA, т.е. a+(b-c) , это тот же результат, что и при традиционном PEMDAS (a+b)-c. Мы знаем алгебраически a+(b-c)=a+b-c=(a+b)-c

-(a+b) , которое мы просверлили, было -a-b настолько сильно отличается от -а+б . Вычитания всегда должны выполняться первыми и по порядку… и если сначала выполняется вычитание или сначала сложение и вычитание, то мы сохраняем это правило.

 1+2-3 а+(б-в)
"="
1+2-3 (а+б)-в
 

И для этого тоже самое. алгебраически

 1-2+3 (1-2)+3 (a-b)+c
"="
1-2+3 (1-2)+3 (а-б)+в
 

И, пожалуй, наконец. 1-2-3 и 1/2/3 И независимо от того, делаете ли вы строго заказанную PEDMSA или традиционную PEMDAS, это (1-2)-c и (1/2)/3 так же есть.

Я не уверен, что это все возможности.

Это может оставить вопрос о том, что объясняет алгебру, например. правило, что

 a*(b/c) = (ab)/c
и
а+(б-в)=(а+б)-в
 

Кроме того, это соглашение по синтаксическому анализу, которое, кажется, было разработано в конце 20-го века, а не фундаментальное правило математики. https://www.quora.com/Is-the-order-of-operations-unclear-for-expressions-like-20-2-5+5

Что такое порядок действий? — Определение, правила и примеры

Порядок действий – это набор правил, которым необходимо следовать в определенном порядке при решении уравнения.

Все мы хорошо знаем четыре основных математических действия: сложение, умножение, деление и вычитание. С детства мы постоянно репетируем задачи, связанные с этими четырьмя операциями. Эти операции используются, от добавления счета за вашу покупку в торговом центре до разделения пиццы на четыре равные части. Но до сих пор мы решали проблемы, связанные с каждой операцией в отдельности.

Что, если у нас есть выражение, в котором все четыре операции работают вместе? Мы сначала умножаем или сначала вычитаем? Это может быть проблематично, если вы будете следовать неправильному подходу. Это может привести к неправильным ответам. Поэтому порядок действий вступил в действие.

Анализ любого математического утверждения с использованием арифметических операций, таких как деление, умножение, сложение и вычитание, в математике называется операциями. Давайте посмотрим на законы порядка операций и посмотрим, насколько хорошо мы можем их вспомнить, используя простые стратегии. В этой статье вы узнаете порядок операций, правила порядка операций, математический порядок операций и решите задачи на порядок операций.

Почему выполняется Порядок операций?

При оценке уравнений в арифметике может потребоваться выполнение множества операций, и упрощение, в конце концов, дает разные результаты. Однако на каждую фразу может быть только один правильный ответ. Мы используем принципы, чтобы упростить любое данное математическое выражение, чтобы найти правильный ответ. Эти принципы основаны на всех основных математических операторах.

С единственной целью всегда получать правильные ответы на любое математическое уравнение, был реализован порядок операций.

Каков порядок действий?

В математике такие операторы, как сложение (+), вычитание (-), умножение (×) и деление (÷), имеют приоритет друг над другом. Мы не можем самостоятельно решить выражение, содержащее любой из двух операторов. Мы должны следовать правилам порядка операций, которые гласят, что в любом выражении, как арифметическом, так и алгебраическом, первыми будут оцениваться скобки. Заказ будет рассчитываться во вторую очередь. Умножение и деление будут оцениваться третьими и, наконец, сложение и вычитание будут упрощены.

Приоритет решения любого выражения упоминается в таблице ниже:

11111111111111111111111111111119. СЕКОТОРЫЙ

Приоритет	Операция
Первая	Бркетс () [{{{{{{{{{{{{{{{{{{{]
Порядки (Экспоненты, Квадратный корень, Кубический корень, Логарифмический и т. д.)
Третий	Деление или умножение (Любая операция, расположенная слева от выражения, будет оцениваться первой)
Четвертая	Сложение или вычитание (в зависимости от того, какая операция находится в левой части выражения, будет оцениваться первой)

Определение порядка операций принципы приоритета, которые мы используем при решении любого математического уравнения, включающего множество операций. Когда между двумя операторами существует подвыражение, должен быть реализован оператор, который появляется первым в таблице, упомянутой в предыдущем разделе.

Давайте теперь разберемся с порядком операций, правило за правилом, в соответствии с установленным приоритетом: операторы, применяемые к выражению. При решении любого выражения всегда двигайтесь от левой стороны к правой. Это поможет вам облегчить упрощение этого выражения. Теперь прочитайте правила, упомянутые ниже, чтобы полностью понять концепцию порядка операций:

Правило 1: Необходимо всегда проверять наличие скобок или круглых скобок в выражении. Чаще всего в математических выражениях встречаются скобки «()», «{}» и «[]». Если термин содержит все три квадратных скобки, то решите уравнение следующим образом:

• Сначала решите термины внутри круглой скобки «()» или круглых скобок.
• Решите условия внутри фигурных скобок ‘{}’ секунды.
• Наконец, решите условия в квадратных скобках «[ ]».

Кроме того, помните, что если в любой из скобок есть несколько операций, обязательно используйте порядок операций для их решения.

Правило 2: После того, как вы решите числа в скобках, найдите любые термины в следующем порядке, такие как возведенные в степень термины, корневые термины, логарифмические термины, тригонометрические термины и т. д., и решите их.

Правило 3: Осталось расположить четыре основных оператора в правильном порядке. Вы можете выполнять умножение или деление в зависимости от того, какой оператор стоит первым с левой стороны выражения.

Правило 4: Последним шагом является добавление или вычитание элементов в том же порядке слева направо.

Если вы помните эти пять правил, значит, вы усвоили порядок действий. Каким бы длинным ни было выражение, вы легко сможете решить его, не задумываясь. Если вы не уверены, что запомните эти правила, есть два простых способа их запомнить. Они известны как BODMAS и PEMDAS. В следующих разделах вы узнаете об этих двух аббревиатурах для порядка операций.

Способы запоминания порядка операций – BODMAS и PEMDAS

Существует два очень важных способа запоминания порядка операций. Они сокращенно называются правилом PEMDAS и правилом BODMAS. Буквы в этих аббревиатурах определяют математические операции. Буква, которая присутствует первой, применяется первой к любому уравнению.

Давайте теперь узнаем, что означает каждая из букв в этих аббревиатурах:

Порядок операций BODMAS

BODMAS — наиболее распространенная аббревиатура для порядка операций. Многие из вас наверняка слышали об этом где-то в своей жизни. В развернутом виде это означает:

• B – Кронштейны ( ), { }, [ ]
• О – Заказ
• D – Отдел (÷)
• M – Умножение (×)
• А – Дополнение (+)
• S – Вычитание (-)

Порядок работы PEMDAS

PEMDAS также является аббревиатурой от порядка работы. Тем не менее, его меньше слышно в нашей повседневной жизни, но он столь же эффективен, как и БОДМАС.

• P – Скобки (), {}, [].
• E – Показатель степени (a2) (Например, здесь a — это число с показателем степени 2 )
• М – Умножение (×)
• Д – Отдел (÷)
• A – означает Дополнение (+)
• S – означает вычитание (-)

Это самый эффективный метод запоминания последовательности событий. Забавная фраза « Пожалуйста, извините, моя дорогая тетя Салли »- хороший способ запомнить PEMDAS.

Оба эти метода используются для упрощения нашего понимания порядка операций. Мы увидим пример порядка операций, чтобы прояснить эту тему.

Каков порядок операций в математике?

Порядок операций — это правило, определяющее правильную последовательность шагов для вычисления математического выражения. Если у вас есть выражение только с одной операцией (например, только сложение, только вычитание, только умножение или только деление), правильный способ его решения — слева направо. Однако для выражений с несколькими операциями необходимо соблюдать порядок операций.

Пример порядка операций

Давайте рассмотрим различные примеры, упомянутые ниже, чтобы понять точность правил, используемых в порядке операций.

1. Для оценки арифметических операторов

Выражение 1: 2 + 3 x 5 

• Правильный способ: Правильный способ решить это выражение — сначала умножить 3 x 5 = 15, а затем добавить 2 к результату. 15 + 2 = 17.
• Неверный путь: Если сначала добавить 2 + 3. Получаем 6 х 5 = 30, что неверно при решении этого выражения.

Выражение 2: 15 ÷ 3 x 2 – 6

• Правильный способ: Правильный способ решить это выражение – сначала разделить 15 и 3 = 5, потому что оно ближе к левой части выражения. Затем умножьте 5 на 2 = 10 и вычтите из этого 6, что дает 10 – 6 = 4. 
• Неверный способ:
  Если умножить 3 х 2 = 6, то вычесть из него 6, то получим 15 ÷ 0 = не определено. Это неправильный способ решения этого выражения.

2. Для оценки заказов

Выражение 1: 6 x 32

• Правильный способ: Правильный способ решить это выражение — сначала решить порядок, то есть 32 = 9. Теперь умножьте это на 6. 9 x 6 = 54
• Неверный способ: Если умножить 6 х 3 = 18, то возведем ответ в квадрат, получим 182 = 324, что неверно.

Выражение 2: 2 x sin 30

• Правильный способ: Сначала оцените порядок sin 30 = ½. Теперь умножаем 2 на ответ. 2 х ½ = 1
• Неверный способ: Если умножить 30 на 2 = 60 и решить порядок, то получим sin 60 = 3/2. Какой ответ неверный

3. Для оценки кронштейнов

Выражение 1: (12 + 3) x 4

Решение: В этом выражении мы видим, что скобки присутствуют; следовательно, мы сначала решим содержимое в скобках. Следовательно, 12 + 3 = 15. Теперь умножаем 15 на 4 = 60.

Выражение 2: 4 – 32 ÷ 8

4 – 32 ÷ 8 = 8 – 8 = 0 является решением. (Это правильно. Это правильный способ.) 

Рассмотрим другой подход к тому же выражению.

4 – 32 ÷ 8 = (-28) ÷ 8 = -3,5 (Неверно (это неверный метод)

Выражение 3: 8 x (6 + 6) 

8 x (12) = 96 (Это правильный способ решения скобок.) 

Рассмотрим другой метод для того же выражения. 

8 x (6 + 6) = 48 + 6 = 54 (Это неправильный способ решения скобок.) 

Примечание: Мы должны соблюдать шаблон операторов при выполнении порядка операций над любой данной фразой.

Из вышеупомянутых правил мы узнаем, как выполнять несколько операций, если они входят в одно уравнение. Очень важно изучить эти понятия, чтобы исключить все возможные ошибки при выполнении расчетов. Более того, освоение порядка действий поможет получить больше баллов на экзаменах.