Выражения без скобок — урок. Математика, 2 класс. — «Семья и Школа»
Содержание
Как правильно решить пример без скобок?
Как правильно решить пример без скобок?
Запомните правило:
- Если в примере нет скобок, сначала выполняем действия умножения и деления по порядку, слева направо. …
- Если в примере есть скобки, то сначала мы выполняем действия в скобках, затем умножение и деление, и затем — сложение и вычитание начиная слева направо.
Какое первое действие в примере без скобок?
Если в выражение без скобок входят не только действия сложения и вычитания, но и умножения и деления, или оба этих действия, то сначала выполняют по порядку (слева направо) умножение и деление, а затем сложение и вычитание.
Какие первые действия в математике?
Сначала умножение и деление, затем сложение и вычитание В школе дается следующее правило, определяющее порядок выполнения действий в выражениях без скобок: действия выполняются по порядку слева направо, причем сначала выполняется умножение и деление, а затем – сложение и вычитание.
Что сначала делается сложение или умножение?
При умножении двух разных единиц измерения получается новая единица измерения, при сложении единицы измерения не меняются. При умножении мы получаем эту самую новую единицу измерения. Если она такая же, как и у первого слагаемого, тогда мы можем выполнить сложение. Это просто правило.
Что это вычитание?
Вычитание — операция обратная сложению. Вычитание возможно только, если оба аргумента принадлежат одному множеству элементов (имеют одинаковый тип).
Что такое сложение и вычитание?
Сложение – это объединение объектов в одно целое. Результатом сложения чисел является число, называемое суммой чисел (слагаемых). Вычитание – это такое действие, в котором отнимают меньшее число от большего. Большее число называется уменьшаемым, меньшее – вычитаемым, результат вычитания – разностью.
Как решать дроби Сложение и вычитание?
Чтобы сложить дроби с одинаковыми знаменателями, надо сложить их числители, а знаменатель оставить без изменений.
Чтобы вычесть дроби с одинаковыми знаменателями, надо из числителя первой дроби вычесть числитель второй, а знаменатель опять же оставить без изменений.
Как называется сложение в математике?
Сложение чисел Результат сложения двух или более чисел называется суммой, а сами числа — слагаемыми. … Складываем числа, аналогично положительным, записываем результат со знаком «минус». Например, (-6)+(-5,3)=-(6+5,3)=-11,3. От перестановки мест слагаемых сумма не изменяется a+b=b+a.
Как называется в математике плюс?
Знаки «плюс» и «минус» (+ и −) — математические символы, используемые для обозначения операций сложения и вычитания, а также положительных и отрицательных величин.
Как называется математическое действие Если стоит знак плюс?
В стране математики живут не только цифры и числа, но и разные математические знаки. Сегодня вы с Лисёнком познакомитесь с ними. … В математике это действие называется сложением и ставится знак плюс.
Как называется действие с минусом?
Вычитание – действие обратное сложению. Уменьшаемое – число, из которого вычитают. Вычитаемое – число, которое вычитают. Разность – результат вычитания.
Как называется при умножении?
Так же, как и при сложении и вычитании, числа при умножении имеют свое название. Первое число при умножении называется множитель. Второе число при умножении тоже называется множитель. Результат умножения называют произведение.
Что такое результат умножения?
Умноже́ние — одна из основных математических операций над двумя аргументами (множителями или сомножителями). Иногда первый аргумент называют множимым, а второй множителем; результат умножения двух аргументов называется их произведением.
Как умножить два отрицательных числа?
Умножение отрицательных чисел Правило умножения отрицательных чисел: чтобы умножить два отрицательных числа, нужно перемножить их модули.
Это значит, что для любых отрицательных чисел -a, -b верно равенство: (-а) * (-b) = a * b.
Как умножить натуральное число на отрицательное?
Правило умножения отрицательных чисел заключается в том, что для того, чтобы умножить два отрицательных числа, необходимо перемножить их модули. Данное правило записывается так: для любых отрицательных чисел –a, −b данное равенство считается верным. (−а)⋅(−b)=a⋅b.
Примеры со скобками: какой порядок действий
Помню, в школе на зимние каникулы учительница всегда давала нам большой листок с примерами, которые нужно было решить. Чтобы мы за пару недель не забыли всё, что выучили. Почти все одноклассники вспоминали об этих примерах в воскресенье вечером перед школой. Страдальчески садились за стол и пытались включить мозг. Получалось не всегда. Спустя годы после школы тем более сложно что-то вспомнить. Поэтому у многих даже простые задания вызывают недоумение. Что ж, проверим, хорошо ли тебя натаскала математичка.
А также расскажем, что стоит помнить, решая математические примеры со скобками.
© Depositphotos
Математические примеры со скобками
8 / 4(3 – 1) = ?
Посчитай и скажи, сколько у тебя вышло. Проверить себя можешь в конце статьи. А если возникают затруднения, мы всегда поможем!
Алгоритмы решения примеров
Начнем с простых примеров без скобок. Чтобы решить такие примеры, нужно помнить одно главное правило: все действия выполняются слева направо. Сначала сделай умножение и деление, а затем сложение и вычитание. © Depositphotos
Посчитаем: 5 х 4 – 8 / 2 = ?
Иди слева направо, но помни, что сначала выполняются умножение и деление. Так:
1) 5 х 4 = 20. Это умножение, и оно будет первым, если идти слева направо.
2) 8 / 2 = 4.
Это деление, и, хотя оно идет после вычитания, деление выполняется первым.
3) 20 – 4 = 16. Теперь обычный порядок: после умножения и деления переходим к вычитанию.
Ответ: 5 х 4 – 8 / 2 = 16.
© Depositphotos
Как решать примеры со скобками
Пример может содержать круглые скобки, которые используются для изменения обычного порядка математических действий. Чтобы сделать всё правильно, запомни такие правила.
Сначала проделай все действия, указанные в скобках. Затем — всё остальное слева направо. Первыми всегда, как мы уже говорили, идут умножение и деление, а затем вычитание и сложение. Те же правила применяются к круглым скобкам.
© Depositphotos
Ответ на наш пример
Решая этот пример, легко перепутать порядок действий. Правильный порядок таков: сначала вычисли результат в скобках, затем подели 8 на 4, а результат умножь на то, что получил в скобках.
Итак, ты получишь: 8 / 4(3 – 1) = 8 / 4 х 2 = 2 х 2 = 4.
© Depositphotos
А ты получил правильный ответ? Делись с нами в комментариях.
Поделиться
Екатерина Кукиб
Редактор, который не пишет статьи, а просто общается с читателем как с хорошим другом. Главные ориентиры в жизни — свобода и безбарьерность. Катя любит людей и их истории, которые собирает для своей собственной, чтобы потом рассказать ее миру. Любимая книга — «Искусство любить» Эриха Фромма.
0.1.1 — Порядок работы
Акроним PEMDAS, или мнемоника « p аренда e извините m y d ear a unt S ally», иногда используется, чтобы помочь учащимся запомнить основной порядок операций, где P = круглые скобки, E = показатели степени (и квадратные корни), M = умножение, D = деление, A = сложение и S = вычитание.
При выполнении ряда математических операций начинайте в скобках.
Затем вычислите любые показатели степени или квадратные корни. Затем умножение и деление. И, наконец, сложение и вычитание. Для более глубокого ознакомления мы рекомендуем урок «Порядок операций» Академии Хана.
СкобкиПоказатель степени и квадратный кореньУмножение и делениеСложение и вычитание
В этом курсе мы будем часто использовать дроби. При работе с дробями можно представить, что операции в числителе заключены в скобки, а операции в знаменателе — в скобках. Ниже приведены несколько примеров математических операций, которые будут применяться в этом курсе. Мы узнаем о применении этих операций позже в курсе, здесь мы сосредоточимся только на математических операциях. 9* = 2,080\).
Сначала мы подставим заданные значения.
\(5,770 \pm 0,355(2,080)\)
В скобках нет операций, степеней или квадратных корней, поэтому следующим шагом будет умножение.
\(5,770 \pm 0,697\)
Символ ± говорит об использовании как вычитания, так и сложения.
\(5,770 — 0,697 = 5,073\)
\(5,770 + 0,697 = 6,467\)
Доверительный интервал (5,073, 6,467).
Пример: объединенная доля Раздел
Пример: тестовая статистика для доли Раздел
Статистические данные теста для проверки гипотезы пропорции одной выборки могут быть вычислены с использованием уравнения \(z = \frac {\hat p — p_0}{\sqrt{\frac{p_0 (1-p_0)}{n}}} \). Давайте проработаем эту формулу, используя следующие значения: \(\шляпа p = 0,87\), \(p_0 = 0,8\) и \(n=100\).
Сначала мы подставим заданные значения.
\(z = \frac {0,87 — 0,8}{\sqrt{\frac{0,8 (1- 0,8)}{100}}}\)
В первых шагах мы будем работать с числителем и знаменателем отдельно . Начнем с числителя, который содержит только вычитание.
\(z = \frac {0,07}{\sqrt{\frac{0,8 (1- 0,8)}{100}}}\)
Теперь сосредоточимся на знаменателе. Операция в скобках должна выполняться первой.
\(z = \frac {0,07}{\sqrt{\frac{0,8 (0,2)}{100}}}\)
В знаменателе мы можем сначала работать с вершиной дроби,
\(z = \frac {0,07}{\sqrt{\frac{0,16}{100}}}\)
Найдите дробь под квадратным корнем в знаменателе.
\(z = \frac {0,07}{\sqrt{0,0016}}\)
Затем извлеките квадратный корень из знаменателя.
\(z = \frac {0.07}{0.04}\)
И, наконец, разделите числитель на знаменатель.
\(z = 1,75\)
Экспоненты, умножение и сложение – MathFour
Рубрики: Алгебра; Будьте первым, кто поделится своими мыслями — оставьте комментарий ниже!
Это четвертая книга из серии Объяснение порядка действий.
Чтобы ознакомиться с другими статьями этой серии, нажмите здесь, чтобы перейти к введению.
Изображение из Википедии
Порядок операций можно свести к трем «настоящим» операциям.
Скобки — это просто способ сгруппировать элементы, а не настоящая операция. Поэтому они не считаются реальной операцией.
Поскольку деление — это просто умножение, перевернутое с ног на голову, нам не нужно включать его отдельно. Точно так же вычитание — это сложение на слуху. Так что его тоже выкидываем.
Теперь у нас их всего три: показатели степени, умножение и сложение.
Экспоненты — это быстрый способ умножения.
В предыдущей статье о запоминании правил экспоненты я записал это видео о экспонентах:
Вы видите, что 3 x 3 x 3 x 3 равно 3 4 . Экспонента — это сокращение для умножения.
Умножение — это быстрый способ сложения.
Точно так же, когда мы перегружены сложением одних и тех же чисел снова и снова, как в видео, 4 + 4 + 4 + 4 + 4, мы можем использовать умножение, чтобы сократить это: 5 x 4.
Следуйте сокращению эволюция.
Эволюция быстрого доступа выглядит следующим образом:
- Сначала появилось дополнение.
- Затем мы создали умножение, чтобы упростить сложение.
- Затем мы создали показатели степени, чтобы упростить умножение.
Итак, когда вы занимаетесь арифметикой, мы должны сначала использовать «недавние» сокращения (возведение в степень), затем «старые» сокращения (умножение), а затем «обычные» арифметические действия (сложение). Помните, что вычитание — это сложение, а деление — это умножение.
И имейте в виду, что нам нужно следить за группировкой или чем-либо изолированным скобками, барами абсолютного значения или дробью. Инструменты группировки/изоляции всегда важнее других правил работы.
Изображение из Википедии
Что, если ваш ответ не совпадает с ответом на обратной стороне книги?
В некоторых учебниках умножение выполняется перед делением. Это означает, что задача 9 3 x 2 будет показывать другой ответ (3/2) на страницах решения этого учебника, чем тот, который вы получили бы после ОоО, которое я здесь описываю (6).
Докажи, что ты умнее второклассника, раскусив хитрый пример
Бывает, что самым сложным неожиданно оказывается самое простое. И мы сейчас говорим не о рецепте человеческого счастья и тайнах атомных ядер. Возьмем порядок действий в примерах. Его проходят в начальных классах средней школы и по идее должны помнить всю жизнь.
Но тем не менее миллионы людей в Сети снова и снова ломают копья вокруг довольно незатейливых математических выражений. Причем удивительное разнообразие ответов ставит под сомнение сам статус математики, как царицы точных наук.
Предлагаем и тебе возможность проверить себя, назвать верный ответ и освежить в памяти подзабытые знания из старых школьных учебников.
Порядок действий в примерах
Увидев предлагаемый пример в Facebook*, я, честно говоря, растерялся. Почти 8 миллионов комментариев под задачкой на три действия? О чём тут спорить? Это же математика!
Однако реальность часто превосходит даже самые смелые фантазии. А ответы пользователей соцсети просто ставят в тупик. Рассмотрим самые распространенные, сохраняя логику и написание их авторов.
«Я думаю, что все комментирующие хотя бы доучились до 4 класса. Спасибо, я проходил. 1 0 − 1 0 х 1 0 + 1 0 = 0 х 10 + 10 = 0 + 10 = 10»
© Depositphotos
«Хороший ответ 10», — утверждает один из комментаторов. Согласны, в нумерологии 10 – хорошее число, обещающее удачу и счастье. Вот только подходит ли 10 на роль правильного ответа?
Прокручиваем ленту дальше. «Это очень просто. Чтобы решить проблему, мы делаем (10-10) × (10 + 10) = 0 × 20 = 0, тогда как любое число × на 0 = 0.
Результат — 0!»
«По правилам в первую очередь 10 х 10 = 100. 10 минус 100 т.к. 100 больше = 90 и 90 + 10 = 100». Хм… С первой частью сложно не согласиться, но потом логика машет нам ручкой и полностью теряется из виду. А мы продолжаем дальше.
Опытные пользователи пошли особенным путем и спросили совета у Калькулятора Google. Умная программа сразу заключила 10 х 10 в скобки и выдала ответ «-80».
Что говорят правила?
Порядок вычисления выражений определяется двумя простыми правилами. Во-первых, при отсутствии скобок действия выполняются по порядку слева направо. Во-вторых, сначала выполняется умножение и деление, а затем — сложение и вычитание.
© Depositphotos
Если в выражении есть скобки, то сначала выполняются действия в скобках, следом в установленном порядке умножение и деление, затем сложение и вычитание. В этом примере нет скобок, но есть вычитание, умножение и сложение. Помня о приоритете умножения, начнем с него.
10 – 10 x 10 + 10 = 10 – 100 + 10
Теперь всё, что осталось, — это сложение и вычитание, которые выполняем слева направо. Вычитание стоит первым, когда мы смотрим на уравнение слева направо, поэтому сначала вычитаем.
10 – 10 x 10 + 10 = 10 – 100 + 10 = -90 + 10
Наконец, последний шаг — сложение.
10 – 10 x 10 + 10 = 10 – 100 + 10 = -90 + 10 = -80
Ответ: -80. А какой результат получился у тебя? Возможно, мы где-то просчитались и допустили ошибку? Выскажи свое мнение на этот счет.
© Depositphotos
Напомним, что не так давно настоящий переполох в Интернете вызвал еще один пример: 8 / 2 (2 + 2) = ? Одни пользователи уверяют, что в итоге должно получиться шестнадцать. Другие же правильным ответом считают единицу. И те и другие приводят свои доводы. Но кто из них прав?
Tags: takprostoВдохновениеДействияЛогикаМатематикаПравилаПримеры
Должны ли мы сначала умножать или складывать?
Вопрос задан: г-ном Нельсоном Леднером
Оценка: 4,7/5 (54 голоса)
Со временем математики пришли к соглашению о наборе правил, называемых порядком операций, чтобы определить, какую операцию выполнить первой .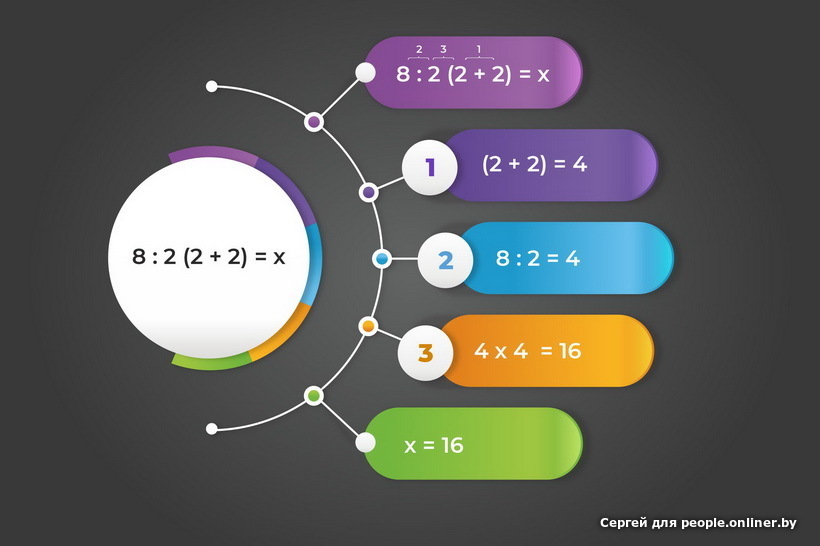
Когда выражение включает только четыре основные операции, действуют следующие правила: Умножайте и делите слева направо. Складывать и вычитать слева направо.
Вы начинаете с умножения или сначала добавляете?
Ответ: Правильный ответ: 56. Порядок операций можно запомнить по аббревиатуре PEMDAS, которая означает: круглые скобки, показатели степени, умножение и деление слева направо, сложение и вычитание слева направо. В этой задаче нет круглых скобок, поэтому начните с показателями степени .
Почему мы умножаем перед сложением?
Учащиеся должны были ответить своими словами, что соответствует концепции: Умножение и деление равны выполняется перед сложением и вычитанием , чтобы преобразовать группы элементов в промежуточные итоги одинаковых элементов, которые можно объединить для получения итога.
Какая математическая операция идет первой?
Сначала мы решаем любые операции внутри круглых или квадратных скобок . Во-вторых, мы решаем любые показатели.
В-третьих, мы решаем все умножение и деление слева направо. В-четвертых, мы решаем все операции сложения и вычитания слева направо.
Имеет ли значение, что вы сначала делите или умножаете?
Умножение и деление можно выполнять вместе. Другими словами, не имеет значения, делаете ли вы сначала деление или умножение , но они должны выполняться после круглых скобок и показателей степени, а также перед сложением и вычитанием.
В математике какая операция выполняется первой Умножение или деление
Найдено 15 связанных вопросов
Имеет ли значение, в каком порядке вы умножаете?
Неважно, в каком порядке вы умножаете числа .
Ответ всегда один и тот же. 3 x 4 x 5 всегда равно 3 x 5 x 4 или даже 5 x 4 x 3.
Применяется ли Bodmas, если нет скобок?
Вопросы теста BODMAS. Правила БОДМАС легче всего понять с некоторой практикой и примерами. Попробуйте эти расчеты самостоятельно, а затем откройте окно (нажмите на символ + слева), чтобы увидеть работу и ответы. В этом расчете нет скобок или порядков .
Каковы четыре правила математики?
Четыре правила математики: сложение, вычитание, умножение и деление .
Каков правильный порядок операций?
Порядок операций — это правило, указывающее правильную последовательность шагов для вычисления математического выражения. Мы можем запомнить порядок, используя PEMDAS: Скобки, Экспоненты, Умножение и деление (слева направо), Сложение и вычитание (слева направо) .
Каков порядок математических уравнений?
Чтобы помочь учащимся в Соединенных Штатах запомнить этот порядок операций, учителя заучивают в них аббревиатуру PEMDAS: круглые скобки, показатели степени, умножение, деление, сложение, вычитание .
Вы умножаете или добавляете, чтобы найти площадь?
Площадь – это измерение поверхности формы. Чтобы найти площадь прямоугольника или квадрата нужно умножить длину и ширину прямоугольника или квадрата. Площадь А равна х умножить на у.
Каковы правила добавления?
Дополнение: обратите внимание, что величина числа со знаком совпадает с его абсолютным значением. При добавлении положительного числа и положительного числа: Добавьте величины . Результат положительный. При добавлении отрицательного числа и отрицательного числа: Добавьте величины.
Что такое правило Бодмаса в математике?
Правило BODMAS — это аббревиатура, используемая для запоминания порядка операций, которым необходимо следовать при решении математических выражений . Это означает B — скобки, O — порядок степеней или корней, D — деление, M — умножение, A — сложение и S — вычитание.
Вы умножаете перед сложением без скобок?
Поскольку 4 × 4 = 16 , а после того, как скобок не осталось, , мы выполняем умножение перед сложением .
Этот набор скобок дает еще один ответ. Итак, когда задействованы круглые скобки, правила порядка операций таковы: Выполняйте операции в круглых скобках или группируйте символы.
Что означает число 2 в третьей степени?
Объяснение: 2 в 3-й степени можно записать как 2 3 = 2 × 2 × 2 , так как 2 умножается на себя 3 раза. … В общем, x n означает, что x умножается сам на себя n раз.
В бодмасе деление предшествует умножению?
Возвращаясь к приведенному выше примеру, правильным ответом будет первый ответ, поскольку он следует правилам БОДМАС: деление может быть выполнено до умножения и должно выполняться перед сложением, а умножение предшествует сложению.
Вы всегда используете порядок операций?
Всегда начинайте с операций, содержащихся в скобках . … В любых скобках вы следуете порядку операций, как и в любой другой части математической задачи. Здесь у нас есть две операции: сложение и умножение.
Поскольку умножение всегда идет первым, мы начнем с умножения 6 ⋅ 2 .
Правильно ли выбран Пемдас или Бодмас?
BODMAS означает скобки, порядок, деление, умножение, сложение и вычитание. BIDMAS и PEMDAS делают то же самое, что и , но используют разные слова. BODMAS объясняет «порядок операций» в математике, а BIDMAS и PEMDAS делают то же самое, но используют немного разные слова.
Как упростить порядок операций?
При упрощении сначала выполнять все выражения в скобках, , затем все показатели степени, затем все операции умножения и деления слева направо и, наконец, все операции сложения и вычитания слева направо.
Какое золотое правило решения уравнений?
Делайте с одной частью уравнения то же, что и с другой!
Уравнение похоже на весы. Если мы что-то надеваем или снимаем с одной стороны, шкала (или уравнение) становится несбалансированной. Решая математические уравнения, мы всегда должны поддерживать сбалансированность «шкалы» (или уравнения), чтобы обе стороны ВСЕГДА были равны .
Что такое основа математики?
Как правило, счет, сложение, вычитание, умножение и деление называются основными математическими операциями.
Какое основное правило математики?
Четыре основных математических правила: сложение, вычитание, умножение и деление .
Почему Бодмас не прав?
Неправильный ответ
Его буквы обозначают скобки, порядок (значение степени), деление, умножение, сложение, вычитание. … Он не содержит скобок, степеней, деления или умножения, поэтому мы будем следовать BODMAS и сделать сложение с последующим вычитанием : Это ошибочно.
Как работает правило Бодмаса?
Правило BODMAS гласит, что мы должны сначала вычислить скобки (2 + 4 = 6), затем порядки (5 2 = 25), затем любое деление или умножение (3 x 6 (ответ на скобки) = 18) и, наконец, любое сложение или вычитание (18 + 25 = 43). Дети могут получить неправильный ответ 35, работая слева направо.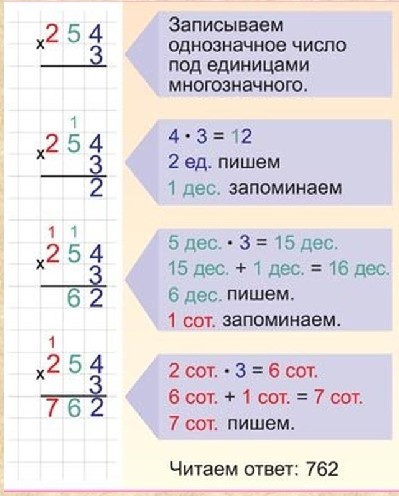
Всегда ли следует использовать Bodmas?
Когда вы завершаете математическое числовое предложение, включающее несколько различных операций, BODMAS помогает вам узнать, в каком порядке их выполнять. Все в скобках должно быть завершено сначала , затем порядок, за которым следует любое деление или умножение и, наконец, сложение или вычитание.
Похожие вопросы
- 33Два числа умножаются на 72?
- 30Будут ли размножаться каллы?
- 32Является ли умножение дробей тем же, что и деление?
- 18Что такое умножение в математике?
- 22Всегда ли нужно умножать перед сложением?
- 37Можно ли умножать непохожие термины?
- 18Размножается ли спаржа?
- 27Какой оператор используется для умножения чисел?
- 45При обычном приготовлении пищи споры бактерий размножаются?
- 27 Два числа умножаются на 24?
Реклама
Популярные вопросы
- 34Was ist lcn fernseher?
- 38 Качественные ли лодки wellcraft?
- 39Что такое определение перигастрального?
- 19Куда девается соль для посудомоечных машин?
- 21Можно ли пресвитерианам есть мясо?
- 30Что такое нейтропенический тифлит?
- 21Открыт ли аэропорт Ньюбурга?
- 22Надаль играет на Уимблдоне-2021?
- 16Что такое доктрина после получения доказательств?
Сложение, вычитание, умножение и деление значений в элементе управления
InfoPath 2010 InfoPath 2013 Больше.
..Меньше
Вы можете помочь своим пользователям заполнять формы на основе вашего шаблона формы, используя формулы для вычисления значения элемента управления на основе данных, которые пользователь вводит в другие элементы управления. Вычисления могут включать сложение, вычитание, умножение и деление значений. Например, если вы разрабатываете шаблон формы, который подрядчики по электроснабжению будут использовать для подачи заявок на получение разрешений, вы можете добавить формулу в элемент управления, который автоматически вычисляет общую стоимость, которую подрядчик должен заплатить за заявку, путем умножения количества разрешений в приложение по цене каждого разрешения.
В этой статье
Что такое формула?
Использование двух и более операторов в формуле
Вставка математической формулы в элемент управления
Что такое формула?
Формула — это выражение XPath, состоящее из значений, полей или групп, функций и операторов, используемых для вычисления и отображения других значений.
Формулы можно использовать для решения следующих задач:
Расчет математических значений на основе значений, указанных при разработке шаблона формы, или значений, которые пользователи вводят в элементы управления при заполнении форм на основе вашего шаблона формы..
Показать определенные даты и время.
Отображение значений, которые пользователи вводят в один элемент управления, в другой элемент управления.
Установите значение по умолчанию для поля или элемента управления.
org/ListItem»>Запустить правило на основе значения, рассчитанного по формуле.
Каждое выражение XPath, используемое в формуле, представляет собой комбинацию значений, функций и операторов, результатом которой является одно значение. Формула может содержать несколько выражений. Вы можете думать о формуле как о предложении, состоящем из одной или нескольких фраз, где каждая фраза представляет одно выражение в формуле.
На следующем рисунке показана связь между формулой и выражением.
Функция — это выражение, возвращающее значение на основе результатов вычисления. Значения, используемые в функциях, называются аргументами. Вы можете использовать стандартные функции XPath 1.0, включенные в InfoPath, а также некоторые функции, специфичные для InfoPath. Найдите ссылки на дополнительные сведения о функциях InfoPath в разделе См. также .
Верх страницы
Использование двух или более операторов в формуле
Если формула содержит два или более математических оператора, InfoPath выполняет расчет в соответствии с приоритетом оператора.
В следующем списке показан порядок выполнения операций:
Вычисления в скобках
Вычисления умножения и деления
Вычисления сложения и вычитания
Если формула содержит два оператора с одинаковым приоритетом, вычисления выполняются слева направо.
Например, представьте, что вы создаете шаблон формы заявки на получение разрешения, в котором есть текстовое поле, отображающее общую стоимость всех разрешений, представленных в заявке. Значения, требуемые этой формулой, берутся из других текстовых полей формы. Текстовое поле, отображающее общую стоимость, содержит следующую формулу:
txtPermit1Qty * txtPermitCost1 + txtPermit2Qty * txtPermitCost2 /txtNumberOfPermits
Эта формула включает операторы сложения (+), умножения (*) и деления (/). В соответствии с приоритетом операторов вычисления умножения и деления выполняются перед вычислением сложения. Поскольку операторы умножения и деления имеют одинаковый приоритет, вычисление умножения выполняется перед оператором деления, поскольку оператор умножения расположен слева от оператора деления. Формула рассчитывается таким образом:
Значение в txtPermit1Qty умножается на значение в txtPermitCost1 .
Результат расчета на шаге 1 добавляется к результатам расчета на шаге 2.
org/ListItem»>Значение в txtPermit2Qty умножается на значение в txtPermitCost2 , а затем этот результат делится на значение в txtNumberOfPermits .
Чтобы управлять порядком вычислений, заключите вычисление, которое вы хотите выполнить первым, в круглые скобки. Вычисления в скобках выполняются перед вычислениями вне скобок. Помещайте вычисления со скобками слева от вычислений без скобок. Вычисления во вложенных скобках выполняются от внутренних к внешним скобкам.
Например, рассмотрим следующую формулу:
((txtPermit1Qty * txtPermitCost1) + (txtPermit2Qty * txtPermitCost2))/txtNumberOfPermits
В этом расчете значение, полученное в результате умножения значений в txtPermit1Qty и txtPermitCost1 , добавляется к значению, полученному в результате умножения значений в txtPermit2Qty и txtPermitCost2 .
Затем сумма этого расчета делится на значение в txtNumberOfPermits 9.0004 .
Верх страницы
Вставка математической формулы в элемент управления
Дважды щелкните элемент управления или поле, для которого вы хотите создать формулу.
Перейдите на вкладку Данные .
Щелкните Вставить формулу .
Чтобы вставить значение или математический оператор в формулу, введите значение или символ математической операции в поле Формула .
Список математических операций
Операция
Символ
Добавить
+
Вычесть
—
Умножить
*
Разделить
/
Примечание.
Если в формуле используется оператор деления (/), убедитесь, что перед ним и после него есть пробел. Если перед оператором деления и после него нет пробела, InfoPath может интерпретировать «/» как разделитель шагов расположения XPath, а не как оператор деления.Совет: Математические формулы обычно используют в качестве аргументов целые или десятичные значения. Чтобы избежать пустых значений в формуле, установите флажок Считать пустые значения равными нулю в категории Дополнительно в диалоговом окне Параметры формы .
Чтобы проверить правильность синтаксиса формулы, в диалоговом окне Вставить формулу щелкните Проверить формулу .
Моя формула содержит ошибки
Щелкните Показать подробности в диалоговом окне Microsoft Office InfoPath , чтобы просмотреть ошибки в формуле.
Ниже приведены некоторые предложения по устранению этих ошибок:Если вы используете функцию в своей формуле, убедитесь, что вы используете правильные аргументы для функции. Некоторым функциям требуются поля или группы, в то время как другим функциям требуются указанные значения в качестве аргументов. Найдите ссылки на дополнительную информацию о функциях в См. также раздел .
Удалите формулу и введите ее заново, чтобы убедиться, что она введена правильно.
Чтобы проверить изменения, нажмите Preview на панели инструментов Standard или нажмите CTRL+SHIFT+B.
Если в формуле используется оператор деления (/), убедитесь, что перед ним и после него есть пробел. Если перед оператором деления и после него нет пробела, InfoPath может интерпретировать «/» как разделитель шагов расположения XPath, а не как оператор деления.
Ниже приведены некоторые предложения по устранению этих ошибок: