Деление в столбик — объяснение и примеры…
Привет, мой друг, тебе интересно узнать все про деление в столбик — объяснение , тогда с вдохновением прочти до конца. Для того чтобы лучше понимать что такое деление в столбик — объяснение , настоятельно рекомендую прочитать все из категории Арифметика.
Деление — Арифметическое действие, по к-оторому узнается, сколько раз одно число содержится в другом.
Если вы родитель , то объясните ребенку, что, в математике, действие, противоположное умножению, называется «деление».
Оперируя таблицей умножения, продемонстрируйте ученику на любом примере взаимосвязь между умножением и делением.
Пример: 3х4=12. результатом умножения является произведение двух чисел. После этого объясните, что операция деления, является обратной операции умножения и проиллюстрируйте это наглядно.
В нашем пример разделите получившееся произведение «12» – на любой из множителей – «3» или «4», и результатом всегда будет другой, не использовавшийся в операции множитель, то есть «4» или «3».
Также нужно знать термины, используемые в операции деления – «делимое», «делитель» и «частное».
Для деления чисел из двух и более цифр (знаков) применяют деление в столбик.
Посмотрим на примере как делить столбиком.
Вычислить:
Для начала запишем делимое и делитель в столбик . Об этом говорит сайт https://intellect.icu . Выглядеть это будет так:
Их частное (результат) будем записывать под делителем. У нас это цифра 8.
Начинаем делить 512 на 8 следующим образом:
- Определяем неполное частное. Для этого слева направосравниваем цифры делимого и делитель.
Берем 5. Цифра 5 меньше 8, значит нужно взять еще одну цифру из делимого.
- 51 больше 8. Значит это неполное частное. Ставим точку в частном (под уголком делителя). Для того, чтобы избежать ошибок, не забывайте определять количество цифр в частном.
Для этого посчитаем сколько цифр осталось в делимом, после неполного частного.
 У нас после 51 стоит только одно цифра 2. Значит и добавляем в результат еще одну точку.
У нас после 51 стоит только одно цифра 2. Значит и добавляем в результат еще одну точку. - Приступаем к делению. Вспоминая таблицу умножения на 8, находим ближайшее к 51 произведение.
6 x 8 = 48
Записываем цифру 6 в частное.Записываем 48 под 51.
При записи под неполном частным самая правая цифра неполного частного должна стоять над самой правой цифрой произведения.
Между 51 и 48 слева поставим «-» (минус). Вычтем по правилам вычитания в столбик 48 и под чертой запишем результат.
- В остатке получилось 3. Сравним остаток с делителем. 3 меньше 8.
Если остаток получился больше делителя, значит мы ошиблись в расчете и есть произведение более близкое, чем то, которое взяли мы.
Спишем из делимого 512 цифру 2 к 3.
Число 32 больше 8. И опять по таблице умножения на 8, найдем ближайшее произведение.
8 x 4 = 32В остатке получился ноль.
 Значит числа разделились нацело (без остатка).
Значит числа разделились нацело (без остатка).
Как ты считаеешь, будет ли теория про деление в столбик — объяснение улучшена в обозримом будующем? Надеюсь, что теперь ты понял что такое деление в столбик — объяснение и для чего все это нужно, а если не понял, или есть замечания, то нестесняся пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Арифметика
Из статьи мы узнали кратко, но емко про деление в столбик — объяснение
Деление столбиком. Онлайн калькулятор | Математика
- Как записывать деление в столбик
- Как делить столбиком
- Деление столбиком с остатком
- Калькулятор деления столбиком
Как записывать деление в столбик
Деление многозначных чисел легче всего выполнять столбиком.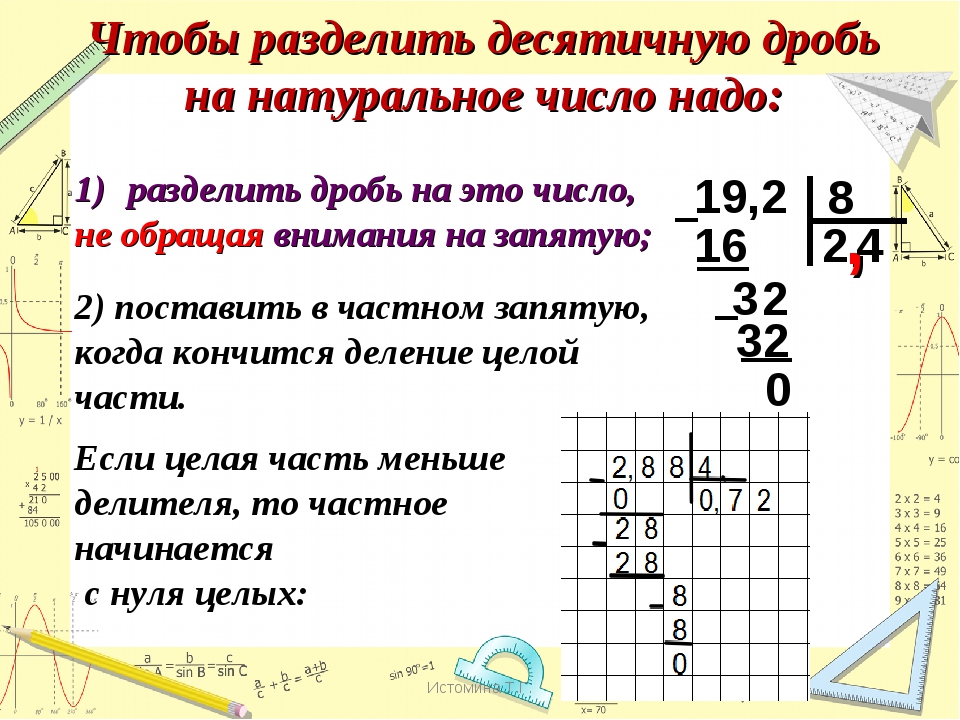 Деление столбиком иначе называют деление уголком.
Деление столбиком иначе называют деление уголком.
Перед тем как начать выполнение деления столбиком, рассмотрим подробно саму форму записи деления столбиком. Сначала записываем делимое и справа от него ставим вертикальную черту:
За вертикальной чертой, напротив делимого, пишем делитель и под ним проводим горизонтальную черту:
Под горизонтальной чертой поэтапно будет записываться получающееся в результате вычислений частное:
Под делимым будут записываться промежуточные вычисления:
Полностью форма записи деления столбиком выглядит следующим образом:
Как делить столбиком
Допустим, нам нужно разделить 780 на 12, записываем действие в столбик и приступаем к делению:
Деление столбиком выполняется поэтапно. Первое, что нам требуется сделать, это определить неполное делимое. Смотрим на первую цифру делимого:
это число 7, так как оно меньше делителя, то мы не можем начать деление с него, значит нужно взять ещё одну цифру из делимого, число 78 больше делителя, поэтому мы начинаем деление с него:
В нашем случае число 78 будет неполным делимым, неполным оно называется потому, что является всего лишь частью делимого.
Определив неполное делимое, мы можем узнать сколько цифр будет в частном, для этого нам нужно посчитать, сколько цифр осталось в делимом после неполного делимого, в нашем случае всего одна цифра — 0, это значит, что частное будет состоять из 2 цифр.
Узнав количество цифр, которое должно получиться в частном, на его месте можно поставить точки. Если при завершении деления количество цифр получилось больше или меньше, чем указано точек, значит где-то была допущена ошибка:
Приступаем к делению. Нам нужно определить сколько раз 12 содержится в числе 78. Для этого мы последовательно умножаем делитель на натуральные числа 1, 2, 3, …, пока не получится число максимально близкое к неполному делимому или равное ему, но не превышающее его. Таким образом мы получаем число 6, записываем его под делитель, а из 78 (по правилам вычитания столбиком) вычитаем 72 (12 · 6 = 72). После того, как мы вычли 72 из 78, получился остаток 6:
Обратите внимание, что остаток от деления показывает нам, правильно ли мы подобрали число. Если остаток равен делителю или больше него, то мы не правильно подобрали число и нам нужно взять число побольше.
Если остаток равен делителю или больше него, то мы не правильно подобрали число и нам нужно взять число побольше.
К получившемуся остатку — 6, сносим следующую цифру делимого — 0. В результате, получилось неполное делимое — 60. Определяем, сколько раз 12 содержится в числе 60. Получаем число 5, записываем его в частное после цифры 6, а из 60 вычитаем 60 (12 · 5 = 60). В остатке получился нуль:
Так как в делимом больше не осталось цифр, значит 780 разделилось на 12 нацело. В результате выполнения деления столбиком мы нашли частное — оно записано под делителем:
780 : 12 = 65.
Рассмотрим пример, когда в частном получаются нули. Допустим нам нужно разделить 9027 на 9.
Определяем неполное делимое — это число 9. Записываем в частное 1 и из 9 вычитаем 9. В остатке получился нуль. Обычно, если в промежуточных вычислениях в остатке получается нуль, его не записывают:
Сносим следующую цифру делимого — 0. Вспоминаем, что при делении нуля на любое число будет нуль.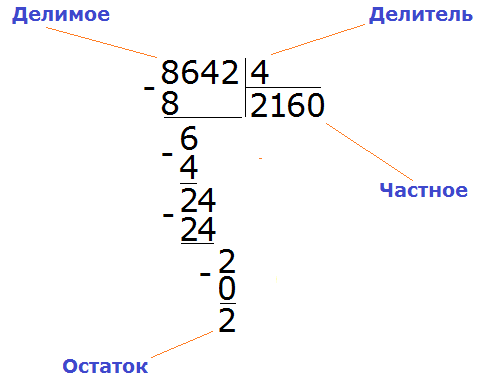 Записываем в частное нуль (0 : 9 = 0) и в промежуточных вычислениях из 0 вычитаем 0. Обычно, чтобы не нагромождать промежуточные вычисления, вычисление с нулём не записывают:
Записываем в частное нуль (0 : 9 = 0) и в промежуточных вычислениях из 0 вычитаем 0. Обычно, чтобы не нагромождать промежуточные вычисления, вычисление с нулём не записывают:
Сносим следующую цифру делимого — 2. В промежуточных вычислениях вышло так, что неполное делимое (2) меньше, чем делитель (9). В этом случае в частное записывают нуль и сносят следующую цифру делимого:
Определяем, сколько раз 9 содержится в числе 27. Получаем число 3, записываем его в частное, а из 27 вычитаем 27. В остатке получился нуль:
Так как в делимом больше не осталось цифр, значит число 9027 разделилось на 9 нацело:
9027 : 9 = 1003.
Рассмотрим пример, когда делимое оканчивается нулями. Пусть нам требуется разделить 3000 на 6.
Определяем неполное делимое — это число 30. Записываем в частное 5 и из 30 вычитаем 30. В остатке получился нуль. Как уже было сказано, нуль в остатке в промежуточных вычислениях записывать не обязательно:
Сносим следующую цифру делимого — 0. Так как при делении нуля на любое число будет нуль, записываем в частное нуль и в промежуточных вычислениях из 0 вычитаем 0:
Так как при делении нуля на любое число будет нуль, записываем в частное нуль и в промежуточных вычислениях из 0 вычитаем 0:
Сносим следующую цифру делимого — 0. Записываем в частное ещё один нуль и в промежуточных вычислениях из 0 вычитаем 0. Так как в промежуточных вычислениях, вычисление с нулём обычно не записывают, то запись можно сократить, оставив только остаток — 0. Нуль в остатке в самом конце вычислений обычно записывают для того, чтобы показать, что деление выполнено нацело:
Так как в делимом больше не осталось цифр, значит 3000 разделилось на 6 нацело:
3000 : 6 = 500.
Деление столбиком с остатком
Пусть нам требуется разделить 1340 на 23.
Определяем неполное делимое — это число 134. Записываем в частное 5 и из 134 вычитаем 115. В остатке получилось 19:
Сносим следующую цифру делимого — 0. Определяем, сколько раз 23 содержится в числе 190. Получаем число 8, записываем его в частное, а из 190 вычитаем 184. Получаем остаток 6:
Получаем остаток 6:
Так как в делимом больше не осталось цифр, деление закончилось. В результате получилось неполное частное 58 и остаток 6:
1340 : 23 = 58 (остаток 6).
Осталось рассмотреть пример деления с остатком, когда делимое меньше делителя. Пусть нам требуется разделить 3 на 10. Мы видим, что 10 ни разу не содержится в числе 3, поэтому записываем в частное 0 и из 3 вычитаем 0 (10 · 0 = 0). Проводим горизонтальную черту и записываем остаток — 3:
3 : 10 = 0 (остаток 3).
Калькулятор деления столбиком
Данный калькулятор поможет вам выполнить деление столбиком. Просто введите делимое и делитель и нажмите кнопку Вычислить
.
длинная дивизия
длинная дивизияПоказать рекламу
Скрыть рекламу
О рекламе
Ниже
Процесс выписан полностью.
Вы часто будете видеть другие версии, которые, как правило, являются просто укороченной версией процесса ниже .
Вы также можете увидеть это в Long Division Animation.
Посмотрим как это делается с помощью:
- число, на которое нужно разделить, называется делимое
- Число, на которое делится другое число, называется делителем
И вот:
| 4 ÷ 25 = 0 остаток 4 | Первая цифра делимого (4) делится на делитель. | |
| Целое число помещается вверху. Любые остатки в этот момент игнорируются. | ||
| 25 × 0 = 0 | Ответ из первой операции: умножить на делитель. Результат помещается под числом, разделенным на. | |
| 4 − 0 = 4 | Теперь мы вычитаем нижнее число из верхнего числа. | |
Сократите следующую цифру делимого. | ||
| 42 ÷ 25 = 1 остаток 17 | Разделите это число на делитель. | |
| Целое число помещается вверху. Любые остатки в этот момент игнорируются. | ||
| 25 × 1 = 25 | Результатом вышеописанной операции является , умноженное на на делитель. Результат помещается под последним числом, на которое делится. | |
| 42 − 25 = 17 | Теперь мы вычитаем нижнее число из верхнего числа. | |
| Сократите следующую цифру делимого. | ||
| 175 ÷ 25 = 7 остатка 0 | Разделите это число на делитель. | |
Целое число помещается вверху. Любые остатки
в этот момент игнорируются. | ||
| 25 × 7 = 175 | Результатом вышеописанной операции является , умноженное на на делитель. Результат помещается под числом, разделенным на. | |
| 175 — 175 = 0 | Теперь мы вычитаем нижнее число из верхнего числа. | |
| Больше нет цифр для записи. Ответ должен быть 17 |
Рабочие листы длинного деления
Copyright © 2017 MathsIsFun.com
Как сделать длинное деление с 2 цифрами + Пример
В сегодняшней статье мы собираемся объяснить
как решать двузначное деление.Перед тем, как начать учиться решать двузначное деление, важно, чтобы вы ознакомились с этими терминами, потому что мы будем использовать их позже.
Дивиденд: число, которое делится.
Делитель: число, на которое делится делимое.
Частное: результат деления.
Остаток: сумма, оставшаяся после деления.
Увидев это, вы знаете, где разместить каждую цифру в дивизионе. Теперь нам нужно выполнить следующие шаги:
- Возьмите первые цифры делимого, столько же цифр, сколько и у делителя. Если число, взятое из делимого, меньше делителя, нужно взять следующую цифру делимого.
- Разделите первое число делимого (или два первых числа, если на предыдущем шаге была другая цифра) на первую цифру делителя. Запишите результат этого деления в пространстве частного.
- Умножьте цифру частного на делитель, запишите результат под делимым и вычтите его. Если вы не можете, потому что делимое меньше, вам придется выбирать меньшее число в частном, пока оно не сможет вычитаться.
- После вычитания отбросить следующую цифру делимого

Это концепция, но мы рассмотрим ее на примере.
Мы собираемся решить следующее двузначное деление:
- Возьмем первые цифры делимого: в данном случае 57. Но так как 57 меньше 73, вы должны взять еще одну цифру: 573.
- Чтобы разделить 573 на 73, берем первые две цифры делимого: 57 и делим их на первую цифру делителя:
57 ÷ 7 = 8
- Запишите 8 в частном и умножьте на делитель:
8 x 73 = 584
Но 584 больше, чем 573; следовательно, 8 «не подходит». Вы должны выбрать предыдущее число и снова умножить:
7 x 73 = 511
511 меньше, чем делимое; поэтому 7 «подходит». Мы пишем 511 под цифрами делимого, а затем делим и вычитаем:
- Отбросьте следующую цифру делимого, то есть 8. Теперь вам нужно разделить 628 на 73. Повторите предыдущие шаги:
Разделите первые две цифры делимого на первую цифру делителя и запишите это в месте частного:
62 ÷ 7 = 8
Умножьте эту цифру на делитель:
8 x 73 = 584
584 меньше 628; следовательно, мы можем вычесть:
628 – 584 = 44
Результат этого деления 78 и остаток 44.
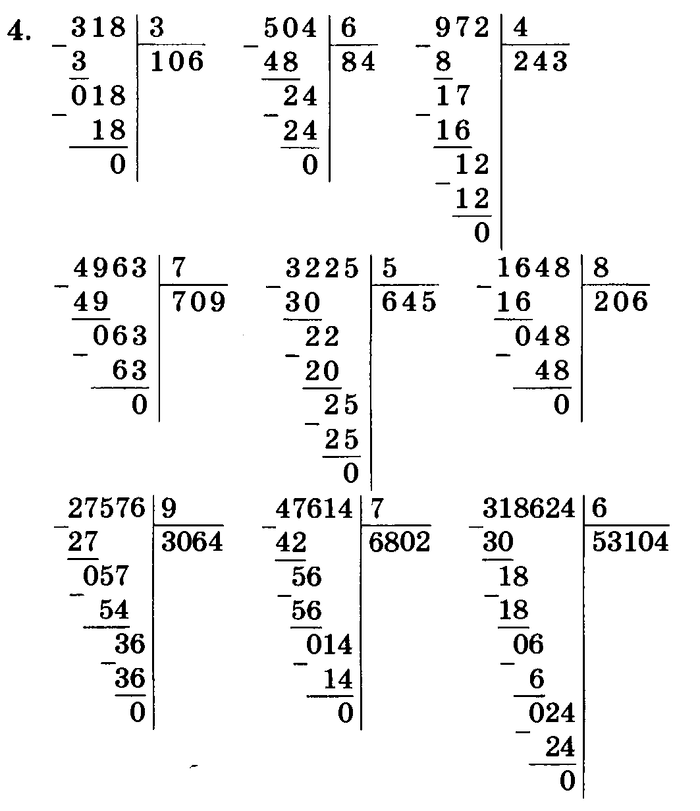 У нас после 51 стоит только одно цифра 2. Значит и добавляем в результат еще одну точку.
У нас после 51 стоит только одно цифра 2. Значит и добавляем в результат еще одну точку. Значит числа разделились нацело (без остатка).
Значит числа разделились нацело (без остатка).