Деление «в столбик» — теперь по-русски 🙂 – Вадим Стеркин
Математика в 3 классе невозможна без поисковых технологий 🙂 Просматривая статистику посещений своего блога осенью 2008 г, я обратил внимание, что с начала сентября в него ежедневно приходят из Google несколько человек по запросу деление в столбик. Действительно, я когда-то писал о том, как делят в столбик американцы. Как ни странно, именно эта запись стояла первой в списке результатов поисковика, но она ничем не помогала бедным школьникам и их родителям.
Беглый просмотр других результатов поисковика не выявил алгоритма деления в первой десятке, и даже в русской Википедии статья еще ждала своего автора. Я решил восполнить пробел, не претендуя на полноту изложения материала или профессиональный педагогический подход.
Итак, дорогие школьники, сегодня мы будем делить 861 на 7 в столбик. Если вы еще не знаете, в любой операции деления должно быть делимое, делитель и частное.
В нашем случае 861 – делимое, 7 – делитель, а результат деления – частное. Его и будем искать.
Для начала записываем рядом делимое и делитель, затем разделяем их «уголком».
Теперь нужно внимательно посмотреть на цифры делимого и, двигаясь слева направо, найти в нем наименьшее число, которое больше делителя. Чисел тут три: 8, 86 и 861. Из них наименьшим является 8. Теперь нужно ответить на главный вопрос! Сколько раз наш делитель (7) содержится в числе 8? Один раз. Поэтому смело пишем 1 под чертой – это первая цифра частного, которое мы пытаемся найти.
А где же столбик? Сейчас будет 🙂 Теперь умножаем 7 на 1 и получаем 7. Записывем полученный результат под первым числом делимого и вычитаем в столбик, то есть из 8 вычитаем 7. Получаем 1.
Если вы все сделали правильно, результат вычитания должен быть меньше делителя. Если больше, значит вы неправильно определили, сколько раз 7 содержится в 8. Поскольку результат вычитания меньше делителя, нам нужно его увеличить для продолжения нашего нелегкого труда.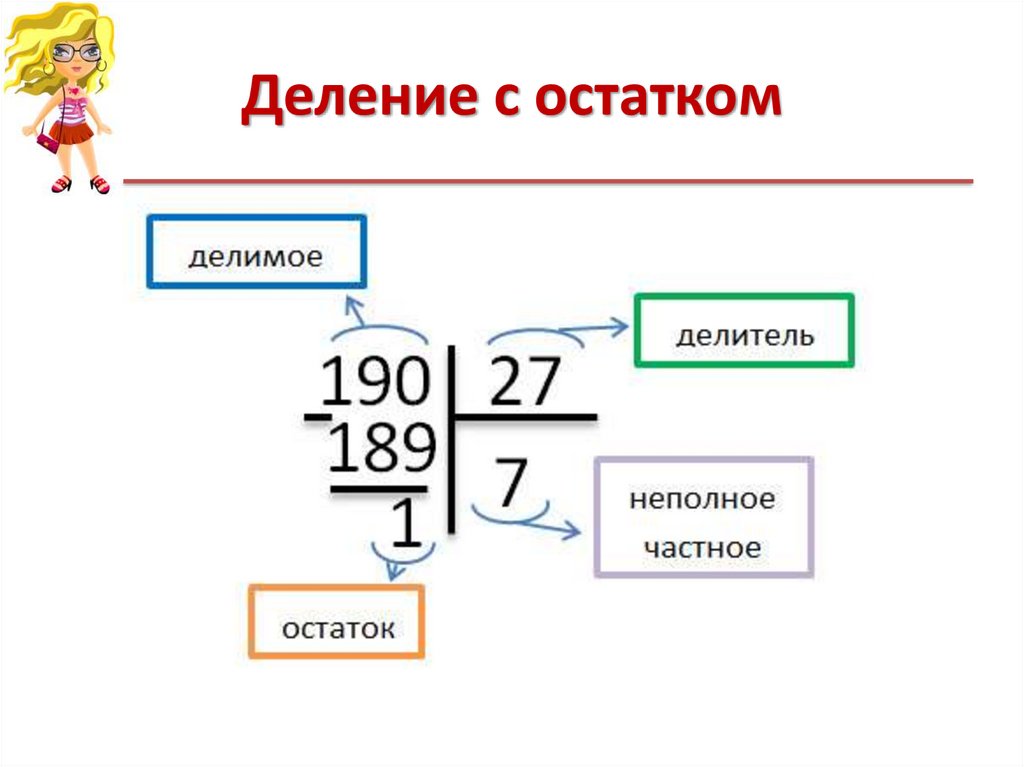
И делать это мы будем за счет следующей цифры делимого. Поскольку 8 мы уже использовали, берем 6 и приписываем к единице.
Теперь отвечаем на уже знакомый вопрос. Сколько раз 7 содержится в 16? Два раза. Приписываем двойку к единице под чертой — это вторая цифра частного. Умножаем 7 на 2, получаем 14 и записываем результат под 16.
Дальше идем по уже знакомому пути. Вычитаем 14 из 16, получаем 2 (2 меньше 7, значит все сделано правильно). Используем третью и последнюю цифру делимого – 1, сносим ее вниз и приписываем к двойке, получая 21.
Снова отвечаем на знакомый вопрос. Сколько раз 7 содержится в 21? Три раза. Пишем тройку под чертой. Умножаем 7 на 3, получаем 21 и записываем в столбик под 21. Вычитаем 21 из 21, получаем 0. Ура, деление выполнено без остатка! Ответ – 123.
Если вы использовали все цифры делимого, а ноль так и не получился, значит либо деление без остатка невозможно, либо вы ошиблись в арифметике.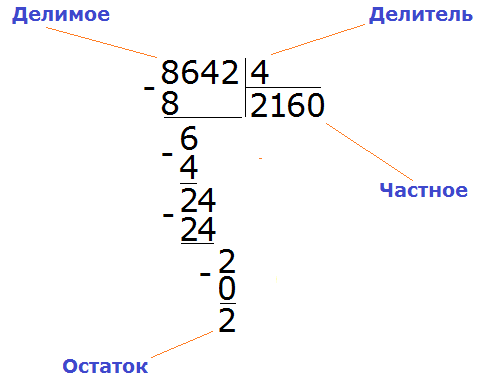
Выполните проверку… при помощи калькулятора – Пуск – Выполнить – calc.
Конец урока 🙂
Математика. Деление уголком | Сайт Леонида Некина
Деление «уголком» — это, на мой взгляд, самая тяжелая, самая нудная тема во всей школьной математике. Тут нам придется всерьез поднапрячься. Пусть, однако, нас вдохновляет мысль, что весь последующий материал будет значительно легче и приятнее.
Прежде всего, рассмотрим деление на однозначное число. Допустим, мы хотим вычислить значение выражения
$648 / 2$.
Пользуясь свойствами умножения, мы можем расписать делимое таким образом:
$648 =$
$6$ $\,\cdot\,100~+$ $4$ $\,\cdot\,10~+~$ $8$ $~=$
$3$ $\,\cdot\,$ $2$ $\,\cdot\,100~+~$ $2$ $\,\cdot\,$ $2$ $\,\cdot\,10~+~$ $4$ $\,\cdot\,$ $2$ $~=$
$($ $3$ $\,\cdot\,100~+~$ $2$ $\,\cdot\,10~+~$ $4$ $)\,\cdot\,$ $2$ $~=$
$3$ $2$ $4$ $\,\cdot\,$ $2$ .
После этого становится очевидно, что частное от деления равно
$648 / 2 = 324$.
Но это мы взяли самый что ни на есть простейший случай, когда каждую отдельно взятую цифру делимого можно поделить на делитель.
$156 / 2 =$ ?
Здесь первая цифра оказалась меньше делителя. Поэтому, расписывая делимое, мы не будем отрывать ее от второй цифры:
$156~=$
$15$ $\,\cdot\,10~+~$ $6$ .
Поскольку число $15$ не делится нацело на $2$, придется нам прибегнуть к делению с остатком. Представим результат такого деления в виде:
$15$ $~=~$ $7 \cdot 2$ $~+~$ $1$ $~=~$ $14$ $~+~$ $1$ .
Теперь мы можем продолжать расписывать наше делимое дальше:
$156 =$
$15$ $\,\cdot\,10~+~$ $6$ =
( $14$ $~+~$ $1$ )$\,\cdot\,10~+~$ $6$ $~=$
$14$ $\,\cdot\,10~+~$ $1$ $\,\cdot\,10~+~$ $6$ $~=$
$14$ $\,\cdot\,10~+~$ $16$ $~=$
$7$ $\,\cdot\,$ $2$ $\,\cdot\,10~+~$ $8$ $\,\cdot\,$ $2$ $~=$
( $7$ $\,\cdot\,10~+~$ 8 )$\,\cdot\,$ $2$ $~=$
$7$ $8$ $\,\cdot\,$ $2$ .
Отсюда моментально получаем ответ:
$156 / 2 = 78$.
Такого рода расчеты можно проводить в уме и сразу же писать ответ. Но мы сейчас перепишем их в виде краткой таблицы.
Умение составлять такие таблицы нам пригодится, когда мы займемся делением на многозначные числа, когда всё окажется не так просто. Делимое и делитель запишем так:
$1$ | $5$ | $6$ | $2$ |
|
|
|
|
|
|
При делении первых двух разрядов ( $15$ ) на двойку получается $7$ плюс еще какой-то остаток. С этим остатком мы разберемся чуть позже, а пока запишем семерку под чертой снизу от делителя (здесь у нас со временем будет выписан полный ответ):
$1$ | $5$ | $6$ | $2$ |
|
|
|
| $7$ |
|
Умножаем на эту семерку наш делитель ( $2$ ) и записываем ответ ( $14$ ) под первыми двумя разрядами делимого ( $15$ ):
$1$ | $5$ | $6$ | $2$ |
|
$1$ | $4$ |
| $7$ |
|
Теперь настало время вычислить остаток от деления $15$ на $2$ .
Он равен, очевидно,
$15$ $~-~$ $2$ $\,\cdot\,$ $7$ $~=~$ $15$ $~-~$ $14$ .
У нас уже всё подготовлено, чтобы выполнить это вычитание «столбиком»:
$1$ | $5$ | $6$ | $2$ |
|
$1$ | $4$ |
| $7$ |
|
| $1$ |
|
|
|
У нас получается единица , к которой мы приписываем шестерку из следующего разряда делимого:
$1$ | $5$ | $6$ | $2$ |
|
$1$ | $4$ |
| $7$ |
|
| $1$ | $6$ |
|
|
В результате такого приписывания у нас получается число $16$ .
Мы делим его на наш делитеть ( $2$ ) и получаем $8$ . Эту восьмерку пишем в строке ответа, под чертой снизу от делителя:
$1$ | $5$ | $6$ | $2$ |
|
$1$ | $4$ |
| $7$ | $8$ |
| $1$ | $6$ |
|
|
Ответ мы получили, однако правила составления таблицы таковы, что нам надо добавить в нее еще две строки. Мы должны формальным образом убедиться, что не потеряли остаток от деления. Умножаем делитель ( $2$ ) на последнюю цифру ответа ( $8$ ), приписываем результат ( $16$ ) снизу к нашей таблице в последние два разряда делимого:
$1$ | $5$ | $6$ | $2$ |
|
$1$ | $4$ |
| $7$ | $8$ |
| $1$ | $6$ |
|
|
| $1$ | $6$ |
|
|
Вычитаем последнюю строку из предпоследней и получаем $0$:
$1$ | $5$ | $6$ | $2$ |
|
$1$ | $4$ |
| $7$ | $8$ |
| $1$ | $6$ |
|
|
| $1$ | $6$ |
|
|
|
| $0$ |
|
|
Этот последний ноль есть не что иное, как остаток от деления, который образовался бы в том случае, если бы мы рассматривали деление с остатком:
$156 : 2 = 78~(\text{ост.
}~0)$.
Чтобы получше это понять, возьмем похожий пример, в котором, однако, остаток не равен нулю:
$157 : 2 = 78~(\text{ост.}~1)$.
Таблица для этого примера выглядит так:
$1$ | $5$ | $7$ | $2$ |
|
$1$ | $4$ |
| $7$ | $8$ |
| $1$ | $7$ |
|
|
| $1$ | $6$ |
|
|
|
| $1$ |
|
|
Здесь, опять-таки, остаток стоит в последней строке.
$157~=$
$14$ $\,\cdot\,10~+~$ $17$ $~=$
$7$ $\,\cdot\,$ $2$ $\,\cdot\,10~+~$ $8$ $\,\cdot\,$ $2$ $~+~1~=$
( $7$ $\,\cdot\,10~+~$ $8$ )$\,\cdot\,$ $2$ $~+~1~=$
$7$ $8$ $\,\cdot\,$ $2$ $~+~1$
Теперь мы готовы к тому, чтобы делить (нацело или с остатком) на многозначные числа. Это делается при помощи подобной же таблицы (именно из-за ее особого вида данная процедура получила название деление «уголком»). Допустим, требуется выполнить деление с остатком:
$135674 : 259~=~$?
Приступаем к заполнению таблицы:
| $1$ | $3$ | $5$ | $6$ | $7$ | $4$ | $2$ | $5$ | $9$ |
|
|
|
|
|
|
|
|
|
|
В данном случае, чтобы найти первую цифру частного, надо взять первые четыре цифры делимого ( $1356$ ) и получившееся число поделить (с остатком) на делитель ( $259$ ).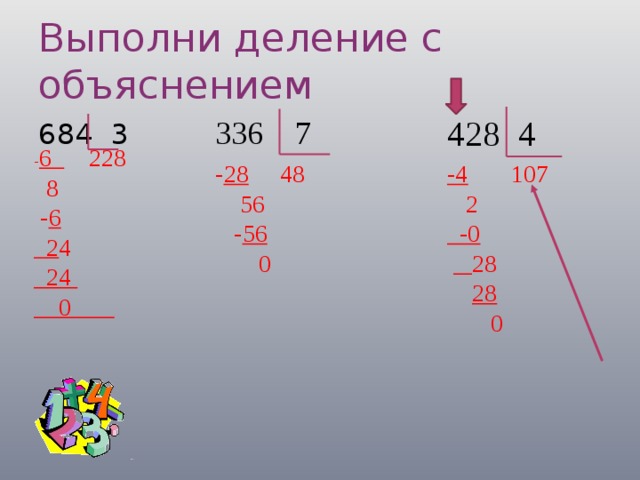
Почему надо взять именно первые четыре цифры делимого? Потому что если бы мы взяли хотя бы на одну цифру меньше, то получившееся число ( $135$ ) оказалось бы меньше делителя ( $259$ ), а это не то, что нам надо. Итак, возьмем первые четыре цифры делимого и рассмотрим следующее деление с остатком:
$1356$ : $259$ = ?
Тут нам помогут приближенные вычисления, для которых, как мы знаем, вовсе необязательно, чтобы числа делились друг на друга нацело:
$1356$ / $259$ $~\approx 1356 / 300 \approx 1500 / 300 = 15 / 3~=~$ $5$ .
Зная результат приближенного деления, мы можем предположить, что, скорее всего,
$1356$ : $259$ = $5$ (остаток — пока неважно какой).
Конечно, абсолютной уверенности у нас нет. Здесь вместо пятерки вполне может стоять четверка или шестерка , однако вряд ли мы ошиблись больше, чем на одну единицу. Имея это в виду, тем не менее берем эту пятерку и заносим ее в нашу таблицу в строку ответа. После этого умножаем на нее делитель ( $259$ ) и при этом записываем ответ под делимым в подходящие разряды:
| $1$ | $3$ | $5$ | $6$ | $7$ | $4$ | $2$ | $5$ | $9$ |
| $1$ | $2$ | $4$ |
|
|
|
|
|
|
$259$ $~\cdot~$ $5$ = | $1$ | $2$ | $9$ | $5$ |
|
| $5$ |
|
|
Здесь «маленькие» цифры — это побочный продукт процедуры умножения: мы познакомились с ними, когда учились умножать «в столбик».
После того как умножение выполнено, они становятся больше не нужны: на них можно просто не обращать внимания. Выражение $259$ ∙ $5$ , написанное слева от таблицы, помещено сюда только ради пояснения того, что мы делаем. К таблице оно, собственно, не принадлежит, и в будущем мы такие пояснения выписывать не будем. Тут важно отметить, что результат нашего умножения $1295$ оказался меньше записанного над ним числа $1356$ , составленного из первых четырех цифр делимого. Если бы это было не так, то это означало бы, что приближенное деление дало нам завышенный результат. Нам надо было бы тогда зачеркнуть пятерку в строке ответа, на ее место поставить четверку — после чего зачеркнуть и переделать все наши последующие вычисления. Но нам на этот раз повезло, и ничего переделывать не требуется.
Теперь выполняем вычитание в столбик и получаем:
| $1$ | $3$ | $5$ | $6$ | $7$ | $4$ | $2$ | $5$ | $9$ |
| $1$ | $2$ | $4$ |
|
|
|
|
|
|
$259$ $~\cdot~$ $5$ = | $1$ | $2$ | $9$ | $5$ |
|
| $5$ |
|
|
|
|
| $6$ | $1$ |
|
|
|
|
|
Внимательно приглядимся к полученной разности ( $61$ ).
Очень важно, что она оказалась меньше делителя ( $259$ ). В противном случае мы пришли бы к выводу, что приближенное деление дало нам заниженный результат и нам пришлось бы теперь исправлять в строке ответа пятерку на шестерку , а также переделывать все последующие вычисления. К счастью, этого не случилось. Приближенное вычисление нас не подвело, и мы теперь совершенно точно знаем, что,
$1356$ : $259$ = $5$ (ост. $61$ ).
Возвращаемся к таблице. К нашему остатку ( $61$ ) приписываем семерку из следующего разряда делимого и приступаем к нахождению второй цифры ответа. Это делается с помощью точно такой же процедуры, что и раньше. Потом — очередь за третьей цифрой. В конце концов таблица принимает такой вид:
| $1$ | $3$ | $5$ | $6$ | $7$ | $4$ | $2$ | $5$ | $9$ |
| $1$ | $2$ | $4$ |
|
|
|
|
|
|
$259$ $~\cdot~$ $5$ = | $1$ | $2$ | $9$ | $5$ |
|
| $5$ | $2$ | $3$ |
|
|
| $6$ | $1$ | $7$ |
|
|
|
|
|
|
| $1$ | $1$ |
|
|
|
|
|
$259$ $~\cdot~$ $2$ $~=~$ |
|
| $5$ | $1$ | $8$ |
|
|
|
|
|
|
|
| $9$ | $9$ | $4$ |
|
|
|
|
|
|
| $1$ | $2$ |
|
|
|
|
$259$ $~\cdot~$ $3$ $~=~$ |
|
|
| $7$ | $7$ | $7$ |
|
|
|
|
|
|
| $2$ | $1$ | $7$ |
|
|
|
Можно выписывать окончательный ответ:
$135674 : 259 = 523~(\text{ост}.
~217)$.
Самая большая неприятность в делении «уголком» состоит в том, что приближенные вычисления, к которым приходится прибегать по ходу дела, не дают сразу гарантированно правильного результата и нуждаются иногда в последующей коррекции. Впрочем, по мере тренировки, у нас выработается особое чутье и мы будем уже сразу почти наверняка знать, какие цифры следует писать в строке ответа, чтобы потом ничего больше не надо было исправлять и переделывать.
Разумеется, нам будут попадаться случаи, когда частное содержит нули. Каждый такой ноль позволит сделать в таблице небольшие сокращения. Вот пример такой таблицы:
$2$ | $6$ | $2$ | $7$ | $4$ | $0$ | $8$ | $7$ |
|
|
$2$ | $2$ |
|
|
|
|
|
|
|
|
$2$ | $6$ | $1$ |
|
|
| $3$ | $0$ | $2$ | $0$ |
|
| $1$ | $7$ | $4$ |
|
|
|
|
|
|
| $1$ | $1$ |
|
|
|
|
|
|
|
| $1$ | $7$ | $4$ |
|
|
|
|
|
|
|
|
| $0$ |
|
|
|
|
|
Как и в случае умножения «в столбик», для того чтобы было удобнее писать «маленькие» цифры, нам может понадобиться
лист со специальной линовкой для вычислений (формат pdf).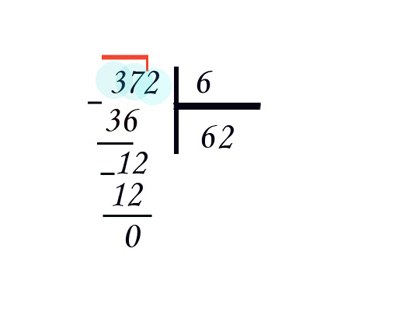
Теперь остается только тренироваться, тренироваться и тренироваться.
Конспект
Деление «уголком». Рассмотрим пример:
делимое : делитель = частное (остаток такой-то).
Наша задача — найти частное и остаток, если известны делимое и делитель. Решаем эту задачу в несколько шагов, на каждом из которых мы находим одну цифру частного.
Шаг первый. Берем в делимом столько цифр спереди, чтобы они составляли число, которое при делении на делитель дает однозначное число и еще какой-то (промежуточный) остаток. Выполнив такое деление, выписываем полученное однозначное число в качестве первой цифры частного, а к промежуточному остатку приписываем в конец первую из оставшихся цифр делимого. В результате такого приписывания мы получаем число, которое мы передаем для дальнейшей «обработки» во второй шаг.
Шаг второй. Число, поступившее для «обработки» из предыдущего шага, делим на делитель. В результате получаем однозначное число и какой-то еще промежуточный остаток.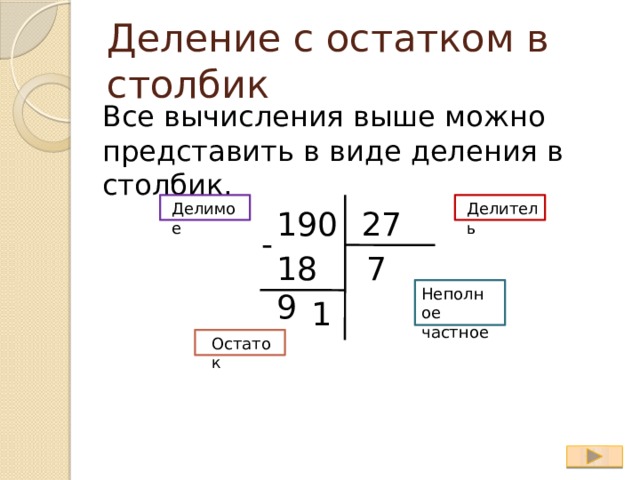
Однозначное число мы записываем в качестве следующей цифры частного, а к промежуточному остатку приписываем в конец первую из оставшихся цифр делимого и передаем получившееся число для дальнейшей «обработки» в следующий шаг.
Описание последующих шагов в точности совпадает с описанием второго шага. Мы останавливаемся, когда в делимом больше не остается цифр для приписывания к очередному промежуточному остатку. К этому времени частное оказывается полностью выписанным, а последний промежуточный остаток и есть окончательный остаток в нашем исходном примере.
Из «бесконечного» сборника типовых упражнений
Деление нацело на однозначное число
Деление с остатком на однозначное число
Деление с остатком на однозначное число с возможным «приписыванием» нулей
Деление нацело на двузначное число
Деление с остатком на двузначное число
Деление нацело на трехзначное число
Деление с остатком на трехзначное число
Как делить десятичные дроби — пустышки
Авторы: Марк Зегарелли и
Обновлено: 27 сентября 2022 г.
Учебник по математике и предварительной алгебре для чайников с онлайн-практикой Изучить книгу Купить на Amazon Переместить десятичную точку в делителе и делимом. Превратите делитель (число, на которое вы делите) в целое число, переместив десятичную точку до упора вправо. При этом переместите запятую в делимом (число, которое вы делите) на такое же количество знаков вправо. Поместите десятичную точку в частное (ответ) непосредственно над тем местом, где теперь стоит десятичная точка в делимом. Разделите как обычно, тщательно выстраивая частное так, чтобы десятичная точка встала на свое место. Выровняйте каждую цифру частного сразу после последней цифры делимого, используемого в этом цикле. Как и при целочисленном делении, иногда десятичное деление не работает равномерно в конце. Однако с десятичными дробями вы никогда не записываете остаток. Вместо этого добавьте достаточно нулей в конце, чтобы округлить частное до определенного числа знаков после запятой. Цифра справа от цифры, до которой вы округляете, указывает, нужно ли округлять в большую или меньшую сторону, поэтому вам всегда нужно вычислять деление на один дополнительный разряд. Разделите следующее: 9,152 / 0,8 = ? 11.44 . Для начала напишите задачу как обычно: Превратите 0,8 в целое число 8, переместив запятую на одну позицию вправо. Теперь вы готовы делить. Просто будьте осторожны, чтобы правильно выстроить частное, чтобы десятичная точка встала на свое место. Разделите следующее: 21,9/ 0,015 = ? 1460. Настройте задачу как обычно: Обратите внимание, что к делимому добавлены два завершающих нуля, потому что вам нужно переместить десятичные точки в каждом числе на три позиции вправо. Снова поместите десятичную точку в частном непосредственно над тем местом, где она теперь появляется в делимом, 21900: Теперь вы готовы делить. Тщательно выровняйте частное, чтобы десятичная точка встала на свое место: Несмотря на то, что деление получается даже после того, как вы вписываете цифру 6 в частное, вам все равно нужно добавить замещающий ноль, чтобы десятичная точка стояла в правильном месте. Разделите эти два десятичных знака: 9,345 / 0,05 = ? Решите следующее деление: 3,15 / 0,021 = ? Выполните следующее десятичное деление, округлив до одного знака после запятой: 6,7 / 10,1. Найти решение, округляя до сотых: 9.13 / 4.25. 9,345/0,05 = 186,9. Для начала напишите задачу как обычно: Превратите делитель (0,05) в целое число, переместив запятую на два знака вправо. При этом переместите запятую в делимом (9,345) на два знака вправо. Поместите десятичную точку в частное прямо над тем местом, где она теперь появляется в делимом: Теперь вы готовы делить. Будьте осторожны, чтобы правильно выстроить частное, чтобы десятичная точка встала на свое место. 3,15 / 0,021 = 150. Напишите задачу как обычно: Вам нужно переместить десятичную точку в делителе (0,021) на три знака вправо, поэтому добавьте дополнительный нуль в конце делимого (3,15), чтобы расширить его до трех знаков после запятой: Теперь вы можете переместить обе десятичные точки на три позиции вправо. Поместите запятую в частном над запятой в делимом: Разделите, соблюдая правильное построение частного: Не забудьте вставить в частное замещающий ноль, чтобы десятичная точка оказалась в правильном месте. 6,7/10,1 = 0,7. Для начала напишите задачу как обычно: Превратите делитель (10.1) в целое число, переместив запятую на один разряд вправо. При этом переместите запятую в делимом (6.7) на один разряд вправо: Задача требует округлить частное до одного знака после запятой, поэтому заполните делимое нулями в конце до двух знаков после запятой: Теперь можно делить: Округлить частное до одного десятичного знака: 9,13/4,25 = 2,15. Сначала напишите задачу как обычно: Превратите делитель (4.25) в целое число, переместив запятую на два знака вправо. При этом переместите запятую в делимом (9.13) на два знака вправо: В задаче предлагается округлить частное до сотых, поэтому заполните делимое нулями в конце до трех знаков после запятой: Теперь разделите, тщательно выстраивая частное: Округлить частное до сотых: Марк Зегарелли — учитель математики и подготовки к экзаменам, который написал множество книг по базовой математике и предварительной алгебре в For Dummies 9. СтенограммаЧасто задаваемые вопросыИнформационный бюллетеньПрактика Эй, ребята! Добро пожаловать в это видео о делении десятичных дробей! Деление десятичных дробей может показаться не самым полезным инструментом, но на самом деле оно может пригодиться в нескольких ситуациях повседневной жизни. Теперь вам может быть интересно, когда деление десятичных дробей может быть полезным. Допустим, у вас на банковском счету было 26,84 доллара, и вы хотели купить бензин для своей машины, не выходя за рамки бюджета. Каждый галлон стоит 3,69 доллара.и вы хотели бы сказать обслуживающему персоналу, сколько галлонов залить в вашу машину. Сколько галлонов газа вы должны просить? Или, скажем, вы строите дом и вам нужны куски дерева длиной 4,85 фута. В таких ситуациях вам поможет способность делить числа на десятичные дроби. Давайте начнем с простого примера. Скажем, вы хотели разделить 4,5 на 0,5. Первым делом вы должны написать задачу, как и любую другую задачу на деление в длину. Это должно выглядеть так: Самый простой способ сделать это — умножить каждое число в выражении на 10. Как правило, каждый раз, когда вы умножаете число на 10, вы перемещаете десятичную точку на один разряд вправо. Если мы умножим 0,5 и 4,5 на 10, мы получим: Вам может быть интересно, нужно ли нам что-то делать, чтобы изменить этот ответ. В конце концов, мы изменили оба числа в нашем выражении. Как ответ может быть правильным для нашего исходного выражения? Однако, если вы достанете свой калькулятор, вы увидите, что деление 4,5 на 0,5, наше исходное выражение, также дает 9., точно так же, как деление 45 на 5. Рассмотрим более сложный пример: разделим \(15,75\дел 3,5\). Помните ключевое правило при делении чисел на десятичные дроби — вам нужно сделать то же самое с обоими числами в выражении. Как мы уже упоминали, нам нужно сделать то же самое с обоими числами, поэтому теперь мы умножаем 3,5 на 10 дважды (или на 100). Мы перемещаем десятичную дробь на два знака вправо и добавляем ноль, чтобы заполнить пустое место. Итак, теперь у нас есть \(1575\div 350\). Итак, когда мы умножаем, \(4\times 0=0\), и мы умножаем \(4\times 5\), чтобы получить \(20\). Надеюсь, это видео было полезным! Увидимся, ребята, в следующий раз! Сложение и вычитание десятичных знаков | Умножение десятичных дробей 
Чтобы округлить десятичную дробь до Заполнить дивиденд нулями до Целое число Один десятичный знак Один десятичный знак Два десятичных знака Два десятичных знака Три десятичных знака Примеры вопросов
При этом запятую в числе 9,1526 переместите на один разряд вправо. Поставьте запятую в частном прямо над тем местом, где она попадает в 91,25: Практические вопросы
Ниже приведены ответы на практические вопросы:
Об этой статье
Эта статья взята из книги:
Об авторе книги:
Серия 0024. Эту статью можно найти в категории:
Как делить десятичные дроби (видео и практические вопросы)
В местном магазине продаются большие бревна длиной 28 футов. В магазине задаешься вопросом: сколько деревяшек можно вырезать из каждого бруса? Деление десятичных дробей
.5 4.5
При решении этой задачи было бы значительно проще работать с целыми числами вместо десятичных знаков .
Теперь вы должны решить \(45\div 5\), как обычно. Поскольку это относительно простая задача, нам не нужно проходить этапы деления в большую сторону.
\(5\умножить на 9=45\). Деление десятичных дробей на десятичные дроби
3,5 15,75
Первый шаг — умножить каждого числа на 10, чтобы превратить эти числа в целые десятичные дроби. Начиная с 3,5, это даст нам 35. Однако, если мы посмотрим на другое число в нашем выражении, 15,75, мы заметим, что однократного умножения его на 10 недостаточно. Это дало бы нам 157,5, что все еще не является целым числом. Так что же нам делать в этом случае?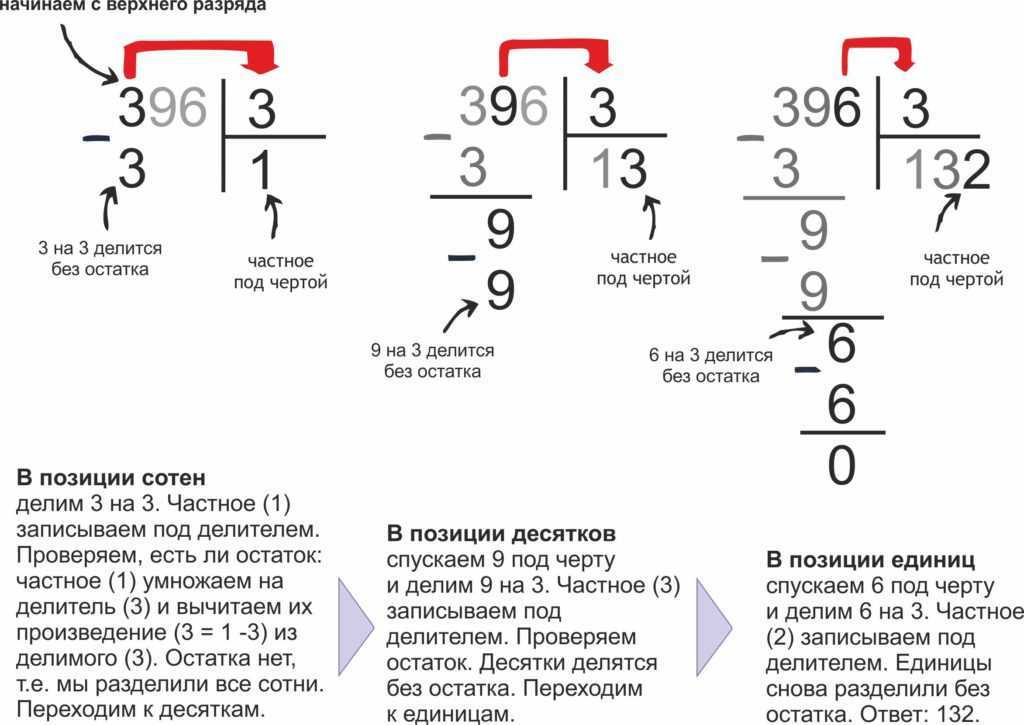
Чтобы сделать 15,75 целым числом, нам нужно дважды умножить его на 10, или, можно сказать, нам нужно умножить его на 100. Это фактически сдвигает десятичный разряд на два знака вправо, давая нам 1575. 350 1,575
Проблема теперь в длинном делении. 350 не входит в число 1, 15 или 157, поэтому нам нужно угадать, сколько раз оно входит в число 1575. 350 входит в 1000 примерно 3 раза, поэтому 4 будет хорошей оценкой количества раз, когда оно входит в 1575. Давайте сделаем небольшое умножение, чтобы перепроверить. \(350\умножить на 4\).
Переносим \(2\), \(4\умножить на 3=12\), затем добавляем \(2\), что дает нам \(14\). Итак, у нас есть \(1400\), что лучше всего подходит для \(1575\). Итак, теперь мы пишем \(4\) над нашим \(5\), так что теперь у нас есть \(1,575-1,400\), что оставляет нас с остатком \(175\). \(\phantom{0,00}\)4 350 1,575 1,400 \(\phantom{0,}\ )175
Итак, теперь мы хотим обязательно добавить десятичную дробь после 4 сверху. \ (\ phantom {0,00} \) 4. \ (\ phantom {0} \) 350 1 575,0 \ 4005333.0 \phant. {.0}\) \(\phantom{0,}\)1,750
Теперь методом проб и ошибок разделим \(1,750\div 350\). Учитывая, что мы видели ранее, что \(350\times 4=1400\), мы можем видеть, что \(350\times 5\) даст нам ровно \(1750\), что означает, что мы добавляем \(5 \) сразу после десятичного знака рядом с нашим \(4\).
Это дает нам окончательный ответ \(4.5\). \(\фантом{0,00}\)4,5 350 1,575,0 1,400 \ (\ Phantom {.0} \) \ (\ Phantom {0,} \) 1,750 191477777777777777777777777777777777777777777777 ,}\)1,750 \(\phantom{0,000}\)0
Хотя деление десятичных дробей поначалу может показаться сложной задачей, помните, что оно, по сути, то же самое, что и обычное деление в длинную. Не забывайте о стратегии, которую мы обсуждали, чтобы превратить наши числа с десятичными знаками в целые числа: умножьте оба числа в выражении на число, кратное 10, чтобы переместить десятичную точку столько раз, сколько необходимо. Обращайтесь с обоими числами одинаково, и вы обязательно получите правильный ответ. Часто задаваемые вопросы
Q
Как вы делите десятичные дроби?
A
Разделите десятичные числа, умножив оба числа на коэффициент 10, чтобы делитель больше не имел десятичного значения.
Затем используйте длинное деление, чтобы разделить как обычно. Поместите десятичную точку в частном непосредственно над десятичной точкой в делимом.
пр. 7,205 ÷ 0,05=
Умножьте оба числа на 100, чтобы избавиться от десятичной части в делителе.
720.5 ÷ 5
Затем используйте длинное деление для деления.
7,205 ÷ 0,05 = 144,1
Q
Как вы делите десятичные дроби на целые числа?
A
Разделите десятичные дроби на целые числа так же, как вы делите целые числа друг на друга, но поставьте десятичную точку в ответе на то же место, что и в исходном числе.
пр. 8,342 ÷ 2=
Q
Как делить десятичные дроби без калькулятора?
A
Деление десятичных дробей с использованием длинного деления, обязательно умножение на произведение 10, если в делителе есть десятичная дробь. Поместите запятую в частном прямо над тем местом, где она стоит в делимом.
пр. 182,35 ÷ 0,5
Сначала умножьте оба числа на 10, чтобы в делителе (0,5) не было десятичной дроби.
1 823,5 ÷ 5
Затем используйте деление в длинном столбце.
Q
Как вы делите десятичные дроби с помощью моделей?
A
Чтобы разделить десятичные дроби с использованием моделей, сначала заштрихуйте первое число, ваше делимое. Затем обведите группы второго числа, вашего делителя. Количество обведенных групп — это ваш ответ или частное.
пр. 2,5 ÷ 0,5
Имеется 5 групп, поэтому 2,5 ÷ 0,5 = 5.
Q
Что вы делаете с остатком при делении десятичных дробей?
А
Если при делении десятичных дробей есть остаток, добавьте нули в конец делимого и продолжайте делить, пока не останется остатка.
пр. 9.67 ÷ 5
Информационный бюллетень
Скачать информационный бюллетень
Практические вопросы
Вопрос №1:
Что такое \(23,95÷5\)?
3,76
4,79
6,42
5,87
Показать ответ
Ответ:
Правильный ответ: 4,7.
Чтобы разделить десятичное число на целое число, выполните длинное деление, как если бы вы делили два целых числа, но поставьте десятичную точку в ответе на то же место, где она находится в делимом.
Скрыть ответ
Вопрос №2:
Что такое \(1,437÷2\)?
2,136
2,874
0,2413
0,7185
Показать ответ
Ответ:
. Чтобы разделить десятичное число на целое число, выполните длинное деление, как если бы вы делили два целых числа, но поставьте десятичную точку в ответе на то же место, где она находится в делимом. Если оно делится неравномерно, прибавьте 0 к концу делимого и продолжайте делить до тех пор, пока не останется остатка.
Скрыть ответ
Вопрос №3:
Что такое \(69,27÷0,3\)?
230,9
176,3
17,63
23,09
Показать ответ
Ответ:
Правильный ответ 9.