Как решать столбиком: Ошибка 403 — доступ запрещён

Содержание

Деление многочленов столбиком онлайн

Примеры решенийРанг матрицыМетод КрамераУмножение матриц Определитель матрицы Метод обратной матрицы Обратная матрица Метод Гаусса онлайн LU разложение матрицы Производная онлайн

Для любых многочленов f(x) и g(x), g(x) ≠ 0, существуют единственные полиномы q(x) и r(x), такие что f(x)/g(x)=q(x)+r(x)/g(x).

Алгоритм деления в столбик применяется в частности при нахождении интегралов.

Решение онлайн
Видеоинструкция

Инструкция. Для получения решения в онлайн режиме необходимо ввести числитель и знаменатель.

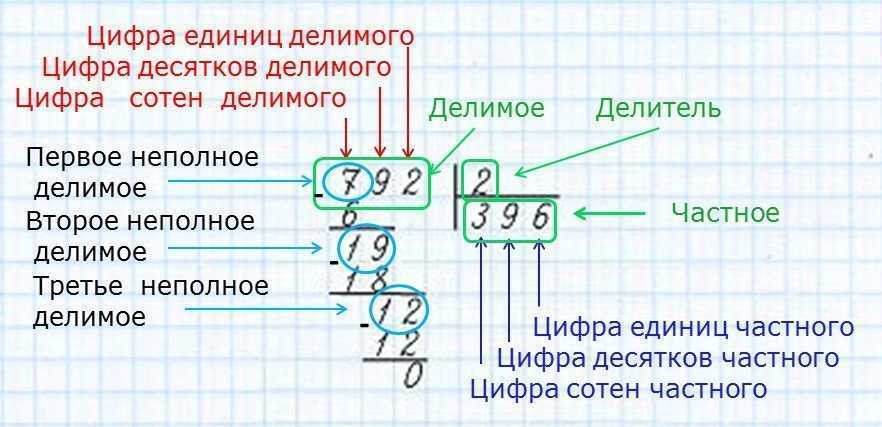
При оформлении в качестве переменной использовать xtzupλ

Пример деления в столбик.

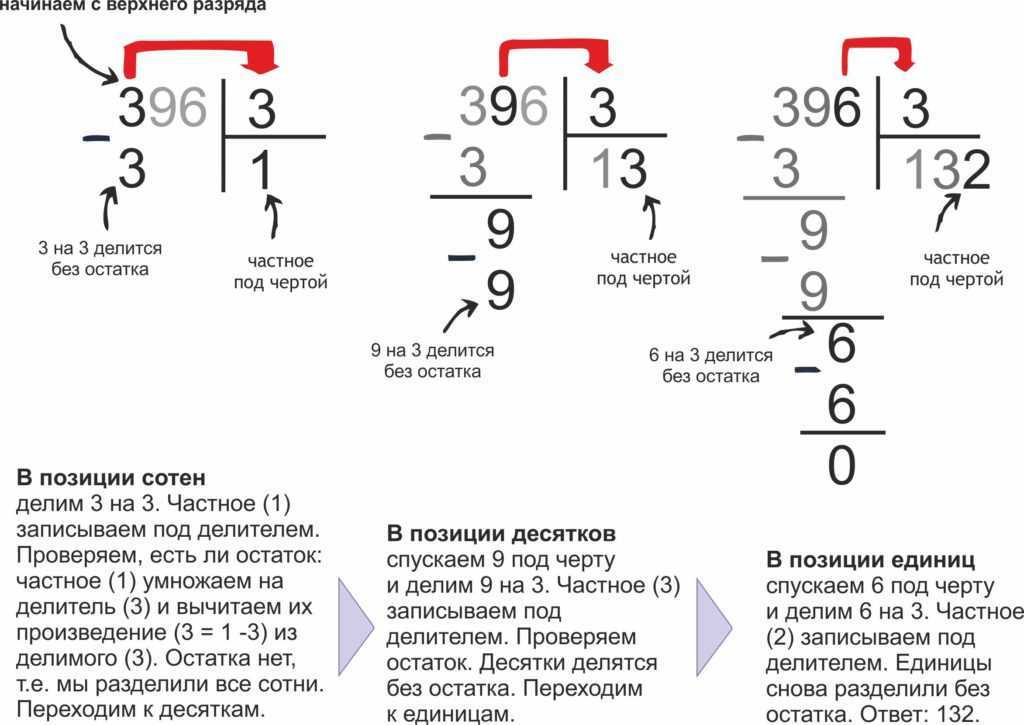
Найти частное деления и остаток многочлена:

№1.

x³ -12x²-42	x^-3
x³ -3x²	x²
-9x²-42

№2.

x³ -12x²-42	x^-3
x³ -3x²	x² -9x
-9x²-42
-9x² + 27x
-27x^-42

№3.

x³ -12x²-42	x^-3
x³ -3x²	x² -9x^-27
-9x²-42
-9x² + 27x
-27x^-42
-27x^{+ 81}
-123

Целая часть: x² -9x^{-27
Остаток: -123}

Таким образом, ответ можно записать как:
см. также и другие примеры решение столбиком.

Пример №1. Найти частное и остаток от деления многочлена на многочлен:
P(x)=2x⁵+3x³-x²+4x+1, Q(x)=2x²-x+1

Пример №2. Не производя деление найти остаток от деления многочлена на двучлен:
P(x)=-x⁴+6x³-2x²+x-2, Q(x)=x-6
Решение. Выделим общий множитель (x-6).
-x³(x-6)-2x(x-6)-12x+x-2 = -x³(x-6)-2x(x-6)-11(x-6)-66-2 = -x³(x-6)-2x(x-6)-11(x-6)-68

Остаток от деления: -68/(x-6)

Задать свои вопросы или оставить замечания можно внизу страницы в разделе Disqus.
Можно также оставить заявку на помощь в решении своих задач у наших проверенных партнеров (здесь или здесь).

Урок «Запись сложения в строчку и столбиком»

Урок Математики.

Учебник: А. Л. Чекин 2 класс.– М..: Академкнига, 2013.

Тема: Запись сложения в строчку и столбиком

Тип урока: урок открытия нового знания

Цель урока: создать условия для знакомства с алгоритмом записи сложения в столбик без перехода через разряд.

Задачи:

1) Создать учебную ситуацию, которая приведёт к постановке учебной задачи.

2) Формировать умение записывать сложение в столбик

3) Развитие умения использовать алгоритм сложения чисел в столбик

4) Развивать умение анализировать, сравнивать, сопоставлять и обобщать.

5) Развивать умение осознавать свои трудности и стремиться к их преодолению.

6) Воспитывать внимание, умение работать в паре, умение слушать, участвовать в диалоге, в дискуссии.

7) Воспитывать интерес к математике

Ход урока

I. Организационный момент

II. Актуализация знаний

1. Минутка чистописания

— Сегодня мы пропишем две цифры. Отгадайте какие. Первая из них состоит из двух полуовалов. Это цифра… . (цифра 3) Напишите её.

— Вторая цифра похожа на лебедя. Правильно – это цифра 2. Запишите рядом, не пропуская клетки.

— Какое число у вас получилось? Пропишите так же до конца строки. Оцените свою работу. Если вам нравится, как вы написали, поставьте на полях карандашом +, если не очень – . (

Самооценка)

— Что вы можете сказать об этом числе? (Двузначное, в нём 2 единицы, 3 десятка)

2. Математический диктант.

— Запишите число, в котором 2 дес. и 5 ед.; 4 дес. и 7ед.; 5 дес., а ед. на 3 больше; 8 дес., а ед. на 2 меньше; 3 дес. и 0 ед.; 4 ед. и 5 дес. (Дети пишут в тетради)

— Поменяйтесь с соседом тетрадями и проверьте. (Взаимопроверка, сравнение с образцом)

3. Создание «ситуации успеха».

1. — Рассмотрите записи на доске

24+ 10

24+31

243+125

-Что общего у всех выражений? (Все на сложение)

— Сформулируйте правило сложения двузначных чисел. (Правило поразрядного сложения: единицы складываем с единицами, десятки с десятками.)

— Выполните поразрядное сложение чисел. (Фронтальная работа, комментированное письмо у доски, способ отработан и затруднения не должно быть)

24+10= (20+4)+10=(20+10)+4=30+4=34

24+31=(20+4)+(30+1)=(20+30)+(4+1)=50+5=55

243+125=(200+40+3)+(100+20+5)=(200+100)+(40+20)+(3+5)=300+60+8= 368

— Как вы думаете, если мы так будем решать каждый пример, много ли успеем на уроке? (ответы детей)

-Как же быть? Может быть, у кого-то появилась идея, как найти сумму данных чисел быстрее? (Записать другим способом, в столбик)

-Откуда вы это узнали?

4. Постановка темы и цели урока

— Определите тему и цель урока. (Способ сложения в столбик, научиться записывать и решать выражения на сложение в столбик)

III. Открытие нового способа действия.

1. -Кто сможет записать выражение 38 + 41 в столбик и решить его? (Объяснение ребёнка у доски)

-Какие правила записи и решения в столбик вы запомнили? (

при условии, если записано и решено верно; если неверно, организуется фронтальное обсуждение)

-Почему не можете записать в столбик и решить это выражение? Что не умеем и чему должны научиться?

— Что надо знать, чтобы записать и решить выражение в столбик?

— Существуют правила записи сложения в столбик и мы с ними сейчас познакомимся.

ФИЗМИНУТКА

2. Работа с учебником

-Рассмотрите образцы сложения двузначных чисел в столбик на с. 36 №2

-Назовите первое и второе слагаемое, значение этой суммы.

-Запишем первое слагаемое. Каждая цифра записана в своей клеточке.

-Где запишем второе слагаемое? При сложении в столбик удобно записывать числа одно под другим, десятки под десятками, а единицы под единицами. Тогда становится видно, какие разрядные единицы нужно складывать.

Знак сложения записывается сбоку на пересечении клеточек.

— Какой знак заменяет знак равно? Проводим черту под всем числом. Ответ записывается прямо под чертой, вниз отступать не нужно.

-С какого разряда начинаем складывать? Складываем сначала единицы, а потом десятки и т.д.

-Как удобнее складывать в столбик или в строчку? Почему?

3. Первичная проверка понимания. Составление алгоритма действия. (Работа в группах.)

-Давайте еще раз воспроизведем пошагово собственные действия, когда вы решали этот пример.

-Предлагаю вам составить алгоритм способа сложения чисел столбиком.

(У каждой группы набор карточек с записью без пошаговой нумерации. )

Алгоритм сложения в столбик.

— Выполни поразрядное сложение, начиная с разряда единиц

— Проведи снизу черту

— Запиши данную сумму столбиком так, чтобы одинаковые разряды слагаемых находились друг под другом

Проверка (Приложение 1)

— Прочитайте свой алгоритм сложения чисел в столбик.

— У кого получилась такая же работа? Кто выполнил по другому?

— Прочитайте. Почему вы так решили? (уч-ся объясняют свой выбор)

— Сравните алгоритм способа сложения столбиком, составленный вами с алгоритмом, который записан в учебнике стр. 39 №3.

— Каких сведений не было в ваших работах? (При необходимости делают поправки в составленных работах)

IV. Первичное закрепление.

-Давайте проверим, как «работает» этот способ на других примерах?

1. Учебник стр.36 №3 (Приложение 2)

— Для каждой из данных сумм, записанных в столбик, сделайте запись в строчку.

— Какое выражение вызвало у вас затруднение?

(Во втором примере (29+46) происходит переход через разряд. 9+6=15, 5 пишем под единицами, 1дес. запоминаем, 2дес.+4дес.=6дес.. Прибавляем к 6дес.1дес., который запомнили. Получаем 7дес.5ед., 75.)

2. Учебник стр. 36 №4

— Для каждой из данных сумм сделайте запись столбиком так, чтобы каждый разряд второго слагаемого располагался под соответствующим разрядом первого слагаемого. То есть нужно записать в столбик.

— С какими трудностями столкнулись? (Обратить внимание на выражение 823+76, во втором слагаемом отсутствуют единицы сотен).

— Поменяйтесь с соседом тетрадями и проверьте. (Взаимопроверка)

Гимнастика для глаз

Глазки видят все вокруг,

Обведу я ими круг.

Глазкам видеть всё дано-

И где дверь, и где окно.

Обведу я ими круг,

Погляжу на мир вокруг!

V. Контроль

— Откройте печатную тетрадь на странице 20 № 3 и выполните сложение в столбик.

( по вариантам)

514+254 420+262 207+81 35+243

234+415 514+342 341+143 234+432

1 вариант-1 и 3 столбик

2 вариант-2 и 4 столбик (Взаимопроверка, сравнение с образцом)

— Проверьте правильность выполнения задания.

-Оцените выполнение данного задания. Как вы оценили свою работу?

-Кто из вас выполнил задания без ошибок? Молодцы!

-Допустил 1-2 ошибки?

-Кто допустил больше 3-х ошибок? Что посоветуете себе?

VI. Рефлексия.

— Какую цель ставили перед собой на уроке? (Научиться записывать и выполнять сложение чисел столбиком)

— Справились с этой задачей? (Да, справились.)

— Как выполнить сложение чисел столбиком?

— Что было интересным для вас?

— Что получилось? Какие трудности были?

— Как оцениваете свою работу на уроке? Кто доволен своей работой на уроке?

— Кто не доволен? Почему?

— Что бы хотели пожелать себе и своим товарищам на следующий урок?

— Спасибо за урок. Урок окончен.

VII. Д/з.

1. Асмолов А.Г. Формирование универсальных учебных действий в основной школе: от действия к мысли, — М. Издательство: Просвещение, 2011 Серия: Стандарты второго поколения

2. Цукерман Г.А. Формирование умения самоконтроля у учащихся: Методические рекомендации. – Омск, 1985. -154с.

3. Чекин А. Л. Математика. 2 класс. Часть 2 – М..: Академкнига, 2013.

Алгоритм сложения в столбик.

1. Запиши данную сумму столбиком так, чтобы одинаковые разряды слагаемых находились друг под другом.

2. Проведи снизу черту.

3. Выполни поразрядное сложение, начиная с разряда единиц.

KS2 Математика 4–5 классы Методы работы со столбцами

Как складывать и вычитать?

Когда нам нужно складывать большие числа, наиболее полезно учитывать разрядное значение каждой цифры. Это означает, что мы можем затем сложить вместе все единицы, десятки, сотни и тысячи и убедиться, что мы сгруппировали вместе все одинаковые значения.

Использование столбцов для сложения

Чтобы убедиться, что мы складываем правильные цифры, мы можем расположить наши числа так, чтобы они были в столбцах. Мы должны всегда выстраивать единицы, десятки, сотни и тысячи друг с другом, чтобы сложить их вместе.

Когда числа расположены в правых столбцах, мы складываем цифры и помещаем ответ ниже, начиная с единиц и двигаясь влево. Если мы получаем больше десяти в качестве ответа на сумму, мы добавляем лишнее в следующий столбец слева. Например, 5 единиц плюс 7 единиц дают 12 единиц. Это 1 десяток и 2 единицы, поэтому 1 десяток будет добавлен к столбцу десятков.

Использование столбцов для вычитания

поэтому они в столбцах. Мы всегда должны выстраивать единицы, десятки, сотни и тысячи друг с другом, чтобы убедиться, что мы вычитаем правильные вещи. Большее общее число должно идти выше меньшего общего числа.

Когда числа расположены в правильных столбцах, мы вычитаем число ниже из числа выше и записываем ответ ниже. Если число, которое мы вычитаем, больше, чем число, которое у нас есть, мы должны «позаимствовать» значение из следующего столбца. Например, 5 единиц минус 7 единиц сделать невозможно, поэтому мы должны взять 10 из следующего столбца слева и сделать 15 минус 7.

Сложение и вычитание: методы столбцов мы делаем сейчас?

Теперь, когда вы можете складывать и вычитать числа до 4 цифр, вы можете отвечать на такие вопросы:

1) Что такое 1234 + 4321?

2) В городе Литтсвоппинг проживает 4351 человек. После наводнения 234 человека переезжают из Литлсвопинга в Биддлстон, где раньше проживало 653 человека. Сколько человек сейчас живет в каждом городе?

3) Миссис Смит открывает прилавок для школьной благотворительной ярмарки. Она берет 2145 фунтов во второй половине дня на ярмарке. Она потратила 9 фунтов4 на материалы для киоска, а затем на следующий день получил пожертвование в размере 652 фунтов стерлингов. Сколько она в итоге отдала на благотворительность?

Hyperlinks

Добавление
Maths — это весело
BBC Bitesize

Нажмите здесь для Maths Maths Home Page

. Клика

Национальная учебная программа

Учащиеся должны научиться:

складывать и вычитать числа, содержащие до 4 цифр, используя формальные письменные методы столбцового сложения и вычитания, где это применимо
оценивать и использовать обратные операции для проверки ответов на вычисления решение, какие операции и методы использовать и почему.

Как вычитать методом столбца

Энциклопедия>Числа и количества>Арифметика>Сложение и вычитание>Как вычитать методом столбца

Когда вы вычитаете два числа, используя метод столбца, вы вычитаете число в нижней части столбца из числа над ним в столбце. Когда вы вычитаете, вы можете оказаться в ситуации, когда число, которое вы вычитаете, больше, чем число, из которого вы вычитаете. В подобных случаях приходится брать взаймы (иногда это называется перегруппировкой). Ниже вы найдете метод вычитания без заимствования и метод вычитания с заимствованием.

Правило

Вычитание без заимствования

1.: Убедитесь, что числа установлены в соответствии с методом столбца.
2.: Начните с цифр в крайней правой колонке. Вычтите нижнее число из верхнего числа и запишите ответ под чертой.
3.: Перейти к следующему столбцу слева. Вычтите нижнее число из верхнего числа и запишите ответ под чертой.
4.: Продолжайте делать это, пока не закончатся столбцы. Вы нашли ответ! Если есть место, в котором «отсутствует» число, вы можете просто заполнить его цифрой 0,9.0102

Пример 1

Вычисление 46–42, 658–134 и 98,43–61,10

Когда вы окажетесь в ситуации, когда вам нужно вычесть больше, чем у вас есть, вам придется заимствовать из столбца слева . Вычитание большего, чем у вас есть, означает, что число в верхней части столбца меньше, чем число под ним. Если число в верхней части столбца, из которого вы берете взаймы, равно 0, вам нужно перейти на другой столбец влево и взять взаймы из верхнего числа. Тогда можно поставить 9над 0 и 10 над столбцом, который нужно было заимствовать для начала. Вот подробное объяснение, как это сделать: