Как умножить три дроби: Умножение обыкновенных дробей — урок. Математика, 6 класс.

.

Учитывая это, можно деление выполнять по следующему правилу.

Чтобы разделить одно число на другое, нужно делимое умножить на число, обратное делителю.

Пример 1.

.

Пример 2.

Пример 3.

.

10. Примеры на все действия с обыкновенными дробями. Решение примеров на все действия с дробями выполняют с помощью записи по отдельным действиям или записи цепочкой.

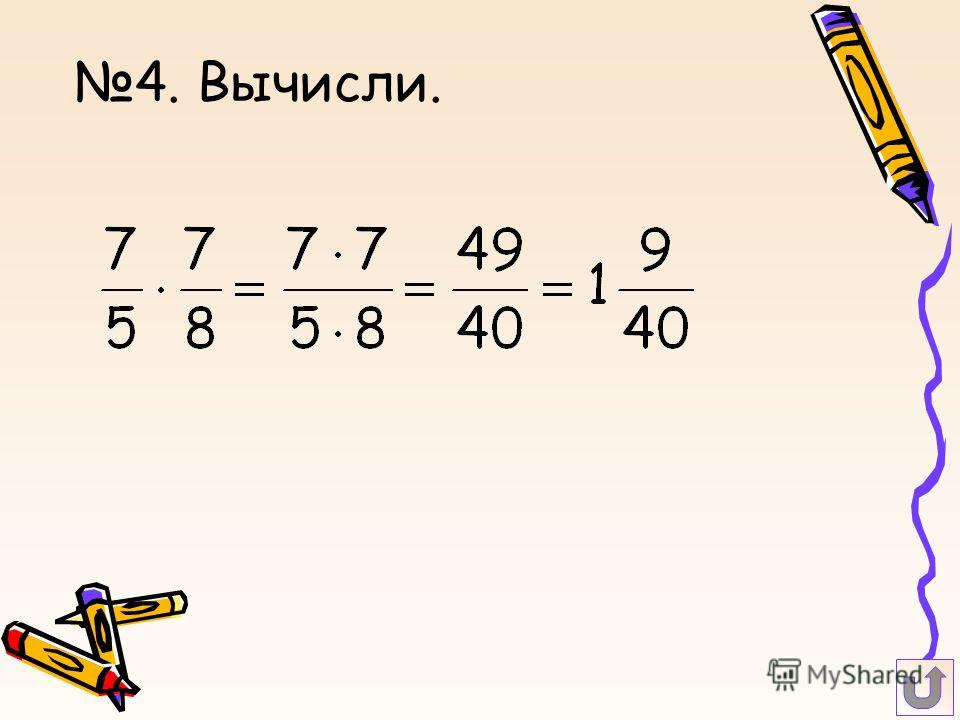
Пример. Вычислить:

Решение по частям.

Ответ. 1.

Пример вычисления цепочкой:

⇦ Ctrl предыдущая страница / следующая страница Ctrl ⇨

ГЛАВНАЯ СТРАНИЦА / МЕНЮ САЙТА / СОДЕРЖАНИЕ ДАННОЙ СТАТЬИ 

1) привести данные дроби к наименьшему общему знаменателю; 2) сравнить (сложить, вычесть) полученные дроби — Студопедия

Поделись  

правило умножения обыкновенных дробей:

умножение дроби на дробь дает дробь, числитель которой равен произведению числителей умножаемых дробей, а знаменатель равен произведению знаменателей.

То есть, умножению обыкновенных дробей a/b и c/d отвечает формула .

правило умножения обыкновенной дроби на натуральное число:

умножение дроби на натуральное число дает дробь, числитель которой равен произведению числителя умножаемой дроби на натуральное число, а знаменатель равен знаменателю умножаемой дроби. С помощью букв правило умножения дроби a/b на натуральное число n имеет вид .

правило деления обыкновенной дроби на натуральное число:

Чтобы разделить дробь на натуральное число, нужно знаменатель умножить на это число, а числитель оставить без изменений.

Пример:

правило деления обыкновенных дробей:

чтобы разделить обыкновенную дробь a/b на дробь c/d нужно делимое умножить на число, обратное делителю. С помощью букв озвученное правило умножения обыкновенных дробей записывается так: .

Смешанное число – это число, равное сумме натурального числа

n и правильной обыкновенной дроби a/b, и записанное в виде . При этом число n называют целой частью числа, а число a/b называют дробной частью числа.

Чтобы из неправильной дроби выделить целую часть надо:

1. разделить с остатком числитель на знаменатель;

2. полученное неполное частное записываем в целую часть дроби;

3. остаток записываем в числитель дроби;

4. делитель записываем в знаменатель дроби

Чтобы представить смешанное число в виде неправильной дроби, нужно:

1. умножить его целую часть на знаменатель дробной части;

2. к полученному произведению прибавить числитель дробной части;

3. записать полученную сумму числителем дроби, а знаменатель дробной части оставить без изменения.

Пример:

правило сложения смешанного и натурального числа :

чтобы сложитьсмешанное число и натуральное число, надо к целой части смешанного числа прибавить данное натуральное число, а дробную часть оставить без изменения. Немного поясним это правило. Пусть нам нужно провести сложение смешанного числа и натурального числа n. Любое смешанное число равно сумме целой и дробной части, поэтому , а свойства сложения позволяют последнюю сумму переписать в виде .

Чтобы сложить смешанные дроби, надо:

1. привести дробные части этих чисел к наименьшему общему знаменателю;

2. отдельно сложить целые части и отдельно дробные части;

3. если при сложении дробных частей получилась неправильная дробь, выделить целую часть из этой дроби и прибавить ее к полученной целой части;

4. сократить полученную дробь.

Чтобы выполнить вычитание смешанных чисел, надо:

1. привести дробные части этих чисел к наименьшему общему знаменателю;
2. если дробная часть уменьшаемого меньше дробной части вычитаемого, превратить ее в неправильную дробь, уменьшив на единицу, целую часть;
3. отдельно выполнить вычитание целых частей и отдельно дробных частей;
4. сократить полученную дробь.

Умножение смешанных чисел: Для того, чтобы выполнить умножение смешанных чисел, надо их записать в виде неправильных дробей, а затем воспользоваться правилом умножения дробей.

Деление смешанных чисел: Для того, чтобы выполнить деление смешанных чисел, надо их записать в виде неправильных дробей, а затем воспользоваться правилом деления дробей.



Каковы правила умножения дробей?

Обновлено 21 декабря 2020 г.

Автор Lisa Maloney

Умножение — одна из самых простых операций, которые вы можете выполнять с дробями, потому что вам не нужно беспокоиться о том, имеют ли дроби одинаковые знаменатели или нет; просто перемножьте числители вместе, умножьте знаменатели вместе и упростите полученную дробь, если это необходимо. Однако есть несколько вещей, на которые следует обратить внимание, включая смешанные числа и отрицательные знаки.

Умножение по прямой

Первое и самое важное правило умножения дробей заключается в том, что вы умножаете только числитель × числитель и знаменатель × знаменатель. Если у вас есть две дроби 2/3 и 4/5, их перемножение даст новую дробь:

\frac{2 × 4}{3 × 5}

, что упрощается до:

\frac{8} {15}

На этом этапе вы бы упростили, если бы могли, но поскольку числа 8 и 15 не имеют общих множителей, дальнейшее упрощение этой дроби невозможно.

Другие примеры, включая умножение дробей, которые необходимо уменьшить, смотрите в видео ниже:

Знаки минуса

Если вы умножаете дроби с отрицательными членами, убедитесь, что вы несете эти отрицательные знаки по вашим расчетам. Например, если вам даны две дроби -3/4 и 9/6, вы должны перемножить их вместе, чтобы создать новую дробь:

\frac{-3 × 9}{4 × 6}

Какой получается:

\frac{-27}{24}

Поскольку −27 и 24 имеют общий множитель 3, вы можете разложить 3 как из числителя, так и из знаменателя, и у вас останется:

\frac{-9}{ 8}

Обратите внимание, что -9/8 представляет собой значение, сильно отличающееся от 9/8. Если бы этот отрицательный знак потерялся по пути, ваш ответ был бы неправильным.

Да, вы можете умножать неправильные дроби

Взгляните еще раз на только что приведенный пример. Вторая дробь 9/6 — неправильная дробь. Или, другими словами, его числитель был больше знаменателя. Это совсем не меняет того, как работает ваше умножение, хотя, в зависимости от вашего учителя или особенностей задачи, над которой вы работаете, вы можете предпочесть упростить результат последнего примера, который сам по себе является неправильной дробью, до смешанное число:

\frac{-9}{8} = -1 \, \frac{1}{8}

Умножение смешанных чисел

Это прекрасно ведет к обсуждению того, как умножать смешанные числа: Преобразовать смешанное число в неправильную дробь и умножить как обычно, как описано в последнем примере. Например, если вам дана дробь 4/11 и смешанное число 5 2/3 для умножения, вы должны сначала умножить целое число 5 на 3/3 (это число 1 в виде дроби). которое имеет тот же знаменатель, что и дробная часть смешанного числа), чтобы преобразовать его в дробь:

5 × \frac{3}{3} = \frac{15}{3}

Затем добавьте дробную часть смешанного числа, получив:

5 \,\frac{2}{3} = \frac{15}{3} + \frac{2}{3} = \frac{17}{3}

Теперь вы готовы перемножить две дроби вместе:

\frac{17}{3 } × \frac{4}{11}

Умножение числителя на знаменатель дает:

\frac{17 × 4}{3 × 11}

Что упрощается до:

\frac{68}{33}

Вы не можете больше упрощать члены этой дроби, но если хотите, вы можете преобразовать ее обратно в смешанное число:

2 \, \frac{2}{33}

Умножение обратно делению

Вот удобный трюк: если вы знаете, как умножать на дроби, вы уже знаете, как делить на дроби. Просто переверните вторую дробь вверх ногами и умножьте ее вместо того, чтобы делить. Итак, если у вас есть:

\frac{3}{4} ÷ \frac{2}{3}

Это то же самое, что написать:

\frac{3}{4} × \frac{3}{ 2}

, которые затем можно умножить как обычно.

Умножение дробей — УРОКИ МАТЕМАТИИ КЕЙТ

Вы видите ярлык, который мы могли бы использовать? Чтобы найти ответ без диаграммы, мы можем перемножить числители вместе (1 x 1 = 1) и умножить вместе знаменатели (2 x 4 = 8), чтобы получить ответ.

Давайте рассмотрим еще один пример, чтобы увидеть, применимо ли это сокращение. Допустим, у нас есть 2/3 умножить на 4/5. Это означает, что нам нужно 2/3 дроби 4/5. Начнем с картинки 4/5. 4/5 означает, что целое было разделено на 5 равных частей, и у нас есть 4 из 5 равных частей.

Если мы хотим найти 2/3 от 4/5, это означает, что нам нужно найти 2/3 заштрихованной части выше. Для этого мы можем разбить прямоугольник на 3 равные строки. Чтобы найти 2/3, нам нужны 2 строки из 3.

Так что же такое 2/3 от 4/5? Когда мы разделили коробку на 3 ряда, мы образовали прямоугольник размером 5 х 3. Это дает нам в общей сложности 15 равных частей. Нам нужны только 2/3 заштрихованной части, поэтому нам нужно подсчитать только то, что заштриховано в 2 из 3 рядов (внутри фиолетового прямоугольника, показанного выше). Мы видим, что это дает нам 8 одинаковых частей из 15: 8/15.

Вы видите ярлык? Чтобы найти ответ, мы можем перемножить числители вместе (2 х 4 = 8) и умножить знаменатели вместе (3 х 5 = 15).

​Как умножать дроби

Вам не нужно рисовать каждый раз, когда вы перемножаете две дроби. Вместо этого используйте ярлык. Чтобы умножить дроби вместе, вы просто умножаете прямо. Перемножьте числители вместе. Затем умножьте знаменатели вместе. Наконец, упростите свой ответ, если это необходимо.

​15 и 56 не имеют общих делителей, кроме 1, поэтому дробь не нужно упрощать. Вот пример, где дробь можно упростить:

.

Есть еще один вариант, который может быть проще. Вместо упрощения в конце можно упростить в начале. Если вы сначала упростите, может быть легче увидеть общие факторы с меньшими числами в начале.

Не имеет значения, упростите ли вы первое или последнее, в итоге вы получите один и тот же ответ. Выберите способ, который кажется вам самым простым.

Умножение дробей на целые числа

Что делать, если только одно число является дробью, а другое — целым числом? Превратите целое число в дробь, используя 1 в качестве знаменателя. Деление на 1 не меняет числа, поэтому любое целое число можно переписать с 1 в знаменателе. После того, как вы записали целое число в виде дроби, вы можете выполнить шаги по умножению дробей.

​Умножение на смешанное число

Одно или оба числа, которые вы умножаете, могут быть смешанными числами. Прежде чем умножать, запишите смешанное число как неправильную дробь.

Умножение дробей. — tutomath.ru репетитор по математике

Чтобы правильно умножить дробь на дробь или дробь на число, нужно знать простые правила. Эти правила сейчас разберем подробно.

Умножение обыкновенной дроби на дробь.

Чтобы умножить дробь на дробь необходимо посчитать произведение числителей и произведение знаменателей этих дробей.

\(\bf \frac{a}{b} \times \frac{c}{d} = \frac{a \times c}{b \times d}\\\)

Рассмотрим пример:
Мы числитель первой дроби умножаем с числителем второй дроби, также и знаменатель первой дроби умножаем со знаменателем второй дроби.

\( \frac{6}{7} \times \frac{2}{3} = \frac{6 \times 2}{7 \times 3} = \frac{12}{21} = \frac{4 \times 3}{7 \times 3} = \frac{4}{7}\\\)

Дробь \( \frac{12}{21} = \frac{4 \times 3}{7 \times 3} = \frac{4}{7}\\\) сократили на 3.

Умножение дроби на число.

Для начала вспомним правило, любое число можно представить в виде дроби \( \bf n = \frac{n}{1}\) .

Воспользуемся этим правилом при умножении.

\(5 \times \frac{4}{7} = \frac{5}{1} \times \frac{4}{7} = \frac{5 \times 4}{1 \times 7} = \frac{20}{7} = 2\frac{6}{7}\\\)

Неправильную дробь \(\frac{20}{7} = \frac{14 + 6}{7} = \frac{14}{7} + \frac{6}{7} = 2 + \frac{6}{7}= 2\frac{6}{7}\\\) перевели в смешанную дробь.

Другими словами, при умножении числа на дробь, число умножаем на числитель, а знаменатель оставляем без изменения. Пример:

\(\frac{2}{5} \times 3 = \frac{2 \times 3}{5} = \frac{6}{5} = 1\frac{1}{5}\\\\\) \(\bf \frac{a}{b} \times c = \frac{a \times c}{b}\\\)

Умножение смешанных дробей.

Чтобы перемножить смешанные дроби, нужно сначала каждую смешанную дробь представить в виде неправильно дроби, а потом воспользоваться правилом умножения. Числитель умножаем с числителем, знаменатель умножаем со знаменателем.

Пример:
\(2\frac{1}{4} \times 3\frac{5}{6} = \frac{9}{4} \times \frac{23}{6} = \frac{9 \times 23}{4 \times 6} = \frac{3 \times \color{red} {3} \times 23}{4 \times 2 \times \color{red} {3}} = \frac{69}{8} = 8\frac{5}{8}\\\)

Умножение взаимно обратных дробей и чисел.

Дробь \(\bf \frac{a}{b}\) является обратной для дроби \(\bf \frac{b}{a}\), при условии a≠0,b≠0.
Дроби \(\bf \frac{a}{b}\) и \(\bf \frac{b}{a}\) называются взаимно обратными дробями. Произведение взаимно обратных дробей равно 1.
\(\bf \frac{a}{b} \times \frac{b}{a} = 1 \\\)

Пример:
\(\frac{5}{9} \times \frac{9}{5} = \frac{45}{45} = 1\\\)

Вопросы по теме:
Как умножить дробь на дробь?
Ответ: произведение обыкновенных дробей является умножение числитель с числителем, знаменатель со знаменателем. Чтобы получить произведение смешанных дробей нужно перевести их в неправильную дробь и перемножить по правилам.

Как выполнить умножение дробей с разными знаменателями?
Ответ: не важно одинаковые или разные знаменатели у дробей, умножение происходит по правилу нахождения произведения числитель с числителем, знаменатель со знаменателем.

Как умножать смешанные дроби?
Ответ: в первую очередь надо перевести смешанную дробь в неправильную дробь и далее находить произведение по правилам умножения.

Как умножить число на дробь?
Ответ: число умножаем с числителем, а знаменатель оставляем тот же.

Пример №1:
Вычислите произведение: а) \(\frac{8}{9} \times \frac{7}{11}\) б) \(\frac{2}{15} \times \frac{10}{13}\)

Решение:
а) \(\frac{8}{9} \times \frac{7}{11} = \frac{8 \times 7}{9 \times 11} = \frac{56}{99}\\\\\)
б) \(\frac{2}{15} \times \frac{10}{13} = \frac{2 \times 10}{15 \times 13} = \frac{2 \times 2 \times \color{red} {5}}{3 \times \color{red} {5} \times 13} = \frac{4}{39}\)

Пример №2:
Вычислите произведения числа и дроби: а) \(3 \times \frac{17}{23}\) б) \(\frac{2}{3} \times 11\)

Решение:
а) \(3 \times \frac{17}{23} = \frac{3}{1} \times \frac{17}{23} = \frac{3 \times 17}{1 \times 23} = \frac{51}{23} = 2\frac{5}{23}\\\\\)
б) \(\frac{2}{3} \times 11 = \frac{2}{3} \times \frac{11}{1} = \frac{2 \times 11}{3 \times 1} = \frac{22}{3} = 7\frac{1}{3}\)

Пример №3:
Напишите число обратное дроби \(\frac{1}{3}\)?
Ответ: \(\frac{3}{1} = 3\)

Пример №4:
Вычислите произведение двух взаимно обратных дробей: а) \(\frac{104}{215} \times \frac{215}{104}\)

Решение:
а) \(\frac{104}{215} \times \frac{215}{104} = 1\)

Пример №5:
Могут ли взаимно обратные дроби быть:
а) одновременно правильными дробями;
б) одновременно неправильными дробями;
в) одновременно натуральными числами?

Решение:
а) чтобы ответить на первый вопрос приведем пример. Дробь \(\frac{2}{3}\) правильная, обратная ей дробь будет равна \(\frac{3}{2}\) – неправильная дробь. Ответ: нет.

б) практически при всех переборах дробей это условие не выполняется, но существуют некоторые числа, которые выполняют условие быть одновременно неправильной дробью. Например неправильная дробь \(\frac{3}{3}\) , обратная ей дробь равна \(\frac{3}{3}\). Получаем две неправильные дроби. Ответ: не всегда при определённых условиях, когда числитель и знаменатель равны.

в) натуральные числа – это числа которые мы используем при счете, например, 1, 2, 3, …. Если возьмем число \(3 = \frac{3}{1}\), то обратная ей дробь будет \(\frac{1}{3}\). Дробь \(\frac{1}{3}\) не является натуральным числом. Если мы переберем все числа, получать обратное число всегда дробь, кроме 1. Если возьмем число 1, то обратная ей дробь будет \(\frac{1}{1} = \frac{1}{1} = 1\). Число 1 натуральное число. Ответ: могут быть одновременно натуральными числами только в одном случае, если это число 1.

Пример №6:
Выполните произведение смешанных дробей: а) \(4 \times 2\frac{4}{5}\) б) \(1\frac{1}{4} \times 3\frac{2}{7}\)

Решение:
а) \(4 \times 2\frac{4}{5} = \frac{4}{1} \times \frac{14}{5} = \frac{56}{5} = 11\frac{1}{5}\\\\ \)
б) \(1\frac{1}{4} \times 3\frac{2}{7} = \frac{5}{4} \times \frac{23}{7} = \frac{115}{28} = 4\frac{3}{7}\)

Пример №7:
Могут ли два взаимно обратных числа быть одновременно смешанными числами?

Рассмотрим на примере. Возьмем смешанную дробь \(1\frac{1}{2}\), найдем для нее обратную дробь, для этого переведем ее в неправильную дробь \(1\frac{1}{2} = \frac{3}{2}\) . Обратная ей дробь будет равна \(\frac{2}{3}\) . Дробь \(\frac{2}{3}\) является правильной дробью. Ответ: взаимно обратные две дроби одновременно смешанными числами быть не могут.

Калькулятор Умножения 3 Дробей — Онлайн Калькулятор Умножения 3 Дробей

Калькулятор Умножения 3 Дробей помогает найти конечный продукт

Что такое Калькулятор Умножения 3 Дробей?

Калькулятор умножения трех дробей — это бесплатный онлайн-инструмент, который поможет вам умножить любые три дроби за несколько секунд. В Калькуляторе умножения на 3 дроби введите значения всех трех дробей и найдите их произведение одним щелчком мыши.

Калькулятор умножения 3 дробей

Как пользоваться калькулятором умножения 3 дробей?

Выполните следующие простые шаги и научитесь пользоваться калькулятором:

• Шаг 1:  Введите значение всех трех дробей в соответствующем поле.
• Шаг 2:  Нажмите «Умножить» .
• Шаг 3:  Будет отображаться произведение этих трех дробей.
• Шаг 4:  Нажмите «Сброс» , чтобы очистить поле и ввести новый набор дробей.

Как умножать дроби?

Чтобы умножить две или более дроби, выполните следующие действия:

• Умножьте числители
• Умножить знаменатели
• Сократите полученную дробь до наименьшего члена.

Другой способ умножения дробей состоит в том, чтобы исключить общие множители в числителе и знаменателе, а затем умножить оставшиеся числа. Этот метод более полезен для простого умножения трех или более дробей.

Хотите найти сложные математические решения за считанные секунды?

Воспользуйтесь нашим бесплатным онлайн-калькулятором, чтобы решить сложные вопросы. С Cuemath находите решения простыми и легкими шагами.

Записаться на бесплатный пробный урок

Пример 1:

Найдите произведение: 2/3 × 3/4 × 4/5.

Решение:

Один из способов найти произведение трех дробей состоит в том, чтобы умножить числители и знаменатели, а затем упростить дробь.

Получаем, 2/3 × 3/4 × 4/5

= 24/60

= 2/5

Другой способ умножить эти три дроби — сначала убрать общие множители в числителе и знаменателе, а затем затем умножьте числа, оставшиеся в числителе и знаменателе.

Итак, мы можем сократить 3 и 4 из числителей и знаменателей, и произведение будет 2/5.

Пример 2:

Найдите произведение: 4/6 × 7/5 × 8/4.

Решение:

Один из способов найти произведение трех дробей состоит в том, чтобы умножить числители и знаменатели, а затем упростить дробь.

Получаем, 4/6 × 7/5 × 8/4

= 224/120

= 28//15

Пример 3:

Найдите произведение: 8/5 × 6/8 5/11.

Решение:

Один из способов найти произведение трех дробей состоит в том, чтобы умножить числители и знаменатели, а затем упростить дробь.

Получаем, 8/5 × 6/8 × 5/11

= 240/440

= 6/11

Теперь воспользуйтесь калькулятором и найдите произведение данного набора дробей:

• 12/13 × 23/46 × 14/5
• 3/5 × 7/4 × 5/7

• Умножение дробей
• Дроби
• Числитель
• Знаменатель

Видео с вопросами: Умножение трех смешанных чисел

Расшифровка видеозаписи

Вычислите полтора раза три и три четверти умножить на одну и семь девятых.

Эти номера считаются смешанными. А чтобы умножить три смешанных числа, нам нужно преобразовать их в неправильные дроби. Неправильная дробь — это дробь, у которой числитель — большее число, а знаменатель — меньшее число.

Итак, как мы сказали, чтобы умножить три смешанных числа, нам нужно преобразовать их в неправильные дроби, а затем умножить числители вместе, умножить знаменатели вместе, а затем упростить.

Итак, давайте начнем преобразовывать эти смешанные числа в неправильные дроби. Итак, полтора, давайте перепишем единицу так, чтобы она имела знаменатель, равный двум. Два больше двух равно одному.

А это полтора. Итак, нам нужно два на два с половиной. Итак, нам нужно добавить половину. Когда мы складываем дроби, мы добавляем числители и сохраняем знаменатели, если они одинаковы.

Итак, мы получаем три половинки. Теперь продолжим. Три и три четверти, так как же мы можем переписать три как нечто большее, чем четыре? Что ж, мы можем взять четыре умножить на три и сделать из них 12, потому что полная противоположность, 12, разделенная на четыре, даст нам три.

Таким образом, 12 четвертей равны трем, а затем мы прибавляем три четверти. Итак, 12 плюс три равно 15. И мы сохраняем наш общий знаменатель, то есть пятнадцать четвертых.

Один и семь девятых, один мы можем переписать как девять на девять плюс семь девятых. Складываем числители и получаем 16, сохраняем знаменатель и получаем девять. Итак, у нас есть 16 девятых. Итак, как мы уже говорили ранее, нам нужно умножить все наши неправильные дроби, умножив все числители вместе и умножив все знаменатели вместе.

Трижды умножить на 15, умножить на 16, будет 720. И дважды четыре, умножить на девять, будет 72. Мы уменьшим это число и получим 10. Теперь мы можем сделать это другим способом. При умножении чисел мы можем упростить, прежде чем умножать числа.

Три можно упростить до девяти. Сколько раз три идет девять? Он входит в девять три раза, а затем входит в себя один раз. Итак, продолжаем искать.

Теперь у нас может возникнуть соблазн сказать, что двойка и четверка внизу могут упростить, но для упрощения это должно быть число из числителя и число из знаменателя. Они не могут находиться ни в одном числителе, ни в одном знаменателе.

Итак, здесь мы рассматриваем четыре из 16. Мы также могли сделать два из 16. Теперь не оба, вам нужно выбрать один набор для упрощения. Итак, четыре входит в число 16 четыре раза, а затем входит в себя один раз.