Как записать в столбик умножение с нулями: Как правильно умножать натуральные числа столбиком

Как правильно умножать натуральные числа столбиком

Оглавление

Время чтения:  10 минут

691

Умножение натуральных чисел в столбик – это способ, который позволит перемножить без калькулятора любые многозначные числа. Чтобы пользоваться таким методом на практике, нужно знать правила его применения. Рассмотрим подробнее умножение разных чисел в теории и на примерах.

Основные закономерности умножения столбиком

Есть ряд математических правил, которые нужно помнить, чтобы успешно пользоваться таким методом умножения:

• Во-первых, нужно знать наизусть таблицу умножения, и, не задумываясь использовать ее.
• Во-вторых, не стоит забывать правила умножения на нуль. Нуль часто встречается в двух и трехзначных числах, а значит, будет выступать в качестве одного из множителей.
• Помним, что \[x \times 0=0\]
• Под x мы понимаем любое натуральное число.
• Прежде, чем решать примеры на умножение в столбик, стоит вспомнить правила сложения в столбик и потренироваться суммировать числа.
• Повторить понятие разряда и сравнения любых натуральных цифр.

Как записывать множители при решении примеров на умножение столбиком

Залогом правильного решения задачи будет умение правильно записывать выражение столбиком. Здесь придерживаемся следующих правил:

1. В качестве первого множителя записывается цифру, которая имеет больший разряд.
2. Во второй строке (под первым множителем) записывается второй множитель. Здесь важно строго соблюдать закономерность сопоставления разрядов. Это значит, что десятки пишутся под десятками, единицы под единицами, и никак иначе.
3. Записав все множители друг под другом, нужно подвести горизонтальную черту, которая отделит их от ответа.

Рассмотрим на примере, как записать такое выражение.

На примере мы видим, как соблюдаются разряды при умножении четырехзначной цифры на трехзначную.

Теперь, чтобы научиться умножать в столбик, потребуется разобраться, как происходит умножение и как записывается результат. Начнем с умножения многозначного множителя на однозначный.

Как происходит умножение двузначных чисел в столбик на однозначные

Если требуется решить пример на умножение многозначного натурального числа на однозначное, легко можем применить данный метод. Процесс решения сразу рассмотрим ниже.

Разберем алгоритм действий:

1. Записываем множители в столбик, строго соблюдая разряды. Единицы пишем под единицами, следовательно, 2 под 4.
2. Перемножаем их по порядку, так же соблюдая разряд. Сначала перемножаем на 2 единицы, потом десятки, потом сотни. Полученный результат вписываем под чертой.

Здесь стоит отметить, что в образце приведены числа, при перемножении которых результат не превысил 10. В том случае, если при перемножении мы получаем двузначный ответ, то записываем только единицы. Десятки запоминаем и прибавляем к результату, который получится при перемножении следующего разряда. Если количество разрядов закончилось, а остались неучтенные десятки, они просто вписываются крайней левой цифрой.

Умножение в столбик с нулями

Если нам потребуется решить пример по математике, где один из множителей имеет на конце нули, действовать придется несколько иначе. Рассмотрим на конкретном примере.

Условие: нам нужно умножить 5400 на 7.

Первым делом нужно правильно записать выражение:

\[\begin{array}{r} \times \begin{array}{r} 5400\\ 7\\ \end{array} \\ \hline \begin{array}{r} \end{array} \end{array}\]

Здесь нужно обратить внимание на то, что под нулями множитель не записывается.

Следующий этап решения примера в столбик – умножение без учета нулей.

\[\begin{array}{r} \times \begin{array}{r} 5400\\ 7\quad\\ \end{array} \\ \hline \begin{array}{r} 378 \quad \end{array} \end{array}\]

Теперь вспоминаем, что у нас осталось два неучтенных нуля. Их просто переносим вниз за черту.

\[\begin{array}{r} \times \begin{array}{r} 5400\\ 7\quad\\ \end{array} \\ \hline \begin{array}{r} 37800 \end{array} \end{array}\]

В итоге получаем: 5400×7=37800

Нет времени решать самому?

Наши эксперты помогут!

Контрольная

| от 300 ₽ |

Реферат

| от 500 ₽ |

Курсовая

| от 1 000 ₽ |

Как умножать столбиком, если в примере два многозначных числа

Чтобы понять, как умножать в столбик многозначные числа, возьмем задание и рассмотрим алгоритм его решения.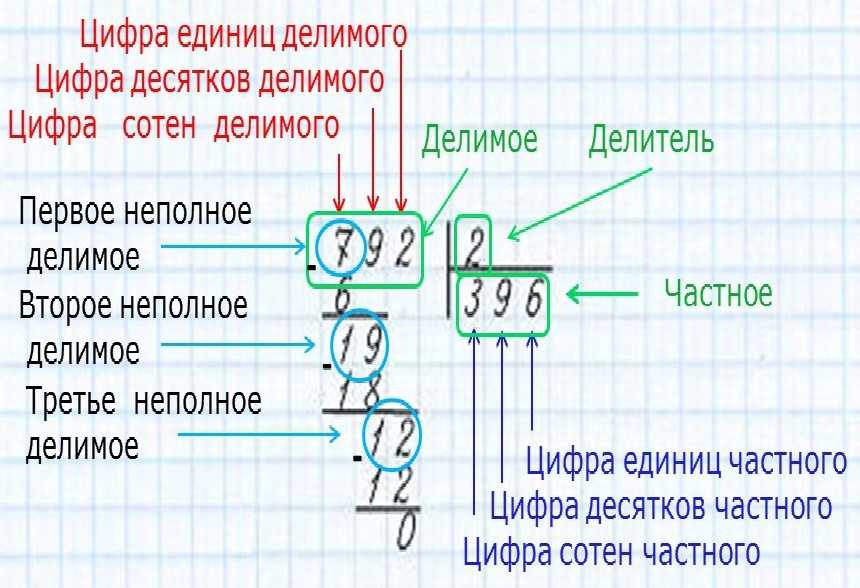 Предположим, нам нужно умножить 8063 на 207.

Решение:

1. Первое действие – записывать множители правильно. Первым записывается множитель, имеющий больше разрядов. В нашем случае – 8063. Под ним записывается второй множитель – 207. Не забываем о строгом соблюдении разрядов. Если нам придется решать примеры, в которых оба множителя имеют равное количество разрядов, записывать их можно в любом порядке.
2. Следующий шаг – перемножение единиц. Это значит, что умножаем 3 на 7, потом 6 на 7, и так далее все разряды первого множителя на единицы второго. Полученный результат будет считаться промежуточным. В некоторых источниках его называют неполным произведением.
   
3. Следующий этап – перемножение десятков. Так как во втором множителе мы имеем нуль в десятках, его просто пропускаем. Согласно правилам, при умножении на нуль все равно получим нуль.
   
4. Следующий этап – перемножение сотен. В итоге мы получим второе неполное произведение или второй промежуточный результат. Его нужно записать под первым промежуточным результатом таким образом, как показано ниже.
   В итоге мы получили два неполных произведения. Задания на умножение столбиком содержат столько промежуточных результатов, сколько разрядов во втором множителе. У нас получилось два, так как в десятках мы имеем нуль, и его пропускаем. Если бы вместо него была любая другая натуральная цифра, мы бы записали три неполных произведения друг под другом со сдвигом влево.
   
5. Завершающий этап – сложение всех полученных промежуточных результатов. Для этого не нужно переписывать их в отдельный пример. Достаточно просто вписать слева знак суммы – плюс и подвести дополнительную черту.

   Под чертой будем записывать полученное в итоге сложения семизначный результат, который и будет ответом.

Таким образом, можно записать выражение:

8063×207=1669041

Можно сказать, что для быстрого и верного решения заданий на умножение в столбик нужно на отлично знать таблицу умножения, помнить правила сложения в столбик, а также помнить основные математические термины.

Под основными терминами понимаются следующие:

• Однозначное число – это число, состоящее из одной цифры (например, 6).
• Двухзначная цифра – это та, в составе которой два натуральных числа (например, 28), и т.д.
• Разряд – это позиция, которую занимает число в комбинации с другими числами. Разряд отсчитывается с конца.
• Разряд единиц – это концовка любого многозначного числа. Перед ним находится разряд десятков, далее разряд сотен, и т.д.

Например, число 4657.

7 – разряд единиц;

5 – разряд десятков;

6 – разряд сотен;

4 – разряд тысяч.

Определение

Умножение – это арифметическое действие, в процессе которого перемножаются два составляющих – множители. Результат данного действия называется произведением.

Чтобы разобраться, как решать умножение в столбик, нужно помнить и основные правила этого математического действия.

1. Перестановка мест множителей не влияет на результат.
   \[x \times y=y \times x\]
2. Произведение трех и более множителей будет иметь идентичное значение, даже если любую группу заменить произведением.
   \[x \times y \times z=(x \times y) \times z\]
3. Умножение на нуль всегда дает нуль.

Есть еще одна категория примеров, на которую стоит обратить внимание. Это перемножение множителей, на конце каждого из которых есть нули. В таких примерах часто допускаются ошибки. Независимо от количества нулей на конце многозначных натуральных чисел, нужно действовать в последовательности, описанной на примере ниже.

Пример умножения чисел столбиком

Пример

Условие: 34500×230

Первым делом нужно записать пример в столбик таким образом, чтобы натуральные числа, отличные от нуля, расположились друг под другом.

\[\begin{array}{r}\times\begin{array}{r}34500\\230\\\end{array}
\\\hline\begin{array}{r}\end{array}\end{array}\]

После того, как мы записали пример в столбик, мы можем просто перемножить множители в соответствие с
правилами перемножения многозначных чисел, без учета нулей.

В ходе вычислений у нас должно получиться два неполных, или промежуточных результата.

\[\begin{array}{r}\times\begin{array}{r}34500\\230\\\end{array}
\\\hline\begin{array}{r}\end{array}\\+1035\\690\\\hline\end{array}\]

Последний этап – сложение двух промежуточных результатов и переписывание справа нулей. Нулей мы напишем столько, сколько имеют оба множителя, а именно, три.

\[\begin{array}{r}\times\begin{array}{r}34500\\230\\\end{array} \\\hline\begin{array}{r}\end{array}\\+1035\\690\\\hline7935000\end{array}\]

В итоге получаем, что 34 500×230=7 935 000

Анализируя вышеперечисленный пример, можно сказать, что перемножить в столбик можно любые без исключения числа, если руководствоваться правилами математики. Умножение двузначных чисел в столбик – это школьная программа, освоив которую, примеры научится решать любой ребенок, ученик четвертого класса.

Умножение в столбик. Распределительный, переставной, связующий законы умножения в 2023 году

Что такое умножение? Компоненты действия умножения

Умножение – это арифметическое действие, заключающееся в нахождении суммы одинаковых слагаемых.

Компоненты или названия чисел при умножении: множимое, множитель, произведение. Число, являющееся слагаемым, называется множимым; число, показывающее, сколько таких одинаковых слагаемых, называется множителем. Результат действия, то есть число, найденное при умножении, называется произведением. Множимое и множитель иногда называют одним словом сомножители.

Запись действия умножения:

Необходимо умножить 4 на 5. В математике запись будет выглядеть: 4×5 = 20. Знак умножения «×» или «·»

Чтобы умножить 4 на 5, необходимо 5 раз добавить число 4 или найти сумму пяти одинаковых слагаемых (числа 4).

4 + 4 + 4 + 4 + 4 = 20

В этом случае 4 будет множеным, 5 – множителем, 20 – произведением.

В буквенном выражении между множеным и множителем принято не ставить знак умножения:

Правила, свойства и законы умножения

Есть 3 основных закона умножения: переместительный, сочетательный и распределительный.

Иногда их называют свойствами, например распределительное свойство умножения.

Переместительный закон умножения

От перестановки множимого и множителя произведение не меняется.

То есть, если мы переставим местами множители, то результат умножения останется без изменений. 5×6 = 6×5

В буквенном выражении переместительный закон умножения можно записать следующим образом (a, b, c – сомножители):

 

Сочетательный закон умножения

Произведение не изменится, если любую группу рядом множителей заменить их произведением.

То есть при умножении нескольких чисел можно объединять или соединять (от этого название закона) их в группы.

Распределительный закон умножения

Чтобы умножить сумму на число, можно умножить на это число каждое слагаемое и образовавшиеся произведения добавить

(5 + 2 +3) × 7 = 5 × 7 + 2 × 7 + 3 × 7 = 35 + 14 +21 = 70

Распределительный закон также можно использовать при вычитании:

(9 – 6) × 5 = 9 × 5 – 6 × 5 = 45 – 30 = 15

Умножение произведения на число и числа на произведение

Чтобы умножить произведение нескольких чисел на определенное число, достаточно один из множителей произведения умножить на это число, оставив другие сомножители без изменения. Умножая число на произведение, достаточно умножить данное число на один из множителей произведения.

Например, 25 × (13 × 4) = (25 × 4) × 13 = 100 × 13 = 1300

Правило действует и для большего количества множителей: 20 × (9 × 5 × 12) = (20 × 5) × 9 × 12 = 100 × 9 × 12 = 10800

Умножение на 0: правило

Свойство умножения на нуль: При умножении любого числа на 0 произведение будет равно 0. То есть, если множимое или множитель равны нулю, то произведение также будет равно нулю.

0 × 0 = 0

5 × 0 = 0

0 × 86 = 0

0 × b = 0 при любом значении переменной b

Умножение на 1

1 × b = b при любом значении переменной b

Правило: при умножении на единицу получим второй сомножитель, который не равен 1. Если множимое равно единице, то произведение равно множителю. Если множитель равен единице, то произведение будет равно множимому.

1 × 1 = 1

1 × 47 = 47

256 × 1 = 256

Умножение на 10, на 100 и т.

д.

При умножении натурального числа на 10, 100, 1000 и т.д., необходимо приписать к этому числу справа столько нулей, сколько их есть в числе, на которое умножаем.

49 × 10 = 490

325 × 1000 = 325000

Умножение многоцифровых чисел

Умножим трехзначное число на однозначное 354 × 3

Мы можем разложить 354 на следующие слагаемые: 300 + 50 + 4 и умножить каждый разряд на 3 (согласно распределительному закону умножения): (300 + 50 + 4) × 3 = 300 × 3 + 50 × 3 + 4 × 3 = 900 + 150 +12 = 1062

Второй способ – выполнение умножения, начиная с низших разрядов. 354×3 – начинаем с умножения единиц: 4×3 = 12, записываем 2, а 1 десяток запоминаем, чтобы добавить его к произведению десятков. 5 десятков умножаем на 3, получим 15 десятков + 1 десяток = 16 десятков, записываем 6, а десять десятков или 1 сотню запоминаем, чтобы добавить в разряд сотен. В разряде сотен умножаем 3 сотни на 3, получим 9 сотен и добавляем еще 1 сотню = 10 сотен. Результат умножения: 1062

Умножение в столбик: умножение трехзначного числа на трехзначное

Пример 1.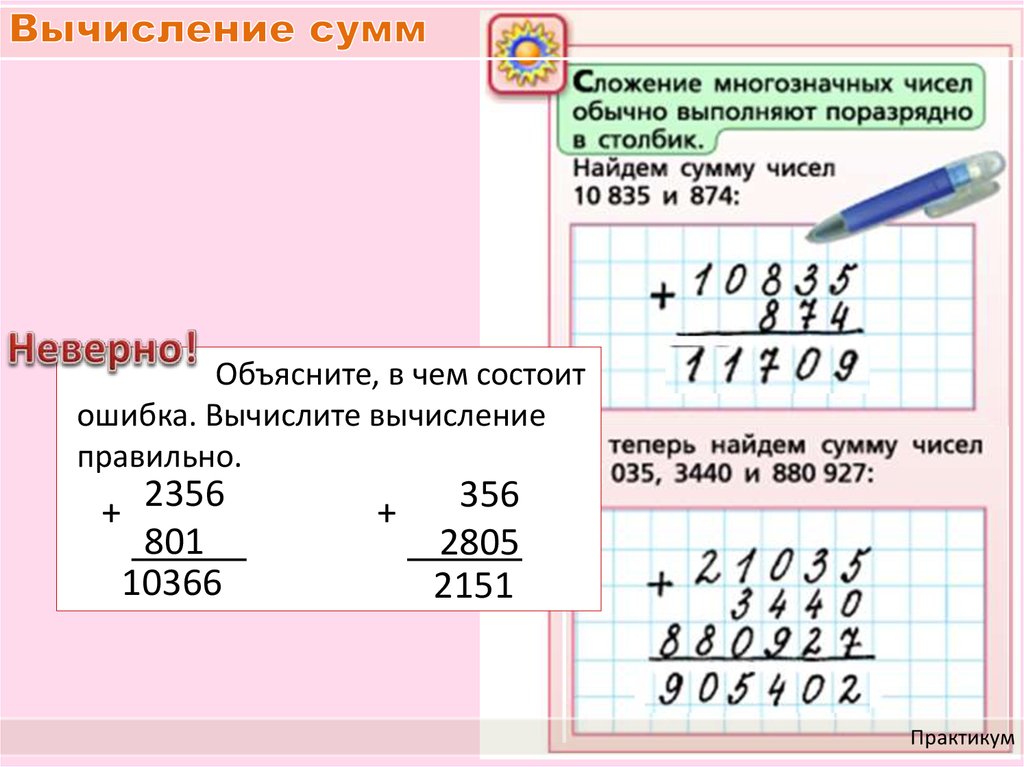 Необходимо умножить 423 × 334

Выполняя умножение в столбик, сначала умножаем множимое на единицы множителя: 423×4 = 1692, данное число называется первым промежуточным произведением. Далее нам необходимо умножить множимое на десятки множителя: 423×3 = 1269 (второе промежуточное произведение). Умножим множимое на разряд сотен: 423×3 = 1269 (третье промежуточное произведение).

При записи умножения в столбик первое промежуточное произведение записываем под разрядом единиц, второй – под разрядом десятков, третий – под разрядом сотен. После этого добавляем промежуточные произведения поразрядно, начиная с разряда единиц.

Калькулятор умножения в столбик

Пример 2. Необходимо умножить 126 × 209.

Сначала начинаем умножение с разряда единиц: умножаем 126 на 9, получим 1134; записываем, начиная с разряда единиц. В этом примере используем правило умножения на 0 и запишем промежуточное произведение в виде трех нулей, справа налево, начиная с разряда десятков. Умножив 126 на 2, получим 252 и запишем, начиная с сотен.

Подытожим основные правила умножения в столбик:

При умножении в столбик сначала находим первое промежуточное произведение – для этого умножаем множимое на разряд единиц множителя. Промежуточное произведение следует начинать подписывать под той разрядной единицей, на которую выполняется умножение. То есть, если мы умножаем разряд единиц (9 из предыдущего примера), то промежуточное произведение записываем так, чтобы последняя цифра промежуточного произведения была под разрядом единиц. Далее умножаем множимое на разряд десяток множителя. Последняя цифра второго промежуточного произведения должна быть под разрядом десятков (в нашем примере под 0). Третий шаг – умножаемое множимое на разряд сотен множителя и записываем промежуточное произведение. После этого добавляем промежуточные произведения по правилу добавления в столбик.

Умножение в столбик на натуральные числа, оканчивающиеся нулями

Для упрощения действия следует выполнить умножение в столбик без учета нулей, а до произведения чисел справа нужно дописать столько нулей, сколько их есть во всех множителях вместе.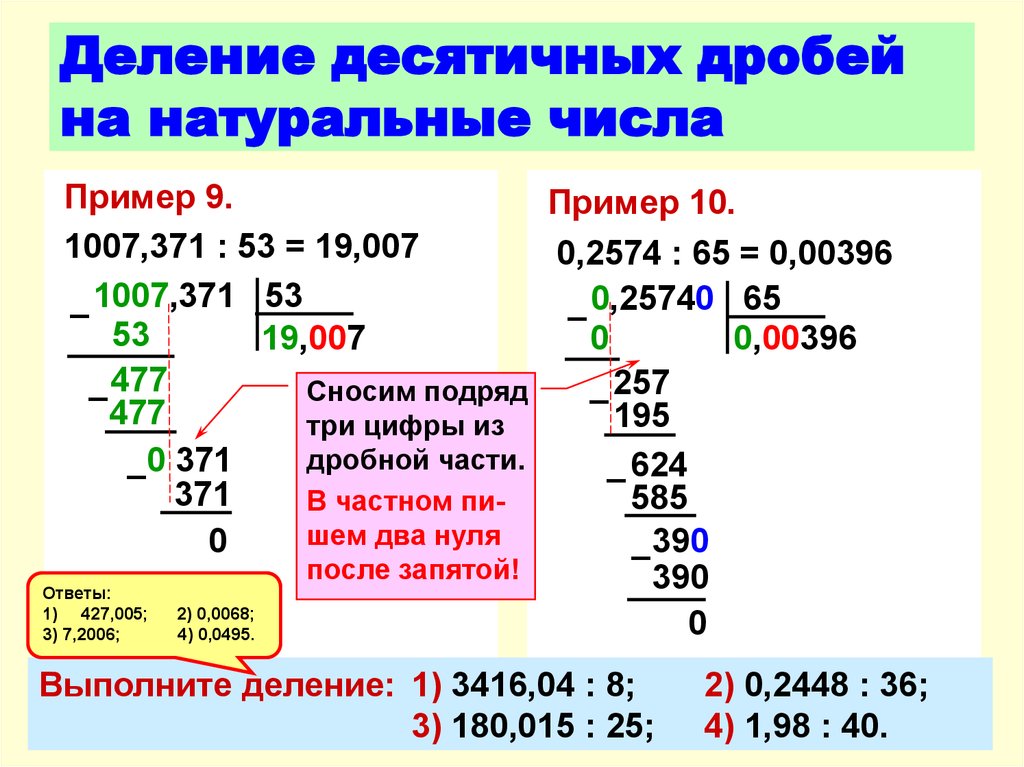

Например, 5600 × 230

При умножении в столбик мы записали 56×23, в результате получили 1288 и дописываем справа три нуля, результат умножения – 1288000

Проверка умножения

Чтобы проверить правильность умножения нужно:

• Переставить местами множители и выполнить действие умножения. Если результат будет одинаковым, то действие выполнено правильно.
• Разделить произведение на один из множителей. Если в результате получим второй множитель, то действие исполнено правильно. О делении натуральных чисел читайте в следующем уроке

Как быстро умножать большие числа?

Существует несколько способов быстрого умножения, рассмотрим их с помощью примеров.

Умножение на число, близкое к единице определенного разряда (до 10, 100, 1000 и т.д.).

206 × 98 = 206 × (100 – 2) = 206 × 100 – 206 × 2 = 20600 – 412 = 20188

9103 × 1004 = 9103 × (1000 + 4) = 9103000 + 36412 = 9139412

В данном типе примеров мы расписываем приближенное число к единице определенного разряда как сумму или разность чисел (98 = 100 – 2; 1004 = 1000 + 4), а также используем распределительный закон умножения.

Умножение на 9, 99, 999 и т.д.

Правило: Чтобы умножить на число, записанное девятками (9 или 99, или 999 и т.д.), нужно к множимому приписать справа столько нулей, сколько девяток в множителе, и от результата вычесть множимое.

685 × 9 = 6850 – 685 = 6165

32 × 99 = 3200 – 32 = 3168

27 × 999 = 27000 – 27 = 26973

Умножение двузначного числа на 11

При умножении двузначного числа на 11 следует учесть, сумма цифр данного числа меньше 10, больше или равна десяти.

Чтобы умножить двузначное число, сумма цифр которого меньше 10, на 11, нужно между цифрами числа написать сумму его цифр.

63 × 11 = 693

25 × 11 = 275

Чтобы умножить на 11 двозначное число, сумма цифр которого больше или равна 10, нужно между цифрой десятков, увеличенной на 1, и цифрой единиц написать избыток суммы цифр числа сверх 10.

76 × 11 = 836

7+6=13 > 10 , поэтому результат будет: цифру десятков увеличиваем на 1, записываем 7+1 = 8, между цифрами 7 и 6 прописываем 3 (7+6-10=3), цифру единиц – 6 записываем без изменений. В результате получим произведение 836

Умножение чисел до 20

Если для умножения чисел до 10 можно использовать таблицу умножения, то для выполнения расчетов с двузначными числами в пределах 20 следует воспользоваться алгоритмом, описанным ниже.

Умножим 14 на 17

• К одному из чисел добавляем количество единиц второго: 14 + 7 = 21
• Полученное число умножаем на 10: 21×10 = 210
• Добавляем произведение единиц двух чисел: 210 + 4×7 = 238

14 × 17 = (14 + 7) × 10 + 4 × 7 = 238

Правильность этого метода можно доказать и проверить: 14 × 17 =

(10 + 4 ) × (10 + 7) = 10 × 10 + 10 × 4 + 10 ×7 + 4 × 7 = 10 × (10 + 4 + 7) + 4 × 7 = 238

В этом случае число 10 считается опорным числом.

Знак умножения на клавиатуре

Чаще всего знак умножения отображают крестиком «×» или точкой «·», реже используют звездочку «*».

На клавиатуре можно набрать знак звездочки* сочетанием клавиш Shift+8

Если вам нужен знак ×, можно использовать символ Unicode (Вставка/Символы), код: 00D7. Код 00B7 — отображает знак «·»

NumberNut.com: Арифметика: Умножение: Двузначные числа

Числа и подсчет| Арифметика |Дроби и десятичные дроби|Предварительная алгебра|Карта сайта

Мы немного схитрили, введя какое-то двух- и трехзначное умножение в нашу переносную секцию. Однако мы работали с простыми цифрами. Правила просты, если вы умножаете двузначное число на однозначное. Умножьте единицы на , а затем умножьте на десятки.

Пример:
32 x 3 = ?
Умножить единицы: 3 x 2 = 6
Умножить десятки: 3 x 3 = 9
32 x 3 = 96

В этом примере не было переноски/перегруппировки. Если у вас есть перенос, вам нужно будет выполнить схему «Умножить — Перенести — Умножить — Добавить».

Пример:
96 x 8 = ?
УМНОЖИТЬ ЕДИНИЦЫ: 6 x 8 = 48
НАПИСАТЬ И НОСИТЬ: Напишите «8» и отнесите «4»
УМНОЖИТЕ ДЕСЯТКИ: 8 x 9 = 72
ДОБАВИТЬ: Добавьте переносимую сумму. 72 + 4 = 76
ЗАПИСАТЬ: Запишите «76»
Ответ: 96 x 8 = 768

Итак, что произойдет, если у вас есть два двузначных числа для ваших делителей ? Хотя это займет немного больше времени, решить проблему несложно. Вам просто нужно решить две задачи на умножение, а затем сложить ответы. Что? Как это могло быть так просто? Давай посмотрим.

Пример:
96 x 28 = ?
Часть 1: Умножьте 8 x 96.
Ответ: Из приведенного выше примера мы знаем, что ответ равен 768.

Часть 2: Умножьте 2 x 96.
(1) 6 x 2 = 12
(2) Напишите «2» и перенесите «1»
(3) 2 x 9 = 18
(4) Доп. 18 + 1 = 19
(5) Напишите «19»
Ответ: 96 х 2 = 192

Часть 3: Добавьте два ответа.
Как вы думаете, теперь можно просто сложить два значения? Нет! Есть одна хитрость. Когда вы умножаете вторую часть, добавьте к этому ответу «0», потому что вы умножаете значение из столбца десятков (2). Если это из десятков, добавьте ноль. Если это из сотен, вы должны добавить два нуля.

768 + 1920 = 2688 (видите, как мы добавили «0» к значению «192»?)

Запишем в вертикальном (вверх-вниз) формате. Вам будет проще увидеть настройку.

96 x 28 768 + 192 0 2668

Может быть трудно понять, когда эта идея выражена словами, но сама концепция проста. Если ваш второй множитель (или нижний) состоит из двух цифр, вы решаете две задачи на умножение. В следующем разделе вы быстро увидите, что если ваш второй множитель состоит из трех цифр, вы решите три задачи на умножение.

Вторая идея, которую следует знать, заключается в том, что перед добавлением ответов необходимо добавить несколько нулей. При умножении первого значения не добавляйте нули. Когда вы умножаете значение десятков, добавляйте один ноль в конце ответа.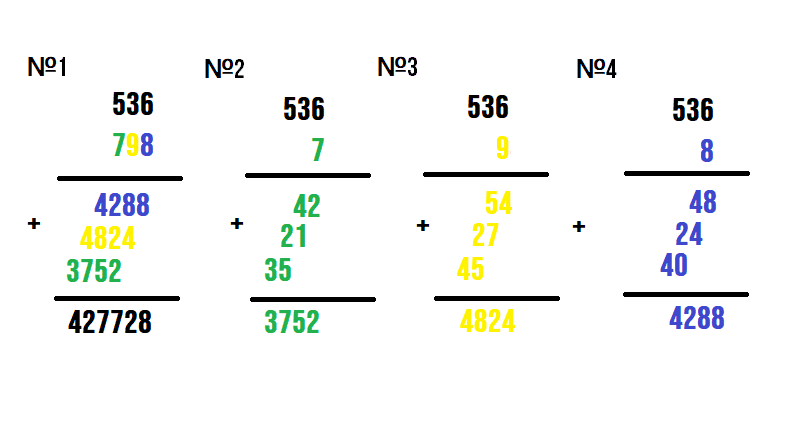 Добавьте два нуля, если есть значение сотен, и три нуля для значения из разряда тысяч. Вы видите шаблон с нулями? Посмотрите, как быстро числа могут стать действительно большими, когда вы их умножаете?

Пример:

352 x 231 352 1056 0 + 704 00 81 312

Извините за использование таких больших чисел. Нам нужно показать вам образец. Все умножение было очень простым. Самая сложная задача на умножение, которую мы решали, была 5×3. Когда у вас большие проблемы, просто наберитесь терпения и выполните все шаги.

► СЛЕДУЮЩАЯ СТРАНИЦА ПО АРИФМЕТИКЕ
► ВЕРНУТЬСЯ НА НАЧАЛО СТРАНИЦЫ

► Или выполните поиск на сайтах…

---

• Обзор
• Операции
• Дополнение
• Вычитание
• Умножение
• от 1 до 10
• Переноска
• Двухзначные номера
• Трехзначные номера
• Несколько значений
• Целые числа
• Отдел
• Мероприятия

---

---

Википедия:
https://en. wikipedia.org/wiki/arithmetic
Encyclopædia Britannica:
9988 HTTP./W com:
http://www.encyclopedia.com/topic/arithmetic.aspx

Как умножать столбцы в Excel

Microsoft Excel в первую очередь предназначен для работы с числами, поэтому он предоставляет несколько различных способов выполнять основные математические операции, а также более сложные вычисления. В нашем последнем уроке мы обсуждали, как умножать ячейки в Excel. В этом уроке мы сделаем еще один шаг и посмотрим, как можно быстро умножать целые столбцы.

• Как умножить два столбца в Excel
  • Умножение одного столбца на другой с помощью символа умножения
  • Умножение двух столбцов с помощью функции ПРОИЗВЕД
  • Умножение целых столбцов на формулу массива
• Как умножить столбец на число в Excel
  • Умножение столбца на число по формуле
  • Умножение столбца на одно и то же число с помощью специальной вставки
  • Умножение столбца на число с помощью Ultimate Suite для Excel

Как умножить два столбца в Excel

Как и в случае со всеми основными математическими операциями, в Excel существует несколько способов умножения столбцов. Ниже мы покажем вам три возможных решения, чтобы вы могли выбрать то, которое лучше всего подходит для вас.

Как умножить один столбец на другой с помощью оператора умножения

Самый простой способ умножить 2 столбца в Excel — составить простую формулу с символом умножения (*). Вот как:

1. Умножить две ячейки в первой строке.

   Предположим, ваши данные начинаются со строки 2, где столбцы B и C должны быть умножены. Формула умножения, которую вы поместили в D2, проста: = B2 * C2 .

2. Дважды щелкните маленький зеленый квадратик в нижнем правом углу D2, чтобы скопировать формулу вниз по столбцу до последней ячейки с данными. Сделанный!
   

Поскольку в формуле используются относительные ссылки на ячейки (без знака $), ссылки будут меняться в зависимости от относительного положения строки, в которую копируется формула. Например, формула в D3 меняется на =B3*C3 , формула в D3 становится =B4*C4 и так далее.

Как умножить два столбца с помощью функции ПРОИЗВЕД

Если вы предпочитаете работать с функциями Excel, а не с выражениями, вы можете умножить 2 столбца с помощью функции ПРОИЗВЕД, которая специально разработана для выполнения умножения в Excel.

Для нашего примера набора данных формула выглядит следующим образом:

=ПРОИЗВ(B2:C2)

Как и в случае с символом умножения, ключевым моментом является использование относительных ссылок на ячейки, так что формула может быть правильно настроена для каждый ряд.

Вы вводите формулу в первую ячейку, а затем копируете ее вниз по столбцу, как описано в приведенном выше примере:

Как умножить два столбца с помощью формулы массива

Еще один способ умножить целые столбцы в Excel: используя формулу массива. Пожалуйста, не расстраивайтесь и не пугайтесь слов «формула массива». Этот очень прост и удобен в использовании. Вы просто записываете диапазоны, которые хотите умножить, разделяя их знаком умножения, например:

=B2:B5*C2:C5

Чтобы вставить эту формулу умножения в свои рабочие листы, выполните следующие действия:

1. Выберите весь диапазон, где вы хотите ввести формулу (D2:D5).
2. Введите формулу в строку формул и нажмите Ctrl + Shift + Enter. Как только вы это сделаете, Excel заключит формулу в {фигурные скобки}, что указывает на формулу массива. Ни в коем случае нельзя набирать фигурные скобки вручную, это не сработает.

В результате Excel будет умножать значение в столбце B на значение в столбце C в каждой строке без необходимости копировать формулу вниз.

Этот подход может быть полезен, если вы хотите предотвратить случайное удаление или изменение формулы в отдельных ячейках. При такой попытке Excel выдаст предупреждение о том, что нельзя изменить часть массива.

Как умножить несколько столбцов в Excel

Чтобы умножить более двух столбцов в Excel, вы можете использовать формулы умножения, подобные рассмотренным выше, но включающие несколько ячеек или диапазонов.

Например, чтобы умножить значения в столбцах B, C и D, используйте одну из следующих формул:

• Оператор умножения: =A2*B2*C2
• Функция ПРОИЗВЕД: =ПРОИЗВЕД(A2:C2)
• Формула массива (Ctrl + Shift + Enter): =A2:A5*B2:B5*C2:C5

Как показано на скриншоте ниже, формулы умножают на числа и на проценты одинаково хорошо.

Как умножить столбец на число в Excel

В ситуациях, когда вы хотите умножить все значения в столбце на одно и то же число, выполните одно из следующих действий.

Умножение столбца на число с помощью формулы

Как оказалось, самый быстрый способ выполнить умножение в Excel — использовать символ умножения (*), и эта задача не является исключением. Вот что вы делаете:

1. Введите число для умножения в какой-нибудь ячейке, скажем, в ячейке B1.

   В этом примере мы собираемся умножить столбец чисел на проценты. Поскольку во внутренней системе Excel проценты хранятся в виде десятичных чисел, мы можем вставить либо 11%, либо 0,11 в ячейку B1.

2. Напишите формулу для самой верхней ячейки столбца, зафиксировав ссылку на постоянное число знаком $ (например, $B$1).

   В нашем образце таблицы числа, которые нужно умножить, находятся в столбце B, начиная с строки 4, поэтому формула выглядит следующим образом:

   =B4*$B$1

3. Введите формулу умножения в самую верхнюю ячейку (C4).
4. Дважды щелкните маленький зеленый квадратик в правом нижнем углу ячейки формулы, чтобы скопировать формулу вниз по столбцу до тех пор, пока в левой части есть какие-либо данные. Вот и все!
   

Как работает эта формула

Вы используете абсолютную ссылку на ячейку (например, $B$1), чтобы зафиксировать координаты столбца и строки ячейки с числом, на которое нужно умножить, чтобы эта ссылка не изменилась при копировании формулы в другие клетки.

Вы используете относительную ссылку на ячейку (например, B4) для самой верхней ячейки в столбце, чтобы эта ссылка менялась в зависимости от относительного положения ячейки, в которую копируется формула.

В результате формула в C5 меняется на =B5*$B$1 , формула в ячейке C6 изменится на =B6*$B$1 и так далее.

Наконечник. Если вы умножаете столбец на постоянное число, которое вряд ли изменится в будущем, вы можете указать это число непосредственно в формуле, например: =B4*11% или =B4*0,11 .

Умножение столбца чисел на одно и то же число с помощью специальной вставки

Если вы хотите получить результат в виде значений, а не формул, выполните умножение с помощью Специальная вставка > Умножение элемента .

1. Скопируйте числа, которые вы хотите умножить, в столбец, где вы хотите вывести результаты. В этом примере мы копируем значения продаж (B4:B7) в столбец НДС (C4:C7), потому что мы не хотим переопределять исходные данные о продажах.
2. Введите постоянное число для умножения в какую-нибудь пустую ячейку, скажем, B1. На данный момент ваши данные будут выглядеть примерно так:
   
3. Выберите ячейку с постоянным номером (B1) и нажмите Ctrl + C, чтобы скопировать ее в буфер обмена.
4. Выберите ячейки, которые вы хотите умножить (C4:C7).
5. Нажмите Ctrl + Alt + V, затем M, что является ярлыком для Специальная вставка > Умножение , а затем нажмите Enter.

   Или щелкните правой кнопкой мыши выделение, выберите Специальная вставка. .. в контекстном меню, выберите Умножение в разделе Операции и нажмите OK.
   

В любом случае Excel будет умножать каждое число в диапазоне C4:C7 на значение в ячейке B1 и возвращать результаты в виде значений, а не формул:

Примечание. В некоторых ситуациях вам может потребоваться переформатировать результаты специальной вставки. В приведенном выше примере мы умножили столбец чисел на проценты, и Excel отформатировал результаты как проценты, а они должны быть числами. Чтобы это исправить, выделите получившиеся ячейки и примените к ним нужный числовой формат, в данном случае Валюта .

Умножение столбца на число с помощью Ultimate Suite for Excel

Подобно специальной вставке, этот метод умножения возвращает значения, а не формулы. В отличие от специальной вставки, Ultimate Suite for Excel удобен и интуитивно понятен. Вот как можно за пару кликов умножить столбец чисел на другое число:

1. Выберите все ячейки, которые вы хотите умножить. Если вы хотите сохранить исходные значения, скопируйте их в другой столбец, где вы хотите получить результаты, и выберите эти ячейки.
2. На ленте Excel перейдите на вкладку Инструменты Ablebits > группу Вычислить .
3. Выберите знак умножения (*) в поле Операция , введите число для умножения в поле Значение и нажмите кнопку Вычислить .

В качестве примера рассчитаем бонус в размере 5% от наших продаж. Для этого мы копируем значения продаж из столбца B в столбец C, а затем либо:

• Выберите знак умножения (*) в поле Operation и введите 0,05 в поле Value (0,05 представляет 5% потому что 5 процентов — это пять частей от ста).
• Выберите знак процента (%) в поле Операция и введите 5 в поле Значение .

Оба метода умножают правильно и дают одинаковые результаты:

В отличие от специальной функции вставки Excel, Ultimate Suite сохраняет исходный формат валюты, поэтому дальнейшая корректировка результатов не требуется.