Какое действие делается первым умножение или сложение: Какое из действий (умножение, деление, сложение или вычитание) нужно выполнить первым, определяя значение выражения (31⋅1−0):31+81…

Двоичная арифметика : сложение, вычитание, умножение, деление

 

Выполнение арифметических действий в любых позиционных системах счисления производится по тем же правилам, которые используются в десятичной системе счисления.

Так же, как и в десятичной системе счисления, для выполнения арифметических действий необходимо знать таблицы сложения (вычитания) и умножения.

Таблица сложения, вычитания и умножения для двоичной системы счисления

Сложение	Вычитание	Умножение
0 + 0 = 0	0 — 0 = 0	0 ∙ 0 = 0
0 + 1= 1	1 — 0 = 1	0 ∙ 1 = 0
1 + 0 = 1	1 — 1 = 0	1 ∙ 0 = 0
1 + 1 = 10	10 — 1 = 1	1 ∙ 1 = 1

Сложение двоичных чисел

Сложение в двоичной системе счисления выполняется по тем же правилам, что и в десятичной. Два числа записываются в столбик с выравниванием по разделителю целой и дробной части и при необходимости дополняются справа незначащими нулями. Сложение начинается с крайнего правого разряда. Две единицы младшего разряда объединяются в единицу старшего.

Пример: 1011,1₂ + 1010,11₂

Интересна также ситуация, когда складываются больше двух чисел. В этом случае возможен перенос через несколько разрядов.
Пример: 111,1₂ + 111₂ + 101,1₂

При сложении в разряде единиц (разряд 0) оказывается 4 единицы, которые, объединившись, дают 100₂. Поэтому из нулевого разряда в первый разряд переносится 0, а во второй — 1.
Аналогичная ситуация возникает во втором разряде, где с учетом двух перенесенных единиц получается число 5 = 101₂. 1 остается во втором разряде, 0 переносится в третий и 1 переносится в четвёртый.

Вычитание двоичных чисел

В случаях, когда занимается единица старшего разряда, она дает две единицы младшего разряда. Если занимается единица через несколько разрядов, то она дает по одной единице во всех промежуточных нулевых разрядах и две единицы в том разряде, для которого занималась.
Пример: 10110,01₂ — 1001,1₂

Умножение и деление двоичных чисел

Зная операции двоичной арифметики, можно переводить числа из двоичной системы счисления в любую другую.
Пример: Перевести число 101111011₂ в десятичную систему счисления.
Поскольку 10₁₀ = 1010₂, запишем

Полученные остатки,  1001₂ = 9₁₀,  =111₂ = 7₁₀,  11₂ = 3₁₀. Искомое число 101111011₂ = 379₁₀.

Назад: Представление данных и архитектура ЭВМ

4.2 — Арифметические вычисления с использованием арифметических операторов

Все, что мы сделали до сих пор, — это сложили вместе переменные. Конечно, мы могли бы также вычитать, умножать, делить или возводить в степень переменные. Нам просто нужно убедиться, что мы используем символы, которые распознает SAS. Это:

Эксплуатация	Символ	Заявление о присвоении	Действия предприняты
дополнение	+	a = b + c ;	добавить b и c
вычитание	—	a = b — c ;	вычесть c из b
умножение	*	a = b * c ;	умножить на б и в
отделение	/	a = b / c ;	разделить b на c
возведение в степень	**	а = б ** в ;	возвести b в степень c
отрицательный префикс	—	= — ;	взять минус b

Как и в других языках программирования, в операторе присваивания можно выполнять более одной операции. Операции выполняются так же, как и для любого математического выражения, а именно:

• сначала выполняется возведение в степень, затем умножение и деление и, наконец, сложение и вычитание
• если в одном и том же выражении встречаются несколько экземпляров сложения, несколько экземпляров вычитания или сложения и вычитания, операции выполняются слева направо
• , если несколько экземпляров умножения, несколько экземпляров деления или умножение и деление встречаются вместе в одном выражении, операции выполняются слева направо
• если в одном выражении встречается несколько экземпляров возведения в степень, операции выполняются справа налево
Сначала выполняется
• операций в скобках

Это последняя пуля, которую, я думаю, будет полезно знать. Если вы используете круглые скобки, чтобы специально указать SAS, что вы хотите вычислить в первую очередь, вам не нужно так сильно беспокоиться о других правилах. Давайте рассмотрим два примера.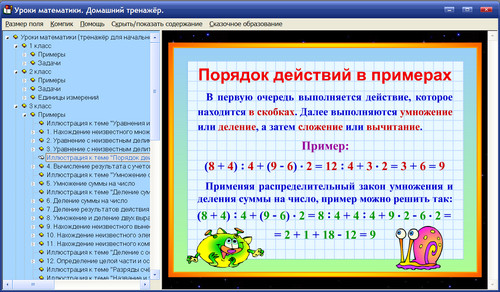

Следующий пример содержит вычисление, иллюстрирующее стандартный порядок операций. Предположим, преподаватель статистики вычисляет итоговую оценку, взвешивая средний балл за экзамен на 0,6, балл за проект на 0,2 и итоговый экзамен на 0,2. Следующая программа SAS иллюстрирует, как преподаватель (неправильно) вычисляет итоговых оценок учащихся:

 оценки DATA;
входное имя $ 1-15 e1 e2 e3 e4 p1 f1;
финал = 0,6*e1+e2+e3+e4/4 + 0,2*p1 + 0,2*f1;
ДАННЫЕ;
Александр Смит 78 82 86 6997 80
Джон Саймон 88 72 86 . 100 85
Патрисия Джонс 98 92 92 99 99 93
Джек Бенедикт 54 63 71 49 82 69
Рене Портер 100 62 88 74 98 92
;
БЕГ;
PROC PRINT данные = оценки;
имя переменной e1 e2 e3 e4 p1 f1 final;
БЕГ; 

Ну да ладно, так что инструктор должен придерживаться статистики, а не математики. Как видно из заявления о задании, преподаватель пытается указать SAS усреднить четыре экзаменационных балла, сложив их и разделив на 4, а затем умножив результат на 0,6. Давайте посмотрим, что вместо этого делает SAS. Запустить и запустить   программу SAS и просмотрите результат, чтобы узнать, сможете ли вы выяснить, что сделала SAS, скажем, для первого студента Александра Смита. Если вы все еще не уверены, еще раз просмотрите правила порядка операций. Правила говорят нам, что SAS first:

• берет первую экзаменационную оценку Александра 78 и умножает ее на 0,6, чтобы получить 46,8
• берет четвертый экзаменационный балл Александра 69 и делит его на 4, чтобы получить 17,25
• берет оценку проекта Александра 97 и умножает ее на 0,2, чтобы получить 19.4
• берет итоговый экзаменационный балл Александра 80 и умножает его на 0,2, чтобы получить 16,0

Затем SAS выполняет все сложения:

 46,8 + 82 + 86 + 17,25 + 19,4 + 16,0 

, чтобы получить окончательный результат 267,45. Теперь, может быть, это окончательная оценка, которую хочет Александр, но она все равно в корне неверна. Давайте посмотрим, сможем ли мы помочь инструктору по статистике, воспользовавшись последним правилом, согласно которому операции в скобках выполняются в первую очередь.

Следующий пример содержит вычисление, иллюстрирующее стандартный порядок операций. Предположим, преподаватель статистики вычисляет итоговую оценку, взвешивая средний балл за экзамен на 0,6, балл за проект на 0,2 и итоговый экзамен на 0,2. Следующая программа SAS иллюстрирует, как преподаватель (правильно) вычисляет итоговых оценок учащихся:

 оценок DATA;
входное имя $ 1-15 e1 e2 e3 e4 p1 f1;
финал = 0,6*((e1+e2+e3+e4)/4) + 0,2*p1 + 0,2*f1;
ДАННЫЕ;
Александр Смит 78 82 86 6997 80
Джон Саймон 88 72 86 . 100 85
Патрисия Джонс 98 92 92 99 99 93
Джек Бенедикт 54 63 71 49 82 69
Рене Портер 100 62 88 74 98 92
;
БЕГ;
PROC PRINT данные = оценки;
имя переменной e1 e2 e3 e4 p1 f1 final;
БЕГ; 

Давайте еще раз разберем расчет окончательного результата Александра. Оператор присваивания для final сообщает SAS:

• сначала сложить четыре экзаменационных балла Александра (78, 82, 86, 69), чтобы получить 315
• , а затем разделите эти 315 на 4, чтобы получить средний балл за экзамен 78,75
• , а затем умножьте средний экзаменационный балл 78,75 на 0,6, чтобы получить 47,25
• , а затем возьмите оценку проекта Александра 97 и умножьте ее на 0,2, чтобы получить 19,4
• , а затем возьмите итоговый экзаменационный балл Александра 80 и умножьте его на 0,2, чтобы получить 16,0

Затем SAS выполняет сложение последних трех элементов:

 47,25 + 19,4 + 16,0 

, чтобы получить окончательный результат 82,65. Там это звучит гораздо лучше. Извините, Александр.

Запустить и запустить   программу SAS, чтобы узнать, как мы это сделали. Просмотрите результаты процедуры печати, чтобы убедиться, что окончательные оценки были рассчитаны в соответствии с пожеланиями преподавателя.

Кстати, обратите внимание еще раз, что SAS присваивает отсутствующее значение окончательной оценке для Джона Саймона.

В этом последнем примере мы подсчитали средние баллы студентов за экзамен, сложив их четыре экзаменационные оценки и разделив на 4. Вместо этого мы могли бы воспользоваться одной из многих числовых функций, доступных в SAS, а именно функцией СРЕДНЯЯ функция.

Ключевые слова для математических операций

Первым шагом в решении текстовой задачи всегда является чтение задачи. Вы должны уметь переводить слов в математические символы, сосредоточив внимание на ключевых словах, которые указывают на математические процедуры, необходимые для решения задачи, — как на операцию, так и на порядок выражения. Точно так же, как вы можете перевести испанский язык на английский, вы можете перевести английские слова в символы, язык математики. Многие (если не все) ключевые слова, обозначающие математические операции, являются знакомыми словами.

Для начала вы переводите английские фразы в алгебраических выражений. Алгебраическое выражение представляет собой набор чисел, переменных, операций и символов группировки. Вы переведете неизвестное число как переменную x или n . Символы группировки обычно представляют собой набор круглых скобок, но они также могут быть наборами скобок или фигурных скобок.

При переводе выражений необходимо хорошо знать основные ключевые слова, которые преобразуются в математические операции: ключевые слова сложения, ключевые слова вычитания, ключевые слова умножения и ключевые слова деления, которые рассматриваются в следующих четырех разделах.

Добавление ключевых слов

Вот некоторые распространенные примеры дополнительных ключевых слов:

• СУММА _____ И _____

• ВСЕГО _____ И _____

• _____ ПЛЮС _____

• _____ УВЕЛИЧИЛСЯ НА _____

• УСИЛЕНИЕ

• ПОДЪЕМ

• ДОПОЛНИТЕЛЬНО

• УВЕЛИЧЕНИЕ НА

Первые два ключевых слова (СУММА и ИТОГО) называются ведущие ключевые слова потому что они ведут выражение. Вторые два ключевых слова (ПЛЮС и УВЕЛИЧЕНИЕ НА) — это ключевые слова, которые указывают точное размещение знака плюс. Последние четыре ключевых слова встречаются в текстовых задачах и могут указывать на сложение.

Если выражение начинается с ведущих ключевых слов СУММА или ИТОГО, ведущее ключевое слово определяет соответствующее И. Затем знак плюс физически заменяет И в выражении.

Пример 1: Переведите следующее: сумма пяти и числа

Следующие шаги помогут вам перевести эту проблему:

1. Подчеркните слова до и после И, когда они соответствуют ведущему ключевому слову СУММА ИЗ.

• сумма пяти и числа

2. Обведите ведущее ключевое слово и укажите соответствующее И, которое оно определяет.

3. Переведите каждое подчеркнутое выражение и замените AND знаком плюс.

• Выражение переводится как 5 + x .

Пример 2: Переведите следующее: сумма числа и минус три

Используйте следующие шаги для перевода этой проблемы:

1. Ключевое слово ВСЕГО ИЗ является ведущим ключевым словом, определяющим И, поэтому подчеркните слова до и после И: «число» и «минус три».

• сумма числа и отрицательной тройки

2. Обведите ведущее ключевое слово и укажите соответствующее И, которое оно определяет.

3. Переведите каждое подчеркнутое выражение и замените AND знаком плюс.

• Выражение переводится как x + −3.

Пример 3: Переведите следующее: сумма семи и отрицательных четырех

Переведите этот пример следующим образом:

1. Слово СУММА является ведущим ключевым словом, определяющим И, поэтому подчеркните слова до и после И: «семь» и «минус четыре».

• сумма семи и минус четыре

2. Обведите ведущее ключевое слово и укажите соответствующее И, которое оно определяет.

3. Переведите каждое подчеркнутое выражение и замените AND знаком плюс.

• Выражение переводится как 7 + −4.

Напоминание: Ключевое слово AND переводится как «плюс», потому что ведущее ключевое слово SUM OF. С другими ведущими ключевыми словами (обсуждаемыми в следующих разделах) И может означать другие вещи. Также обратите внимание, что вы не упрощаете выражение и получаете «3» за ответ, потому что вы просто переводите слова в символы, а не выполняете математические операции.

Два других ключевых слова в списке дополнительных ключевых слов, PLUS и INCREASED BY, могут быть правильно переведены с помощью стратегии прямого перевода . В стратегии прямого перевода вы переводите каждое слово в соответствующий ему алгебраический символ, по одному, в том же порядке, как написано, как показано в примере 4.

Пример 4: Переведите следующее: число, увеличенное на двадцать четыре

• Выражение переводится как x + 24,

Некоторые дополнительные ключевые слова, такие как ПРИБЫЛЬ, БОЛЬШЕ, УВЕЛИЧЕНИЕ и ПОВЫШЕНИЕ, обычно встречаются в задачах-рассказах, как в примере 5.

Пример 5: Переведите следующую сюжетную задачу в математическое выражение о весе полузащитника: Защитный полузащитник весил двести двадцать два фунта в начале весенней тренировки. Он набрал семнадцать фунтов после четырех недель тренировок с командой.

• Выражение переводится как 222 + 17.

Примечание: Не все числа, упомянутые в словесной задаче, должны быть включены в математическое выражение. Число «четыре» — это просто интересный факт, а не информация, необходимая для написания выражения о весе полузащитника.

Вам также может быть интересно, почему ответ не 239 фунтов. Это потому, что вопрос просит вас перевести проблему истории в математическое выражение, а не оценивать выражение.

Пример 6: Переведите следующую текстовую задачу в математическое выражение о текущей почасовой оплате кассира: Кассир в бакалейной лавке зарабатывал 6,25 доллара в час. Он получил прибавку в размере 25 центов в час.

• Выражение переводится как 6,25 + 0,25.

Примечание: Почасовая оплата указана в долларах, а надбавка — в центах. Каждый раз, когда вы добавляете два числа, которые имеют единиц , убедитесь, что оба числа измеряются в одних и тех же единицах; если это не так, преобразуйте одно из чисел в те же единицы, что и другое. Измерение обоих чисел в одних и тех же единицах называется 9.0008 однородных единиц. В этом примере вы конвертируете его надбавку, 25 центов, в 0,25 доллара, поскольку его почасовая оплата измеряется в долларах, а не в центах, поэтому надбавка также должна быть в долларах.

Вычитание ключевых слов

Ключевые слова на вычитание также включают ведущие ключевые слова, ключевые слова, которые можно переводить по одному слову за раз, и ключевые слова, встречающиеся в задачах-рассказах. Посмотрите на следующий список ключевых слов вычитания:

• РАЗНИЦА МЕЖДУ _____ И _____

• _____ МИНУС _____

• _____ УМЕНЬШИЛСЯ НА _____

• ПОТЕРЯ

• МЕНЬШЕ

• МЕНЬШЕ

• ЗАБЕРИТЕ

Одно ключевое слово вычитания (РАЗНИЦА МЕЖДУ) представляет собой выражение, состоящее из двух частей, которое начинается с ведущего ключевого слова, определяющего соответствующее И. Вы можете использовать те же методы подчеркивания и обведения ключевых слов, которые показаны в предыдущем разделе, для перевода этих выражений.

Пример 7: Переведите следующее: разница между четырьмя и шестью

Вот как вы переводите Пример 7:

1. Поскольку ключевое слово РАЗНИЦА МЕЖДУ является ведущим ключевым словом, определяющим соответствующее И, подчеркните слова до и после И: «четыре» и «шесть».

• разница между четырьмя и шестью

2. Обведите ведущее ключевое слово и укажите соответствующее И, которое оно определяет.

3. Переведите каждое подчеркнутое выражение и замените И знаком минус.

• Выражение переводится как 4 – 6.

Примечание: И не всегда переводится как сложение. Здесь РАЗНИЦА МЕЖДУ — это ведущее ключевое слово, которое определяет, что И означает вычитание.

Другие ключевые слова вычитания, такие как MINUS и DECREASED BY, используют стратегию прямого перевода. Пример 8 представляет собой задачу на вычитание слов, которая переводится по одному ключевому слову за раз в точном порядке выражения.

Пример 8: Переведите следующее: двадцать четыре уменьшить на число

• Выражение переводится как 24 – x .

В задаче на вычитание вы можете найти ключевые слова на вычитание LOSS, LESS, FEWER и TAKE AWAY, как показано в примере 9.

Пример 9: Переведите следующую текстовую задачу в математическое выражение о текущей стоимости материалов на стройплощадке: Строительная компания хранила на строительной площадке материалы на сумму 1253 доллара. Компания понесла убытки в размере 300 долларов из-за ущерба, нанесенного ураганом.

• Выражение переводится как 1 253 – 300.

Умножение ключевых слов

Вот некоторые распространенные примеры ключевых слов умножения:

• УМНОЖИТЬ _____ НА _____

• ПРОДУКТ _____ И _____

• _____ РАЗ _____

• ДВОЙНОЙ _____

• ДВАЖДЫ _____

• ТРОЙНОЙ _____

• ПРОЦЕНТ _____

• ДОЛЯ _____

Для двух ключевых слов умножения, MULTIPLY и PRODUCT OF, ведущее ключевое слово определяет соответствующее BY или AND, как показано в примере 10.

Пример 10: Переведите следующее: произведение семи и числа

Переведите этот пример следующим образом:

1. Поскольку ПРОИЗВЕДЕНИЕ является ведущим ключевым словом, которое соответствует И, подчеркните слова до и после И: «семь» и «число».

• произведение семи и числа

2. Обведите ведущее ключевое слово и укажите соответствующее И, которое оно определяет.

3. Переведите каждое подчеркнутое выражение и замените AND знаком времени.

• Выражение переводится как 7 × x .

Примечание: Имейте в виду, что И не всегда означает сложение. Ключевое слово PRODUCT OF определяет, что И в этом выражении означает умножение.

Выражение умножения, переведенное методом прямого перевода, показано в примере 11.

Пример 11: Переведите следующее: число, умноженное на пятнадцать

Выражение переводится как x x 15.

Некоторые ключевые слова умножения, такие как DOUBLE, TWICE и TRIPLE, преобразуются в число и операцию умножения, как показано в примерах 12 и 13.

Пример 12: Переведите следующее: дважды число

Выражение преобразуется в 2 × x .

Пример 13: Переведите следующую текстовую задачу в математическое выражение: У Дженнифер в банке было 15 долларов. За следующие две недели она удвоила свои деньги.

Выражение преобразуется в 2 × 15.

Одним из ключевых слов, указывающих на умножение, является OF. Однако в текстовых задачах вы можете увидеть более одного употребления слова «из». Единственная OF, которая указывает на умножение, — это та, которая следует за ключевым словом PERCENT, знаком процента, ключевым словом FRACTION или дробью. См. примеры 14 и 15.

Пример 14: Переведите следующее: двадцать пять процентов от четырехсот долларов

Выражение переводится как 0,25 × 400.

Примечание: Помните, что перед умножением процент заменяется десятичной дробью.

Пример 15: Переведите следующее: одна треть от двадцати семи

Выражение переводится как .

Ключевые слова раздела

Некоторые распространенные примеры ключевых слов разделения:

• ЧАСТЬ _____ И _____

• РАЗДЕЛИТЬ _____ НА _____

• _____ ДЕЛИТСЯ НА _____

• ДЕЛИМ НА ПОЛОВИНУ

• ПО

Некоторым людям трудно различить ключевые слова ПРОИЗВЕДЕНИЕ ИЗ и ЧАСТНОЕ ИЗ. Вот подсказка, которая поможет вам запомнить, какое из них указывает на деление, а какое на умножение: ЧАСТНОЕ — более сложное слово, чем «ПРОИЗВЕД», а деление — более сложная операция, чем умножение.

Помните: Ведущие ключевые слова определяют соответствующее И или BY для обозначения деления, обычно обозначаемого символом ÷.

Пример 16: Переведите следующее: частное семи и числа

1. Поскольку ключевое слово ЧАСТНОЕ ИЗ является ведущим ключевым словом, определяющим И, подчеркните слова до и после И: «семь» и «число».

• частное семи и число

2. Обведите ведущее ключевое слово и укажите соответствующее И, которое оно определяет.

3. Переведите каждое подчеркнутое выражение и замените И знаком деления.

• Выражение переводится как 7 ÷ n .

Примечание: Здесь ключевое слово ЧАСТНОЕ определяет И для обозначения деления.

Пример 17: Переведите следующее: разделите минус тридцать шесть на девять

1. Поскольку слово DIVIDE является ведущим ключевым словом, определяющим BY, подчеркните слова до и после BY: «минус тридцать шесть» и «девять».

• минус тридцать шесть разделить на девять

2. Обведите ведущее ключевое слово и укажите соответствующий BY, который оно определяет.

3. Переведите каждое подчеркнутое выражение и замените BY знаком деления.

• Выражение переводится как .

Примечание: Первое число идет в числителе при использовании дроби для обозначения деления. Число в числителе (-36) помещается внутри «дома» при использовании длинного символа деления.

Некоторые ключевые слова раздела можно переводить по одному слову. Вместо этого вы просто следуете предложению и заменяете его алгебраическими обозначениями по ходу дела.

Пример 18: Переведите следующее: число, деленное на 16

Выражение переводится как .

Часто в сюжетных задачах ключевым словом, указывающим на деление, является PER. Когда в сюжетной задаче требуется указать скорость транспортного средства в милях в час, настройте выражение, чтобы разделить количество миль на количество часов. Вы не только напрямую переводите «мили» ÷ «часы», но также определяете количество миль и количество часов, находя их в другом месте задачи. См. пример 19.

Пример 19: Переведите следующую текстовую задачу в математическое выражение о скорости: Требуется три часа, чтобы проехать 150 миль до дома бабушки.