Негосударственное общеобразовательное учреждение Средняя общеобразовательная школа

Метод люшера: Восьмицветовой тест Люшера — Пройти онлайн тест

alexxlab

Исследование адаптации методом Люшера

Исследование адаптации методом Люшера — определение эмоционального состояния ребенка в школе, наличия положительных и отрицательных эмоций в различных учебных ситуациях. Выявляется эмоциональная самооценка ребенка.

Психолог раскладывает перед ребенком цветные карточки на чистом листе бумаге А4 в произвольном порядке.

Инструкция

1. Посмотри внимательно и ответь на вопросы, на какой из этих цветов больше всего похоже твое настроение, когда ты утром идешь в школу? Чаще всего, обычно. Назови или покажи пальцем.
2. А дома в выходные дни?
3. На какой из этих цветов больше всего похоже твое настроение, когда ты сидишь на уроке?
4. А когда отвечаешь у доски?
5. А перед контрольной или проверочной работой?
6. Когда с ребятами на перемене играешь или общаешься?
7. Когда с учителем разговариваешь?

            А теперь выбери из этих цветов тот, который больше всего нравится тебе, кажется красивее других (психолог убирает карточку, выбранную ребенком).

А из оставшихся? (снова убирает карточку, выбранную ребенком, и т.д.).

Определение эмоционального отношения ребенка к школьным ситуациям

При выборе синего, зеленого, красного, желтого цветов отмечаются положительное отношение, установка, эмоциональное состояние, хорошее настроение.
При выборе черного цвета отмечаются отрицательное отношение, негативизм, резкое неприятие того, что происходит, преобладание плохого настроения.
При выборе серого цвета отмечаются нейтральное отношение, отсутствие эмоций, пассивное неприятие, равнодушие, опустошенность, ощущение ненужности.
При выборе коричневого цвета отмечаются тревога, беспокойство, напряжение, страх, неприятные физиологические ощущения (болит живот, голова, подташнивает и пр.).
При выборе фиолетового цвета отмечаются инфантилизм, капризы, неустойчивость установок, безответственность, сохранение «позиции ребенка».

Определение эмоциональной самооценки ребенка

Если общий цветовой выбор ребенка начинается с синего, зеленого, красного, желтого цветов, то в этом случае самооценка у ребенка позитивная, он отождествляет себя с хорошими детьми.
Если общий цветовой выбор начинается с черного, серого, коричневого цветов, то в этом случае у ребенка негативная самооценка, он отождествляет себя с плохими людьми, сам себе не нравится.
Если общий цветовой выбор начинается с фиолетового цвета, то в этом случае у ребенка инфантильная самооценка, личностная незрелость, сохранение установок и манеры поведения, свойственных младшему возрасту.

Интерпретация результатов

ЦВЕТ

Красный

Желтый

Зелёный

Фиолетовый

Синий

Коричневый

Чёрный

Серый

Место цвета
в норме

1

2

3

4

5

6

7

8

Место цвета
в выборе ребёнка

3

8

2

1

5

7

4

6

Разность

2

6

1

3

1

3

2

ЭС = 2 + 6 + 1 + 3 + 0 +1 + 3 + 2= 18

20 — преобладание отрицательных эмоций. У ребенка доминируют плохое настроение и неприятные переживания. Плохое настроение свидетельствует о нарушении адаптационного процесса, о наличии проблем, которые ребенок не может преодолеть самостоятельно. Преобладание плохого настроения может нарушать сам процесс обучения, но свидетельствует о том, что ребенок нуждается в психологической помощи.

10 — эмоциональное состояние в норме. Ребенок может радоваться, печалиться, поводов для беспокойства нет, адаптация протекает в целом нормально.

0 — преобладание положительных эмоций. Ребенок весел, счастлив, настроен оптимистично, пребывает в состоянии эйфории.

Анализ

При выборе ребенком коричневого, серого цветов во всех семи случаях и фиолетового цвета в ситуациях «самочувствие дома, общая установка по отношению к школе, взаимоотношение с классным руководителем» — ставится 0 баллов.

При выборе черного цвета — 1 балл.

При выборе синего, зеленого, красного, желтого — 1 балл.

Высокий уровень адаптации: ответы ребенка оцениваются в 6-7 баллов — общее эмоциональное отношение ребенка к школе положительное.

Средний уровень адаптации: ответы оцениваются в 4-5 баллов — возможно проявление негативного отношения как в целом к школе, так и к отдельным сторонам учебного процесса.

Низкий уровень адаптации: ответы оцениваются в 0-3 балла — у ребенка преобладает негативное отношение к школе.

Эмоциональное состояние ребенка в школе анализируется отдельно.

Оригинальный цветовой тест Люшера //Психологическая газета

Разрабатывая свой цветовой тест, Макс Люшер стремился к тому, чтобы тест не рассматривался в будущем специалистами, которые захотят использовать его в своей работе, как проективный тест, который каждый человек сможет интерпретировать по-разному. Его точка зрения, изложенная в материалах описания цветового теста, заключается в том, чтобы опираться при тестировании и оценке полученных результатов на научный подход. Эмоциональность измеряется с помощью физиологических объективных реакций. По информации, размещённой на официальном сайте Макса Люшера: «72 цвета теста Люшера являются объективными показателями с точно измеряемой частотой, они абсолютно одинаковы для всех возрастов и всех культур. Цвета Люшера воспринимаются объективно и не проецируются, поэтому тест Люшера — это физиологически обоснованный, объективный тест, и не является «проективным» тестом». Исключая субъективное влияние на этапе тестирования, обработки и анализа полученных результатов специалист может взглянуть на ситуацию с научной точки зрения, а также идентифицировать причину и психо-вегетативную структуру недугов или симптомов без вмешательства толкований и проекций, дифференцировать конституциональные особенности, актуальное состояние, составить рекомендации и др.

История создания теста Люшера

Историю создания теста необходимо рассказывать, начиная с предыстории. Ведь создание собственного подхода к исследованию человеческой психики не одномоментный акт – ему предшествуют годы поисков, проб, ошибок, размышлений, открытий, которые, в конце концов, складываются в некое единое целое… Макс Люшер заинтересовался внутренним миром человека довольно рано и его интерес был практическим – школьником он изучал труды Фрейда, читал Аристотеля, изучал тайны физиогномики, графологии.

Уже в 16 лет он имел возможность по специальному разрешению посещать лекции и семинары по психологии и философии в университете Базеля. А в 18 лет он познакомился с известным тестом своего соотечественника Германа Роршаха и разработал метод, позволивший оценивать с помощью этого теста логику мышления. Школьный психолог профессор Пробст, который преподавал в университете тест Роршаха, помог ему получить дополнительные каникулы в школе для описания этого нового метода. Параллельно он выразил желание, чтобы Макс Люшер продолжал его исследования в области цветовой диагностики, которую он в свое время разработал для теста Роршаха. Приступив к изучению внутреннего мира человека, Макс Люшер достаточно быстро отверг эмпирический метод исследования и предпочел опираться на логический подход. Десятки лет были потрачены на поиски наиболее подходящих и точных психологических терминов для категорий регуляционной психологии. Он понимал, что в отличие от общепринятой и психоаналитической терминологии они не могут быть ни телесными, ни пространственными, ни временными (как например, оральный, фаллический, интровертированный, архетип).

Психология цвета интересовала его сначала лишь в связи с тестом Роршаха. Так как изначально ему не удалось быстро решить поставленную задачу, он с присущей ему настойчивостью ухватился за эту проблему и потратил 5 лет с 1941 по 1946 на эксперименты, пока не смог найти достаточно логичного объяснения. Он пришел к выводу, с которым не соглашались многие его предшественники, что чувственное ощущение при восприятии цвета объективно и универсально, и лишь симпатия по отношению к цвету субъективна. Благодаря этому различению появляется возможность посредством тестовых цветов объективно измерить субъективное состояние человека.

Профессор психиатрии Джон Штеелин предоставил (1941) школьнику Максу Люшеру неограниченный доступ к пациентам и их историям болезни. Таким образом, у него появилась возможность исследовать и разрабатывать свою цветовую диагностику на пациентах и детях из наблюдательных классов в специализированных школах. Эта работа длилась в течение шести лет.

По счастливой случайности Карл Мишер — генеральный директор концерна Ciba, крупнейшего в то время химического предприятия в Базеле, лично заинтересовался психологией цвета и предоставил в распоряжение Люшера лабораторию, материалы и помощь в разработке специальных тестовых цветов, продолжавшуюся около пяти лет. Он проверил около 4500 цветовых стимулов, выполненных из различного материала (бумага, металл, дерево, пленка, шелк, шерсть) и поставил с 1941 по 1946 г.г. огромное большое число экспериментов в поисках цветов, которые бы точно соответствовали его психологической системе.

Будучи студентом в возрасте 22 — 24 лет (1945 – 1947) он руководил психодиагностической оценкой персонала в психотехническом институте в Базеле. За время работы там он понял, что цветовая диагностика не только является наиболее простым и быстрым методом (по сравнению с общепринятыми в этой области тестами), но и дает возможность получать более дифференцированные и очевидные результаты.

В 1947 году в возрасте 23 лет Макс Люшер изложил свою цветовую диагностику в Лозанне на первом после второй мировой войны всемирном конгрессе по психологии. Таким образом, его цветовой тест получил международную известность, а его теория была опубликована в сборнике трудов конгресса «Диагностика характера». Благодаря этому Макс Люшер получил возможность преподавать свою психологию цвета в 1949 и в 1950 г.г. на кафедре психологии в Сорбонне и в министерстве по труду в Париже. Его диссертация «Цвет как инструмент психодиагностики» (1949) была высоко оценена профессорами психиатрии, философии и психологии со следующим комментарием: «Эта работа войдет в историю психологии».

После получения ученой степени он работал (1949) в швейцарском антропологическом институте, который в течение трех лет финансировал подготовку будущих профессоров философии для университетов Швейцарии. В это время в течение трех лет он читал лекции в постоянно переполненном актовом зале университета в Базеле. Одновременно с этим он вел психотерапевтическую практику, используя главным образом толкование сновидений, которое он изучал в Париже.

Благодаря публикации в одном из швейцарских журналов статьи о цветовой психологии в 1952 г. крупнейший немецкий медиа-концерн пригласил его в качестве консультанта в Гамбург. Впоследствии он получил большое количество контрактов на консультирование всемирно известных рекламных агентств и ведущих немецких индустриальных гигантов. Это позволило ему получить дополнительные демографические и кросс-культуральные данные по тесту Люшера благодаря большим статистическим исследованиям (подготовлено по материалам сайта Института Люшера).

Представляя цветовой тест в России в своем послании участникам Саммита психологов, Макс Люшер отметил, что цветовая психология логична и объективна: «Я хочу объяснить Вам свое понимание цветов, физическое и психологическое. Будет большой ошибкой полагать, что значения цветов субъективны, это далеко не так. Правильное восприятие цветов – это восприятие объективное и их интерпретация не субъективна. Я хочу объяснить Вам свое понимание влияния и значения цветов. Прежде всего, мы должны опасаться основной ошибки многих людей. Цвета не субъективны, восприятие цветов объективно для всех — мужчин и женщин, стариков и молодых, европейцев, азиатов и американцев. Например, этот оранжево-красный будет оранжево-красным для любого человека во всём мире, а этот темно-синий абсолютно всеми будет восприниматься как тёмно-синий. Итак, Вы должны запомнить: цвета определяются объективно. Перейдем к интерпретациям и ассоциациям. Например, считать, что красный цвет является волнующим, потому что это цвет крови или темно-синий является успокаивающим, потому что это цвет ночи – это, безусловно, нонсенс. Первое, что мы должны сделать – найти тот язык, на котором мы могли бы объяснить то, как мы думаем и как мы чувствуем. Для этого нужно учесть специальные категории. Для любого человека в мире существует два варианта.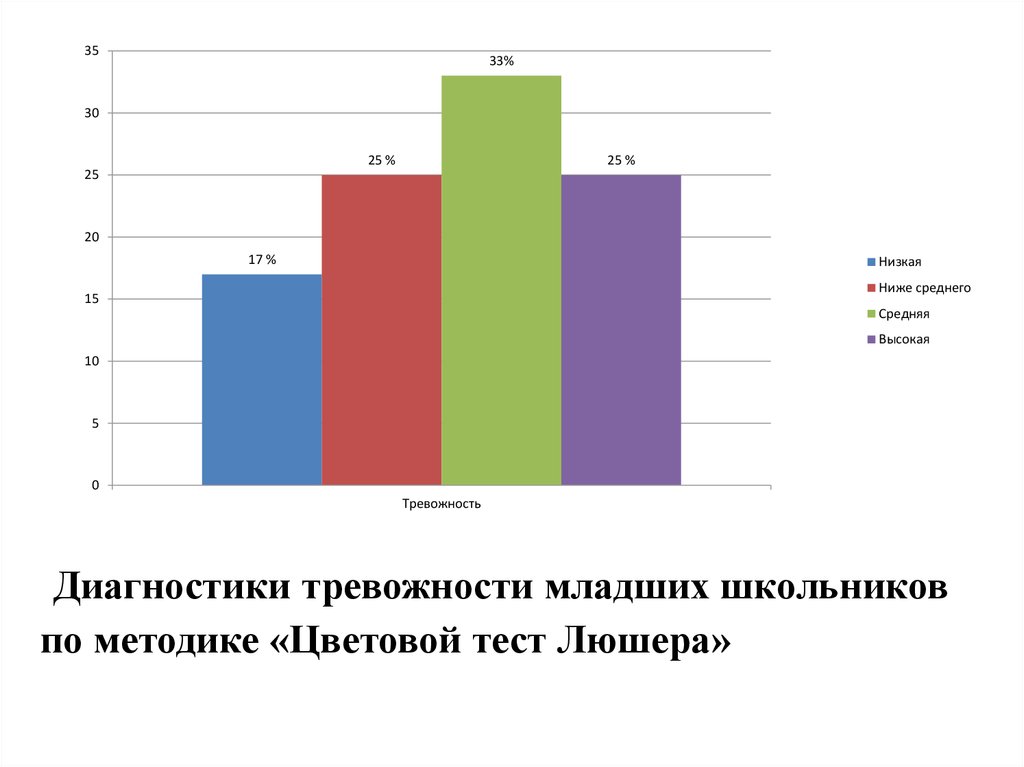 Мы можем либо воспринимать, постигать что-то и это можно назвать рецептивным вариантом или вариантом чувственного восприятия. Другой вариант – противоположный. Мы можем что-то делать или организовывать и это будет директивный вариант. Итак, первыми категориями того, что мы видим и делаем, могут быть либо восприятие, рецепция, либо управление, дирекция. Однако есть ещё одно измерение. Есть вещи постоянные, константные, например, мои родители, которые всегда были и будут моими родителями, это неизменно. Противоположность этому – вещи изменчивые, вариабельные: облака или различные знакомства. Эти вещи изменчивы. Так мы получаем следующие категории: рецептивные – директивные и константные – вариабельные. Если мы попробуем их изобразить, то на горизонтальной прямой окажутся варианты директивные и рецептивные, а на вертикальной внизу окажутся константные и наверху – вариабельные. Так мы можем получить четыре квадрата. Эти четыре квадрата – своего рода классический критерий, который люди использовали всегда (4 элемента: огонь, вода, воздух, земля; 4 темперамента – холерик, сангвиник, флегматик, меланхолик, 4 времени года – весна, лето, осень, зима, четыре стороны света – север, запад, юг, восток). Почему всегда четыре? Всё это потому, что мы думаем и чувствуем по этой структуре и она является основной наших чувств и мыслей. Теперь подумаем, какой цвет больше всего подходит понятиям директивности и вариабельности? Это оранжево-красный. Какой цвет является противоположным и подходящим для рецептивности и константности? Темно-синий. Какой цвет соответствует директивной и константной позиции? Сине-зеленый. Какой цвет вариабельный и рецептивный? Это желтый цвет. Цветовой тест Люшера использует объективные цвета для измерения эмоциональности личности. И здесь всё различно: один предпочитает оранжево-красный, он возбуждённый и всегда готов действовать, а другой человек не любит оранжево-красный, считая его агрессивным и неприятным. Люди, не любящие оранжево-красный, не разделяющие этого волнения, обычно изнурены, депрессивны и так далее. Итак, используя объективные цвета, мы задаём вопрос: какой цвет вы предпочитаете, какой любите или не любите? И получается, что люди, любящие определенный цвет, хотели бы быть похожими на этот цвет, а люди, не любящие определенный цвет, не любят и эмоции этого цвета. И это – основа цветового теста Люшера: с помощью объективного инструмента – цветов, мы измеряем субъективное состояние личности. Я надеюсь, что всё, объясненное мной, пусть даже в очень кратком виде, понравилось вам и было для вас полезно». (видеозапись обращения Макса Люшера и доклад профессора Андреаса Эдельмана, сотрудника Института медицинской психодиагностики Макса Люшера).

Институт цветовой диагностики Люшера — партнер IX Саммита психологов, который состоится 31 мая — 2 июня 2015 года в Санкт-Петербурге – профессор Андреас Эдельман проведёт мастер-класс «Цветовой тест Люшера: возможности применения в кризисной ситуации».
Перед Саммитом в Институте «Иматон» будет проходить обучающий семинар «Подлинный тест Люшера. Возможности практического применения (медицинская и педагогическая практика, управление персоналом и индивидуальный коучинг)». Подробнее о программе семинара

 

Рассеяние двух частиц в условиях квантования конечного объема с использованием базиса плоских волн

  • М. Люшер, Объемная зависимость энергетического спектра в массивных квантовых теориях поля. 1. Стабильные состояния частиц , Общ. Мат. физ. 104 (1986) 177 [ВДОХНОВЕНИЕ].

  • М. Люшер, Объемная зависимость энергетического спектра в массивных квантовых теориях поля. 2. Состояния рассеяния , Общ. Мат. физ. 105 (1986) 153 [ВДОХНОВЕНИЕ].

  • М. Люшер, Два состояния частиц на торе и их связь с матрицей рассеяния , Nucl. физ. B 354 (1991) 531 [ВДОХНОВЕНИЕ].

    Артикул ОБЪЯВЛЕНИЯ MathSciNet Google Scholar

  • К. Руммукайнен, С.А. Готлиб, Фазовые сдвиги резонансного рассеяния на решетке без покоя , Nucl. физ. Б 450 (1995) 397 [hep-lat/9503028] [INSPIRE].

  • С. ч. Ким, К. Т. Сачрайда и С. Р. Шарп, Эффекты конечного объема для двухадронных состояний в движущихся системах отсчета , Nucl.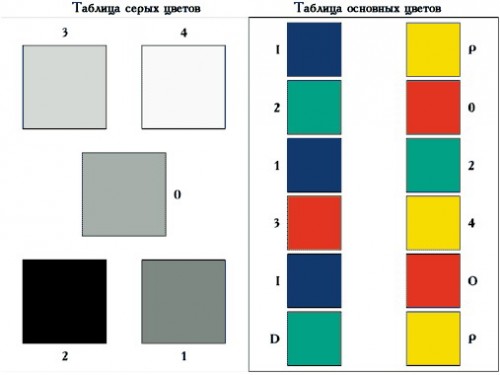 физ. B 727 (2005) 218 ​​[hep-lat/0507006] [INSPIRE].

  • M. Gokeler et al., Фазы рассеяния для мезонных и барионных резонансов на общих решетках с подвижной системой отсчета , Phys. Ред. D 86 (2012) 094513 [arXiv:1206.4141] [INSPIRE].

    Артикул ОБЪЯВЛЕНИЯ Google Scholar

  • T. Luu and M.J. Savage, Извлечение фазовых сдвигов рассеяния в более высоких парциальных волнах из расчетов КХД на решетке , Phys. Ред. D 83 (2011) 114508 [arXiv:1101.3347] [INSPIRE].

    Артикул ОБЪЯВЛЕНИЯ Google Scholar

  • Z. Fu, Формула Руммукайнена-Готлиба для двухчастичной системы с различной массой , Физ. Ред. D 85 (2012) 014506 [arXiv:1110.0319] [INSPIRE].

    Артикул ОБЪЯВЛЕНИЯ Google Scholar

  • Л. Лесковец и С. Преловсек, Фазовые сдвиги рассеяния для двух частиц с разной массой и ненулевым полным импульсом в решеточной КХД , Phys. Ред. D 85 (2012) 114507 [arXiv:1202.2145] [INSPIRE].

    Артикул ОБЪЯВЛЕНИЯ Google Scholar

  • Р. А. Брицено, Двухчастичные многоканальные системы в конечном объеме с произвольным спином , Phys. Ред. D 89 (2014) 074507 [arXiv:1401.3312] [INSPIRE].

    Артикул ОБЪЯВЛЕНИЯ Google Scholar

  • М. Лаге, У.-Г. Мейснер и А. Русецкий, Метод измерения длины рассеяния антикаона на нуклоне в решеточной КХД , Phys. лат. Б 681 (2009) 439 [arXiv:0905.0069] [ВДОХНОВЕНИЕ].

    Артикул ОБЪЯВЛЕНИЯ Google Scholar

  • S. He, X. Feng and C. Liu, Два состояния частиц и элементы S-матрицы в многоканальном рассеянии [ВДОХНОВЛЯТЬ].

  • М. Т. Хансен и С. Р. Шарп, Многоканальное обобщение формулы Леллоуша-Люшера , Phys. Версия D 86 (2012) 016007 [arXiv:1204.0826] [INSPIRE].

    Артикул ОБЪЯВЛЕНИЯ Google Scholar

  • М. Деринг, У. Г. Мейснер, Э. Осет и А. Русецкий, Скалярные мезоны, движущиеся в конечном объеме, и роль парциального волнового смешивания , Eur. физ. J. A 48 (2012) 114 [arXiv:1205.4838] [INSPIRE].

    Артикул ОБЪЯВЛЕНИЯ Google Scholar

  • X. Feng, X. Li and C. Liu, Два состояния частиц в асимметричном ящике и фазы упругого рассеяния , Phys. Ред. D 70 (2004) 014505 [hep-lat/0404001] [INSPIRE].

  • Р. А. Брицено, Дж. Дж. Дудек и Р. Д. Янг, Процессы рассеяния и резонансы в КХД на решетке , Rev. Mod. физ. 90 (2018) 025001 [arXiv:1706.06223] [INSPIRE].

    Артикул ОБЪЯВЛЕНИЯ MathSciNet Google Scholar

  • М. Май, М. Деринг и А. Русецкий, Многочастичные системы на решетке и киральные экстраполяции: краткий обзор , Eur. физ. J. ST 230 (2021) 1623 [arXiv:2103.00577] [INSPIRE].

    Артикул Google Scholar

  • Х.-Х. Чен, В. Чен, С. Лю и С.-Л. Zhu, Состояния пентакварка и тетракварка со скрытым очарованием , Phys. Представитель 639 (2016) 1 [arXiv: 1601.02092] [ВДОХНОВЕНИЕ].

    Артикул ОБЪЯВЛЕНИЯ MathSciNet Google Scholar

  • Ф.-К. Го, К. Ханхарт, У.-Г. Мейснер, К. Ван, К. Чжао и Б.-С. Zou, Адронные молекулы , Rev. Mod. физ. 90 (2018) 015004 [arXiv:1705.00141] [INSPIRE].

    Артикул ОБЪЯВЛЕНИЯ Google Scholar

  • Н. Брамбилла и др., Состояния X Y Z: экспериментальный и теоретический статус и перспективы , Phys. Представитель 873 (2020) 1 [arXiv:1907.07583] [ВДОХНОВЕНИЕ].

    Артикул ОБЪЯВЛЕНИЯ Google Scholar

  • П. Ф. Бедак, И. Сато и А. Уокер-Лауд, Поправки на конечный объем к π-π рассеянию , Phys. Ред. D 73 (2006) 074501 [hep-lat/0601033] [INSPIRE].

  • И. Сато и П. Ф. Бедак, Помещение двух нуклонов в ящик: экспоненциально подавленные поправки к формуле Люшера , Phys. Ред. D 76 (2007) 034502 [hep-lat/0702021] [INSPIRE].

  • M. Jansen, H.W. Hammer and Y. Jia, Поправки на конечный объем к энергии связи X(3872) , Phys. Ред. D 92 (2015) 114031 [arXiv:1505.04099] [INSPIRE].

    Артикул ОБЪЯВЛЕНИЯ Google Scholar

  • М. Деринг, У.-Г. Мейснер, Э. Осет и А. Русецкий, Унитаризованная киральная теория возмущений в конечном объеме: скалярный мезонный сектор , Eur. физ. J. A 47 (2011) 139 [arXiv:1107.3988] [INSPIRE].

    Артикул ОБЪЯВЛЕНИЯ Google Scholar

  • З.-Х. Го, Л. Лю, У.-Г. Мейснер, Дж. А. Оллер и А. Русецкий, . Киральное исследование резонанса a 0 (980) и фазовых сдвигов πη-рассеяния в свете недавнего моделирования решетки , Физ. Ред. D 95 (2017) 054004 [arXiv:1609.08096] [INSPIRE].

    Артикул ОБЪЯВЛЕНИЯ Google Scholar

  • З. -Х. Го, Л. Лю, У.-Г. Мейснер, Дж. А. Оллер и А. Русецкий, К точному определению амплитуд рассеяния очарованных и светлых псевдоскалярных мезонов , Eur. физ. J. C 79 (2019) 13 [arXiv:1811.05585] [INSPIRE].

    Артикул ОБЪЯВЛЕНИЯ Google Scholar

  • М. Альбаладехо, Дж. А. Оллер, Э. Осет, Г. Риос и Л. Рока, Рассмотрение ππ-рассеяния в конечных объемах и пределы извлечения фазовых сдвигов из КХД на решетке , JHEP 08 (2012) 071 [arXiv:1205.3582] [ВДОХНОВЕНИЕ].

    Артикул ОБЪЯВЛЕНИЯ Google Scholar

  • Х.-Х. Чен и Э. Осет, ππ-взаимодействие в ρ-канале в конечном объеме , Phys. Ред. D 87 (2013) 016014 [arXiv:1202.2787] [ВДОХНОВЕНИЕ].

  • Дж. М. М. Холл, А. С. П. Хсу, Д. Б. Лейнвебер, А. В. Томас и Р. Д. Янг, Матричная гамильтонова модель конечного объема для системы ∆ → Nπ , Phys. Ред. D 87 (2013) 094510 [arXiv:1303.4157] [INSPIRE].

    Артикул ОБЪЯВЛЕНИЯ Google Scholar

  • Ж.-Ж. Ву, Т. С. Х. Ли, А. В. Томас и Р. Д. Янг, Метод гамильтониана конечного объема для взаимодействия связанных каналов в решеточной КХД , Phys. Ред. C 90 (2014) 055206 [arXiv:1402.4868] [INSPIRE].

    Артикул ОБЪЯВЛЕНИЯ Google Scholar

  • Z.-W. Лю, В. Камле, Д. Б. Лейнвебер, Ф. М. Стоукс, А. В. Томас и Дж.-Дж. Ву, Гамильтониан эффективное исследование теории поля N ∗ ( 1535 ) резонанса в решеточной КХД , Физ. Преподобный Летт. 116 (2016) 082004 [arXiv:1512.00140] [INSPIRE].

  • Ю. Ли, Дж.-Дж. Ву, Д. Б. Лейнвебер и А. В. Томас, Гамильтонова эффективная теория поля в удлиненном или движущемся конечном объеме , Phys.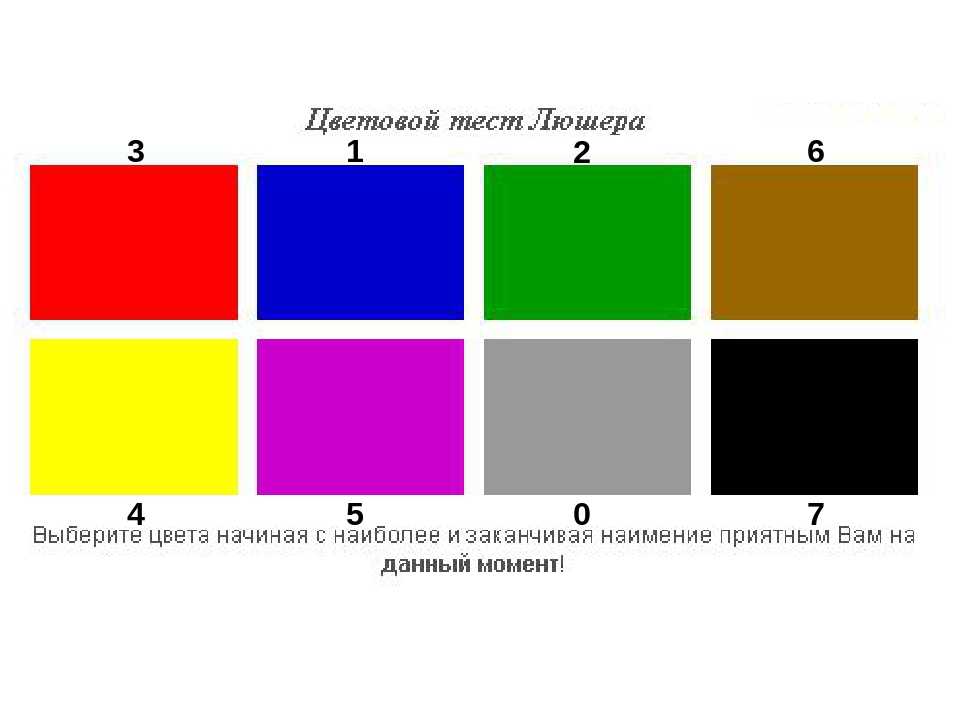 Ред. D 103 (2021) 094518 [arXiv:2103.12260] [INSPIRE].

    Артикул ОБЪЯВЛЕНИЯ MathSciNet Google Scholar

  • К. Морнингстар и др., Оценка двухчастичной K -матрицы для множественных парциальных волн и каналов распада по энергиям конечного объема , Nucl. физ. B 924 (2017) 477 [arXiv:1707.05817] [INSPIRE].

    Артикул ОБЪЯВЛЕНИЯ МАТЕМАТИКА Google Scholar

  • Ю. Ли, Дж.-Дж. Wu, CD Abell, DB Leinweber and AW Thomas, Парциальное смешивание волн в гамильтоновой теории эффективного поля , Phys. Ред. D 101 (2020) 114501 [arXiv:1910.04973] [ВДОХНОВЕНИЕ].

    Артикул ОБЪЯВЛЕНИЯ MathSciNet Google Scholar

  • Ф. X. Ли, А. Александру и Р. Бретт, Проверка условия квантования конечного объема для двух бесспиновых частиц , arXiv: 2107. 04430 [INSPIRE].

  • F. X. Lee, C. Morningstar and A. Alexandru, Энергетический спектр двухчастичного рассеяния в периодическом ящике , Междунар. Дж. Мод. физ. C 31 (2020) 2050131 [INSPIRE].

    Артикул ОБЪЯВЛЕНИЯ MathSciNet Google Scholar

  • R. A. Briceno, Z. Davoudi and T. C. Luu, Двухнуклонные системы в конечном объеме: (I) условия квантования , Phys. Ред. D 88 (2013) 034502 [arXiv:1305.4903] [INSPIRE].

    Артикул ОБЪЯВЛЕНИЯ Google Scholar

  • C. Morningstar et al., Расширенные адронные и двухадронные операторы определенного импульса для расчета спектра в решеточной КХД , Phys. Ред. D 88 (2013) 014511 [arXiv:1303.6816] [INSPIRE].

    Артикул ОБЪЯВЛЕНИЯ Google Scholar

  • В. Бернар, М. Лаге, У.-Г. Мейснер и А. Русецкий, Резонансные свойства из энергетического спектра конечного объема , JHEP 08 (2008) 024 [arXiv:0806.4495] [ВДОХНОВЕНИЕ].

    Артикул ОБЪЯВЛЕНИЯ Google Scholar

  • М. Дрессельхаус, Г. Дрессельхаус и А. Йорио, Теория групп: приложение к физике конденсированного состояния , SpringerLink, Springer, Германия (2007).

  • М. Деринг, Х. В. Хаммер, М. Май, Дж. Ю. Панг, t. А. Русецкий и Дж. Ву, Трехчастичный спектр в конечном объеме: роль кубической симметрии , Физ. Ред. D 97 (2018) 114508 [arXiv:1802.03362] [INSPIRE].

  • Коллаборация Hadron Spectrum, Эффективное решение многоканального детерминанта Люшера посредством разложения по собственным значениям , Phys. Ред. D 101 (2020) 114505 [arXiv:2001.08474] [INSPIRE].

  • Э. Эпельбаум, Х.-В. Хаммер и У.-Г. Meissner, Современная теория ядерных сил , Rev. Mod. физ. 81 (2009) 1773 [arXiv:0811.1338] [ВДОХНОВЕНИЕ].

    Артикул ОБЪЯВЛЕНИЯ Google Scholar

  • Р. Махлейдт и Д. Р. Энтем, Киральная эффективная теория поля и ядерные силы , Phys. Представитель 503 (2011) 1 [arXiv:1105.2919] [ВДОХНОВЕНИЕ].

    Артикул ОБЪЯВЛЕНИЯ Google Scholar

  • Э. Эпельбаум, Х. Кребс и П. Рейнерт, Высокоточные ядерные силы от хиральных ТЭС: состояние дел, проблемы и перспективы , Фронт. в физ. 8 (2020) 98 [arXiv:1911.11875] [ВДОХНОВЕНИЕ].

    Артикул ОБЪЯВЛЕНИЯ Google Scholar

  • E. Epelbaum, H. Krebs and U. G. Meißner, Прецизионный нуклон-нуклонный потенциал пятого порядка в киральном расширении , Phys. Преподобный Летт. 115 (2015) 122301 [arXiv:1412.4623] [INSPIRE].

    Артикул ОБЪЯВЛЕНИЯ Google Scholar

  • P. Reinert, H. Krebs and E. Epelbaum, Полулокальные импульсные регуляризованные киральные двухнуклонные потенциалы до пятого порядка , Eur. физ. J. A 54 (2018) 86 [arXiv:1711.08821] [INSPIRE].

    Артикул ОБЪЯВЛЕНИЯ Google Scholar

  • Энтем Д. Р., Махлейдт Р., Носик Ю., Высококачественные двухнуклонные потенциалы до пятого порядка кирального расширения , Физ. Ред. C 96 (2017) 024004 [arXiv:1703.05454] [INSPIRE].

    Артикул ОБЪЯВЛЕНИЯ Google Scholar

  • Э. Эпельбаум, В. Глокль и У.-Г. Meissner, Улучшение сходимости кирального расширения для ядерных сил. 2. Низкие фазы и дейтрон , Eur. физ. J. A 19 (2004) 401 [nucl-th/0308010] [INSPIRE].

  • В. Бару, К. Ханхарт, М. Хоферихтер, Б. Кубис, А. Ногга и Д. Р. Филлипс, Прецизионный расчет порога π − d-рассеяния, длин πN-рассеяния и правила сумм ГМО , Nucl. физ. A 872 (2011) 69 [arXiv:1107.5509] [INSPIRE].

    Артикул ОБЪЯВЛЕНИЯ Google Scholar

  • P. Reinert, H. Krebs и E. Epelbaum, Прецизионное определение констант пион-нуклонного взаимодействия с использованием теории эффективного поля , Phys. Преподобный Летт. 126 (2021) 092501 [arXiv:2006.15360] [INSPIRE].

    Артикул ОБЪЯВЛЕНИЯ Google Scholar

  • Э. Эпельбаум, В. Глокль и У.-Г. Meissner, Улучшение сходимости кирального расширения для ядерных сил. 1. Периферийные фазы , Евро. физ. J. A 19 (2004) 125 [nucl-th/0304037] [INSPIRE].

  • В. Г. Дж. Стокс, Р. А. М. Кломп, М. К. М. Рентмистер и Дж. Дж. де Сварт, Парциально-волновой анализ всех данных нуклон-нуклонного рассеяния ниже 350 МэВ , Phys. C 48 (1993) 792 [INSPIRE].

    Артикул ОБЪЯВЛЕНИЯ Google Scholar

  • M. Mai, M. Döring, C. Culver and A. Alexandru, Трехчастичная унитарность в сравнении с конечным объемом π + π + π спектр из 903 решетки + 903 решетки QCD , Физ. Версия D 101 (2020) 054510 [arXiv:1909.05749] [INSPIRE].

    Артикул ОБЪЯВЛЕНИЯ Google Scholar

  • I. Fachruddin, C. Elster and W. Gloeckle, Нуклон-нуклонное рассеяние в трехмерном подходе , Nucl. физ. A 689 (2001) 507 [nucl-th/0104027] [INSPIRE].

  • В. Г. Дж. Стокс и Дж. Дж. Де Сварт, Взаимодействие магнитных моментов в нуклон-нуклонном фазовом сдвиге , Физ. Ред. C 42 (1990) 1235 [INSPIRE].

    Артикул ОБЪЯВЛЕНИЯ Google Scholar

  • Дж. Дж. Дудек, Р. Г. Эдвардс и К. Э. Томас, Фазовые сдвиги S- и D-волн в рассеянии пи-пи изоспина-2 в КХД на решетке , Phys. Ред. D 86 (2012) 034031 [arXiv:1203.6041] [INSPIRE].

    Артикул ОБЪЯВЛЕНИЯ Google Scholar

    9{\ast } \) (2317) из решётки QCD , JHEP 02 (2021) 100 [arXiv:2008.06432] [INSPIRE].

  • В. Бару, Э. Эпельбаум, А. А. Филин, Дж. Гегелия, Низкоэнергетические теоремы для нуклон-нуклонного рассеяния при нефизических массах пионов , Phys. Ред. C 92 (2015) 014001 [arXiv:1504.07852] [INSPIRE].

    Артикул ОБЪЯВЛЕНИЯ Google Scholar

  • В. Бару, Э. Эпельбаум и А. А. Филин, Низкоэнергетические теоремы для нуклон-нуклонного рассеяния на M π = 450 МэВ , Физ. Ред. C 94 (2016) 014001 [arXiv:1604.02551] [INSPIRE].

    Артикул ОБЪЯВЛЕНИЯ Google Scholar

  • В. Бернар, Н. Кайзер и У. Г. Мейснер, Киральная теория возмущений при наличии резонансов: приложение к пи-пи и пи-К-рассеянию , Nucl. физ. Б 364 (1991) 283 [ВДОХНОВЕНИЕ].

    Артикул ОБЪЯВЛЕНИЯ Google Scholar

  • П. К. Брунс и У.-Г. Meissner, Инфракрасная регуляризация для полей со спином 1 , Eur. физ. J. C 40 (2005) 97 [hep-ph/0411223] [INSPIRE].

  • Р. М. Волошин, А. Д. Джексон, Сравнение трехмерных релятивистских уравнений рассеяния , Nucl. физ. Б 64 (1973) 269 [ВДОХНОВЕНИЕ].

    Артикул ОБЪЯВЛЕНИЯ Google Scholar

  • Л. Кастильехо, Р. Х. Далиц и Ф. Дж. Дайсон, Уравнение рассеяния Лоу для заряженных и нейтральных скалярных теорий , Phys. 101 (1956) 453 [INSPIRE].

    Артикул ОБЪЯВЛЕНИЯ МАТЕМАТИКА Google Scholar

  • Дж. А. Оллер, Э. Осет и Дж. Э. Паломар, Форм-факторы векторов пиона и каона , Phys. Ред. D 63 (2001) 114009 [hep-ph/0011096] [INSPIRE].

  • Дж. Гассер и Х. Лейтвайлер, Киральная теория возмущений: расширения в массе странного кварка , Nucl. физ. B 250 (1985) 465 [ВДОХНОВЕНИЕ].

    Артикул ОБЪЯВЛЕНИЯ Google Scholar

  • Г. Эккер, Дж. Гассер, А. Пич и Э. де Рафаэль, Роль резонансов в киральной теории возмущений , Nucl. физ. B 321 (1989) 311 [ВДОХНОВЕНИЕ].

    Артикул ОБЪЯВЛЕНИЯ Google Scholar

  • Extended Twisted Mass, коллаборация ETM, ρ-резонанс от N f = 2 КХД на решетке, включая физическую массу пиона , Phys. лат. B 819 (2021) 136449 [arXiv:2006.13805] [INSPIRE].

  • П. Эстабрукс и А. Д. Мартин, Анализ фазового сдвига ππ ниже порога \(K\overline{K} \) , Nucl. физ. B 79 (1974) 301 [ВДОХНОВЕНИЕ].

  • S. D. Protopopescu et al., ππpartial wave analysis from reactions π + p → π + π − ∆ ++ and π + р → К + К − ∆ ++ по 7 . 1 ГэВ/c , Физ. Ред. D 7 (1973) 1279 [INSPIRE].

  • Сотрудничество ETM, Хранилище данных , https://github.com/urbach/datarhonf2.

  • Ф. Джеймс, Минимизация функций MINUIT и анализ ошибок: справочное руководство, версия 94.1 , CERN-D-506 (1994).

  • Филин А.А., Бару В., Эпельбаум Э., Кребс Х., Меллер Д. и Райнерт П., Извлечение радиуса заряда нейтрона из точного расчета радиуса структуры дейтрона , Phys. Преподобный Летт. 124 (2020) 082501 [arXiv:1911. 04877] [INSPIRE].

    Артикул ОБЪЯВЛЕНИЯ Google Scholar

  • Филин А.А., Меллер Д., Бару В., Эпельбаум Э., Кребс Х. и Райнерт П., Высокоточный расчет заряда дейтрона и квадрупольных формфакторов в киральной теории эффективного поля , Физ. Ред. C 103 (2021) 024313 [arXiv:2009.08911] [INSPIRE].

    Артикул ОБЪЯВЛЕНИЯ Google Scholar

  • Коллаборация NPLQCD, Дейтрон и экзотические двухчастичные связанные состояния из решеточной КХД , Phys. Ред. D 85 (2012) 054511 [arXiv:1109.2889] [INSPIRE].

  • Коллаборация HAL КХД, Двухбарионные потенциалы и H-дибарион из моделирования КХД на решетке с тремя ароматами , Нукл. физ. A 881 (2012) 28 [arXiv:1112.5926] [INSPIRE].

  • Т. Ямадзаки, К. -и. Исикава, Ю. Курамаси и А. Укава, Ядра гелия, дейтрон и динейтрон в 2 + 1 флейворной решетке КХД , Phys. Ред. D 86 (2012) 074514 [arXiv:1207.4277] [INSPIRE].

    Артикул ОБЪЯВЛЕНИЯ Google Scholar

  • Т. Ямадзаки, К.-и. Исикава, Ю. Курамаси и А. Укава, 9 лет0004 Исследование зависимости энергии связи легких ядер от массы кварка в решетке аромата 2 + 1 КХД , Phys. Ред. D 92 (2015) 014501 [arXiv:1502.04182] [INSPIRE].

    Артикул ОБЪЯВЛЕНИЯ Google Scholar

  • K. Orginos, A. Parreno, M.J. Savage, S.R. Beane, E. Chang and W. Detmold, Две нуклонные системы на m π ∼ QCD

  • 405 решетка{\mathrm{phys}} \) : Первый расчет КХД на решетке со стохастическим лапласианским методом Хевисайда , Phys. Ред. C 103 (2021) 014003 [arXiv:2009.11825] [INSPIRE].

    Артикул ОБЪЯВЛЕНИЯ Google Scholar

  • Z. Davoudi et al., Ядерные матричные элементы из решеточной КХД для электрослабых и нестандартных процессов , Phys. Представитель 900 (2021) 1 [arXiv:2008.11160] [ВДОХНОВЕНИЕ].

    Артикул ОБЪЯВЛЕНИЯ МАТЕМАТИКА Google Scholar

  • Коллаборация NPLQCD, Легкие ядра и гиперядра из квантовой хромодинамики в пределе SU(3) ароматическая симметрия , Phys. Ред. D 87 (2013) 034506 [arXiv:1206.5219] [INSPIRE].

  • Н. Барнеа, Л. Контесси, Д. Газит, Ф. Педерива и У. ван Колк, Эффективная теория поля для ядер решетки , Физ. Преподобный Летт. 114 (2015) 052501 [arXiv:1311.4966] [INSPIRE].

    Артикул ОБЪЯВЛЕНИЯ Google Scholar

  • C. Drischler et al., К обоснованию ядерной физики в КХД , Prog. Часть. Нукл. физ. 121 (2021) 103888 [arXiv:1910.07961] [ВДОХНОВЕНИЕ].

    Артикул Google Scholar

    • Согласованность метода конечных объемов Люшера и метода HAL КХД для двухбарионных систем в решеточной КХД

    Согласованность между методом конечных объемов Люшера и методом HAL КХД для двухбарионных систем в решеточной КХД

    Скачать PDF

    Скачать PDF

    • Обычная статья — Теоретическая физика
    • Открытый доступ
    • Опубликовано:
    • The HAL QCD collaboration,
    • Takumi Iritani 1 ,
    • Sinya Aoki 2,3 ,
    • Takumi Doi 1,4 ,
    • Tetsuo Hatsuda 1,4 ,
    • Yoichi Ikeda 5 ,
    • Такаши Иноуэ 6 ,
    • Нориёси Исии 5 ,
    • Хидекацу Нэмура 5 и
    • …
    • Кенджи Сасаки 2  

    Журнал физики высоких энергий том 2019 , Номер статьи: 7 (2019) Процитировать эту статью

    • 363 доступа

    • 20 цитирований

    • 1 Альтметрический

    • Сведения о показателях

    Аннотация

    Существует два метода изучения двухбарионных систем в решеточной КХД: прямой метод, который извлекает собственные энергии из плато временной корреляционной функции, и метод HAL КХД, который извлекает наблюдаемые из нелокального потенциала, связанного с пространственно-временной корреляцией. функция. Хотя теоретически эти два метода должны давать одинаковые результаты, сообщалось о качественном различии наблюдаемых данных при моделировании КХД на решетке. Недавно мы указали в [1, 2], что отделение основного состояния от возбужденных состояний имеет решающее значение для получения разумных результатов в первом, в то время как оба состояния обеспечивают полезные сигналы для наблюдаемых во втором. В этой статье мы идентифицируем вклад каждого состояния в прямом методе путем разложения двухбарионных корреляционных функций на собственные моды конечного объема, полученные методом HAL КХД. Как и в наших предыдущих исследованиях, мы рассматриваем систему ΞΞ в 1 S 0 канал на м π = 0,51 ГэВ в (2+1)-ароматной решетке КХД с использованием пристеночных и размытых кварковых источников с пространственными протяженностями, La = 3,6, 4,8. фм. Показано, что «псевдоплато» на ранних временных срезах ( t = 1 ∼ 2 фм) от размытого источника в прямом методе действительно возникает из-за контаминации возбужденных состояний, а плато с насыщением основного состояния реализовано только на т > 5 ∼ 15 фм, что соответствует обратной величине наименьшей энергии возбуждения. Мы также показываем, что двухбарионный оператор можно оптимизировать, используя собственные моды конечного объема, так что (i) энергетические спектры конечного объема из метода HAL КХД согласуются со спектрами временной корреляционной функции с оптимизированными операторами и ( ii) правильные спектры конечного объема будут доступны в прямом методе только в том случае, если используются высокооптимизированные операторы. Таким образом, мы заключаем, что давний вопрос о согласованности между методом конечных объемов Люшера и методом HAL КХД для двух барионов теперь решен, по крайней мере, для рассматриваемой здесь конкретной системы: они количественно согласуются друг с другом только в том случае, если возбужденное загрязнение правильно удалены в бывшем.

    Скачайте, чтобы прочитать полный текст статьи

    Ссылки

    1. Сотрудничество HAL QCD, T. Iritani et al. , Mirage in Temporal Correlation functions for Baryon-Baryon Interactions in Lattice QCD , JHEP 10 (2016) 101 [arXiv:1607.06371] [ВДОХНОВЕНИЕ].

    2. Коллаборация HAL КХД, Т. Иритани и др., Связаны ли два нуклона в КХД на решетке для масс тяжелых кварков? Проверка непротиворечивости с помощью формулы конечного объема Люшера , Физ. Ред. D 96 (2017) 034521 [arXiv:1703.07210] [ВДОХНОВЕНИЕ].

    3. Т. Ямадзаки, К.-и. Ishikawa, Y. Kuramashi and A. Ukawa, Исследование зависимости энергии связи от массы кварка для легких ядер в решетке аромата 2+1 КХД , Phys. Ред. D 92 (2015) 014501 [arXiv:1502.04182] [ВДОХНОВЕНИЕ].

      ОБЪЯВЛЕНИЕ Google Scholar

    4. NPLQCD коллаборация, М.Л. Wagman et al. , Барион-барионные взаимодействия и спин-ароматная симметрия из квантовой хромодинамики решетки , Phys. Ред. D 96 (2017) 114510 [arXiv:1706.06550] [ВДОХНОВЕНИЕ].

    5. Коллаборация CalLat, E. Berkowitz et al., Двухнуклонное рассеяние высших парциальных волн на решеточной КХД , Phys. лат. Б 765 (2017) 285 [arXiv:1508.00886] [ВДОХНОВЕНИЕ].

    6. М. Люшер, Объемная зависимость энергетического спектра в массивных квантовых теориях поля. 1. Стабильные состояния частиц , Общ. Мат. физ. 104 (1986) 177 [ВДОХНОВЕНИЕ].

    7. М. Люшер, Объемная зависимость энергетического спектра в массивных квантовых теориях поля. 2. Состояния рассеяния , общ. Мат. физ. 105 (1986) 153 [ВДОХНОВЕНИЕ].

    8. М. Люшер, Два состояния частиц на торе и их связь с матрицей рассеяния , Nucl. физ. B 354 (1991) 531 [ВДОХНОВЕНИЕ].

      Артикул ОБЪЯВЛЕНИЯ MathSciNet Google Scholar

    9. Н. Исии, С. Аоки и Т. Хацуда, Ядерная сила из решетчатой ​​КХД , Phys. Преподобный Летт. 99 (2007) 022001 [nucl-th/0611096] [INSPIRE].

    10. С. Аоки, Т. Хацуда и Н. Исии, Теоретические основы ядерных сил в КХД и их приложения к центральным и тензорным силам в КХД-моделировании закаленных решеток , Prog. Теор. физ. 123 (2010) 89 [arXiv:0909.5585] [ВДОХНОВЕНИЕ].

      Артикул ОБЪЯВЛЕНИЯ МАТЕМАТИКА Google Scholar

    11. HAL Сотрудничество КХД, Н. Исии и др., Адрон-адронные взаимодействия из волновой функции Намбу-Бете-Солпитера в мнимом времени на решетке , Phys. лат. B 712 (2012) 437 [arXiv:1203.3642] [ВДОХНОВЕНИЕ].

    12. Коллаборация HAL КХД, С. Аоки и др., Решетчатый подход КХД к ядерной физике , PTEP 2012 (2012) 01A105 [arXiv:1206.5088] [ВДОХНОВЕНИЕ].

    13. С. Аоки, КХД на решетке и ядерная физика , в Современные перспективы КХД на решетке: квантовая теория поля и высокопроизводительные вычисления. Proceedings, International School, 93rd Session , Les Houches, France, 3–28 августа 2009 г., стр. 591–628 (2010) [arXiv:1008.4427] [INSPIRE].

    14. Коллаборация NPLQCD, S.R. Beane et al., Легкие ядра и гиперядра из квантовой хромодинамики в пределе SU(3) Flavor Symmetry , Физ. Ред. D 87 (2013) 034506 [arXiv:1206.5219] [ВДОХНОВЕНИЕ].

    15. Сотрудничество HAL КХД, T. Inoue et al., Потенциалы двух барионов и H-дибарион из моделирования КХД с 3 ароматами , Nucl. физ. A 881 (2012) 28 [arXiv:1112.5926] [ВДОХНОВЕНИЕ].

    16. А. Фрэнсис, Дж. Р. Грин, П.М. Junnarkar, C. Miao, T.D. Rae and H. Wittig, Решетчатая КХД, исследование дибариона H с использованием гексакваркового и двухбарионного интерполяторов , arXiv:1805.03966 [ВДОХНОВЕНИЕ].

    17. T. Iritani для коллаборации с HAL КХД, Барионные взаимодействия в решеточной КХД: прямой метод против потенциального метода HAL КХД , PoS(LATTICE2016)107 (2016) [arXiv:1610.09779] [INSPIRE].

    18. С. Аоки, Т. Дои и Т. Иритани, Проверка работоспособности связанных состояний NN в КХД решетки с формулой конечного объема Люшера — Раскрытие симптомов ложных плато — , EPJ Web Conf. 175 (2018) 05006 [arXiv:1707. 08800] [ВДОХНОВЕНИЕ].

      Артикул Google Scholar

    19. Т. Иритани для коллаборации с HAL КХД, Двухбарионные системы из метода HAL КХД и миража во временной корреляции прямого метода , EPJ Web Conf. 175 (2018) 05008 [arXiv:1710.06147] [ВДОХНОВЕНИЕ].

    20. Сотрудничество HAL QCD, Т. Иритани и др., Систематика потенциала HAL КХД при низких энергиях в решеточной КХД , Phys. Ред. D 99 (2019) 014514 [arXiv:1805.02365] [ВДОХНОВЕНИЕ].

    21. Г. Паризи, Стратегия вычисления спектра адронных масс , Phys. Представитель 103 (1984) 203 [ВДОХНОВЕНИЕ].

      Артикул ОБЪЯВЛЕНИЯ Google Scholar

    22. Г.П. Lepage, The Analysis of Algorithms for Lattice Field Theory , in From Actions to Answers: Proceedings of the TASI 1989 , T. Degrand and D. Toussaint eds., World Scientific, Сингапур (1990) [CLNS-89-971 ] [ВДОХНОВЛЯТЬ].

    23. https://en.wikipedia.org/wiki/Sanity_check.

    24. К. Мурано, Н. Исии, С. Аоки и Т. Хацуда, Нуклон-нуклонный потенциал и его нелокальность в решетке КХД , Прогр. Теор. физ. 125 (2011) 1225 [arXiv:1103.0619] [ВДОХНОВЕНИЕ].

      Артикул ОБЪЯВЛЕНИЯ МАТЕМАТИКА Google Scholar

    25. К. Нисидзима, Формулировка полевых теорий составных частиц , Phys. Ред. 111 (1958) 995 [ВДОХНОВЕНИЕ].

      Артикул ОБЪЯВЛЕНИЯ MathSciNet МАТЕМАТИКА Google Scholar

    26. W. Zimmermann, О проблеме связанного состояния в квантовой теории поля , Nuovo Cim. 10 (1958) 597 [ВДОХНОВЕНИЕ].

      Артикул ОБЪЯВЛЕНИЯ MathSciNet МАТЕМАТИКА Google Scholar

    27. Р. Хааг, Квантовые теории поля с составными частицами и асимптотическими условиями , Phys. Ред. 112 (1958) 669 [ВДОХНОВЕНИЕ].

      Артикул ОБЪЯВЛЕНИЯ MathSciNet МАТЕМАТИКА Google Scholar

    28. Т. Ямадзаки, К.-и. Исикава, Ю. Курамаси и А. Укава, Ядра гелия, дейтрон и динейтрон в решетке аромата 2+1 КХД , Phys. Ред. D 86 (2012) 074514 [arXiv:1207.4277] [ВДОХНОВЕНИЕ].

      ОБЪЯВЛЕНИЕ Google Scholar

    29. Т. Дои и М.Г. Эндрес, Единый алгоритм сжатия для мультибарионных корреляторов на решетке , Вычисл. физ. коммун. 184 (2013) 117 [arXiv:1205.0585] [ВДОХНОВЕНИЕ].

      Артикул ОБЪЯВЛЕНИЯ MathSciNet Google Scholar

    30. Коллаборация NPLQCD, K. Orginos et al., Две нуклонные системы на m π ∼ 450 МэВ из КХД на решетке , Физ. Ред. D 92 (2015) 114512 [arXiv:1508.07583] [ВДОХНОВЕНИЕ].

    31. Коллаборация NPLQCD, S.R. Beane et al., Комментарий к статье «Связаны ли два нуклона в КХД на решетке для масс тяжелых кварков? — Проверка работоспособности с помощью формулы конечного объема Люшера — , arXiv:1705.09239 [INSPIRE].

    32. М. Люшер и У. Вольф, Как рассчитать матрицу упругого рассеяния в двумерных квантовых теориях поля с помощью численного моделирования , Нукл. физ. B 339 (1990) 222 [ВДОХНОВЕНИЕ].

      Артикул ОБЪЯВЛЕНИЯ MathSciNet Google Scholar

    33. Р.А. Брицено, Дж.Дж. Дудек и Р.Д. Янг, Процессы рассеяния и резонансы в КХД на решетке , Rev. Mod. физ. 90 (2018) 025001 [arXiv:1706.06223] [ВДОХНОВЕНИЕ].

      Артикул ОБЪЯВЛЕНИЯ MathSciNet Google Scholar

    34. Сотрудничество HAL QCD, S. Gongyo et al., Самый странный дибарион из решетки QCD , Phys. Преподобный Летт. 120 (2018) 212001 [arXiv:1709.00654] [ВДОХНОВЕНИЕ].

    35. HAL КХД коллаборация, Т. Иритани и др., N Ω дибарион из решеточной КХД вблизи физической точки , arXiv:1810.03416 [INSPIRE].

    36. Сотрудничество HAL QCD, T. Inoue et al., Strange Nuclear Physics из КХД на решетке , in 13th International Conference on Hypernuclear and Strange Particle Physics (HYP 2018) , Портсмут, Вирджиния, США, 24–29 июня 2018 г. [arXiv:1809.08932] [INSPIRE].

    37. T. Amagasa et al., Совместное использование данных решетчатой ​​КХД в широко распространенной файловой системе , J. Phys. конф. сер. 664 (2015) 042058 [ВДОХНОВЕНИЕ].

      Артикул Google Scholar

    38. http://www.lqcd.org/ildg.

    39. http://www.jldg.org.

    40. Columbia Physics System (CPS), http://usqcd-software.github.io/CPS.html.

    41. Bridge++, http://bridge.kek.jp/Lattice-code/.

    42. М. Шрек и Х. Фогт, Фиксация кулоновской, Ландау и максимально абелевой калибровки в решетчатой ​​КХД с использованием нескольких графических процессоров , Вычисл. физ. коммун. 184 (2013) 1907 [arXiv:1212.5221] [ВДОХНОВЕНИЕ].

      Артикул ОБЪЯВЛЕНИЯ MathSciNet МАТЕМАТИКА Google Scholar

    43. T. Boku et al., Многоблочный/многоядерный предобуславливатель SSOR для кваркового решателя QCD для компьютера K , PoS(LATTICE2012)188 (2012) [arXiv:1210.7398] [INSPIRE].

    44. М. Терай и др., Настройка производительности решетчатого кода КХД на узле компьютера K (на японском языке), IPJ Trans. Доп. вычисл. Сист. 6 (2013) 43.

    Скачать ссылки

    Открытый доступ

    Эта статья распространяется в соответствии с лицензией Creative Commons Attribution License (CC-BY 4. 0), которая разрешает любое использование, распространение и воспроизведение на любом носителе при условии указания автора(ов) и источника.

    Информация об авторе

    Авторы и организации

    1. RIKEN Nishina Center, Wako, 351-0198, Japan

      Takumi Iritani, Takumi Doi & Tetsuo Hatsuda

    2. Центр гравитационной физики, Институт теоретической физики им. Киото, 606-8502, Япония

      Синья Аоки и Кенджи Сасаки

    3. Центр вычислительных наук Университета Цукуба, Цукуба, 305-8577, Япония

      Синья Аоки

    4. Междисциплинарная теоретическая и математическая научная программа RIKEN (iTHEMS), Вако, 351-0198, Япония

      Такуми Дои и Тецуо Хацуда

    5. Исследовательский центр ядерной физики (RCNP), Осакский университет, Осака, 567-0047, Япония

      Ёити Икэда, Нориёси Исии и Хидэкацу Нэмура

    6. Университет Нихон, Колледж наук о биоресурсах, Канагава, 252-0880, Япония

      Такаши Иноуэ

      7. s 91

      1. Такуми Иритани

        Посмотреть публикации автора

        Вы также можете искать этого автора в PubMed Google Scholar

      2. Sinya Aoki

        Просмотр публикаций автора

        Вы также можете искать этого автора в PubMed Google Scholar

      3. Takumi Doi

        Просмотр публикаций автора

        Вы также можете искать этого автора в PubMed Google Scholar

      4. Тецуо Хацуда

        Просмотр публикаций автора

        Вы также можете искать этого автора в PubMed Google Scholar

      5. Yoichi Ikeda

        Просмотр публикаций автора

        Вы также можете искать этого автора в PubMed Google Scholar

      6. Takashi Inoue

        Просмотр публикаций автора

        Вы также можете искать этого автора в PubMed Google Scholar

      7. Noriyoshi Ishii

        Посмотреть публикации автора

        Вы также можете искать этого автора в PubMed Google Scholar

      8. Hidekatsu Nemura

        Просмотр публикаций автора

        Вы также можете искать этого автора в PubMed Google Scholar

      9. Kenji Sasaki

        Просмотр публикаций автора

        Вы также можете искать этого автора в PubMed Google Scholar

      Consortia

      Сотрудничество HAL QCD

      Автор, ответственный за переписку

      Такуми Иритани.

      Дополнительная информация

      ArXiv ePrint: 1812.08539

      Права и разрешения

      Открытый доступ Эта статья находится под лицензией Creative Commons Attribution 4.0 International License, которая разрешает использование, совместное использование, адаптацию, распространение и воспроизведение на любом носителе или в любом формате. , при условии, что вы укажете первоначальных авторов и источник, предоставите ссылку на лицензию Creative Commons и укажите, были ли внесены изменения.

      Изображения или другие сторонние материалы в этой статье включены в лицензию Creative Commons на эту статью, если иное не указано в кредитной строке материала. Если материал не включен в лицензию Creative Commons статьи, а ваше предполагаемое использование не разрешено законом или выходит за рамки разрешенного использования, вам необходимо получить разрешение непосредственно от правообладателя.

      Чтобы просмотреть копию этой лицензии, посетите https://creativecommons.

    Добавить комментарий

    Ваш адрес email не будет опубликован. Обязательные поля помечены *