От частного к общему метод: Чем индукция отличается от дедукции? — все самое интересное на ПостНауке

Содержание

Индукция – Гуманитарный портал

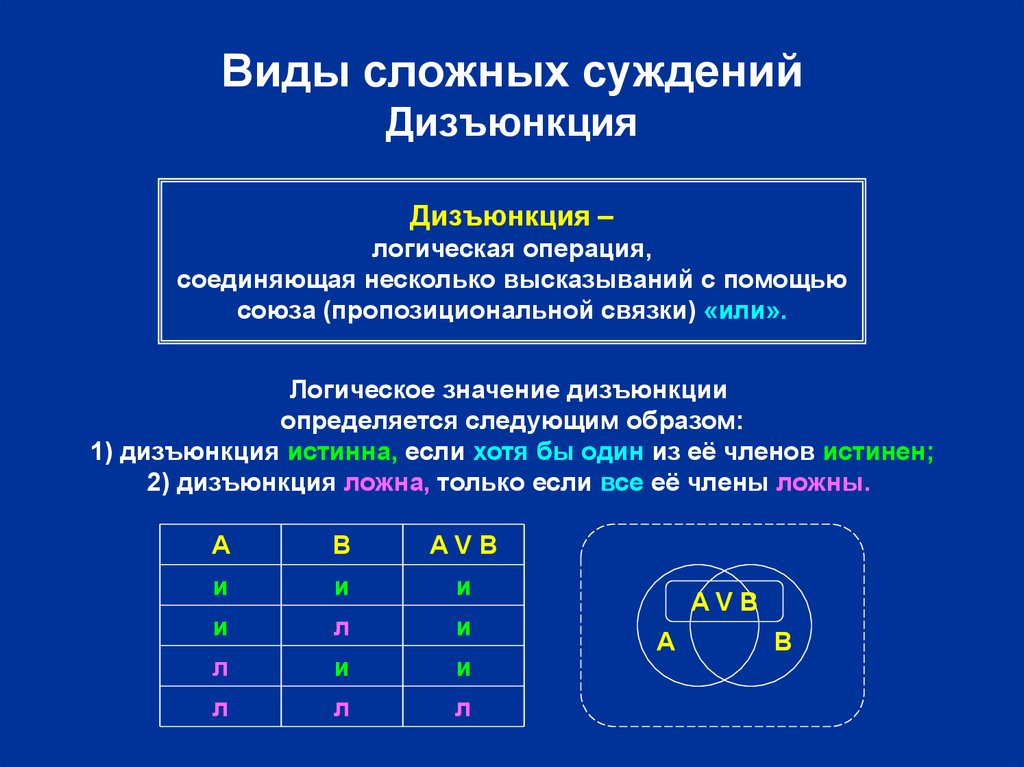
Индукция — это познавательная процедура, посредством которой из сравнения наличных фактов выводится обобщающее их утверждение. В научном поиске (см. Методы научного познания) индукция предполагает движение познания от единичных утверждений об отдельных фактах к положениям, носящим более общий характер. В логике (см. Логика) термин «индукция» используется как синоним более точного, но более громоздкого, термина «индуктивное рассуждение» и понимается в более узком смысле: как умозаключение, в котором общий вывод строится на основе частных посылок. При этом посылки могут подтверждать или подразумевать истину, но не гарантируют её получения. Этим индукция принципиально отличается от дедукции (см. Дедукция), посредством которой из истинных посылок при соблюдении правил логического вывода всегда получаются истинные заключения.

Наиболее широко используемая разновидность индуктивных рассуждений — это перечислительные рассуждения, то есть рассуждения, содержащие переход от посылок, утверждающих, что все известные объекты из некоторой совокупности

A обладают свойством P, к заключению, утверждающему, что все — в том числе и неизвестные — объекты из A обладают P.

Другая широко распространённая разновидность индуктивных рассуждений — рассуждения, содержащие переход от посылок, утверждающих, что некий объект A обладал свойством P в каждый момент времени, предшествующий настоящему, к заключению, утверждающему, что A будет обладать P в будущем.

Индукция широко используется во всех областях научного познания, играя важную роль при построении эмпирических знаний и переходе от эмпирического знания к теоретическому. В науке основой индукции являются опыт, эксперимент и наблюдение, в ходе которых собираются отдельные факты. Затем, изучая эти факты, анализируя их, исследователь устанавливает общие и повторяющиеся признаки ряда явлений, входящих в определённый класс. На этой основе он строит индуктивное умозаключение, в качестве посылок которого выступают суждения о единичных объектах и явлениях с указанием их повторяющегося признака, и суждение о классе, включающем данные объекты и явления. В качестве вывода получают суждение, в котором признак, выявленный у совокупности единичных объектов, приписывается всему классу.

Ценность индуктивных выводов состоит в том, что они обеспечивают переход от единичных фактов к общим положениям, позволяют обнаруживать зависимости между явлениями, строить эмпирически обоснованные гипотезы и приходить к обобщениям.

В индуктивных рассуждениях различают полную и неполную индукцию:

Полная индукция — это индукция, в которой делается заключение о том, что всем представителям класса изучаемых объектов принадлежит свойство P, на основании полученной при опытном исследовании информации о том, что каждому представителю изучаемого класса принадлежит свойство P. Умозаключения полной индукции являются дедуктивными в том смысле, что заключение в них следует из посылок с логической необходимостью: при истинности посылок, применяя известные правила логики, мы не можем получить ложного заключения. Полная индукция применима в тех случаях, когда класс изучаемых объектов обозрим и все объекты этого класса могут быть перечислены. Таким образом, она подразумевает изучение каждого из объектов, входящих в класс, и нахождение на этой основе их общих характеристик. Однако в ряде случаев просто нет необходимости рассматривать абсолютно все предметы того или иного класса, в других случаях это невозможно сделать в силу необозримости класса изучаемых явлений или же в силу ограниченности человеческой практики. В таких ситуациях применяют неполную индукцию.

Неполная индукция — это индукция, в которой делается заключение о том, что всем представителям класса изучаемых объектов принадлежит свойство P, на том основании, что некоторым представителям изучаемого класса принадлежит свойство P. Таким образом, она подразумевает изучение ограниченного числа объектов какого-либо определённого класса, поскольку, как правило, число всех случаев практически необозримо, а теоретическое доказательство для бесконечного числа этих случаев невозможно. Неполная индукция уже не является логически обоснованным рассуждением, так как с точки зрения логики справедливы только такие заключения, для получения которых не требуется никакой новой информации, кроме той, что содержится в посылках, но заключение неполной индукции говорит всегда больше, чем могут сказать её посылки. В этом, собственно, заключается познавательный смысл индукции — абстрагирующая работа мысли помогает получить новое знание при недостатке имеющихся [практических] знаний. Неполнота индукции может обусловливаться не только числом посылок (неполнота в отношении числа посылок), но и их характером (неполнота в отношении характера посылок).
Существуют две разновидности неполной индукции: популярная индукция (или индукция через простое перечисление) и научная индукция:
1. Популярная индукция строится как обобщение ряда наблюдений за сходными явлениями, в которых фиксируется какой-либо повторяющийся признак. Фиксация нового признака у ряда объектов происходит здесь, как правило, без предварительного плана исследований: обнаружив сходный признак у первых попавшихся предметов некоторого класса и не встретив ни одного противоречащего случая, переносят указанный признак на весь класс предметов. Отсутствие противоречащего случая является главным основанием для принятия индуктивного вывода.
  Обнаружение же такого случая опровергает индуктивное обобщение. Вывод, полученный путём индукции через простое перечисление, обладает сравнительно малой степенью достоверности и при продолжении исследований, основанном на расширении класса изученных случаев, часто может оказаться ошибочным. Поэтому популярная индукция может применяться в научном исследовании при выдвижении первых и приближённых гипотез. К ней часто прибегают на первых этапах знакомства с новым классом объектов, но в целом она не может служить надёжной основой для получаемых наукой индуктивных обобщений. Такие обобщения строятся главным образом на базе научной индукции.
2. Научная индукция характеризуется поиском причинных зависимостей между явлениями и стремлением обнаружить существенные признаки объектов, объединяемых в класс. Выделяют три основных вида научной индукции:
  1. Индукция через отбор случаев. В отличие от популярной индукции, где учитывается лишь количество исследуемых случаев, индукция через отбор случаев принимает во внимание особенности каждой их группы.
  2. Индукция через исследование причинных связей. Научная индукция широко используется и как метод нахождения причинных связей путём изучения некоторой совокупности обстоятельств, предшествующих наблюдаемому явлению. Варьируя обстоятельства и осуществляя каждый раз наблюдение за некоторым явлением, исследователь устанавливает его причину. Такой способ характеризует в частности многие виды экспериментального изучения объектов.
  3. Индукция через изучение единственного представителя некоторого класса.
    Научная индукция может строиться не только на основе изучения ряда явлений или объектов, входящих в некоторый класс, но и на основе изучения единственного представителя указанного класса. В этом случае при рассуждении о принадлежности или отсутствии определённого признака у объекта не должны использоваться такие его индивидуальные свойства, которые отличают его от других предметов того же класса.

Указанные разновидности неполной индукции играют исключительно важную роль в научном познании. Неполная индукция позволяет сократить научный поиск и прийти к общим положениям, раскрытию закономерностей, не дожидаясь, пока будут подробно исследованы все явления данного класса. Однако она заключает в себе и существенную ограниченность, состоящую в том, что вывод неполной индукции чаще всего не даёт достоверного знания. В меньшей степени это относится к научной индукции, некоторые разновидности которой дают достоверные выводы, целиком же — к популярной индукции. Знание, полученное в рамках неполной индукции, обычно является проблематичным, вероятностным. Отсюда возникает возможность многочисленных ошибок, являющихся следствием поспешных обобщений. Подобного рода обобщения особенно характерны для ранних стадий научного исследования. Проблематичный характер большинства индуктивных выводов требует их многократной проверки практикой, сопоставления с опытом следствий, выводимых из индуктивного обобщения. По мере того, как эти следствия совпадают с результатом опыта, увеличивается степень достоверности индуктивного вывода.

В этом процессе обоснование знаний, полученных путём индукции, обязательно предполагает движение от индуктивных обобщений к тому или иному частному случаю. Такого рода вывод представляет собой уже дедуктивное умозаключение. Тем самым индукция дополняется дедукцией, что и обеспечивает переход от вероятностного к достоверному знанию.

Поскольку индукция тесно связана с развитием опытного познания, она стала применяться уже в глубокой древности, хотя теоретически её простейшие формы начали анализироваться только в античной философии, в частности Сократом, который ввёл понятие индуктивных рассуждений, и Аристотелем, который рассматривал их как вспомогательные средства обоснования посылок силлогизмов (см. Силлогизм). У Аристотеля понимание индукции связывается с обобщением наблюдений и означает, по существу, способ умозаключения, посредством которого производится восхождение от частного к общему. Этот аристотелевский взгляд восприняли философы эпикурейской школы, защищавшие индукцию в споре со стоиками как единственный авторитетный метод доказательства законов природы.

Дальнейшее развитие теории индукции отмечается лишь в Новое время, когда активный рост науки, обусловленный накоплением, обобщением и систематизацией обширного эмпирического материала, поставил вопрос об исследовании способов научного открытия, а сами виды индуктивных рассуждений стали изучаться на предмет их надёжности. Важное значение в этом отношении имели сочинения Ф. Бэкона, который начал систематическое изучение индуктивных процедур, рассматривая их как единственно научный способ познания и противопоставив индукцию умозрительным рассуждениям. Поскольку методы аристотелевской силлогистики и индукция через простое перечисление подтверждающих случаев не могли быть использованы для анализа эмпирических обобщений, Бэкон в противовес «Органону» Аристотеля создаёт свой «Новый Органон» (1620), в котором излагает «каноны индукции» как методы открытия новых истин в науке. Позднее теория индукции развивалась в работах Дж. Ст. Милля, который предложил пять методов индуктивных рассуждений (каноны индукции Бэкона-Милля), посредством которых выводятся заключения о причинных связях между явлениями: метод сходства; метод различия; объединённый метод сходства и различия; метод остатков; метод сопутствующих изменений. Указанные индуктивные методы являются известными примерами правдоподобных рассуждений (см. Рассуждения правдоподобные). Впоследствии они получили ряд уточнений в работах других исследователей. Однако с помощью «канонов индукции» можно было сделать лишь относительно простые эмпирические обобщения и установить логические отношения между наблюдаемыми свойствами явлений. Когда наука стала исследовать более глубокие законы, раскрывающие сущность и внутренние механизмы явлений, стало очевидным, что эмпирические методы, опирающиеся на индукцию, не в состоянии этого сделать хотя бы потому, что здесь необходимо обращение к абстрактным, теоретическим понятиям. В связи с этим радикально изменился взгляд на индукцию, и вместо логики открытия она стала рассматриваться как метод проверки и обоснования гипотез. В рамках гипотетико-дедуктивного метода (см. Метод гипотетико-дедуктивный) именно эмпирически проверяемые следствия гипотезы могут быть проверены и подтверждены с помощью индуктивно установленных фактов. Такой взгляд на индукцию нашёл наиболее яркое выражение в неопозитивистской концепции, в которой контекст обоснования резко противопоставляется контексту открытия. Задача логики и философии науки сводится при этом исключительно к обоснованию нового знания, процесс же открытия целиком относится к психологии научного творчества. Поскольку заключение индукции логически не следует из посылок, постольку между ними можно установить лишь вероятностное отношение, которое определяется как семантическая степень подтверждения заключения его посылками. Отсюда задачей индукции является не изобретение правил открытия новых научных истин, а поиск объективных критериев подтверждения гипотез их эмпирическими посылками, а если возможно, то определение количественной степени подтверждения. С этой точки зрения другие недедуктивные рассуждения (аналогия, статистические выводы) можно также отнести к индукции в том смысле, что их заключения имеют лишь вероятностный характер и могут быть анализируемы в рамках более широкой вероятностной логики. Однако при этом остаётся в тени эвристическая функция индукции, которая широко применяется для получения обобщений из фактов.

С философской точки зрения наибольший интерес представляет проблема обоснования индукции — нахождения рационального базиса для признания легитимности индуктивных рассуждений. Важность проблемы обусловлена важностью индуктивных рассуждений для современной науки. Её успешное решение предполагает нахождение ответа на вопрос, на каком основании мы признаем некоторые из индуктивных рассуждений приемлемыми, несмотря на то, что во всяком индуктивном рассуждении истинность посылок не гарантирует истинности заключения. Все ответы, предложенные со времени поставившего этот вопрос Д. Юма, оказались безуспешными — всякая попытка обоснования индукции, предложенная до настоящего момента, в неявной форме предполагала легитимность индукции. В настоящее время определённой популярностью пользуется рассмотрение проблемы индукции, предложенное П. Стросоном, утверждающим, что проект обоснования индукции самопротиворечив. Согласно Стросону, обоснование индукции равносильно приданию индуктивным рассуждениям статуса дедуктивных. В то же время основная ценность индуктивных рассуждений заключается в том, что — в отличие от дедуктивно правильных рассуждений — они позволяют нам получать новую информацию; таким образом, обоснование индукции равносильно утверждению, что индуктивные рассуждения, вопреки очевидности, не приводят к получению новой информации, что, согласно Стросону, абсурдно. В последние годы делаются попытки дополнить индукцию некоторыми предпосылками или разрешающими процедурами, обеспечивающими более надёжные выводы в конкретных областях исследования. В этом же направлении ведётся анализ репродуктивных рассуждений, где поиск идёт не от гипотез к следствиям, а, напротив, от следствий к гипотезам. Подобные приёмы уменьшают риск ошибки при индукции, но в принципе индукция — исключая полную и математическую — всегда остаётся умозаключением вероятностным. В современной логике и философии науки интерес к теории индукции поддерживается прикладными исследованиями.

Аристотель. Аналитики первая и вторая. — М., 1952.
Бэкон Ф. Новый органон. — Л., 1938.
Гаек П., Гавранек Т. Автоматическое образование гипотез. — М., 1984.
Гемпепь К. Логика объяснения. — М., 1998.
Джевонс У. С. Основы науки. Трактат о логике и научном методе. — СПб. 1881.
Кайберг Г. Вероятность и индуктивная логика. — Л., 1978.
Карнап Р. Философские основания физики. — М., 1971.
Котарбиньский Т. Лекции по истории логики. — М., 1963.
Лазарев Ф. В. Проблема точности естественнонаучного знания. — «Вопросы философии», 1968, № 9.
Милль Д. С. Система логики силлогистической и индуктивной. — М., 1914.
Минто В. Дедуктивная и индуктивная логика. — М., 1905.
Пойя Д. Математика и правдоподобные рассуждения. — М., 1957.
Пятницын Б. Н., Субботин А. Л. Соображения о построении индуктивной логики. — «Вопросы философии», 1969, № 2.
Рутковский Л, В. Критика методов индуктивного доказательства. — В книге: Избранные труды русских логиков XIX века. — М., 1956.
Рассел Б. Человеческое познание. Его сфера и границы. — М., 1957.
Уемов А. И. Индукция и аналогия. — Иваново, 1956.
Финн В. К. Синтез познавательных процедур и проблема индукции. — «Научно-техническая информация», № 1–2, 1998, с. 3–52.
Франк Ф. Философия науки. — М., 1960.
Carnap R. The Logical Foundations of Probability, 2 ed. — Chicago, 1957.
Induction, Acceptance and Rational Belief. Ed. by М. Swain. — Dordrecht, 1970.
Gordon М. O uspawiedliwieniu indukcji. — Warszawa, 1964.
Keynes J. М. A Treatise on Probability. — L., 1952.
Nicod J. Le probleme logique de l’induction. — P., 1961.
The Problem of Inductive Logic. — Amsterdam, 1986.
Wright G. H. The Logical Problem of Induction, 2 ed. — Oxford, 1957.

Индуктивные и дедуктивные методы обучения

Главная>Книги по педагогике>Оглавление

Индуктивные и дедуктивные методы обучения характеризуют исключительно важную особенность методов — способность раскрывать логику движения содержания учебного материала. Применение индуктивных или дедуктивных методов означает вьибор определенной логики раскрытия содержания изучаемой темы — от частного к общему или от общего к частному.
(…) Индуктивное изучение темы особенно полезно в тех случаях, когда материал носит преимущественно фактический характер или связан с формированием понятий, смысл которых может стать ясным лишь в ходе индуктивных рассуждений. Широко применимы индуктивные методы при изучении технических устройств и выполнении практических заданий.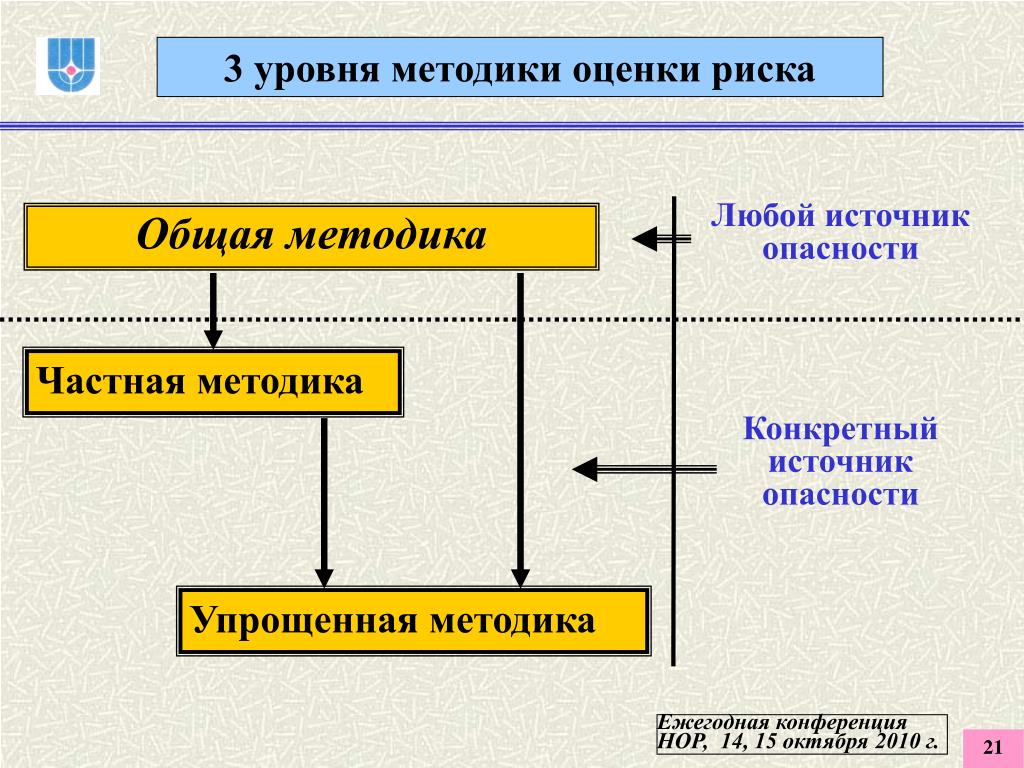 Индуктивным методом решаются многие математические и физические задачи, особенно когда учитель считает необходимым самостоятельно подвести учащихся к усвоению некоторой более обобщенной формулы. Слабость индуктивных методов обучения состоит в том, что они требуют большего времени на изучение нового материала, чем дедуктивные. Они в меньшей мере способствуют развитию абстрактного мышления, так как опираются на конкретные факты, опыты и другие данные.
(…) Дедуктивный метод способствует более быстрому прохождению учебного материала, активнее развивает абстрактное мышление.
Применение его особенно полезно при изучении теоретического материала, при решении задач, требующих выявления следствий из некоторых более общих положений. Например, таким образом могут быть изучены газовые законы Бойля—Мариотта и Гей-Люссака, которые являются следствием из общего уравнения состояния идеального газа. Таким же методом могут быть изучены следствия, вытекающие из молекулярно-кинетической, электронной и других теорий.
В. В. Давыдовым и Д. Б. Элькониным доказана возможность дедуктивного построения обучения уже в начальной школе с применением более высоких, чем обычно, теоретических обобщений. Они ищут такую логику построения содержания учебного материала при формировании научных понятий, при которой ученики прежде всего обнаруживают генетически исходную всеобщую связь, определяющую целостную структуру всей совокупности подобных понятий. Так, для математических понятий всеобщей основой выступают общие отношения величины, для школьной грамматики роль такой всеобщей основы выполняют отношение формы и значения слова. Поскольку эти общие связи можно выразить в виде моделей (формул, графических схем), то школьников учат использовать эти модели. Такой подход позволяет ученикам раньше усваивать знания общего и абстрактного характера и уже из них выводить более частные и конкретные знания. Но это не означает, что необходимо перейти к дедуктивному изучению всего материала начальной школы. Должно быть найдено его рациональное сочетание с индуктивным подходом, так как без индуктивного подхода нельзя успешно подготовить школьников к трудовой деятельности, к проведению опытов, доступных исследований лабораторного типа.
Как видно из характеристики деятельности преподавателя и учеников, при использовании дедуктивного или индуктивного методов обучения применяются ранее описанные словесные, наглядные и практические методы, а также репродуктивные или проблемно-поисковые методы, но при этом содержание учебного материала раскрывается определенным логическим образом — индуктивно или дедуктивно. Поэтому можно говорить об индуктивно или дедуктивно построенной беседе, о репродуктив-но или поисково построенной практической работе, о проблемно и дедуктивно построенном рассказе и т. д. Здесь мы еще раз убеждаемся в том, что «метод обучения» — понятие многоаспектное. В реально используемой в данный момент системе методов обучения сочетаются несколько условно выделяемых в классификации методов. И то, что мы говорим о применении дедуктивного или индуктивного метода в данной ситуации, определяется ведущей дидактической задачей, поставленной педагогом на данном этапе обучения. Если, например, учитель решил сконцентрировать внимание на развитии дедуктивного мышления обобщенного характера, то он использует дедуктивный метод, сочетая его с проблемно-поисковым, реализуемым посредством специально построенной беседы.
Заметим, что мы ограничили перечень логических методов обучения двумя видами — дедуктивным и индуктивным. Сделано это лишь для большей доступности целостной классификации методов обучения. В принципе же к этой подгруппе методов организации учения относятся и методы учебного анализа, учебного синтеза, учебной аналогии, выявления причинно-следственных связей и др.

www.p-lib.ru

Педагогика. / Под ред. Ю.К. Бабанского. — М.: Просвещение, 1983.

Главная>Книги по педагогике>Оглавление

Дедуктивное рассуждение против индуктивного рассуждения

Вам не нужно быть Шерлоком Холмсом, чтобы использовать свои способности к дедуктивным рассуждениям… или это будут индуктивные рассуждения?

В чем разница между индуктивным и дедуктивным рассуждениями?

В ходе научного процесса дедуктивное рассуждение используется для достижения логического и истинного вывода. Другой тип рассуждений, индуктивный, также широко используется. Люди часто путают дедуктивное рассуждение с индуктивным; однако важные различия разделяют эти два пути до логического завершения.

Что такое дедуктивное рассуждение?

Дедуктивное рассуждение, также известное как дедукция, является основной формой рассуждения. Он начинается с общего утверждения или гипотезы и исследует возможности прийти к конкретному логическому заключению, согласно Норману Герру , профессору среднего образования Калифорнийского государственного университета в Нортридже. Метод использует дедукцию для проверки гипотез и теорий, которые предсказывают определенные результаты, если они верны, говорит доктор Сильвия Вассертейл-Смоллер , исследователь и почетный профессор Медицинского колледжа Альберта Эйнштейна.

«Мы идем от общего — теории — к конкретному — наблюдениям», — сказал Вассертейл-Смоллер Live Science.

В дедуктивном рассуждении есть первая посылка, затем вторая посылка и, наконец, вывод (вывод, основанный на рассуждениях и доказательствах). Распространенной формой дедуктивного рассуждения является силлогизм, в котором два утверждения — большая посылка и второстепенная посылка — вместе достигают логического заключения. Например, за большой посылкой «Каждое А есть В» может следовать второстепенная посылка: «Этот С есть А». Эти утверждения привели бы к заключению: «Этот C есть B». Силлогизмы считаются хорошим способом проверки дедуктивных рассуждений, чтобы убедиться, что аргумент действителен.

Изображение 1 из 3

Вот как работает дедуктивное мышление. Чтобы вывод был верным, гипотеза должна быть обоснованной. (Изображение предоставлено Shutterstock) Это правда, это паук. (Изображение предоставлено Shutterstock) И поскольку у всех пауков 8 ног, у этого должно быть 8 ног. Это пример дедуктивного рассуждения, которое верно, потому что исходная посылка верна. (Изображение предоставлено Shutterstock)

Например, «У всех пауков восемь ног. Тарантул — это паук. Следовательно, у тарантулов восемь ног». Чтобы дедуктивное рассуждение было правильным, гипотеза должна быть верной. Предполагается, что утверждения «У всех пауков восемь ног» и «тарантул — это паук» верны. Поэтому вывод логичен и верен. В дедуктивных рассуждениях, если что-то верно для класса вещей в целом, это также верно для всех членов этого класса.

Дедуктивные выводы надежны, если посылки верны, согласно Herr. Аргумент «Все лысые мужчины — дедушки. Гарольд лысый. Следовательно, Гарольд — дедушка» логически верен, но неверен, поскольку исходная посылка ложна.

Гравюра на дереве, на которой Шерлок Холмс изучает улики со своим другом доктором Ватсоном. Знаменитый сыщик был полностью посвящен дедуктивным рассуждениям и известен тем, что говорил: «Устраните все другие факторы, и то, что останется, должно быть правдой». (Изображение предоставлено: Художественная иллюстрация Сидни Пэджета, автора сэра Артура Конан Дойля/Getty)

(открывается в новой вкладке)

Что такое индуктивное рассуждение

Индуктивное рассуждение движется от наблюдения к обобщению и теории. (Изображение предоставлено: Designer491/Getty)

В то время как дедуктивное рассуждение начинается с предпосылки, которая доказана наблюдениями, индуктивное рассуждение извлекает вероятную (но не точную) предпосылку из конкретных и ограниченных наблюдений. Есть данные, а потом из данных делаются выводы; это называется индуктивной логикой, согласно Университет Иллинойса в Спрингфилде.

«В индуктивном выводе мы идем от частного к общему. Мы делаем много наблюдений, выявляем закономерность, делаем обобщение и выводим объяснение или теорию», — сказал Вассертейл-Смоллер в интервью Live Science. «В науке происходит постоянное взаимодействие между индуктивным выводом (основанным на наблюдениях) и дедуктивным выводом (основанным на теории), пока мы не будем все ближе и ближе приближаться к «истине», к которой мы можем только приблизиться, но не установить с полной уверенностью. »

Другими словами, надежность вывода, сделанного с помощью индуктивной логики, зависит от полноты наблюдений. Например, предположим, что у вас есть мешок с монетами; вы вытаскиваете из мешка три монеты, и каждая монета — пенни. Затем, используя индуктивную логику, вы можете предположить, что все монеты в мешке — пенни». будет правдой.

Вот еще пример: «Пингвины — это птицы. Пингвины не умеют летать. Следовательно, все птицы не умеют летать.» Вывод не следует логически из утверждений.

Тем не менее, индуктивное рассуждение занимает свое место в научном методе , и ученые используют его для формирования гипотез и теорий . Затем дедуктивное рассуждение позволяет им применять теории к конкретным ситуациям.

Примеры дедуктивных рассуждений

Вот несколько примеров дедуктивных рассуждений:

Основная предпосылка: У всех млекопитающих есть позвоночник.
Второстепенная предпосылка: Люди — это млекопитающие.
Вывод: У людей есть позвоночник.

Основное помещение: Все птицы откладывают яйца.
Второстепенная предпосылка: Голуби — это птицы.
Вывод: Голуби откладывают яйца.

Основная предпосылка: Все растения осуществляют фотосинтез.
Второстепенная предпосылка: Кактус — это растение.
Вывод: Кактус осуществляет фотосинтез.

Дедуктивное рассуждение движется от общего утверждения к конкретному логическому заключению. В этом случае, если все растения используют фотосинтез, а кактусы являются растениями, то все кактусы используют фотосинтез, что является допустимым примером дедуктивного рассуждения. (Изображение предоставлено: mikroman6/Getty)

Примеры индуктивных рассуждений

Вот несколько примеров индуктивных рассуждений:

Данные: Каждое лето я вижу светлячков на заднем дворе.
Гипотеза: Этим летом я, вероятно, увижу светлячков на своем заднем дворе.

Данные: Я часто простужаюсь, когда люди вокруг меня болеют.
Гипотеза: Простуда заразна.

Данные: Каждая собака, которую я встречаю, дружелюбна.

Гипотеза: Большинство собак обычно дружелюбны.

Если каждая собака, которую вы встречаете, дружелюбна, разумно предположить, что большинство собак обычно дружелюбны.

Это пример индуктивного рассуждения. (Изображение предоставлено Салли Анскомб/Гетти)

Что такое абдуктивное рассуждение

Другая форма научного рассуждения, которая отличается от индуктивного и дедуктивного рассуждения, — это абдуктивное. Абдуктивные рассуждения обычно начинаются с явно неполного набора наблюдений и переходят к наиболее вероятному из возможных объяснений данных, и (открывается в новой вкладке) по данным Колледжа Бьютт (открывается в новой вкладке) в Оровилле, Калифорния. Он основан на выдвижении и проверке гипотез с использованием наилучшей доступной информации. Это часто влечет за собой обоснованное предположение после наблюдения явления, для которого нет четкого объяснения.

Например, человек заходит в гостиную и находит на полу разорванные бумаги. Собака этого человека весь день была одна в квартире. Человек заключает, что собака порвала бумаги, потому что это наиболее вероятный сценарий. Возможно, документы уничтожил член семьи, у которого был ключ от квартиры, или это сделал хозяин дома, но наиболее вероятным выводом является собачья теория.

Абдуктивные рассуждения полезны для формирования гипотез, подлежащих проверке. Абдуктивные рассуждения часто используются врачами, которые ставят диагноз на основании результатов анализов, и присяжными, принимающими решения на основе представленных им доказательств.

Дополнительные ресурсы

В этом руководстве от Scholastic (откроется в новой вкладке) представлены идеи для обучения детей младшего возраста всему научному мышлению. PBS собрала несколько видеоклипов и игр (открывается в новой вкладке) о дедуктивных и индуктивных рассуждениях. Эта книга, написанная Кристофером Муром (открывается в новой вкладке), содержит информацию о том, как использовать научные рассуждения в классе.

Алина Брэдфорд — автор статей для Live Science. За последние 16 лет Алина освещала все, от лихорадки Эбола до андроидов, и писала статьи о здоровье, науке и технике для крупных изданий. Она имеет несколько сертификатов по охране здоровья, безопасности и спасению жизни от Университета штата Оклахома. Цель Алины в жизни – перепробовать как можно больше впечатлений. На сегодняшний день она была пожарным-добровольцем, диспетчером, подменным учителем, художником, уборщиком, автором детских книг, пиццерией, координатором мероприятий и многим другим.