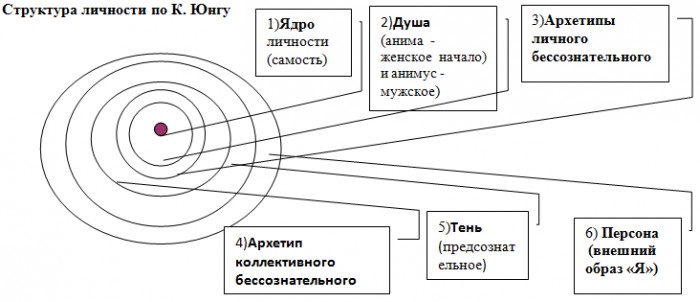
Структура личности по Юнгу
Эго – это сознательный ум. Оно строится из сознательных перцепций, воспоминаний, мыслей и чувств. Эго отвечает за чувство идентичности и непрерывности и с точки индивидуального человека рассматривается как центр сознания.
Личное бессознательное – это регион, примыкающий к Эго. Он состоит из переживаний, некогда бывших сознательными, но вытесненных, подавленных, забытых или игнорируемых, и из переживаний, которые при появлении своем были слишком слабы, чтобы произвести впечатление на уровне сознания. Содержание личного бессознательного доступно сознанию: между личным бессознательным и эго идет сильное «двустороннее движение».
Коллективное (или трансперсональное) бессознательное – наиболее сильная и влиятельная психическая система, и в патологических случаях она перекрывает эго и личное бессознательное (К. Юнг, 1936, 1943, 1945). Коллективное бессознательное – хранилище скрытых воспоминаний, унаследованных от предков;
 Оно почти полностью отделено от личного в жизни индивида, и, по-видимому, универсально. Коллективное бессознательное – врожденное, расовое основание всей структуры личности. На нем вырастают эго, личное бессознательное и другие индивидуальные приобретения.
Оно почти полностью отделено от личного в жизни индивида, и, по-видимому, универсально. Коллективное бессознательное – врожденное, расовое основание всей структуры личности. На нем вырастают эго, личное бессознательное и другие индивидуальные приобретения.Структурные компоненты коллективного бессознательного называются архетипы (доминанты, изначальные образы, имаго, мифологические образы, поведенческие паттерны). Архетип – это универсальная мыслительная форма (идея), содержащая значительный эмоциональный элемент. Эта мыслительная форма создает образы или видения, в обычной бодрствующей жизни соответствующие некоторым аспектам сознательной ситуации. Например, архетип матери продуцирует образ матери, который затем идентифицируется с реальной матерью.
Предполагается, что в коллективном бессознательном содержится множество архетипов. Хотя все архетипы могут быть рассмотрены как автономные динамические системы, относительно независимые от остального в личности, некоторые развились настолько, что в полной мере оправдывают отношение к себе как к отдельным системам внутри личности.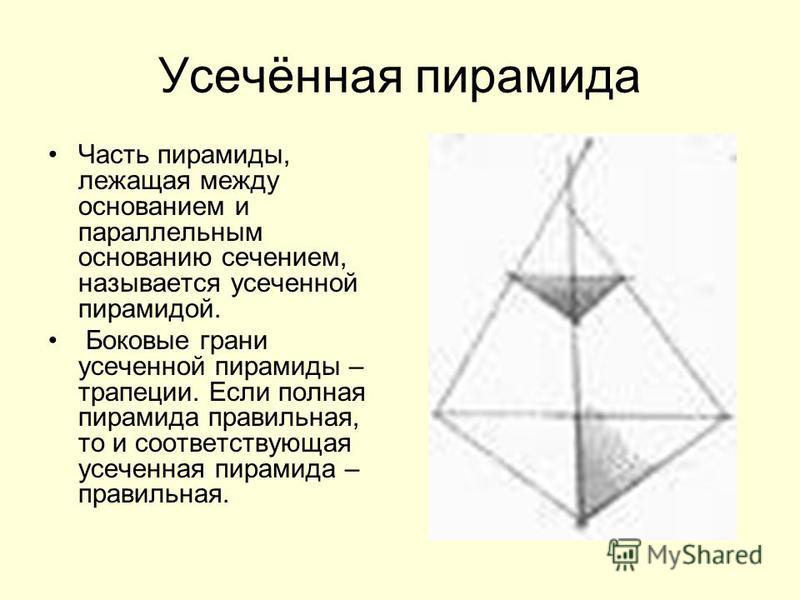 Это: Персона, Анима, Анимус, Тень.
Это: Персона, Анима, Анимус, Тень.
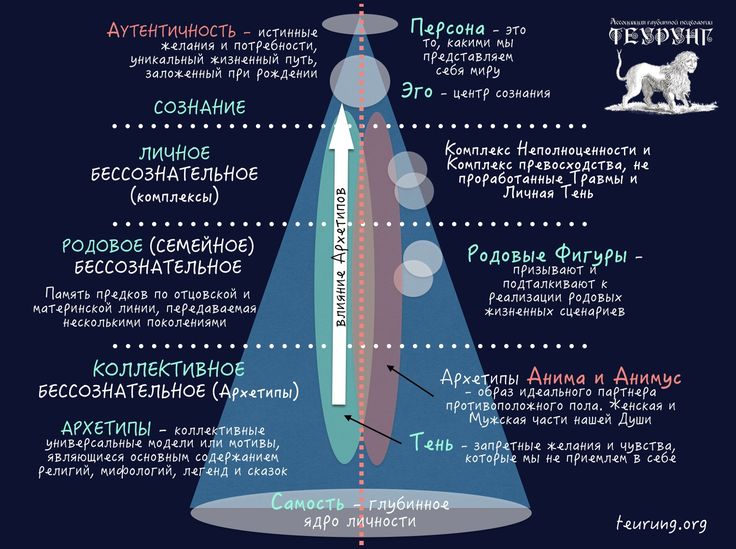
Персона – это то, каким мы представляем себя миру. Она включает наши социальные роли, индивидуальный стиль выражения. Персона имеет как позитивный, так и негативный аспекты. Доминирующая Персона может подавлять, даже задушить индивидуальность. Те, кто отождествляет себя со своей Персоной, начинают видеть себя только с точки зрения своих поверхностных социальных ролей или фасада. К. Юнг называл также Персону архетипом конформности. Вместе с тем Персона не только негативна, она защищает Эго и душу в целом от различных социальных сил и направленных на нее покушений. Персона – прекрасное орудие коммуникации.
Анимус, анима. К.Юнг постулирует бессознательные структуры, которые представляют интросексуальную связь в душе каждого. Фемининный архетип в мужчине называется Анима, маскулинный в женщине – Анимус. Эти архетипы не только являются причиной наличия у представителей каждого пола черт противоположного; они также действуют как коллективные образы, мотивирующие представителей каждого пола на то, чтобы понять представителей другого и ответить.
Архетип Тень – центр личного бессознательного, фокус для материала, который был вытеснен из сознания. Он включает тенденции, желания, воспоминания, переживания, которые отрицаются индивидуумом как несовместимые с его персоной или противоречащие социальным стандартам и идеалам.
Самость – это центр личности, вокруг которого группируются все остальные системы.
Она удерживает эти системы вместе и обеспечивает личности единство, равновесие и стабильность. Самость – это цель, к которой люди постоянно стремятся, но которой редко достигают. Прежде, чем самость воплотится, необходимо, чтобы различные компоненты личности прошли полное развитие и индивидуализацию. По мнению К. Юнга личность может достичь равновесия лишь в результате длительного процесса психологического созревания, называемого им индивидуализацией.источник
Читайте нас в удобном формате
Telegram | Facebook | Instagram | Tags
Двоичные таблицы Юнга / Хабр
Итак, как и обещал, продолжение темы о таблицах Юнга. Напомню, что под таблицей Юнга понимается числовая матрица, обладающая некоторыми специальными свойствами. Матрица – это двумерный массив. И вот тут должен возникнуть естественный вопрос – а почему, собственно, массив должен быть двумерным? А что, если мы попробуем реализовать на тех же принципах таблицу размерности три, или четыре
Напомню, что под таблицей Юнга понимается числовая матрица, обладающая некоторыми специальными свойствами. Матрица – это двумерный массив. И вот тут должен возникнуть естественный вопрос – а почему, собственно, массив должен быть двумерным? А что, если мы попробуем реализовать на тех же принципах таблицу размерности три, или четыре
! О том, куда приведет нас такое обобщение, можно прочитать под катом…
Одномерные таблицы Юнга
Прежде, чем устремлять размерность таблицы Юнга к бесконечности, давайте посмотрим, что у нас остается «за спиной». Меньше двойки только единица (не считая нуля, но таблица Юнга нулевой размерности – это что-то типа нуль-пространства – никто не знает что это такое, но звучит красиво).

Подъем и спуск элементов (базовые операции над таблицами Юнга) в данном случае сводятся к линейному просмотру таблицы справа налево (подъем) или слева направо (спуск):
def MoveUp(X, i):
while i>0 and X[i]>X[i-1]:
X[i], X[i-1] = X[i-1], X[i]
i -= 1
def MoveDown(X, n):
i = 0
while i+1<n and X[i]a>X[i+1]:
X[i], X[i-1] = X[i-1], X[i]
i += 1
Сам алгоритм сортировки практически ничем не отличается от того, который был описан здесь.
def YoungSort(X, n):
for i in range(1,n):
MoveUp(X,i)
for i in range(1,n):
X[0], X[n-i] = X[n-i], X[0]
MoveDown(X,n-i)
Внимательный читатель заметит, что первый цикл в данной сортировке есть ни что иное, как стандартная сортировка вставкой. Правда, результат – последовательность упорядоченная по убыванию. Поэтому, второй цикл выполняет хитрое реверсивное обращение данной последовательности. Понятно, что это обращение можно было бы выполнить и поэффективнее, но сейчас наша цель – попытаться обобщить понятие таблицы Юнга на случай произвольной размерности, поэтому оптимизация одного конкретного случая (да еще такого простого) не имеет смысла.
Понятно, что это обращение можно было бы выполнить и поэффективнее, но сейчас наша цель – попытаться обобщить понятие таблицы Юнга на случай произвольной размерности, поэтому оптимизация одного конкретного случая (да еще такого простого) не имеет смысла.
Обобщенные таблицы Юнга
Примем за определение обобщенной таблицы Юнга следующее: таблицей Юнга называется частично упорядоченный почти заполненный числовой массив размерности d.
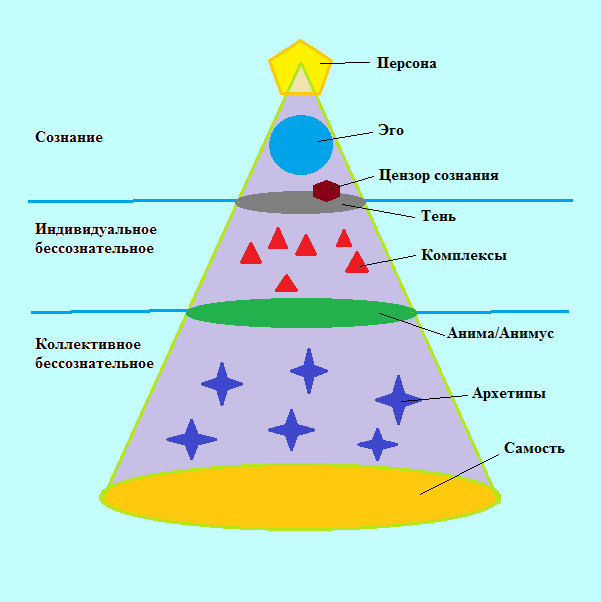 Таким образом, если все индексы ячейки ненулевые, то у нее имеется ровно d верхних соседей, а если все индексы нулевые, то соседей сверху нет – такой элемент назовем вершиной таблицы Юнга.
Таким образом, если все индексы ячейки ненулевые, то у нее имеется ровно d верхних соседей, а если все индексы нулевые, то соседей сверху нет – такой элемент назовем вершиной таблицы Юнга.Тогда, частичная упорядоченность означает, что значение любого элемента таблицы Юнга не больше значений всех его верхних соседей в этой таблице.
Почти заполненность означает, что если некоторая ячейка таблицы Юнга является заполненной (т.е. содержит некоторое значение), то и все ее верхние соседи также являются заполненными.
Нетрудно показать, что вдоль каждой размерности (когда все индексы, кроме одного, зафиксированы) значения ячеек таблицы Юнга образуют невозрастающую последовательность. Как следствие, самый большой элемент таблицы всегда располагается в ее вершине.
К сожалению, визуализация уже трехмерных таблиц Юнга сопряжена со значительными трудностями, поэтому читателю предлагается включить свое многомерное воображение, помогая ему (воображению) при необходимости картинками обычных двумерных таблиц Юнга.

Операции подъема и спуска обобщаются очевидным образом. При подъеме некоторого элемента перебираются все его соседи сверху, если обнаруживаются соседи с меньшими значениями, то из них выбирается наименьший, он меняется местами с текущим и процесс продолжается для нового текущего элемента. Если значения всех верхних соседей больше текущего, то подъем закончен. Пример подъема элемента в трехмерной таблице Юнга приведен на рисунке (показан только фрагмент таблицы).
Спуск выполняется аналогично, но перебираются все соседи снизу (ячейки, для которых текущая является верхним соседом) и из них выбирается наибольший.
Используя данные две операции, можно реализовать вставку нового элемента в таблицу и удаление наибольшего элемента из таблицы. А уже с помощью вставки и удаления просто реализуется сортировка. Реализация подъема и спуска, в принципе, не должная вызывать особых трудностей даже для d-мерных таблиц, но, все-таки, сначала попытаемся оценить сложность данных двух операций.
Будем предполагать, что каждый индекс d-мерной таблицы Юнга изменяется от 0 до m-1. Возьмем наихудший случай – таблица заполнена до конца (число элементов n=m d), требуется поднять последний ее элемент, который (так получилось) является наибольшим. Т.е. в конце подъема этот элемент должен оказаться на вершине таблицы. Т.к. в процессе подъема на каждой итерации уменьшается на единицу ровно один индекс элемента, то всего придется выполнить порядка dm итераций. На каждой итерации выполняется один обмен, и не более d сравнений (при просмотре соседей). Итого, одна операция подъема (в худшем случае) обойдется нам в O(d2m) действий. Это значит, что n таких операций будут стоить уже O(d2mn) действий. С учетом того, что n=md, получаем следующую оценку сложности сортировки с помощью d-мерной таблицы Юнга: O(d2n1+1/d).
Хорошая новость – с увеличением d уменьшается показатель степени 1+1/d: 2 (одномерная таблица Юнга), 1.

Двоичные таблицы Юнга
Хотя мы и показали, что даже в лучшем случае сортировка с помощью таблиц Юнга не дотягивает до асимптотической оптимальности, мы все же попытаемся реализовать лучшую из таких таблиц, т.е. таблицу размерности d=log2n, которую будем называть двоичной таблицей Юнга. Пусть такая таблица и не может использоваться для организации эффективной сортировки, тем не менее, возможно кому-нибудь удастся найти ей и полезное применение. А кроме всего прочего, реализация двоичной таблицы Юнга просто является хорошим упражнением по программированию.
А кроме всего прочего, реализация двоичной таблицы Юнга просто является хорошим упражнением по программированию.
Сначала давайте формализуем понятие двоичной таблицы Юнга. Будем называть двоичной таблицу Юнга размерности d, в которой каждый индекс может принимать всего два значения 0 и 1. Если обозначить через n емкость такой таблицы, то получим, что n=2d или d=log2n. Примеры таких таблиц для небольших значений d показаны на следующем рисунке. Ага, скажет проницательный читатель, да ведь это гиперкубы размерности d! И будет совершенно прав.
Теперь давайте развернем такой гиперкуб в линейный массив, используя стандартную схему расположения многомерных массивов в памяти – быстрее всего меняется младший индекс. Для примера рассмотрим таблицу размерности d=3 с предыдущего рисунка.
Что мы видим – индексы, трактуемые как числа в двоичной системе счисления, образуют последовательность 0, 1, 2, 3 и т.д. То есть, мы получили простой алгоритм преобразования координат ячейки в двоичной таблице Юнга в координаты этой же ячейки в линеаризованной таблице. Ну а с битами мы работать-то умеем! Кажется, умеем…
Ну а с битами мы работать-то умеем! Кажется, умеем…
Ключевыми понятиями таблицы Юнга являются верхние и нижние соседи ячеек. Применительно к двоичной таблице Юнга эти понятия определяются следующим образом: ячейка с индексом i (в линеаризованной таблице) называется верхним соседом ячейки с индексом j, если битовое представление числа i совпадает с битовым представлением числа j, за исключением ровно одного бита, который в j равен единице, а в i – нулю. Соответственно, ячейка j в данном определении будет нижним соседом ячейки i. Например, ячейка с номером 6=1102 является верхним соседом ячейки с номером 7=1112, и нижним соседом ячейки с номером 2=0102.
Подъем и спуск элементов
Операции подъема и спуска определяются точно так же, как они были определены выше для обобщенных таблиц. Чтобы реализовать эти операции для двоичных таблиц в силу только что сделанного определения верхних и нижних соседей, нам нужен эффективный алгоритм перебора всех единичных (подъем) или нулевых (спуск) битов заданного целого числа. Специально для тех, кому лень думать в этом направлении, имеется замечательная книжка Генри Уоррена «Алгоритмические трюки для программистов», где имеются интересующие нас формулы. Итак, чтобы обнулить крайний справа единичный бит числа x, используется операция x&(x-1). Для замены крайнего с правого нуля на единицу используется аналогичная операция x|(x+1). Этих операций (плюс немного танцев с бубном) оказывается достаточно для организации перебора всех единиц (нулей) в заданном целом числе.
Специально для тех, кому лень думать в этом направлении, имеется замечательная книжка Генри Уоррена «Алгоритмические трюки для программистов», где имеются интересующие нас формулы. Итак, чтобы обнулить крайний справа единичный бит числа x, используется операция x&(x-1). Для замены крайнего с правого нуля на единицу используется аналогичная операция x|(x+1). Этих операций (плюс немного танцев с бубном) оказывается достаточно для организации перебора всех единиц (нулей) в заданном целом числе.
Реализация
Ниже приведена реализация операций подъема и спуска элементов для двоичной таблицы Юнга, представленной вектором X.
def MoveUp(X, i):
while True:
t = i
j = i
while j: # цикл по всем единичным битам числа i
k = j-1
l = k&i
if X[t]>X[l]: t = l # нашли нового большего соседа
j = k&j
if i==t: return # подъем закончен
X[i], X[t] = X[t], X[i] # поднимаем элемент
i = t
При спуске соседи перебираются в порядке возрастания их номеров, поэтому при обнаружении первого пустого соседа (с номером большим размера таблицы) перебор заканчивается.
def MoveDown(X, n):
i = 0
while True:
t = i
j = i
while True: # цикл по всем нулевым битам
k = j+1
l = k|i
if l>=n: break # все оставшиеся нижние соседи - пустые
if X[t]<X[l]: t = l # нашли нового меньшего соседа
j = k|j
if i==t: return # приехали
X[i], X[t] = X[t], X[i]
i = t
Сама сортировка выполняется по уже стандартной схеме.
def YoungTableauSort(X, n):
for i in range(1,n): # собираем таблицу Юнга
MoveUp(X,i)
for i in range(1,n): # упорядочиваем последовательность
X[0], X[n-i] = X[n-i], X[0]
MoveDown(X,n-i)
Вместо заключения
Итак, чего же мы добились? Кто-то скажет, что ничего особенного, и будет по своему прав. Сортировка явно не дотягивает до оптимальной, проигрывая, например, пирамидальной сортировке, устроенной на аналогичных принципах.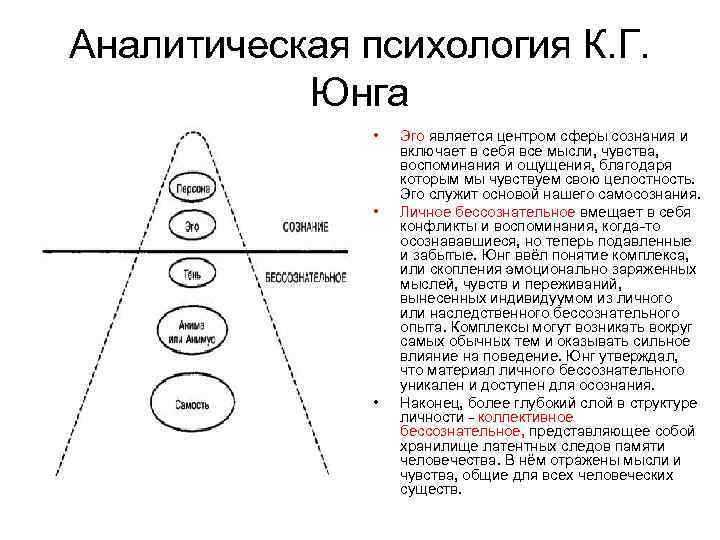 По тем же причинам, реализация АТД Очередь с приоритетом на основе двоичных таблиц Юнга уступает аналогичной реализации с помощью пирамид. Ко всему прочему, переход от стандартных таблиц к двоичным убил, наверное, единственное преимущество таблиц Юнга над пирамидами — поиск произвольного элемента. Напомню, что в двумерных таблицах такой поиск выполняется за время O(n1/2), а вот в двоичных таблицах поиск произвольного значения потребует почти полного перебора всей таблицы, т.е. линейного по n времени. С другой стороны, как говорится, кто не рискует, тот не пьет шампанского. Мы попытались придумать новый алгоритм сортировки и нам это удалось. Да еще и с такой редкой производительностью O(nlog2n)! И еще, у автора все-таки теплится надежда, что такая красивая структура данных просто обязана иметь какие-нибудь интересные и полезные свойства, которые возможно удастся открыть кому-нибудь из читателей. Спасибо за внимание!
По тем же причинам, реализация АТД Очередь с приоритетом на основе двоичных таблиц Юнга уступает аналогичной реализации с помощью пирамид. Ко всему прочему, переход от стандартных таблиц к двоичным убил, наверное, единственное преимущество таблиц Юнга над пирамидами — поиск произвольного элемента. Напомню, что в двумерных таблицах такой поиск выполняется за время O(n1/2), а вот в двоичных таблицах поиск произвольного значения потребует почти полного перебора всей таблицы, т.е. линейного по n времени. С другой стороны, как говорится, кто не рискует, тот не пьет шампанского. Мы попытались придумать новый алгоритм сортировки и нам это удалось. Да еще и с такой редкой производительностью O(nlog2n)! И еще, у автора все-таки теплится надежда, что такая красивая структура данных просто обязана иметь какие-нибудь интересные и полезные свойства, которые возможно удастся открыть кому-нибудь из читателей. Спасибо за внимание!
Литература:
- Кормен Т. и др.
 — Алгоритмы. Построение и анализ, 2009
— Алгоритмы. Построение и анализ, 2009 - Фултон У. — Таблицы Юнга, 2006
- Уоррен Г. — Алгоритмические трюки для програмистов, 2004
PS: Кстати, вполне допускаю мысль, что все описанное выше уже когда-то кем-то открыто. Буду очень признателен, если у кого-нибудь есть такого рода информация и он готов ей поделиться!
| ||||||||||||||||||||||||
молодая пирамида | TikTok Search
TikTokUpload
For You
Following
yung_pyramid
yung_pyramid
Throw some sad boy shit on this #music #cashapp13plus #sad #duet #fyp #yungpyramid #soh #openverse #imscaredofthedark
989 лайков, 19 комментариев. Видео в TikTok от yung_pyramid (@yung_pyramid): «Добавьте немного грустного мальчишеского дерьма в эту #музыку #cashapp13plus #sad #duet #fyp #yungpyramid #soh #openverse #imscaredofthedark». оригинальный звук.
Видео в TikTok от yung_pyramid (@yung_pyramid): «Добавьте немного грустного мальчишеского дерьма в эту #музыку #cashapp13plus #sad #duet #fyp #yungpyramid #soh #openverse #imscaredofthedark». оригинальный звук.
2689 просмотров|
оригинальный звук — yung_pyramid
.kobe222
B🤎
🫶🏽🫶🏽
TikTok видео от B🤎 (@.kobe222): «🫶🏽». Я настоящий юный строитель пирамид из 208🔪 | Настоящий молодой строитель пирамид из 208💪🏽. Мне не нравится тот, кто начал эту тенденцию.
327 просмотров|
I dislike whoever started this trend — Jama
<3mudcravers
Allen
The youngest pyramid in the world,d u want to live in it #TikTokBrushes #art #pyramid #foryou #fypシ #house #youngset
15,2 тыс.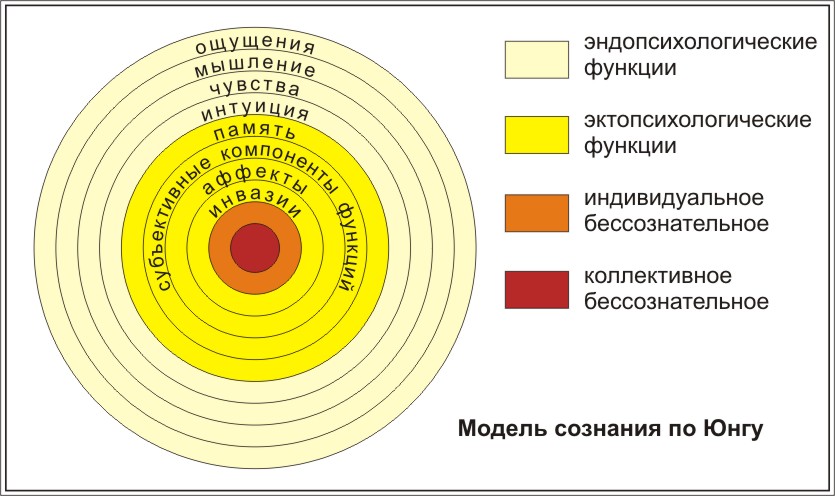 лайков, 361 комментарий. Видео TikTok от Аллена (@mudcravers): «Самая молодая пирамида в мире, ты хочешь в ней жить #TikTokBrushes #art #pyramid #foryou #fypシ #house #youngset». Спаз.
лайков, 361 комментарий. Видео TikTok от Аллена (@mudcravers): «Самая молодая пирамида в мире, ты хочешь в ней жить #TikTokBrushes #art #pyramid #foryou #fypシ #house #youngset». Спаз.
391,1 тыс. просмотров|
Spaz — Mr. 2-17 & DRIPPY PRODUCTIONS
youngzeiss
Young ZEISS
Die Drehpyramide ist bestandteil des Grundkurses an der Drehmaschine #youngzeiss #zerspanungsmechaniker #drehen #job
273 Likes , 6 комментариев. Видео TikTok от Young ZEISS (@youngzeiss): «Die Drehpyramide ist bestandteil des Grundkurses an der Drehmaschine #youngzeiss #zerspanungsmechaniker #drehen #job». Unsere Aufgabe: Дрепирамид энтгратен — Yazan erklärt wie. Летний день.
26,8 тыс. просмотров|
Летний день — TimTaj
byrondempsey
Byron Dempsey
Пирамиды настолько продвинуты для такого древнего общества… что вы думаете? ЭП. 37 #пирамиды #заговор #история #drivenyoung
37 #пирамиды #заговор #история #drivenyoung
2,8 тыс. лайков, 48 комментариев. Видео в TikTok от Байрона Демпси (@byrondempsey): «Пирамиды настолько продвинуты для такого древнего общества… что вы думаете? EP. 37 #pyramids #conspiracy #history #drivenyoung». ЧУЖИЕ построили пирамиды?. Париж.
23,6 тыс. просмотров|
Paris — Else
civilisationsforgotten
Civilisations Forgotten
You can’t argue this one #pyramids #lostcivilization #ancient #sphinx #fyp #ancientegypt #youngerdryas #ancienthistory #engineering
2,5 тыс. лайков, 144 комментария. Видео TikTok от Civilizations Forgotten (@civilisationsforgotten): «С этим не поспоришь #pyramids #lostcivilization #ancient #sphinx #fyp #ancientegypt #yougerdryas #ancienthistory #engineering». ДОКАЗАТЕЛЬСТВА того, что пирамиды были построены в 10 500 г. до н.э. 📜. оригинальный звук.
ДОКАЗАТЕЛЬСТВА того, что пирамиды были построены в 10 500 г. до н.э. 📜. оригинальный звук.
73,6 тыс. просмотров|
Оригинальный звук — Цивилизации забыты
Hottaudy
Райан
Блажены, чтобы найти мою карьеру So Young😍 #pyramischeme #Marykay #FORYOU 5 #MARYKAY #FORYOOU 5555555555.HALISBY #FORYOU 55555555.HALIZ. «Я счастлив, что моя карьера такая молодая😍 #pyramidscheme #marykay #foryou #xyzbca». I Lived (Сделано популярным OneRepublic) [Вокальная версия].
3201 просмотр|
I Lived (Сделано популярным OneRepublic) [Вокальная версия] — Party Tyme Karaoke
civilisationsforgotten
Civilisations Forgotten
This puts it back to the younger dryas #sphinx #pyramids #lostcivilization #ancient #fyp #architecture #history #youngerdryas
577 лайков, 25 комментариев.
 — Алгоритмы. Построение и анализ, 2009
— Алгоритмы. Построение и анализ, 2009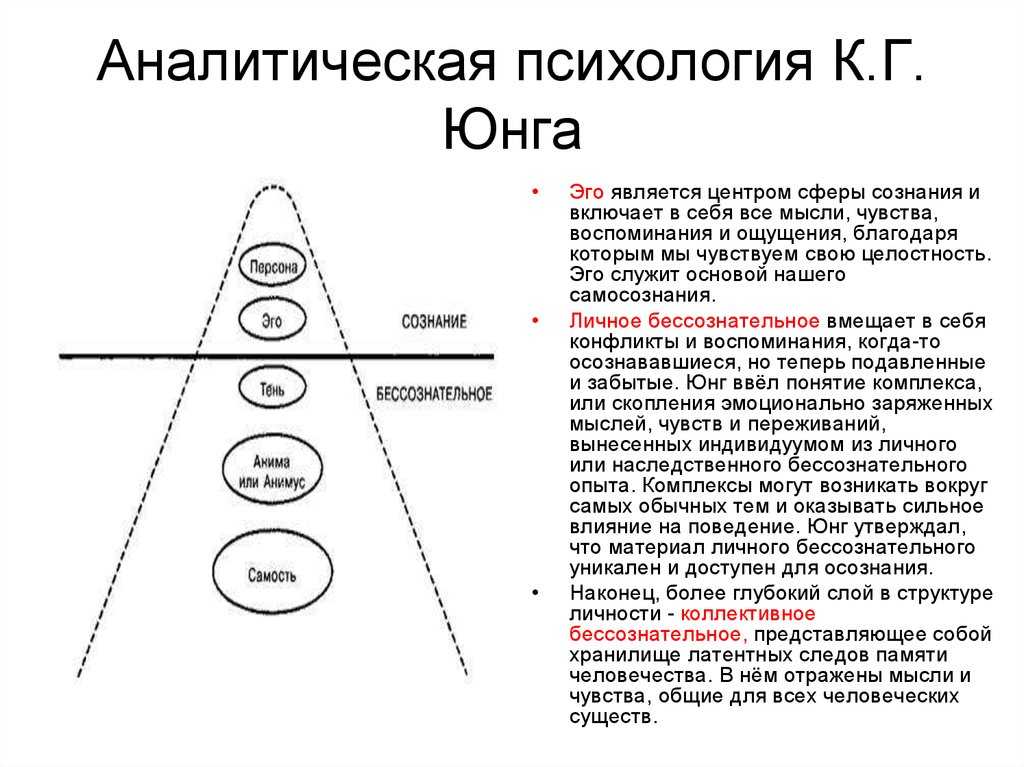 )
)
 Зарегистрируйтесь сегодня!
Зарегистрируйтесь сегодня!