Правила решения примеров: Ошибка 403 — доступ запрещён

Содержание

Основные правила математики с примерами. 5 класс

Содержание

Натуральные числа
Сравнение натуральных чисел
Свойства сложения
Формула пути
Корень уравнения
Правила решения уравнений
Отрезок, прямая, луч
Угол, биссектриса угла
Углы: развернутый, прямой, острый, тупой
Многоугольники. Равные фигуры
Треугольники: остроугольный, прямоугольный, тупоугольный
Треугольники: равнобедренный, равносторонний, разносторонний

Прямоугольник. Квадрат. Периметр
Умножение. Свойства умножения
Деление. Деление с остатком
Площадь. Площадь квадрата, прямоугольника
Объем. Объем прямоугольного параллелепипеда, куба
Дроби: правильная, неправильная, сравнение дробей
Сложение и вычитание дробей с одинаковыми знаменателями
Сложение и вычитание смешанных чисел
Преобразование неправильной дроби в смешанное число

Преобразование смешанного числа в неправильную дробь
Десятичные дроби: свойства, сравнение, округление
Десятичные дроби: сложение, вычитание
Десятичные дроби: умножение, деление
Среднее арифметическое
Процент

Натуральные числа

Числа 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12 и т. д., которые используют при счете предметов, называют натуральными.

Сравнение натуральных чисел

Число 0 меньше любого натурального числа.

0<1, 0<100

Из двух натуральных чисел, которые имеют разное количество цифр большим является то, у которого количество цифр больше.

4352⏟4>999⏟3

Из двух натуральных чисел с одинаковым количеством цифр большим является то, у которого больше первая (при чтении слева направо) из неодинаковых цифр

3561>3559

Свойства сложения

Переместительный закон:

15+10=10+15

Сочетательный закон:

(23+15)+25=23+(15+25)

Формула пути

S=V·t,где S — пройденный путь, V — скорость движения, t — время, за которое пройден путь S

= 50км, = 2ч, = 25км/ч

, 50км = 25км/ч· 2ч

, 25км/ч = 50км : 2ч

, 2ч = 50км : 25км/ч

Корень уравнения

Корнем (решением) уравнения называют число, которое при подстановке его вместо буквы превращает уравнение в верное числовое равенство.

2·x+10=16

x = 3 — корень, так как 2·3+10=16

Что значит «Решить уравнение»

Решить уравнение — это значит найти все его корни или убедиться, что их вообще нет.

Правила решения уравнений

Чтобы найти неизвестное слагаемое, надо из суммы вычесть известное слагаемое.

20слагаемое+xслагаемое=100суммаx = 100 — 20x = 80

Чтобы найти неизвестное уменьшаемое, надо к разности прибавить вычитаемое.

xуменьшаемое—10вычитаемое=40разностьx = 40 + 10x = 50

Чтобы найти неизвестное вычитаемое, надо из уменьшаемого вычесть разность.

50уменьшаемое—xвычитаемое=40разностьx = 50 — 40x = 10

Чтобы найти неизвестный множитель, надо произведение разделить на известный множитель.

xмножитель·7множитель=56произведениеx = 56 : 7x = 8

Чтобы найти неизвестное делимое, надо делитель умножить на частное.

xделимое:8делитель=9частноеx = 9 · 8x = 72

Чтобы найти неизвестный делитель, надо делимое разделить на частное.

42делимое:xделитель=7частноеx = 42 : 7x = 6

Отрезок, прямая, луч

Отрезок

Отрезок — часть прямой, ограниченная двумя точками(концами) и все точки между этими концами(внутренние точки отрезка)

Свойство длины отрезка

Если на отрезке отметить точку , то длина отрезка равна сумме длин отрезков и .

Равные отрезки

Два отрезка называют равными, если они совмещаются при наложении.

Свойство прямой

Через две точки проходит только одна прямая.

Измерить отрезок

Измерить отрезок означает подсчитать, сколько единичных отрезков в нем помещается

Ломаная

Ломаная — геометрическая фигура, состоящая из отрезков, последовательно соединенных друг с другом

Луч

Луч (полупрямая) — это геометрическая фигура, часть прямой, состоящая из точки(начала луча) и всех точек прямой, лежащих по одну сторону от начала луча.В названии луча присутствуют две буквы, например, . Причем первая буква всегда обозначает точку начала луча, поэтому менять местами буквы нельзя.

Угол, биссектриса угла

Угол

Фигуру, образованную двумя лучами, имеющими общее начало, называют углом.

Равные углы

Два угла называют равными, если они совмещаются при наложении.

Свойство величины угла

Если между сторонами угла ∠ провести луч , то градусная мера ∠ равна сумме градусных мер углов ∠ и ∠, то есть ∠ = ∠+ ∠.

Биссектриса угла

Луч, который делит угол на два равных угла, называется биссектрисой угла.

Углы: развернутый, прямой, острый, тупой

Развернутый угол

Угол, стороны которого образуют прямую, называют развернутым. Градусная мера развернутого угла равна 180°.

Прямой угол

Угол, градусная мера которого равна 90°, называют прямым.

Острый угол

Угол, градусная мера которого меньше 90°, называют острым.

Тупой угол

Угол, градусная мера которого больше 90°, но меньше 180°, называют тупым.

Многоугольники.

Равные фигуры

Равные многоугольники

Два многоугольники называют равными, если они совмещаются при наложении.

Равные фигуры

Две фигуры называют равными, если они совмещаются при наложении.

Треугольники: остроугольный, прямоугольный, тупоугольный

Остроугольный треугольник

Если все углы треугольника острые, то его называют остроугольным треугольником.

Прямоугольный треугольник

Если один из углов треугольника прямой, то его называют прямоугольным треугольником.

Тупоугольный треугольник

Если один из углов треугольника тупой, то его называют тупоугольным треугольником.

Треугольники: равнобедренный, равносторонний, разносторонний

Равнобедренный треугольник

Если две стороны треугольника равны, то его называют равнобедренным треугольником.

Равносторонний треугольник

Если три стороны треугольника равны, то его называют равносторонним треугольником.

Периметр равностороннего треугольника

Если сторона равностороннего треугольника равна , то его периметр вычисляют по формуле

Разносторонний треугольник

Если три стороны треугольника имеют разную длину, то его называют разносторонним треугольником.

Прямоугольник. Квадрат. Периметр

Прямоугольник

Если в четырехугольнике все углы прямые, то его называют прямоугольником.

Свойство прямоугольника

Противоположные стороны прямоугольника равны.

Периметр прямоугольника

Если соседние стороны прямоугольника равны и , то его периметр вычисляют по формуле

Квадрат

Прямоугольник, у которого все стороны равны, называют квадратом.

Периметр квадрата

Если сторона квадрата равна , то его периметр вычисляют по формуле .

Умножение. Свойства умножения

Умножение

Произведением числа на натуральное число , которое не равно 1, называют сумму, состоящую из слагаемых, каждый из которых равен . В равенства числа и называют множителями, а число и запись — произведением.

Если один из двух множителей равен 1, то произведение равно второму множителю.

Если один из множителей равен нулю, то произведение равно нулю.

Если произведение равно нулю, то хотя бы один из множителей равен нулю.

Свойства умножения

Переместительный закон умножения:

Сочетательный закон умножения:

Распределительное свойство умножения относительно сложения:

2·(3+10) = 2·3 + 2·103·11 + 3·4 = 3·(11 + 4)

Распределительное свойство умножения относительно вычитания:

2·(15—7) = 2·15 — 2·73·10 — 3·4 = 3·(10 — 4)

Деление. Деление с остатком

Деление

Для натуральных чисел равенство является правильным, если является правильным равенство

15 : 5 = 3 -правильное равенство, так как равенство 5 · 3 = 15 верное

В равенстве число называют делимым, число — делителем, число и запись — частным от деления, отношением, долей.

На ноль делить нельзя.

Для любого натурального числа правильными являются равенства:

Деление с остатком

, где — делимое, — делитель, — неполное частное, — остаток, .

154делимое=50делитель · 3неполное частное + 4остаток, 4<50

Если остаток равен нулю, то говорят, что число делится нацело на число .

Площадь. Площадь квадрата, прямоугольника

Свойства площади фигуры

Равные фигуры имеют равные площади;

Площадь фигуры равна сумме площадей фигур, из которых она состоит.

Площадь прямоугольника

Площадь прямоугольника равна произведению длин его соседних сторон, выраженных в одних и тех же единицах.

Площадь квадрата

где — площадь квадрата, — длина его стороны.

Объем. Объем прямоугольного параллелепипеда, куба

Свойства объема фигуры

Равные фигуры имеют равные объемы;
Объем фигуры равен сумме объемов фигур, из которых она состоит.

Объем прямоугольного параллелепипеда

где — объем параллелепипеда, , и — его измерения, выраженные в одних и тех же единицах;

, где — площадь поверхности прямоугольного параллелепипеда.

где — площадь основания параллелепипеда, — его высота.

Объем куба

где — объем куба, — длина его ребра.

Дроби: правильная, неправильная, сравнение дробей

Правильная дробь

Дробь, числитель которой меньше знаменателя, называют правильной

Неправильная дробь

Дробь, числитель которой больше знаменателя или равен ему, называют неправильной.

Сравнение дробей

Из двух дробей с одинаковыми знаменателями больше та, числитель которой больше, и меньше та, числитель которой меньше.

Из двух дробей с одинаковыми числителями больше та, знаменатель которого меньше, и меньшая та, знаменатель которой больше.

Все правильные дроби меньше единицы, а неправильные — больше или равны единице.

Любая неправильная дробь больше любой правильной дроби.

Сложение и вычитание дробей с одинаковыми знаменателями

Чтобы найти сумму двух дробей с одинаковыми знаменателями, нужно сложить их числители, а знаменатель оставить тот же.

Чтобы найти разность двух дробей с одинаковыми знаменателями, надо из числителя уменьшаемого вычесть числитель вычитаемого, а знаменатель оставить тот же.

Сложение и вычитание смешанных чисел

Чтобы найти сумму двух смешанных чисел, надо отдельно сложить их целые и дробные части.

Чтобы найти разность двух смешанных чисел, надо от целой и дробной части уменьшаемого вычесть соответственно целую и дробную части вычитаемого.

Преобразование неправильной дроби в смешанное число

Чтобы неправильную дробь, числитель которой не делится нацело на знаменатель, преобразовать в смешанное число, нужно

числитель разделить на знаменатель;
полученное неполное частное записать как целую часть смешанного числа, а остаток — как числитель его дробной части.

227= смешанное число? 7322—211 227=317

Преобразование смешанного числа в неправильную дробь

Чтобы преобразовать смешанное число в неправильную дробь нужно

целую часть числа умножить на знаменатель дробной части;
к полученному произведению прибавить числитель дробной части;
эту сумму записать как числитель неправильной дроби;
в его знаменателе записать знаменатель дробной части смешанного числа.

523= неправильная дробь?523=5*3+23=15+23=173

Десятичные дроби: свойства, сравнение, округление

Свойства десятичной дроби

Если к десятичной дроби справа приписать любое количество нулей, то получим дробь, равную данной.

Значение дроби, которая заканчивается нулями, не изменится, если последние нули в его записи отбросить.

2,23 = 2,230 = 2,230000005,50000=5,50000=5,5

Сравнение десятичных дробей

Из двух десятичных дробей больше та, у которой целая часть больше.

Чтобы сравнить две десятичные дроби с равными целыми частями и разным количеством цифр после запятой, надо

с помощью приписывания нулей справа уравнять количество цифр в дробных частях,
после чего сравнить полученные дроби поразрядно.

Сравнить 5,03 и 5,0375.5,03⏟2=5,0300⏟4 и 5,0375⏟4 ; 5,0300 < 5,0375.

Округление десятичных дробей

Для того чтобы десятичную дробь округлить до единиц, десятых, сотых и т. д., надо

все следующие за этим разрядом цифры отбросить.
если при этом первая из цифр, которые отбрасывают равна 0,1, 2, 3, 4, то последнюю из цифр, которые оставляют, не меняют;
если же первая из цифр, которые отбрасывют, равна 5, 6, 7, 8, 9, то последнюю из цифр, которые оставляют, увеличивают на единицу.

Округлить 5,248 и 3,952:а) до десятых:5,248≈5,2; 3,952≈4,0;б) до сотых:5,248≈5,25;3,952≈3,95.

Десятичные дроби: сложение, вычитание

Сложение десятичных дробей

Чтобы найти сумму двух десятичных дробей, нужно:

уравнять количество цифр после запятых;
записать слагаемые друг под другом так, чтобы каждый разряд второго слагаемого оказался под соответствующим разрядом первого слагаемого;
сложить полученные числа так, как складывают натуральные числа;
поставить в полученной сумме запятую под запятыми.

Сложить 2,5 и 3,623.2,500⏟3 и 3,263⏟3;2,500+3,2635,763

Вычитание десятичных дробей

Чтобы найти разность двух десятичных дробей, нужно:

уравнять количество цифр после запятых;
записать вычитаемое под уменьшаемым так, чтобы каждый разряд вычитаемого оказался под соответствующим разрядом уменьшаемого;
выполнить вычитание так, как вычитают натуральные числа;
поставить в полученной разности запятую под запятыми.

Вычесть 3,27 и 3,009.3,270⏟3 и 3,009⏟3;3,270—3,0090,261

Десятичные дроби: умножение, деление

Умножение десятичных дробей

Чтобы перемножить две десятичные дроби, надо:

перемножить их как натуральные числа, не обращая внимания на запятые;
в полученном произведении отделить запятой справа столько цифр, сколько их стоит после запятых в обоих множителях вместе.

Умножить 1,5 и 2,25.2×2,2511,5+1125225·33,375 —количество цифр после запятой

Чтобы умножить десятичную дробь на 10, 100, 1000 и т. д., надо в этой дроби перенести запятую вправо на 1, 2, 3 и т. д. цифры.

Умножить 1,235 на 10, 100, 1000.а) на 10:1,235 ×10⏟1=12,35б) на 100:1,235 ×100⏟2 = 123,5в) на 1000:1,235 ×1000⏟3=1235,0 = 1235

Чтобы умножить десятичную дробь на 0,1; 0,01; 0,001 и т. д., надо в этой дроби перенести запятую влево соответственно на 1, 2, 3 и т. д. цифры.

Умножить 512,3 на 0,1, 0,01 и 0,001.а) на 0,1:512,3 ×0,1⏟1=51,23б) на 0,01:512,3 ×0,01⏟2=5,123в) на 0,001:512,3 ×0,001⏟3=0,5123

Деление десятичных дробей

Чтобы разделить десятичную дробь на десятичную, надо:

перенести в делимом и в делителе запятую вправо на столько цифр, сколько их содержится после запятой в делителе;

выполнить деление на натуральное число.

Разделить 24,2 на 0,02.24,2 : 0,02⏟ 2= 2420,0 : 2 = 2420 : 2 = 1210.

Чтобы разделить десятичную дробь на 10, 100, 1000 и т. д., надо в этой дроби перенести запятую влево на 1, 2, 3 и т. д. цифры.

Разделить 25,5 на 10, 100, 1000.а) на 10:25,5 : 10⏟1=2,55;б) на 100:25,5 : 100⏟2=0,255;в) на 1000:25,5 : 1000⏟3=0,0255;

Среднее арифметическое

Средним арифметическим нескольких чисел называют результат деления сумму этих чисел на количество слагаемых.

Найти среднее арифметическое чисел 15, 25 и 20.

15+25+20⏞сумма чисел3⏟количество чисел = 603= 20

Примечание:

Задача. Автомобиль 200 км ехал со скоростью 50 км/ч. Затем 120 км он ехал со скоростью 30 км/ч. Найти среднюю скорость.

Здесь

Vсредняя =Sобщtобщ .

1) 200 + 120 = 320(км) -весь путь;

2) 200 : 50 = 4(ч) — время, затраченное на 1-ую часть пути;

3) 120 : 30 = 4(ч) — время, затраченное на 2-ую часть пути;

4) 4 + 4 = 8(ч) — все время;

5) 320 : 8 = 40(км/ч) — средняя скорость.

Ответ: 40 км/ч.

Процент

Процентом называют сотую часть величины или числа 1%=

Найти 4% от числа 20.20 : 100 = 0,2 (0,2 —это 1% от числа 20);0,2 × 4 =0,8( 0,8—искомое число).Или 4% = 4100 = 0,04;0,04 ×20 = 0,8.

Решение примеров со скобками

Метки

Математика Мозг Ум Цифры Школа

Решение примеров со скобками дети проходят уже во втором классе. И хотя все эти знания впоследствии многократно закрепляются при решении всё более сложных примеров, но иногда ощутимого результата это не дает. И ребенок так и не усваивает главные принципы решения. А потому и во взрослом возрасте не может с такими заданиями совладать.

Сегодня редакция «Так Просто!» предлагает решить несколько примеров со скобками. Попутно вспомним, каких правил в этом деле следует придерживаться. Да и в целом такая небольшая математическая разминка довольно полезна для ума. А потому советуем регулярно решать интересные задачки и примеры как взрослым, так и детям.

Первое задание кажется довольно простым. Однако скобки способны запутать даже признанных хорошистов, не говоря уже о троечниках, тем более двоечниках. Постарайся пошагово решить этот пример, не сделав ни единой ошибки.
Во втором задании снова-таки есть и скобки, и деление, и умножение. Однако похоже, что выполнять математические операции придется в другом порядке. Попробуй вспомнить необходимые правила, которых нужно придерживаться в этой ситуации. И помни, что правильный ответ только один.
Третий пример выглядит более сложным. Но если знать, какие действия в каком порядке выполнять, то и здесь легко найти правильный ответ. Также не забудь свериться с нашими объяснениями и ответами во второй части статьи.

Объяснения и ответы

В первую очередь напомним простые правила, о которых многие взрослые люди уже вполне могли забыть. Если в примере отсутствуют скобки, то все математические операции выполняются слева направо. Но при этом деление и умножение выполняем сразу, а сложение и вычитание позже.

В примерах со скобками всё чуть сложнее, но не намного. Тут сперва выполняем всё в скобках (как описано выше), а затем выполняем все математические операции слева направо, учитывая, что деление и умножение снова-таки имеют более высокий приоритет.

Учитывая описанные алгоритмы, в первом задании сначала выполняем действия в скобках, потом делим, а только в самом конце умножаем. Таким образом получаем: 10 ÷ 5 × 2 = 2 × 2 = 4.
Во втором примере сначала выполняем действия в скобках, потом умножаем, а только напоследок делим. В итоге наш пример приобретает следующий вид: 10 × 4 ÷ 2 = 40 ÷ 2 = 20.
Теперь последний пример наверняка уже не кажется читателю таким страшным, как прежде. Сперва высчитываем, что в скобках у нас 10 – 2 × 3 = 10 – 6 = 4. Тогда весь пример решается так: 4 + 2 × 4 = 4 + 8 = 12.
© Depositphotos

Надеемся, что теперь решение примеров со скобками не будет представлять для тебя трудную задачку. А если же эти задания считаешь слишком простыми, то попробуй решить более сложные примеры, которые мы публиковали совсем недавно. Сможешь не наделать ошибок? Не забудь поделиться своими решениями в комментариях.

Десять простых правил решения любой проблемы

Добро пожаловать! Сделайте три глубоких вдоха, каждый раз с силой выдыхая воздух через нос. Теперь вы готовы к этому приключению. Давайте погрузимся прямо и поразмыслим над предпосылкой этого сообщения в блоге.

Лично мне не нравится слово «решать». Что это вообще значит? И это уже второй раз, когда я использую это слово. Слово «решить» подразумевает всякую чепуху, например завершение или существование решения. Давайте переделаем это как: новые озарения, позитивный рефрейминг или просто «а-а-а!» . Эти «проблемы» тоже могут быть какими угодно: эмоциональными (внешними или внутренними), научными или исследовательскими, художественными, писательскими. Если вам так хочется, просто назовите это проблемой.

Кто бы ни писал этот пост в блоге, он, конечно, много говорит… Нам действительно нужно идти, иначе у нас не хватит времени. Знаешь что, давайте начнем снова. Добро пожаловать в:

Десять простых правил для Sol.. (кашель) Десять простых правил для того, чтобы сказать «а-ха!» чаще

Идеи в этом блоге не являются оригинальными. О так называемой педагогике решения проблем написано гораздо больше. Нет намерения или желания быть исчерпывающим или равномерно представлять идеи в литературе. Я решил выделить идеи, которые я считаю любопытными, интересными и полезными. Некоторые другие люди и места, где вы можете найти эти идеи:

Polya – How To Solve It

Zeitz – Искусство и ремесло решения проблем

Engel – Стратегии решения проблем

Ньюпорт – Глубокая работа

Ньюпорт – Так хорошо, что они не могут вас игнорировать

Стейнхардт – Исследование как стохастический процесс принятия решений

Дарвин – Жизнь и письма, автобиографическая глава

Артур Конан Дойл – Различные произведения

Правило 1: Знайте, что вы застряли

Чтобы решить проблему, нам нужно знать, что у нас есть проблема.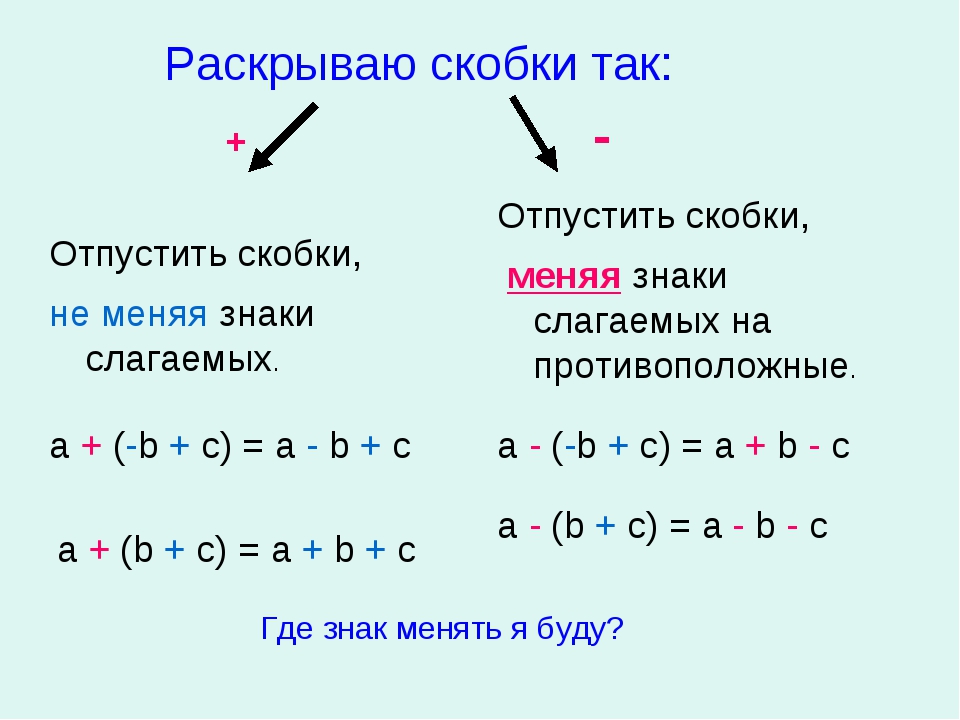 Это может быть легкомысленным замечанием, но не всегда очевидно, что мы находимся в пасти проблемы. Например, я переписывал это последнее предложение около двадцати раз, прежде чем понял, что застрял на том, что хотел сказать. Ключевые признаки того, что вы застряли:

Я не знаю, что делать дальше.
Понятия не имею.
Почему это не работает?

Однако это может быть и более тонко. Неоднократные попытки снова и снова без прогресса также застревают. Один сценарий, в котором я виновен, следующий: я хочу решить проблему, но вместо этого занимаюсь другими делами. Я называю этот последний пункт пассивным зависанием . Чтобы знать, что мы застряли, мы должны понимать, что решение не является немедленным. Чтобы стать лучше, я рекомендую громко говорить «Я застрял» всякий раз, когда это уместно. Другие могут предпочесть записать это на стикере или в лабораторном журнале, записать на диктофон или прокричать своему терапевту. Итак, резюмируя: определить, что у вас есть проблема, имейте в виду, что решение не будет немедленным, заявите, что вы застряли.

Правило 2: Поймите проблему

Часто проблема сложна, потому что мы не уверены, что нас просят или просим себя сделать. Плохо определенные проблемы редко приводят к быстрому «ага!» . Тратить время на то, чтобы понять проблему, — это пренебрегаемая часть процесса решения проблемы, несмотря на множество ностальгических воспоминаний о том, что «я даже не понимаю проблему». Как правило, существует множество стратегий демистификации. Один из способов — перефразировать задачу несколькими способами, каждый раз используя все более и более простой язык. Другой рисует картинку или диаграмму. Я часто спрашиваю себя: достаточно ли у меня информации, чтобы двигаться вперед? Наконец, рефакторинг проблемы может быть полезен; то есть изменение структуры задачи, чтобы сделать ее более понятной.

Правило 3: Изображение Решение

Даже если бы вы нашли решение, узнали бы вы его? Предположим, кто-то спросил вас, сколько будет семь, умноженное на восемь, и вы почесали затылок. Затем они продолжают говорить пятьдесят шесть. Вы бы тогда сказали «да, конечно» или «ага!». Рисунок решения может быть удивительно проницательным. Не имеет значения, если решение в конечном итоге будет отличаться от того, что вы нарисовали — просто спросите Да Винчи — оно все равно может быть полезным. Представление решения помогает нам понять, что мы нашли сокровище. Это также облегчает решение проблем в обратном направлении. Например, предположим, что я не знаю ответа на число семь, умноженное на восемь. Я представляю ответ в виде числа, скажем, 100. Я знаю, что 100 — это 10, умноженное на 10. Я уже усвоил несколько вещей. Я ищу число, и это число, вероятно, меньше 100.

Правило 4: Упрощение и специализация

Немногие книги рецептов говорят: «Ну, а теперь испеки торт». Обычно есть список ингредиентов и список маневров. Ингредиенты без каких-либо инструкций или инструкции без каких-либо ингредиентов привели бы в бешенство. Маловероятно, что мы быстро придем к торту, взяв ингредиенты случайным образом. Разбивка проблемы на более мелкие шаги может пролить свет, а решение каждой подзадачи по одному — более управляемая задача. Возможно, вы захотите сделать 7-ярусный свадебный торт. Вместо того, чтобы браться за эту задачу, почему бы не попробовать сначала однослойную губку Виктория? Рассмотрение конкретного сценария вашей проблемы может выявить ее составные части. Математики часто называют эти частные случаи или базисными случаями.

Правило 5: Думай как ученый

Несмотря на то, что не все проблемы являются научными, мышление ученого может быть полезным. Как (хороший) ученый вы выдвигаете гипотезы о своей проблеме. Для каждого ранжируйте их по степени правдоподобности. Пример: (1) я обнаружил конкретный пограничный случай, который сломал C++ (2) я неправильно написал lnegth. Другой пример (1) Моя сестра злится конкретно на меня (2) Моя сестра злится на что-то, а я просто случайно присутствую. Я позволю вам решить, какие из них более вероятны. Начните с самых простых способов и исключите те, которые неразумны или маловероятны. Наконец, составьте план и выполните его. Знайте, что вы собираетесь делать, и у вас должна быть причина для этого.

Правило 6: Угадай и проверь

Мы можем просто парализоваться, не зная, в каком направлении двигаться. Во-первых, вернитесь к правилу 5, прежде чем пытаться что-то еще. Если мы все еще застряли, то давайте просто попробуем хотя бы что-нибудь . Кто-то должен был первым смешать муку и воду или яйца и сахар. Попытка сделать что-то, в чем мы мало уверены, может вызвать неприятные чувства. Будьте готовы чувствовать себя некомфортно или глупо — плохой ответ все равно может быть полезен. Мы можем промахнуться, но тогда мы сможем ориентироваться вокруг этого. Как только вы сделали предположение, не забудьте проверить , если мы добились какого-либо прогресса – узнали ли мы что-нибудь новое о проблеме?

Правило 7: Вспомогательные задачи

Возможно, для некоторых сложных задач мы пока не достигли большого прогресса. В этом сценарии мы можем рассмотреть решение другой проблемы. Здесь мы ищем аналогичные или связанные проблемы, которые, возможно, уже были решены кем-то другим, или путь может быть более подходящим для предыдущих правил. С другой стороны, мы можем варьировать текущую задачу. Мы можем спросить себя, легче ли вариант задачи. Например, если мы репетируем фортепианную пьесу, возможно, мы можем сначала попробовать ее очень медленно.

Правило 8: Отправляйтесь на прогулку

Окружающая среда влияет на то, как мы думаем и воспринимаем. Многие люди утверждают, что генерируют свои лучшие идеи в определенных местах — на ум приходит душ. Другие рекомендуют долгую прогулку. Если вы отправитесь на прогулку, обратите внимание, как трудно удерживать абстрактные идеи. Позвольте себе отвлечься и замечайте вещи, которые находятся как рядом, так и далеко. Узнайте, что работает для вас, попробовав различные возмущения в вашей среде. Найдите Ватсона и выведите его на прогулку — объясните ему свою проблему.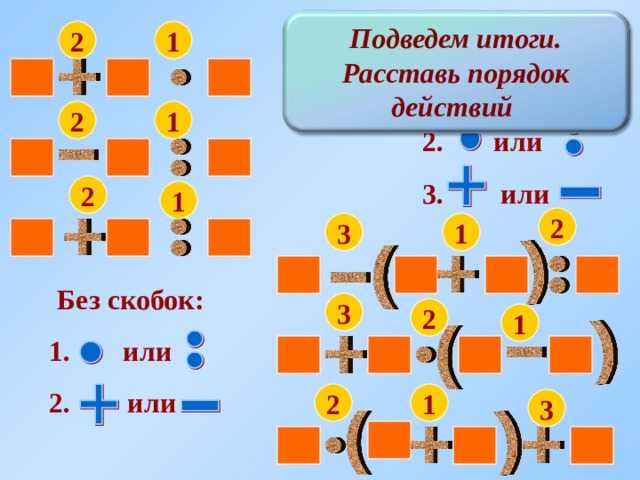 Это также возможность нарушить ваши ритмы. Даже такая безобидная вещь, как письмо карандашом, а не ручкой, может изменить ваше мышление.

Правило 9: Медитируйте

Решение проблем может привести к нежелательным или отвлекающим эмоциям. Разочарование, гнев и беспомощность — это лишь некоторые из них. Отсутствие осознанной ясности или внимания может помешать вам сосредоточиться на своей проблеме. Попробуйте переформулировать эмоции. Вы, вероятно, злитесь, потому что ожидали решить проблему к этому моменту. Понимание того, что это означает, что вы недооценили проблему, и она была более существенной, чем вы сначала подумали, и, следовательно, более захватывающей, может переориентировать разум. Обратите внимание на свои чувства и помните о своих мыслительных процессах. Как вы пришли? Я рекомендую взять книгу по медитации или осознанности. Вот быстрое упражнение для начинающих: Три глубоких вдоха — с силой выталкивайте воздух через нос. Теперь вдохните, считая до четырех, через нос. Обратите внимание на ощущение дыхания внутри ноздрей и давление снаружи ноздрей. Следите за движением диафрагмы. Задержите дыхание, считая до четырех, и выдохните, считая до шести. На этот раз обратите внимание на давление на диафрагму и внутреннюю часть ноздрей. В течение всего процесса старайтесь осознавать непрерывность дыхания и четко определять конец вдоха и начало конца выдоха. Замечайте отвлекающие факторы и избавляйтесь от них.

Правило 10: размышление

Теперь пришло время подумать и проанализировать процесс. Откуда у тебя твой «а-ха!» мгновений? Вытекали ли они из чего-то конкретного? Что-нибудь вызвало и «а-а-а!» момент? Какие стратегии сработали и не сработали для вас? Когда вам не удавалось двигаться вперед? В каких моментах вы были отброшены назад? Будьте критичны в процессе рецензирования, но не сбрасывайте со счетов что-то только потому, что на этот раз это не сработало. Цель состоит в том, чтобы добраться до точки, в которой вы можете предсказать стратегию будущих проблем.

Итак, это были мои 10 простых правил . Теперь у вас есть рецепт, пришло время написать свой собственный.

Оливер Крук, отзывы приветствуются на сайте Oliver.crook на stats.ox.ac.uk.

Оливер Крук

Решение уравнения. Методы, приемы и примеры

Решение уравнения включает в себя нахождение значений неизвестных переменных в данном уравнении. Условие равенства двух выражений удовлетворяется значением переменной. Решение линейного уравнения с одной переменной дает единственное решение, решение линейного уравнения с двумя переменными дает два результата. Решение квадратного уравнения дает два корня. Существует множество методов и процедур, применяемых при решении уравнения. Давайте подробно обсудим методы решения уравнения по одному.

1.	В чем смысл решения уравнений?
2.	шагов решения уравнения
3.	Решение уравнений с одной переменной
4.	Решение квадратного уравнения
5.	Решение рационального уравнения
6.	Решение радикального уравнения
7.	Часто задаваемые вопросы о решении уравнений

В чем смысл решения уравнений?

Решение уравнений вычисляет значение неизвестной переменной, все еще уравновешивая уравнение с обеих сторон. Уравнение — это условие для переменной, при котором два выражения в переменной имеют одинаковое значение. Значение переменной, для которой выполняется уравнение, называется решением уравнения. Уравнение остается тем же, если поменять местами левую и правую части. Выделяется переменная, для которой нужно найти значение, и получается решение. Решение уравнения зависит от того, с каким типом уравнения мы имеем дело. Уравнения могут быть линейными уравнениями, квадратными уравнениями, рациональными уравнениями или радикальными уравнениями.

шагов решения уравнения

Цель решения уравнения состоит в том, чтобы найти значение переменной, удовлетворяющее условию истинности уравнения. Чтобы изолировать переменную, выполняются следующие операции, все еще уравновешивающие уравнение с обеих сторон. Таким образом, левая сторона остается равной правой, и, в конце концов, баланс не нарушается.

Добавление свойства равенства: Добавьте одинаковое число к обеим сторонам. Если a = b, то a + c = b + c
Свойство равенства вычитания: вычитание одинакового числа с обеих сторон. Если a = b, то a — c = b — c
Свойство равенства умножения: умножить одно и то же число с обеих сторон. Если a = b, то ac = bc
Свойство равенства деления: Делим на одно и то же число в обе стороны. Если a = b, то a/c = b/c (где c ≠ 0)

После выполнения этого систематического уравновешивающего метода решения уравнения с помощью серии идентичных арифметических операций с обеих сторон уравнения мы разделяем переменную на одной из сторон, и последним шагом является решение уравнения.

Решение уравнений с одной переменной

Линейное уравнение одной переменной имеет вид ax + b = 0, где a, b, c — действительные числа. При решении линейного уравнения выполняются следующие шаги.

Удалите скобки и при необходимости используйте свойство распределения.
Упростите обе части уравнения, объединив одинаковые члены.
Если есть дроби, умножьте обе части уравнения на наименьший общий знаменатель всех дробей.
Если есть десятичные дроби, умножьте обе части уравнения на меньшую степень 10, чтобы преобразовать их в целые числа.
Перенесите переменные члены в одну часть уравнения, а постоянные члены в другую, используя свойства равенства сложения и вычитания.
Сделать коэффициент переменной равным 1, используя свойства равенства умножения или деления.
изолируйте переменную и получите решение.

Рассмотрим следующий пример: 3(x + 4) = 24 + x

Мы упрощаем LHS, используя свойство дистрибутивности.

3x + 12 = 24 + x

Сгруппируйте одинаковые термины вместе, используя метод транспонирования. Это становится 3x — x = 24-12

. Упрощаем дальше ⇒ 2x = 12

. Используйте свойство равенства деления, 2x/2 = 12/2

, изолируем переменную x. x = 6 является решением уравнения.

Используйте любой из следующих методов, чтобы упростить линейное уравнение и найти неизвестную переменную. Метод проб и ошибок, метод балансировки и метод транспонирования используются для выделения переменной.

Решение уравнения методом проб и ошибок

Предположим, что 12x = 60. Чтобы найти x, мы интуитивно пытаемся найти, что число, умноженное на 12, равно 60. Мы находим, что 5 — это искомое число. Решить уравнения методом проб и ошибок не всегда просто.

Решение уравнения методом уравновешивания

Нам нужно изолировать переменную x для решения уравнения. Для ее решения воспользуемся методом разделения переменных или методом балансировки. Рассмотрим уравнение 2x + 3 = 17,9. 0003

Сначала мы исключаем 3 на первом шаге. Чтобы сохранить баланс при решении уравнения, мы вычитаем 3 из каждой части уравнения.

Таким образом, 2x + 3 — 3 = 17 — 3

У нас есть 2x = 14

Теперь, чтобы изолировать x, мы делим на 2 с обеих сторон. (Свойство равенства деления)

2x/2 = 14/2

x = 7

Таким образом, мы изолируем переменную, используя свойства равенства при решении уравнения в методе уравновешивания.

Решение уравнения методом транспонирования

Решая уравнение, мы меняем стороны чисел. Этот процесс называется транспонированием. При перестановке числа мы меняем его знак или выполняем обратную операцию. Рассмотрим 5y + 2 = 22.

Нам нужно найти y, поэтому изолируем его. Следовательно, мы переносим число 2 на другую сторону. Уравнение принимает следующий вид:

5y = 22-2

5y = 20

Теперь, переставив 5 на другую сторону, мы обратим операцию умножения на деление. у = 20/5 = 4

Решение квадратного уравнения

Существуют уравнения, которые дают более одного решения. Квадратные многочлены имеют степень два, а нули квадратного многочлена представляют собой квадратное уравнение.

Рассмотрим (x+3) (x+2)= 0. Это квадратично по своей природе. Мы просто приравниваем каждое из выражений в LHS к 0.

Либо x+3 = 0, либо x+2 =0.

Мы получаем x = -3 и x = -2.

Квадратное уравнение имеет вид ax ² + bx + c = 0. Решение квадратного уравнения дает два корня: α и β.

Шаги, необходимые для решения квадратного уравнения:

Путем выполнения метода квадратов
По методу факторизации
Методом формулы

Путем выполнения метода квадратов

Решить уравнение квадратного типа путем выполнения метода квадратов довольно просто, поскольку мы применяем наши знания об алгебраическом тождестве: (a+b) ²

Запишите уравнение в стандартной форме ax ² + bx + c = 0.
Разделите обе части уравнения на a.
Переместить постоянный член на другую сторону
Добавьте квадрат половины коэффициента x с обеих сторон.
Дополните левую часть квадратом и упростите правую часть.
Извлеките квадратный корень из обеих сторон и найдите x.

Для получения дополнительной информации о решении уравнений (квадратичных) путем заполнения квадратов, нажмите здесь.

Методом факторизации

Решая уравнение квадратного типа методом факторизации, выполните шаги, описанные здесь. Запишите данное уравнение в стандартной форме и, разделив средние члены, разложите уравнение на множители. Перепишите полученное уравнение как произведение двух линейных множителей. Приравняйте каждый линейный множитель к нулю и найдите x. Рассмотрим 2x ² + 19х + 30 = 0. Это стандартная форма ax ² + bx + c = 0.

Разделите средний член таким образом, чтобы произведение членов было равно произведению коэффициента x ² и c и суммы из терминов должно быть b. Здесь произведение слагаемых должно быть 60, а сумма должна быть 19. Таким образом, разделите 19x на 4x и 15x (поскольку сумма 4 и 15 равна 19, а их произведение равно 60).

2x ² + 4x + 15x + 30 = 0

Вычтите общий делитель из первых двух членов и общие делители из двух последних членов.

2x(x ^{+ 2) + 15(x + 2) = 0}

Снова факторизуем (x+2), получаем

(x ^{+ 2)(2x + 15) = 0}

x = — 2 и x = -15/2

Решение квадратного уравнения включает такие шаги при разделении средних членов при факторизации.

Формульным методом

Решение уравнения квадратного типа по формуле

x = [-b ± √[(b ² -4ac)]/2a помогает найти корни квадратного уравнения ax ² + bx + c = 0. Подставляя значения a, b и c в формулу, мы приходим к решению.

Рассмотрим пример: 9x ² -12 x + 4 = 0

a = 9, b = -12 и c = 4

x = [-b ± √[(b ² -4ac)] /2a

= [12 ± √[((-12) ² -4×9×4)] / (2 × 9)

= [12 ± √(144 — 144)] / 18

= (12 ± 0)/18

х = 12/18 = 2/3

Решение рационального уравнения

Уравнение, в знаменателе которого есть хотя бы одно полиномиальное выражение, называется рациональным уравнением. Решение рационального уравнения включает следующие шаги. Приведите дроби к общему знаменателю, а затем решите уравнение числителей.

Рассмотрим x/(x-1) = 5/3

При перекрестном умножении получаем

3x = 5(x-1)

3x = 5x — 5

3x — 5x = — 5

90 002 -2x = -5

x = 5/2

Решение радикального уравнения

Уравнение, в котором переменная находится под радикалом, называется радикальным уравнением. Решение уравнения, которое является радикалом, включает несколько шагов. Выразите данное радикальное уравнение через индекс радикала и уравновесьте уравнение. Решите для переменной.

Рассмотрим √(x+1) = 4

Теперь возведите обе стороны в квадрат, чтобы сбалансировать. [ √(x+1)] ² = 4 ²

(x+1) = 16

Таким образом, x = 16-1 =15

Важные замечания по решению уравнений: 9 0003

Решение уравнение находит значение переменной в уравнении.
Решение уравнения удовлетворяет условию данного уравнения.
Решить уравнение линейного типа можно и графически.
Если правая часть уравнения равна нулю, то для решения уравнения просто начертите на графике левую часть уравнения, и точка пересечения x на графике будет решением(ями).

☛ Статьи по теме:

Калькулятор решений уравнений
Синхронные линейные уравнения
Линейные уравнения и неравенства с одной переменной
Простые уравнения и их приложения

Часто задаваемые вопросы о решении уравнений

Что такое решение уравнения?

Решение уравнения — это нахождение значений неизвестных переменных в данном уравнении. Процесс решения уравнения зависит от типа уравнения.

Какие этапы решения уравнений?

Определите тип уравнения: линейное, квадратичное, логарифмическое, показательное, радикальное или рациональное.

Удалите скобки, если они есть в данном уравнении. Примените распределительное свойство.
Добавьте одинаковое количество на обе стороны
Вычесть одинаковое число с обеих сторон
Умножить одинаковое число с обеих сторон
Разделить на одно и то же число в обе стороны.

Золотое правило решения уравнения?

Определен тип уравнения. Если это линейное уравнение, используется метод разделения переменных или метод транспонирования. Если это квадратное уравнение, то используется достраивание квадратов, разбиение средних членов с помощью факторизации или по формульному методу.

Как вы используете 3 шага в решении уравнения?

3 шага решения уравнения:

удалить скобки, если они есть, используя свойство распределения,
упростить уравнение, добавляя или вычитая одинаковые члены,
выделение переменной и ее решение.

Как вы решаете линейные уравнения?

Решая линейное уравнение, мы изолируем переменную, значение которой нужно найти.