Почему минус на минус дает плюс?
«Враг моего врага — мой друг».
Проще всего ответить: «Потому что таковы правила действий над отрицательными числами». Правила, которые мы учим в школе и применяем всю жизнь. Однако учебники не объясняют, почему правила именно такие. Мы сначала постараемся понять это, исходя из истории развития арифметики, а потом ответим на этот вопрос с точки зрения современной математики.
Давным-давно людям были известны только натуральные числа: 1, 2, 3, … Их использовали для подсчета утвари, добычи, врагов и т. д. Но числа сами по себе довольно бесполезны — нужно уметь с ними обращаться. Сложение наглядно и понятно, к тому же сумма двух натуральных чисел — тоже натуральное число (математик сказал бы, что множество натуральных чисел замкнуто относительно операции сложения). Умножение — это, по сути, то же сложение, если мы говорим о натуральных числах. В жизни мы часто совершаем действия, связанные с этими двумя операциями (например, делая покупки, мы складываем и умножаем), и странно думать, что наши предки сталкивались с ними реже — сложение и умножение были освоены человечеством очень давно.
Без вычитания, конечно, тоже не обойтись. Но на практике мы, как правило, вычитаем из большего числа меньшее, и нет нужды использовать отрицательные числа. (Если у меня есть 5 конфет и я отдам сестре 3, то у меня останется 5 – 3 = 2 конфеты, а вот отдать ей 7 конфет я при всем желании не могу.) Этим можно объяснить, почему люди долго не пользовались отрицательными числами.
В индийских документах отрицательные числа фигурируют с VII века н.э.; китайцы, видимо, начали употреблять их немного раньше. Их применяли для учета долгов или в промежуточных вычислениях для упрощения решения уравнений — это был лишь инструмент для получения положительного ответа. Тот факт, что отрицательные числа, в отличие от положительных, не выражают наличие какой-либо сущности, вызывал сильное недоверие. Люди в прямом смысле слова избегали отрицательных чисел: если у задачи получался отрицательный ответ, считали, что ответа нет вовсе.
Рассмотрим для примера уравнение 7x – 17 = 2x – 2. Его можно решать так: перенести члены с неизвестным в левую часть, а остальные — в правую, получится 7x – 2x = 17 – 2, 5x = 15, x = 3. При таком решении нам даже не встретились отрицательные числа.
Но можно было случайно сделать и по-другому: перенести слагаемые с неизвестным в правую часть и получить 2 – 17 = 2x – 7x, (–15) = (–5)x. Чтобы найти неизвестное, нужно разделить одно отрицательное число на другое:
Что демонстрирует этот нехитрый пример? Во-первых, становится понятна логика, которой определялись правила действий над отрицательными числами: результаты этих действий должны совпадать с ответами, которые получаются другим путем, без отрицательных чисел.
Во-вторых, допуская использование отрицательных чисел, мы избавляемся от утомительного (если уравнение окажется посложнее, с большим числом слагаемых) поиска того пути решения, при котором все действия производятся только над натуральными числами. Более того, мы можем больше не думать каждый раз об осмысленности преобразуемых величин — а это уже шаг в направлении превращения математики в абстрактную науку.
Правила действий над отрицательными числами сформировались не сразу, а стали обобщением многочисленных примеров, возникавших при решении прикладных задач. Вообще, развитие математики можно условно разбить на этапы: каждый следующий этап отличается от предыдущего новым уровнем абстракции при изучении объектов. Так, в XIX веке математики поняли, что у целых чисел и многочленов, при всей их внешней непохожести, есть много общего: и те, и другие можно складывать, вычитать и перемножать. Эти операции подчиняются одним и тем же законам — как в случае с числами, так и в случае с многочленами.
Потом обнаружились другие совокупности математических объектов, над которыми можно производить такие операции: формальные степенные ряды, непрерывные функции… Наконец, пришло понимание, что если изучить свойства самих операций, то потом результаты можно будет применять ко всем этим совокупностям объектов (такой подход характерен для всей современной математики).
В итоге появилось новое понятие: кольцо. Это всего-навсего множество элементов плюс действия, которые можно над ними производить. Основополагающими здесь являются как раз правила (их называют аксиомами), которым подчиняются действия, а не природа элементов множества (вот он, новый уровень абстракции!). Желая подчеркнуть, что важна именно структура, которая возникает после введения аксиом, математики говорят: кольцо целых чисел, кольцо многочленов и т. д. Отталкиваясь от аксиом, можно выводить другие свойства колец.
Мы сформулируем аксиомы кольца (которые, естественно, похожи на правила действий с целыми числами), а затем докажем, что в любом кольце при умножении минуса на минус получается плюс.
Кольцом называется множество с двумя бинарными операциями (т. е. в каждой операции задействованы два элемента кольца), которые по традиции называют сложением и умножением, и следующими аксиомами:
- сложение элементов кольца подчиняется переместительному (A + B = B + A для любых элементов A и B) и сочетательному (A + (B + C) = (A + B) + C) законам; в кольце есть специальный элемент 0 (нейтральный элемент по сложению) такой, что A + 0 = A, и для любого элемента A есть противоположный элемент (обозначаемый (–A)), что A + (–A) = 0;
- умножение подчиняется сочетательному закону: A·(B·C) = (A·B)·C;
- сложение и умножение связаны такими правилами раскрытия скобок: (A + B)·C = A·C + B·C и A·(B + C) = A·B + A·C.
Заметим, что кольца, в самой общей конструкции, не требуют ни перестановочности умножения, ни его обратимости (т. е. делить можно не всегда), ни существования единицы — нейтрального элемента по умножению. Если вводить эти аксиомы, то получаются другие алгебраические структуры, но в них будут верны все теоремы, доказанные для колец.
Теперь докажем, что для любых элементов A и B произвольного кольца верно, во-первых, (–A)·B = –(A·B), а во-вторых (–(–A)) = A. Из этого легко следуют утверждения про единицы: (–1)·1 = –(1·1) = –1 и (–1)·(–1) = –((–1)·1) = –(–1) = 1.
Для этого нам потребуется установить некоторые факты. Сперва докажем, что у каждого элемента может быть только один противоположный. В самом деле, пусть у элемента A есть два противоположных: B и С. То есть A + B = 0 = A + C. Рассмотрим сумму A + B + C. Пользуясь сочетательным и переместительным законами и свойством нуля, получим, что, с одной стороны, сумма равна B: B = B + 0 = B + (A + C) = A + B + C, а с другой стороны, она равна C: A + B + C = (A + B) + C = 0 + C = C.
Значит, B = C.
Заметим теперь, что и A, и (–(–A)) являются противоположными к одному и тому же элементу (–A), поэтому они должны быть равны.
Первый факт получается так: 0 = 0·B = (A + (–A))·B = A·B + (–A)·B, то есть (–A)·B противоположно A·B, значит, оно равно –(A·B).
Чтобы быть математически строгими, объясним еще, почему 0·B = 0 для любого элемента B. В самом деле, 0·B = (0 + 0) B = 0·B + 0·B. То есть прибавление 0·B не меняет сумму. Значит, это произведение равно нулю.
А то, что в кольце ровно один ноль (ведь в аксиомах сказано, что такой элемент существует, но ничего не сказано про его единственность!), мы оставим читателю в качестве несложного упражнения.
Ответил: Евгений Епифанов
§ Вычитание отрицательных чисел. Вычитание рациональных чисел
Координатная прямая Координаты точек на числовой оси Сложение отрицательных чисел Вычитание отрицательных чисел Умножение отрицательных чисел Деление отрицательных чисел
Как известно вычитание — это действие, противоположное сложению.
Если «a» и «b» — положительные числа, то вычесть из числа «a» число «b», значит найти такое число «c», которое при сложении «с» числом «b» даёт число «a».
a − b = с или с + b = a
Определение вычитания сохраняется для всех рациональных чисел. То есть вычитание положительных и отрицательных чисел можно заменить сложением.
Запомните!
Чтобы из одного числа вычесть другое, нужно к уменьшаемому прибавить число противоположное вычитаемому.
Или по другому можно сказать, что вычитание числа «b» — это тоже самое сложение, но с числом противоположным числу «b».
a − b = a + (−b)
Пример.
6 − 8 = 6 + (− 8) = −2
Пример.
0 − 2 = 0 + (−2) = −2
Запомните!
Стоит запомнить выражения ниже.
0 − a = − a
a − 0 = a
a − a = 0
Как видно из примеров выше вычитание числа «b» — это сложение
с числом противоположным числу «b».
Это правило сохраняется не только при вычитании из бóльшего числа меньшего, но и позволяет из меньшего числа вычесть большее число, то есть всегда можно найти разность двух чисел.
Разность может быть положительным числом, отрицательным числом или числом ноль.
Примеры вычитания отрицательных и положительных чисел.
- −3 − (+ 4) = −3 + (−4) = −7
- 5 − (−3) = 5 + (+ 3) = 8
Удобно запомнить правило знаков, которое позволяет уменьшить количество скобок.
Знак «плюс» не изменяет знака числа, поэтому, если перед скобкой стоит плюс, то знак в скобках не меняется.
+ (+ a) = + a
+ (−a) = −a
Знак «минус» перед скобками меняет знак числа в скобках на противоположный.
−(+ a) = − a
−(−a) = + a
Из равенств видно, что если перед и внутри скобок
стоят одинаковые знаки, то получаем «+», а если знаки разные, то
получаем «−».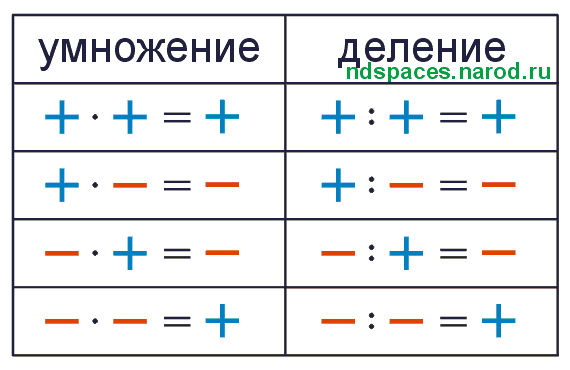
(−6) + (+ 2) − (−10) − (− 1) + (− 7) = −6 + 2 + 10 + 1 − 7 = − 13 + 13 = 0
Правило знаков сохраняется и в том случае, если в скобках не одно число, а алгебраическая сумма чисел.
a − (− b + c) + (d − k + n) = a + b − c + d − k + n
Обратите внимание, если в скобках стоит несколько чисел и перед скобками стоит знак «минус», то должны меняться знаки перед всеми числами в этих скобках.
Чтобы запомнить правило знаков можно составить таблицу определения знаков числа.
Правило знаков для чисел
| + (+) = + | + (−) = − |
| − (−) = + | − (+) = − |
Или выучить простое правило.
Запомните!
Минус на минус даёт плюс.
Плюс на минус даёт минус.
Координатная прямая Координаты точек на числовой оси Сложение отрицательных чисел Вычитание отрицательных чисел Умножение отрицательных чисел Деление отрицательных чисел
Правило знаков — Math28
Содержание
Определение положительного или отрицательного знака Знаки, сопровождающие числа, очень важны, так как они указывают, положительное это число или отрицательное.
Чтобы определить, является ли число положительным, слева от числа ставится крест, хотя во многих случаях знак не ставится, и считается, что оно положительное, с другой стороны, чтобы определить, является ли число отрицательным, средний тире или черта ставится слева от числа.
+ 3 ← Положительный
— 3 ← Отрицательный
Примечание : Для положительного числа слева от числа у нас нет другого числа, которое можно оставить без знака.
В числовой строке вы можете увидеть разницу между числом с положительным знаком и числом с отрицательным знаком.
- -1
- 0
- 1
Ноль считается нейтральным числом, слева от нуля предыдущей строки соответствуют отрицательные числа до самой бесконечности (-inf), а справа от нуля положительные числа до самой бесконечности (+inf). обдуманный
Законы или правила знаков
Закон или правило знаков указывает на знак, преобладающий при выполнении операций двух одинаковых или разных знаков, и применяется по-разному для различных математических операций:
Правило знаков для сложения и вычитания- При сложении двух положительных чисел результат будет иметь положительный знак.
3 + 5 = 8 - При сложении или вычитании двух чисел, одно с положительным знаком, а другое с отрицательным знаком, результат будет иметь знак наибольшего числа.
5 — 6 = — 1 - При сложении или вычитании двух чисел, одно с отрицательным знаком, а другое с положительным знаком, результат будет иметь знак наибольшего числа.
— 7 + 4 = — 3 - При вычитании двух отрицательных чисел результат будет иметь отрицательный знак.
— 5 — 4 = — 9
Упрощение вышеизложенного:
положительный + отрицательное = наибольшее число
отрицательное + положительное = наибольшее число
отрицательное y отрицательное = отрицательное
Узнать больше о: « Сумма » →
Узнать больше о: « Вычитание » →
Правило знаков для умножения и деления- При умножении или делении двух положительных чисел результат будет иметь положительный знак.
(+) х (+) = +
(+) ÷ (+) = + - При умножении или делении двух чисел, одно с положительным знаком, а другое с отрицательным знаком, результат будет иметь отрицательный знак.
(+) х (-) = —
(+) ÷ (-) = — - При умножении или делении двух чисел, одно с отрицательным знаком, а другое с положительным знаком, результат будет иметь отрицательный знак.
(-) х (+) = —
(-) ÷ (+) = — - При умножении или делении двух отрицательных чисел результат будет иметь положительный знак.
(-) х (-) = +
(-) ÷ (-) = +
Узнать больше о: « Умножение » →
Узнать больше о: « Подразделение » →
Правило знаков для потенцирования- Если показатель степени равен даже , результатом будет знак положительный .
(+) пар = +
(-) пар = + - Если показатель степени равен , нечетное , результат сохранит знак основного числа.
(+) импар = +
(-) импар = —
Узнать больше о: «Экспонент » →
Операции с числами со знаком
Операции с числами со знакомОперации с подписанными номерами | ||
Дополнение Вычитание Умножение Подразделение
| ||
| Дополнение Правила | Примеры |
Когда
добавив два числа с одинаковыми знаками, сложите значения и сохраните общее
знак. | 1. (+3) + (+5) = + 8 2. 4 + 6 = 10 3. (-3) + (-5) = — 8 4. — 4 + (- 6 ) = -10 |
| Когда сложив два числа с разными знаками, вычесть значения и использовать знак большего числа. | 1. (+3) + (-5) = -2 2. (-3) + (+5) = +2 3. 4 + (- 6 ) = -2 4. — 4 + 6 = 2 |
Дополнение Вычитание Умножение Подразделение верх | |
| Вычитание Правила | Примеры |
Изменить
оператор вычитания для сложения и изменения знака числа
что сразу следует. Соблюдайте правила добавления изложенные
выше. (т.е. сложить наоборот) | 1. (+3) — (-5) = (+3) + (+5) = 8 2. (-3) — (+5) = (-3) + (-5) = — 8 3. 4 — (- 6 ) = 4 + (+ 6 ) = 10 4. — 4 — 6 = — 4 + (- 6) = — 10 |
Дополнение Вычитание Умножение Подразделение верх | |
| Умножение Правила | Примеры |
Когда
при умножении двух чисел с одинаковым знаком произведение положительно. (+)(+) = + (-)(-) = +
| 1. (+3) (+5) = +15 2. (4)( 6) = 24 3. (-3) + (-5) = +15 4. — 4(- 6 ) = 24 |
| Когда
при умножении двух чисел с разными знаками произведение отрицательно. (+)(-) = — (-)(+) = —
| 1. (+3) (-5) = -15 2. 4 (-6 ) = 24 3. (-3) (+5) = -15 4. |
Дополнение Вычитание Умножение Подразделение верх | |
| Отдел Правила | Примеры |
| Когда
при делении двух чисел с одинаковым знаком частное положительно. (+)/(+) = + (-)/(-) = +
| 1. (+3) (+5) = +15 2. (4)( 6) = 24 3. |
—
4 ( 6 ) =
-24 