Урок математики «Правило порядка выполнения действий в выражениях со скобками» | План-конспект урока по математике (3 класс) по теме:
Технологическая карта урока
Ф. И. О. педагога: Морозова Елена Федоровна
Предмет: Математика, УМК «Школа 21 века»
Класс: 3а
Тип урока: Урок «открытия новых знаний»
Тема: Правило порядка выполнения действий в выражениях со скобками.
Цель: Изучить порядок выполнения действий в выражениях со скобками и научить выполнять алгоритм на практике.
Задачи:
1.Уметь решать математические выражения со скобками
2.Уметь применять алгоритм на практике
Название этапа | Деятельность учителя | Деятельность учащихся | УУД |
1.Мотивирование (самоопределение) к учебной деятельности | Здравствуйте, ребята. Посмотрите, друг другу в глаза, улыбнитесь друг другу, шёпотом пожелайте товарищу хорошего рабочего настроения на весь урок. Теперь посмотрите на меня, я тоже желаю вам удачи на этом уроке, потому что «с малой удачи начинается большой успех». Займите свои рабочие места. Ребята, обратите внимание, у вас на столах лежат карточки с заданиями и смайлики красного, зеленого и голубого цвета. Зеленые смайлики вы будете поднимать, если ответ верный, и вы соглашаетесь со своими товарищами, желтые – сомневаетесь или вам надо еще подумать, а голубые, если не соглашаетесь или ответ не верный. С карточками мы будем работать в течение урока. Откройте тетради, запишите число. Классная работа | Желают удачи друг другу, хорошего рабочего настроения. Садятся за парты Проверяют наличие иллюстративного материала Записывают | Личностные: |
2. | — Скажите, пожалуйста, что нового вы узнали на прошлом уроке? (слайд 1) Сейчас я предлагаю проверить, как хорошо вы усвоили правило. Посмотрите на экран. Здесь даны выражения со скобками и без скобок. В каких выражениях можно отбросить скобки? Запишите эти выражения без скобок. В остальных выражениях определите порядок действий. (слайд 2) (43+57)+20= 18:(27:3)= (72-6)-2= 4*(2*3)= 94-8*8= 4*(8+1)+(25-16):3 — 81:(36:4)= Какие выражения вы записали без скобок? Почему? В каких выражениях нельзя отбросить скобки? Почему? Каков порядок действий в других выражениях? Каков порядок действий в выражении, которое не содержит скобок, а только знаки + или-, * или : | Правило с.116 Вычитание и деление не обладают сочетательным и переместительным свойством. Поэтому в таких выражениях, как 9:(3:3), 12-(7-4) скобки переставлять или отбрасывать нельзя. Объяснение учеников Два выражения можно записать без скобок. (43+57)+20=120 4*(2*3)=24 Решая эти примеры, я использовал переместительное и сочетательное свойство сложения и умножения, т.к. эти свойства дают возможность записывать выражения, содержащие только умножение и сложение без скобок и выполнять вычисления в любом порядке. В остальных примерах скобки отбросить нельзя, поэтому вычисления делаем сначала в скобках, потом умножение деление, сложение вычитание. 18:(27:3)=2 (72-6)-2=66 Первым- умножение и деление, потом сложение вычитание и дальше по порядку, слева направо. 94-8*8=30 | Коммуникативные: |
3.Выявление места и причины затруднения | Ребята, у нас осталось последнее выражение. Сможете его решить? Почему? Чтобы решить это выражение, что должны знать?(правило) | Думают и выявляют место и причину затруднения: Не знаем, как выполнять действия в таких выражениях; не знаем последовательность действий в выражении. | Познавательные: Регулятивные: |
4Построение проекта выхода из затруднения | Значит, что сегодня мы должны изучить на уроке? Сформулируем тему урока «Порядок выполнения действий в выражениях со скобками (слайд 3) Цель нашего урока? Изучить правило выполнения действий в выражении и научиться вычислять значение выражения со скобками. | Формулируют тему и цель урока Правило выполнения действий в выражении Порядок выполнения действий в выражениях со скобками Научиться вычислять значение выражений. | Регулятивные: |
5.Реализация построенного проекта | Как будем решать это выражение? Предлагаю обсудить все возможные варианты решения в группах. Для этого используем сингапурскую структуру СИНГЛ-РАУНД-РОБИН. Итак, ваши предположения. (спросить по желанию). Какую версию выдвинул ученик по плечу? (спросить оного из учащихся) Ребята, у вас получилось две версии: решить выражение по порядку выполнения математических действий и вторая -разделить выражение на части. Рассмотрим первую версию. Для этого вспомним, по какому правилу мы выполняем математические действия в выражениях содержащих скобки, деление и умножение, сложение и вычитание. Запишите выражение в тетрадь, определим порядок действий в выражении. (слайд 4) 4*(8+1) + (25-16):3 — 81:(36:4)= Подпишем над выражением цифры в порядке выполнения действий. Сколько действий у нас получилось? Значит, сколько примеров мы должны решить? Мы можем в них запутаться? Ребята, давайте разберем 2 версию, которую вы высказали, может она окажется более простой и удобный? Попробуем разбить выражение на части. Как определить каждую часть? Где будут границы частей? (слайд 5) Посмотрите на экран, вам подсказка. Что изменилось в нашем выражении? Знаки + и- стали красного цвета. Почему я их выделила красным цветом? Знаки заключены в скобки? Значит, по ним мы будем определять границы частей выражения. Итак, как мы будем проводить разбивку выражения на части? (слайд 6) Какое выражение сейчас получилось? Из скольких частей состоит теперь выражение? Можем мы решить такое выражение? Как? Прежде чем вы вычислите значения выражения, я попрошу вас снова поработать в группах. Ребята, прежде, как решить это выражение, давайте составить план или алгоритм выполнения действий в таких выражениях. У вас на столах лежат карточки с описанием математических действий. Выберите правильное действие и разложите карточки по порядку выполнения математических действий. Почему убрали одну карточку. Какие алгоритмы у вас получились? Как вы думаете, у вас получились правильные алгоритмы? Как и где, мы это можем проверить? Откроем учебник на с. Поднимите карточки, у кого алгоритм составлен верно. (слайд 7) Теперь мы знаем алгоритм решения этого выражения, поэтому сейчас вычислим значение выражения. (слайд 8)Правильное решение на доске. У вас такой же ответ? | Обсуждают возможные варианты ответа на вопрос, используя структуру СИНГЛ-РАУНД-РОБИН. Объяснение учеников: Сосчитать слева направо по порядку; сосчитать сначала в скобках; разделить выражение на части и т.д. 1.В скобках 2. умножение и деление, 3. сложение вычитание 4. дальше по порядку, слева направо Один ученик у доски записывает выражение и определяет порядок действий 4 1 7 2 5 8 6 3 4*(8+1)+(25-16):3 — 81:(36:4)= 8 действий да ученик решает у доски Знаки + и — стали красного цвета знаки +, или – будут определять границы части; Сначала в выражении нужно найти знаки + или – не заключенные в скобки. Затем начинаем разбивать выражение на части слева направо, от начала до первого из знаков — это первая часть выражения, от первого знака до второго — это вторая часть, от второго знака до конца выражения. Сверху выделяем части карандашом (выделить на доске) Из трех. Да. Сначала сосчитать каждую часть, а затем выполнить действия слева направо. Составляют алгоритм в группах с раздаточным материалом. 1.Находим в выражении все знаки + или — , не заключенные в скобки – это будут границы частей выражения. 2.Определяем количество частей в выражении, от начала до первого знака + или — , не заключенных в скобки 3.Выполняем вычисления каждой части выражения. а) в скобках б) умножение/деление; в) сложение/вычитание). 4. Остальные действия в выражении выполняют слева направо 5.Выполняем вычисления каждой части выражения. а) сложение/вычитание б) умножение/деление; в) в скобках ( карточку с неверным описанием убирают) Поднимают сигнальные карточки По эталону, прочитать правило. Читают правило Поднимают сигнальные карточки. Один ученик решает у доски Поднимают сигнальные карточки | Регулятивные: |
6.Первичное закрепление с проговариванием во внешней речи | (слайд 9) Ребята, выражение вы решили успешно, поэтому сейчас я предлагаю отработать навыки решения выражений со скобками. У вас на столах карточки с математическими заданиями. Запишите их в тетрадь и разбейте выражения на части. 6*6 + 45: (13-4) + 48:8= (154-128) -(20:5+3)+152= Физкультминутка | Проговаривая алгоритм, разбивают выражения на части у доски (фронтальная работа) | Познавательные |
7.Самостоятельная работа с проверкой по эталону | С.117 №11 2*3*4 — (20:5+3)+152= 607- 6*6: (13-4) +(48:8)= Поменяйтесь тетрадями с соседом по лицу. (слайд 10) Вывод на экран эталона Оцените работу товарища, подняв карточки. (проверить учащихся, выполнивших 2 примера) | Выполняют задание, сильные ученики-2 примера Меняются тетрадями Дети поднимают сигнальные карточки | Регулятивные: |
8.Включение в систему знаний и повторение | (слайд 11) Задача с.119 № 16 На базе было 260 кг.вишни. В школьные буфеты отправили 8 ящиков по 6 кг.вишни,в детские сады -7 ящиков по 5 кг. и в кафе-9 ящиков по 8 кг. Сколько вишни отправили на базы Сколько вишни осталось на базе? Как записать одним выражением? | Решают (1 ученик у доски). Было-260 кг Б.-8 ящ. по 6 кг, Д.с.—7 ящ. по 5 кг. К. — 9 ящ. по 8 кг. Сколько вишни отправили с базы? Сколько вишни осталось на базе? 8*6+7*5+9*8=155 260-166=105 кг Запись одним выражением 260-(8*6+7*5+9*8)=105 | Познавательные: |
9. | Ребята, наш урок подходит к завершению. Запишите Домашнее задание Уч. с.118 №14, 1-2 выражение вычислить двумя способами. Первый -определить порядок действий и вычислить по порядку( не вычисляли), второй путем разбиения выражения на части. И скажите, какой способ вычисления значения выражения удобнее. Какую задачу ставили? Удалось решить поставленную задачу? Каким способом? Где можно применить новые знания? Что на уроке у вас хорошо получалось? Над чем ещё надо поработать? Я прошу вас взять в руки красные и синие смайлики и оценить свою работу на уроке. Кому всё понятно и хорошее настроение – поднимите зеленый, а если у вас остались вопросы, желтый, кто не понял тему — красный. Ребята, я благодарю вас за работу, и тоже хочу оценить вашу работу на уроке. Скажите, какое событие ждет нашу страну в феврале 2014 года? За победу спортсменам вручают золотые, серебряные и бронзовые медали. Давайте улыбнёмся друг другу и скажем спасибо. Урок закончен | Научиться решать выражения, содержащие скобки. Научились выделять части выражения и решать по порядку, слева направо. Зимняя олимпиада | Регулятивные |
Конспект урока ««Порядок выполнения действий в выражениях без скобок и со скобками».»
Тема урока: «Порядок выполнения действий в выражениях без скобок и со скобками».
Цель урока: создать условия для закрепления умений применять знания о порядке выполнения действий в выражениях без скобок и со скобками в различных ситуациях, умений решать задачи выражением.
Задачи урока.
Образовательные:
— закрепить знания учащихся о правилах выполнения действий в выражениях без скобок и со скобками; формировать у них умение пользоваться этими правилами при вычислении конкретных выражений; совершенствовать вычислительные навыки; повторить табличные случаи умножения и деления;
Развивающие:
— развивать вычислительные навыки, логическое мышление, внимание, память, познавательные способности учащихся,
коммуникативные навыки;
Воспитательные:
— воспитывать толерантное отношение друг к другу, взаимное сотрудничество,
культуру поведения на уроке, аккуратность, самостоятельность, воспитывать интерес к занятиям математикой.
Формируемые УУД:
Регулятивные УУД:
работать по предложенному плану, инструкции;
выдвигать свои гипотезы на основе учебного материала;
осуществлять самоконтроль.
Познавательные УУД:
знать правила порядка выполнения действий:
уметь разъяснить их содержание;
понимать правило порядка выполнения действий;
находить значения выражений согласно правилам порядка выполнения;
действий, используя для этого текстовые задачи;
записывать решение задачи выражением;
применять правила порядка выполнения действий;
уметь применять полученные знания при выполнении контрольной работы.
Коммуникативные УУД:
слушать и понимать речь других;
выражать свои мысли с достаточной полнотой и точностью;
допускать возможность различных точек зрения, стремиться понимать позицию собеседника;
работать в команде разного наполнения (паре, малой группе, целым классом), участвовать в обсуждениях, работая в паре;
Личностные УУД:
устанавливать связь между целью деятельности и её результатом;
определять общие для всех правила поведения;
уметь осознанно и внимательно читать задания;
выражать способность к самооценке на основе критерия успешности учебной деятельности.
Планируемый результат:
Предметные:
Знать правила порядка выполнения действий.
Уметь разъяснить их содержание.
Уметь решать задачи с помощью выражений.
Личностные:
Уметь проводить самооценку на основе критерия успешности учебной деятельности.
Метапредметные:
Уметь определять и формулировать цель на уроке с помощью учителя; проговаривать последовательность действий на уроке; работать по коллективно составленному плану; оценивать правильность выполнения действия на уровне адекватной ретроспективной оценки; планировать своё действие в соответствии с поставленной задачей; вносить необходимые коррективы в действие после его завершения на основе его оценки и учёта характера сделанных ошибок; высказывать своё предположение(Регулятивные УУД).
Уметь оформлять свои мысли в устной форме; слушать и понимать речь других; совместно договариваться о правилах поведения и общения в школе и следовать им (Коммуникативные УУД).
Уметь ориентироваться в своей системе знаний: отличать новое от уже известного с помощью учителя; добывать новые знания: находить ответы на вопросы, используя учебник, свой жизненный опыт и информацию, полученную на уроке (Познавательные УУД).
Ход урока
1. Организационный момент.
Чтоб урок наш стал светлее,
Мы поделимся добром.
Вы ладони протяните,
В них любовь свою вложите,
Ей с друзьями поделитесь
И друг другу улыбнитесь.
— Займите свои рабочие места.
Открыли тетради, записали число и классная работа.
2. Актуализация знаний.
— На уроке нам с вами предстоит подробно рассмотреть порядок выполнения арифметических действий в выражениях без скобок и со скобками.
Устный счёт.
Игра «Найди правильный ответ».
( У каждого ученика лист с числами)
55 | 56 | 57 | 58 | 59 | 60 | 61 |
62 | 63 | 64 | 65 | 66 | 67 | 68 |
69 | 70 | 71 | 72 | 73 | 74 | 75 |
76 | 77 | 78 | 79 | 80 | 81 | 82 |
83 | 84 | 85 | 86 | 87 | 88 | 89 |
90 | 91 | 92 | 93 | 94 | 95 | 96 |
97 | 98 | 99 | 100 | 101 | 102 | 103 |
— Я читаю задания, а вы, выполнив в уме действия, должны полученный результат, т. е. ответ, зачеркнуть крестиком.
е. ответ, зачеркнуть крестиком.
Я задумала число, из него вычла 80, получила 18. Какое число я задумала? (98)
Я задумала число, к нему прибавила 12, получила 70. Какое число я задумала? (58)
Первое слагаемое 90, второе слагаемое 12. Найдите сумму. (102)
— Соедините полученные результаты.
— Какую геометрическую фигуру вы получили? ( Треугольник)
— Расскажите, что вы знаете о данной геометрической фигуре. (Имеет 3 стороны, 3 вершины, 3 угла)
— Продолжаем работать по карточке.
Найдите разность чисел 100 и 22. (78)
Уменьшаемое 99, вычитаемое 19. Найдите разность. (80).
Возьмите число 25 4 раза. (100)
— Начертите внутри треугольника еще 1 треугольник, соединяя полученные результаты.
— Сколько треугольников получилось? (5)
3. Работа над темой урока. Наблюдение за изменением значения выражения от порядка выполнения арифметических действий
Наблюдение за изменением значения выражения от порядка выполнения арифметических действий
В жизни мы постоянно выполняем какие-либо действия: гуляем, учимся, читаем, пишем, считаем, улыбаемся, ссоримся и миримся. Эти действия мы выполняем в разном порядке. Иногда их можно поменять местами, а иногда нет. Например, собираясь утром в школу, можно сначала сделать зарядку, затем заправить постель, а можно наоборот. Но нельзя сначала уйти в школу, а потом надеть одежду.
А в математике обязательно ли выполнять арифметические действия в определенном порядке?
Давайте проверим
Сравним выражения:
8-3+4 и 8-3+4
Видим, что оба выражения совершенно одинаковы.
Выполним действия в одном выражения слева направо, а в другом справа налево. Числами можно проставить порядок выполнения действий (рис. 1).
Рис. 1. Порядок действий
В первом выражении мы сначала выполним действие вычитания, а затем к результату прибавим число 4.
Запишем.
8-3+4=5+4=9
Во втором выражении сначала найдем значение суммы, а потом из 8 вычтем полученный результат 7.
8-3+4=8-7=1
Видим, что значения выражений получаются разные.
Сделаем вывод: порядок выполнения арифметических действий менять нельзя.
Порядок выполнения арифметических действий в выражениях без скобок
Узнаем правило выполнения арифметических действий в выражениях без скобок.
Если в выражение без скобок входят только сложение и вычитание или только умножение и деление, то действия выполняют в том порядке, в каком они написаны.
Потренируемся.
Рассмотрим выражение
38-10+6
В этом выражении имеются только действия сложения и вычитания. Эти действия называют действиями первой ступени.
Выполняем действия слева направо по порядку (рис. 2).
Рис. 2. Порядок действий
Рассмотрим второе выражение
24:3*2
В этом выражении имеются только действия умножения и деления – это действия второй ступени.
Выполняем действия слева направо по порядку (рис. 3).
Рис. 3. Порядок действий
В каком порядке выполняются арифметические действия, если в выражении имеются не только действия сложения и вычитания, но и умножения и деления?
Если в выражение без скобок входят не только действия сложения и вычитания, но и умножения и деления, или оба этих действия, то сначала выполняют по порядку (слева направо) умножение и деление, а затем сложение и вычитание.
Рассмотрим выражение.
18:2-2*3+12:3
Рассуждаем так. В этом выражении имеются действия сложения и вычитания, умножения и деления. Действуем по правилу. Сначала выполняем по порядку (слева направо) умножение и деление, а затем сложение и вычитание. Расставим порядок действий.
1 4 2 5 3
18:2-2*3+12:3
Вычислим значение выражения.
1 4 2 5 3
18:2-2*3+12:3=9-6+4=3+4=7
Порядок выполнения арифметических действий в выражениях со скобками
В каком порядке выполняются арифметические действия, если в выражении имеются скобки?
Если в выражении имеются скобки, то сначала вычисляют значение выражений в скобках.
Рассмотрим выражение.
30 + 6 * (13 — 9)
Мы видим, что в этом выражении имеется действие в скобках, значит, это действие выполним первым, затем по порядку умножение и сложение. Расставим порядок действий.
3 2 1
30 + 6 * (13 — 9)
Вычислим значение выражения.
3 2 1
30+6*(13-9)=30+6*4=30+24=54
Правило выполнения арифметических действий в выражениях без скобок и со скобками
Как нужно рассуждать, чтобы правильно установить порядок арифметических действий в числовом выражении?
Прежде чем приступить к вычислениям, надо рассмотреть выражение (выяснить, есть ли в нём скобки, какие действия в нём имеются) и только после этого выполнять действия в следующем порядке:
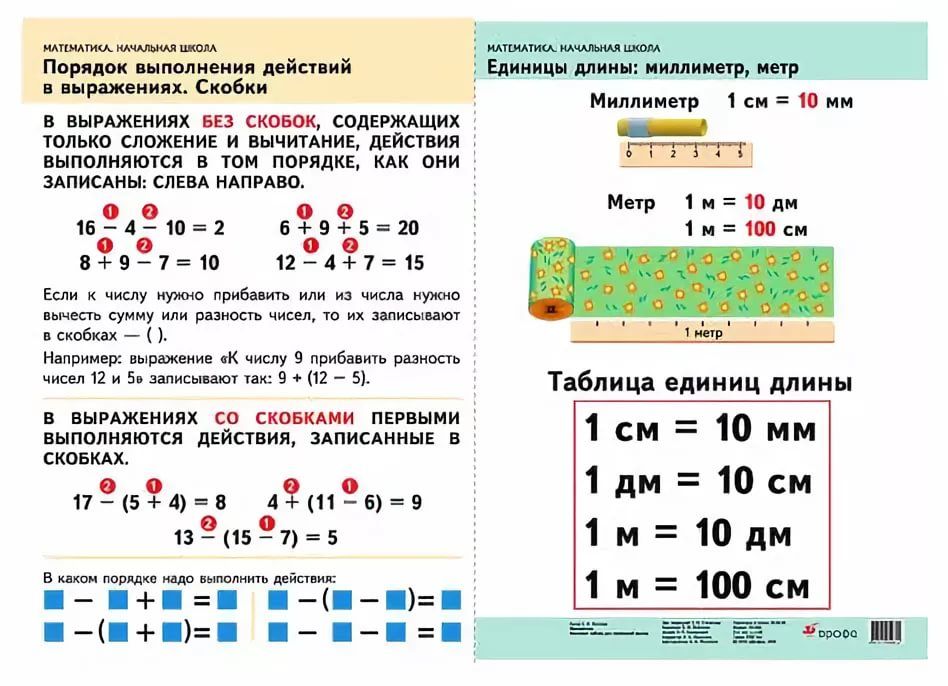
1. действия, записанные в скобках;
2. умножение и деление;
3. сложение и вычитание.
Схема поможет запомнить это несложное правило (рис. 4).
Рис. 4. Порядок действий
4. Закрепление Выполнение тренировочных заданий на изученное правило
Закрепление Выполнение тренировочных заданий на изученное правило
Потренируемся.
Рассмотрим выражения, установим порядок действий и выполним вычисления.
43 — (20 — 7) +15
32 + 9 * (19 — 16)
2 * 9 — 18:3
Будем действовать по правилу. В выражении 43 — (20 — 7) +15 имеются действия в скобках, а также действия сложения и вычитания. Установим порядок действий. Первым действием выполним действие в скобках, а затем по порядку слева направо вычитание и сложение.
43 — (20 — 7) +15 =43 — 13 +15 = 30 + 15 = 45
В выражении 32 + 9 * (19 — 16) имеются действия в скобках, а также действия умножения и сложения. По правилу первым выполним действие в скобках, затем умножение (число 9 умножаем на результат, полученный при вычитании) и сложение.
32 + 9 * (19 — 16) =32 + 9 * 3 = 32 + 27 = 59
В выражении 2*9-18:3 отсутствуют скобки, зато имеются действия умножения, деления и вычитания. Действуем по правилу. Сначала выполним слева направо умножение и деление, а затем от результата, полученного при умножении, вычтем результат, полученный при делении.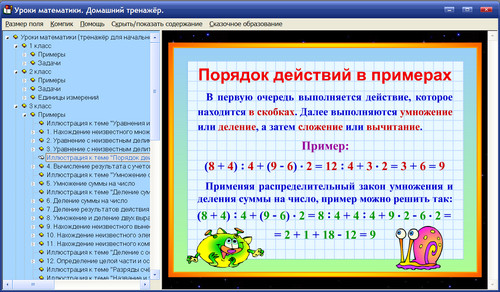 То есть первое действие – умножение, второе – деление, третье – вычитание.
То есть первое действие – умножение, второе – деление, третье – вычитание.
2*9-18:3=18-6=12
Узнаем, правильно ли определен порядок действий в следующих выражениях.
4 3 1 2
37 + 9 — 6 : 2 * 3 =
3 1 2
18 : (11 — 5) + 47=
1 3 2
7 * 3 — (16 + 4)=
Рассуждаем так.
3 4 1 2
37 + 9 — 6 : 2 * 3 =
В этом выражении скобки отсутствуют, значит, сначала выполняем слева направо умножение или деление, затем сложение или вычитание. В данном выражении первое действие – деление, второе – умножение. Третье действие должно быть сложение, четвертое – вычитание. Вывод: порядок действий определен верно.
Найдем значение данного выражения.
3 4 1 2
37+9-6:2*3 =37+9-3*3=37+9-9=46-9=37
Продолжаем рассуждать.
3 1 2
18:(11-5)+47=
Во втором выражении имеются скобки, значит, сначала выполняем действие в скобках, затем слева направо умножение или деление, сложение или вычитание. Проверяем: первое действие – в скобках, второе – деление, третье – сложение. Вывод: порядок действий определен неверно. Исправим ошибки, найдем значение выражения.
Проверяем: первое действие – в скобках, второе – деление, третье – сложение. Вывод: порядок действий определен неверно. Исправим ошибки, найдем значение выражения.
2 1 3
18:(11-5)+47=18:6+47=3+47=50
Рассуждаем далее.
1 3 2
7*3-(16+4)=
В этом выражении также имеются скобки, значит, сначала выполняем действие в скобках, затем слева направо умножение или деление, сложение или вычитание. Проверяем: первое действие – в скобках, второе – умножение, третье – вычитание. Вывод: порядок действий определен неверно. Исправим ошибки, найдем значение выражения.
2 3 1
7*3-(16+4)=7*3-20=21-20=1
Выполним задание.
Расставим порядок действий в выражении, используя изученное правило (рис. 5).
Рис. 5. Порядок действий
Мы не видим числовых значений, поэтому не сможем найти значение выражений, однако потренируемся применять изученное правило.
Действуем по алгоритму.
В первом выражении имеются скобки, значит, первое действие в скобках. Затем слева направо умножение и деление, потом слева направо вычитание и сложение.
Затем слева направо умножение и деление, потом слева направо вычитание и сложение.
Во втором выражении также имеются скобки, значит, первое действие выполняем в скобках. После этого слева направо умножение и деление, после этого – вычитание.
Проверим себя (рис. 6).
Рис. 6. Порядок действий
5. Подведение итогов.
— Сегодня на уроке мы познакомились с правилом порядка выполнения действий в выражениях без скобок и со скобками. В ходе выполнения заданий определяли, зависит ли значение выражений от порядка выполнения арифметических действий, узнали, отличается ли порядок арифметических действий в выражениях без скобок и со скобками, потренировались в применении изученного правила, искали и исправляли ошибки, допущенные при определении порядка действий.
Standards for Mathematical Practice — Стандарты содержания (Департамент образования CA)
Департамент образования Калифорнии
- Преподавание и обучение
- Тестирование и отчетность
- Финансы и гранты
- Данные и статистика
- Специализированные программы
- Поддержка обучения
- Профессиональное обучение
- Дом
- Государственный совет по образованию
- Отказ от прав, стандарты и рамки
- Стандарты содержания
Стандарты математической практики описывают различные виды знаний, которые преподаватели математики на всех уровнях должны стремиться развивать у своих учащихся.
Общие базовые стандарты штата Калифорния по математике
Стандарты математической практики
Стандарты математической практики описывают различные знания, которые преподаватели математики на всех уровнях должны стремиться развивать у своих учащихся. Эти практики основаны на важных «процессах и навыках», имеющих давнее значение в математическом образовании. Первыми из них являются стандарты процессов NCTM для решения проблем, рассуждений и доказательств, коммуникации, представления и связей. Во-вторых, это направления математического мастерства, указанные в отчете Национального исследовательского совета Adding It Up: адаптивное мышление, стратегическая компетентность, концептуальное понимание (понимание математических понятий, операций и отношений), процедурная беглость (навык гибкого, точного и эффективно и надлежащим образом) и продуктивная предрасположенность (привычная склонность считать математику разумной, полезной и стоящей в сочетании с верой в усердие и собственную эффективность).
Разбираться в проблемах и настойчиво решать их.
Подкованные в математике учащиеся начинают с того, что объясняют себе смысл задачи и ищут пути ее решения. Они анализируют данные, ограничения, отношения и цели. Они строят предположения о форме и значении решения и планируют путь решения, а не просто пытаются найти решение. Они рассматривают аналогичные проблемы и пробуют частные случаи и более простые формы исходной задачи, чтобы получить представление о ее решении. Они контролируют и оценивают свой прогресс и при необходимости меняют курс. Учащиеся постарше могут, в зависимости от контекста задачи, преобразовывать алгебраические выражения или менять окно просмотра на своем графическом калькуляторе, чтобы получить необходимую им информацию. Подкованные в математике учащиеся могут объяснять соответствия между уравнениями, словесными описаниями, таблицами и графиками или рисовать диаграммы важных функций и взаимосвязей, графически отображать данные и искать закономерности или тенденции.
- Рассуждать абстрактно и количественно .
Математически подкованные учащиеся понимают величины и их отношения в проблемных ситуациях. Они привносят две взаимодополняющие способности в решение проблем, связанных с количественными отношениями: способность деконтекстуализировать — абстрагировать данную ситуацию и представлять ее символически, а также манипулировать репрезентирующими символами так, как если бы они жили собственной жизнью, не обязательно обращая внимание на свои референты, — и способность контекстуализировать, делать паузы по мере необходимости в процессе манипулирования, чтобы исследовать референты для задействованных символов. Количественное рассуждение влечет за собой привычки создавать последовательное представление проблемы; рассмотрение задействованных единиц; обращать внимание на значение величин, а не только на то, как их вычислять; знание и гибкое использование различных свойств операций и объектов.
Количественное рассуждение влечет за собой привычки создавать последовательное представление проблемы; рассмотрение задействованных единиц; обращать внимание на значение величин, а не только на то, как их вычислять; знание и гибкое использование различных свойств операций и объектов. - Придумывать жизнеспособные аргументы и критиковать рассуждения других .
Подкованные в математике учащиеся понимают и используют заявленные предположения, определения и ранее установленные результаты при построении аргументов. Они строят предположения и выстраивают логическую последовательность утверждений, чтобы исследовать истинность своих предположений. Они способны анализировать ситуации, разбивая их на случаи, а также могут распознавать и использовать контрпримеры. Они обосновывают свои выводы, сообщают их другим и отвечают на аргументы других. Они индуктивно рассуждают о данных, выдвигая правдоподобные аргументы, учитывающие контекст, из которого эти данные возникли.
- Модель с математикой .
Учащиеся, хорошо разбирающиеся в математике, могут применять математику, которую они знают, для решения проблем, возникающих в повседневной жизни, обществе и на рабочем месте. В младших классах это может быть так же просто, как написать уравнение сложения для описания ситуации. В средних классах учащийся может применять пропорциональные рассуждения, чтобы спланировать школьное мероприятие или проанализировать проблему в сообществе. К старшей школе учащийся может использовать геометрию для решения задачи проектирования или использовать функцию для описания того, как одна интересующая величина зависит от другой. Подкованные в математике учащиеся, которые могут применять то, что они знают, спокойно делают предположения и приближения, чтобы упростить сложную ситуацию, понимая, что позже они могут потребовать пересмотра. Они способны определять важные величины в практической ситуации и отображать их отношения, используя такие инструменты, как диаграммы, двусторонние таблицы, графики, блок-схемы и формулы. Они могут математически анализировать эти отношения, чтобы делать выводы. Они обычно интерпретируют свои математические результаты в контексте ситуации и размышляют о том, имеют ли результаты смысл, возможно, улучшая модель, если она не достигла своей цели.
В младших классах это может быть так же просто, как написать уравнение сложения для описания ситуации. В средних классах учащийся может применять пропорциональные рассуждения, чтобы спланировать школьное мероприятие или проанализировать проблему в сообществе. К старшей школе учащийся может использовать геометрию для решения задачи проектирования или использовать функцию для описания того, как одна интересующая величина зависит от другой. Подкованные в математике учащиеся, которые могут применять то, что они знают, спокойно делают предположения и приближения, чтобы упростить сложную ситуацию, понимая, что позже они могут потребовать пересмотра. Они способны определять важные величины в практической ситуации и отображать их отношения, используя такие инструменты, как диаграммы, двусторонние таблицы, графики, блок-схемы и формулы. Они могут математически анализировать эти отношения, чтобы делать выводы. Они обычно интерпретируют свои математические результаты в контексте ситуации и размышляют о том, имеют ли результаты смысл, возможно, улучшая модель, если она не достигла своей цели.
- Стратегически используйте соответствующие инструменты .
Подкованные в математике учащиеся рассматривают доступные инструменты при решении математической задачи. Эти инструменты могут включать карандаш и бумагу, конкретные модели, линейку, транспортир, калькулятор, электронную таблицу, систему компьютерной алгебры, статистический пакет или программное обеспечение для динамической геометрии. Профессиональные учащиеся достаточно хорошо знакомы с инструментами, соответствующими их классу или курсу, чтобы принимать обоснованные решения о том, когда каждый из этих инструментов может быть полезен, признавая как получаемое понимание, так и их ограничения. Например, математически подкованные старшеклассники анализируют графики функций и решений, построенные с помощью графического калькулятора. Они обнаруживают возможные ошибки, стратегически используя оценку и другие математические знания. Создавая математические модели, они знают, что технологии позволяют визуализировать результаты различных предположений, исследовать последствия и сравнивать прогнозы с данными.
- Следить за точностью .
Математически подкованные ученики стараются точно общаться с другими. Они стараются использовать четкие определения в обсуждениях с другими и в собственных рассуждениях. Они заявляют о значении выбранных ими символов, включая последовательное и уместное использование знака равенства. Они внимательно относятся к указанию единиц измерения и маркировке осей, чтобы прояснить соответствие с количествами в задаче. Они рассчитывают точно и эффективно, выражают числовые ответы с точностью, соответствующей контексту задачи. В начальных классах учащиеся дают тщательно сформулированные объяснения друг другу. 2 + x + 1) может привести их к общей формуле суммы геометрического ряда. Работая над решением задачи, математически подкованные ученики контролируют процесс, уделяя внимание деталям. Они постоянно оценивают обоснованность своих промежуточных результатов.
2 + x + 1) может привести их к общей формуле суммы геометрического ряда. Работая над решением задачи, математически подкованные ученики контролируют процесс, уделяя внимание деталям. Они постоянно оценивают обоснованность своих промежуточных результатов.
Связь стандартов математической практики со стандартами математического содержания
Стандарты математической практики описывают способы, с помощью которых развивающиеся студенты-практики, изучающие дисциплину математики, все чаще должны взаимодействовать с предметом по мере роста их математической зрелости и опыта во всем начальный, средний и старший школьный годы. Разработчики учебных программ, оценок и профессионального развития должны учитывать необходимость соединения математических практик с математическим содержанием в обучении математике.
Стандарты математического содержания представляют собой сбалансированное сочетание процедуры и понимания. Ожидания, которые начинаются со слова «понимать», часто являются особенно хорошей возможностью связать практику с содержанием.
В этом отношении те стандарты содержания, которые устанавливают ожидание понимания, являются потенциальными «точками пересечения» между Стандартами математического содержания и Стандартами математической практики. Эти точки пересечения должны быть смещены в сторону центральных и генеративных концепций школьной программы по математике, которые в наибольшей степени заслуживают времени, ресурсов, новаторской энергии и внимания, необходимых для качественного улучшения учебной программы, обучения, оценки, профессионального развития и достижений учащихся в математика.
Вопросы: Отдел учебной программы и учебных ресурсов | [email protected] | 916-319-0881
Последнее рассмотрение: среда, 13 июля 2022 г. Поделиться этой страницей За последние 60 дней нет опубликованных материалов.
Математика
Государственный совет по образованию имеет право принимать академические стандарты для каждой предметной области в классах K–12. Совет штата принял новые государственные стандарты по математике в апреле 2016 года, и они впервые будут внедрены в классах в 2017-18 учебном году. Математические стандарты были разработаны, чтобы гарантировать, что выпускники Теннесси готовы к строгим требованиям математического понимания в колледже и карьере.
Загрузить Академические стандарты штата Теннесси по математике
Чтобы обеспечить эффективное обучение в классе, департамент создал учебные документы по математике. Эти документы были разработаны в соответствии со стандартами математики, в которых, по данным штата, учащиеся испытывали наибольшие затруднения, и являются необязательными дополнениями для рассмотрения педагогами. Цель этих документов — предоставить учителям примеры обучения на всех уровнях успеваемости, чтобы помочь педагогам определить глубину концептуального понимания учащимся математических стандартов штата Теннесси. Вы можете получить доступ к этим документам, используя раскрывающееся меню ниже.
Цель этих документов — предоставить учителям примеры обучения на всех уровнях успеваемости, чтобы помочь педагогам определить глубину концептуального понимания учащимся математических стандартов штата Теннесси. Вы можете получить доступ к этим документам, используя раскрывающееся меню ниже.
Восемь стандартов математической практики являются важным компонентом стандартов математики для каждого класса и курса, K–12. Стандарты математической практики описывают разновидности знаний, склада ума и продуктивных склонностей, которые педагоги стремятся развить у всех учащихся.
- Разбираться в проблемах и настойчиво решать их
- Рассуждать абстрактно и количественно
- Придумывать жизнеспособные аргументы и критиковать рассуждения других
- Модель с математикой
- Стратегически используйте соответствующие инструменты
- Следите за точностью
- Ищите и используйте структуру
- Ищите и выражайте регулярность в повторяющихся рассуждениях
Четыре стандарта грамотности для математических навыков также являются неотъемлемым компонентом стандартов математики K–12. Коммуникация в математике использует навыки грамотности в чтении, словарном запасе, разговорной речи, а также
Коммуникация в математике использует навыки грамотности в чтении, словарном запасе, разговорной речи, а также
аудировании и письме. Ниже приведены четыре навыка грамотности, необходимые для математических навыков:
- Использовать несколько стратегий чтения
- Понимать и использовать правильный математический словарь
- Обсуждать и формулировать математические идеи
- Запись математических аргументов
Примечание: Совет по образованию штата устанавливает требования для окончания средней школы (см. Правила для средних школ 2.103). В соответствии с правилом SBE учащиеся должны достичь четырех математических единиц уровня средней школы, чтобы получить аттестат о среднем образовании, включая алгебру I, алгебру II и геометрию (или эквивалентные курсы, интегрированная математика I, II и III) и один дополнительный курс математики помимо алгебры I. Посмотреть список курсов, необходимых для окончания средней школы, можно здесь.

 Актуализация знаний и фиксирование индивидуального затруднения
Актуализация знаний и фиксирование индивидуального затруднения Сначала нужно выполнить действия в скобках
Сначала нужно выполнить действия в скобках — не знаем правило
— не знаем правило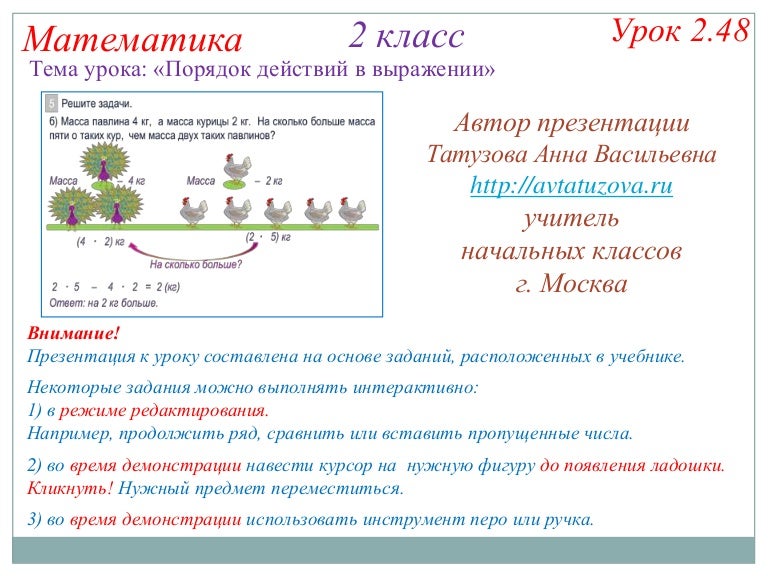 Сначала думаем, затем начинаем проговаривать ответ по кругу, начиная с участника №1.
Сначала думаем, затем начинаем проговаривать ответ по кругу, начиная с участника №1. Как будем разбивать?
Как будем разбивать? 117 прочитаем памятку.
117 прочитаем памятку.

 Проверьте.
Проверьте.  Рефлексия учебной деятельности на уроке
Рефлексия учебной деятельности на уроке Я вручаю вам золотые и серебряные звезды (вручение звезд)
Я вручаю вам золотые и серебряные звезды (вручение звезд) Количественное рассуждение влечет за собой привычки создавать последовательное представление проблемы; рассмотрение задействованных единиц; обращать внимание на значение величин, а не только на то, как их вычислять; знание и гибкое использование различных свойств операций и объектов.
Количественное рассуждение влечет за собой привычки создавать последовательное представление проблемы; рассмотрение задействованных единиц; обращать внимание на значение величин, а не только на то, как их вычислять; знание и гибкое использование различных свойств операций и объектов.
 В младших классах это может быть так же просто, как написать уравнение сложения для описания ситуации. В средних классах учащийся может применять пропорциональные рассуждения, чтобы спланировать школьное мероприятие или проанализировать проблему в сообществе. К старшей школе учащийся может использовать геометрию для решения задачи проектирования или использовать функцию для описания того, как одна интересующая величина зависит от другой. Подкованные в математике учащиеся, которые могут применять то, что они знают, спокойно делают предположения и приближения, чтобы упростить сложную ситуацию, понимая, что позже они могут потребовать пересмотра. Они способны определять важные величины в практической ситуации и отображать их отношения, используя такие инструменты, как диаграммы, двусторонние таблицы, графики, блок-схемы и формулы. Они могут математически анализировать эти отношения, чтобы делать выводы. Они обычно интерпретируют свои математические результаты в контексте ситуации и размышляют о том, имеют ли результаты смысл, возможно, улучшая модель, если она не достигла своей цели.
В младших классах это может быть так же просто, как написать уравнение сложения для описания ситуации. В средних классах учащийся может применять пропорциональные рассуждения, чтобы спланировать школьное мероприятие или проанализировать проблему в сообществе. К старшей школе учащийся может использовать геометрию для решения задачи проектирования или использовать функцию для описания того, как одна интересующая величина зависит от другой. Подкованные в математике учащиеся, которые могут применять то, что они знают, спокойно делают предположения и приближения, чтобы упростить сложную ситуацию, понимая, что позже они могут потребовать пересмотра. Они способны определять важные величины в практической ситуации и отображать их отношения, используя такие инструменты, как диаграммы, двусторонние таблицы, графики, блок-схемы и формулы. Они могут математически анализировать эти отношения, чтобы делать выводы. Они обычно интерпретируют свои математические результаты в контексте ситуации и размышляют о том, имеют ли результаты смысл, возможно, улучшая модель, если она не достигла своей цели.
 2 + x + 1) может привести их к общей формуле суммы геометрического ряда. Работая над решением задачи, математически подкованные ученики контролируют процесс, уделяя внимание деталям. Они постоянно оценивают обоснованность своих промежуточных результатов.
2 + x + 1) может привести их к общей формуле суммы геометрического ряда. Работая над решением задачи, математически подкованные ученики контролируют процесс, уделяя внимание деталям. Они постоянно оценивают обоснованность своих промежуточных результатов.