Умножения двузначных чисел в уме – искусство счета
Люди всегда стремились найти лучшие способы выполнения вычислений. Чем стремительнее развивается прогресс, тем более актуальными становятся высокие математические способности. Даже тот человек, карьера которого не предполагает работу с цифрами, ежедневно вынужден прибегать к счету в уме. Походы за покупками, оплата коммунальных счетов, планирование семейного бюджета – все это требует большого количество подсчетов. Конечно, можно полагаться на технику, ведь в каждом современном смартфоне присутствует калькулятор. Но все же стоит помнить, что умение быстро считать – это возможность существенно оптимизировать свои собственные ресурсы, поэтому развивать такие навыки важно.
Умножение в уме
В современном мире цифры окружают нас везде. Ежедневно мы не задумываясь выполняем десятки и даже сотни простых арифметических действий, но, стоит только столкнуться с более сложными числовыми операциями, и большинство людей машинально потянется к калькулятору. Мало кто хочет тратить время на сложные подсчеты в уме, когда с помощью информационных технологий произвести их можно за считанные секунды. Но что делать, если смартфона, калькулятора или листа бумаги с ручкой нет, а что-то посчитать нужно срочно? На помощь приходят методы счета в уме.
Мало кто хочет тратить время на сложные подсчеты в уме, когда с помощью информационных технологий произвести их можно за считанные секунды. Но что делать, если смартфона, калькулятора или листа бумаги с ручкой нет, а что-то посчитать нужно срочно? На помощь приходят методы счета в уме.
Складывать и вычитать устно – этому человек учится еще в школе. Со временем, удается научиться без труда производить вычисления даже с большими значениями. Конечно, это утверждение справедливо только для простых операций, таких как сложение и вычитание, а вот умножение освоить уже не так легко. В школе от детей требуется научиться умножать только на множитель от одного до десяти, а более сложные подсчеты допустимо производить на бумаге. Таким образом, ученикам не прививается умение выполнять умножение больших чисел в уме, этим навыкам можно обучиться только дополнительно.
Умение быстро считать очень полезно, так как оно используется ежедневно. Поэтому сегодня придумано множество подходов к счету.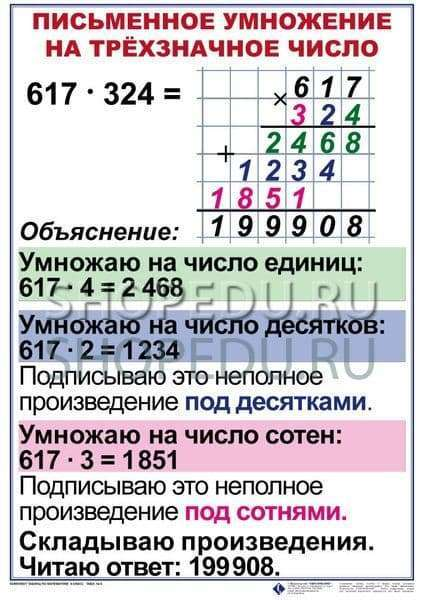 Чаще всего люди используют различные математические приемы, которые позволяют производить умножение устно. Они имеют свои плюсы и минусы, но все же позволяют получить правильный ответ без использования подручных средств. Чтобы определить, насколько эти способы эффективны и продуктивны в повседневных реалиях, нужно рассмотреть каждый из них отдельно.
Чаще всего люди используют различные математические приемы, которые позволяют производить умножение устно. Они имеют свои плюсы и минусы, но все же позволяют получить правильный ответ без использования подручных средств. Чтобы определить, насколько эти способы эффективны и продуктивны в повседневных реалиях, нужно рассмотреть каждый из них отдельно.
Популярные методы устного умножения
Сегодня существует сразу несколько способов умножения в уме. Они не универсальны, но позволяют достаточно успешно производить операции с двузначными числами. Чтобы подобрать для себя оптимальный, лучше ознакомиться с самыми популярными из них:
Вариант 1. Умножение в столбик
Этот вариант отлично подходит тем, кто способен хорошо запоминать и удерживать в памяти сразу несколько промежуточных результатов вычислений. Благодаря этому подходу можно легко производить операции между двузначными числами. Рассмотрим данный вид счета на примере выражения 34*63.
Сначала необходимо умножить 34 на единицы второго числа: 34*3=102.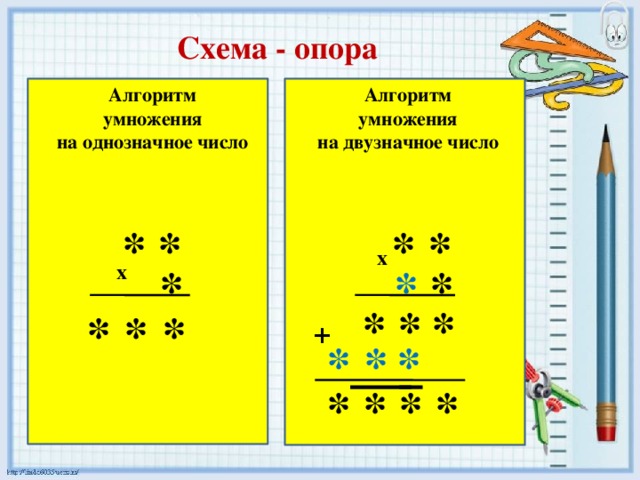 Запоминаем это значение. Затем повторяем операцию уже с десятками множителя: 34*60=2040. Теперь требуется просто сложить результаты наших вычислений: 102+2040=2142
Запоминаем это значение. Затем повторяем операцию уже с десятками множителя: 34*60=2040. Теперь требуется просто сложить результаты наших вычислений: 102+2040=2142
Вариант 2. Умножение с разложением на десятки и единицы
Этот вариант также требует хорошей памяти. Рассмотрим его на примере прошлого выражения 34*63.
Сначала требуется разложить числа на десятки и единицы, у нас получится: (30+4)*(60+3). Далее мы перемножаем между собой десятки: 30*60=1800. Запоминаем этот результат. Затем необходимо умножить десятки первого значения на единицы второго и наоборот: (30*3)+(60*4)=330. Теперь наступает самая сложная часть, главное – не сбиться. Нам нужно сложить результаты наших первых двух примеров и прибавить к ним произведение единиц перемножаемых чисел. Получится следующее выражение: 1800+330+4*3=2142.
Вариант 3. Умножение с большими числами
Этот вид вычислений больше подходит для тех двузначных чисел, которые близки к 100. Рассмотрим этот способ на примере выражения 88*95.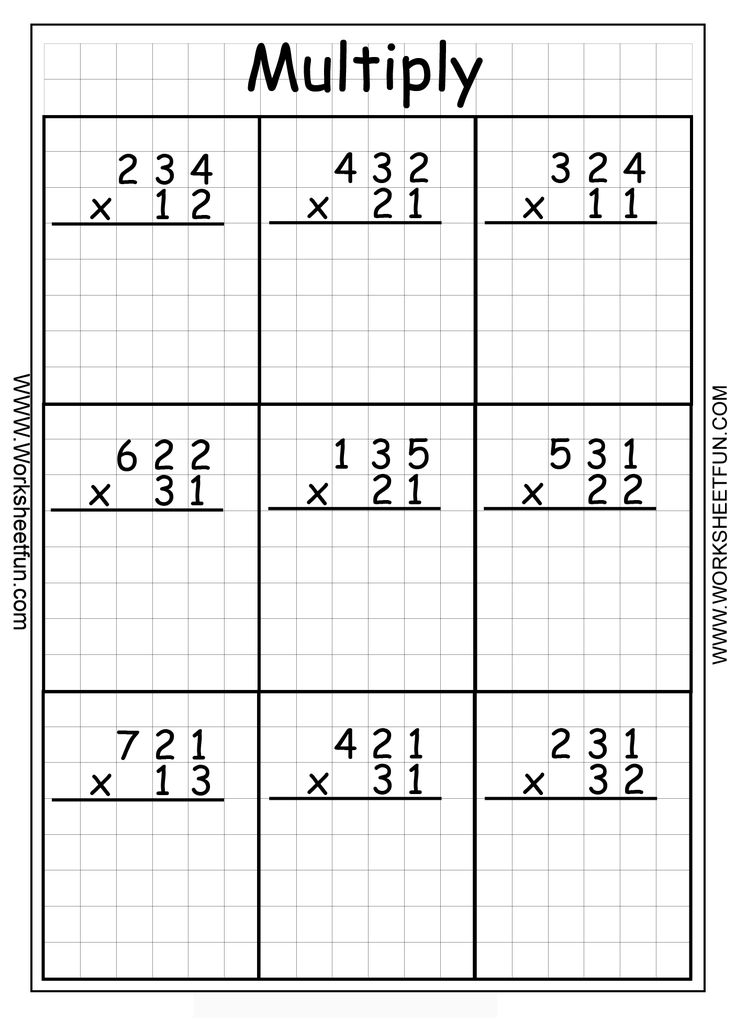
Сначала нужно представить каждое из этих значений как разность 100 и другого числа: 100-a=88 и 100-b=95, a=12, b=5. Так у нас получится (100-12)*(100-5). Теперь нужно произвести следующие вычисления: 88-b и 95-a, 88-5 и 95-12, получится 83 в обоих случаях. Это значение нужно запомнить. Теперь нам нужно найти a*b=12*5=60. Наш итоговый ответ будет состоять из четырех цифр от полученных ранее ответов: 83 и 60, получается 8360.
Иногда в результате подсчетов получается, что второе итоговое значение имеет три знака, а не два. Допустим, у нас получились числа 12 и 345. В этом случае нужно сложить вторую и третью цифру так, чтобы получилось 1545.
Это основные методы устного умножения. Но можно ли их назвать простыми? Несмотря на то, что при усердных тренировках удастся освоить любой из этих подходов, все же они будут требовать хорошей памяти и высокой концентрации. К тому же, не всегда допустимо проводить операции с многозначными числами с помощью данных методов. Лучше постараться найти для себя другие, более простые способы счета.
Быстрое умножение в уме больших чисел
Математики всех времен искали простые методы быстрого устного счета. Умножение и деление, в отличие от сложения и вычитания, являются более сложными операциями. Поэтому производить такие подсчеты в уме без должной подготовки сложно, тем более когда речь идет о многозначных числах. Проблема устного умножения в том, что не существует какого-либо универсального способа, который бы подходил вне зависимости от ситуации.
Мозг обычного человека не способен работать также быстро, как калькулятор. Мы склонны терять концентрацию, сбиваться, забывать результаты промежуточных операций. Поэтому стандартные способы устного умножения мало пригодны для повседневных задач. Они скорее являются хорошей разминкой для мозга, чем удобным инструментом. Но что делать, если быстро считать без подручных средств все же хочется?
Благодаря интернету можно найти немало информации по этому вопросу. Сегодня существует множество методик, позволяющих научиться складывать, вычитать, умножать и даже делить с моментальной скоростью. Но самым популярным направлением устного счета является ментальная арифметика. Ее неоспоримым плюсом является то, что она дается детям даже легче, чем взрослым.
Но самым популярным направлением устного счета является ментальная арифметика. Ее неоспоримым плюсом является то, что она дается детям даже легче, чем взрослым.
Лучший способ научиться устному счету
Ментальная арифметика – это не только уникальный способ счета без подручных средств. В основе этой методики лежит равнозначное развитие как левого полушария мозга, отвечающего за логику и анализ, так и правого, которое контролирует работу воображения и фантазии. Несмотря на то, что освоить ментальную арифметику может любой желающий, она все же больше подходит для изучения в раннем возрасте. Именно в детстве можно приобрести навыки, которые не забудутся со временем и сохранятся на всю жизнь.
Обучение ментальной арифметике – длительный процесс, который требует усидчивости и нацеленности на результат. Пройдет немало времени, пока ребенок сможет полностью освоить программу и научиться не только складывать и вычитать, но и умножать и делить многозначные числа. Родителям не всегда удается контролировать периодичность занятий своего ребенка, а также следить за тем, чтобы он выполнял все необходимые упражнения. Этим обусловлен рост популярности групповых занятий ментальной арифметикой в центрах дополнительного развития детей.
Этим обусловлен рост популярности групповых занятий ментальной арифметикой в центрах дополнительного развития детей.
Ученики, обучающиеся по этому направлению, сначала осваивают вычисления на древних счетах – абакусе. Когда базовые навыки закрепятся, наступает время для перехода к следующему, более сложному этапу. Теперь ученик постепенно привыкает представлять абакус в своем воображении и производить подсчеты уже на нем. Именно так и удается развить навык быстрого счета.
Благодаря занятиям ментальной арифметикой ребенок повышает успеваемость в школе, ведь теперь ему доступны не только простые вычисления в уме, но и быстрое умножение и деление. Количество времени, которое он тратит на выполнение домашних заданий, также сокращается. Так удается добиться большей продуктивности образовательного процесса в школе и дома. Навыки, приобретенные благодаря ментальной арифметике, сохранятся навсегда, что очень пригодится во взрослой жизни.
Математика Умножение двузначного числа на однозначное
Материалы к уроку
Конспект урока
|
27.
|
|
|
Организационный этап
Математика вновь к вам пришла. Сегодня сама царица Математика приглашает нас в свою страну. Без конца твердят нам в школе: Сегодня на уроке мы будем учиться умножать двузначное число на однозначное.
|
|
|
Этап подготовки учащихся к активному сознательному усвоению знаний
Устный счёт
Всё считается со счета. И отправляемся в небольшое путешествие по стране Математике.
Задание 1 Посмотрите перед нами бурная математическая речка Слагайка, чтобы её переплыть, нужно заменить суммой разрядных слагаемых следующие числа: 15, 27, 38 Проверьте себя. Задание 2 В стране Математике много интересного. Перед нами горы Считалы, чтобы на них подняться, нужно выполнить задание. Выберите выражение, значение которого равно 0. 1) 48 : 8 · 6 — 6 2) 48 : (1 · 6) + 6 3) 48 : 8 · (6 — 6) 4) 48 : 8 · 6 : 6 Проверьте себя.
Задание 3 В конкурсе портретов царицы Математики приняли участие: 5 учеников первого класса, каждый ученик предоставил по две работы. 7 учеников второго класса, каждый ученик предоставил по две работы. 10 учеников третьего класса, каждый ученик предоставил по три работы. Сколько работ от каждого класса было на выставке?
Какое количество работ предоставлено от учеников 2 класса? 7 · 2 = 14 Какое количество работ предоставлено от учеников 3 класса? 10 · 3 = 30
|
|
|
Этап усвоения новых знаний
Ребята, смотрите, перед нами океан Знаний. И где-то там вдалеке есть остров Умножения. Побывать там нам поможет царица Математика. Научимся умножать двузначное число на однозначное. 42 умножаем на 6. 1. Раскладываем первый множитель на разрядные слагаемые. Что такое 42? Это 40 и 2. 2. Применяем распределительный закон умножения: умножаем каждое разрядное слагаемое на второй множитель, а полученные результаты складываем. 42 ∙ 6 = (40 ∙ 6) + (2 ∙ 6) = 240 + 12 = 252
Запомните, чтобы умножить двузначное число на однозначное: 1. Нужно разложить первый множитель на разрядные слагаемые. 2. Применить распределительный закон умножения: умножить каждое разрядное слагаемое на второй множитель, а полученные результаты сложить. Решим пример с объяснением. 17 умножить на 4. Дальше применяем распределительный закон умножения: умножаем каждое разрядное слагаемое на второй множитель, а полученные результаты складываем. 10 умножаем на 4, получается 40, 7 умножаем на 4, получается 28, 40 плюс 28, получается 68. Молодцы! Для решения примеров подобного вида можно использовать последовательность команд, которые нужно выполнять поочерёдно или можно использовать алгоритм:
|
|
|
Путешествуем дальше по стране Математике. Вот мы с вами уже находимся на острове Умножения. Посмотрите повсюду деревья, на которых растут числовые выражения, сорвем парочку.
Задание 1 Найдите произведение чисел 24 и 3; 19 и 4 Проверьте себя и оцените свои успехи. 24 · 3 = (20 + 4) · 3 = 20 · 3 + 4 · 3 = 60 + 12 = 72 19 · 4 = (10 + 9) · 4 = 10 · 4 + 9 · 4 = 40 + 36 = 76 |
|
|
Задание 2 Ребята, на острове Умножения растут даже цветы математические с задачами. На четырёх клумбах по пять кустов гвоздик и по шесть кустов роз. Сколько всего кустов на клумбах? Решите задачу, сделав схематический рисунок. Проверьте себя и оцените свои успехи.
Решить данное выражение можно двумя способами: 1 способ: умножим число на каждое слагаемое и полученные результаты сложим. (5 + 6) · 4 = 5 · 4 + 6 · 4 = 20 + 24 = 44 (к. 2 способ: вычислим сумму и умножим ее на число: (5 + 6) · 4 = 11 · 4 = 44 (к.) Ответ: на клумбах всего 44 куста.
Интересно задачи решать, У каждой задачи свой сюжет, И надо найти на вопрос ответ.
Во время путешествия все, конечно, проголодались, подкрепимся фруктами, решив задачу. 21 ученик получил по 3 груши. Сколько всего груш было? Решите задачу без краткой записи. Проверьте себя.
Ответ: всего было 63 груши.
Задание от царицы Математики на внимание. Посмотрите на запись математических выражений и запишите только верное выражение. 17 · 2 = (10 + 7) · 2 = 10 · 2+ 7 = 20 + 7 = 34 17 · 2 = (10 + 7) · 2 = 10 · 2 + 7 · 2 = 20 + 14 = 34 Проверьте себя.
|
|
|
Этап подведения итогов
Для того чтобы умножить двузначное число на однозначное нужно:
|
|
|
Рефлексия
Ребята, наше путешествие по стране Математике подходит к концу. Красный. Я работал на уроке с желанием, был уверен в себе. Желтый. Я работал на уроке с желанием, но чувствовал какое-то неудобство, волнение, но мне было интересно. Синий. Я работал на уроке без желания, боялся отвечать и выполнять работу….
Спасибо за работу! |
|
Остались вопросы по теме? Наши репетиторы готовы помочь!
Подготовим к ЕГЭ, ОГЭ и другим экзаменам
Найдём слабые места по предмету и разберём ошибки
Повысим успеваемость по школьным предметам
Поможем подготовиться к поступлению в любой ВУЗ
Выбрать репетитора
Как умножать двузначные числа: стратегии и идеи для игр
Когда я заканчивал учебный год с моим третьеклассником, мы потратили некоторое время, работая над умножением и пытаясь закрепить факты умножения. Но наряду со знанием того, что означает умножение, и важностью знания фактов, я также хотел, чтобы он увидел, как мы можем распространить это знание на , умножая двузначные числа, и дальше . Хотя вид таких больших задач на умножение может пугать, это не обязательно. Узнать простые, но мощные стратегии для того, как с легкостью умножать двузначные числа . Затем вы можете применить эти идеи к еще большим числам и умножению десятичных дробей.
Но наряду со знанием того, что означает умножение, и важностью знания фактов, я также хотел, чтобы он увидел, как мы можем распространить это знание на , умножая двузначные числа, и дальше . Хотя вид таких больших задач на умножение может пугать, это не обязательно. Узнать простые, но мощные стратегии для того, как с легкостью умножать двузначные числа . Затем вы можете применить эти идеи к еще большим числам и умножению десятичных дробей.
* Обратите внимание : Этот пост содержит партнерские ссылки, которые поддерживают работу этого сайта. Подробное описание читайте здесь.*
Как умножать двузначные числа: используйте модель площадиМой любимый метод умножения двузначных цифр — это нарисовать модель площади
0004 . Это полезно, потому что дает наглядное представление о том, что представляет собой проблема.
Кроме того, впоследствии его можно будет применить к более сложным задачам, включая многочлены умножения в алгебре.
Один из способов представить умножение как площадь прямоугольника. Это означает, что в любой заданной задаче на умножение вы можете думать о каждом множителе как о длине и ширине прямоугольника.
Допустим, мы хотим умножить 24 x 35. Вы можете начать с рисования прямоугольника шириной 24 и длиной 35.
В этот момент вы можете подумать: «Хорошо, отлично. Теперь это коробка, но как, черт возьми, это поможет мне ее решить??»
Ну, тогда вы можете разбить коробку на части , которые легче решить, как будто вы раскрашиваете область по одной небольшой секции .
Например, я могу разделить ширину на 20 и 4, затем я могу разделить 35 на 30 и 5, например:
Теперь у меня есть меньшие прямоугольные секции, которые мне легче умножать. Например, начиная с самого большого прямоугольника, мы имеем 30 х 20 = 600:9.0007
Затем я могу продолжить с остальными ячейками:
30 х 4 = 120,
И 5 х 20 = 100,
И, наконец, 5 х 4 = 20.
Теперь, когда я нашел площадь каждого маленького участка, я могу сложить их вместе , чтобы найти общую площадь (или окончательное решение исходной задачи умножения двузначного числа: 24 x 35): 600 + 120 + 100 + 20 = 840
Преимущества использования модели площадиЭто наглядное изображение также полезно, поскольку оно показывает, что умножение больших чисел дает более крупные ответы, что видно на рисунке (большие участки всего прямоугольника).
Другая замечательная особенность этого метода заключается в том, что дети могут разбить исходный прямоугольник на миллионами различных способов . Они могут делать то, что имеет для них наибольший смысл, или использовать любые задачи на умножение, которые им будет легче всего решить в уме.
Нет «правильного» или «неправильного» пути. Это дает детям свободу разобраться в проблеме самостоятельно и исследовать ее по-своему.
И если вы видите, что они склонны всегда выбирать одну и ту же стратегию (например, разделение десятков и единиц), попросите их решить ее другим способом. Это заставит их подумайте о других способах декомпозиции чисел , которые могли бы работать лучше или сделать решение проблемы проще и эффективнее.
Это заставит их подумайте о других способах декомпозиции чисел , которые могли бы работать лучше или сделать решение проблемы проще и эффективнее.
Кроме того, это дает им дополнительную практику умножения. 😉
Чтобы узнать больше о настройке и решении с использованием моделей площадей, см. эту статью и скачайте бесплатный шаблон.
Как умножать двузначные числа: использовать разрядное значение для нахождения частичных произведенийЕще одна полезная стратегия, которую могут использовать дети, не обученные формальному алгоритму, — использовать 9.0003 поместите значение, чтобы разбить задачу на части и решить ее по частям .
Это похоже на использование модели области, но не включает визуал.
Это может быть особенно полезно, когда одно из чисел включает младшие, легко умножаемые цифры, такие как 2 или 3.
Например, предположим, что вы хотите умножить 78 x 12.
Вместо этого вы можете представить это как (78 х 10) + (78 х 2).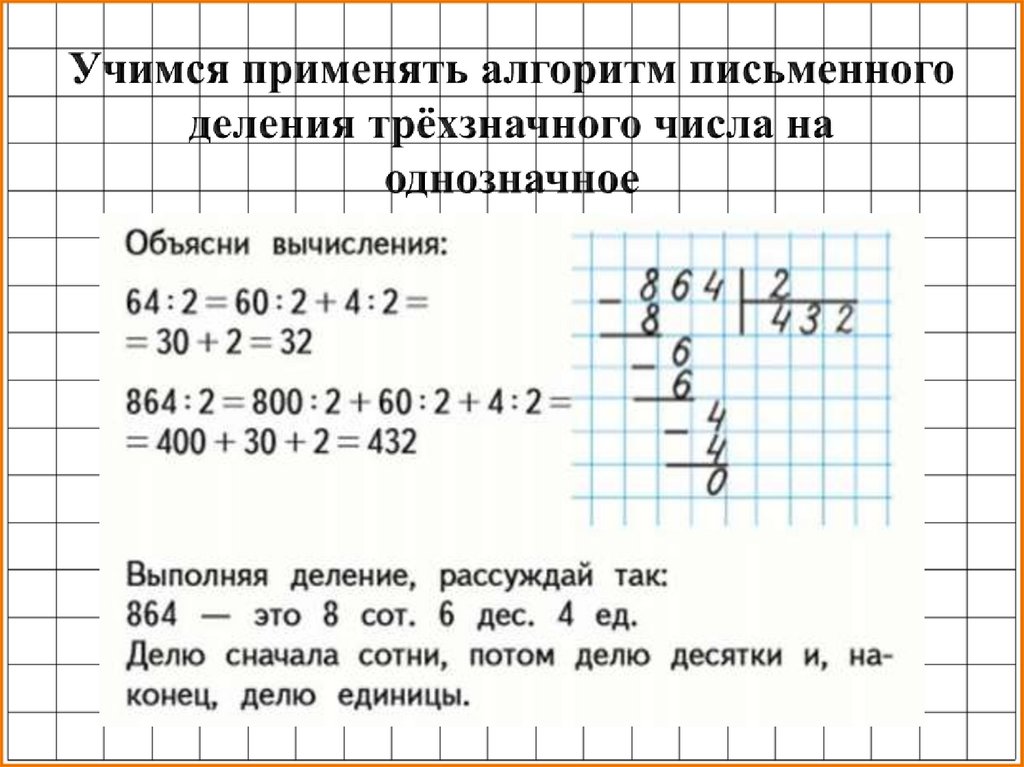
Умножить на десять несложно, и это даст вам 780.
Умножение на 2 равно удвоению, поэтому 78 x 2 = 156
Затем вы можете просто сложить частичные произведения вместе , чтобы получить 780 + 156 = 936
Вот еще один пример: 48 x 14
В этом примере мы можем думать об этом как (48 x 10) + (48 x 4)
Первая часть проста, давая нам 48 x 10 = 480
Умножение 48 x 4 не так просто сделать в уме, но затем его можно разбить на 48 x 2, а затем снова x 2.
Другими словами, 48 х 2 = 96 и тогда 96 х 2 = 192
Тогда снова мы можем сложите частичные произведения вместе , чтобы получить 480 + 192 = 672
Как умножать двузначные числа: используя формальный алгоритмпосредством задач умственного вычисления вы можете ввести формальный алгоритм .
Я предлагаю поделиться этим последним, потому что, если дети уже хорошо понимают, как работать с двузначными числами и умножать их, алгоритм не так страшен.
Если на самом деле, это, скорее всего, будет иметь смысл для большинства детей. Потому что теперь это не похоже на случайные правила, которым нужно следовать и помнить, а на удобный способ денди отслеживать то, что они раньше делали в своей голове.
Итак, если вы не знакомы, вот пошаговый пример умножения двузначных цифр с использованием традиционного алгоритма . Допустим, теперь мы хотим умножить 34 x 62.
Шаг первый: выровняйте все цифрыСначала выровняйте все числа в соответствии с их разрядностью.
Шаг второй: Умножьте на цифру единицЗатем начните с , умножая каждую цифру верхнего числа на цифру единиц (в данном случае 2). В этом примере у нас есть 4 x 2 = 8 (запишите это в единицах), а затем 3 (что на самом деле означает 30) x 2 = 6 (что на самом деле означает 60). Затем вы записываете 6 в разряде десятков.
Шаг третий: добавьте нулевой заполнитель Затем поместите ноль под столбцом единиц , когда вы начнете умножать 34 на 6 (что на самом деле означает 60).
Причина этого нуля в том, что вы не просто умножаете 34 на 6. Вы умножаете 34 x 60 . Другими словами, кратно десяти , поэтому мы знаем, что должны иметь этот ноль там .
Шаг четвертый: Умножение на десяткиЗатем вы можете умножить каждую цифру на 6 .
Это дает 6 х 4 (что на самом деле 60 х 4) = 24 (что на самом деле 240).
Поскольку это на самом деле представляет 240, 4 идет в столбце десятков в нашем решении, а затем мы «переносим» 2, то есть помещаем его в столбец десятков вверху.
Я обычно записываю это как «+2» , а не просто как 2, потому что часто дети забывают, должны ли они сложить это или умножить.
Затем мы умножаем 3 x 6 = 18 и к добавляем 2 , чтобы получить 20 (что на самом деле представляет собой 2000, потому что мы на самом деле умножили 30 x 60 и добавили к нему еще 200).
Следовательно, мы получаем 2040 во второй строке нашего ответа.
Затем, как и в случае с частичными произведениями, мы складываем вместе две строки решений , чтобы получить 68 + 2040 = 2,108
Когда я учу своих детей В этой процедуре я обычно записываю каждый шаг как частичный продукт по мере решения проблемы. Это позволяет им увидеть, откуда берутся все числа, почему мы добавляем ноль и почему мы складываем строки ответов вместе для окончательного ответа.
Затем я позволяю им практиковаться, используя любой метод или стратегию, которые наиболее эффективны и удобны для них!
Умножение двузначных чисел: идеи для игрЕсли вы хотите, чтобы ваши дети попрактиковались в умножении двузначных чисел, вот несколько игр, которые могут вам понравиться.
- Распечатанные настольные игры для тренировки двузначного умножения
- Многоразрядное умножение страниц вырезания и вставки
- Настольные игры с многозначным умножением
И обязательно ознакомьтесь с этой стратегией, которая поможет детям понять и увидеть закономерности при умножении больших чисел: Как умножать большие числа с помощью таблиц
Надеюсь, вы нашли это полезным и, возможно, даже узнали новых способа умножения двузначных чисел. числа !
числа !
Математические идеи никогда не заканчиваются
Если вам понравился этот пост, вам понравится быть частью сообщества Math Geek Mama! Каждую неделю я отправляю электронное письмо с забавными и увлекательными математическими идеями, бесплатными ресурсами и специальными предложениями. Присоединяйтесь к более чем 163 000 читателей, поскольку мы помогаем каждому ребенку добиться успеха и преуспеть в математике! ПЛЮС, получи мою БЕСПЛАТНУЮ электронную книгу, 5 математических игр, в которые можно играть СЕГОДНЯ , в подарок вам !
2-значное умножение — Шаги
LearnPracticeDownload
2-значное умножение или двузначное умножение выполняется путем расположения чисел таким образом, что заданные числа располагаются одно под другим. Двузначное число можно умножить на однозначное, на другое двузначное число, на трехзначное число и так далее. Давайте узнаем больше о двузначном умножении, шагах для умножения и решим несколько примеров, чтобы лучше понять концепцию.
Давайте узнаем больше о двузначном умножении, шагах для умножения и решим несколько примеров, чтобы лучше понять концепцию.
| 1. | Что такое двузначное умножение? |
| 2. | 2-значное умножение на 2-значное |
| 3. | 2-значное умножение с перегруппировкой |
| 4. | Часто задаваемые вопросы по двузначному умножению |
Что такое двузначное умножение?
2-значное умножение — это метод умножения двузначных чисел, упорядоченных по двум разрядам, то есть единицам и десяткам. Способ умножения чисел такой же, как и умножения однозначных цифр. Однако в двузначных числах мы умножаем каждую цифру по одной на множитель. Это означает, что множитель сначала умножается на разряд единиц множимого, а затем на разряд десятков множимого. Давайте узнаем об умножении 2 цифр на 1 цифру и 2 цифры на 2 цифры умножения в следующих разделах.
Умножение 2-значных чисел на 1-значное
Умножение 2-значных чисел на 1-значные очень просто. Давайте разберемся в этом, используя следующие шаги и пример.
Пример: Умножить 23 × 2
- Шаг 1: Поместите однозначное число под двузначным. Это делает однозначное число множителем. Умножьте однозначное число (множитель) на единицу множимого. Здесь 2 — это множитель, а единица множимого равна 3. Таким образом, 2 × 3 = 6. Это частичное произведение (6) будет помещено под колонку единиц.
- Шаг 2: Теперь умножьте множитель на разряд десятков множимого. Здесь 2 — это множитель, а цифра десятков множимого равна 2. Это означает, что 2 × 2 = 4. Это частичное произведение (4) будет помещено в столбец десятков. Следовательно, 23 × 2 = 46 .
Теперь давайте научимся умножать двузначные числа на двузначные числа.
2-значное умножение на 2-значное
Умножение 2 цифр на 2 цифры означает, что оба числа, которые нужно умножить, состоят из двух цифр. Умножение начинается с разряда единиц, а затем переходит к разряду десятков. Цифры располагаются одна под другой. Хотя любое из двух чисел можно поместить сверху или снизу, предпочтительнее поместить меньшее число снизу, потому что это облегчает умножение. Давайте разберемся с этим умножением с помощью следующего примера. Умножим 34 × 12. В этом случае пусть 34 будет множимым, а 12 — множителем.
Умножение начинается с разряда единиц, а затем переходит к разряду десятков. Цифры располагаются одна под другой. Хотя любое из двух чисел можно поместить сверху или снизу, предпочтительнее поместить меньшее число снизу, потому что это облегчает умножение. Давайте разберемся с этим умножением с помощью следующего примера. Умножим 34 × 12. В этом случае пусть 34 будет множимым, а 12 — множителем.
- Шаг 1: Поместите множимое (34) сверху, а множитель (12) под ним, как показано на рисунке выше. Умножьте цифру единиц множителя на множимое. Здесь 34 — множимое, а цифра единиц 12 — 2. Это даст 34 × 2 = 68. Это первое частичное произведение, которое будет помещено в одну строку.
- Шаг 2: Умножьте множимое на разряд десятков множителя. Здесь 34 — это множимое, а цифра десятков множителя равна 1. Это будет 34 × 1 = 34. Следует отметить, что нам нужно поместить ноль под цифрой единиц частичного произведения, а затем записать второе частичное произведение.
 товар. (Этот 0 помещен здесь, потому что мы на самом деле умножаем 34 на 10 на этом шаге). Таким образом, мы получаем 340 здесь.
товар. (Этот 0 помещен здесь, потому что мы на самом деле умножаем 34 на 10 на этом шаге). Таким образом, мы получаем 340 здесь. - Шаг 3: Добавьте оба частичных продукта, чтобы получить конечный продукт. Это будет 68 + 340 = 408.
Теперь давайте узнаем о двузначном умножении, в котором у нас есть переносы.
2-значное умножение с перегруппировкой
Двузначное умножение с перегруппировкой или переносом происходит при переносе числа вперед. Давайте поймем это на следующем примере и шагах. Умножим 45 × 6,
- Шаг 1: Умножьте множитель на единицу множимого. Здесь множимое равно 45, цифра единиц в числе 45 равна 5, а множитель равен 6. Таким образом, это будет 6 × 5 = 30.
- Шаг 2: Поскольку произведение, полученное на шаге 1, равно 30, мы перенесем 3 в предыдущий столбец десятков и запишем 0 под столбцом единиц как частичное произведение.
- Шаг 3: Теперь мы умножим множитель на разряд десятков множимого.
 Здесь разряд десятков множимого равен 4, а множитель равен 6. Таким образом, это будет 6 × 4 = 24. На этом этапе нам нужно добавить число, которое было перенесено на предыдущем шаге. Это означает 24 + 3 = 27. Таким образом, конечный продукт равен 270,9.0221
Здесь разряд десятков множимого равен 4, а множитель равен 6. Таким образом, это будет 6 × 4 = 24. На этом этапе нам нужно добавить число, которое было перенесено на предыдущем шаге. Это означает 24 + 3 = 27. Таким образом, конечный продукт равен 270,9.0221
Двузначное умножение с десятичными дробями очень похоже на обычное умножение с использованием нескольких правил десятичных чисел. Давайте узнаем больше об этом в следующем разделе.
Двузначное умножение с десятичными дробями
Двузначное умножение с десятичными дробями выполняется так же, как и обычное умножение двузначных цифр с учетом правил десятичных чисел. При умножении таких чисел мы можем игнорировать десятичную точку, пока не получим окончательный результат. После получения окончательного результата подсчитываем количество знаков после запятой в обоих числах, складываем их и в соответствии с этим ставим запятую. Разберем это на примере и умножим 2,5 × 1,1
- Шаг 1: Расположите числа вертикально в соответствии со значением разряда.
 Не выравнивайте числа по десятичной точке.
Не выравнивайте числа по десятичной точке. - Шаг 2: Умножьте разряд единиц множителя на множимое. Здесь 25 × 1 = 25, .
- Шаг 3: Поместите ноль под цифрой единиц частичного произведения.
- Шаг 4: Умножьте разряд десятков множителя на множимое. Это будет 25. Поместите это рядом с 0 под частичным произведением.
- Шаг 5: Добавьте два продукта, чтобы получить конечный продукт. Здесь 25 + 250 = 275, .
- Шаг 6: Поместите десятичную точку через 2 знака справа в конечном продукте. Поскольку множимое и множитель имеют по 1 десятичному знаку, получается 1 + 1 = 2 десятичных знака. Поэтому ставим запятую через 2 знака справа и получаем 2,5 × 1,1 = 2,75
☛ Связанные темы
- Вычитание 2 цифр
- 2-значное дополнение
- 3-значное дополнение
- 3-значное вычитание
- 3-значное умножение
- 4-значное дополнение
- 4-значное вычитание
- Умножение и деление целых чисел
Примеры двузначного умножения
Пример 1: Найдите произведение 67 × 20.
Решение: Давайте разберемся с этим двузначным умножением, используя следующие шаги.
- Умножить 0 на 7 и 6.
- Поместите ноль под цифрой единиц частичного произведения.
- Умножить 2 на 7 и 6.
- Добавьте продукты, чтобы получить окончательный ответ.
Следовательно, 67 × 20 = 1340.
Пример 2: Умножить 31 × 7
Решение: Выполним это двузначное умножение, используя следующие шаги.
- Умножить 7 на 1, то есть 7 × 1 = 7
- Теперь умножьте 7 на 3, то есть 7 × 3 = 21
- Запишите их вместе как 217
- Следовательно, 31 × 7 = 217
Пример 3: Укажите истинное или ложное значение умножения 2-значного числа.
а.) 10 × 11 = 110
б.) 20 × 20 = 40
Решение:
а.) Верно, 10 × 11 = 110
б.) Ложь, 20 × 20 = 400
перейти к слайдуперейти к слайдуперейти к слайду
Разбивайте сложные концепции с помощью простых визуальных средств.
Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций.
Записаться на бесплатный пробный урок
Практические вопросы по умножению двузначных чисел
перейти к слайдуперейти к слайду
Часто задаваемые вопросы о двузначном умножении
Что такое двузначное умножение?
Двузначное умножение — это метод умножения двузначного числа на другое число. Числа располагаются друг под другом для выполнения умножения. Число, написанное сверху, называется множимым, а число, написанное ниже, — множителем. Двузначные числа можно умножать на однозначные числа, двузначные числа и так далее.
Как выполнить двузначное умножение?
Следующие шаги объясняют процесс двузначного умножения. Например, давайте умножим 42 × 3
- Расположите числа одно под другим так, чтобы большее число (42) было сверху, а меньшее (3) — под ним. Итак, 3 становится множителем, а 42 — множимым.

- Начните умножать множитель с разряда единиц множимого. Здесь 3 будет умножено на 2, что даст 3 × 2 = 6. Это 6 будет записано как частичное произведение.
- Затем умножьте 3 на разряд десятков множимого, то есть 4, что будет 3 × 4 = 12. Теперь, записав оба произведения вместе, конечный продукт будет 42 × 3 = 126
Как выполнить двузначное умножение с переносом?
Двузначное умножение с переносом выполняется, когда произведение одного столбца больше 9. Лишняя цифра переносится в следующий столбец и прибавляется к этому конкретному произведению. Например, давайте умножим 45 × 7.
- Поместите 45 сверху и 7 под ним, чтобы 45 стало множимым, а 5 стало множителем.
- Умножьте 7 на 5, и вы получите 7 × 5 = 35. Поскольку произведение представляет собой двузначное число 35, мы перенесем 3 в столбец десятков и запишем 5 под столбцом единиц как частичное произведение.
- Теперь умножьте множитель на разряд десятков множимого.
 Здесь разряд десятков множимого равен 4, а множитель равен 7. Таким образом, это будет 7 × 4 = 28. На этом этапе нам нужно добавить число, которое было перенесено на предыдущем шаге. Это означает 28 + 3 = 31. Таким образом, конечный продукт равен 315.
Здесь разряд десятков множимого равен 4, а множитель равен 7. Таким образом, это будет 7 × 4 = 28. На этом этапе нам нужно добавить число, которое было перенесено на предыдущем шаге. Это означает 28 + 3 = 31. Таким образом, конечный продукт равен 315.
Как умножить 2-значное на 1-значное?
Умножение 2 цифр на 1 цифру выполняется так же, как и умножение одной цифры. Например, умножим 13 × 2,9.0007
- Двузначное число (13) записывается сверху, а однозначное (2) — снизу, поэтому 13 становится множимым, а 2 — множителем.
- Начинаем умножать младшую цифру (множитель) на единицу множимого. Здесь мы умножим 2 на 3, что будет 2 × 3 = 6. Мы запишем это 6.
- Затем мы идем дальше и умножаем нижнюю цифру (множитель) на разряд десятков множимого. Здесь 2 × 1 = 2. Это также будет записано вместе с произведением, полученным на предыдущем шаге. Итак, это даст произведение 13 × 2 = 26,9.0221
Как выполнить двузначное умножение на двузначное?
Умножение двух цифр на две цифры — это процесс умножения, при котором двузначное число умножается на другое двузначное число. Например, умножим 23 × 14.
Например, умножим 23 × 14.
- Поместите 23 сверху и 14 под ним, чтобы 23 стало множимым, а 14 — множителем.
- Умножьте разряд единиц множителя на множимое. Здесь 23 — множимое, а цифра единиц 14 — 4. После умножения 23 на 4 мы получаем 23 × 4 = 9.2. Это первый неполный товар, который будет размещен в одной строке.
- Умножьте множимое на разряд десятков множителя. Это означает, что мы умножим 23 на 1, и получится 23 × 1 = 23. Следует отметить, что нам нужно поставить ноль под цифрой единиц частичного произведения, а затем написать рядом с ним второе частичное произведение. (Этот 0 помещен здесь, потому что мы фактически умножаем 23 на 10 на этом шаге.) Таким образом, мы получаем здесь 230.
- Теперь мы добавим оба частичных продукта, чтобы получить конечный продукт. это будет 92 + 230 = 322.
- Следовательно, конечный продукт равен 23 × 14 = 322.
Как умножить 3-значное на 2-значное?
Умножение 3-значного на 2-значное означает, что мы умножаем 3-значное число на 2-значное число.
 Умножение двузначного числа на однозначное
Умножение двузначного числа на однозначное
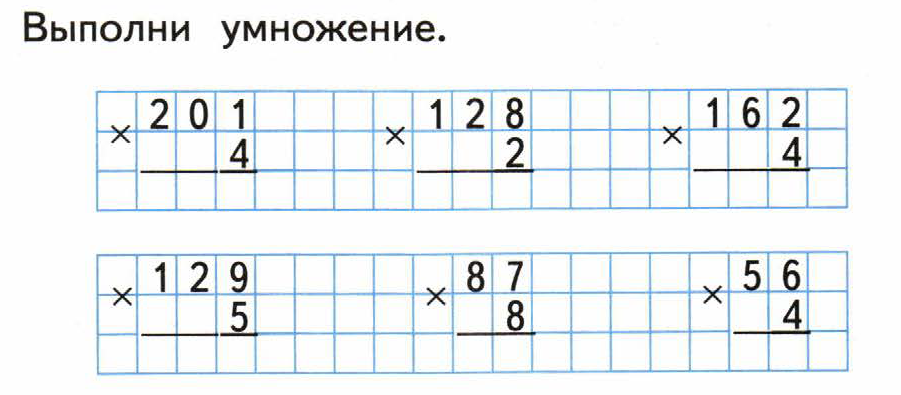

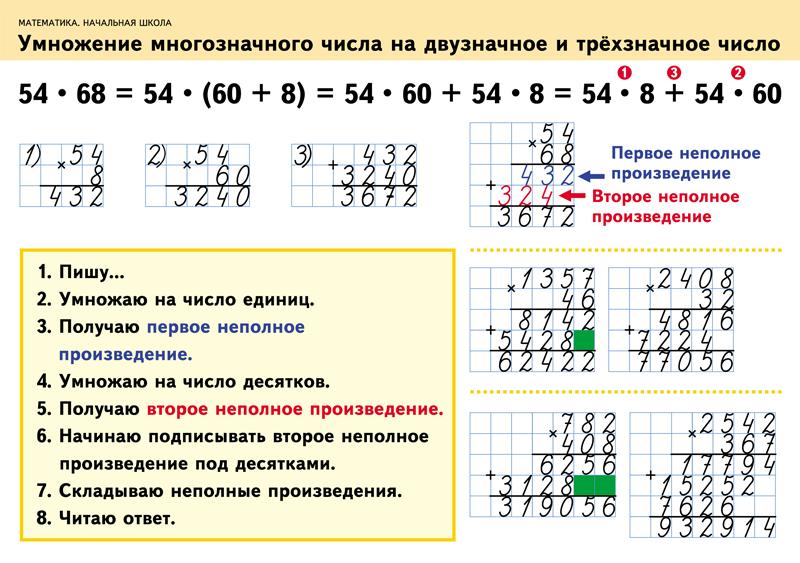

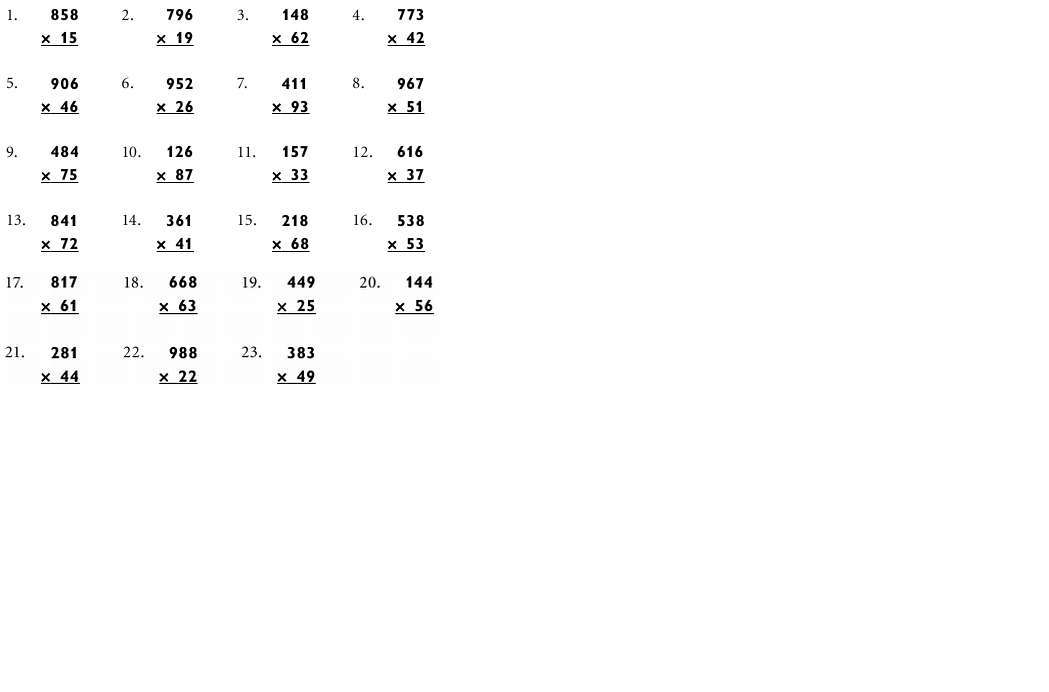 )
) )
) Но мы туда ещё обязательно вернёмся, ведь осталось ещё много математических вершин, которые мы не покорили. На прощание царица Математика дарит нам цветы, выберите себе тот, который вам подходит по итогам урока, и нарисуйте его у себя в тетради.
Но мы туда ещё обязательно вернёмся, ведь осталось ещё много математических вершин, которые мы не покорили. На прощание царица Математика дарит нам цветы, выберите себе тот, который вам подходит по итогам урока, и нарисуйте его у себя в тетради.