Этапы | Деятельность учителя | Деятельность учащихся | УУД | |||||||||||||||
1.Орг.момент. | Здравствуйте, ребята. Сегодня урок математики буду вести я. Зовут меня Элина Рафиковна. Давайте проверим вашу готовность к уроку. На столах у вас должен лежать пенал, тетрадь по математике и учебник. Садитесь. Математика – Царица всех наук, Тебе с ней подружиться советую, мой друг. Если сложные законы в школе изучаешь, То любые трудности ты преодолеваешь. | Настраиваются на работу. Проверяется готовность к уроку. | Личностные — учебно-познавательный интерес к новому учебному материалу; -ориентация на понимание причин успеха в учебной деятельности; | |||||||||||||||
2. | Открываем тетрадь -Какое сегодня число? -Правильно, отступаем 4 клетки вниз и записываем число и «классная работа». 2. Чистописание. Сейчас я буду называть правильные ответы. Ваша задача: если ответ в ваших тетрадях правильный – сделать хлопок ладошами, если же нет – исправить его.
Итог по таблице. Возможные варианты ответов детьми. Ответ на 1вопрос – верю. 2 вопрос — верю. 3 вопрос — не верю. 4 вопрос – не верю. Какие вопросы для вас оказались сложными? Почему? На эти вопросы мы должны в конце урока дать себе точные ответы. Ребята, на доске написаны примеры. Вы должны их решить. 840:4= (80 дес:4 ед=21 дес) =210 630:3= (60 дес:3 ед=21 дес) =210 240:6=(24 дес:6=4 дес)=40 420:3=(300+120):3=100+40=140 720:4=(400+320):4=100+80=180 960:3=(900+60):3=300+30=320 864:2= (800+60+4):2=400+30+2=432??? Какой пример у вас вызвал трудность в решении? Почему? Как мы поступаем, если вычислять устно трудно? Верно, так чему же мы сегодня будем учиться? Кто сформулирует тему урока? Какие цели поставим перед собой? Сейчас я вам расскажу еще один способ деления подобных примеров. Такая форма записи есть и для деления столбиком. В делении это еще называется “деление уголком”, потому что знак деления заменяется углом. Слева стоит делимое, над чертой стоит делитель, а под чертой – частное. А теперь давайте решим тот пример, с которым у вас возникли трудности. 864:2=(800+60+4)=400+30+2=432 А по другому запишем столбиком | Ученик отвечает: Сегодня 12 мая. Отступают две клетки вниз и записывают число 12 11, 22, 33, 44, 55, 66, 77, 88, 99. 700, 700, 400, 30, 1100, 130, 700, 1000. 3 и 4. 3 вопрос, так как других способов решения пока не знаю. 4 вопрос, так как не знаком с короткой записью — уголком. Решают, по окончании проговаривают вместе с учителем каждый пример. Последний, потому все примеры оканчивались на 0, а это число не оканчивается на 0. Вычисляем письменно Выполнять деление письменно Делить столбиком Приемы письменного деления Узнать про новый прием деления Нет. Слушают. | Коммуникативные УУД -формирование умения объяснять свой выбор, строить фразы, отвечать на поставленный вопрос, аргументировать; | |||||||||||||||
6.Физминутка | -А теперь давайте разомнемся (видео) | Выполняют упражнения | ||||||||||||||||
7. Работа с учебником 8.Итог урока. Рефлексия деятельности. | -Откройте учебник на странице 92 Прочтите информацию Выполни деление, записывая решение столбиком 936:3 486:2 848:4 555:5 -Молодец! Садись. -А теперь решим задачу. Прочитайте текст задачи Читает учитель: -На старом станке токарь изготовил 96 деталей за 6 ч, а на новом станке за 4 ч. На сколько деталей больше он стал изготавливать за 1 ч? -О чем идет речь в задаче? -О каких станках идет речь в задаче? -По сколько деталей было изготовлено на каждом из станков? -Сколько часов требуется, чтобы изготовить 96 деталей на старом станке? -А на новом? -Что нужно узнать в задаче? -Мы будем составлять краткую запись в таблице, какие колонки будут в нашей таблице? -Запишем условие задачи на доске. -Ребята, если мы знаем, что токарь изготавливает на старом станке 96 деталей за 6 часов, можем ли мы узнать, сколько он изготавливает за 1 час? Каким действием? -А мы также можем узнать, сколько деталей за час изготавливает токарь на новом станке? Каким действием? -Как узнать, на сколько деталей больше токарь начал изготавливать на новом станке за 1 ч? -Молодцы. Теперь запишем решение Давайте решим еще одну задачу. -Прочитайте текст задачи. Читает учитель: Периметр квадрата 28 см. Найди длину одной его стороны и площадь. -О какой геометрической фигуре идет речь? -Охарактеризуйте квадрат -Что известно о периметре? -Что такое периметр? -Что нужно найти? Запишите условие задачи на доске. -Если у нас квадрат с одинаковыми сторонами, а можем ли мы узнать длину одной стороны? Каким действием? Правильно, молодцы. Что нужно сделать, чтобы найти площадь квадрата? Запишите решение на доске. Самостоятельно решите примеры. 1 ряд решает 1 строчку, второй – 2, третий, соответственно – 3. СЛОЖЕНИЕ И ВЫЧИТАНИЕ ОНИ РЕШАЮТ ТОЖЕ В СТОЛБИК ПРОВЕРЬ ЕЩЕ РАЗ РЕШЕНИЕ, ПОТОМУ ЧТО Я ВИЖУ ПЛОХО ЭТИ ЗАПИСИ Ребята, на столе у вас лежат три кружочка. Поднимите зеленый, если у вас не возникало трудностей и вам все понравилось. Желтый – если было не все понятно. Красный – если сегодняшний материал вам не ясен, нужна помощь учителя. Что мы должны были с вами научиться делать? Выполнили ли мы с вами задачу сегодняшнего урока? | Ученики открывают учебник на странице 92 Выходят по одному к доске и решают при помощи «уголка» 312, 243, 212, 111 Сначала читает ученик. О деталях и станках. О старом и новом. По 96. 6 часов 4 часа На сколько деталей больше он стал изготавливать за 1 ч 1 колонка – за 1 час 2 колонка – кол-во часов 3 колонка – кол-во деталей Ученик записывает у доски, потом садится. Да. Нам нужно 96 деталей разделить на 6 часов. Да. Нужно 96 деталей разделить на 4 часа. Из количества деталей, которое изготавливается в час на новом станке, вычесть количество деталей, которое изготавливается в час на старом станке. Читает ученик О квадрате Четырехугольник, у которого все стороны и углы равны. 28 см Сумма длин всех сторон Длину одной стороны и площадь Ученик записывает: Ркв=28см а=? см S=? см Да. Если периметр квадрата равен 28 см, то нужно 28 разделить на 4, получится 7. Для этого одну сторону умножить на другую. 7*7=49 Ученик записывает. Решают. Дети поднимают кружок, тем самым они дают ответ, было ли ему трудно на уроке. Научиться делить уголком Да Дети встают, собирают принадлежности и идут на перемену. | Регулятивные -контроль в форме сличения способа действия и его результата с заданным эталоном; оценка своих знаний |
Математика Проверка деления с остатком
Материалы к уроку
Конспект урока
|
33.
|
|
||
|
Организационный этап
Прозвенел уже звонок, Сегодня мы вспомним правила деления с остатком, будем учиться выполнять проверку деления с остатком. |
|
||
|
Этап подготовки учащихся к активному сознательному усвоению знаний
Устный счёт
Любая в математике работа, Задание 1 Делить – это здорово,
21, 22, 23, 24, 25, 26, 27, 28, 30, 33 Проверьте себя.
Во второй столбик Задание 2 от весёлой Любознайки Если пример делится с остатком, вы поднимаете красную сигнальную карту, если делится без остатка — зеленую. 19 : 8…. делится с остатком (красная) Задание 3 от Размышлялкина Решите задачу. Проверьте себя. 1) 78 — 29 = 49 деталей пошло на 7 вагонов Вычислите. Проверьте себя. 75 : 5 = 13 |
|
||
|
Этап усвоения новых знаний
Чтоб ошибки при делении избежать, Как же проверить деление с остатком? 1. Сравниваем делитель и остаток. Остаток должен быть меньше, чем делитель. Выполним деление с остатком и проверим его. 47 : 6 Рассуждайте так: Найдём остаток: 47 — 42 = 5 47 : 6 = 7 (ост. 5) Выполним проверку. |
|
||
|
Этап закрепления новых знаний
Задание 1 Выполните деление с остатком и сделайте проверку.
|
|
||
|
Задание 2 Ребята, Любознайка решила примеры. 29 : 4 = 7 (ост. 1) Проверьте себя. В примере 13 : 4 = 2 (ост. 5) есть ошибка: остаток при делении должен быть меньше делителя. Решите правильно и сделайте проверку. 13 : 4 = 3 (ост. 1) Задание 3 Посчитайте лепестки на цветах. На одном цветке их пять. 5 ∙ 7 = 35 лепестков. |
|
||
|
Этап подведения итогов
Давайте повторим основные правила деления с остатком. Вспомним основные правила проверки: |
|||
|
Рефлексия
Если на уроке вам было всё понятно, нарисуйте лепестки красного цвета, если понятно, но не совсем, то лепестки желтого цвета, а если не понятно ничего – зелёные лепестки. Спасибо за работу! |
|
Остались вопросы по теме? Наши репетиторы готовы помочь!
Подготовим к ЕГЭ, ОГЭ и другим экзаменам
Найдём слабые места по предмету и разберём ошибки
Повысим успеваемость по школьным предметам
Поможем подготовиться к поступлению в любой ВУЗ
Выбрать репетитораОставить заявку на подбор
Именование фактологических семейств – Элементарная математика
Чтобы попрактиковаться в математических фактах, соединив семейства фактов с массивами.
Материалы
Нет
Обзор
Нарисуйте на доске массив точек, например массив 3 на 5. Спросите учащихся о семействе фактов, которое описывает массив. В этом примере семейство фактов будет 3 × 5 = 15, 5 × 3 = 15, 15 ÷ 3 = 5 и 15 ÷ 5 = 3. Нарисуйте другие массивы с достаточно малыми размерами, чтобы поддерживать быстроту этой деятельности, и продолжайте спрашивать учащихся о семействе фактов, которое описывает массив. Когда учащиеся освоятся, вы можете дать член семейства фактов, например 4 × 3 = 12, и попросить учащихся описать соответствующий массив, а затем дать другие члены семейства фактов. В этом примере подойдет массив из 4 строк и 3 столбцов или массив из 3 строк и 4 столбцов. Другими членами семейства фактов являются 3 × 4 = 12, 12 ÷ 3 = 4 и 12 ÷ 4 = 3,9.0004
Когда учащиеся освоятся, вы можете дать член семейства фактов, например 4 × 3 = 12, и попросить учащихся описать соответствующий массив, а затем дать другие члены семейства фактов. В этом примере подойдет массив из 4 строк и 3 столбцов или массив из 3 строк и 4 столбцов. Другими членами семейства фактов являются 3 × 4 = 12, 12 ÷ 3 = 4 и 12 ÷ 4 = 3,9.0004
О последовательности
В части 1 учащимся предлагается визуализировать массивы меньших размеров и назвать семейство фактов, описывающее каждый массив. Часть 2, и расширение переходит к либо , именующему семейство фактов из визуализации массива , либо , описывающему массив из знания факта из семейства фактов.
Часть 1
Давайте изобразим несколько массивов и назовем семейство фактов, описывающее каждый из них. Например, я думаю о массиве, который имеет 3 строки и 5 столбцов. Какое семейство фактов описывает этот массив?
(5 × 3 = 15, 3 × 5 = 15, 15 ÷ 5 = 3 и 15 ÷ 3 = 5)
Примеры:
- 2 строки и 4 столбца (2 × 4 = 8, 4 × 2 = 8, 8 ÷ 4 = 2, 8 ÷ 2 = 4)
- 2 строки и 2 столбца (2 × 2 = 4, 4 ÷ 2 = 2)
- 3 ряда и 2 столбца (3 × 2 = 6, 2 × 3 = 6, 6 ÷ 3 = 2, 6 ÷ 2 = 3)
- 3 ряда и 3 столбца (3 × 3 = 9, 9 ÷ 3 = 3)
- 3 ряда и 4 столбца (3 × 4 = 12, 4 × 3 = 12, 12 ÷ 4 = 3 и 12 ÷ 3 = 4)
Пока дети наслаждаются своим мастерством, не стесняйтесь повторять.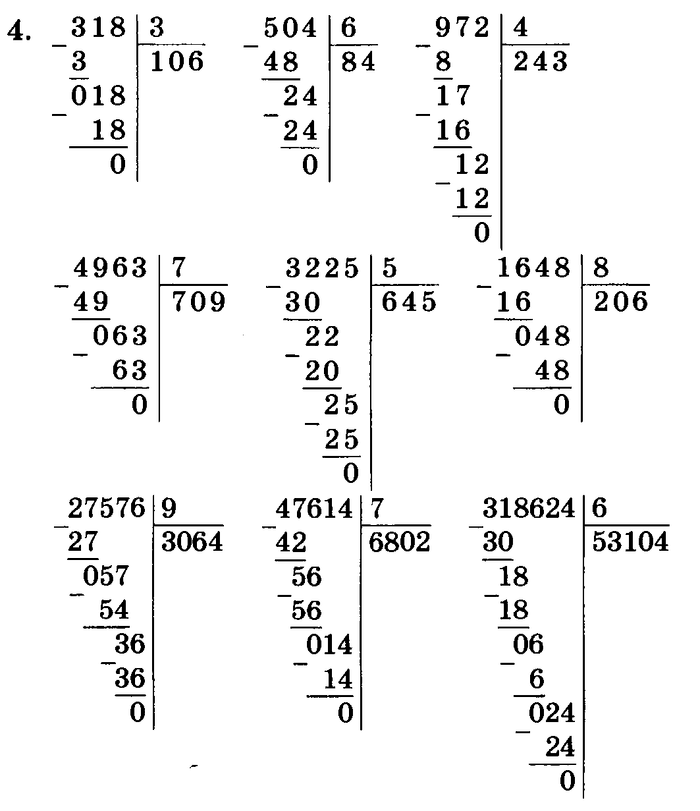 Когда дети хотят большего, попробуйте Часть 2.
Когда дети хотят большего, попробуйте Часть 2.
Часть 2
Давайте рассмотрим более крупные массивы и их семейства фактов. На этот раз вам будет предоставлен массив для изображения или член семейства фактов. Если вам дан массив для изображения, вы назовете членов его семейства фактов. Если дан факт, вы описываете массив, связанный с этим фактом, и называете других членов семейства фактов. Вот так!
Примеры:
- 6 рядов и 5 столбцов (6 × 5 = 30, 5 × 6 = 30, 30 ÷ 5 = 6, 30 ÷ 6 = 5)
- 6 рядов и 3 столбца (6 × 3 = 18, 3 × 6 = 18, 18 ÷ 3 = 6, 18 ÷ 6 = 3)
- 6 x 6 = 36 (опишите массив с 6 строками и 6 столбцами, 36 ÷ 6 = 6)
- 7 рядов и 6 столбцов (7 × 6 = 42, 6 × 7 = 42, 42 ÷ 6 = 7, 42 ÷ 7 = 6)
- 7 x 4 = 28 (опишите массив из 7 строк и 4 столбцов, 4 × 7 = 28, 28 ÷ 4 = 7, 28 ÷ 7 = 4)
- 7 рядов и 7 столбцов (7 × 7 = 49, 49 ÷ 7 = 7)
Как всегда, когда дети кажутся взволнованными новой задачей, двигайтесь дальше.
Extension
Теперь мы представим еще большие массивы и их семейства фактов.
Примеры:
- 10 строк и 8 столбцов (10 × 8 = 80, 8 × 10 = 80, 80 ÷ 8 = 10, 80 ÷ 10 = 8)
- 11 × 10 (описать массив с 11 строками и 10 столбцами, 10 × 11 = 110, 110 ÷ 10 = 11, 110 ÷ 11 = 10)
- 11 строк и 11 столбцов (11 × 11 = 121, 121 ÷ 11 = 11)
- 12 × 10 (описать массив с 12 строками и 10 столбцами, 10 × 12 = 120, 120 ÷ 10 = 12, 120 ÷ 12 = 10)
- 12 рядов и 12 столбцов (12 × 12 = 144, 144 ÷ 12 = 12)
Как преподавать дивизион — простое пошаговое руководство
- Дом
- >
- Блог
- >
- Как преподавать деление — простое пошаговое руководство
Джессика Камински
8 минут чтения
27 апреля 2022 г.
Деление является четвертым среди первых четырех основных математических операций, которые должен освоить ребенок. Эти математические операции сложения, вычитания, умножения и деления. Они составляют основу всех математических задач. Изучение первых трех операций не является обязательным для ребенка, чтобы понять деление, но, как мы увидим, они необходимы. Однако научить ребенка делению не так сложно, как может показаться.
Концепция деления
Как указано выше, деление может показаться сложным, но это проще, чем вы думаете. Как правило, разделение влечет за собой разделение поровну в соответствии с количеством необходимых групп. По этой причине вы можете связать разделение с идеей разделения поровну.
Например, несколько элементов могут поровну распределяться между группами. Практический пример: разделить 9 яблок (количество предметов) между 3 друзьями (3 группы), при этом у каждого друга будет 3 яблока.
Основная концепция деления лучше понимается с помощью методов группировки и совместного использования. Деление также называют обратным умножению или процессом многократного вычитания.
Деление также называют обратным умножению или процессом многократного вычитания.
Как научить ребенка делению
Обучение делению или обучение делению не так сложно, как кажется. Родитель или учитель может освоить простой подход к эффективному объяснению деления. Следовательно, ребенок может быстро понять концепцию довольно легко.
Ниже приведен пошаговый процесс обучения делению от базовой концепции деления до полного деления. Этот подход предполагает постепенный процесс, облегчающий оценку того, как ребенок справляется с проблемами деления.
Примечание. Крайне важно, чтобы ваше обучение было интересным и увлекательным, чтобы повысить его эффективность.
Шаг 1: Знакомство с основами деления
Чтобы ребенок понял деление, ему необходимо понять основы деления.
Во-первых, познакомьте ребенка с концепцией деления как способом поделиться. Естественно, при таком подходе ребенку легче понять деление. Поэтому вводите для практики такие предметы, как конфеты.
Во-вторых, физически попросите ребенка разделить количество конфет на более мелкие группы. Например, если у вас есть 8 конфет, попросите ребенка разделить их на 4 небольшие равные группы. Это значит, что в каждой группе должно быть равное количество предметов (конфет). В этом случае 8 — это делимое (оно представляет общее количество элементов/объектов), а 4 — делитель. по 2 конфеты в каждой группе; следовательно, 8 разделить на 4 группы равно 2.
Когда-то ребенок научился группировать, теперь вы можете вводить символы деления. Для обозначения деления потребуется записать знак деления (÷) и косую черту (/). Кроме того, вы должны произнести это вслух, записывая на листе. Это делает процесс видимым для ребенка и улучшает понимание. Из приведенного выше сценария 8 разделить на 4 можно записать как 8÷4 или 8/4.
Теперь, если ребенок знает принцип умножения, ему будет еще проще объяснить деление. Вы поможете им понять, что деление противоположно умножению. Поэтому используйте таблицы умножения, чтобы проиллюстрировать этот процесс.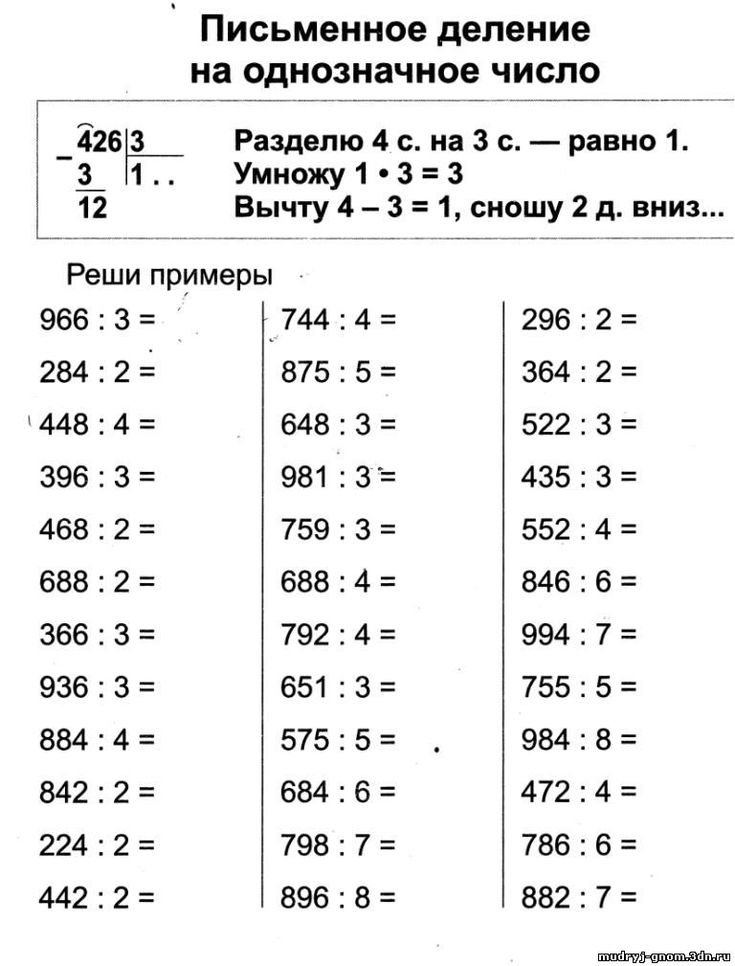 Например, проверьте по таблице умножения 2×4 = 8, а затем проиллюстрируйте, что 8÷4= 2. Затем сделайте 2×3=6 и 6÷3=2. Вы должны делать это несколько раз, пока ребенок не поймет связь между умножением и делением.
Например, проверьте по таблице умножения 2×4 = 8, а затем проиллюстрируйте, что 8÷4= 2. Затем сделайте 2×3=6 и 6÷3=2. Вы должны делать это несколько раз, пока ребенок не поймет связь между умножением и делением.
Наконец, оцените способности вашего ребенка к обучению, дав ему несколько простых задач на деление. Однако убедитесь, что вы используете числа, которые делятся без остатка. Например, 12÷4, 6÷3, 8÷2, 15÷5 и т. д. Вы можете помочь им повторить этот шаг от разделения конфет на группы до использования таблицы умножения.
Шаг 2: Выработка деления с остатками
Если ребенок уже понимает основы деления, в том числе как делить числа нацело, вы можете перейти к следующему шагу. Этот шаг влечет за собой работу с остатками, где числа не могут быть разделены поровну.
Чтобы разработать концепцию остатков в делении, используйте такие предметы, как конфеты и кубики. Начните с подсчета определенного количества конфет, которые нельзя разделить на равные группы или разделить поровну. Например, попросите ребенка разделить 9 конфет на группы по 4 или разделить 15 конфет на группы по 6.
Например, попросите ребенка разделить 9 конфет на группы по 4 или разделить 15 конфет на группы по 6.
В первом сценарии остаток будет равен 1, потому что в каждой из 4 групп будет по две конфеты. Во втором примере останется 3 конфеты, потому что в каждой из 6 групп будет по 2 конфеты. Это понятие помогает ребенку понять, что некоторые числа остаются при делении и называются остатками.
Затем вы должны записать задачу на деление на листе. Например, 9÷4=2 остатка 1 и 15÷6=2 остатка 3.
Чтобы сделать обучение делению с остатком более эффективным, предложите ребенку больше задач на деление, таких как 7÷2, 10÷3, 15÷4, 20÷7, 25÷10 и т. д. Конечная цель состоит в том, чтобы ребенок/ученик тренировался до тех пор, пока он не сможет объяснить, почему у него есть остатки в каждой группе без вашей помощи. Вы можете разрешить им использовать конфеты или другие предметы, если им нужно сгруппироваться.
Шаг 3: Обучение длинному делению
Как указывалось ранее, обучение детей делению — это постепенный процесс. Поэтому, если ребенок успешно справился с двумя предыдущими шагами, пора переходить на другой уровень, т. е. на деление в длину. Изучение длинного деления немного технично. Тем не менее, ребенок, который уже понимает основные операции, обратные таблице умножения и остаткам, может легко решить деление в столбик.
Поэтому, если ребенок успешно справился с двумя предыдущими шагами, пора переходить на другой уровень, т. е. на деление в длину. Изучение длинного деления немного технично. Тем не менее, ребенок, который уже понимает основные операции, обратные таблице умножения и остаткам, может легко решить деление в столбик.
Обычно длинное деление повторяет основные шаги деления, умножения, вычитания и опускания до следующей цифры.
Чтобы научить детей делению на четные, начните знакомить их с понятием четного деления. Каждая сотня, десяток и единица без остатка делятся на делитель. Ребенок привыкает знать и упражняться, сколько раз делитель входит в различные цифры делимого.
Следующий шаг в делении в длинное число включает остаток и использует понятия умножения и вычитания. Вы применяете умножение и вычитание в самом простом месте в самом конце деления, то есть в той колонке, где у вас есть остаток. Однако, если у вас есть остаток в десятках в алгоритме длинного деления, вы делите, умножаете, вычитаете, а затем переходите к следующей цифре.
Разделить:
следовательно, мы получили 1 (размещено над длинным знаком деления). Мы также можем сказать, что 2 разделить на 2 равно 1.
Умножить и вычесть:
Теперь давайте вычислим оставшиеся 54.
2×2=4, запишем 4 под 5 и вычтем, чтобы найти остаток . Остаток 1 из 10.
Опустите следующую цифру
Затем опустите 4 цифры рядом с 1 из десяти оставшихся. Теперь у вас есть 14.
Теперь разделите два на 14. Повторится та же самая концепция умножения, где 2×7= 14. Запишите 7 над знаком деления и 14 под 14. Снова произойдет вычитание, в результате чего 14-14 =0
Следовательно, частное 254 на 2 равно 127.
Последняя мысль
Деление может быть трудным для изучения, особенно для детей, которые взаимодействуют с ним впервые. Тем не менее, описанный выше подход касается того, как шаг за шагом перейти от основ к полному делению. Самое главное, стоит отметить, что обучение детей делению — это постепенный процесс.
 Актуализация
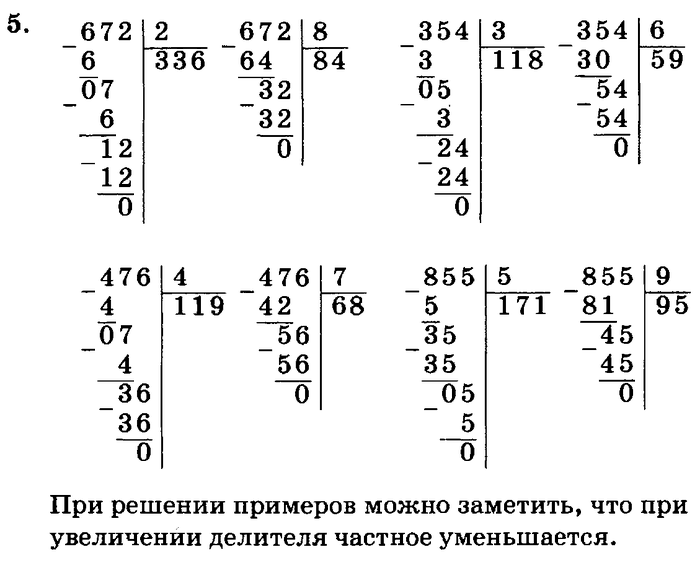
Актуализация Деление – это операция, в результате которой получается число (частное) которое при умножении на делитель дает делимое.
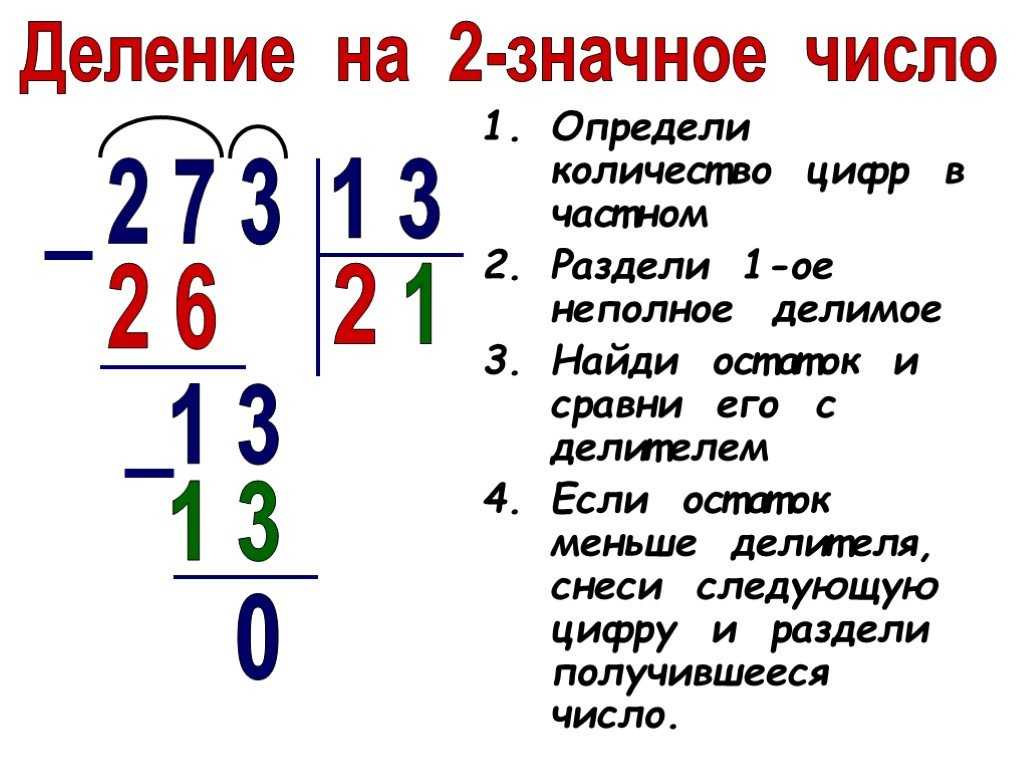
Деление – это операция, в результате которой получается число (частное) которое при умножении на делитель дает делимое. Способ называется «деление уголком».
Способ называется «деление уголком».


 Проверка деления с остатком
Проверка деления с остатком


 9)
9)
