Примеры двухзначные на двухзначные: Примеры по математике для 1, 2, 3 класса — «Семья и Школа»

Как объяснить ребенку вычитание и сложение двузначных чисел

Схема проезда

Контакты

Главная

Блог

Как объяснить ребенку вычитание и сложение двузначных чисел

Обучение ребенка вычитанию и сложению – сложный, многоэтапный процесс, начинающийся с изучения однозначных чисел и переходящий в двухзначные, с постепенным изучением моментов, когда происходит переход через десяток. Чтобы научить ребенка быстро считать двузначные числа следует пройти каждый этап последовательно. Использование разных способов обучения, преимущественно в игровой форме, дает возможность сделать весь процесс интересным для малыша, что положительно скажется на результатах.

Вычитание двузначных чисел с переходом через разряд

Объяснить ребенку вычитание двузначных чисел легче с использованием игровых методов. Это позволит сконцентрировать внимание на процессе и улучшит усвоение пройденного материала. Не стоит сразу начинать с больших чисел, лучше начать первые шаги с минимальных чисел, постепенно увеличивая.

Важным является такой момент – ребенок не сможет сразу считать в уме, даже когда речь идет о небольших числах. Лучше использовать листок бумаги, части конструктора, компьютер или другие дополнительные средства, где малыш сможет делать требуемые пометки. Следует уделить внимание изучению порядка образования десятков, вплоть до ста. Это поможет при обучении сложению и вычитанию с переходом через разряд, а не только в пределах одного десятка. Освоив счет в пределах десяти, можно переходить к изучению более сложных действий, используя одну из методик или комбинируя их.

Разделение чисел при вычете

При вычете из двузначного числа однозначного с переходом через разряд можно использовать разделение. Объясните ребенку, что от целого десятка отнимать будет легче, и достаточно разделить однозначное число таким образом, чтобы отняв одну из его частей получить 10, и уже потом вычесть вторую часть. В результате чадо быстро освоит такой счет, научившись правильно разделять числа и получать конечный результат.

Такой способ хорошо подходит в тех случаях, когда освоен счет до 10, а также малыш знаком с числами минимум до 20. Проводить занятия следует в игровой форме, используя расходные материалы или специальные компьютерные игры.

---

Использование геометрических фигур для визуализации чисел

Распространенный вариант, когда десятки обозначаются треугольниками, а единицы – точками. Достаточно объяснить ребенку значение фигур и привести несколько примеров. После этого можно приступать к тренировкам, начиная с простых заданий, используя числа до 20, постепенно усложняя их.

Для начального уровня это подходящий вариант, позволяющий проводить расчеты быстро и понятно. Однако может возникнуть сложность, когда при вычете следует отнимать дополнительный десяток (например, 54-35=19). Важно объяснить малышу тонкость такого момента. Отнимать двузначные числа таким способом лучше, избегая подобных ситуаций или же регулярно показывать примеры ребенку для лучшего освоения.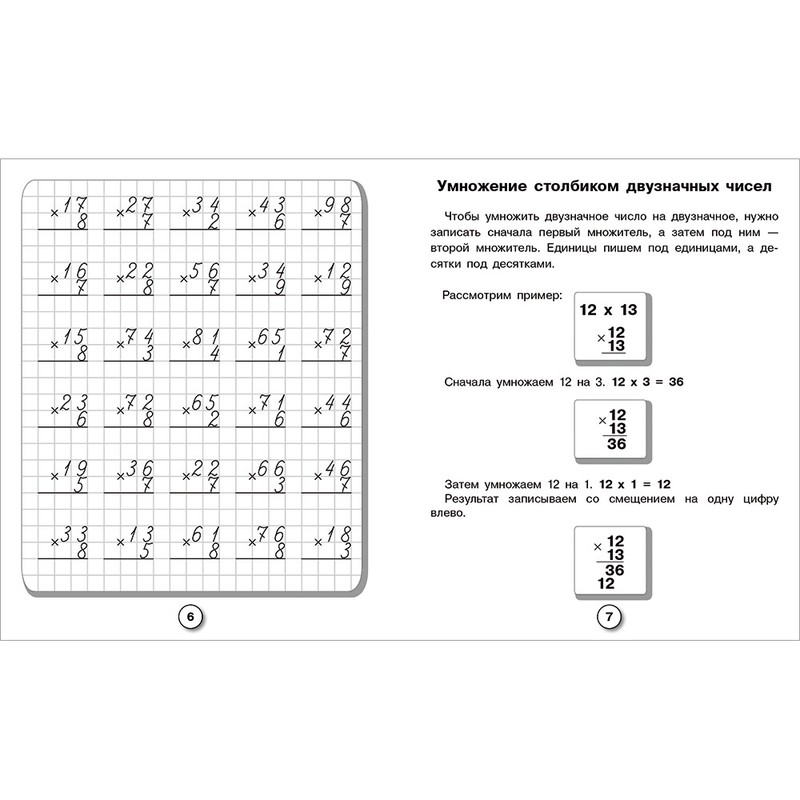

---

Отнимание с помощью Lego

Для применения этого способа можно использовать Lego Duplo, рассчитанный для этих целей, или обычные кубики конструктора, предварительно пронумеровав их. С их помощью можно решать сложные задачи, включая те, в которых происходит переход через десяток.

Достаточно отобразить требуемые числа с помощью соответствующих цифр (например 25-19). Чтобы понятнее ребенку объяснить тонкость, достаточно разделить их на более мелкие (10,10, 5 и 10, 5, 4). Ребенок легко усваивает, что 10-10=0, и сможет убрать лишние десятки. Оставшееся уравнение в дальнейшем решается легко (10 и 5 – 5 и 4). Ребенку остается посчитать 10-4, получив конечный результат.

---

Сложение двухзначных чисел

Объяснить ребенку сложение двузначных чисел обычно проще, нежели вычет, даже в тех случаях, когда идет прибавление дополнительного десятка после сложения. Способов обучения вполне достаточно для того, чтобы выбрать наиболее подходящий для вашего малыша.

Важно – занятие всех детей дошкольного возраста должно проходить в игровой форме.

Разделение чисел

Одним из простых способов обучения является разделение чисел на десятки и единицы. Это помогает и в том случае, когда происходит прибавление десятка после сложения единиц. Например 25+36 ребенок запишет как 10+10+10+10+10+6+5 и получит результат 50+5+6. После этого происходит сложение 5+6=11. Снова разложив 11 на 10+1 получается 50+10+1=61. Дети легко воспринимают такой способ и быстро учатся использовать его даже при подсчетах в уме.

---

Используйте решение «в столбик»

Это значительно упростит процесс подсчета вашему малышу. Так ребенок проще воспринимает десятки и единицы, может делать пометки о дополнительных десятках и прочие необходимые записи. Прибавлять двузначные числа таким образом легче и вскоре ребенок сможет проводить необходимые операции в уме.

Использование этого метода возможно и для изучения вычета.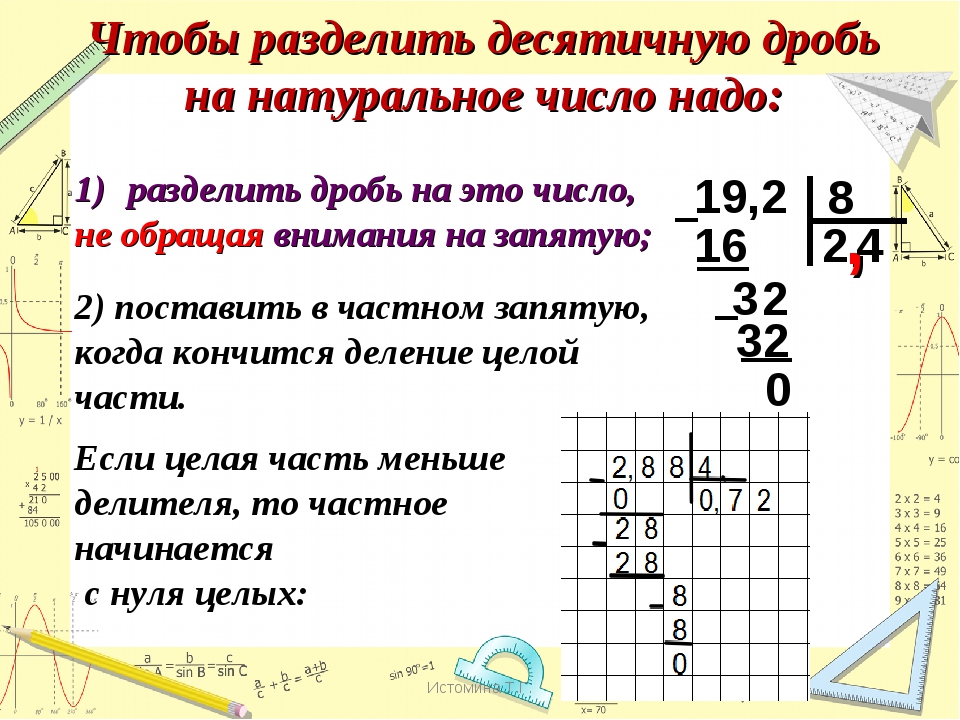

---

Применение онлайн-игр для обучения

Сегодня существует множество мини-игр, которые направленны на помощь родителям в обучении ребенка. Их использование дает возможность малышу быстро и с интересом освоить основные азы счета, включая случаи, когда происходит сложение двухзначных чисел с переходом через разряд.

Решать примеры с двузначными числами таким образом довольно легко, ведь в большинстве случаев на первом этапе идет пояснение того, как следует проводить все действия, показываются примеры, и только потом можно приступать к решению заданий. Можно использовать вариант, когда в игре предложены варианты ответа, однако в таком случае ребенок может пытаться угадывать правильный ответ не проводя подсчеты. В случае ошибки, необходимо помочь ребенку понять, почему он ее совершил, и объяснить, как стоит делать правильно.

Онлайн флеш-игра по математике «Двузначные числа» генерирует случайные двузначные числа, которые ребенку следует просуммировать и выбрать правильный результат. Также можно вписывать его вручную, с помощью мыши или цифровой панели клавиатуры.

---

Научить ребенка складывать и вычитать двузначные числа на самом деле несложно. Достаточно проводить регулярные занятия, длительность которых будет 10-20 минут, и уже через небольшой промежуток времени ваш малыш добьется неплохих показателей. Использование тренировочных заданий в повседневной жизни позволит лучше усвоить все правила и быстрее развить возможность счета в уме даже больших двухзначных чисел.

Еще из блога:

Чем занять ребенка от 5 до 8 лет дома и на улице

Подробнее

Книги для детей от 2 месяцев до 14 лет – какие читать

Подробнее

Чем занять ребенка летом?

Подробнее

Одаренные дети — как определить и развить их способности

Подробнее

Последние новости

Мастер-класс в ТРК «ТРИНИТИ»

Оставьте заявку и мы свяжемся с вами

Оставьте свой телефон, мы обязательно вам перезвоним

Сложение натуральных чисел в столбик: правила, примеры

Sign in

Password recovery

Восстановите свой пароль

Ваш адрес электронной почты

MicroExcel. ru Математика Арифметика Сложение двузначных, трехзначных и многозначных чисел столбиком

В данной публикации мы рассмотрим правила и практические примеры того, каким образом можно складывать столбиком натуральные числа (двузначные, трехзначные и многозначные).

• Правила сложения в столбик
• Примеры сложения в столбик

Правила сложения в столбик

Два и более числа с любым количеством разрядов можно сложить в столбик. Для этого:

1. Пишем первое число (для удобства начинаем с того, у которого больше разрядов).
2. Под ним записываем второе число так, чтобы цифры одного и того же разряда обоих чисел располагались строго друг под другом (т.е. десятки под десятками, сотни под сотнями и т.д.).
3. Аналогичным образом записываем третье и последующие числа, если они есть.
4. Чертим горизонтальную линию, которая будет отделять слагаемые от суммы.
5. Приступаем к сложению цифр – отдельно для каждого разряда суммируемых чисел (справа налево), записываем результат под чертой в том же столбце. При этом, если сумма столбца оказалась двузначной, в нем пишем последнюю цифру, а первую переносим в следующий разряд (слева), т.е. прибавляем к цифрам, содержащимся в нем (см. пример 2). Иногда в результате такого действия в сумме появляется еще один более старший разряд, которого изначально не было (см. пример 4). В редких случаях, когда слагаемых много, может потребоваться перенос не на один, а на несколько разрядов.

Примеры сложения в столбик

Пример 1

Сложим двузначные числа: 41 и 57.

Пример 2

Найдем сумму чисел: 37 и 28.

Пример 3

Вычислим сумму двузначного и трехзначного чисел: 56 и 147.

Пример 4

Просуммируем трехзначные числа: 485 и 743.

Пример 5

Сложим двузначные, трехзначные и четырехзначные числа: 62, 341, 578 и 1209.

ЧАЩЕ ВСЕГО ЗАПРАШИВАЮТ

Таблица знаков зодиака

Нахождение площади трапеции: формула и примеры

Нахождение длины окружности: формула и задачи

Римские цифры: таблицы

Таблица синусов

Тригонометрическая функция: Тангенс угла (tg)

Нахождение площади ромба: формула и примеры

Нахождение объема цилиндра: формула и задачи

Тригонометрическая функция: Синус угла (sin)

Геометрическая фигура: треугольник

Нахождение объема шара: формула и задачи

Тригонометрическая функция: Косинус угла (cos)

Нахождение объема конуса: формула и задачи

Таблица сложения чисел

Нахождение площади квадрата: формула и примеры

Что такое тетраэдр: определение, виды, формулы площади и объема

Нахождение объема пирамиды: формула и задачи

Признаки подобия треугольников

Нахождение периметра прямоугольника: формула и задачи

Формула Герона для треугольника

Что такое средняя линия треугольника

Нахождение площади треугольника: формула и примеры

Нахождение площади поверхности конуса: формула и задачи

Что такое прямоугольник: определение, свойства, признаки, формулы

Разность кубов: формула и примеры

Степени натуральных чисел

Нахождение площади правильного шестиугольника: формула и примеры

Тригонометрические значения углов: sin, cos, tg, ctg

Нахождение периметра квадрата: формула и задачи

Теорема Фалеса: формулировка и пример решения задачи

Сумма кубов: формула и примеры

Нахождение объема куба: формула и задачи

Куб разности: формула и примеры

Нахождение площади шарового сегмента

Что такое окружность: определение, свойства, формулы

Числа до 2 цифр — определение, разрядное значение

В двузначных числах есть только два разряда — разряд единиц и разряд десятков.

Каждое число, состоящее более чем из 1 цифры, имеет разные цифры, описываемые их разрядными значениями. Двузначные числа начинаются с 10 и заканчиваются на 99. Другими словами, наименьшее двузначное число — 10, а наибольшее двузначное число — 99.

1.	Что такое двузначные числа?
2.	Как записывать числа до 2 цифр?
3.	Общие ошибки чисел до 2 цифр
4.	Часто задаваемые вопросы о номерах до 2 цифр

Что такое двузначные числа?

Двузначные числа — это числа, состоящие из двух цифр, которые начинаются с цифры 10 и заканчиваются цифрой 99. Они не могут начинаться с нуля, потому что в этом случае это будет считаться однозначной цифрой. Цифра в разряде десятков может быть любым числом от 1 до 9. Например, 45, 78, 12 — двузначные числа.

Разрядное значение в двузначных числах

Разрядное значение — это положение каждой цифры в числе. Когда мы говорим об однозначных числах, есть только одно разрядное значение, которое является разрядом единиц. Когда мы подходим к двузначным числам, есть два разряда — единицы и десятки. Обратите внимание на следующий рисунок, на котором показано двузначное число 23, написанное вместе с его разрядными значениями. Цифра 2 стоит на месте десятков и означает 20, а цифра 3 стоит на месте единиц и означает 3.

Присвоение разрядных значений

Мы знаем, что разрядное значение числа говорит о позиции цифры. В двузначных числах единственными разрядами являются десятки и единицы.

Давайте посмотрим на следующий набор чисел, чтобы понять сочетание единиц и десятков:

а.) 33 ⇒ 3 десятка + 3 единицы = (3 × 10) + (3 × 1) = 30 + 3 = 33

б.) 18 ⇒ 1 десяток + 8 единиц = (1 × 10) + (8 × 1) = 10 + 8 = 18

в.) 27 ⇒ 2 десятка + 7 единиц = (2 × 10) + ( 7 × 1) = 20 + 7 = 27

Как записывать числа до 2 цифр?

Двузначные числа можно записывать в виде цифр, прописью и в расширенной форме. Например, 45 — это двузначное число. Давайте посмотрим, как это можно записать тремя способами.

• В цифровой форме: 45
• Прописью: сорок пять
• В развернутом виде: 40+5

Двузначные числа в словах

Когда числа записываются словами с помощью разрядных значений, это помогает нам писать их по буквам. Самое маленькое двузначное число — 10, которое записывается как десять. После этого числа от 11 до 20 записываются как 11 – одиннадцать, 12 – двенадцать, 13 – тринадцать, 14 – четырнадцать, 15 – пятнадцать, 16 – шестнадцать, 17 – семнадцать, 18 – восемнадцать, 19.- девятнадцать, а 20 — двадцать. После этого они записываются как 21 — двадцать один, 22 — двадцать два, 23 — двадцать три и так далее, пока не дойдет до 30 — тридцать, и тот же образец следует после тридцати, сорока и так далее.

Двузначные числа в расширенной форме

Расширенная форма числа помогает узнать о его составляющих. Развернутую форму двузначного числа можно показать по-разному.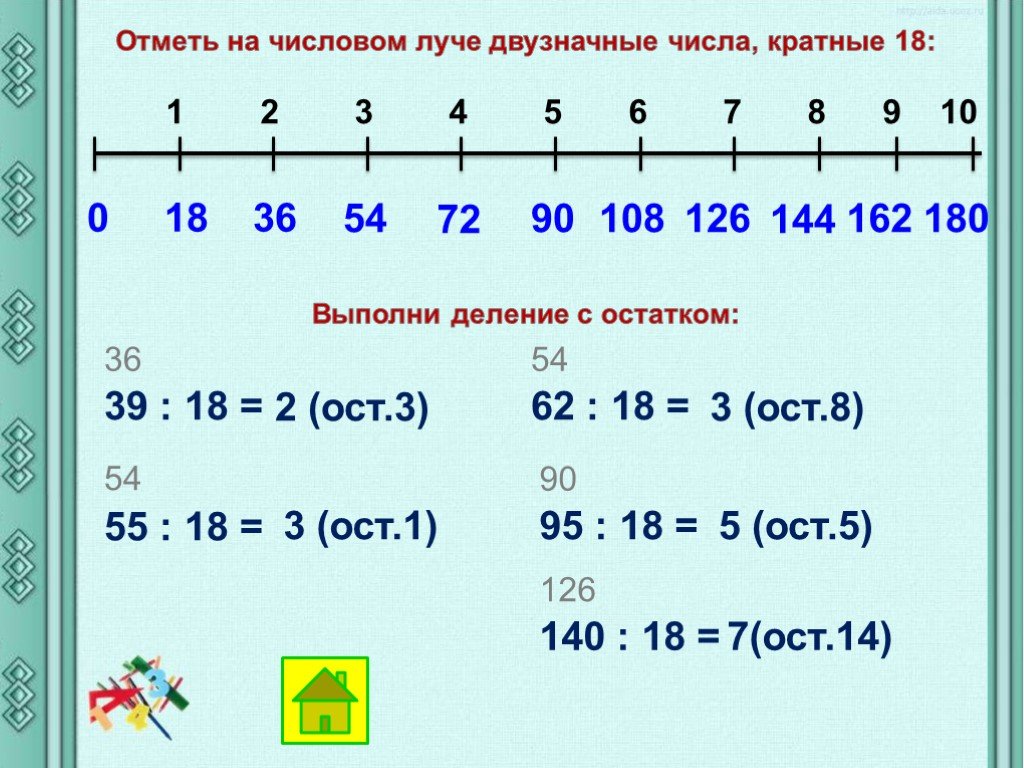 Рассмотрим двузначное число 57.

• Число 57 можно записать в одной форме как 57 = (5 × десятков) + (7 × единиц)
• По-другому это можно записать как 57 = (5 × 10) + (7 × 1)
• Третий способ записать 57 в расширенной форме: 57 = 50 + 7.

Общие ошибки чисел до 2 цифр

• Дети часто могут назвать все числа до 99 (или 100), но могут ошибаться, когда их просят найти большее число между двумя числами. Они повторяют числа от 1 до 100 так, как будто выучили буквы алфавита. Если это произойдет, то найти большее число между 14 и 15 так же сложно, как найти большую букву между С и D. Дети должны понимать, что, в отличие от букв, числа связаны друг с другом. 15 ровно на единицу больше, чем 14. Для этого можно использовать числовые линии и цветные счетчики, чтобы связать звук с количеством.
• Дети склонны ошибаться при работе с числами при изменении разряда десятков. Например, при переходе от 19 к 20, от 29 к 30, от 39 к 40 и т. д. Часто двузначные числа вводятся без привязки к разрядным значениям. Хотя это облегчает запоминание чисел, это может быть не лучшей стратегией, поскольку дети не видят числа, составленные из общего набора цифр от 0 до 9. В этом случае можно использовать счеты для моделирования чисел и основания. -10 блоков могут быть использованы, чтобы помочь им визуализировать числа.
• Дети делают ошибки при написании или чтении чисел словами, особенно от одиннадцати до девятнадцати. Нет никакой замены практике. Дети должны практиковаться в написании названий чисел. Как правило, при небольшой преднамеренной и целенаправленной практике эту ошибку можно легко исправить.

Советы по числам до 2 цифр

Ниже приведены некоторые советы и рекомендации по числам до 2 цифр.

• При умножении любого однозначного числа (от 1 до 9) на 10 получается двузначное число. Например, 4 × 10 = 40
• Наименьшее двузначное число, состоящее только из одной цифры, равно 11.
• Наименьшее двузначное число, состоящее из двух разных цифр, равно 10. (10 также является наименьшим двузначным числом)
• Наибольшее двузначное число, использующее только одну цифру, равно 99. (99 также является наибольшим двузначным числом).
• Наибольшее двузначное число, использующее все разные цифры, равно 98.
• В двузначных числах есть только два разряда: десятки и единицы.
• Есть девяносто «двухзначных чисел», начиная с 10-99.

Вот список всех чисел до 2 цифр от 10 до 99.

Наименьшее двузначное число

Наименьшее двузначное число — 10, поскольку предыдущее число — 9, которое является однозначным числом.

Наибольшее двузначное число

Наибольшее двузначное число — 99, поскольку следующее число — 100, которое является трехзначным числом.

Важные примечания

Ниже приведены некоторые важные примечания, связанные с числами до 2 цифр, которые мы изучали в этой статье.

• Наименьшее двузначное число — 10, а наибольшее двузначное число — 99.
• Всего девяносто двузначных чисел.
• Двузначное число не может начинаться с 0, так как в этом случае оно будет считаться однозначным.

☛ Статьи по теме

• Номера до 3 цифр
• Номера до 4 цифр
• Номера до 5 цифр
• Номера до 6 цифр
• Номера до 7 цифр
• Номера до 8 цифр
• Номера до 9 цифр
• Номера до 10 цифр

 

Примеры двузначных чисел

1. Пример 1: В чем разница между самым большим двузначным числом и числом 20?

   Решение: Наибольшее двузначное число = 99
   Разница между 99 и 20 составляет 99 — 20 = 79

   .

2. Пример 2: Создайте двузначное число, в котором 7 — это разряд десятков, а 5 — разряд единиц. Запишите номер в развернутой форме и напишите его номерное название.

   Решение: Если 7 в разряде десятков и 5 в разряде единиц, число равно 75.
   Расширенная форма 75 = 70 + 5. Это также можно записать как (7 десятков) + (5 единиц) или (7 × 10) + (5 × 1) 9.0185 Имя числа 75 — это семьдесят пять.

3. Пример 3: Запишите первые четыре «двузначных числа» и последние четыре «двузначных числа».

   Решение: Первые четыре двузначных числа: 10, 11, 12, 13.

   Последние четыре двузначных числа: 96, 97, 98, 99.

перейти к слайдуперейти к слайдуперейти к слайду

Отличное обучение в старшей школе с использованием простых подсказок

Увлекаясь зубрежкой, вы, скорее всего, забудете понятия. С Cuemath вы будете учиться визуально и будете удивлены результатами.

Записаться на бесплатный пробный урок

Практические вопросы по числам до 2 цифр

 

перейти к слайдуперейти к слайду

Часто задаваемые вопросы о номерах до 2 цифр

Что такое двузначные числа в математике?

Число называется двузначным, если оно состоит из двух цифр, в которых разряд десятков должен стоять от 1 до 9, оно не может начинаться с нуля, потому что в этом случае оно станет однозначным числом. Например, 35, 45, 60, 11 и так далее — двузначные числа.

Сколько существует двузначных чисел?

Всего существует девяносто двузначных чисел, начиная с 10 и заканчивая 99. Это означает, что наименьшее двузначное число равно 10, а самое большое двузначное число равно 99.

Какое самое большое 2- Цифровой номер?

Самое большое двузначное число — 99, а следующее число — 100, которое является трехзначным числом.

Какое самое маленькое двузначное число?

Наименьшее двузначное число — 10, поскольку предыдущее число — 9, то есть однозначное число.

Какое наибольшее двузначное число делится на 10?

Самое большое двузначное число, которое делится на 10, — это 90. Хотя самое большое двузначное число — 99, оно не делится на 10.

Какое наибольшее двузначное число можно составить из 8 и 6?

Наибольшее двузначное число, которое можно составить из 8 и 6, равно 86. Поскольку 8 больше 6, поэтому мы оставляем 8 на разряде десятков и 6 на разряде единиц. Следовательно, 86 — это самое большое двузначное число, состоящее из цифр 8 и 6.

Напишите расширенную форму данного двузначного числа 65.

Расширенную форму числа 65 можно представить как 60 + 5. Это также можно записать как 6 десятков + 5 единиц или (6 × 10) + (5 × 1).

Сколько десятков в двузначном числе 20?

В данном числе 20 цифра 2 стоит на месте десятков. Следовательно, в числе 20 2 десятка. Это можно записать как 20 = 2 десятка + 0 единиц.

Могут ли двузначные числа начинаться с 0?

Нет, двузначные числа не могут начинаться с 0. Разряд десятков в двузначном числе не может быть нулем, это может быть любое число от 1 до 9, в противном случае оно будет считаться однозначным числом. Например, 05, 06, 07 — все однозначные числа, а 56, 78, 79 — двузначные числа.

Каковы разрядные значения в числах до 2 цифр?

Значение разряда помогает определить положение цифр. В двузначных числах всего два разряда — десятки и единицы. Например, в числе 98 9 стоит на месте десятков, а 8 — на месте единиц.

Какое самое большое двузначное простое число?

Самое большое двузначное простое число — 97, потому что 97 имеет только 2 делителя, 1 и 97.

Скачать БЕСПЛАТНЫЕ учебные материалы

Скачать бесплатные рабочие листы KG

Рабочий лист чисел

NumberNut.com: Арифметика: Сложение: двузначные числа

Числа и подсчет| Арифметика |Дроби и десятичные числа|Предварительная алгебра|Карта сайта

Добавление двузначных чисел аналогично добавлению однозначных значений, просто вы выполняете процесс сложения более одного раза. Когда вы складываете двузначные числа, вы добавляете столбцы вместе, а не все числа. Например, вам не хотелось бы пытаться сложить в уме 78 и 57 как полные числа. Легче разбить эти цифры на кусочки размером с укус. Вы должны начать с добавления чисел в столбец единиц, а затем перейти к добавлению чисел в столбец десятков . Этот пример был немного сложным, потому что он включает переноску. Давайте рассмотрим несколько простых примеров…

24 + 45 = 69
37 + 11 = 48
82 + 6 = 88

Вот еще один способ увидеть проблему. Вам будет легче решить их в формате по вертикали (вверх и вниз), когда вы начнете с сложения. Гораздо легче увидеть, как числа выстраиваются в столбцы. В этом примере сумма в столбце единиц составляет девять (9), а в столбце десятков — шесть (6).

24 + 45 69

Не забывайте всегда работать влево. Вы будете записывать свои добавления с выровненными столбцами, а затем начнете добавлять. Если вы обнаружите, что один столбец не имеет значения для десятков, ничего страшного. Просто представьте, что это ноль. Любое число, добавленное к нулю, есть само.

82 + 6 88

Следующей задачей при сложении двузначных чисел будет добавление чисел, включающих , переносящих , или , перегруппировывающих . Мы уже немного говорили о переносе в предыдущем уроке. Если сумма из столбца единиц больше девяти (9), вы переносите «1» в следующий столбец слева.

Что делать, если у вас проблема 78 + 57? Вы бы начали с столбца единиц (8 + 7 = 15). Запишите «5» в своем ответе и переместите «1» в столбец десятков. Ваш следующий шаг — добавить все значения из столбца десятков (1 + 7 + 5). Эта сумма равна «13», которую вы бы записали в своем ответе. Ваша окончательная сумма будет «135».

Пример:

78 + 57 ? 1   78 + 57 5 78 + 57 13 5

Другие примеры:
48 + 32 = 80
(8+2=10, запишите 0 и перенесите 1, 1+4+3=8)

29 + 29 = 58
(9+9=18, записать 8 и перенести 1, 1+2+2=5)

95 + 16 = 111
(5+6=11, запишите 1 и перенесите 1, 1+9+1=11)

75 + 87 = 162
(5+7=12, запиши 2 и перенеси 1, 1+7+8=16)

► СЛЕДУЮЩАЯ СТРАНИЦА ПО АРИФМЕТИКЕ
► ВЕРНУТЬСЯ НА НАЧАЛО СТРАНИЦЫ

► Или выполните поиск на сайтах.