Примеры по математике для 1, 2, 3 класса
1-й класс 2-й класс 3-й класс1 класс
В первом классе начинается обучение счёту. Сначала ученикам дают примеры в пределах первой десятки — сложение и вычитание. Когда примеры с однозначными числами решаются уверенно — добавляются примеры с переходом через десяток.
Для тренировки навыков устного счёта удобно воспользоваться генератором примеров:
Примеры на сложение и вычитание в пределах 10
Вычитание однозначных чисел
Примеры на сложение и вычитание в пределах 20
Сложение и вычитание однозначных и двузнычных чисел
Примеры на сложение и вычитание в пределах 100
Сложение и вычитание двузначных чисел
2 класс
Во втором классе изучают таблицу умножения, постепенно проходя каждую цифру доводят навыки умножение для автоматизма.
Для лучшего запоминания рекомендутся давать много разнообразных примеров вперемешку. В это поможет генератор примеров на умножение:
Примеры на умножение однозначных чисел
Сумма не превышает 10
Примеры на умножение однозначных и двузначных чисел
Сумма не превышает 10
Помимо умножения во втором классе появляются примеры с пропусками значений — прообраз уравнений с одним неизвестным. В примерах с пропусками значений сначала необходимо правильно подобрать математическое действие, и только потом можно решить пример. Довести навыки счёта до автоматизмав поможет генератор примеров с пропусками значений.
Примеры на сложение и вычитание с пропусками двузначных и однозначных чисел
Сумма не превышает 10
Примеры на сложение и вычитание с пропусками двузначных чисел
Сумма не превышает 10
Примеры на сложение и вычитание с пропусками в пределах 1000
Сложение двузначных чисел с суммой не превышащей 100
Более слодные примеры — неравенства, где для решения нужно вычислить значения в левой и правой части.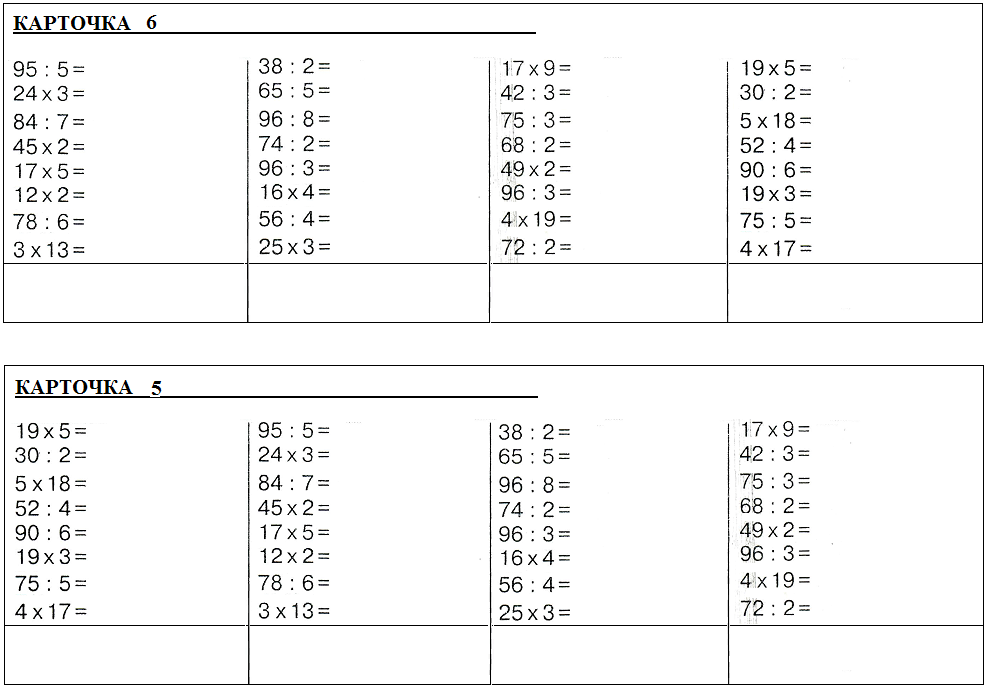 Это усложнённый вариант обычных примеров.
Это усложнённый вариант обычных примеров.
Неравенства с примерами с однозначными числами
Сумма не превышает 10
Неравенства с примерами с двузначными числами
Сумма не превышает 10
3 класс
В третьем классе продолжается отработка навыков счёта. Примеры становятся более сложными, и для их решения применяется решение в столбик. Для развития навыков быстрого счёта рекомендутся давать ученику большое количество разнообразных примеров. Их можно взять здесь:
Примеры на сложение и вычитание в пределах 1000
Сложение двузначных чисел с суммой не превышащей 100
Примеры на сложение и вычитание в пределах 10000
Сложение двузначных чисел с суммой не превышащей 1000
Примеры на сложение и вычитание с пропусками в пределах 1000
Сложение двузначных чисел с суммой не превышащей 1000
Примеры на сложение и вычитание с пропусками в пределах 10000
Сложение двузначных чисел с суммой не превышащей 10000
Примеры на умножение в третьем классе включают уже двузначные числа.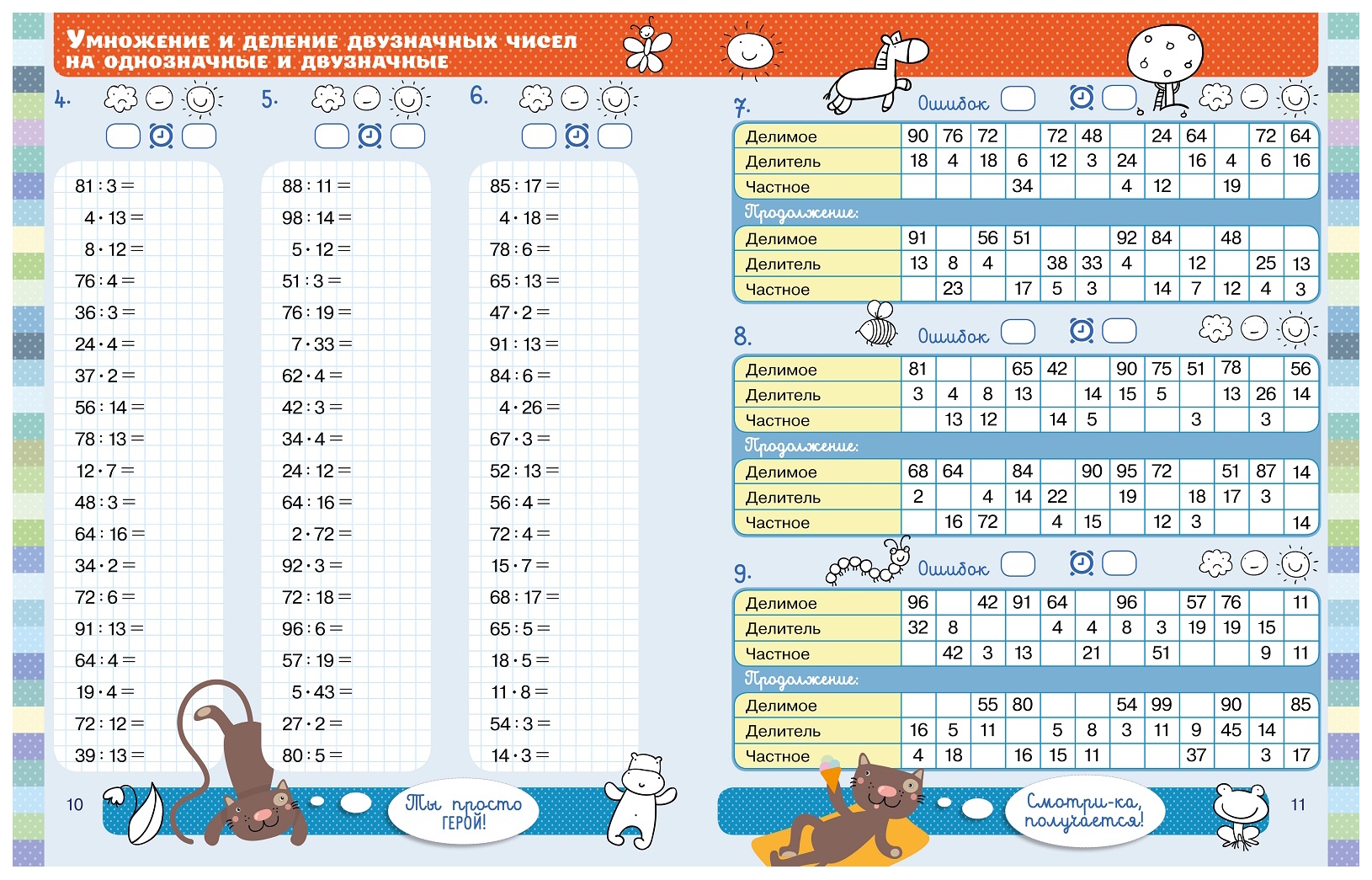 Также полезно отработать счёт с «опорными» числами, которые часто встречаются в различных расчётах.
Также полезно отработать счёт с «опорными» числами, которые часто встречаются в различных расчётах.
Примеры на умножение однозначных и двузначных чисел
Сумма не превышает 10
Примеры на умножение опорных чисел «12», «15», «25», «75», «125»
Сумма не превышает 10
Примеры онлайн на сложение и вычитание двузначных чисел
Онлайн примеры на сложение и вычитание двузначных чисел позволяют выбрать сложность примеров: без перехода через десяток, с некоторыми переходами через десяток, и с обязательным переодом через десяток.
Для успешного овладения устными счётомнеобходима практика. Он-лайн примеры позволяют наработать практику устного счёта. Для этого школьнику даются неповторяющиеся примеры на сложение и вычитание, и прорешаве несколько десятков примеров он доведёт навыки устного счёта до автоматизма.
К сожалению, «зубрёжка» в устном счёте — это главный элемент: вы не должны каждый раз считать в уме результат, он должен автоматически выдаваться из памяти.
Примеры можно разделить по степени сложности: лёгкие – это примеры без перехода через десяток, сложные – с обязательным переходом, обычные – слагаемые выбираются случайным образом.
| Настройка генератора примеров |
|---|
|
Образец примеров
76 + 22
97 — 73
80 + 14
20 — 10
26 + 71
46 — 42
20 — 11
36 + 61
36 + 38
71 — 26
59 — 18
57 — 57
50 + 37
71 — 5
16 + 63
85 — 26
21 + 57
82 — 29
23 — 5
31 — 29
64 + 7
59 — 20
20 — 6
56 — 2
98 — 25
29 — 4
74 — 68
10 + 5
18 — 16
70 + 14
45 — 40
33 — 20
34 + 34
81 + 6
24 + 47
22 + 9
33 + 26
54 + 7
58 + 23
49 — 17
36 + 60
27 — 4
94 — 18
5 + 74
94 — 39
89 — 31
45 + 50
47 + 33
79 — 20
81 — 66
69 + 3
83 — 79
92 — 5
78 + 4
28 — 1
88 — 41
9 — 1
2 + 86
3 + 14
25 + 28
23 + 71
63 — 13
83 — 37
44 + 1
43 — 35
7 + 47
86 — 54
69 + 22
53 + 36
79 — 43
54 + 33
77 — 62
38 + 61
57 + 29
35 + 47
3 + 30
30 — 13
95 + 1
98 — 24
11 — 6
90 — 23
46 + 20
97 — 71
43 — 25
58 + 2
28 — 6
17 + 57
30 — 24
37 + 59
47 + 6
24 + 48
13 + 15
87 — 14
44 — 35
58 + 17
3 + 15
50 — 20
87 — 79
72 — 34
26 + 44
28 + 54
64 — 26
39 + 35
51 + 39
82 — 50
11 — 7
30 + 35
85 + 14
25 + 29
16 + 77
9 + 30
13 + 8
17 — 17
82 — 78
9 + 20
16 + 4
56 + 26
85 — 22
96 — 10
99 — 9
3 + 60
36 — 2123 + 14
61 + 32
62 — 8
98 — 96
69 — 59
99 — 57
60 — 4
98 — 8
90 — 35
92 — 18
26 + 66
41 + 15
31 — 30
76 — 36
23 + 21
67 — 23
79 — 73
32 + 64
54 — 54
1 + 28
43 — 15
41 + 47
52 + 43
33 + 31
86 — 76
94 — 2
36 — 36
81 — 26
68 + 3
61 — 42
19 — 12
40 — 13
38 — 20
11 + 72
28 + 28
76 — 52
45 + 46
46 + 49
19 + 65
11 — 2
12 + 49
16 + 43
22 + 1
68 — 58
5 + 93
62 — 14
57 — 15
69 + 3
19 + 63
96 — 77
46 — 3
80 — 73
52 — 31
96 — 29
34 + 48
96 — 2
2 + 12
2 + 97
51 — 4
93 — 5
6 + 70
59 — 18
30 + 12
9 + 6
41 — 22
25 — 19
25 + 2
61 — 40
79 — 30
37 + 50
58 — 3
79 — 58
30 — 4
4 + 25
4 + 9
96 — 56
33 + 64
60 + 8
99 — 51
81 — 61
1 + 32
4 + 20
89 — 15
87 — 38
77 — 51
5 + 22
63 — 20
43 — 26
24 + 64
48 + 7
39 + 9
12 + 76
19 + 44
90 — 38
53 + 2
20 — 13
88 — 9
72 — 10
27 + 35
35 + 50
93 — 89
23 + 20
77 — 64
65 + 26
47 — 20
11 + 12
70 — 54
43 + 37
78 — 60
29 + 50
98 — 59
66 + 12
55 — 4
34 + 26
66 — 7
56 + 43
49 — 41
42 + 39
14 + 27
50 — 39
26 + 46
91 — 71
94 — 63
49 — 36
54 — 52
25 + 45
3 + 57
35 + 25
27 + 24
90 — 1
68 + 31
40 — 27
56 — 2
6 + 50
32 + 32
59 + 14
47 — 25
27 + 67
64 + 24
99 — 83
61 + 16
32 — 31
18 + 80
16 + 24
17 + 21
11 + 18
91 — 13
42 — 29
87 — 43
12 + 54
67 — 67
31 + 26
21 + 66
61 — 39
14 — 11
45 + 24
88 + 11
81 — 15
13 — 6
8 + 69
36 — 11
6 + 77
26 — 25
96 — 20
45 — 4
57 — 11
42 — 23
73 — 48
57 + 26
77 — 13
73 + 16
48 + 39
54 — 5
87 — 42
95 — 80
38 — 4
12 + 53
94 — 52
83 + 15
11 + 84
5 + 48
59 — 21
94 — 36
93 — 69
36 + 47
69 — 37
21 + 42
36 — 22
23 + 13
59 — 52
65 + 13
97 — 94
27 — 21
65 + 17
47 + 30
20 — 8
38 — 4
9 + 66
70 + 13
32 + 61
14 + 49
32 + 65
7 + 53
47 + 4
35 — 26
11 + 58
66 — 58
87 — 3
69 — 45
76 — 23
33 + 41
85 — 20
37 — 21
35 + 8
2 + 78
30 + 41
43 — 9
51 — 2
18 + 69
63 — 24
27 + 66
38 — 20
73 — 67
26 + 26
2 + 43
86 — 55
50 — 7
94 — 15
52 + 45
36 — 21
18 — 14
15 + 30
84 — 36
23 — 3
25 + 12
57 — 26
79 — 77
78 — 30
82 + 2
3 + 80
91 — 58
28 + 34
4 + 30
41 + 34
83 — 65
25 + 49
80 — 68
7 + 92
95 — 63
5 + 63
38 — 23
56 — 39
97 — 40
42 + 7
35 + 20
70 — 57
57 — 52
47 + 4
10 + 59
6 — 2
7 + 92
29 — 7
71 — 21
45 + 9
22 + 23
83 — 9
67 — 8
50 — 40
40 + 42
85 + 2
53 — 29
9 + 75
46 — 33
39 — 34
40 + 51
54 + 40
67 — 63
81 — 21
72 — 41
96 — 83
47 — 41
48 — 3
11 + 28
32 + 3
11 + 58
84 — 15
64 + 5
5 + 77
95 — 22
64 — 35
26 + 37
80 + 2
67 + 7
40 — 14
48 — 41
31 + 43
19 + 24
34 + 20
41 + 4
33 + 50
44 — 26
46 — 15
9 + 52
50 + 32
73 — 47
75 — 9
38 + 21
98 — 79
16 + 53
13 + 20
24 + 2
19 + 24
99 — 26
48 + 24
91 — 44
53 — 38
39 — 34
66 — 44
50 — 29
83 — 26
71 — 34
44 + 4
37 + 10
20 + 42
9 + 49
12 + 85
78 + 1
48 + 37
77 — 62
48 — 16
51 + 21
18 + 26
92 — 71
93 — 4
98 — 8
95 — 80
13 + 71
65 — 62
18 + 26
27 — 7
54 + 22
3 + 87
87 — 77
72 — 12
2 + 45
85 — 25
62 — 45
12 + 57
14 + 37
32 + 50
89 — 19
53 + 14
80 — 21
93 — 74
44 — 26
11 + 62
62 — 15
4 + 59
91 — 11
56 + 23
51 + 22
43 + 47
77 — 53
94 — 23
52 + 27
77 + 9
9 + 79
81 — 76
68 + 14
50 — 13
26 + 35
70 + 11
92 — 6
84 — 72
Урок 43.
 приём деления для случаев вида 87 : 29, 66 : 22 — Математика — 3 класс
приём деления для случаев вида 87 : 29, 66 : 22 — Математика — 3 классМатематика, 3 класс
Урок № 43. Приём деления для случаев вида 87 : 29, 66 : 22
Перечень вопросов, рассматриваемых в теме:
1. Как разделить двузначное число на двузначное?
2. Как выполнить деление вида 87 : 29, 66 : 22?
3. Как проверить правильность результата деления?
Глоссарий по теме:
Деление – это обратное действие умножению
Умножение – это сложение одинаковых слагаемых.
Метод подбора – это способ деления двузначного числа на двузначное, при котором частное подбираем последовательно и проверяем умножением.
Обязательная и дополнительная литература:
1. Моро М. И., Бантова М. А. и др. Математика 3 класс. Учебник для общеобразовательных организаций М.; Просвещение, 2017, C-18.
2. Петерсон Л. Г. Математика 3 класс. Часть 2. – М.: Ювента, 2013– 96 C., С-86.
3. Марченко И. С. Справочник школьника по математике: 1 – 4 классы. – М.: Эксмо, 2014. С. 160, (Светлячок) С. 50.
С. Справочник школьника по математике: 1 – 4 классы. – М.: Эксмо, 2014. С. 160, (Светлячок) С. 50.
Теоретический материал для самостоятельного изучения
Рассмотрим решение задачи.
Высота дома тридцать два метра, а высота дерева – шестнадцать метров. Во сколько раз дом выше дерева?
Чтобы узнать во сколько раз дом выше, надо тридцать два разделить на шестнадцать. Получится два, в два раза. Выполнить такое деление можно
используя взаимосвязь умножения и деления. Это поможет научиться делить двузначное число на двузначное методом подбора частного.
Рассмотрим пример 48 : 12
Пробуем в частном два и проверяем. Двенадцать умножить на два получится двадцать четыре — не подходит. Пробуем- три. Двенадцать умножить на три равно тридцать шесть, тоже не подходит. Пробуем четыре. Двенадцать умножаем на четыре, получается сорок восемь, подходит. Значит, сорок восемь разделить на двенадцать получится четыре.
48 : 12
12 ∙ 2 = 24 не подходит
12 ∙ 3 = 36 не подходит
12 ∙ 4 = 48 подходит
Значит,
48 : 12 = 4
В случае деления числа шестьдесят шесть на двадцать два, подбираем число, на которое надо умножить двадцать два, чтобы получилось шестьдесят шесть. Это число три.
Это число три.
66 : 22
22 ∙ 3 = 66
66 : 22 = 3, так как 22 ∙ 3 = 66
Умножение нужно использовать для проверки правильности вычислений.
88 : 11 = 8, так как 11 ∙ 8 = 88
Чтобы делать меньше проб при подборе частного, нужно обратить внимание на последнюю цифру в делимом и делителе. В делимом цифра один , в делителе — цифра семь. В таблице умножения на семь находим число двадцать один (ведь один последняя цифра в делимом). Чтобы получить двадцать один, нужно семь умножить на три. Три – пробное число. Выполняем проверку.
81 : 27 = 3
Делимое 81 — последняя цифра 1
Делитель 27 — последняя цифра 7
7 ∙ 3 = 21 Проверка: 27 ∙ 3 = 81
Частное найдено, верно.
Выполним тренировочные задания
Вставьте пропущенные числа:
54 : 27 = ____ , так как 27 ∙ ___ = 54;
Ответ: 54 : 27 = 2 , так как 27∙ 2 = 54.
Зачеркните пример с ошибкой:
38 : 19 = 2
42 : 14 = 2
64 : 16 = 3
Ошибка в примере 42 : 14 = 2 и 64 : 16 = 3
Расшифруйте, расставляя ответы в порядке возрастания, название одного из самых высоких деревьев в мире:
Я 78 : 26
С 99 : 33
В 78 : 13
Й 64 : 16
К 84: 12
О 70 : 14
Е 88 : 11
Ответ:
11 8 7 6 5 4 3
С Е К В О Й Я
Деление двузначного числа на однозначное.
 Примеры
ПримерыСначала рассмотрим способ деления двузначного числа на однозначное, когда в делимом количество десятков и количество единиц делится на делитель.
Чтобы разделить двузначное число на однозначное, надо двузначное число представить в виде суммы разрядных слагаемых и разделить эту сумму на однозначное число.
Например, чтобы найти значение выражения:
56 : 2
сначала записываем двузначное число 56 в виде суммы разрядных слагаемых:
50 + 6,
то есть просто разбиваем число 56 на сумму пяти десятков и шести единиц. Затем делим сумму 50 + 6 на число 2:
(50 + 6) : 2 = 50 : 2 + 6 : 2 = 25 + 3 = 28,
значит 56 : 2 = 28.
Примеры:
1) 39 : 3 = (30 + 9) : 3 = 30 : 3 + 9 : 3 = 10 + 3 = 13;
2) 75 : 5 = (70 + 5) : 5 = 70 : 5 + 5 : 5 = 14 + 1 = 15;
3) 68 : 4 = (60 + 8) : 4 = 60 : 4 + 8 : 4 = 15 + 2 = 17.
Теперь рассмотрим способ деления двузначного числа на однозначное, когда в делимом количество десятков и количество единиц по отдельности не делятся на делитель.
Чтобы разделить двузначное число на однозначное, надо двузначное число представить в виде суммы слагаемых и разделить эту сумму на однозначное число.
Рассмотрим выражение:
52 : 4.
В данном случае разрядные слагаемые числа 52 (50 и 2) не делятся на 4. Значит первый способ вычислений здесь не подходит. Тогда можно подобрать ближайшее к 52 круглое число, которое делится на 4, это будет число 40. Заменяем делимое 52 на сумму:
40 + 12.
Затем делим сумму 40 + 12 на число 4:
(40 + 12) : 4 = 40 : 4 + 12 : 4 = 10 + 3 = 13,
значит 52 : 4 = 13.
Примеры:
1) 96 : 8 = (80 + 16) : 8 = 80 : 8 + 16 : 8 = 10 + 2 = 12;
2) 51 : 3 = (30 + 21) : 3 = 30 : 3 + 21 : 3 = 10 + 7 = 17;
3) 84 : 7 = (70 + 14) : 7 = 70 : 7 + 14 : 7 = 10 + 2 = 12.
Как видно из примеров, при делении двузначного числа на однозначное используется:
- представление числа в виде суммы двух чисел или суммы разрядных слагаемых,
- правило деления суммы на число,
- знание таблицы умножения.
«Сложение и вычитание двузначных чисел» (2-й класс)
Тема: «Сложение и вычитание
двузначных чисел».
Цели:
- закрепить умения представлять двузначные числа в виде суммы разрядных слагаемых; повторить соотношение между частью и целым; закрепить умения решать текстовые задачи.
- научить складывать двузначные числа с двузначными без перехода через разряд;
- развивать внимательность, мышление; воспитывать чувства взаимопомощи и взаимовыручки.
Оборудование: графические карточки
для обозначения чисел, таблицы-схемы задач,
конверты с заданием, Приложение 1 (компьютерная
презентация с использованием фрагментов сказки
«Гуси-лебеди»).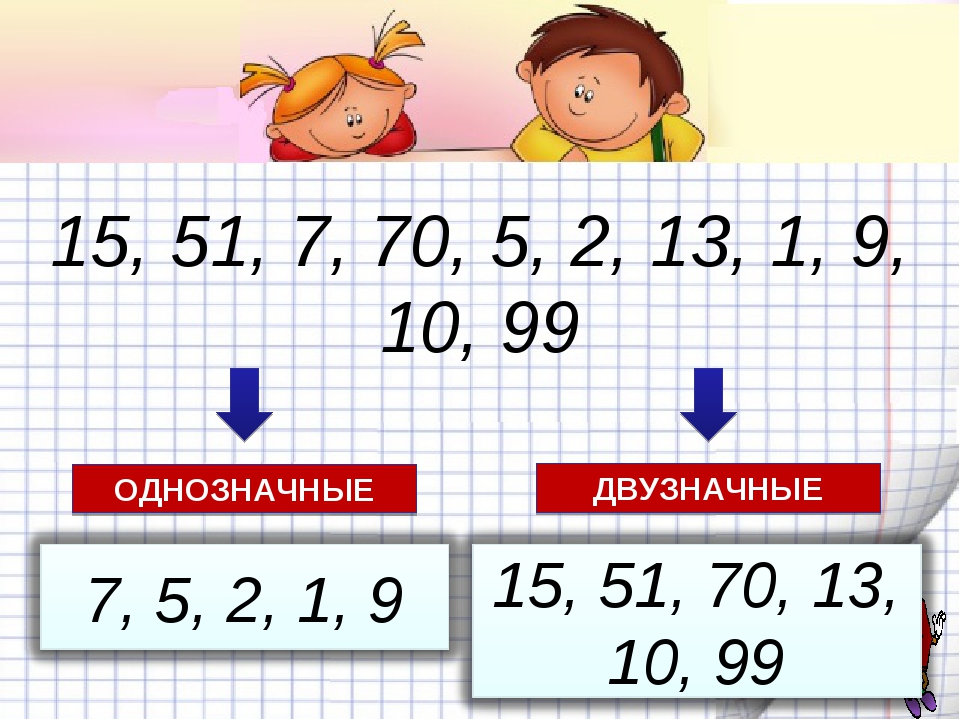
ХОД УРОКА
1. Оргмомент
– Подготовились к уроку:
Долгожданный дан звонок –
Начинается урок.
Тут примеры и задачи
Игры, шутки, всё для вас!
Пожелаю вам удачи –
За работу, в добрый час!
2. Работа над пройденным материалом
На доске:
4 22 10 20 18 6 12 2 24 8 16 26 14
– Назовите числа в порядке возрастания.
Запишите их в тетрадь.
– Что вы заметили, переписывая эти числа? (Каждое
следующее число больше предыдущего на 2 единицы).
– На какие две группы мы сможем разбить этот ряд? (На
двузначные и однозначные числа)
– Чем отличается однозначное число от
двузначного? (Для записи однозначного числа
требуется один знак (цифра), для двузначного –
два)
– Как называется первый справа разряд у
двузначного числа? (Разряд единиц)
– Как называется второй справа разряд у
двузначного числа? (Разряд десятков)
– Ребята, как вы думаете, зачем нам нужно знать
разряды? (Безошибочно уметь решать любые
примеры)
– Назовите разрядные слагаемые чисел.
На доске:
35 это 3 д. и 5 ед.
92…
56…
Работа по учебнику
– Выполним задание № 1(в). Заполним «пустые» окошки. (Выборочно пригласить отвечать у доски)
48 = 40 + … 70 + 3 = … 21 = 1 + …
96 = … + 6 5 + 80 = … 39 = … + …
3. Объявление новой темы урока и её задач
– Сегодня мы продолжим работу с двузначными числами, научимся правильно складывать и вычитать их.
4. Работа над новым материалом (образец на наборном полотне)
– Посмотрим, как графически записан пример.
– Что обозначают треугольники?. .. (Десятки)
.. (Десятки)
– Что обозначают точки?… (Единицы)
– Прочитаем пример.
Чтение с места: Двадцать четыре плюс тринадцать
равно тридцать семь.
– Запишем его с помощью цифр: 24 + 13 = 37.
– Как сложить двузначные числа?
(Дети высказывают своё мнение)
– Чтобы сложить…
ПРАВИЛО-ВЫВОД
– На доске графически записан следующий пример.
– Прочитаем его.
…Сорок пять минус четырнадцать равно тридцать
один.
– Запишем его с помощью цифр 45 –14 = 31
– Сделаем вывод: чтобы вычесть двузначные
числа, нужно из единиц вычесть единицы, а из
десятков – десятки.
– Прочитаем на с. 68 правило…
5. Физкультминутка
Мы дружно потрудились
Немного устали
Быстро все сразу
За партами встали.
Руки поднимем, потом разведём.
В ладоши похлопаем, потом их встряхнём.
Направо посмотрим, налево посмотрим
И очень глубоко всей грудью вздохнём!
(Можно повторить)
6. Закрепление (Приложение 1)
– За время нашего отдыха к нам
прибежали за помощью герои сказки «Гуси-лебеди».
Это Машенька и её братец Иванушка. Сестрица с
братцем добежали до молочной реки. Видят: летят
гуси-лебеди. Попросили у речки:
– Речка, матушка, спрячь нас!
Речка: Если справитесь с моим
заданием, то я вас укрою.
– Ребята, поможем Машеньке с братцем, быстро
выполним задание №2.
Речка укрыла их кисельным бережком. Гуси-лебеди
не увидали, пролетели мимо. Девочка с братцем
дальше побежала, но вот воротились гуси-лебеди.
Что делать, кого просить о помощи…
… Видят яблоню…
Яблоня: Если вы ребята сможете
самостоятельно решить примеры, то я помогу
спрятаться…
1 вариант – 1 столбик
2 вариант – 2 столбик
1 вариант: 2 вариант:
36 +
42
69 – 21
44 –
13
72 + 24
52 +
15
85 – 43
Работа в парах
– Ребята проверим, правильно ли мы выполнили
задание, выручили детей.
– Обменялись тетрадями, проверили друг у друга.(1
в. проверяет 2 в., а 2 в. проверяет 1 в.)
Яблоня заслонила ветвями, прикрыла листами…
Пролетели гуси мимо, а девочка с братцем дальше
побежали. Добежали до печки. Видят, опять
гуси-лебеди летят…
Печь. Печка дала самое трудное
задание. Не обойтись Машеньке с братом без нашей
помощи.
Прочитать задачи, выбрать правильно схему к ним и
подобрать верное решение. Это задание №4
– Прочитаем 1-ю задачу. Выберем нужную схему.
Найдем решение и т. д. 2-ю и 3-ю задачи.
– Мы помогли героям сказки. Печь спрятала детей.
Гуси-лебеди полетали-полетали,
покричали-покричали и ни с чем улетели к Бабе
Яге. Сестрица с братцем счастливые прибежали
домой, где их ждали отец с матерью и подарки.
– Хорошие дела и поступки вознаграждаются! За
работу на уроке, за помощь героям сказки вам
также «подарки». Подарок у каждого в конверте –
это игра «Танаграм». Условие игры подскажет задание
№5* «г»
Подарок у каждого в конверте –
это игра «Танаграм». Условие игры подскажет задание
№5* «г»
7. Итог
– С какими числами мы работали на уроке? (С
двузначными)
– Как сложить двузначные числа?
– Как вычесть двузначные числа?
Очень жаль, что путь недолог,
Возвращаться нам пора,
Но на следующем уроке
Вновь продолжиться игра!
– Всем спасибо! Урок окончен.
Как научиться быстро считать в уме любые числа: техники устного счета
Устный счет – занятие, которым в наше время себя утруждает все меньшее количество людей. Гораздо проще достать калькулятор на телефоне и вычислить любой пример.
Но так ли это на самом деле? В этой статье мы представим математические лайфхаки, которые помогут научиться быстро складывать, вычитать, умножать и делить числа в уме. Причем оперируя не единицами и десятками, а минимум двухзначными и трехзначными числами.
Причем оперируя не единицами и десятками, а минимум двухзначными и трехзначными числами.
После освоения методов из этой статьи идея лезть в телефон за калькулятором уже не покажется такой хорошей. Ведь можно не тратить время и посчитать все в уме гораздо быстрее, а заодно размять мозги и произвести впечатление на окружающих (противоположного пола).
Итак, добро пожаловать в увлекательный мир вычислений! Мы собрали советы от наших авторов о том, как улучшить устный счет и стать математическим героем и гением. Кстати, если вам интересна математика, вы можете почитать статью «Пределы для чайников» в нашем блоге.
Предупреждаем! Если вы обычный человек, а не вундеркинд, то для развития навыка счета в уме понадобятся тренировки и практика, концентрация внимания и терпение. Сначала все может получаться медленно, но потом дело пойдет на лад, и вы сможете быстро считать в уме любые числа.
Гаусс и устный счет
Карл Фридрих Гаусс
Одним из математиков с феноменальной скоростью устного счета был знаменитый Карл Фридрих Гаусс (1777-1855). Да-да, тот самый Гаусс, который придумал нормальное распределение.
Да-да, тот самый Гаусс, который придумал нормальное распределение.
По его собственным словам, он научился считать раньше, чем говорить. Когда Гауссу было 3 года, мальчик взглянул на платежную ведомость своего отца и заявил: «Подсчеты неверны». После того как взрослые все перепроверили, выяснилось, что маленький Гаусс был прав.
В дальнейшем этот математик достиг немалых высот, а его труды до сих пор активно используются в теоретических и прикладных науках. До самой смерти большую часть вычислений Гаусс производил в уме.
Здесь мы не будем заниматься сложными расчетами, а начнем с самого простого.
Сложение чисел в уме
Чтобы научиться складывать в уме большие числа, нужно уметь безошибочно складывать числа до 10. В конечном счете любая сложная задача сводится к выполнению нескольких тривиальных действий.
Чаще всего проблемы и ошибки возникают при сложении чисел с «переходом через 10». При сложении (да и при вычитании) удобно применять технику «опоры на десяток». Что это? Сначала мы мысленно спрашиваем себя, сколько одному из слагаемых не хватает до 10, а потом прибавляем к 10 оставшуюся до второго слагаемого разность.
Что это? Сначала мы мысленно спрашиваем себя, сколько одному из слагаемых не хватает до 10, а потом прибавляем к 10 оставшуюся до второго слагаемого разность.Например, сложим числа 8 и 6. Чтобы из 8 получить 10, не хватает 2. Затем к 10 останется прибавить 4=6-2. В итоге получаем: 8+6=(8+2)+4=10+4=14
Основная хитрость со сложением больших чисел – разбить их на разрядные части, а потом сложить эти части между собой.
Пусть нам нужно сложить два числа: 356 и 728. Число 356 можно представить как 300+50+6. Аналогично, 728 будет иметь вид 700+20+8. Теперь складываем:
356+728=(300+700)+(50+20)+(8+6)=1000+70+14=1084
Вычитание чисел в уме
Вычитание чисел тоже будет даваться легко. Но в отличие от сложения, где каждое число разбивается на разрядные части, при вычитании «разбить» нужно только то число, которое мы отнимаем.
Но в отличие от сложения, где каждое число разбивается на разрядные части, при вычитании «разбить» нужно только то число, которое мы отнимаем.
Например, сколько будет 528-321? Разбиваем число 321 на разрядные части и получаем: 321=300+20+1.
Теперь считаем: 528-300-20-1=228-20-1=208-1=207
Попробуйте визуализировать процессы сложения и вычитания. В школе всех учили считать в столбик, то есть сверху вниз. Один из способов перестроить мышление и ускорить счет – считать не сверху вниз, а слева направо, разбивая числа на разрядные части.Умножение чисел в уме
Умножение – это многократное повторение числа. Если нужно умножить 8 на 4, это значит, что число 8 нужно повторить 4 раза.
8*4=8+8+8+8=32
Так как все сложные задачи сводятся к более простым, нужно уметь умножать все однозначные числа. Для этого существует отличный инструмент – таблица умножения. Если вы не знаете эту таблицу на зубок, то мы настоятельно рекомендуем первым делом выучить ее и только потом приниматься за практику устного счета. К тому же учить там, по сути, нечего.
Для этого существует отличный инструмент – таблица умножения. Если вы не знаете эту таблицу на зубок, то мы настоятельно рекомендуем первым делом выучить ее и только потом приниматься за практику устного счета. К тому же учить там, по сути, нечего.
Таблица умножения
Умножение многозначных чисел на однозначные
Сначала потренируйтесь в умножении многозначных чисел на однозначные. Пусть нужно умножить 528 на 6. Разбиваем число 528 на разряды и идем от старшего к младшему. Сначала умножаем, а потом складываем результаты.
528=500+20+8
528*6=500*6+20*6+8*6=3000+120+48=3168
Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы
Умножение двузначных чисел
Здесь тоже нет ничего сложного, только нагрузка на краткосрочную память немного больше.
Перемножим 28 и 32. Для этого сведем всю операцию к умножению на однозначные числа. Представим 32 как 30+2
28*32=28*30+28*2=20*30+8*30+20*2+8*2=600+240+40+16=896
Еще один пример. Умножим 79 на 57. Это значит, что на нужно взять число «79» 57 раз. Разобьем всю операцию на этапы. Сначала умножим 79 на 50, а потом – 79 на 7.
- 79*50=(70+9)*50=3500+450=3950
- 79*7=(70+9)*7=490+63=553
- 3950+553=4503
Умножение на 11
Вот хитрый прием быстрого устного счета, который поможет умножить любое двузначное число на 11 с феноменальной скоростью.
Проверим и умножим 54 на 11.
Возьмите любое двузначное число, умножьте его на 11 и убедитесь сами — эта хитрость работает!
Возведение в квадрат
С помощью другого интересного приема устного счета можно легко и быстро возводить двузначные числа в квадрат. Особенно просто это делать с числами, которые заканчиваются на 5.
Результат начинается с произведения первой цифры числа на следующую за ней по иерархии. То есть, если эту цифру обозначить через n, то следующей за ней по иерархии цифрой будет n+1. Результат заканчивается на квадрат последней цифры, то есть квадрат 5.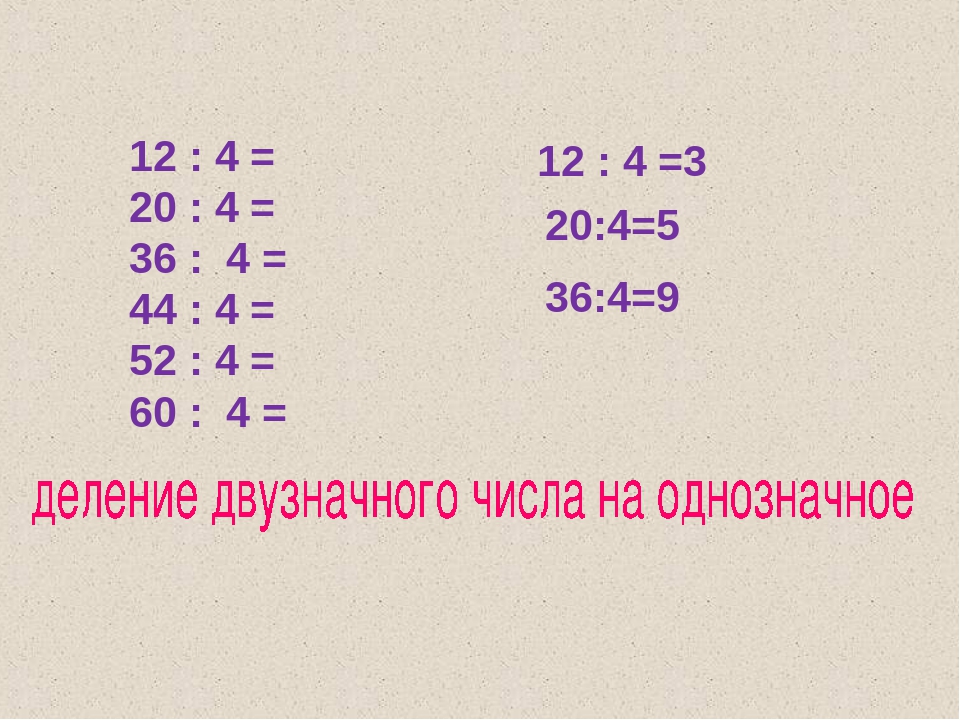
Проверим! Возведем в квадрат число 75.
Раньше все считали без калькуляторов
Деление чисел в уме
Осталось разобраться с делением. По сути, это операция, обратная умножению. С делением чисел до 100 никаких проблем вообще возникать не должно – ведь есть таблица умножения, которую вы знаете на зубок.
Деление на однозначное число
При делении многозначных чисел на однозначное необходимо выделить максимально большую часть, которую можно разделить с помощью таблицы умножения.
Например, есть число 6144, которое нужно разделить на 8. Вспоминаем таблицу умножения и понимаем, что на 8 будет делиться число 5600. Представим пример в виде:
6144:8=(5600+544):8=700+544:8
Далее из числа 544 также выделяем максимально большое число, которое делится на 8. Имеем:
Имеем:
544:8=(480+64):8=60+64:8
Осталось разделить 64 на 8 и получить результат, сложив все результаты деления
64:8=8
6144:8=700+60+8=768
Деление на двузначное число
При делении на двузначное число нужно пользоваться правилом последней цифры результата при умножении двух чисел.
При умножении двух многозначных чисел последняя цифра результата умножения всегда совпадает с последней цифрой результата умножения последних цифр этих чисел.
Например, умножим 1325 на 656. По правилу, последняя цифра в получившемся числе будет 0, так как 5*6=30. Действительно, 1325*656=869200.
Теперь, вооружившись этой ценной информацией, рассмотрим деление на двузначное число.
Сколько будет 4424:56?
Первоначально будем пользоваться методом «подгона» и найдем пределы, в которых лежит результат. Нам нужно найти число, которое при умножении на 56 даст 4424. Интуитивно попробуем число 80.
56*80=4480
Значит, искомое число меньше 80 и явно больше 70. Определим его последнюю цифру. Ее произведение на 6 должно заканчиваться цифрой 4. Согласно таблице умножения, нам подходят результаты 4 и 9. Логично предположить, что результатом деления может быть либо число 74, либо 79. Проверяем:
79*56=4424
Готово, решение найдено! Если бы не подошло число 79, второй вариант обязательно оказался бы верным.
Картина Н.П. Богданова-Бельского «Устный счёт. В народной школе С. А. Рачинского»
Полезные советы
В заключение приведем несколько полезных советов, которые помогут быстро научиться устному счету:
- Не забывайте тренироваться каждый день;
- не бросайте тренировки, если результат не приходит так быстро, как хотелось бы;
- скачайте мобильное приложение для устного счета: так вам не придется самостоятельно придумывать себе примеры;
- почитайте книги по методикам быстрого устного счета. Существуют разные техники устного счета, и вы сможете овладеть той, которая лучше всего подходит именно вам.
Польза устного счета неоспорима. Тренируйтесь, и с каждым днем вы будете считать все быстрее и быстрее. А если вам понадобится помощь в решении более сложных и многоуровневых задач, обращайтесь к специалистам студенческого сервиса за быстрой и квалифицированной помощью!
Деление столбиком на двузначное число.
 Видео #
Видео #Деление столбиком или, правильнее сказать, письменный прием деления уголком, школьники проходят уже в третьем классе начальной школы, но зачастую этой теме уделяется так мало внимания, что к 9-11 классу не все ученики могут им свободно пользоваться.
Деление столбиком на двузначное число проходят в 4 классе, как и деление на трехзначное число, а далее этот прием используется только как вспомогательный при решении каких-либо уравнений или нахождении значения выражения.
Очевидно, что уделив делению столбиком больше внимания, чем заложено в школьной программе, ребенок облегчит себе выполнение заданий по математике вплоть до 11 класса. А для этого нужно немногое — понять тему и позаниматься, порешать, держа алгоритм в голове, довести навык вычисления до автоматизма.
Для начала повторим кратко, как делить столбиком на однозначное число:
А что если деление с остатком? Смотрим в следующем видео:
youtube.com/embed/Tn-W851Arxs» frameborder=»0″ allow=»accelerometer; autoplay; encrypted-media; gyroscope; picture-in-picture» allowfullscreen=»»/>Алгоритм деления столбиком на двузначное число
Как и при делении на однозначное число, будем последовательно переходить от деления более крупных счетных единиц к делению более мелких единиц.
1. Находим первое неполное делимое. Это число, которое делится на делитель с получением числа больше или равного 1. Это значит, что первое неполное делимое всегда больше делителя. При делении на двузначное число в первом неполном делимом минимум 2 знака.
Примеры 768:24. Первое неполное делимое 76
265:53 26 меньше 53, значит не подходит. Нужно добавить следующую цифру (5). Первое неполное делимое 265.
2. Определяем количество цифр в частном. Для определения числа цифр в частном следует помнить, что неполному делимому соответствует одна цифра частного, а всем остальным цифрам делимого — еще по одной цифре частного.
Примеры 768:24. Первое неполное делимое 76. Ему соответствует 1 цифра частного. После первого неполного делителя есть еще одна цифра. Значит в частном будет всего 2 цифры.
265:53. Первое неполное делимое 265. Оно даст 1 цифру частного. Больше в делимом цифр нет. Значит в частном будет всего 1 цифра.
15344:56. Первое неполное делимое 153, а после него еще 2 цифры. Значит в частном будет всего 3 цифры.
3. Находим цифры в каждом разряде частного. Сначала найдем первую цифру частного. Подбираем такое целое число, чтобы при умножении его на наш делитель получилось число, максимально приближенное к первому неполному делимому. Цифру частного записываем под уголок, а значение произведения вычитаем столбиком из неполного делителя. Записываем остаток. Проверяем, что он меньше делителя.
Затем находим вторую цифру частного. Переписываем в строку с остатком цифру, следующую за первым неполным делителем в делимом. Полученное неполное делимое снова делим на делитель и так находим каждое последующее число частного, пока не закончатся цифры делителя.
Полученное неполное делимое снова делим на делитель и так находим каждое последующее число частного, пока не закончатся цифры делителя.
4. Находим остаток (если есть).
Если цифры частного закончились и получился остаток 0, то деление выполнено без остатка. В ином случае значение частного записывается с остатком.
Так же выполняется деление на любое многозначное число (трехзначное, четырехзначное и т. д.)
Разбор примеров на деление столбиком на двузначное число
Сначала рассмотрим простые случаи деления, когда в частном получается однозначное число.
— Найдем значение частного чисел 265 и 53.
Первое неполное делимое 265. Больше в делимом цифр нет. Значит в частном будет однозначное число.
Чтобы было легче подобрать цифру частного, разделим 265 не на 53, а на близкое круглое число 50. Для этого 265 разделим на 10, будет 26 (остаток 5). И 26 разделим на 5, будет 5 (остаток 1). Цифру 5 нельзя сразу записывать в частном, поскольку это пробная цифра. Сначала нужно проверить, подойдет ли она. Умножим 53*5=265. Мы видим, что цифра 5 подошла. И теперь можем ее записать в частном под уголок. 265-265=0. Деление выполнено без остатка.
Цифру 5 нельзя сразу записывать в частном, поскольку это пробная цифра. Сначала нужно проверить, подойдет ли она. Умножим 53*5=265. Мы видим, что цифра 5 подошла. И теперь можем ее записать в частном под уголок. 265-265=0. Деление выполнено без остатка.
Значение частного чисел 265 и 53 равно 5.
Иногда при делении пробная цифра частного не подходит, и тогда ее нужно менять.
— Найдем значение частного чисел 184 и 23.
В частном будет однозначное число.
Чтобы было легче подобрать цифру частного, разделим 184 не на 23, а на 20. Для этого разделим 184 на 10, будет 18 (остаток 4). И 18 разделим на 2, будет 9. 9 – это пробная цифра, мы ее сразу писать в частном не будем, а проверим, подойдет ли она. Умножим 23*9=207. 207 больше, чем 184. Мы видим, что цифра 9 не подходит. В частном будет меньше 9. Попробуем, подойдет ли цифра 8. Умножим 23*8=184. Мы видим, что цифра 8 подходит. Можем ее записать в частном. 184-184=0.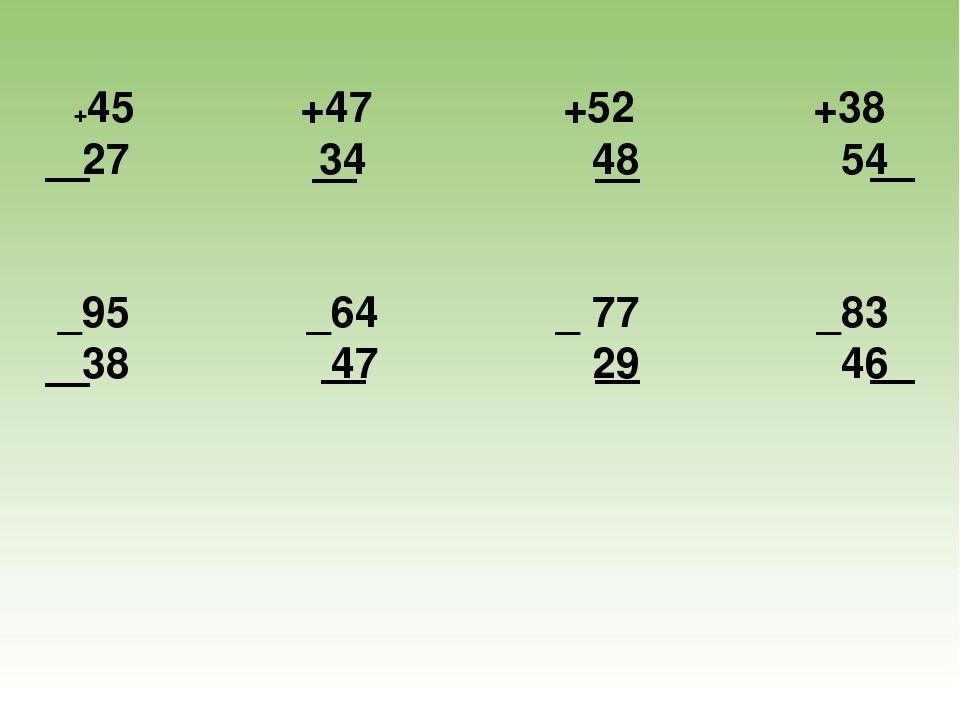 Деление выполнено без остатка.
Деление выполнено без остатка.
Значение частного чисел 184 и 23 равно 8.
Рассмотрим более сложные случаи деления.
— Найдем значение частного чисел 768 и 24.
Первое неполное делимое – 76 десятков. Значит, в частном будут 2 цифры.
Определим первую цифру частного. Разделим 76 на 24. Чтобы легче было подобрать цифру частного, разделим 76 не на 24, а на 20. То есть нужно 76 разделить на 10, будет 7 (остаток 6). И 7 разделим на 2, получится 3 (остаток 1). 3 – это пробная цифра частного. Сначала проверим, подойдет ли она. Умножим 24*3=72 . 76-72=4. Остаток меньше делителя. Значит, цифра 3 подошла и теперь мы ее можем записать на месте десятков частного. 72 пишем под первым неполным делимым, между ними ставим знак минус, под чертой записываем остаток.
Продолжим деление. Перепишем в строку с остатком цифру 8, следующую за первым неполным делимым. Получим следующее неполное делимое – 48 единиц. Разделим 48 на 24. Чтобы было легче подобрать цифру частного, разделим 48 не на 24, а на 20. То есть разделим 48 на 10, будет 4 (остаток 8). И 4 разделим на 2, будет 2. Это пробная цифра частного. Мы должны сначала проверить, подойдет ли она. Умножим 24*2=48. Мы видим, что цифра 2 подошла и, значит, можем ее записать на месте единиц частного. 48-48=0, деление выполнено без остатка.
Разделим 48 на 24. Чтобы было легче подобрать цифру частного, разделим 48 не на 24, а на 20. То есть разделим 48 на 10, будет 4 (остаток 8). И 4 разделим на 2, будет 2. Это пробная цифра частного. Мы должны сначала проверить, подойдет ли она. Умножим 24*2=48. Мы видим, что цифра 2 подошла и, значит, можем ее записать на месте единиц частного. 48-48=0, деление выполнено без остатка.
Значение частного чисел 768 и 24 равно 32.
— Найдем значение частного чисел 15344 и 56.
Первое неполное делимое – 153 сотни, значит, в частном будут три цифры.
Определим первую цифру частного. Разделим 153 на 56. Чтобы легче было подобрать цифру частного, разделим 153 не на 56, а на 50. Для этого разделим 153 на 10, будет 15 (остаток 3). И 15 разделим на 5, будет 3. 3 – это пробная цифра частного. Помните: ее нельзя сразу записывать в частном, а нужно сначала проверить, подойдет ли она. Умножим 56*3=168. 168 больше, чем 153. Значит, в частном будет меньше, чем 3. Проверим, подойдет ли цифра 2. Умножим 56*2=112. 153-112=41. Остаток меньше делителя, значит, цифра 2 подходит, ее можно записать на месте сотен в частном.
Проверим, подойдет ли цифра 2. Умножим 56*2=112. 153-112=41. Остаток меньше делителя, значит, цифра 2 подходит, ее можно записать на месте сотен в частном.
Образуем следующее неполное делимое. 153-112=41. Переписываем в ту же строку цифру 4, следующую за первым неполным делимым. Получаем второе неполное делимое 414 десятков. Разделим 414 на 56. Чтобы удобнее было подобрать цифру частного, разделим 414 не на 56, а на 50. 414:10=41(ост.4). 41:5=8(ост.1). Помните: 8 – это пробная цифра. Проверим ее. 56*8=448. 448 больше, чем 414, значит, в частном будет меньше, чем 8. Проверим, подойдет ли цифра 7. Умножим 56 на 7, получится 392. 414-392=22. Остаток меньше делителя. Значит, цифра подошла и в частном на месте десятков можем записать 7.
Пишем в строку с новым остатком 4 единицы. Значит следующее неполное делимое – 224 единицы. Продолжим деление. Разделим 224 на 56. Чтобы легче было подобрать цифру частного, разделим 224 на 50. То есть сначала на 10, будет 22 (остаток 4). И 22 разделим на 5, будет 4 (остаток 2). 4 – это пробная цифра, проверим ее, подойдет ли она. 56*4=224. И мы видим, что цифра подошла. Запишем 4 на месте единиц в частном. 224-224=0, деление выполнено без остатка.
И 22 разделим на 5, будет 4 (остаток 2). 4 – это пробная цифра, проверим ее, подойдет ли она. 56*4=224. И мы видим, что цифра подошла. Запишем 4 на месте единиц в частном. 224-224=0, деление выполнено без остатка.
Значение частного чисел 15344 и 56 равно 274.
Пример на деление с остатком
Чтобы провести аналогию, возьмем пример, похожий на пример выше, и отличающийся лишь последней цифрой
— Найдем значение частного чисел 15345:56
Делим сначала точно так же, как в примере 15344:56, пока не дойдем до последнего неполного делимого 225. Разделим 225 на 56. Чтобы легче было подобрать цифру частного, разделим 225 на 50. То есть сначала на 10, будет 22 (остаток 5). И 22 разделим на 5, будет 4 (остаток 2). 4 – это пробная цифра, проверим ее, подойдет ли она. 56*4=224. И мы видим, что цифра подошла. Запишем 4 на месте единиц в частном. 225-224=1, деление выполнено с остатком.
Значение частного чисел 15345 и 56 равно 274 (остаток 1).
Деление с нулем в частном
Иногда в частном одним из чисел получается 0, и дети зачастую пропускают его, отсюда неправильное решение. Разберем, откуда может взяться 0 и как его не забыть.
— Найдем значение частного чисел 2870:14
Первое неполное делимое — 28 сотен. Значит в частном будет 3 цифры. Ставим под уголок три точки. Это важный момент. Если ребенок потеряет ноль, останется лишняя точка, которая заставит задуматься, что где-то упущена цифра.
Определим первую цифру частного. Разделим 28 на 14. Подбором получается 2. Проверим, подойдет ли цифра 2. Умножим 14*2=28. Цифра 2 подходит, ее можно записать на месте сотен в частном. 28-28=0.
Получился нулевой остаток. Мы обозначили его розовым для наглядности, но записывать его не нужно. Переписываем в строку с остатком цифру 7 из делимого. Но 7 не делится на 14 с получением целого числа, поэтому записываем на месте десятков в частном 0.
Теперь переписываем в ту же строку последнюю цифру делимого (количество единиц).
70:14=5 Записываем вместо последней точки в частном цифру 5. 70-70=0. Остатка нет.
Значение частного чисел 2870 и 14 равно 205.
Деление нужно непременно проверить умножением.
Примеры на деление для самопроверки
Найдите первое неполное делимое и определите количество цифр в частном.
3432:66 2450:98 15145:65 18354:42 17323:17
Усвоили тему, а теперь потренируйтесь решить несколько примеров столбиком самостоятельно.
1428 : 42 30296 : 56 254415 : 35 16514 : 718
2924 : 68 136576 : 64 710278 : 91 15830 : 293
номеров до 2 цифр | Решенные примеры | Номера
В этом видео вы вместе с Ритой и Джоэлом подсчитываете палки на ферме. Не упустите трюк, который использует Рита, когда палочек больше 10.
Содержание
Мы в Cuemath считаем, что математика — это жизненный навык. Наши эксперты по математике сосредотачиваются на том, «почему» стоит за «что». Учащиеся могут исследовать огромное количество интерактивных листов, наглядных пособий, симуляторов, практических тестов и многого другого, чтобы глубже понять концепцию.
Наши эксперты по математике сосредотачиваются на том, «почему» стоит за «что». Учащиеся могут исследовать огромное количество интерактивных листов, наглядных пособий, симуляторов, практических тестов и многого другого, чтобы глубже понять концепцию.
Забронируйте БЕСПЛАТНОЕ пробное занятие сегодня! и поучаствуйте в онлайн-классе Cuemath LIVE вместе со своим ребенком.
Концепт Видео по номерамПосмотрите это видео о том, как числа знакомят детей Cuemath Way!
Давайте разберемся, почему? за что!
Введение в числа до 2-х цифр
Мы начинаем считать числа на пальцах наших рук в очень молодом возрасте, а затем переходим к использованию суперкомпьютеров для вычисления очень больших чисел.
Каким бы ни было количество цифр в числе, правильное расположение каждой цифры является наиболее важным.
Сегодня мы поговорим о двузначных числах, но перед этим познакомимся с однозначными числами.
Есть 10 однозначных чисел — \ (0,1,2,3,4,5,6,7,8 \) и \ (9 \)
Все двузначные или двузначные числа, которые мы обсудим, являются комбинациями любых двух из девяти из этих десяти чисел.
Да, 0 не всегда считается, и мы вернемся к этому позже.
Посмотрите это моделирование, чтобы увидеть, как двузначное число представлено в блоках и стержнях.
10 собранных вместе блоков образуют стержень.
10 единиц равно 1 десятке.
Большая идея: числа до 2-х цифр Простая идея: стоимость чисел
Каждое число, состоящее из более чем одной цифры, должно иметь разные цифры, описываемые их разрядами .
Разрядные значения, которые мы используем, — это единицы, десятки, сотни, тысячи, десять тысяч и так далее.
Вы заметите, что каждое из следующих подряд значений разряда в десять раз больше предыдущего.
Когда мы ограничиваемся 2-значными числами, мы имеем дело только с двумя разрядами — единиц — и десятков — .
Допустим, вы покупаете мороженое в магазине, и к вам на обед приходят 5 друзей.
Включая родителей, вам нужно 5 \ (+ \) You \ (+ \) Parents = 8 мороженого.
Вы можете пойти в магазин и купить 8 единиц мороженого.
Если вы пригласите весь класс домой, когда будете готовы бросить школу, у вас будет 33 друга \ (+ \) вы \ (+ \) ваши родители = 36 мороженого.
Итак, вы возьмете 3 ванны, чтобы получить эквивалент 30 мороженого.
Кроме того, вы возьмете 6 стаканчиков мороженого, всего получится 36 мороженых.
Именно это и происходит, когда мы создаем двузначные числа.
Присвоение значений мест Таким образом, каждый набор из десяти единиц превращается в число с десятичной ценностью, точно так же, как продавец сделал 1 ванну, объединив 10 чашек мороженого.
Давайте посмотрим на 3 набора чисел, чтобы понять преобразование единиц в комбинацию единиц и десятков:
\ (\ begin {align} & {\ text {33 единицы: 3 десятки + 3 единицы}} \\ & {\ text {8 единиц: 1 десять + 8 единиц}} \\ & {\ text {27 единиц: 2 Десятки + 3 единицы}} \ end {align} \)
Я уверен, что вы смогли разобрать, что только первый правильный.
Во втором неверно разряжаются десятки, а в третьем — единицы.
Вот какие правильные комбинации будут для обоих наборов:
\ (\ begin {align} {3 \ text {Десятки} + 3 \ text {Units} \\ = (3 \ times 10) + (3 \ times 1) \\ = 30 + 3 = 33} \\ { 1 \ text {Десять} + 8 \ text {Единицы} \\ = (1 \ times 10) + (8 \ times 1) \\ = 10 + 8 = 18} \\ {\ text {2 Tens} + 3 \ текст {Единицы} \\ = (2 \ times 10) + (3 \ times 1) \\ = 20 + 3 = 23} \ end {align} \)
\ (\ begin {align} & 33 \ text {units:} \\ & (3 \ times 10) + (3 \ times 1) \\ & = 30 + 3 = 33 \\ & 8 \ text {units:} \\ & (0 \ times 10) + (8 \ times 1) \\ & = 0 + 8 = 8 \\ & 27 \ text {units:} \\ & (2 \ times 10) + (7 \ times 1 ) \\ & = 20 + 7 = 27 \ end {align} \)
Некоторые общие 2-значные числаДавайте посмотрим, знаете ли вы ответы на следующие 5 вопросов:
- Сколько цифр в дюжине?
- Что считается несчастливым числом?
- Что такое оценка?
- Сколько ярдов в длину поле для крикета?
- Какое число равно четверти века?
Ответы на приведенные выше вопросы по порядку: \ (12, 13, 20, 22 \) и \ (25. \) Все эти пять чисел являются двузначными числами.
\) Все эти пять чисел являются двузначными числами.
Есть сомнения, что вы хотите очистить? Получите разъяснения с помощью простых решений на 2-значных числах от наших экспертов по математике в LIVE, персонализированных и интерактивных онлайн-классах Cuemath.
Сделайте своего ребенка экспертом по математике, Забронируйте БЕСПЛАТНЫЙ пробный урок сегодня!
Двухзначный номер
Есть 90 двузначных номеров, начиная с 10-99
Вот список всех 2-значных чисел от 10-99
Как найти количество цифр в числе?
Мы увидели, как с помощью руки можно считать числа от 1 до 10
Мы также можем использовать счетчики, блоки и стержни для подсчета и номеров кадров.
Однозначное число будет содержать только одну цифру от 0 до 9
Двухзначное число будет состоять из двух цифр: одно в разряде десятков, а другое — в разряде единиц.
Пример: 25 — это двухзначное число, где 2 в разряде десятков и 5 в разряде единиц.
Точно так же трехзначное число будет состоять из трех цифр.
Пример: 134 — это трехзначное число, где 1 в разряде сотен, 3 в разряде десятков и 4 в разряде единиц.
Можете ли вы сказать, сколько цифр будет в 5-значном числе?
Насколько это важно?
Значение (или иное) нуля в 2-значных числах
Мы уже знаем, что двузначное число может быть образовано комбинацией двух из 10 цифр от 0 до 10
А как насчет тех чисел, у которых 0 в десятичном значении?
Давайте рассмотрим число, которое образовалось бы из нуля в разряде десяти и пяти в разряде единицы.
Число: \ (\ begin {align} (0 \ times 10) + (5 \ times 1) = 0 + 5 = 5 \ end {align} \)
Цифра десятков не может быть 0, потому что фактически становится однозначным числом.
Но это не тот случай, когда ноль стоит на месте единицы.
Давайте на этот раз попробуем поменять числа и возьмем пять в разряде десятков и ноль в разрядах единиц.
Число: \ (\ begin {align} (5 \ times 10) + (0 \ times 1) = 50 + 0 = 50 \ end {align} \)
Итак, когда дело доходит до нуля, есть девять вариантов, в которых ноль вместо десяти, когда полученное число представляет собой однозначное число, независимо от того, какое число стоит на месте единицы.
Помогите детям воспринимать числа как гибкие величины.
Полезный совет — попросить студентов разбивать числа разными способами.
Напр. 15 — это 10 и еще 5.
При этом 15 — это тоже 14 и еще 1.
Также на 11 и 4 больше.
Играйте в эту игру часто с разными числами.
Начните с маленьких чисел, например 15 и 20, а затем переходите к большим числам, например 32 и 46
Помогите детям освоиться с пропуском до 10
Они должны иметь возможность пропускать счет на 10 из любого числа.
Начните с серии 10, 20, 30, . .. но затем создайте комфорт, попросив учащихся пропустить счет на 10 с любой другой начальной точки.
.. но затем создайте комфорт, попросив учащихся пропустить счет на 10 с любой другой начальной точки.
Например. с 23:23, 33, 43, 53, …
Перечислите числа по 10 в одной строке и по одной во второй строке.
Покажите образцы того, как можно составить числа от 11 до 99, комбинируя десятки и единицы.
Сложные вопросы
- Я двузначное четное число больше 6 + 6 и меньше 15.Найди меня!
- Я — двухзначное число от 50 до 60, и моя единица измерения — это количество сторон квадрата.
- Я — двузначное четное число больше 80 и меньше 90, а сумма моих цифр равна 12. Найди меня!
Дети могут часто произносить все числа до 99 (или 100), но могут ошибаться , когда их просят найти большее число между двумя числами.
Студенты иногда произносят числа от 1 до 100, как если бы они запомнили буквы алфавита.
Если это произойдет, то найти большее число 14 и 15 так же сложно, как найти большую букву между C и D.
Дети должны понимать, что, в отличие от букв, числа связаны друг с другом.
15 ровно на единицу больше 14
Для этого используйте числовые линии, цветные счетчики, чтобы связать звук с количеством.Дети склонны к ошибаться, работая с числами, когда значение разряда десятков меняется на .
Например. при движении с 19 до 20, с 29 до 30, с 39 до 40 и т.д.
Часто двузначные числа вводятся без ссылки на разрядные значения.
Хотя это облегчает запоминание чисел, это, возможно, не лучшая стратегия, поскольку дети не воспринимают числа как составные из общего набора цифр — от 0 до 9
Лучше всего использовать счеты для моделирования чисел и использовать блоки Base-10, чтобы помочь им визуализировать числа.Дети делают ошибки при написании чисел .
Особенно с одиннадцати до девятнадцати.
Практике нет замены.
Дети должны попрактиковаться в написании числовых имен.
Как правило, эту ошибку можно легко исправить с помощью небольшой преднамеренной и целенаправленной практики.
Помогите своему ребенку набрать больше баллов с помощью запатентованного БЕСПЛАТНОГО диагностического теста Cuemath. Получите доступ к подробным отчетам, индивидуальным планам обучения и БЕСПЛАТНОЙ консультации. Попытайтесь пройти тест сейчас.
Решенные примеры
Райан сказал: «В числе 100000 6 цифр». Можете ли вы посчитать количество цифр в номере и подтвердить, прав ли он?
Решение:
Подсчитав количество цифр в 100000, можно заметить, что в числе 5 нулей и 1 единица.
Таким образом, это шестизначное число.
| \ (\ следовательно \) Райан прав |
Номер состоит из двух цифр.
7 в разряде десятков и 5 разрядах.
Что это за номер и напишите его номер имя?
Решение:
Разместим числа в таблице значений разряда.
| Десятичный разряд | Единицы Место |
|---|---|
| 7 | 5 |
Число 75 или семьдесят пять.
| \ (\ следовательно \) Число 75 |
Определите двузначные числа, представленные блоками и стержнями, показанными ниже.
Решение:
Синие стержни представляют место десятков, а желтые блоки — место единиц.
| С. № | Десятки место | Единицы Место | Число |
|---|---|---|---|
| а) | 2 | 8 | 28 |
| б) | 2 | 1 | 21 |
| в) | 1 | 2 | 12 |
| г) | 3 | 0 | 30 |
| \ (\ следовательно \) Цифры: a) 28 b) 21 c) 12 и d) 30 |
Найдите сумму наибольшего двузначного числа и наименьшего двузначного числа.
Найдите количество цифр в найденном числе
Решение:
Наибольшее двузначное число — 99, наименьшее двузначное число — 10
Их сумма равна \ (99 + 10 = 109 \)
109 состоит из 3 цифр, это 3-значное число.
| \ (\ следовательно \) сумма 109 и трехзначное число |
Что является предшественником и преемником разности наибольшего двузначного числа и числа 20?
Решение:
Наибольшее двузначное число = 99
Разница между 99 и 20 равна \ (99-20 = 79 \)
Предшественник 79 — 78, преемник 79 — 80
| \ (\ следовательно \) Предшественник — 78, а преемник — 80 |
Найдите сумму чисел, показанных на счетах.
Решение:
Давайте сначала определим числа, а затем сложим их.
| С. № | Десятки место | Единицы Место | Число |
|---|---|---|---|
| 1 | 3 | 3 | 33 |
| 2 | 2 | 8 | 28 |
| 3 | 1 | 3 | 13 |
| Сумма | 74 | ||
| \ (\ следовательно \) сумма 74 |
Практические вопросы
Вот несколько занятий для вас.
Выберите / введите свой ответ и нажмите кнопку «Проверить ответ», чтобы увидеть результат.
Важные примечания
- Наименьшее двузначное число — 10, а наибольшее двузначное число — 99.

- Всего 90 двузначных чисел.
- 10 единиц составляет 1 Десятку.
- Двузначное число не может начинаться с 0, поэтому разряд десятков может иметь любое число от 1 до 9.
IMO (Международная олимпиада по математике) — это конкурсный экзамен по математике, который ежегодно проводится для школьников. Он побуждает детей развивать свои навыки решения математических задач с точки зрения соревнований.
Вы можете БЕСПЛАТНО скачать образцы работ по оценкам ниже:
Чтобы узнать больше об олимпиаде по математике щелкните здесь
Часто задаваемые вопросы (FAQ)
1.Сколько там двузначных чисел?
Всего 90 двузначных чисел.
2. Как складывать двузначные числа?
- К разряду единиц второго числа прибавляем разряды единиц первого числа.
- Складываем разряды десятков первого числа с разрядами десятков второго числа.

- Если есть переходящий остаток на шаге — 1 прибавьте его к разряду десятков.
\ (\ begin {align}
& 29 \
+ & 34 \
& — \\
= \: & 6 3 \\
& —
\ end {align} \)
3.Какое двузначное число является наибольшим?
Наибольшее двузначное число — 99.
4. Какое первое двузначное число?
Первое двузначное число — 10.
Разделение на двузначное число и пример
Вы уже узнали о делении на двузначное число?
В этом посте мы рассмотрим, как разделить на двузначное число на примере.
Во-первых, давайте рассмотрим части задачи деления:
Теперь мы собираемся выполнить эту же задачу деления шаг за шагом:
1.Подбираем первые цифры делимого. Мы должны выполнить два шага:
- Мы выбираем такое же количество цифр, что и делителя. В данном случае это две цифры.

- Сумма выбранных цифр должна быть больше делителя. Если это не так, мы должны взять другую цифру.
2. Записываем первое число частного.
Теперь мы должны найти число, которое при умножении на делитель (26) дает , равное или меньшее выбранного числа (34), всегда ищет наибольшее кратное, которое соответствует .
Когда мы находим это число, мы помещаем его в частное.
3. Делим первые цифры:
Умножаем частное на делитель, а результат записываем под делимым. Затем мы находим разницу.
( Внимание! Всегда должно быть меньше делителя.)
4. Сбрасываем следующую цифру и повторяем шаги 2 и 3
5. Заканчиваем деление
Продолжаем повторять шаг 4 до тех пор, пока у нас не закончатся цифры, которые нужно сбить.Последнее число, которое у нас осталось под дивидендом, — это остаток. Помните, что остаток всегда должен быть меньше делителя !
Помните, что остаток всегда должен быть меньше делителя !
А вы помните, как делить на двузначное число?
Вы можете узнать больше о делении в предыдущих постах:
А если вы хотите и дальше изучать элементарную математику, попробуйте Smartick Method бесплатно!
Подробнее:
Команда по созданию контента.
Многопрофильная и многонациональная команда, состоящая из математиков, учителей, профессоров и других специалистов в области образования!
Они стремятся создать максимально возможное математическое содержание.
Двузначный делитель в столбике
Это полный урок с примерами и упражнениями о двузначном делителе в столбик, предназначенный для начального обучения в 5-м классе. В первых упражнениях есть сетки для завершения деления и место для учеников, чтобы они могли написать таблицу умножения делителя на полях. Кроме того, существуют проблемы преобразования между дюймами / футами и унциями / фунтами, потому что они решаются с помощью деления.
| Часто бывает полезно написать таблицу умножения делителя перед вы разделяете. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Пример 1. Деление на 16. Вот таблица умножения 16: 3 × 16 = 48 |
16 переходит в 5 нулевых раз, поэтому мы смотрим на 55. Сколько раз 16 входит в 55? Отметьте в таблице на слева. Мы видим, что он входит в число 55 три раза. |
А теперь сколько раз 16 переходит в 76? Из таблицы видно, что это четыре раза. |
Наконец, 16 переходит в 128 ровно 8 раз, а разделение окончено. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
Пример 2. 3 × 32 = 96 |
|
32 переходит в 150
четыре раза. |
32 переходит в 224 семь
раз. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
1. Разделить. Сначала напишите таблица умножения делителя. Проверяйте каждый ответ умножением.
|
2.Делить. Сначала напишите таблица умножения делителя. Проверяйте каждый ответ умножением.
| |||||
| |||||
| |||||
|
3.Делить. Проверяйте каждый ответ умножением.
| ||||
| ||||
| ||||
|
4. Ментальная математика! Если 20 переходит в
800 сорок раз, затем 20 переходит в 820 еще раз,
или 41 раз.В каждом поле используйте верхнюю задачу, чтобы решить нижнюю.
проблема.
| а. 800 ÷ 20 = 820 ÷ 20 = | б. 700 ÷ 50 = 750 ÷ 50 = | г. 150 ÷ 15 = 300 ÷ 15 = |
| г. 480 ÷ 40 = 520 ÷ 40 = | e. 600 ÷ 30 = 690 ÷ 30 = | ф. 1,200 ÷ 60 = 1,320 ÷ 60 = |
5. а. Сколько дюймов в одном футе?
а. Сколько дюймов в одном футе?
г. Преобразовать 245 дюймов в футы и дюймы.
г. Преобразование 387 дюймов в футы и дюймы.
6. а. Сколько унций в одном фунте?
г. Перевести 163 унции в
фунтов
и унции.
г. Перевести 473 унции в
фунтов
и унции.
7. Новорожденный ребенок прибавляет в весе на 9 0 15 15
примерно одна унция в день.
Допустим, малыш прибавил в весе
г.
по этой ставке на ПОЛНЫЙ ГОД.
(На самом деле, у младенцев нет; их
темп роста замедляется.) сколько
фунтов и унций бы ребенок
прибыль за год?
См. Также
Листы с длинным делением
Создавайте неограниченное количество листов для деления в столбик (4-6 классы), в том числе с 2-значными и 3-значными делителями.Рабочие листы могут быть выполнены в формате html или PDF — и то, и другое легко распечатать. Вы также можете настроить их с помощью генератора.
Вы также можете настроить их с помощью генератора.
/worksheets/long_division.php
Этот урок взят из книги Марии Миллер Math Mammoth Multiplication & Division 3 и размещен на сайте www.HomeschoolMath.net с разрешения автора. Авторские права © Мария Миллер.
Рабочие листы для сложения двух цифр | Что такое ?, Примеры и резюме
Не готовы приобрести подписку? Нажмите, чтобы загрузить бесплатный образец. Загрузить образецЗагрузить этот образец
Этот образец предназначен исключительно для участников KidsKonnect!
Чтобы загрузить этот рабочий лист, нажмите кнопку ниже, чтобы зарегистрироваться бесплатно (это займет всего минуту), и вы вернетесь на эту страницу, чтобы начать загрузку!
Зарегистрируйтесь
Уже зарегистрировались? Авторизуйтесь, чтобы скачать. Когда мы научимся складывать однозначные числа, следующим шагом будет научиться складывать двухзначных чисел . Добавка используется в повседневной жизни много раз в день. Когда мы считаем деньги или что-то еще, мы используем сложение. Мы можем складывать сколько угодно чисел.
Добавка используется в повседневной жизни много раз в день. Когда мы считаем деньги или что-то еще, мы используем сложение. Мы можем складывать сколько угодно чисел.
См. Файл фактов ниже для получения дополнительной информации о сложении двух цифр или, альтернативно, вы можете загрузить нашу 28-страничную рабочую таблицу сложения двух цифр для использования в классе или дома. Этот рабочий лист разбит на начальный, средний и продвинутый, что означает, что вы можете выбрать уровень сложности для своего ученика.
Основные факты и информация
Резюме:
- Сложение чисел означает нахождение общего значения или суммы этих чисел вместе взятых.
Пример: 2 + 1 = 3 - Сложение двухзначных чисел: 21+ 31 = 52
- Когда мы прибавляем к числу ноль, число остается неизменным.
Пример: 20 + 0 = 20 - Сложение — одна из самых основных операций, которая поможет нам понять все остальные операции.
Что такое сложение?
- После развития чувства числа детей знакомят с сложением.
 Сложение — одна из четырех основных операций, которым обучают в математике.
Сложение — одна из четырех основных операций, которым обучают в математике. - Четыре основных операции — это сложение, вычитание, умножение и деление. Сложение двух чисел приводит к их общему значению.
- Это означает, что сложением двух чисел мы находим их сумму. Добавка используется в повседневной жизни много раз в день.
- Когда мы считаем деньги или что-то еще, мы используем сложение. Мы можем складывать сколько угодно чисел.
- Дополнение имеет специальный символ «+».
- Вот примеры простого сложения одной цифры:
1 + 4 = 5
7 + 2 = 9
5 + 3 = 8
- Когда мы добавляем ноль к числу, ничего не происходит к номеру. Его значение остается неизменным, как показано ниже:
6 + 0 = 6
0 + 3 = 3
Сложение двух цифр
- Сложение одной цифры очень просто и похоже на подсчет.
- После того, как мы научимся складывать однозначные числа, следующим шагом будет научиться складывать двузначные числа.

- Нам просто нужно выполнить простую процедуру.
- У нас может быть два случая. Добавление либо генерирует перенос, либо не генерирует перенос.
- Сначала мы объясним сценарий, в котором нет переноса. Это относительно проще и похоже на сложение одной цифры.
Вариант I (без переноса)
- Предположим, мы добавляем следующие два числа:
24 + 34
- Начнем с расположения этих двух чисел по вертикали, как показано ниже:
24
34
- Мы делаем это так, чтобы разряды единиц и десятков обоих чисел были выровнены.
- В нашем примере для 24, 4 — это единицы, а 2 — десятки. Аналогично для 34, 4 — это единицы, а 3 — десятки.
- Располагая числа по вертикали, мы получаем единицы над единицей и десятки над десятками.
- После расстановки мы проводим линию под этими числами и ставим знак сложения с левой стороны, как показано:
- Затем мы начинаем складывать числа.
 Мы начинаем справа и складываем два числа в одном месте.
Мы начинаем справа и складываем два числа в одном месте.
4 + 4 = 8
- Записываем ответ под чертой в одном месте.
- Затем мы складываем два числа в разряде десятков.
2 + 3 = 5
- Запишем ответ под линией в разряде десятков, как показано ниже:
Итак, 24 + 34 = 58
Случай II (с переносом)
- Предположим, мы хотим сложить следующие числа:
47 + 35
- Мы снова расположим их по вертикали, как в предыдущем примере:
- Начнем с добавления цифр по одному. место.
7 + 5 = 12
- При сложении мы получаем двузначное число 12.
- Это двузначное число имеет 2 в разряде единицы и 1 в разряде десятков.
- Мы пишем 2 под линией в разряде единиц и используем 1 в качестве переноса и помещаем его поверх 4, как показано ниже:
- Теперь мы складываем две цифры в разряде десятков вместе с цифрой переноса.

4 + 3 + 1 = 8
- Записываем ответ через десятки под чертой.
Итак, 47 + 35 = 82
Важность сложения
- Сложение помогает развивать у детей умственные способности и чувство чисел.
- Используется в повседневной жизни, потому что мы ежедневно складываем числа, предметы, деньги и т. Д.
- Он действует как основа для изучения новых концепций.
Пример:
- Добавьте следующие числа:
14 + 22
- Сначала мы сложим обе цифры в одном месте:
4 + 2 = 6
Затем- складываем цифры в разряде десятков:
1 + 2 = 3
Итак, 14 + 22 = 36
Пример:
- Добавляем следующие числа:
34 + 19
- Мы складываем две цифры в одном месте:
4 + 9 = 13
- Мы пишем 3 на единицу под синей линией и используем 1 как цифру переноса.

- Теперь мы складываем две цифры и перенос в разряде десятков:
3 + 1 + 1 = 5
- Мы пишем 5 в разряде десятков под синей линией.
Итак, 34 + 19 = 53
Пример:
- Предположим, Ник купил 10 розовых и 16 фиолетовых воздушных шаров на день рождения Сары. Сколько всего воздушных шаров он купил?
розовых шаров = 10
фиолетовых шаров = 16
всего шаров = розовых шаров + фиолетовых шаров
всего шаров = 10 + 16
- Сложив цифры на единичных местах, мы получим:
0 + 6 = 6
- Сложив цифры в десятичном разряде, мы получим:
1 + 1 = 2
Итак, общее количество баллов = 26
Рабочие таблицы сложения двух цифр 9000 Это фантастический набор, который включает в себя все, что вам нужно знать о сложении двух цифр на 28 подробных страницах. Это готовых к использованию рабочих листов сложения двух цифр, которые идеально подходят для обучения студентов сложению двух цифр. Когда мы научимся складывать однозначные числа, следующим шагом будет научиться складывать двузначные числа. Добавка используется в повседневной жизни много раз в день. Когда мы считаем деньги или что-то еще, мы используем сложение. Мы можем складывать сколько угодно чисел.
Это готовых к использованию рабочих листов сложения двух цифр, которые идеально подходят для обучения студентов сложению двух цифр. Когда мы научимся складывать однозначные числа, следующим шагом будет научиться складывать двузначные числа. Добавка используется в повседневной жизни много раз в день. Когда мы считаем деньги или что-то еще, мы используем сложение. Мы можем складывать сколько угодно чисел.
Полный список включенных рабочих листов
- Рабочий лист 1 (новичок)
- Рабочий лист 2 (новичок)
- Рабочий лист 3 (новичок)
- Рабочий лист 4 (начинающий
- Рабочий лист 5 (промежуточный)
- Рабочий лист )
- Рабочий лист 7 (средний уровень)
- Рабочий лист 8 (средний уровень)
- Рабочий лист 9 (предварительный)
- Рабочий лист 10 (предварительный)
- Рабочий лист 11 (предварительный)
- Рабочий лист 12 (предварительный)
Ссылка / цитируйте это страница
Если вы ссылаетесь на какой-либо контент на этой странице на своем собственном веб-сайте, используйте приведенный ниже код, чтобы указать эту страницу как первоисточник.
Ссылка будет представлена в виде двухзначных рабочих листов: https://kidskonnect.com — KidsKonnect, 6 марта 2019 г.
Использование с любой учебной программой
Эти рабочие листы были специально разработаны для использования с любой международной учебной программой. Вы можете использовать эти рабочие листы как есть или редактировать их с помощью Google Slides, чтобы сделать их более конкретными в соответствии с вашими уровнями способностей учащихся и стандартами учебной программы.
Сколько имеется 2-значных положительных целых чисел, таких что продукт • PrepScholar GRE
Сколько существует 2-значных положительных целых чисел, произведение двух цифр которых составляет 24 доллара?
- Один
- Два
- Четыре
- Шесть
- Восемь
Итак, вы пытались хорошо сдать экзамены и практиковаться в GRE с помощью PowerPrep online. Но тогда у вас возникло несколько вопросов о количественном разделе — в частности, вопрос 9 второго количественного раздела Практического теста 1.Эти вопросы, проверяющие наши знания о методах подсчета , могут быть довольно сложными, но не бойтесь, PrepScholar вас поддержит!
Но тогда у вас возникло несколько вопросов о количественном разделе — в частности, вопрос 9 второго количественного раздела Практического теста 1.Эти вопросы, проверяющие наши знания о методах подсчета , могут быть довольно сложными, но не бойтесь, PrepScholar вас поддержит!
Изучите вопрос
Давайте поищем в проблеме ключи к разгадке того, что она будет тестировать, поскольку это поможет нам задуматься о том, какой тип математических знаний мы будем использовать для решения этого вопроса. Обращайте внимание на любые слова, которые имеют отношение к математике и на что-нибудь особенное в том, как выглядят числа, и отметьте их на нашей бумаге.
Мы хотим, чтобы подсчитали количество двузначных положительных целых чисел, удовлетворяющих определенному критерию, поэтому мы, вероятно, воспользуемся тем, что мы узнали о Методах подсчета в математике. Давайте будем держать в голове то, что мы узнали об этом навыке, когда мы подойдем к этому вопросу.
Что мы знаем?
Давайте внимательно прочитаем вопрос и составим список того, что мы знаем.
- Мы хотим знать количество 2-значных положительных целых чисел, для которых произведение их цифр составляет 24 доллара США долларов США.
Разработка плана
Ну вроде прямой вопрос.Во-первых, давайте составим список положительных факторов в 24 доллара, так как это не очень длинный список. Мы знаем, что множителей числа $ x $ — это числа, которые можно без остатка разделить на $ x $. Или, другими словами, множители числа $ x $ — это числа, и если мы разделим $ x $ на это число, в результате мы получим целое число. Например, $ 2 $ — множитель $ 8 $, поскольку $ 8/2 = 4 $, а $ 4 $ — целое число. Но $ 2 $ НЕ является множителем в $ 9 $, поскольку $ 9/2 = 4,5 $, а $ 4,5 $ НЕ является целым числом. Итак, для положительных факторов в 24 доллара мы знаем, что:
| $ 24 $ | $ = | $$ 1 · 24 $ |
| $ | $ | |
| $ 24 $ | $ = | $$ 2 · 12 $ |
| $ | $ | |
| $ 24 $ | $ = | $$ 3 · 8 $ |
| $ | $ | |
| $ 24 $ | $ = | $$ 4,6 $ |
| $ | $ |
Итак, множители $ 24 $ следующие: $ 1, 2, 3, 4, 6, 8, 12, \ и 24 $. Затем мы ищем двузначных положительных чисел, в которых цифры умножаются на 24 доллара. Таким образом, мы хотим сохранить только пары факторов, которые мы нашли выше, которые являются однозначными. Это оставляет нам 3 доллара в паре с 8 долларами, а также 4 доллара в паре с 6 долларами. Давайте выясним, как объединить их, чтобы получить полный список двузначных положительных целых чисел, удовлетворяющих ограничению в этом вопросе.
Затем мы ищем двузначных положительных чисел, в которых цифры умножаются на 24 доллара. Таким образом, мы хотим сохранить только пары факторов, которые мы нашли выше, которые являются однозначными. Это оставляет нам 3 доллара в паре с 8 долларами, а также 4 доллара в паре с 6 долларами. Давайте выясним, как объединить их, чтобы получить полный список двузначных положительных целых чисел, удовлетворяющих ограничению в этом вопросе.
Решить вопрос
Одна уловка, которую нам нужно понять, заключается в том, что для любого двузначного целого числа, которое мы получаем здесь, мы можем изменить порядок целых чисел.В конце концов,
, если 3 · 8 = 24 $, то уж точно 8 · 3 = 24 $ тоже. Итак, для двух пар целых чисел ($ 3 $ и $ 8 $, а также $ 4 $ и $ 6 $) двузначные положительные целые числа, произведение их цифр которых составляет $ 24 $, равны: $ 38, 83, 46, \ и 64 $. Поскольку у нас есть , четыре, различных двузначных целых чисел, правильный ответ — C, четыре .
Что мы узнали
Всегда нужно быть осторожным с вопросами Методы подсчета , чтобы не упустить ни одной возможности.Похоже, что в этом вопросе нам поставили ловушку, когда мы забыли поменять местами порядок целых чисел. Легко понять, как кто-то может получить 38 долларов и 46 долларов в качестве двузначных целых чисел и по ошибке выбрать «Два» в качестве правильного ответа. Будьте осторожны и активно ищите все возможности — это отличные советы, как избежать такой ошибки.
Хотите более квалифицированную подготовку к GRE? Подпишитесь на пятидневную бесплатную пробную версию нашей онлайн-программы PrepScholar GRE, чтобы получить доступ к своему индивидуальному плану обучения с 90 интерактивными уроками и более 1600 вопросами GRE.
Есть вопросы? Оставьте комментарий или отправьте нам письмо по адресу [электронная почта защищена].
Добавление однозначных и двузначных чисел без перегруппировки — математика 2-го класса
Научитесь складывать одно- и двухзначные числа без перегруппировки
Итак, вы сложили однозначные числа. ✅
✅
3 + 4 = 7
9 + 2 = 11
Вы также сложили двузначные числа. ✅
10 + 30 = 40
60 + 20 = 80
А теперь, как сложить однозначные и двузначные числа? 🤔
Добавление 1-значных и 2-значных чисел
Давайте узнаем на примере:
31 + 7 = ?
Сначала запишите уравнение в форме столбца .
😃 Совет: Поместите двузначное число вверху.
Затем введите однозначное число внизу.
Нам нужно правильно выровнять цифр , чтобы мы могли правильно сложить!
👆 В этом примере цифры в разряде «Единицы» должны быть выровнены правильно.
Теперь мы можем добавить!
Сначала мы добавляем Единицы.
У нас 8! Пишем 8 в позиции Единицы.
Так как в столбце Десятки всего одно число, мы просто приводим его.
Наш окончательный ответ — 38. Отличная работа!
Давайте попробуем другой пример.
90 + 3 = ?
Давайте сначала сложим числа:
Мы правильно выстроили номера. Теперь мы можем добавить!
У нас 93. Отлично сделано! 💪
Смотри и учись
Первый пример в этом видео поможет вам повторить то, что вы только что узнали.
Теперь вы можете практиковать то, что вы только что узнали.
Сравнение двух- и трехзначных чисел
Сравнение чисел
Сравнение двузначных и трехзначных чисел аналогично сравнению однозначных чисел.По-прежнему действуют те же правила; например, 8 всегда будет больше 5.
При сравнении двузначных и трехзначных чисел вы будете сравнивать цифры, принадлежащие к одним и тем же разрядам. Вот несколько шагов, которые помогут вам в этом.
1.) Начните слева от числа и двигайтесь вправо.
2.) Сравните цифру в разряде сотен в первом числе с цифрой в разряде сотен во втором числе.
3.) Сравните разряд десятков в первом числе с разрядами десятков во втором числе.
4.) Сравните цифру в разряде единиц вашего первого числа с цифрой в разряде единиц вашего второго числа.
Например, давайте попробуем сравнить числа 35 и 85. Начните с самых первых цифр слева: 3 и 8. Какая из них больше? 8 больше. Поскольку вы уже можете сказать, какое число больше, можно остановиться. Вы уже знаете, что 85 больше 35.
А что, если бы вы сравнивали числа 347 и 349? Опять же, вы начинаете с самых левых цифр.В данном случае это цифры в разряде сотен: 3 и 3. Они одинаковы, поэтому вы не можете сказать, какое число больше на данный момент.
Итак, вы переходите к следующим цифрам или цифрам разряда десятков: 4 и 4, которые снова совпадают. Итак, вам нужно проверить цифры в разрядах единиц: 7 и 9. Что больше? 9 больше, что означает, что число 349 больше, чем число 347.
Если два номера имеют разное количество цифр, вы можете автоматически выбрать номер с наибольшим количеством цифр в качестве большего числа.Итак, из двух чисел 23 и 121 число 121 автоматически больше только потому, что оно имеет больше цифр, чем другое число, или 23.







 Делим
на 32. Вот
умножение
таблица из 32:
Делим
на 32. Вот
умножение
таблица из 32:
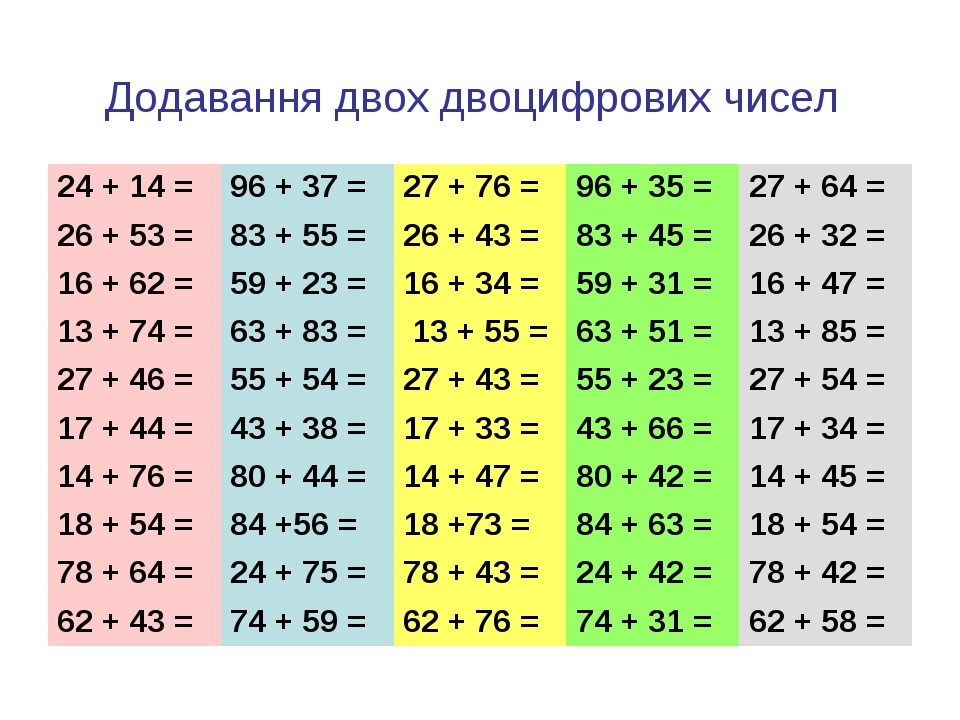 Обратите внимание, есть остаток.
Обратите внимание, есть остаток.



 Сложение — одна из четырех основных операций, которым обучают в математике.
Сложение — одна из четырех основных операций, которым обучают в математике.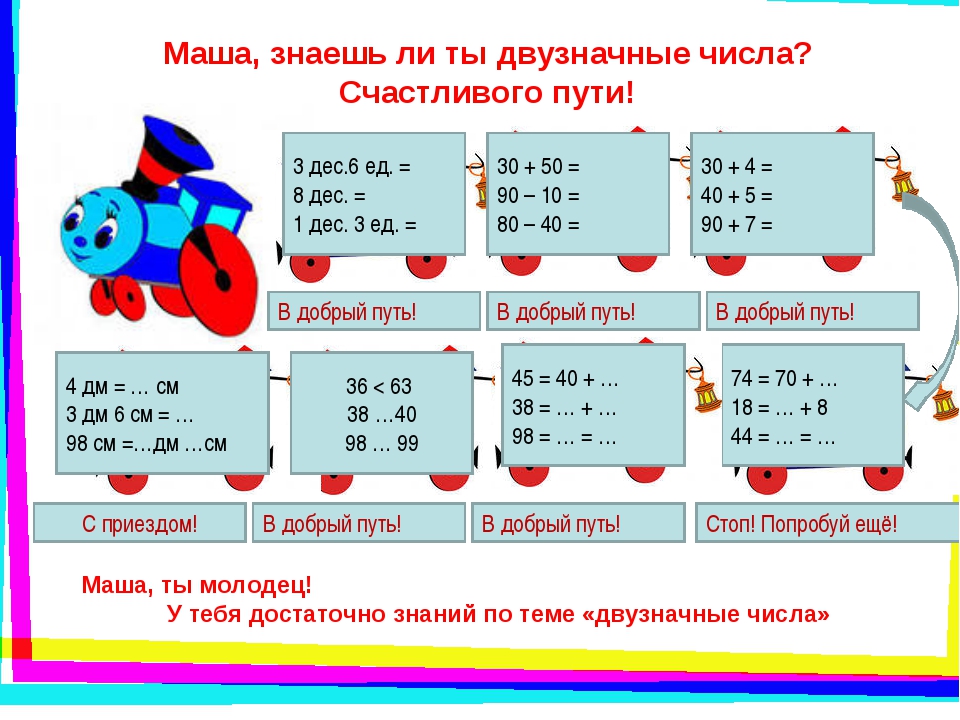
 Мы начинаем справа и складываем два числа в одном месте.
Мы начинаем справа и складываем два числа в одном месте.
