Примеры на деление и умножение в столбик 4 класс: 4 класс. Примеры на умножение многозначных чисел в столбик. Примеры с ответами. Скачать pdf или jpg.

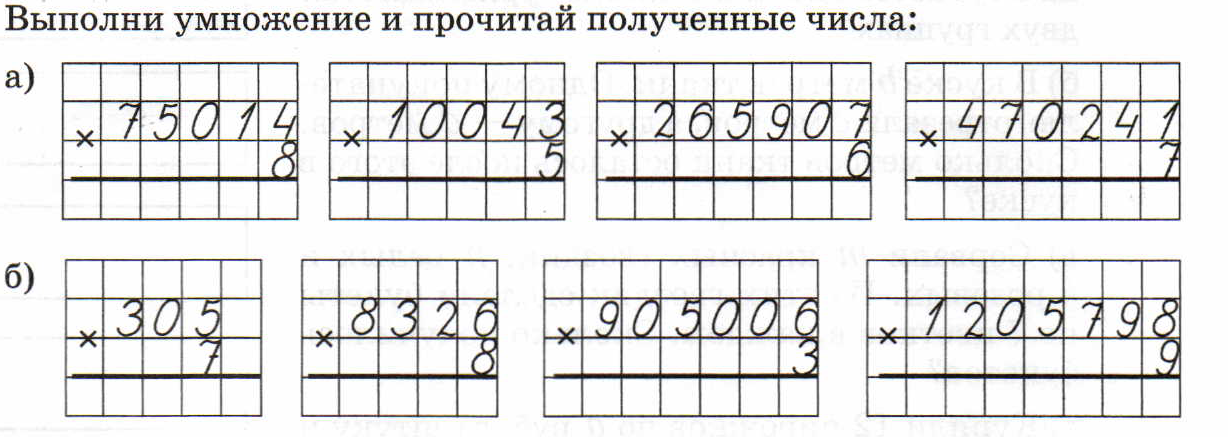
Умножение столбиком многозначных натуральных чисел

Рассмотрим в этой статье как умножать столбиком различные числа — двузначные, трехзначные и другие — большие и маленькие. Если умножать большие числа, то умножать их столбиком, конечно, быстрее и проще всего. Маленькие числа можно умножить и в уме. Рассмотрим умножение столбиком на примере. Умножать в столбик умеет уже и 3, и 4 класс. Начинают вводить такой способ умножения уже в 3 классе, и закрепляют в 4 классе. То есть четвероклассник должен уметь это делать легко и быстро, а для этого надо хорошо знать таблицу умножения. А в 5 классе это уже отработанный навык. В этой статье мы дадим вам алгоритм умножения больших (начиная с двузначных) натуральных чисел и объясним как научить ребенка умножению, как правильно объяснить как считать в столбик.

В статье вы рассмотрите подробное решение примеров столбиком на умножение, повторите таблицу умножения и вспомните как решается любой пример на умножение больших чисел. Мы приведем примеры умножения в столбик натуральных чисел.

Содержание

Умножение двузначных чисел столбиком

Умножим два числа: 25 и 44. Когда мы записываем числа столбиком, важно записать их друг под другом так, чтобы десятки были под десятками, единицы под единицами. Вот так считать в столбик:

Правильная запись умножения столбиком

Теперь начинаем последовательно умножать сначала число 25 на первую четверку (число единиц), получим:

Умножение столбиком двузначных чисел 1 часть — умножили число 25 на число единиц (на 4) — получили 100.

Обратите внимание — число 100 записывается в процессе умножения справа налево — то есть, идем от единиц к десяткам, умножаем сначала 5 на 4, получаем 20, записываем 0 под числом единиц, а число 2 держим в уме. Теперь умножаем 2 на 4, получаем 8, но так как у нас в уме еще 2, то складываем 2 и 8, получаем 10, записываем 10, причем так как мы сейчас умножаем число десятков на число единиц второго числа — на 4, то и число 10 записываем, начиная с числа десятков — 0 под десятками и 1 слева. В итоге получаем 100.

Мы умножили число 25 на число единиц 4 второго числа 44. Теперь сделаем умножение числа 25 на число десятков 4 числа 44. Результат умножения столбиком начнем писать справа налево, то есть начнем писать его под числом десятков, получим:

Умножение в столбик двухзначных чисел

Итак, мы выполнили умножение числа 25 сначала на число единиц — 4 — второго числа 44, а потом на число десятков  — 4 — второго числа 44. Следующим шагом будет сложение этих последовательных результатов умножения. Получим:

Умножение в столбик двузначных чисел результат

Обратите внимание — мы складываем не 100+100, а последовательно числа по разрядам, то есть сначала числа, стоящие на местах единиц (у нас тут один ноль), потом числа стоящие на местах десятков (0+0), числа, стоящие на позиции сотен (1+0) и числа, стоящие на месте тысяч (1). Если число только одно, то мы его просто сносим вниз, мысленно складывая с нулем.

Примеры умножения двузначных чисел

Чтобы лучше разобраться в умножении двузначных чисел столбиком, рассмотрим следующие примеры решения столбиком. Вы сможете рассмотрев каждый пример подробно научиться решать такие примеры:

Пример 1

Умножим число 15 на число 37. Пошаговый алгоритм умножения столбиком:

Умножение двузначных чисел в столбик

Пример 2

Умножим число 23 на число 79. Пошаговый алгоритм умножения столбиком:

Умножение столбиком 23 и 79

Умножение столбиком трехзначных чисел

Для того, чтобы умножать столбиком трехзначные числа — все действия выполняем также, алгоритм не меняется. Только у нас появляется умножение первого (верхнего) числа на число сотен второго (нижнего) числа.

Давайте рассмотрим пример умножения столбиком трёхзначного числа на трехзначное число. Пусть нам нужно умножить 345 на 726. Вот что получится — пошаговый алгоритм:

Умножение столбиком трехзначных чисел

Таким образом, общий принцип ясен и можно перемножать в столбик числа с любым количеством знаков.

Умножение столбиком многозначных натуральных чисел

 

Правильная поразрядная запись умножения столбиком

Теперь рассмотрим, как надо умножать круглые числа. Тут есть небольшая хитрость для удобства умножения.

Умножение столбиком круглых чисел

Когда мы умножаем в уме круглые числа, мы не обращаем при умножении сначала внимания на ноль, например, нам нужно умножить 50 на 30. Мы в уме перемножаем 5 на 3 и просто приписываем два нуля, памятуя о том, что 10 на 10 дают 100.

Значит, если мы будем умножать, скажем 50 на 35, то эти числа в столбик нам удобнее записать не так:

Запись умножения в столбик круглого числа 1

А так:

Умножение в столбик круглого числа

Тогда нам нужно будет просто умножить число 35 на 5 и приписать 0. Здесь мы использовали следующее свойство умножения: от перемены мест множителей произведение не меняется. Поэтому вместо верхнего числа 50, мы записали нижнее число 35 — поменяли их местами.

Итак, мы рассмотрели как умножать в столбик двузначные, трехзначные и любые многозначные натуральные числа, рассмотрели алгоритм умножения в столбик, привели примеры такого умножения.

Не только в столбик: как объяснить ребенку деление

Что должен освоить ребенок сначала — умножение или деление

Некоторые родители считают, что прежде чем начать обучение делению, ребенок должен наизусть знать таблицу умножения.

Как объясняет Галина Корчагина, учитель высшей категории начальных классов московской школы №2005, сначала ребенку действительно лучше раскрыть смысл умножения. Но для этого не нужно зубрить таблицу, главное — понять принцип этого действия. Например, показать на фруктах: две вазы с двумя яблоками в каждой — это четыре яблока (то есть результат умножения 2х2).

«Умножение и деление с начала их изучения целесообразно рассматривать раздельно, поскольку главным при этом является раскрытие не взаимосвязи между ними, а конкретного смысла этих действий», — подчеркивает эксперт.

Как объяснить ребенку деление

Ребенок должен понимать, что такое делимое и делитель, а также как называется результат деления.

Тест: назовите предмет из советского детства

Многие советские школьники удивились бы тем вещам, которые есть у современных детей. В свою очередь…

24 мая 13:33

Галина Корчагина разъясняет: «Деление — это арифметическое действие, с помощью которого можно узнать, сколько раз одно число содержится в другом. Делимое — это число, которое делят. Делитель — это число, на которое делят. Частное — это результат деления».

Лучше всего объяснять ребенку деление в игровой форме, например, с помощью сладостей.

«Малыши вовлекаются в процесс деления с самого раннего возраста, например, когда угощают конфетами друзей, делятся игрушками в песочнице. Поэтому задача родителей заключается в том, чтобы обобщить этот детский опыт для освоения азов арифметики, дать понимание принципа деления — то есть разделения предметов на равные доли. При этом базовыми знаниями, необходимыми для освоения деления в дошкольном возрасте, является понимание, что такое целое, больше и меньше. Если с этими понятиями ребенок знаком, то можно поэтапно объяснять деление в игровой форме», — сообщает педагог.

Эксперт подчеркивает, что для начала нужно показать, что такое деление, с помощью наглядности. В этом поможет игра «Тебе и мне поровну».

1. Малыш получает 6 конфет.

2. Взрослый просит поделить конфеты на двоих так, чтобы у каждого было одинаковое количество.

3. Ребенок раскладывает конфеты по одной, пересчитывая их в обеих кучках.

После того, как конфеты поделены, юный математик еще раз пересчитывает их в каждой кучке, а затем считает, сколько сладостей всего.

В первую очередь ребенок должен освоить деление без остатка, поэтому родителям важно соблюдать определенное условие: делимое и делитель нужно выбирать с определенными пропорциями. Например, шесть конфет (делимое) можно поделить поровну между двумя и тремя людьми (делитель): по три или две конфеты соответственно. А вот проделать то же самое с пятью уже не получится. Так у ребенка формируется представление о том, что такое поровну.

close

100%

Как научить ребенка делить в игровой форме

Галина Корчагина рекомендует вместе с ребенком потренироваться вычислительным навыкам с помощью интересного упражнения «Угостим гостью».

Кукла говорит: «Здравствуйте! Меня зовут Маша. Ко мне в гости пришла подруга Катя, и я хотела ее угостить яблоком. Но у меня только одно яблоко.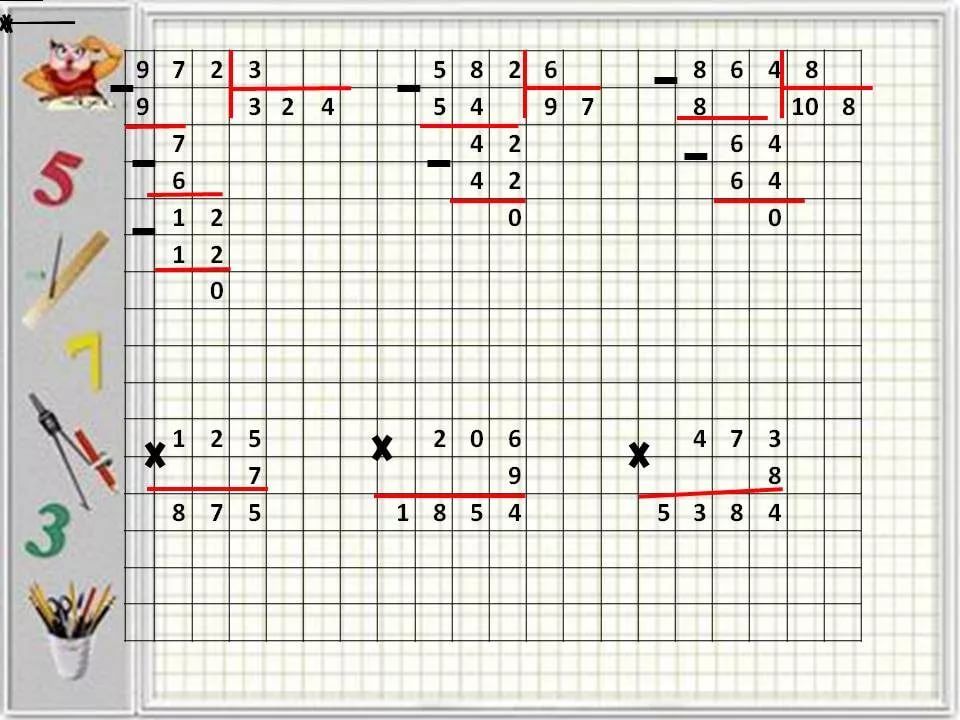 Что делать? Помогите мне, пожалуйста».

Итак, переходим к делению. Берем с ребенком яблоко, намечаем середину и разрезаем пополам. На сколько равных частей мы разделили яблоко? Как можно назвать каждую часть яблока? Пусть ребенок попробует сам ответить на эти вопросы.

Еще одно игровое упражнение от педагога Корчагиной — «Раздели торт на части». Маша пригласила на день рождения медведя и двух волков. Пусть сын или дочь поможет ей поделить торт между друзьями — для этого нужно научиться делить круг на четыре равные части. Ребенок должен ответить на следующие вопросы.

Как отучить ребенка сосать палец: советы педиатра и стоматолога

Большинство детей имеют привычку сосать пальцы – это связано с сосательным рефлексом и стремлением…

05 мая 11:00

На сколько гостей нужно поделить торт? Ответ: на четыре. Какими должны быть части? Ответ: равными, одинаковыми. На сколько частей мы уже умеем делить круг (на примере яблока)? Ответ: на два. Сколько частей получилось? Ответ: два. Как называется каждая часть? Ответ: половина или одна вторая. Что больше: целый круг или его часть? Ответ: целый круг. Что меньше: часть круга или целый круг? Ответ: часть круга. Как получить четыре равные части? Ответ: надо каждую половину разрезать еще раз пополам. Сколько частей получилось? Ответ: четыре. Как можно назвать каждую часть? Ответ: одна четвертая.

close

100%

Как правильно научить ребенка делению в столбик

Анастасия Козлова, преподаватель математики и геометрии онлайн-школы «Синергия», предупреждает: приступать к делению в столбик нужно в том случае, если ребенок уже усвоил таблицу умножения.
Алгоритм деления в столбик лучше разбирать на простом примере, поэтому рассмотрим деление на однозначное число.

Решим пример: 288:4. Эксперт Козлова объясняет принцип деления по пунктам.

1. Сначала нужно определить неполное делимое. Это такая часть числа 288, которая сможет поделиться на 4. В нашем случае это 28. 28 делим на 4. Сколько целых получится? Записываем 7 в частное.

2. Затем нужно умножить полученный результат (то есть 7) на делитель и вычесть его из неполного делимого. 7 x 4=28. Значит, из 28 вычитаем 28. Получаем 0.

3. После этого сносим следующую цифру 8. Повторяем действия: 8 делим на 4. Записываем двойку в частное к семерке, и получаем результат деления: 72.

Педагог уточняет: «При делении ребенок обязательно должен комментировать все свои действия вслух. Так он быстрее усвоит навык».

Деление двузначных чисел на однозначные

Учитель Галина Корчагина рассказала об интересном способе деления, для которого также необходимо знать таблицу умножения.

Алгоритм деления:

1. Заменяем число суммой слагаемых.

2. Делим каждое слагаемое на число.

3. Складываем результаты.

Решим пример: 75:5.

Нужно представить число 75 в виде суммы слагаемых, каждое из которых делится на 5.

Вариант 1. 75:5 = (25+50):5 = 25:5+50:5 = 5+10 = 15

Вариант 2. 75:5 = (45+30):5 = 45:5+30:5 = 9+6 = 15

Умножение и деление с использованием таблицы с примерами

Ключевые понятия

1. Использование таблицы умножения для деления.
2. Связь между умножением и делением
3. Уравнение с недостающим множителем с использованием таблицы умножения
4. Счетные таблицы
5. Семейство фактов для деления

Связь между умножением и делением:

• вместе, чтобы сформировать новую сумму.
• Умножение – это процесс многократного сложения и объединения общего количества        элементов, составляющих группы одинакового размера.
  Делимое = Делитель x Частное + Остаток
  Деление обратно умножению
  5 × 3 = 15
  15 ÷ 3 = 5
  15 ÷ 5 = 3
  Делимое ÷ Делитель = Частное

2 Если мы Уравнение: 9003 хотите узнать об отсутствующем факторе, сначала нам нужно понять определения фактора и продукта.

Продукт:- Ответ, который мы получаем, когда мы умножаем два или более множителя.

Фактор:-    Число, умноженное на другое число, чтобы получить продукт.

Если множитель, умноженный на множитель, равен произведению, а деление противоположно умножению, то мы можем сказать:

Например:

18 ÷ 3 = ?

Решение:

Подумайте, 3 × ? = 18

Три раза какое число равно 18?

3 × 6 = 18

Итак, 18 ÷ 3 = 6

Использование таблицы умножения для деления

Напишите уравнение с отсутствующими множителями, а затем используйте таблицу умножения, чтобы найти 15 ÷ 3.

Решение:

Шаг 1:   Здесь один множитель равен 3, найдите 3 в первый столбец этой таблицы умножения.

Шаг 2:   И продукт равен 15. Следуйте за строкой, в которой находится 3, пока не дойдете до 15.

Шаг 3:   Посмотрите прямо вверх в этот столбец таблицы. Число в верхней части столбца равно 5. Таким образом, недостающий множитель равен 5,9.0035

               3 × 5 = 15

                15 ÷ 3 = 5

Пример:

Напишите уравнение с отсутствующими множителями и используйте таблицу умножения для решения задачи на деление.

12 ÷ 3 = ?

Решение:

Здесь один множитель равен 3

произведение равно 12

Найдем 12 в строке 3

Итак, 12 точка пересечения 3 и 4 3

3 4 034 Другой множитель равен 3 4 034 × 4 = 12              12 ÷ 3 = 4

Отсутствующие числа в таблице

Мы можем найти недостающие множители с помощью умножения или деления

2 × 8 = 16

2 × 5 = 10

2 × 4 = 8

9 × 5 = 35 900 45 900 45 900 4 × 8 = 32

4 × 4 = 16

7 × 8 = 56

7 × 5 = 35

7 × 4 = 28

Используйте таблицу умножения, чтобы помочь.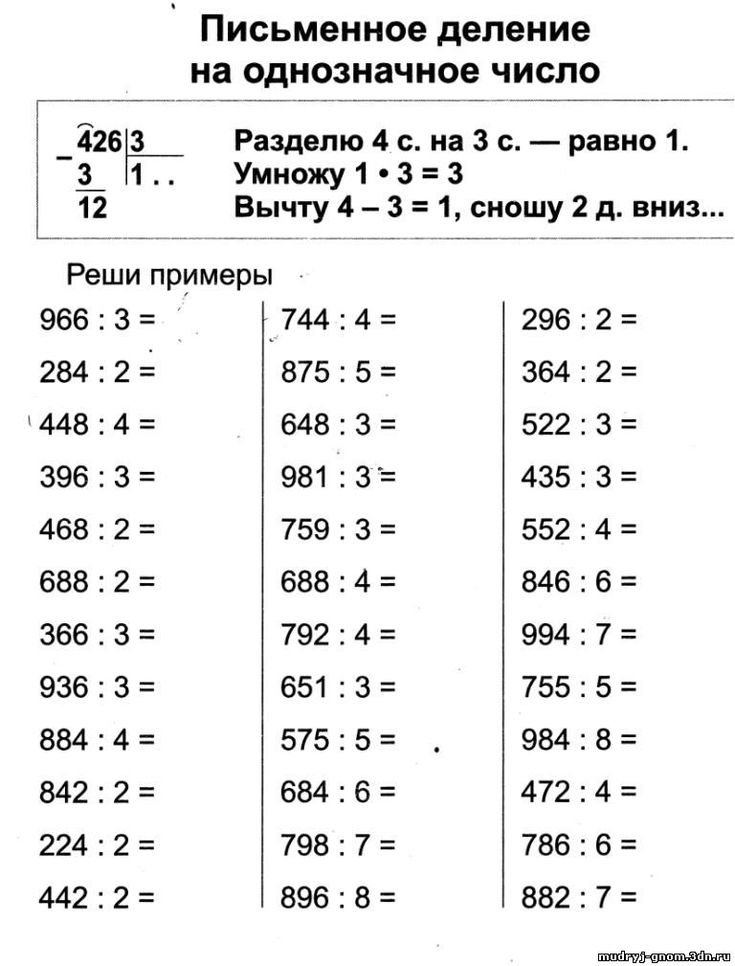

24 ÷ 6 = ____

24 = 6 × ____

Решение:

Здесь один множитель равен 6

произведение равно 24

Используя таблицу, мы можем найти 6 в столбце таблицы.

Двигаемся вперед, пока не получим 24.

Смотрим в эту строку, мы находим, что другой множитель равен 4.

24 ÷ 6 = 4

6 × 4 = 24

Пример:

5 Найдите недостающее

фактор и продукты.

Решение:

2 × 8 = 16

2 × 5 = 10

2 × 7 = 14

5 × 8 = 40

5 × 7 = 35

6 × 5 = 30

9 × 8 = 72

9 × 7 = 63

Счетная таблица

Счетная таблица — это простой способ записи и подсчета частот. Каждое вхождение показано меткой подсчета.

Как рисовать метки учета:

•  Появление каждой информации отмечено вертикальной линией «|»
•  Каждый пятый счет записывается путем зачеркивания предыдущих четырех вертикальных линий как «||||»
•   Это упрощает подсчет результатов.

Пример:

• Сосчитайте предметы, указанные ниже, и подготовьте таблицу.

Давайте создадим итоговую диаграмму для вышеуказанных данных.

Это выглядит намного проще для чтения.

Семейство фактов

Факторы – перемножаемые числа.

                   3 × 7 = 21

Обратная операция  – Противоположная операция, отменяющая другую.

                                      3 × 7 = 21                21 ÷ 7 = 3

Пример: Каковы четыре 4 члена семейства фактов 8 из 4?

4 × 8 = 32

8 × 4 = 32

32 ÷ 8 = 4

32 ÷ 4 = 8

Что мы узнали:

• — это обратное деление.
•  Дивиденд ÷ Делитель = Частное
•  Если множитель, умноженный на множитель, равен произведению, а деление является противоположностью умножения.
•  Произведение / множитель = Отсутствующий множитель
•  Мы можем найти недостающие множители с помощью умножения или деления.
•  Счетная таблица – это простой способ записи и подсчета частот.
•  Каждое вхождение отмечено меткой.
•  Противоположная операция, отменяющая другую, называется обратной операцией.

Умножение и деление в 4-м классе (8–9 лет)

 

В 4-м классе ваш ребенок научится запоминать факты умножения и деления для таблиц умножения до 12 × 12. Они будут использовать разрядность, числовые факты , факторные пары, коммутативность и обратные операции в мысленных вычислениях.

В июне ваш ребенок примет участие в проверке таблицы умножения. Взгляните на нашу контрольную страницу таблицы умножения для 4 класса, чтобы узнать об оценивании и узнать, как вы можете помочь дома.

Ключевое слово в этом разделе — метод площади/сетки.

Чему научится ваш ребенок

Взгляните на требования Национальной учебной программы к умножению и делению в 4-м классе (возраст 8–9 лет):

Знать таблицу умножения до 12 × 12

Ожидается, что ваш ребенок будет знать все свои таблицы умножения до 12 × 12.  Они будут использовать эти знания, чтобы решать задачи на умножение и вычислять соответствующие факты деления (например, если 7 × 8 = 56 , тогда 56 ÷ 7 = 8 ).

Использование фактов о разрядах и числах для решения задач в уме

Ваш ребенок должен быть в состоянии использовать факты умножения для решения вычислений с делением, и ожидается, что он будет использовать известные факты для мысленных вычислений с числами до трех цифр. Например, 600 ÷ 3 = 200 можно вычислить, зная, что 2 × 3 = 6 .

Они также научатся умножать три числа (например, 3 × 4 × 5 = 60 ).

Использование пар факторов и коммутативности в вычислениях в уме

Ваш ребенок выучит термин «пары факторов». Факторная пара — это пара чисел, которые перемножаются, чтобы получить определенное число. Например, 3 и 2 — это пара множителей 6. Ваш ребенок будет использовать эти знания для мысленного решения задач.

Они также будут использовать свои знания коммутативности, чтобы решать задачи на умножение в уме.

Умножение двузначных и трехзначных чисел на однозначные числа

Ваш ребенок будет продолжать практиковать формальные письменные методы умножения и деления. Они будут использовать эти формальные методы для решения вычислений, включающих двузначные и трехзначные числа, умноженные на однозначные числа (например, 73 × 6 и 637 × 8).

Они будут практиковать формальный письменный метод краткого умножения и краткого деления с ответами, представляющими собой целые числа.

Решайте многошаговые задачи, используя правила арифметики

Ожидается, что ваш ребенок будет решать двухшаговые задачи в контексте. Это означает решение текстовых задач, которые включают в себя несколько различных операций и постоянно увеличивающиеся числа.

Ваш ребенок сможет написать утверждения о «равенстве выражений». Звучит сложно, но это просто означает, что они могут увидеть, как один способ отображения расчета имеет ту же ценность, что и другой. Например:

Используя распределительный закон: 39 × 7 = (30 × 7) + (9 × 7).

Используя ассоциативный закон: (2 × 3) × 4 = 2 × (3 × 4).

Ожидается, что ваш ребенок объединит свои знания о числовых фактах и ​​«правилах арифметики», таких как БОДМАС и коммутативность , для решения умственных и письменных вычислений (например, 2 × 6 × 5 = 10 × 6 = 60).

Как помочь дома

Существует множество простых и быстрых способов помочь ребенку понять умножение и деление. Вот лишь несколько идей, которые помогут вашему ребенку в обучении:

 

1. Найдите факты умножения в реальной жизни

Вы можете использовать повседневные ситуации, чтобы попрактиковаться в умножении фактов. Например, если вы находитесь в супермаркете и покупаете три упаковки мультиупаковки чипсов, по 6 штук в каждой, вы можете спросить своего ребенка, сколько всего у вас будет упаковок чипсов. Обсудите, какой расчет они использовали.

Если ваш ребенок сразу знает ответ, спросите его, какие еще числовые факты он знает, знает ли он, что 3 × 6 = 18 . Например, они могут знать, что 18 ÷ 6 = 3 или что 18 ÷ 3 = 6 .

 

2. Используйте разные способы умножения чисел

Поощряйте ребенка использовать множество способов умножения чисел, используя его понимание:

• • Удвоение и деление пополам. Например, если мы знаем 2 × 6 = 12 , тогда мы также знаем
    4 × 6 = 24 , 8 × 6 = 48 и так далее.
  • Коммутативность (т. е. знание того, что мы можем умножать суммы в любом порядке и получать один и тот же ответ). Например, если мы знаем 2 × 6 = 12 , то мы также знаем 6 × 2 = 12 .
  • Обратные операции. Например, если мы знаем 2 × 6 = 12 , то мы также знаем 12 ÷ 2 = 6 и 12 ÷ 6 = 2 .
  • Разрядное значение. Например, если мы знаем 20 × 6 = 120 , тогда мы также знаем 200 × 6 = 1200 , 2 × 0·6 = 1·2 и так далее.

Предложите ребенку составить ментальную карту всех известных им фактов, связанных с фактом умножения 2 × 6 = 12. Он может быть удивлен тем, как много он может получить из одного этого вычисления!

Метод площади/сетки

В школе вашего ребенка научат ряду методов решения задач на умножение, таких как использование физических ресурсов, рисунков и диаграмм, таких как метод площади/сетки. Возьмем пример 65×74:

В методе сетки ваш ребенок будет разделять (разбивать) каждое число, которое нужно умножить. В этом примере они разбивают каждое число на десятки и единицы — 65 разбивается на 60 и 5, а 74 — на 70 и 4. Затем они находят произведение каждой пары чисел перед сложением всех значений вместе:

70 × 60 = 4200

70 × 5 = 350

4 × 60 = 240

4 × 5 = 20

 

4200 + 350 + 240 + 20 = 4810

Ожидается, что ваш ребенок также будет использовать формальные письменные методы, такие как короткое умножение.