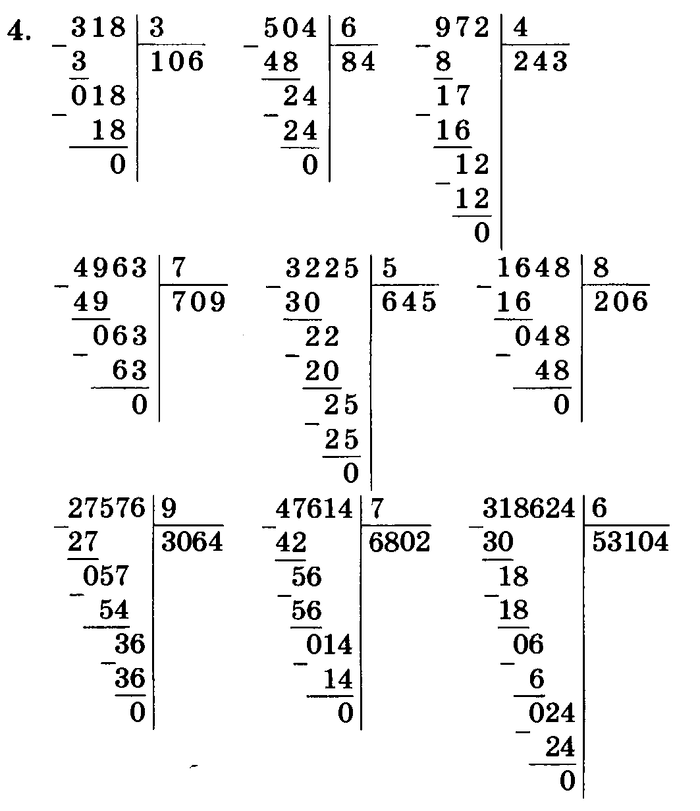
Примеры на умножение. Математика 4 класс.
Примеры на умножение. Математика 4 класс. Задачи по математике 4 класс
MAT-ZADACHI.RU
Математика 4 класс
- Математические диктанты
- Тесты
- Нестандартные задачи
- Логические задачи
- Задачи с ответами
- Примеры
Контрольные работы
- Числа, которые больше 1000. Нумерация
- Итоговая контрольная работа за 1 четверть
- 1 четверть
- 2 четверть
- Итоговая контрольная работа 1
- 3 четверть
- Контрольная работа 1
- 4 четверть
- Деление на двузначное число
- Итоговые контрольные работы за курс начальной школы
- Контрольная работа 1
Математика 4 класс ->> Примеры
Чтобы увидеть решение, наведите на пример курсор мыши.
| 60 * 91 = 5460 | 108 * 63 = 6804 | 31 * 583 = 18073 | 590 * 30 = 17700 | 300 * 47 = 14100 |
| 110 * 49 = 5390 | 92 * 692 = 63664 | 250 * 5 = 1250 | 700 * 3 =2100 | 73 * 80 = 5840 |
| 988 * 99 = 97812 | 930 * 6 = 5580 | 81 * 415 = 33615 | 260 * 40 = 10400 | 690 * 30 = 20700 |
| 4800 * 80 = 384000 | 93 * 40 = 3720 | 0 * 937 = 0 | 150 * 80 = 12000 | 50 * 19 = 950 |
| 98 * 50 = 4900 | 2730 * 7 = 19110 | 14 * 616 = 8624 | 890 * 30 = 26700 | 894 * 70 = 62580 |
| 40 * 277 = 11080 | 2320 * 8 = 18560 | 8960 * 8 = 71680 | 82 * 20 = 1640 | 32 * 50 = 1600 |
| 89 * 80 = 7120 | 87 * 550 = 47850 | 350 * 30 = 10500 | 264 * 29 = 7656 | 4200 * 20 = 84000 |
| 350 * 6 = 2100 | 77 * 60 = 4620 | 130 * 2 = 260 | 710 * 2 = 1420 | 640 * 70 = 44800 |
| 780 * 8 = 6240 | 4300 * 5 = 21500 | 43 * 371 = 15953 | 360 * 5 = 1800 | 46 * 213 = 9798 |
| 950 * 2 = 1900 | 3 * 430 = 1290 | 9600 * 96 = 921600 | 44 * 44 = 1936 | 10 * 12 = 120 |
| 630 * 50 = 31500 | 282 * 73 = 20586 | 660 * 7 = 4620 | 330 * 7 = 2310 | 8500 * 80 = 680000 |
| 40 * 729 = 29160 | 35 * 56 = 1960 | 65 * 369 = 23985 | 32 * 40 = 1280 | 10 * 555 = 5550 |
| 22 * 90 = 1980 | 790 * 50 = 39500 | 40 * 60 = 2400 | 480 * 3 = 1440 | 71 * 30 = 2130 |
| 13 * 20 = 260 | 5100 * 80 = 408000 | 2800 * 50 = 140000 | 8300 * 90 = 747000 | 800 * 8 = 6400 |
| 740 * 9 = 6660 | 15 * 60 = 900 | 390 * 40 = 15600 | 570 * 60 = 34200 | 400 * 80 = 32000 |
| 80 * 14 = 1120 | 480 * 3 = 1440 | 260 * 60 = 15600 | 40 * 210 = 8400 | 46 * 50 = 2300 |
| 790 * 40 = 31600 | 910 * 4 = 3640 | 2200 * 70 = 154000 | 1700 * 50 = 85000 | 40 * 80 = 3200 |
| 42 * 80 = 3360 | 5000 * 30 = 150000 | 47 * 70 = 3290 | 8900 * 70 = 623000 | 580 * 80 = 46400 |
| 6300 * 40 = 252000 | 34 * 90 = 3060 | 9600 * 90 = 864000 | 4000 * 30 = 120000 | 90 * 832 = 74880 |
| 380 * 4 = 1520 | 310 * 8 = 2480 | 56 * 60 = 3360 | 337 * 0 = 0 | 87 * 810 = 70470 |
| 853 * 28 = 23884 | 140 * 3 = 420 | 590 * 60 = 35400 | 37 * 587 = 21719 | 1400 * 60 = 84000 |
| 17 * 184 = 3128 | 300 * 6 = 1800 | 290 * 2 = 580 | 929 * 41 = 38089 | 20 * 90 = 1800 |
| 980 * 60 = 58800 | 100 * 320 = 32000 | 100 * 64 = 6400 | 680 * 20 = 13600 | 42 * 50 = 2100 |
| 25 * 60 = 1500 | 8300 * 60 = 498000 | 550 * 7 = 3850 | 749 * 67 = 50183 | 9 * 20 = 11805 |
| 320 * 5 = 1600 | 140 * 40 = 5600 | 783 * 50 = 39150 | 50 * 500 = 25000 | 859 * 19 = 16321 |
| О * 870 = 0 | 290 * 2 = 580 | 700 * 50 = 35000 | 14 * 576 = 8064 | 68 * 30 = 2040 |
| 428 * 73 = 31244 | 120 * 6 = 720 | 640 * 70 = 44800 | 352 * 40 = 14080 | 11 * 531 = 5841 |
| 300 х 30 = 30030 | 802 * 7 = 5614 | 61 * 90 = 5490 | 750 * 9 = 6750 | 20 * 90 = 1800 |
| 980 * 80 = 78400 | 97 * 20 = 1940 | 500 * 8 = 4000 | 87 * 80 = 6960 | 60 * 67 = 4020 |
| 920 * 70 = 64400 | 7300 * 40 = 292000 | 86 * 70 = 6020 | 770 * 2 = 1540 | 500 * 70 = 35000 |
| ____________________ | ____________________ | ____________________ | ____________________ | ____________________ |
Простые задачи
- Простые задачи на движение
Составные задачи
- Задачи на встречное движение
- Задачи на движение в одном направлении
- Задачи на противоположное движение
- Задачи на нахождение неизвестного по двум разностям
- Задачи на нахождение числа по доле и доли по числу
- Задачи на нахождение площади
- Задачи на сложение и вычитание многозначных чисел
- Задачи на умножение и деление многозначных чисел
- Задачи на приведение к единице и пропорциональное деление
- Задачи на определение цены, количества, стоимости
§ Умножение в столбик.
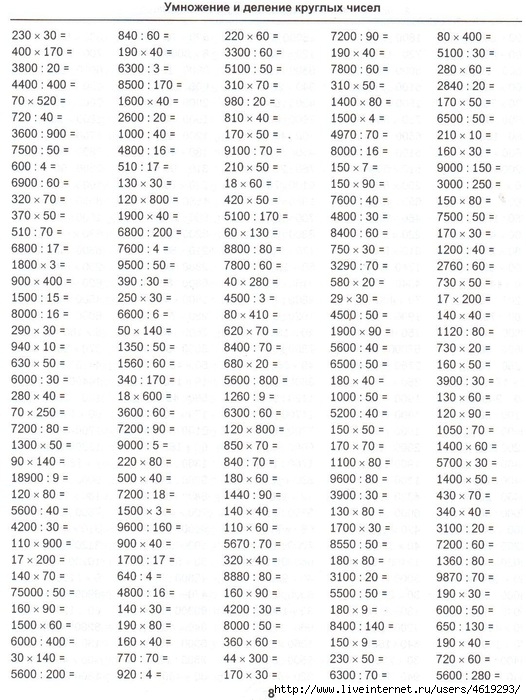Как умножать в столбикПохоже, вы используете блокировщик рекламы. Наш сайт существует и развивается только за счет дохода от рекламы.
Пожалуйста, добавьте нас в исключения блокировщика.
Скрыть меню
На главную страницу
Войти при помощи
Темы уроков
Начальная школа
- Геометрия: начальная школа
- Действия в столбик
- Деление с остатком
- Законы арифметики
- Периметр
- Порядок действий
- Разряды и классы. Разрядные слагаемые
- Счет в пределах 10 и 20
Математика 5 класс
- Взаимно обратные числа и дроби
- Десятичные дроби
- Натуральные числа
- Нахождение НОД и НОК
- Обыкновенные дроби
- Округление чисел
- Перевод обыкновенной дроби в десятичную
- Площадь
- Проценты
- Свойства сложения, вычитания, умножения и деления
- Среднее арифметическое
- Упрощение выражений
- Уравнения 5 класс
- Числовые и буквенные выражения
Математика 6 класс
- Масштаб
- Модуль числа
- Окружность.
Площадь круга - Отношение чисел
- Отрицательные и положительные числа
- Периодическая дробь
- Признаки делимости
- Пропорции
- Рациональные числа
- Система координат
- Целые числа
Площадь кругаАлгебра 7 класс
- Алгебраические дроби
- Как применять формулы сокращённого умножения
- Многочлены
- Одночлены
- Системы уравнений
- Степени
- Уравнения
- Формулы сокращённого умножения
- Функция в математике
Геометрия 7 класс
- Точка, прямая и отрезок
- Что такое аксиома и теорема
Алгебра 8 класс
- Квадратичная функция. Парабола
- Квадратные неравенства
- Квадратные уравнения
- Квадратный корень
- Неравенства
- Системы неравенств
- Стандартный вид числа
- Теорема Виета
Алгебра 9 класс
- Возрастание и убывание функции
- Нули функции
- Область определения функции
- Отрицательная степень
- Среднее
геометрическое
Алгебра 10 класс
- Иррациональные числа
Алгебра 11 класс
- Факториал
Почему все потеряшки прячутся в самом дальнем углу? Потому что найдя их, ты больше их не ищешь.
Народная мудрость
на главную
Введите тему
Русский язык Поддержать сайт
Сложение в столбик Вычитание в столбик Умножение в столбик Деление в столбик
Решим пример:
- Запишем числа столбиком (одно под другим). В верхней строчке — большее число, в нижней — меньшее.
Самая правая цифра (знак) верхнего числа должна стоять над самой правой цифрой нижнего числа. Сбоку слева между числами ставим знак действия. У нас это «×» (знак умножения).
- Сначала умножаем целиком верхнее число на последнюю цифру нижнего числа. Результат записывается
под чертой под самой правой цифрой.
Умножаем число сверху по цифре (знаку) справа налево.
7 · 6 = 42
У нас получилось число большее или равное «10».Поэтому под черту идет только последняя цифра результата. Это «2». Количество десятков произведения (у нас «4 десятка») ставим над соседом слева от «7».
- Умножаем «2» на «6».
2 · 6 = 12
Не забудем, что над «2» стоит «4». Это значит, что к результату умножения (произведению) надо прибавить «4».12 + 4 = 16
«6» записываем под чертой и «1» записываем над «4». - Умножаем «4» на «6».
4 · 6 = 24
К произведению добавляем «1»24 + 1 = 25
- Переходим к умножению числа «427» на «3». Умножаем по тем же правилам, что и на «6».
Запомните!
Результат умножения на вторую цифру необходимо записывать под второй цифрой результата первого действия умножения.
- Полученные числа под чертой складываем по
правилам сложения в столбик.
Теперь освоив умножение столбиком, вы сможете перемножать сколь угодно большие числа.
Сложение в столбик Вычитание в столбик Умножение в столбик Деление в столбик
Массивы, умножение и деление
Массивы, умножение и деление
Дженни Пеннант с помощью Дженни Уэй и Майка Аскью исследует, как можно использовать массив в качестве инструмента мышления, чтобы помочь детям развить глубокое понимание умножения и деления.
Использование массивов для исследования чисел
Массивы — полезные модели для умножения, которые можно использовать различными способами, начиная от хорошо структурированных уроков и заканчивая играми и открытыми исследованиями.
Массив формируется путем организации набора объектов в строки и столбцы. Каждый столбец должен содержать такое же количество объектов, как и другие столбцы, а каждая строка должна иметь такое же количество объектов, как и другие строки.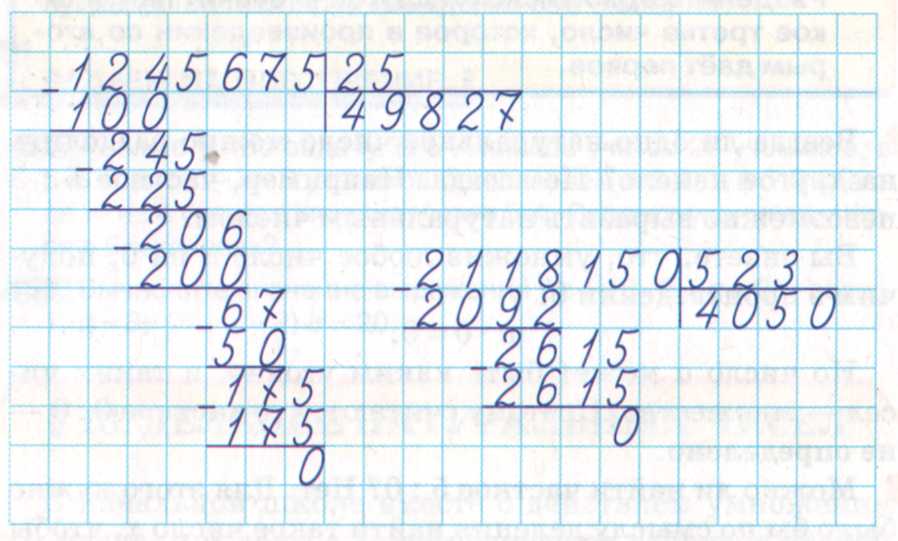
Следующий массив, состоящий из четырех столбцов и трех строк, может использоваться для представления числового предложения 3 x 4 = 12, 4 x 3 = 12, 3 + 3 + 3 + 3 = 12 и 4 + 4 + 4 = 12.
Построение фактов и таблиц умножения
Массивы можно использовать для осмысленного построения фактов умножения. Прежде чем сверлить и запоминать таблицы, дети должны понять, как эти факты получены. Например, постепенно добавляя еще один столбец из трех объектов, дети могут построить для себя таблицы умножения на три. Это представление не только помогает понять процесс, но и дает визуальный образ для детей, чтобы опираться на них, когда они начинают использовать и запоминать факты об основных числах.
Использование массивов для изучения больших чисел
Массивы могут быть полезны для изучения вычислений, таких как 13 x 5, где массив может быть разделен на полезные фрагменты, такие как 10 и 3.
Это означает, что дети могут использовать свои известные количество фактов для выполнения расчетов.
Здесь 13 х 5 = (10 х 5) + (3 х 5).
Через некоторое время рисовать все точки может стать очень утомительно! Затем пустой массив становится очень полезным инструментом, помогающим детям моделировать свое мышление и решать, как выполнять более сложные умножения неформальным способом.
Вот ребенок, использующий пустой массив в качестве инструмента мышления, чтобы помочь ему решить 15 x 14.
Пустой массив помогает детям использовать другие стратегии, такие как компенсация, при выполнении умножения. Здесь, чтобы вычислить 34 х 9, ребенок решил сделать 34 х 10, а затем снять 34 х 1. сеточный метод. Дети могут увидеть, как метод «абстрактной» сетки накладывает массив и формализует пустой массив в стандартную форму.
Деление как операция, обратная умножению
Из четырех операций деление является самой трудной для младших школьников.
Полное понимание деления, как правило, сильно отстает от других операций. Для многих детей возможности исследовать понятие с конкретными материалами ограничены задолго до того, как они узнают взаимосвязь между делением и тремя другими операциями. Одно из таких отношений, обратное отношение
между делением и умножением можно эффективно проиллюстрировать с помощью массивов.
Например; 3×5=15 или 3 строки по 5 составляют 15, могут быть представлены следующим массивом.
Взглянув на массив под другим углом, можно обнаружить обратное, то есть
15÷3=5 или 15, помещенное в 3 строки, дает 5 столбцов — или 5 в каждой строке.
Очевидно, что язык играет важную роль в способности выражать математические отношения, а физический массив поддерживает этот аспект понимания, давая детям конкретный образ, о котором можно говорить.
Помещение математики в контекст реальной жизни с помощью текстовых задач может облегчить как понимание отношений, так и их выражение через слова.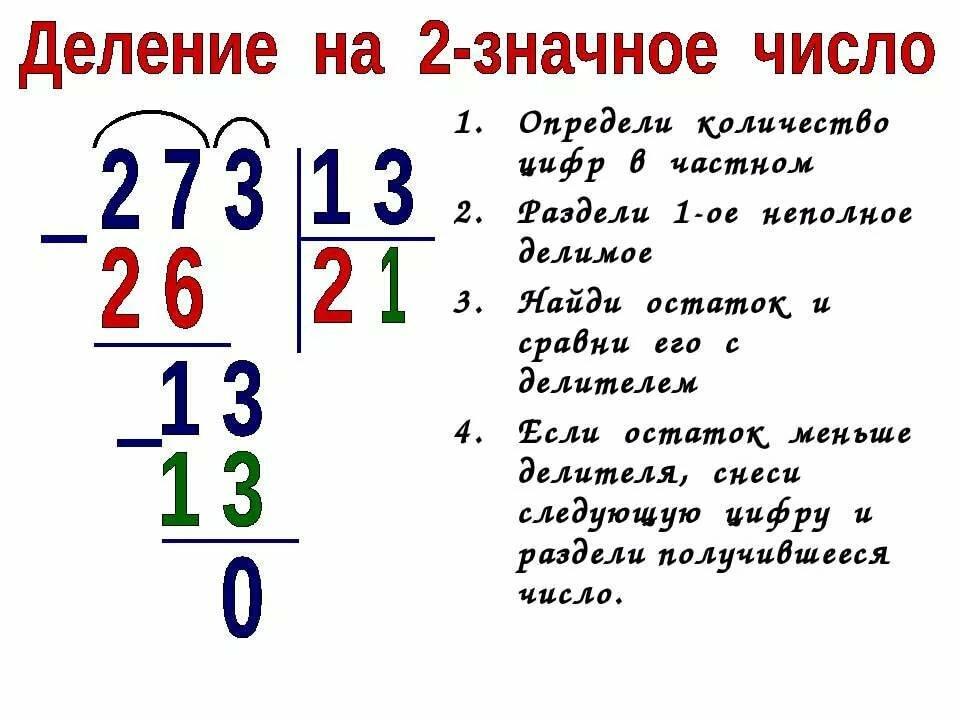
Например, «Садовник посадил 3 ряда по 5 семян. Сколько семян она посадила?» ставит совсем другую задачу, чем «Садовник посадил 15 семян в 3 равных ряда. Сколько семян в каждом ряду?» тем не менее, обе эти текстовые задачи могут быть смоделированы с использованием одного и того же массива.
Дальнейшее изучение массива выявило еще два способа выражения обратных отношений: 5×3=15 и 15÷3=5 .
Текстовые задачи могут быть адаптированы для описания этих операций и выделения сходств и различий между четырьмя выражениями, смоделированными одним массивом.
Использование пустого массива
Предположим, вы хотите вычислить 176 ÷ 8. Мы можем настроить это как массив с отсутствующим значением одной стороны.
Используя известные факты умножения, можно построить значение пропущенной стороны.
Таким образом, ребенок может видеть, что 22 партии по 8 равны 176.
Массив — очень мощный инструмент для поддержки развития детского мышления в отношении умножения и деления.
Дополнительная литература
Чтобы узнать об использовании массивов для иллюстрации числовых свойств, перейдите сюда и прочитайте статью Дженни Уэй под названием «Иллюстрация числовых свойств с помощью массивов».
Вот PDF-версия этой статьи.
Сложение, вычитание, умножение и деление целых чисел
Цели обучения
- Использование сложения, вычитания, умножения и деления при оценке выражений с целыми числами
Работа с целыми числами и выполнение основных вычислений — основа всей математики. Мы предполагаем, что вы помните, как выполнять сложение, вычитание, умножение и деление однозначных чисел. Вы часто будете иметь под рукой калькулятор для выполнения этих расчетов, но быстрое освежение знаний поможет вам лучше понять, как работать с числами, чтобы сложные уравнения не вызывали у вас затруднений.
Дополнение
пример
Добавление: [латекс]28+61[/латекс]
Решение
Чтобы складывать числа, состоящие из более чем одной цифры, часто проще писать числа вертикально в столбцах.
| Запишите числа так, чтобы единицы и десятки располагались вертикально. | [латекс]\begin{array}{c}\hfill 28\\ \\ \hfill \underset{\text{____}}{+61}\end{array}[/latex] |
| Затем добавьте цифры в каждом разряде. Добавьте единицы: [латекс]8+1=9[/латекс] Добавьте десятки: [латекс]2+6=8[/латекс] | [латекс]\begin{array}{c}\hfill 28\\ \\ \hfill \underset{\text{____}}{+61}\\ \hfill 89\end{array}[/latex] |
В предыдущем примере сумма единиц и сумма десятков были меньше [латекс]10[/латекс]. Но что произойдет, если сумма [latex]10[/latex] или больше? Давайте воспользуемся нашей моделью base-[latex]10[/latex], чтобы выяснить это.
На приведенном ниже рисунке показано добавление [латекс]17[/латекс] и [латекс]26[/латекс].
Когда мы добавляем единицы, [латекс]7+6[/латекс], мы получаем [латекс]13[/латекс] единиц. Поскольку у нас их больше, чем [латекс]10[/латекс], мы можем обменять [латекс]10[/латекс] из них на [латекс]1[/латекс] десять.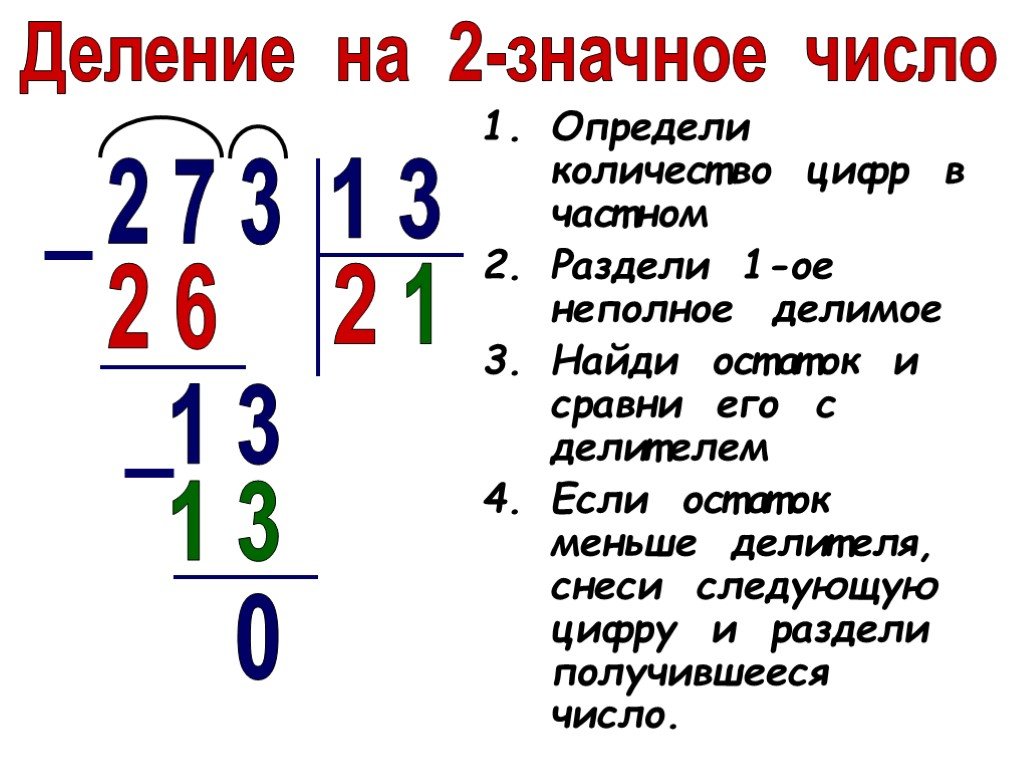
Теперь у нас есть [латекс]4[/латекс] десятки и [латекс]3[/латекс] единицы. Не используя модель, мы показываем это как маленький красный [латекс]1[/латекс] над цифрами в разряде десятков.
Когда сумма в столбце разряда больше, чем [latex]9[/latex], мы переносимся в следующий столбец слева. Перенос — это то же самое, что перегруппировка путем обмена. Например, [latex]10[/latex] единиц для [latex]1[/latex] десяти или [latex]10[/latex] десятков для [latex]1[/latex] сотен.
Сложите целые числа
- Запишите числа так, чтобы каждый разряд располагался вертикально.
- Добавьте цифры в каждое разрядное значение. Работайте справа налево, начиная с места единиц. Если сумма в разряде больше, чем [latex]9[/latex], выполняется перенос к следующему разряду.
- Продолжайте добавлять каждое разрядное значение справа налево, добавляя каждое разрядное значение и перенося при необходимости.
пример
Добавить: [латекс]43+69[/латекс]
Показать ответ
попробуй
попробуй
Если слагаемые имеют разное количество цифр, будьте внимательны, чтобы выровнять соответствующие разрядные значения, начиная с единиц и двигаясь влево.
пример
Добавить: [латекс]1,683+479[/латекс].
Показать ответ
попробуй
Вычитание
Сложение и вычитание являются обратными операциями. Сложение отменяет вычитание, а вычитание отменяет сложение.
Мы знаем [латекс]7 — 3=4[/латекс], потому что [латекс]4+3=7[/латекс]. Знание всех фактов сложения чисел поможет с вычитанием. Затем мы можем проверить вычитание, сложив. В приведенных выше примерах наши вычитания можно проверить сложением.
| [латекс]7-3=4[/латекс] | потому что | [латекс]4+3=7[/латекс] |
| [латекс]13-8=5[/латекс] | потому что | [латекс]5+8=13[/латекс] |
| [латекс]43-26=17[/латекс] | потому что | [латекс]17+26=43[/латекс] |
Чтобы вычесть числа, состоящие из более чем одной цифры, обычно проще писать числа вертикально в столбцах, как мы это делали для сложения.
Выровняйте цифры по разрядности, а затем вычтите каждый столбец, начиная с единиц, и затем работайте влево.
Упражнение
Вычтите, а затем проверьте, добавив: [латекс]89 — 61[/латекс].
Показать ответ
ПОПРОБУЙТЕ
Вычтите целые числа
- Запишите числа так, чтобы каждое разрядное значение располагалось вертикально.
- Вычтите цифры из каждого разряда. Работайте справа налево, начиная с места единиц. Если цифра сверху меньше, чем цифра снизу, заимствуйте по мере необходимости.
- Продолжайте вычитать значение каждого разряда справа налево, при необходимости заимствуя.
- Проверить добавлением.
упражнение
Вычесть: [латекс]43 — 26[/латекс].
Показать ответ
В приведенном выше примере, если мы моделируем вычитание [латекс]26[/латекс] из [латекс]43[/латекс], мы заменим [латекс]1[/латекс] десять на [латекс]10[/латекс] те.
Когда мы делаем это без моделей, мы говорим, что заимствуем [латекс]1[/латекс] из разряда десятков и добавляем [латекс]10[/латекс] к разряду единиц.
попробуйте
Упражнение
Вычтите и затем проверьте, добавив: [латекс]207 — 64[/латекс].
Показать ответ
попробуйте
Упражнение
Вычтите и затем проверьте, добавив: [латекс]2,162 — 479[/латекс].
Показать ответ
попробуйте
Посмотрите видео ниже, чтобы увидеть еще один пример вычитания целых чисел путем выстраивания разрядов.
Умножение
Чтобы умножать без использования моделей, вам нужно знать все факты умножения одной цифры.
Убедитесь, что вы знаете их бегло, прежде чем продолжить изучение этого раздела. В таблице ниже показаны факты умножения.
Каждое поле показывает произведение числа в левом столбце и числа в верхней строке. Если вы не уверены в продукте, смоделируйте его. Важно, чтобы вы запомнили любые факты о числах, которые вы еще не знаете, чтобы вы были готовы умножать большие числа.
| [латекс]x[/латекс] | [латекс]0[/латекс] | [латекс]1[/латекс] | [латекс]2[/латекс] | [латекс]3[/латекс] | [латекс]4[/латекс] | [латекс]5[/латекс] | [латекс]6[/латекс] | [латекс]7[/латекс] | [латекс]8[/латекс] | [латекс]9[/латекс] |
|---|---|---|---|---|---|---|---|---|---|---|
| [латекс]0[/латекс] | [латекс]0[/латекс] | [латекс]0[/латекс] | [латекс]0[/латекс] | [латекс]0[/латекс] | [латекс]0[/латекс] | [латекс]0[/латекс] | [латекс]0[/латекс] | [латекс]0[/латекс] | [латекс]0[/латекс] | [латекс]0[/латекс] |
| [латекс]1[/латекс] | [латекс]0[/латекс] | [латекс]1[/латекс] | [латекс]2[/латекс] | [латекс]3[/латекс] | [латекс]4[/латекс] | [латекс]5[/латекс] | [латекс]6[/латекс] | [латекс]7[/латекс] | [латекс]8[/латекс] | [латекс]9[/латекс] |
| [латекс]2[/латекс] | [латекс]0[/латекс] | [латекс]2[/латекс] | [латекс]4[/латекс] | [латекс]6[/латекс] | [латекс]8[/латекс] | [латекс]10[/латекс] | [латекс]12[/латекс] | [латекс]14[/латекс] | [латекс]16[/латекс] | [латекс]18[/латекс] |
| [латекс]3[/латекс] | [латекс]0[/латекс] | [латекс]3[/латекс] | [латекс]6[/латекс] | [латекс]9[/латекс] | [латекс]12[/латекс] | [латекс]15[/латекс] | [латекс]18[/латекс] | [латекс]21[/латекс] | [латекс]24[/латекс] | [латекс]27[/латекс] |
| [латекс]4[/латекс] | [латекс]0[/латекс] | [латекс]4[/латекс] | [латекс]8[/латекс] | [латекс]12[/латекс] | [латекс]16[/латекс] | [латекс]20[/латекс] | [латекс]24[/латекс] | [латекс]28[/латекс] | [латекс]32[/латекс] | [латекс]36[/латекс] |
| [латекс]5[/латекс] | [латекс]0[/латекс] | [латекс]5[/латекс] | [латекс]10[/латекс] | [латекс]15[/латекс] | [латекс]20[/латекс] | [латекс]25[/латекс] | [латекс]30[/латекс] | [латекс]35[/латекс] | [латекс]40[/латекс] | [латекс]45[/латекс] |
| [латекс]6[/латекс] | [латекс]0[/латекс] | [латекс]6[/латекс] | [латекс]12[/латекс] | [латекс]18[/латекс] | [латекс]24[/латекс] | [латекс]30[/латекс] | [латекс]36[/латекс] | [латекс]42[/латекс] | [латекс]48[/латекс] | [латекс]54[/латекс] |
| [латекс]7[/латекс] | [латекс]0[/латекс] | [латекс]7[/латекс] | [латекс]14[/латекс] | [латекс]21[/латекс] | [латекс]28[/латекс] | [латекс]35[/латекс] | [латекс]42[/латекс] | [латекс]49[/латекс] | [латекс]56[/латекс] | [латекс]63[/латекс] |
| [латекс]8[/латекс] | [латекс]0[/латекс] | [латекс]8[/латекс] | [латекс]16[/латекс] | [латекс]24[/латекс] | [латекс]32[/латекс] | [латекс]40[/латекс] | [латекс]48[/латекс] | [латекс]56[/латекс] | [латекс]64[/латекс] | [латекс]72[/латекс] |
| [латекс]9[/латекс] | [латекс]0[/латекс] | [латекс]9[/латекс] | [латекс]18[/латекс] | [латекс]27[/латекс] | [латекс]36[/латекс] | [латекс]45[/латекс] | [латекс]54[/латекс] | [латекс]63[/латекс] | [латекс]72[/латекс] | [латекс]81[/латекс] |
Мы знаем, что изменение порядка сложения не меняет сумму.
Мы видели, что [латекс]8+9=17[/латекс] совпадает с [латекс]9+8=17[/латекс].
Верно ли это и для умножения? Рассмотрим несколько пар факторов.
[латекс]4\cdot 7=28\quad 7\cdot 4=28[/латекс]
[латекс]9\cdot 7=63\quad 7\cdot 9=63[/latex]
[latex]8\cdot 9=72\quad 9\cdot 8=72[/latex]
При обратном порядке множителей произведение не меняется. Это называется коммутативным свойством умножения.
Коммутативное свойство умножения
Изменение порядка множителей не меняет их произведения.
[латекс]a\cdot b=b\cdot a[/латекс]
пример
Умножить:
[латекс]8\cdot 7[/латекс]
[латекс]7\cdot 8[/латекс]
Показать ответ
попробуй
Чтобы умножать числа, состоящие из более чем одной цифры, обычно проще записывать числа вертикально в столбцы, как мы это делали для сложения и вычитания.
[латекс]\begin{array}{c}\hfill 27\\ \hfill \underset{\text{___}}{\times 3}\end{array}[/latex]
Начнем с умножения [ латекс]3[/латекс] от [латекс]7[/латекс].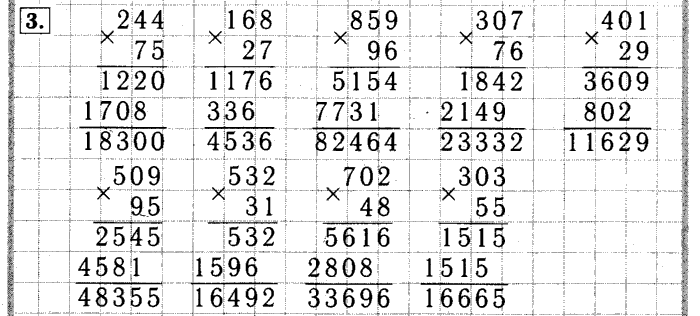
[латекс]3\раз 7=21[/латекс]
Мы пишем [латекс]1[/латекс] в единицах продукта. Мы переносим [латекс]2[/латекс] десятки, написав [латекс]2[/латекс] над разрядом десятков.
Затем мы умножаем [латекс]3[/латекс] на [латекс]2[/латекс] и прибавляем [латекс]2[/латекс] выше разряда десятков к произведению. Итак, [латекс]3\умножить на 2=6[/латекс] и [латекс]6+2=8[/латекс]. Напишите [латекс]8[/латекс] в разряде десятков продукта.
Продукт [латекс]81[/латекс].
Когда мы умножаем два числа с разным количеством цифр, обычно проще написать меньшее число внизу. Можно было бы написать и по-другому, но с этим проще работать.
пример
Умножить: [латекс]15\cdot 4[/латекс]
Показать ответ
попробуй
пример
Умножить: [латекс]286\cdot 5[/латекс]
Показать ответ
попробуй
Когда мы умножаем на число, состоящее из двух и более цифр, мы умножаем на каждую цифру отдельно, работая справа налево.
Каждое отдельное произведение цифр называется частичным произведением. Когда мы пишем частичные произведения, мы должны убедиться, что разрядные значения выровнены.
Умножение целых чисел
- Запишите числа так, чтобы каждый разряд располагался вертикально.
- Умножьте цифры в каждом разряде.
- Вяжите справа налево, начиная с разряда единиц в нижнем ряду.
- Умножьте нижнее число на разряд единиц в верхнем числе, затем на разряд десятков и так далее.
- Если продукт в разрядном значении больше, чем [latex]9[/latex], перенос на следующее разрядное значение.
- Запишите частичные произведения, выровняв цифры разрядов с числами выше.
- Повторите для разряда десятков в нижнем числе, разряда сотен и т. д.
- Вставьте ноль в качестве заполнителя для каждого дополнительного частичного продукта.
- Вяжите справа налево, начиная с разряда единиц в нижнем ряду.
- Добавьте частичные произведения.
пример
Умножить: [латекс]62\влево(87\вправо)[/латекс]
Показать ответ
попробуй
Когда множителей три или более, мы умножаем первые два, а затем умножаем их произведение на следующий множитель. Например:
| умножить | [латекс]8\cdot 3\cdot 2[/латекс] |
| первое умножение [латекс]8\cdot 3[/латекс] | [латекс]24\cdot 2[/латекс] |
| затем умножьте [латекс]24\cdot 2[/латекс] | [латекс]48[/латекс] |
В видео ниже мы обобщаем концепции, представленные на этой странице, включая свойство умножения нуля, свойство идентичности умножения и свойство перестановочности умножения.m
Деление
Мы сказали, что сложение и вычитание являются обратными операциями, потому что одна отменяет другую.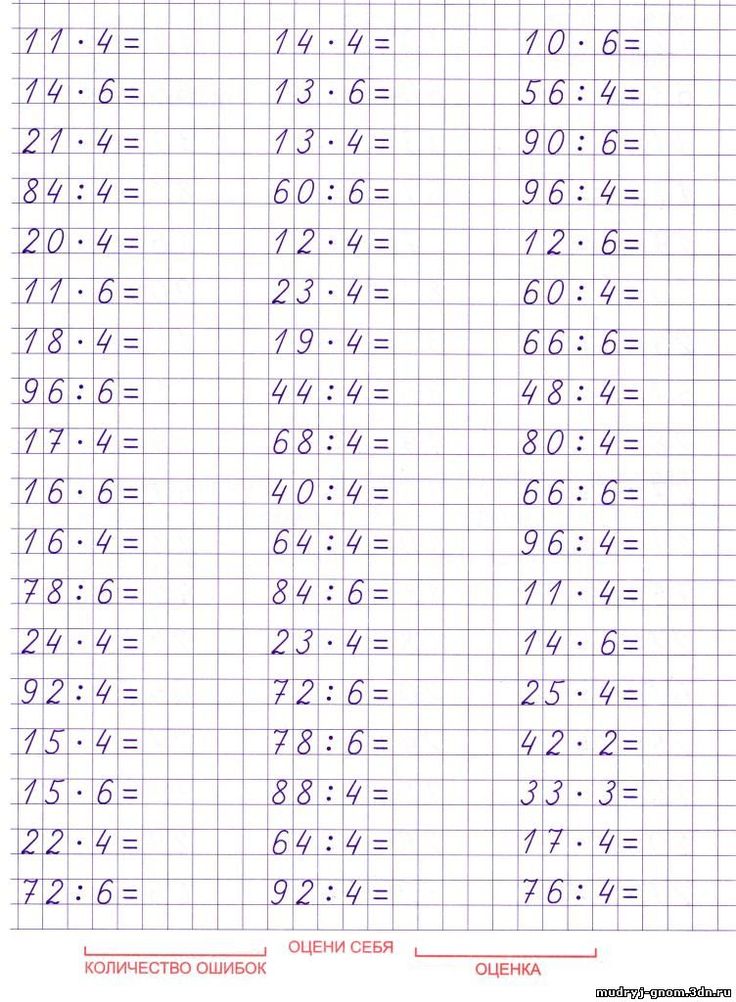
Точно так же деление является обратной операцией умножения. Мы знаем [латекс]12\дел 4=3[/латекс], потому что [латекс]3\cdot 4=12[/латекс]. Знание всех фактов числа умножения очень важно при делении.
Мы проверяем наш ответ на деление, умножая частное на делитель, чтобы определить, равно ли оно делимому. Мы знаем, что [латекс]24\дел 8=3[/латекс] правильный, потому что [латекс]3\cdot 8=24[/латекс].
Пример
Разделить. Затем проверьте умножением.
- [латекс]42\дел 6[/латекс]
- [латекс]\фракция{72}{9}[/латекс]
- [латекс]7\overline{)63}[/латекс]
Решение:
| 1. | |
| [латекс]42\дел 6[/латекс] | |
| Разделите [латекс]42[/латекс] на [латекс]6[/латекс]. | [латекс]7[/латекс] |
| Проверить умножением. [латекс]7\cdot 6[/латекс] | |
| [латекс]42\quad\галочка [/латекс] |
2. | |
| [латекс]\фракция{72}{9}[/латекс] | |
| Разделите [латекс]72[/латекс] на [латекс]9[/латекс]. | [латекс]8[/латекс] |
| Проверить умножением. [латекс]8\cdot 9[/латекс] | |
| [латекс]72\quad\галочка [/латекс] |
| 3. | |
| [латекс]7\overline{)63}[/латекс] | |
| Разделите [латекс]63[/латекс] на [латекс]7[/латекс]. | [латекс]9[/латекс] |
| Проверить умножением. [латекс]9\cdot 7[/латекс] | |
| [латекс]63\quad\галочка [/латекс] |
попробуй
Чему равно частное при делении числа само на себя?
[латекс]\frac{15}{15}=1\text{ потому что }1\cdot 15=15[/latex]
Деление любого числа [латекс]\текст{(кроме 0)}[/латекс] сам по себе дает частное [latex]1[/latex].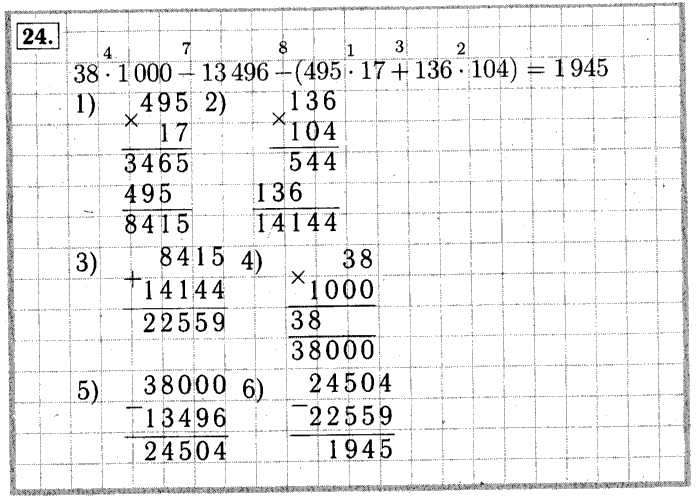
Кроме того, любое число, деленное на [latex]1[/latex], дает частное от числа. Эти две идеи изложены в Свойствах Разделения Единого.
Раздел Свойства одного
| Любое число (кроме 0), деленное само на себя, равно единице. | [латекс]а\дел а=1[/латекс] |
| Любое число, разделенное на единицу, равно числу. | [латекс]а\дел 1=а[/латекс] |
Пример
Разделить. Затем проверьте умножением:
- [латекс]11\дел 11[/латекс]
- [латекс]\фракция{19}{1}[/латекс]
Показать ответ
попробуйте
Предположим, у нас есть [латекс]\текст{\$0}[/латекс], и мы хотим разделить его между [латекс]3[/латекс] людьми. Сколько получит каждый? Каждый человек получит [латекс]\текст{\$0}[/латекс]. Ноль, разделенный на любое число, равен [латекс]0[/латекс].
Теперь предположим, что мы хотим разделить [латекс]\текст{\$10}[/латекс] на [латекс]0[/латекс].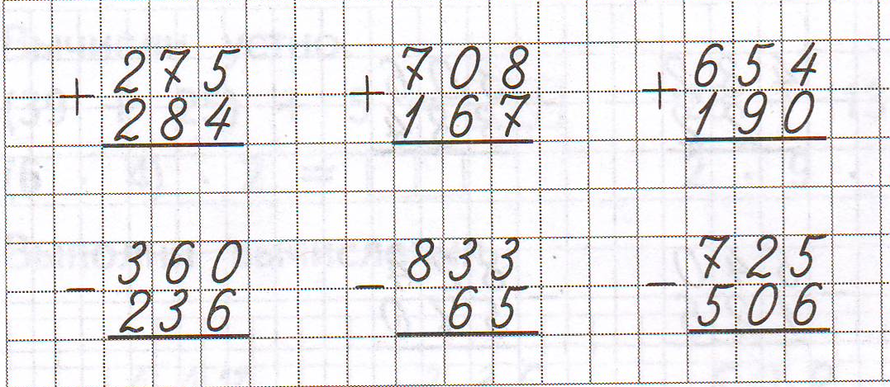
Это означает, что нам нужно найти число, которое мы умножим на [latex]0[/latex], чтобы получить [latex]10[/latex]. Этого не может быть, потому что [латекс]0[/латекс], умноженное на любое число, равно [латекс]0[/латекс]. Говорят, что деление на ноль равно undefined .
Эти две идеи составляют Свойства Разделения Зеро.
Раздел Свойства Зеро
| Ноль, разделенный на любое число, равен [латекс]0[/латекс]. | [латекс]0\дел а=0[/латекс] |
| Деление числа на ноль не определено. | [латекс]а\дел 0[/латекс] не определено |
Другой способ объяснить, почему деление на ноль не определено, состоит в том, чтобы вспомнить, что деление на самом деле представляет собой многократное вычитание. Сколько раз мы можем отнять [латекс]0[/латекс] от [латекс]10?[/латекс] Поскольку вычитание [латекс]0[/латекс] никогда не изменит итоговое значение, мы никогда не получим ответ.
Поэтому мы не можем разделить число на [latex]0[/latex].
Пример
Разделить. Проверить умножением:
- [латекс]0\дел 3[/латекс]
- [латекс]\фракция{10}{0}[/латекс]
Показать ответ
попробуйте
Когда делитель или делимое имеет более одной цифры, обычно проще использовать запись [latex]4\overline{)12}[/latex]. Этот процесс называется длинным делением. Давайте рассмотрим этот процесс, разделив [латекс]78[/латекс] на [латекс]3[/латекс].
The next line reads » data-label=»»>
Мы будем повторять процесс до тех пор, пока в делимом не останется цифр, которые нужно уменьшить. В этой задаче больше не осталось цифр, поэтому деление закончено.
[латекс]\текст{Так} 78\дел 3=26[/латекс].
Проверьте, умножив частное на делитель, чтобы получить делимое. Умножьте [латекс]26\умножить на 3[/латекс], чтобы убедиться, что произведение равно делимому, [латекс]78[/латекс].
[латекс]\begin{array}{c}\hfill \stackrel{1}{2}6\\ \hfill \underset{\text{___}}{\times 3}\\ \hfill 78 \end{ массив}[/латекс]
Да, значит, наш ответ правильный. [latex]\checkmark[/latex]
Деление целых чисел
- Разделить первую цифру делимого на делитель. Если делитель больше первой цифры делимого, разделить первые две цифры делимого по делителю и так далее.
- Запишите частное над делимым.
- Умножьте частное на делитель и запишите произведение под делимым.
- Вычтите этот продукт из дивиденда.
- Сократите следующую цифру делимого.
- Повторяйте с шага 1 до тех пор, пока в делимом не останется цифр, которые нужно уменьшить.
- Проверьте, умножив частное на делитель.
В видео ниже мы показываем еще один пример использования деления в длину.
пример
Разделить [латекс]2,596\дел 4[/латекс]. Проверить умножением:
Показать ответ
попробовать
пример
Разделить [латекс]4,506\дел 6[/латекс]. Проверить умножением:
Показать ответ
попробуй
Посмотрите это видео, чтобы увидеть еще один пример использования деления в длину для деления целого четырехзначного числа на целое двузначное число.
До сих пор все задачи на деление решались равномерно. Например, если бы у нас было [латекс]24[/латекс] печенья и мы хотели сделать пакеты из [латекс]8[/латекс] печенья, у нас было бы [латекс]3[/латекс] пакетов. Но что, если бы было [латекс]28[/латекс] печенья, и мы хотели бы сделать пакеты из [латекс]8?[/латекс] Начните с [латекс]28[/латекс] печенья.
Попробуйте разложить печенье по восемь штук.
Остались группы [latex]3[/latex] из восьми файлов cookie и еще [latex]4[/latex] cookie. Мы называем файлы cookie [latex]4[/latex], которые остались поверх остальных, и показываем их, записывая R4 рядом с [latex]3[/latex]. (R означает остаток.)
Чтобы проверить это деление, мы умножаем [латекс]3[/латекс] на [латекс]8[/латекс], чтобы получить [латекс]24[/латекс], а затем складываем остаток [латекс]4[/латекс].