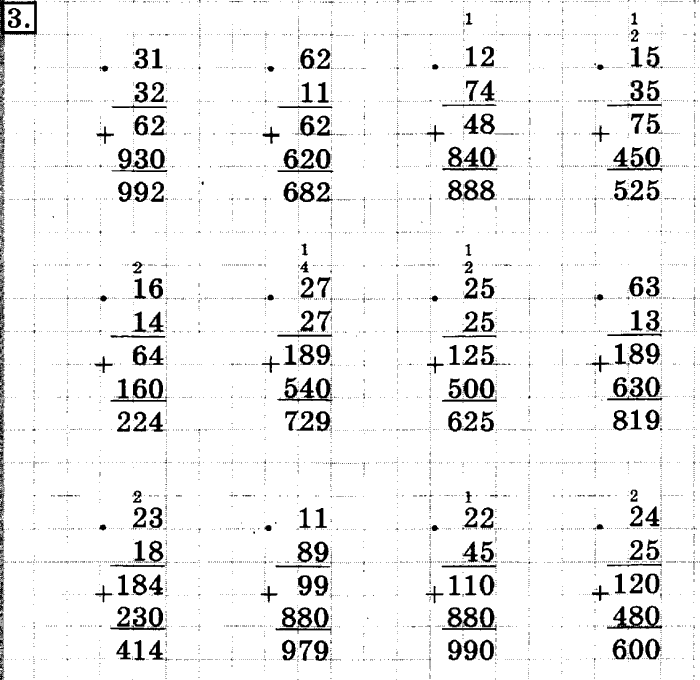
Расставь порядок действий. Найди значение выражения: (72507 + 56736) : (350 – 347) = 560000 : 100 ∙ 8 = 4 ∙ (932 + 17692) : 6 = 500 + (600 – 3 ∙ 100) : 10 = | Расставь порядок действий. Найди значение выражения: 60997 + (6012 + 6228) : 3 = 485 ∙ 2 + 485 ∙ 3 = 82213 ∙ 3 – 12240 : 3 = (40179 – 15395 : 5) ∙ 4 = | Расставь порядок действий. Найди значение выражения: 55440 : 9 – 10460 : 2 = 3546 – 283 ∙ 4 + 819 = 5999 + 903 ∙ 100 : 2 = (56043 – 13032) : (900 : 100) = |
Расставь порядок действий. Найди значение выражения: 41090 : 7 + 11950 : 5 = 240 : 3 ∙ 5 – 399 = 372160 : 4 ∙ 7 – 721 95 = 4 ∙ (728 – 301) : 7 = (286 + 14) : 3 ∙ 5 – 280 = | Расставь порядок действий. 2250 : 9 + 8420 : 2 = 9000 : ( 100 – 90) : 100 ∙ 2 = 283040 : 10 ∙ 3 = 100520 – 470 ∙ 5 + 13980 = 7280 ∙ 6 + 1965 ∙ 3 = | Расставь порядок действий. Найди значение выражения: 11140 : (2076 – 2066) : 2 = 900100 – (735 – 184) ∙ 8 = 3010 – 5614 : 7 + 9042 = 46370 : 5 + 546 ∙ 4 = 1254 + 645 : 5 – 967 = |
Расставь порядок действий. Найди значение выражения: 80115 : 3 ∙ 10 = 40471 ∙ 2 – 4503 ∙ 7 = | Расставь порядок действий. Найди значение выражения: 69580 : 7 – 14280 : 6 = 14110 + 801 : 9 – 7604 = 235 + 4 ∙ (536 : 8) = 12 ∙ (53 – 48) – 84 : 7 = 400000 – 702 ∙ 5 : 10 = | Расставь порядок действий. Найди значение выражения: 7800 – (398 + 507 ∙ 6) = 15 ∙ (54 3 – 84 : 7) = 190 ∙ 2 + (32148 – 16) = 73460 : 5 + 454 ∙ 4 = 8 ∙ (900000 – 896507) : 4 = |
Расставь порядок действий. 13640 : 4 – 6400 : 10 = (90 – 42 : 3 ∙ 2) : 2 = (2700 – 30) ∙ (40 – 32) = (5600 – 12240 : 3) + 145 = 400000 – 702 ∙ 5 : 10 = | Расставь порядок действий. Найди значение выражения: 8130 : 3 – 2640 : 10 = (35400 + 83915) : 5 ∙ 3 = 3152 : 8 ∙ 100 = 40018 – 725 ∙ 10 : 5 = 838008 : 9 – 410960 : 8 = | Расставь порядок действий. Найди значение выражения: 480 : 6 + 360 : 12 = (10200 – 9356) ∙ (81 – 75) = 2448 : 6 + 1854 : 6 = 2758 – 345 ∙ 6 + 369 = 8 ∙ (900000 – 896507) : 4 = |
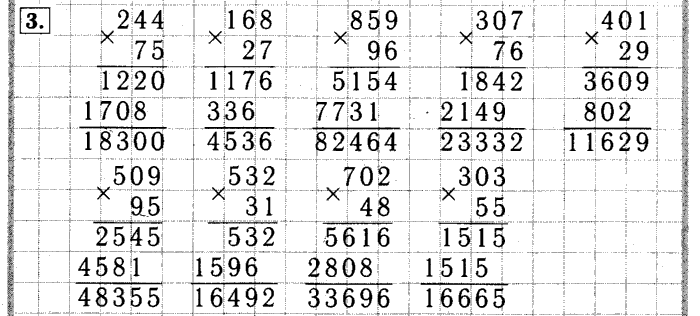
Выполни умножение на однозначное число столбиком: 43127 ∙ 6 36039 ∙ 4 7 ∙ 23844 70 ∙ 94800 Найди значение выражения: 709 + 13200 ∙ 5 = 9 ∙ (5000 – 786) = | Выполни умножение на однозначное число столбиком: 95136 ∙ 3 391005 ∙ 4 9 ∙ 12543 50 ∙ 157300 Найди значение выражения: 400800 — 3980 ∙ 7 = 3 ∙ (90000 – 514 ∙ 4) = | Выполни умножение на однозначное число столбиком: 56482 ∙ 3 341008 ∙ 6 4 ∙ 81429 9 ∙ 930700 Найди значение выражения: 70005 — 5320 ∙ 2 = 9 ∙ (26000 – 1705) = |
Выполни умножение на однозначное число столбиком: 719806 ∙ 4 903040 ∙ 3 9 ∙ 24845 5 ∙ 120605 Найди значение выражения: 27356 — 1607 ∙ 3 = 800 – 640 : 8 + 70 ∙ 4 = | Выполни умножение на однозначное число столбиком: 25482 ∙ 2 374006 ∙ 7 5 ∙ 93748 90 ∙ 17850 Найди значение выражения: 41008 — 1240 ∙ 4 = 7 ∙ (6954 – 1007) = | Выполни умножение на однозначное число столбиком: 15213 ∙ 6 65080 ∙ 4 7 ∙ 31476 70 ∙ 390400 Найди значение выражения: 50786 + 8091 ∙ 3 = 6 ∙ (10000 – 5836) = |
Выполни умножение на однозначное число столбиком: 23452 ∙ 7 36008 ∙ 9 6 ∙ 32749 40 ∙ 82190 Найди значение выражения: 29010 – ( 5000 — 800 ∙ 4) = 17082 ∙ 8 + 1329 = | Выполни умножение на однозначное число столбиком: 36193 ∙ 5 670032 ∙ 8 9 ∙ 56492 70 ∙ 420080 Найди значение выражения: 4689 ∙ 5 + 97308 = 80000 – (4536 + 160 ∙ 3) = | Выполни умножение на однозначное число столбиком: 68715 ∙ 4 90048 ∙ 7 7 ∙ 49873 60 ∙ 72680 Найди значение выражения: 76090 ∙ 4 – 52673 = 5 ∙ (128050 – 73607) = |
Выполни умножение на однозначное число столбиком: 95124 ∙ 2 50804 ∙ 4 9 ∙ 3652 50 ∙ 21470 Найди значение выражения: 90000 — 6 ∙ 2509 = 8 ∙ (7852 + 1308) = | Выполни умножение на однозначное число столбиком: 84308 ∙ 6 536937 ∙ 4 7 ∙ 4030900 50 ∙ 971680 Найди значение выражения: 500000 — 17806 ∙ 4 = (130 ∙ 5 + 72 : 24) ∙ 9 = | Выполни умножение на однозначное число столбиком: 3968719 ∙ 7 130704 ∙ 6 6 ∙ 109765 90 ∙ 700200 Найди значение выражения: 600 — 320 : 4 + 140 ∙ 3 = 90620 ∙ 8 — 8349 = |
Найди значение выражения по действиям: 229372 : 286 ∙ 506 = 82276 : 268 + 228475 : 325 = 76 ∙ (3569 + 2795) – 1247 ∙3 = 162540 : (100236 – 99978) : 63 = | Найди значение выражения по действиям: 416 ∙ 509 + 536469 : 67 = 230441 – (229682 – 228904 : 52) = (52 ∙ 390 – 12863) ∙ (12280 : 40 – 207) = (59531 – 58926) ∙ 6004 – 1221485 = | Найди значение выражения по действиям: 282370 : 302 : 85 ∙ 2004 = 81308 – 308 ∙ (8856 – 8649) = (43512 – 43006) ∙ 805 – 23900 : 25 = 700700 – 6954 ∙ (47923 – 47884) = |
Найди значение выражения по действиям: 507 ∙ 432 + 234 : 26 = (126828 : 542) ∙ (47600 – 406 ∙ 117) = 460 ∙ 308 + 447480 : 132 – 3987 = 1000000 – 136068 : 68 + 4600 ∙ 900 = | Найди значение выражения по действиям: 728 ∙ 468 : 273 : 78 = (47868 + 112812) : 52 + 45948 : 84 = 65254 :79 – 75369 : 97 + 6075 ∙ 42 = 100000 – 12900 : 129 + 19140 : 132 = | Найди значение выражения по действиям: 805 ∙ 282 : (4000 – 3678) ∙ 32 = 76428 – 771840 : 192 + 209160 : 249 = (701020 – 698456) ∙ (208128 : 542) = 671112 : 956 + (600000 – 178688) : 464 = |
Найди значение выражения по действиям: 246 ∙ 812 : (1001 – 673) ∙ 12 = 73689 : 87 – 96064 : 158 + 310726 = (22287 – 308 ∙ 72) : 111 + 3090 = (10200 – 9891) ∙ (70204 – 69874) : 206 = | Найди значение выражения по действиям: 496 ∙ 960 : 372 : 160 = (199430 – 119 ∙ 805) : (148 + 8536 : 88) = 500100 – 356 ∙ 101 + 78052 : 26 ∙ 48 = 30000 – (2486 + 335104 : 476) ∙ 9 = | Найди значение выражения по действиям: 25146 : (428442 : 707 – 255000 : 625) = (64000 : 128 – 3280 : 164 ∙ 15) ∙ 700 = 804 ∙ 705 : 335 : 47 = (162000 – 216 ∙ 750) ∙ (816 : 4) + 1000 = |
Найди значение выражения по действиям: 802 ∙ 406 – 900072 : 18 + 63392 = (35730 + 91800 : 36) : 120 = 180848 : 356 ∙ (19800 – 18900) : 254 = 1285 – 282 ∙ 75 :47 + 14472 : 18 ∙ 12 = | Найди значение выражения по действиям: 532000 : 760 + 407 ∙ 360 – 82008 = (234690 – 306 ∙ 201) : 192 = 71370 : 234 ∙ 243 + 695 ∙ 50 – 2884 : 28 = 3060 ∙ 236 – 184708 + 125125 : 125 = | Найди значение выражения по действиям: 608 ∙ (1263 – 563) : 400 = 127410 : 274 + 307200 : 480 – 1105 = (1015 – 332926 : 818) ∙ (240372 : 396) = 609 ∙ 896 – 545664 + 748616 : 362 = |
Выполни умножение и деление на однозначное число столбиком: 825 : 5 215 ∙ 4 5472 : 4 4238 ∙ 7 4371 : 3 40632 ∙ 8 Найдите неизвестное число, зная, что ½ его часть равна 8. Вся дыня весит 6 кг. Сколько кг весит 1/3 часть дыни? | Выполни умножение и деление на однозначное число столбиком: 576 : 4 3875 ∙ 6 5418 : 3 14398 ∙ 7 6255 : 5 46504 ∙ 4
| Выполни умножение и деление на однозначное число столбиком: 496 : 4 5603 ∙ 6 25632 : 2 3303 ∙ 7 7284 : 6 73504 ∙ 9 Найдите неизвестное число, зная, что ¼ его часть равна 16. Какую долю от метра составляет 1 дм? |
Выполни умножение и деление на однозначное число столбиком: 1225 : 5 728 ∙ 6 726 : 3 1438 ∙ 8 2536 : 4 62008 ∙ 4 Длина всей ленты 10 см. Какова длина ¼ части ленты? Найдите 1/3 часть от суммы 36 и 63. | Выполни умножение и деление на однозначное число столбиком: 828 : 2 487 ∙ 5 4552 : 8 6702 ∙ 9 36204 : 6 31454 ∙ 6
| Выполни умножение и деление на однозначное число столбиком: 456 : 4 1315 ∙ 3 2536 : 2 38524 ∙ 8 82244 : 4 27180 ∙ 6
|
Выполни умножение и деление на однозначное число столбиком: 507 ∙ 4 952 : 7 2014 ∙ 6 1458 : 6 26613 ∙ 8 25656 : 8
| Выполни умножение и деление на однозначное число столбиком: 214 ∙ 6 858 : 6 1708 ∙ 9 5020 : 4 34328 ∙ 5 25256 : 7
| Выполни умножение и деление на однозначное число столбиком: 392 ∙ 5 970 : 5 1438 ∙ 8 1227 : 3 62008 ∙ 7 18504 : 9
|
Выполни умножение и деление на однозначное число столбиком: 237 ∙ 9 984 : 6 4914 ∙ 6 5836 : 4 34807 ∙ 8 13572 : 9 Почтовый голубь в час пролетает 92 км. Сколько километров он пролетит за четверть часа? | Выполни умножение и деление на однозначное число столбиком: 478 ∙ 7 915 : 5 1687 ∙ 9 4872 : 8 43703 ∙ 6 22435 : 7 ¼ стакана сахарного песка весит 60 г. Сколько весит стакан сахарного песка? | Выполни умножение и деление на однозначное число столбиком: 418 ∙ 6 7660 : 4 2718 ∙ 9 5346 : 9 47086 ∙ 7 30402 : 6 Длина куска материи 75 м. |
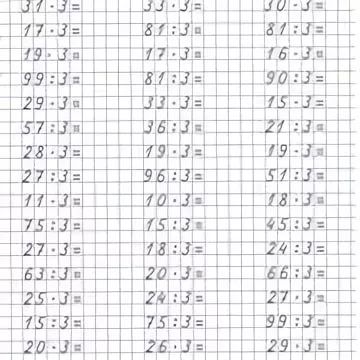
Выполни деление столбиком: 39285 : 45 114021 : 27 48372 : 58 380700 : 45 Зверёк землеройка за сутки съедает 12 г пищи. Сколько весит зверёк, если его масса составляет ¼ массы съеденной пищи? | Выполни деление столбиком: 19980 : 37 525728 :56 6293 : 31 16884 : 42 8844 : 22 20468 : 34 Продолжительность жизни хвои ели 9 лет, а продолжительность жизни хвои сосны 1/3 жизни хвои ели. Сколько лет живёт хвоя сосны? | Выполни деление столбиком: 5472 : 18 26553 : 53 4575 : 15 17575 : 25 65520 : 28 23640 : 24 Сколько километров проходит за ¼ часа поезд, если в час он проходит 64 км? |
Выполни деление столбиком: 173232 : 48 975255 : 79 216 161 : 43 455948 : 62 12896 : 32 72144 : 24 Берёза прожила 50 лет, что составляет 1/5 продолжительности её жизни. | Выполни деление столбиком: 5508 : 36 428910 : 85 33350 : 46 24512 : 16 97312 : 32 144096 : 79 Какую сдачу получит мальчик с 400 руб, если четвёртую часть этих денег он потратил на 2 ручки и 3 ластика? | Выполни деление столбиком: 182056 : 28 128928 : 32 191520 : 95 394680 : 78 13356 : 18 249922 : 62 Продолжительность жизни ежа равна 10 годам, а заяц живёт на 1/5 меньше. Сколько лет живёт заяц? |
4 класс. Моро. Учебник №1. Ответы к стр. 81
Числа от 1 до 1000
Умножение и деление
Деление на однозначное число
Ответы к стр. 81
Объясни приёмы вычисления.
963 : 3 = (900 + 60 + 3) : 3 = 900 : 3 + 60 : 3 + 3 : 3
455 : 5 = (450 + 5) : 5 = 450 : 5 + 5 : 5
Делимое разложили на сумму разрядных слагаемых и использовали правило деления суммы на число: чтобы поделить сумму на число, можно каждое слагаемое поделить на это число и полученные частные сложить.
363. Найди частное и остаток и выполни проверку.
56 : 15 92 : 30 399 : 9 854 : 8 34 : 40
— 56|15 Проверка: ×15
45|3 3
11 — ост. 45
45 + 11 = 56
— 92 |30 Проверка: 30 • 3 + 2 = 92
90 |3
2 — ост.
— 399|9 Проверка: ×44
36 |44 9
—39 396
36
3 — ост. 396 + 3 = 399
— 854|8 Проверка: ×106
8 |106 8
—054 848
48
6 — ост. 848 + 6 = 854
848 + 6 = 854
— 34 |40 Проверка: 40 • 0 + 34 = 34
0 |0
34 — ост.
364. Объясни, что обозначают записи в рамках на полях, и выполни вычисления.
0 : α = 0 − при делении нуля на любое число всегда получается нуль
b : 1 = b − при делении числа на единицу всегда получается данное число
c : c = 1 − при делении числа на само себя всегда получается единица
0 : 45 = 0 208 : 1 = 208 375 : 375 = 1
0 : 964 = 0 342 : 1 = 342 863 : 863 = 1
365. Составь разные задачи по выражению 24 : 6.
1) Миша купил 24 солдатика, а машинок в 6 раз меньше, чем солдатиков. Сколько машинок купил Миша?
24 : 6 = 4 (м. )
)
О т в е т: Миша купил 4 машинки.
2) Мама принесла домой 24 пирожных. Вечером Миша съел шестую часть этих пирожных. Сколько пирожных съел Миша?
24 : 6 = 4 (п.)
О т в е т: Миша съел 4 пирожных.
366. За 2 ч езды на легковой машине обычно расходуется 12 л бензина. На сколько часов езды хватит 48 л бензина, если его расход не изменится?
1) 12 : 2 = 6 (л) − бензина хватает на 1 ч
2) 48 : 6 = 8 (ч) − время, на которое хватит 48 л бензина
О т в е т: на 8 часов.
367. В прошлом году завод изготовил 1400 машин, что на 300 машин меньше, чем в этом году. Поставь вопрос и реши задачу.
Сколько машин изготовил завод за эти 2 года?
1) 1400 + 300 = 1700 (м.) − изготовлено в этом году
2) 1400 + 1700 = 3100 (м.) − изготовлено за 2 года
О т в е т: за 2 года завод изготовил 3100 машин.
368. Одна бригада рабочих заасфальтировала 5 км 060 м шоссе, другая бригада − на 2 км 280 м больше.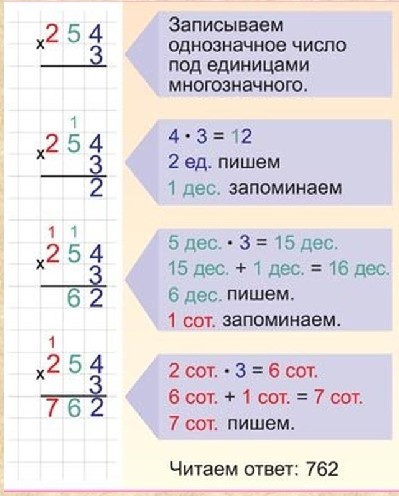 Осталось покрыть асфальтом 965 м шоссе. Какой длины шоссе должны были заасфальтировать эти бригады?
Осталось покрыть асфальтом 965 м шоссе. Какой длины шоссе должны были заасфальтировать эти бригады?
1) 5 км 060 м + 2 км 280 м = 7 км 340 м − заасфальтировала вторая бригада
2) 5 км 060 м + 7 км 340 м + 965 м = 12 км 400 м + 965 м = 13 км 365 м − должны были заасфальтировать
О т в е т: должны были заасфальтировать 13 км 365 м шоссе.
369. 658 : 7 9235 + 4 • (536 : 8) 40077 • 7 − 199099
836 : 4 (2010 − 1065) : 7 • 6 9020 • 6 + 53901
658 : 7 = 94
— 658|7
63 |94
—28
28
0
836 : 4 = 209
— 836|4
8 |209
—036
36
0
9235 + 4 • (536 : 8) = 9235 + 4 • 67 = 9235 + 268 = 9503
— 536|8 ×67 +9235
48 |67 4 268
—56 268 9503
56
0
(2010 − 1065) : 7 • 6 = 945 : 7 • 6 = 135 • 6 = 810
_2010 — 945|7 ×135
1065 7 |135 6
945 —24 810
21
_35
35
0
40077 • 7 − 199099 = 280539 − 199099 = 81440
× 40077 _ 280539
7 199099
280539 81440
9020 • 6 + 53901 = 54120 + 53901 = 108021
× 9020 + 54120
6 53901
54120 108021
370.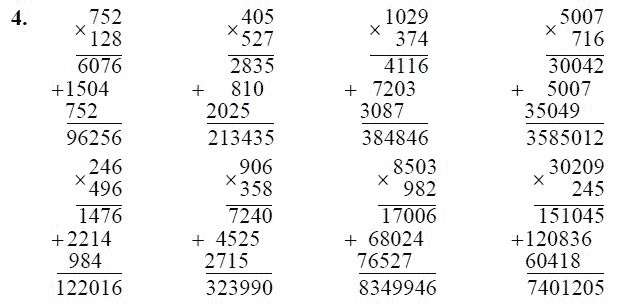 x : 9 = 1000 − 910 100 • x = 2430 − 2030
x : 9 = 1000 − 910 100 • x = 2430 − 2030
x • 9 = 1000 − 910 100 : x = 2430 − 2420.
x : 9 = 1000 − 910 x • 9 = 1000 − 910
x : 9 = 90 x • 9 = 90
x = 90 • 9 x = 90 : 9
x = 810 x = 10
100 • x = 2430 − 2030
100 • x = 400
x = 400 : 100
x = 4
100 : x = 2430 − 2420
100 : x = 10
x = 100 : 10
x = 10
371. На какое однозначное число надо умножить число 12345679, чтобы в результате получить новое число, записанное одними единицами?
Так как у числа 12345679 последняя цифра 9, то при умножении на однозначное число этой цифры, последняя цифра произведения должна быть равна 1. Известен только один случай такого табличного умножения: 9 • 9 = 81 (последняя цифра 1).
Известен только один случай такого табличного умножения: 9 • 9 = 81 (последняя цифра 1).
× 12345679
9
111111111
Вычисли. 693 : 3 468 : 2
— 693|3 — 468|2
6 |239 4 |234
—09 —06
9 6
_03 _08
3 8
0 0
Ответы по математике. Учебник. 4 класс. Часть 1. Моро М. И., Бантова М. А., Бельтюкова М. А., Волкова С. И., Степанова С. В.
Математика. 4 класс
Обзор сложения, вычитания, умножения и деления | 4 класс Математика
В математике есть 4 основных действия : сложение, вычитание, умножение и деление.
Давайте вспомним, что вы уже узнали о них.
Обзор сложения
Сложение объединяет два или более чисел.
Дополнение — это номер, который добавляется к другим номерам.
Знак плюс + это то, что говорит нам о том, что нам нужно добавить.
Знак равенства = говорит нам, что значение слева равно значению справа.
Сумма — это число, которое мы получаем при сложении чисел.
Попробуем сложить числа.
Дополнение Пример 1
6,034 + 2,841 = ?
Складываем числа, используя форму столбца , начиная с разряда единиц:
Каков наш ответ? 😃
Правильно! Это 8875.
6 034 + 2 841 = 8 875
Отличная работа!
Дополнение Пример 2
356 + 297 = ?
Добавим!
На этот раз нам нужно сделать перегруппировка .
Перегруппировка берет 10 из одного разряда и передает его следующему более высокому разряду.
Наша сумма 653. ✅
✅
Отлично! 😎
Теперь приступим к вычитанию.
Вычитание Обзор
Вычитание — это вычитание части числа.
Уменьшаемое — это число, из которого мы вычитаем.
Вычитаемое — это вычитаемое число.
Знак минус говорит нам о вычитании.
Разность — это ответ, который мы получаем при вычитании.
Совет по запоминанию:
Давайте попробуем вычесть некоторые числа. 🤗
🤗
Пример вычитания 1
9,586 — 3,172 = ?
Давайте вычтем числа, используя форму столбца .
Начать вычитание из разряда единиц.
Какая разница или ответ? 🤓
9 586 — 3 172 = 6 414
NICE Work! 👏
Пример вычитания 2
512 — 243 = ?
Вычитаем!
Не забудьте начать вычитание из разряда единиц.
Нам нужно вычесть 3 из 2.
3 больше 2, поэтому мы не можем вычесть сразу. 😕
Нам нужно перегруппировать одну Десятку в Десять Единиц!
Обратите внимание, что нам пришлось перегруппироваться и в разряде десятков.
В путь! 🤗
Давайте теперь рассмотрим умножение и деление.
Просмотр умножения
Умножение складывает одно и то же число снова и снова.
Например:
5 × 2 = 10
Это означает, что 5 групп по 2 круга составляют 10 кругов.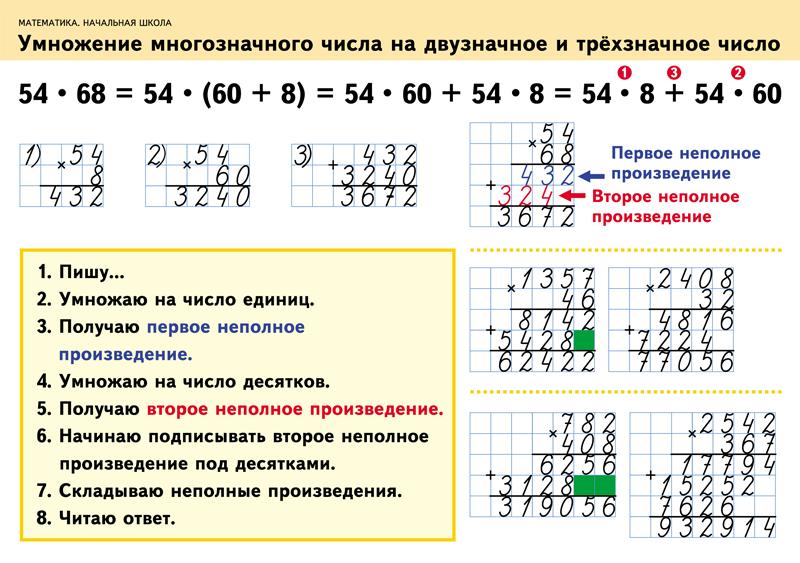
Уравнение умножения состоит из следующих частей:
Множитель и множимое также называются множителями . Это числа, которые мы перемножаем вместе.
Знак умножения говорит нам умножать. Читается как «раз».
Продукт — это ответ, который мы получаем.
Попробуем умножить.
Пример умножения 1
7 × 6 = ?
Вы можете умножать числа, используя повторных сложений.
✅ Мы можем прибавить к себе 7 6 раз, или прибавить к себе 6 7 раз.
7 × 6 = 7 + 7 + 7 + 7 + 7 + 7 = 42
Итак,
7 × 6 = 42
Отличная работа!
Умножение настолько важно, что вы уже должны выучить таблицу умножения! Если нет, то вернемся к нашим урокам умножения в 3-м классе.
Пример умножения 2
268 × 4 = ?
Давайте попробуем умножить эти числа, используя форму столбца .
🔸 Сначала умножаем цифру на разряд единиц на 4.
🔸 Далее мы умножаем цифру в разряде десятков на 4 и добавляем полученное число.
🔸 Наконец, мы умножаем цифру в разряде сотен на 4 и добавляем полученное число.
Какой ответ вы получили?
268 × 4 = 1072
Отличная работа! 👏
Обзор отдела
Подразделение разбивает число на равные группы.
Например, когда мы разделим 10 кругов на 5 равных групп, получим по 2 круга в каждой группе.
10 ÷ 5 = 2
Уравнение деления состоит из следующих частей:
Теперь рассмотрим несколько примеров деления.
Раздел Пример 1
30 ÷ 6 = ?
Мы можем решить эту задачу на деление, используя повторных вычитаний.
✅ Мы начинаем с 30 и снова и снова вычитаем 6 .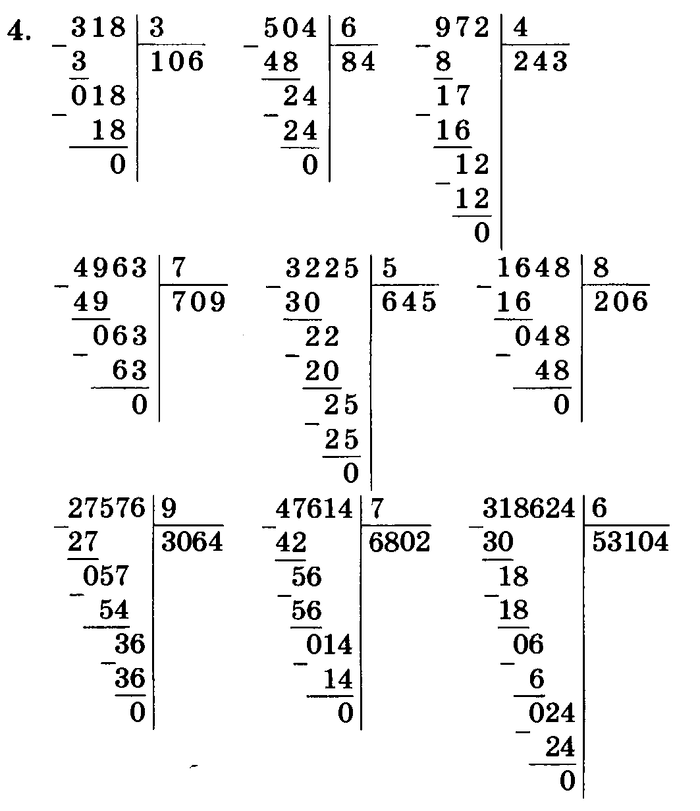 Мы останавливаемся, когда достигаем 0.
Мы останавливаемся, когда достигаем 0.
Количество вычитаний и есть наш ответ.
Сколько раз вы вычитали?
Правильно! 5 раз .
Итак,
30 ÷ 6 = 5
Отлично! 🤗
Совет: Еще проще представить деление как , противоположное умножению.
Только подумайте… 🤔
Сколько раз 6 будет 30?
6 х ? = 30
И вы получите тот же ответ: 5! ✔️
Раздел Пример 2
944 ÷ 8 = ?
Давайте решим этот вопрос, используя длинное деление .
🔸 Начнем с расстановки чисел в длинном делении.
Мы работаем над цифрами по одной.
🔸 Теперь смотрим на первую цифру.
Можете ли вы сказать, сколько восьмерок входит в девятку? 🤔
Очень хорошо! 1 .
Напишите 1 сверху, как частное.
🔸 Запишите произведение 1 и 8 под цифрой 9 .
Теперь вычесть 8 из 9 .
Фантастика! 😎
🔸 Далее, сбиваем следующую цифру и повторяем процесс.
🔸 Наконец, введите последнюю цифру и повторите процесс.
Какой ответ вы получили?
944 ÷ 8 = 118
Отличная работа! 👏
Раздел Пример 3
1,492 ÷ 6 = ?
🔸 Запишем в форме деления 9.0004 .
🔸 Посмотрите на первую цифру, 1.
Делим на наш делитель.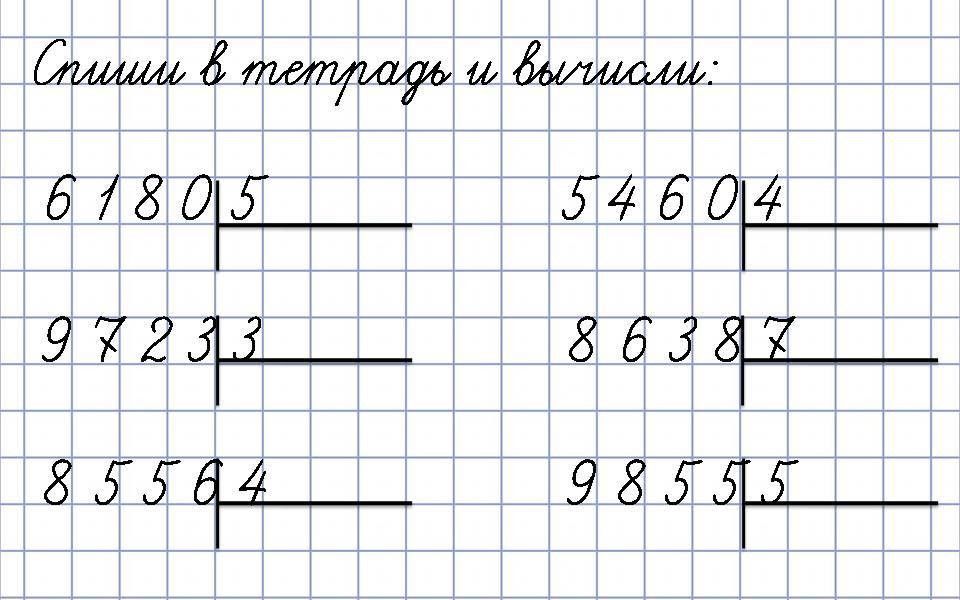
1 ÷ 6 = ?
Мы делим меньшее число на большее.
Итак, наш ответ 0.
Давайте напишем 0 сверху, как частное.
Запишите произведение 0 и 6 под 1.
Вычтите 0 из 1.
Отличная работа! 🤗
Вот важный совет : Не пропускайте при делении первой цифры, даже если она меньше делителя. Работайте над числами по одному, чтобы не запутаться.
🔸 Теперь сбиваем вторую цифру . Затем просто повторите тот же процесс.
🔸 Сократите до третьей цифры . Затем проделайте те же действия еще раз.
Затем проделайте те же действия еще раз.
🔸 Теперь запишите последнюю цифру и выполните те же действия.
Мы дошли до последней цифры, но осталось еще число.
Это наш остаток.
Мы пишем это вверху через «r» или «R» .
Когда мы пишем ответ, мы не учитывать ноль в начале частного.
1 492 ÷ 6 = 248 R4
Отличная работа! 😀
🎉 Вы только что рассмотрели самые важные моменты о сложении, вычитании, умножении и делении.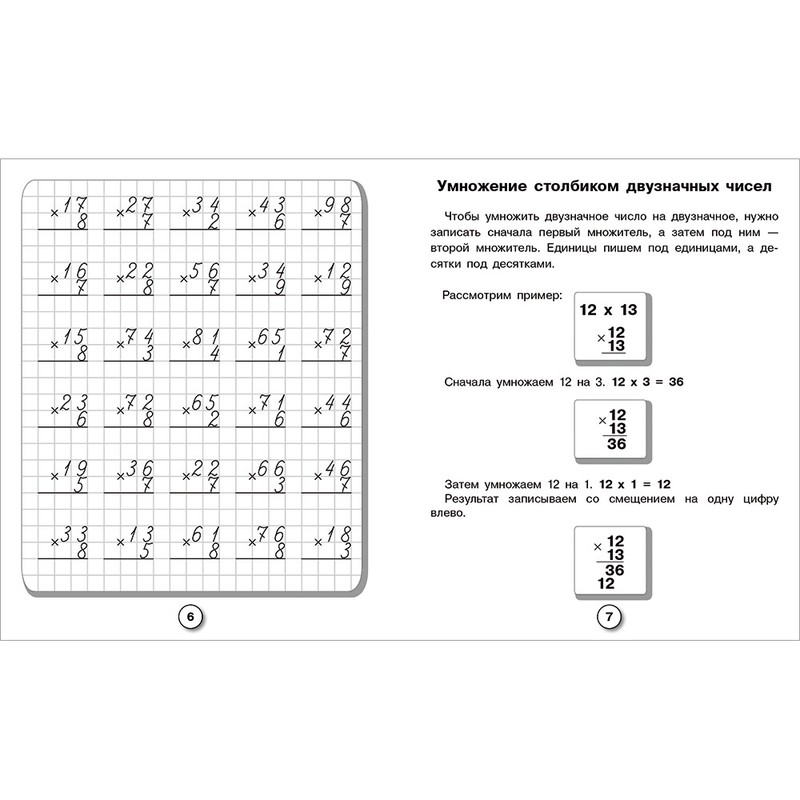 😅
😅
Теперь приступайте к практике. 😀 Это поможет вам помнить дольше.
Символы умножения и деления, выражения и отношения
Цель
Этот модуль развивает понимание умножения и деления, включая обратную связь между двумя операциями, а также когда и как их использовать в ситуациях решения задач. Учащиеся изучают правила представления операций умножения и деления в виде уравнений.
Цели достижения
NA3-6: Запишите и интерпретируйте аддитивные и простые мультипликативные стратегии, используя слова, диаграммы и символы, с пониманием равенства.
Разработка АО и другие учебные ресурсы
Конкретные результаты обучения
- Читать, писать и понимать символы умножения и деления, знак равенства и язык, связанный с этими символами.
- Напишите контекст рассказа для заданных уравнений умножения и деления.
- Знайте, что операция умножения коммутативна.

- Определите связанные факты умножения и деления («семейства фактов»).
- Знать обратную зависимость операций умножения и деления.
- Признать, что деление некоммутативно.
- Правильно используйте слова «фактор» и «продукт»
- Определите коэффициенты заданных сумм.
Описание математики
Эта последовательность уроков устанавливает связь между повторяющимся сложением и умножением. Он вводит деление и исследует взаимосвязь между операциями умножения и деления.
В рамках этих уроков развиваются три основных понимания.
- Учащиеся должны понимать отношения между величинами, представленными уравнениями умножения и деления. Например, 4 x 5 = 20 может представлять собой «четыре количества по пять равны 20» или «20 в четыре раза больше, чем 5».
- Учащиеся должны выучить словарный запас, связанный с умножением и делением, а также значение этих слов. Важная лексика включает множители (числа умножаются), произведение (ответ на умножение), умножение на (умножение одной величины в х раз), равенство (одинаковость количества).

- Умножение также может быть представлено в пространстве. Массивы — это эффективный способ показать структуру и структуру множественных групп и, в данном случае, прочно связать умножение и деление с измерением.
При изучении структуры и модели умножения и деления основное внимание уделяется также развитию раннего понимания числовых свойств . На этих уроках формально исследуется коммутативное свойство умножения (то есть порядок, в котором умножаются числа, не меняет ответ). Распределительное свойство, при котором один или оба фактора разделяются для облегчения вычислений (например, 12 x 55 = 10 x 55 + 2 x 55), является основополагающим для стратегий расчета, включая письменные алгоритмы.
При изучении поведения операций умножения и деления важно, чтобы 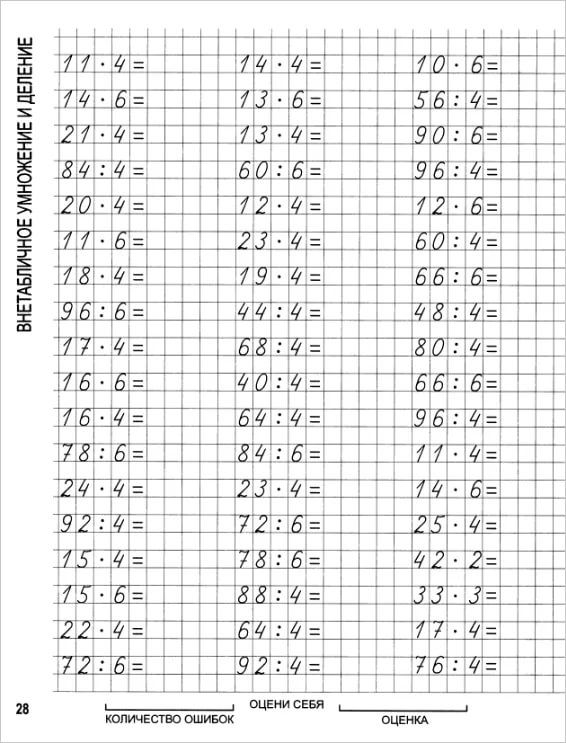
Эта серия уроков посвящена однозначным множителям и делителям. Он признает, что учащиеся должны иметь много возможностей представить умножение и деление. операции для решения текстовых задач. Это подкрепляется глубоким пониманием использования символов и выражений умножения и деления для математического мышления и выражения отношений. Учащиеся также должны уметь создавать контексты, которые может выражать уравнение. Установление связей между языком и символами необходимо для развития правильного понимания математических идей и концепций.
Возможности для адаптации и дифференциации
Возможности обучения в этом модуле можно дифференцировать, предоставляя или удаляя поддержку учащихся и изменяя требования к заданиям. Способы дифференциации включают:
- предоставление физических материалов, чтобы учащиеся могли предвидеть действия и обосновывать свои решения. Использование таких материалов, как кубы, квадратные плитки и диаграммы массивов, для моделирования ситуаций и связывания стратегий, используемых учащимися, с представленными величинами.

- , соединяющие символы и математический словарь, особенно символы умножения и деления (x, ÷) и равенства (=). Явное моделирование правильного использования уравнений и алгоритмов и обсуждение значения символов в контексте.
- изменение сложности используемых чисел. Умножение на такие множители, как два, четыре, пять, десять, и деление на одни и те же делители, как правило, проще, чем на такие множители, как три, шесть, семь, восемь и девять. Подумайте, какие факты умножения ваши ученики будут уверенно применять при решении задач.
- побуждает учащихся сотрудничать в малых группах, делиться и обосновывать свои идеи.
- с использованием технологий, особенно калькуляторов, в прогнозирующих, основанных на шаблонах способах оценки произведений и частных, например. Если ответ на 4 x 8 = 32, будет ли ответ на 32 ÷ 5 больше или меньше 8? Откуда вы знаете? разрешить использование калькуляторов там, где вы хотите, чтобы учащиеся больше сосредоточились на процессе получения разумного ответа или на замечании закономерностей, чем на отработке вычислительных навыков.

Контекст, используемый для этого модуля, — это стеганые одеяла, тиваеваэ и ткань тапа. Подумайте, как вы можете использовать знания сообщества в этом контексте. Есть ли члены сообщества, которых вы могли бы пригласить, чтобы поговорить о культурном происхождении тиваев или тапа? В этих контекстах важно обеспечить подлинность, актуальность и цель важных культурных знаний. Вы можете изменить контекст на ситуации, более соответствующие повседневной жизни, интересам или культурной самобытности ваших учащихся. Массивы распространены в разных культурах, и их можно найти в узорах плитки, текстиле, упаковке, стопках домов и игровых досках для игр. Поощряйте учащихся к творчеству, принимая различные стратегии от других и предлагая учащимся создавать свои собственные проблемы, которые должны решать другие, в значимом контексте.
Необходимые материалы
- Не менее двух прямоугольных стеганых одеял, тиваева или тапа
- Цветные пластиковые квадратные плитки (или маленькие квадратики из картона другого цвета)
- Бумага в клетку
- Калькуляторы
- Кубики Unifix
- Игральные карты
- PowerPoint 1
- PowerPoint 2
- Копи-мастер 1
- Копимастер 2
- Копи-мастер 3
Деятельность
Занятие 1
Занятие 1
- Покажите учащимся два разных прямоугольных лоскутных одеяла.
 Это была бы хорошая возможность взглянуть на любую школьную ткань тапа или панели тукутуку. Кроме того, используйте PowerPoint 1, чтобы показать изображения подходящих стеганых одеял или ткани тапа. Например:
Это была бы хорошая возможность взглянуть на любую школьную ткань тапа или панели тукутуку. Кроме того, используйте PowerPoint 1, чтобы показать изображения подходящих стеганых одеял или ткани тапа. Например:
Разработайте контекст для обучения этому разделу. Это может включать изготовление одеяла или тапы (даже гипотетически) для детского отделения в местной больнице или хосписе. Подумайте, как вы можете использовать знания своих учеников и их сообщества. Могут ли взрослые принести tivaevae, siapo или сделанные ими одеяла или фотографии вещей?
Вовлеките учащихся в обсуждение лоскутных одеял, установив, как создаются узоры. - Спросите: «Какая математика содержится в этих лоскутных одеял?» (например, лоскутное одеяло 3 x 3)
Запишите идеи учащихся в карточке класса. (Это могут быть числа, геометрия, измерения: например, 3 + 3 + 3 = 9, 3 x 3 = 9, 9 квадратов, один большой квадрат, стороны одинаковой длины, 9 разделить на 3 и т. д.). Сравните количество квадратов в разных примерах.
- Выделить операцию и отношения символов (или слов), которые были записаны. Например:
- Напишите каждый символ на отдельном листе бумаги формата А4. Попросите пары учащихся взять по одному листу (один символ), и каждый по очереди запишет в заданный период времени (например, за 2 минуты) , используя слова и картинки/диаграммы , и проведите мозговой штурм всего, что они знают об этом символе. (или слово). Попросите учащихся привести пример того, где можно использовать их символ.
- Попросите учащихся вернуться на коврик, рассаживаясь двумя отдельными группами: группа с операция символов (+ — x ÷) и группа с связью символов (<> =). Попросите выбранные пары учащихся объяснить, почему они сидят на своих местах и какие идеи они записали для своих символов.
В этом обсуждении подчеркните язык , используемый , разработайте понимание того, что такое числовая операция (математический процесс, который изменяет число или сумму), и повторите значение знака равно .
Сохраните листы мозгового штурма для дальнейшего использования.
Занятие 2
- Подготовьте пакеты по 12, 18, 20, 24 и 30 пластиковых плиток, маленькие цветные квадратики из картона или квадратики из ткани. Сделайте их, карандаши и бумагу, доступными для пар учащихся.
Поставьте задачу. «Покажите, , используя диаграммы и уравнения , сколькими различными способами можно расположить эти лоскуты, чтобы сделать «мини-лоскутное одеяло»?»
Предложите учащимся поработать в парах, чтобы записать свои идеи. - Предложите учащимся поделиться своими идеями с парой, у которой было одинаковое количество плиток, и записать все варианты расположения, о которых они не подумали.
- Обменивайтесь идеями в классе, изучайте и записывайте основные понятия в классной таблице. Оставьте эту работу учащегося для занятия 2.
Например: из пакета с 18 «заплатками» (плитками).
В ходе обсуждения опирайтесь на идеи, которыми поделились в Упражнении 1 (см. выше), выделяя и записывая словами эти идеи:
выше), выделяя и записывая словами эти идеи:- Аранжировки «патчей» могут быть записаны с использованием различных операций .
- Умножение с помощью x символ, может отображать ту же идею как многократное сложение (равных количеств), используя символ + .
- Символ для деления или деления на равные группы: ÷ . Он называется символом деления .
- Это расположение с одинаковыми строками и столбцами называется массивом .
- Поза и запись: «9+ 9 = 6 x 3. Вы согласны или не согласны». Попросите пары студентов обсудить это утверждение и обосновать свою позицию (объяснить, почему они согласны или не согласны и откуда они знают, что они правы).
Запишите обоснование ученика, выделив отношение эквивалентности (оба равны 18, всего 18 патчей в обоих массивах). Выделите мультипликативные представления, такие как «9 равно 3 x 3, поэтому 9 + 9 равно 6 x 3».
Выделите мультипликативные представления, такие как «9 равно 3 x 3, поэтому 9 + 9 равно 6 x 3».
Упражнение 3
Напишите два уравнения в таблице классов, одно на умножение и одно на деление.
Например: 6 x 5 = 30 28 ÷ 4 = 7. Прочтите их вместе. Пусть каждый учащийся нарисует схему стеганого одеяла или ткани тапа, представляющую уравнение. Попросите их написать словесное описание того, как стеганое одеяло/ткань представляет собой уравнение.
Упражнение 4
Завершите сеанс просмотром символов операций и взаимосвязей и их значений.
Занятие 2
Занятие 1
- Начните с того, что по крайней мере два ученика поделятся своими схемами одеяла/ткани из предыдущего занятия. Попросите других учащихся записать уравнения, представленные на схеме. Подчеркните тот факт, что математику из реальной жизни можно представить с помощью диаграмм, слов и символов.
- Проанализируйте на классной доске другие ситуации в нашей жизни, когда мы видим и используем умножение или деление.
 Когда учащиеся будут делиться идеями, попросите их назвать конкретные числа. Запишите эти истории, используя схемы и слова.
Когда учащиеся будут делиться идеями, попросите их назвать конкретные числа. Запишите эти истории, используя схемы и слова.
Например: Мы видим умножение, когда:- 12 упаковок по 20 драже упакованы в одну большую упаковку для продажи на школьной ярмарке – четыре упаковки в ряд и три ряда.
- Школа покупает три набора хоккейных клюшек по десять штук в каждом.
- На мараэ мы сидим в четыре ряда по шесть человек.
- Прочитайте сказки еще раз вместе. Попросите учащихся использовать символы для записи уравнений для каждой из историй в своих книгах/на доске/бумаге. Те учащиеся, которые закончат быстро, могут придумать больше контекстных историй. Поощряйте учащихся создавать контекстные истории, отражающие их повседневную жизнь (в отличие от выбора «случайных» чисел).
Предложите парам учащихся поделиться своими уравнениями. Если учащиеся записали, используя многократное сложение, попросите их также записать уравнения умножения.
Упражнение 2
- Просмотрите информацию о символах из сеанса 1, выделив символы операций, + — x ÷ , и символы отношений, равно (=), больше (>) и меньше (<) символы отношений.

Попросите учащихся поработать в парах, используя ситуации из предыдущего задания. Студенты должны обсудить ситуации и посмотреть, сколько уравнений или неравенств они могут написать. Например:
3 x 4 = 4 x 3
3 x 4 < 2 x 10
4 x 6 > 2 x 10 > 4 x 3
Они должны использовать диаграммы, чтобы показать, откуда они знают, что они верны. - Предложите учащимся поделиться своей работой в парах. При этом они должны по очереди читать вслух то, что они написали.
Занятие 3
- Вернитесь к стеганым одеялам/тапа-тканям (изображения). Объясните, что некоторым маленьким детям нравятся лоскутные одеяла с алфавитом, в которых на каждой клеточке изображено что-то, начинающееся с другой буквы алфавита. Поговорите о том, что некоторые из них могут быть. Например: A может изображать яблоко, B — бабочку, C — кошку и так далее.
- Предоставьте учащимся бумагу, карандаши и фломастеры.
Поставьте задачу: Вы собираетесь сделать лоскутное одеяло/ткань с алфавитом, чтобы подарить кому-нибудь. У вас есть время до конца сегодняшней сессии, чтобы спланировать свой дизайн и то, как вы будете располагать свои «квадратные лоскуты» . Где-то в проблеме может быть вызов. Вы выбираете лучший способ решить эту проблему для вашего дизайна стеганого одеяла.
У вас есть время до конца сегодняшней сессии, чтобы спланировать свой дизайн и то, как вы будете располагать свои «квадратные лоскуты» . Где-то в проблеме может быть вызов. Вы выбираете лучший способ решить эту проблему для вашего дизайна стеганого одеяла.
Сколько букв в алфавите? (26)
Почему изготовление одеяла из 26 квадратов может быть проблемой? - Пусть учащиеся поэкспериментируют с 26 квадратами. Они могут нарисовать возможные варианты использования квадратных плиток или кубов. Цифровые инструменты также можно использовать для упорядочивания плиток и представления работ учащихся.
(26 будет состоять только из массивов 1 x 26 или 2 x 13, что нежелательно для лоскутного одеяла такого типа. Учащиеся встретят «остаток» (6 x 4 + 2, 5 x 5 + 1) или найдут некоторые «заплатки» короткие (7 x 4). Примите реалистичные решения для контекста (например, лоскутное одеяло 5 x 5: поместите 2 буквы на одну заплатку, лоскутное одеяло 6 x 4: сделайте его 7 x 4 и включите 2 новых или пустых патчи. )
) - Предложение: Если мы добавим патчи для каждой из цифр 0-9, сколько тогда будет патчей? (26 + 10 = 36)
Посмотрите, какие одеяла вы могли бы сделать тогда.
Попросите учащихся найти все возможные варианты:
1 x 36 2 x 18 3 x 12 4 x 9 6 x 6 Почему?
Занятие 3
Занятие 1
- Предложите учащимся поделиться своими рисунками стеганых одеял с алфавитом для 36 нашивок. Обсудите «оставшуюся проблему» и оцените творческие решения.
Почему было невозможно сделать одеяло с пятью заплатками подряд?
Запишите 36 ÷5 = 7 r 1 и спросите учащихся, что означает r 1 (остаток от 1).
Укажите, что часто задачи на деление решаются неравномерно. Мы называем то, что осталось, , остаток . - Представьте, что у нас есть 26 патчей, и мы пытаемся разместить по шесть патчей в каждом ряду. Один из способов записать эту задачу: 26 ÷ 6 = 4 r2.

- На диаграмме классов быстро нарисуйте массивы, которые были разработаны для 26 патчей.
- Обсудите «размеры» массива, вводя слова факторы и произведение . Модель с примером:
Попросите каждого учащегося записать под своим дизайном лоскутного одеяла то, что находится в рамке выше, регулируя числа для своего дизайна.
Деятельность 2
Напишите на доске 4 36 9.
Вот еще три числа, которые связаны умножением и делением.
Запишите набор уравнений умножения и деления, используя эти числа.Предложите учащимся работать в парах, чтобы составить уравнения и создать массив, представляющий все четыре уравнения. Студенты должны быть готовы обосновать свою позицию (объясняя, откуда они знают, что они правы).
4 x 9 = 36 9 x 4 = 36 36 ÷ 4 = 9 36 ÷ 9 = 4
Свяжите каждое уравнение с массивом 9 x 4, который учащиеся должны узнать из предыдущего задания по созданию лоскутного одеяла. Особое внимание обратите на деление. Например, 36 ÷ 4 = 9дает количество строк, созданных из 36 патчей (площадь), если каждый ряд состоит из четырех патчей.
Особое внимание обратите на деление. Например, 36 ÷ 4 = 9дает количество строк, созданных из 36 патчей (площадь), если каждый ряд состоит из четырех патчей.- Подведите итоги на классной таблице. Например:
- Есть четыре связанных факта только (семейство фактов) и не более.
4 х 7 = 28 7 х 4 = 28 28 ÷ 4 = 7 28 ÷ 7 = 4 - Умножение — это операция «переворота». Вы можете изменить порядок факторов без изменения произведения. (Это как сложение.)
Мы говорим, что умножение (и сложение) равны коммутативный .
4 х 7 = 7 х 4 = 28 - Деление не является коммутативным, т.е. 36 ÷ 4 = 9, но 4 ÷ 36 = 0,1111… (1/9). Частные деления не совпадают (ответ).
Мы говорим, что деление (и вычитание) не коммутативно .
- Есть четыре связанных факта только (семейство фактов) и не более.
Задание 3
- Попросите учащихся сыграть в игру Умножение, рисование и запись в парах . Рассмотрите возможность объединения в пары учащихся с одинаковым уровнем знания таблицы умножения, что будет способствовать развитию туакана-тейна и уверенности учащихся в своих навыках.

Им нужны игральные карты (с цифрами от 2 до 9), карандаш и бумага.
Победителем становится тот, у кого после десяти раундов окажется больше всего пар карточек с одинаковыми продуктами, но изготовленными с использованием разных факторов.
Например: 6 x 4 = 8 x 3 = 24, или 4 x 4 = 2 x 8 = 16
Как играть:
Карты перемешиваются и кладутся лицом вниз в стопку между обоими игроками.
Игроки по очереди переворачивают по три карты из стопки. Это факторы. Игрок возвращает одну карту в низ стопки. Игрок должен написать факт(ы) умножения для двух карт. Они также могут нарисовать массив и записать семейство фактов.
Например: - Учащиеся завершают занятие написанием словесных сценариев для своих наборов уравнений (семейство фактов). Вы можете выбрать работу со студентами, которым нужна дополнительная поддержка, в небольшой группе, в то время как другие студенты будут работать самостоятельно. В конечном счете, все учащиеся должны уметь писать словесные сценарии для наборов уравнений.
 Они могут быть написаны с использованием цифровых инструментов и могут быть смоделированы с использованием материалов (например, счетчиков). Это не обязательно должны быть сценарии квилтинга.
Они могут быть написаны с использованием цифровых инструментов и могут быть смоделированы с использованием материалов (например, счетчиков). Это не обязательно должны быть сценарии квилтинга.
Например: «Было три мешка по пять яблок в каждом. Пятнадцать поделили на три мешка — это пять. Если эти пятнадцать яблок разложить по пяти мешкам, то в каждом окажется по три. Это будет пять лотов по три.
Занятие 4
Занятие 1
Покажите альтернативный набор стеганых одеял или ткани тапа (PowerPoint 2). Например:
Попросите четырех учащихся записать по одному факту каждого из связанных фактов.
(6 х 5 = 30, 5 х 6 = 30, 30 ÷ 5 = 6, 30 ÷ 6 = 5) и объяснить каждый факт со ссылкой на лоскутное одеяло, включая демонстрацию коммутативного (оборотного) свойства умножения. Поверните одеяло, чтобы продемонстрировать это.
Занятие 2
- Раздайте учащимся соединяющие кубики (или цветные фишки).
 Пусть пары учеников возьмут по 48 кубиков. Спросите, какие множители могут составить 48. Запишите возможности, используя умножение; 1 х 48, 2 х 24, 3 х 16 и т. д.
Пусть пары учеников возьмут по 48 кубиков. Спросите, какие множители могут составить 48. Запишите возможности, используя умножение; 1 х 48, 2 х 24, 3 х 16 и т. д. - Попросите одного ученика из каждого ученика смоделировать пару 4 x 12, соединив кубики. Затем пусть его партнер использует те же кубики для моделирования 12 x 4. Обсудите, что получится. (Им нужно было перегруппировать их). Повторите с 6 x 8 и 8 x 6. Подчеркните, что коммутативное свойство включает те же множители и произведение, но требует другого взгляда на массив (т. е. либо строки, либо столбцы образуют одинаковые множества).
- Разложите на карточках факты умножения 48 (Переписчик 1). Задержать 5 раз? и 7 х? Соедините пары уравнений, демонстрирующих свойство коммутативности.
Думаете, это все факты умножения на произведение 48? (Вы можете расположить карты в порядке первого множителя.)
Почему нет 5-кратных и 7-кратных фактов? (Используйте карточки. Учащиеся должны понять, что 48 не входит в число кратных 5 и 7. 48 не делится на 5 и 7).
48 не делится на 5 и 7).
С помощью калькулятора покажите, что 48 ÷ 5 = 9,6 и 48 ÷ 7 = 6,857142857…
Как вы думаете, что показывает десятичная часть произведения? (Остаток, поэтому 48 не делится на 5 и 7) - Попросите учащихся изучить факты умножения с разным количеством кубиков, используя язык тех же множителей и произведений, сосредоточив внимание на перегруппировке. Их исследование может показать, что некоторые числа имеют только два делителя, например 17 и 31. Эти числа являются простыми.
Занятие 3
- Запишите одно знакомое уравнение умножения в таблицу класса. Например, 6 x 2 = 12. Попросите одного из учеников в каждой паре смоделировать это, составив 6 групп по 2 и , соединив кубики вместе в одну линию из 12.
Запишите 12 ÷ 6 = 2. другой ученик в паре разыгрывает это с кубиками.
Предложите учащимся описать, что произошло, и запишите такие идеи, как: это наоборот, деление не умножение, это наоборот, мы вернулись к тому, с чего начали.
Спросите, Всегда ли так? Как мы можем узнать? Принимайте идеи учеников. Они должны включать студентов, изучающих больше примеров. Сделайте вывод, что невозможно проверить все факты умножения и деления. Скажем, идея «отмены» означает, что умножение и деление являются обратными операциями, как включение и выключение выключателя света. Уничтожение друг друга — это именно то, как ведут себя умножение и деление.
Запись « обратная связь» на диаграмме классов. Обсудите слова, похожие на инверсию, например. перевернуть, отменить, вернуть, вернуть и их значение. Установите связь с обратной зависимостью между сложением и вычитанием. Подчеркните, что в каждой паре операций одна операция или действие отменяет другое.
Вернитесь к одеялу в Упражнении 1 (выше) и к записанным уравнениям:
(6 x 6 = 30, 5 x 6 = 30, 30 ÷ 5 = 6, 30 ÷ 6 = 5)
Попросите учащихся объяснить «отмену» (снова обратная связь со ссылкой на лоскутное одеяло. (Это немного сложнее увидеть, потому что этот массив физически нельзя «отменить». Однако вы можете составить ряды из шести кубиков и показать 5 x 6, расположив пять рядов по вертикали Сколько у меня лоскутов? Что произойдет, если я теперь разделю на пять? )
(Это немного сложнее увидеть, потому что этот массив физически нельзя «отменить». Однако вы можете составить ряды из шести кубиков и показать 5 x 6, расположив пять рядов по вертикали Сколько у меня лоскутов? Что произойдет, если я теперь разделю на пять? )Напишите в таблице класса:
Знание того, что умножение и деление являются обратными операциями, полезно, потому что……..
Попросите учащихся предложить причины и записать их, в том числе:
Мы можем использовать умножение, чтобы решить задачи на деление.
Мы можем проверить операции деления с помощью умножения. (Как?)
Занятие 4
Раздайте Copymaster 2 для работы учащихся. Подчеркните обратные операции и необходимость для учащихся показать или объяснить , как умножение помогает решать задачи на деление.
Занятие 5
Занятие 1
Повторите основные выводы из Занятия 4. Предложите учащимся поработать в парах, чтобы поделиться своими решениями задач квилтинга из Занятия 4, Занятие 4. Предложите им задавать друг другу вопросы.
Предложите учащимся поработать в парах, чтобы поделиться своими решениями задач квилтинга из Занятия 4, Занятие 4. Предложите им задавать друг другу вопросы.
Упражнение 2
- Покажите несколько примеров лоскутного одеяла или ткани тапа с помощью PowerPoint 1:
- Напишите в таблице классов:
Одно одеяло из шестнадцати заплаток:
Одно одеяло из тридцати заплаток:
Одно одеяло из сорока пяти заплаток:
Если я переставлю заплатки в один ряд, как будет выглядеть одеяло? (Больше похоже на длинный шарф) - Попросите учащихся записать уравнения умножения для каждого из этих утверждений.
Одно одеяло из шестнадцати заплат: 1 x 16 = 16
Одно одеяло из девяти заплат: 1 x 30 = 30
Одно одеяло из тридцати заплат: 1 x 45 = 45
Если ваши уравнения верны, каковы ответы на 16 ÷ 1 = ☐ , 30 ÷ 1 = ☐ , 45 ÷ 1 = ☐? - Попросите учащихся обсудить свои идеи, а затем объяснить и обосновать свое мнение.
 Связывают ли они деление с вопросом «Сколько столбцов одного патча составляет в общей сложности 16, 30 или 45 патчей?»
Связывают ли они деление с вопросом «Сколько столбцов одного патча составляет в общей сложности 16, 30 или 45 патчей?»
Если ваши уравнения верны, каковы ответы на 16 ÷ 16 = ☐ , 30 ÷ 30 = ☐ , 45 ÷ 45 = ☐?
Связывают ли они деление с вопросом «Сколько рядов по 16 нашивок составляет в общей сложности 16 накладок и т. д.?» - Приведите другие примеры деления числа на единицу и само на себя. Для проверки ответов можно использовать калькуляторы.
Занятие 3
Предложите учащимся работать в группах от 2 до 4 над Это правда? (Переписчик 3 (Цель: различать правильные и неправильные уравнения и выражения умножения и деления и уметь объяснить почему, обосновывая свое решение)
Учащиеся по очереди выбирают утверждение и объясняют его другим в группе, если и почему утверждение является фактом, или если и почему оно неверно (истинно или ложно)
Попросите учащихся создать свои собственные факты или нефакты, связанные с умножением и делением, т.
 Найди значение выражения:
Найди значение выражения:


 продали 1/5 часть этого куска. Сколько метров ткани осталось в куске?
продали 1/5 часть этого куска. Сколько метров ткани осталось в куске? Сколько лет живёт берёза?
Сколько лет живёт берёза?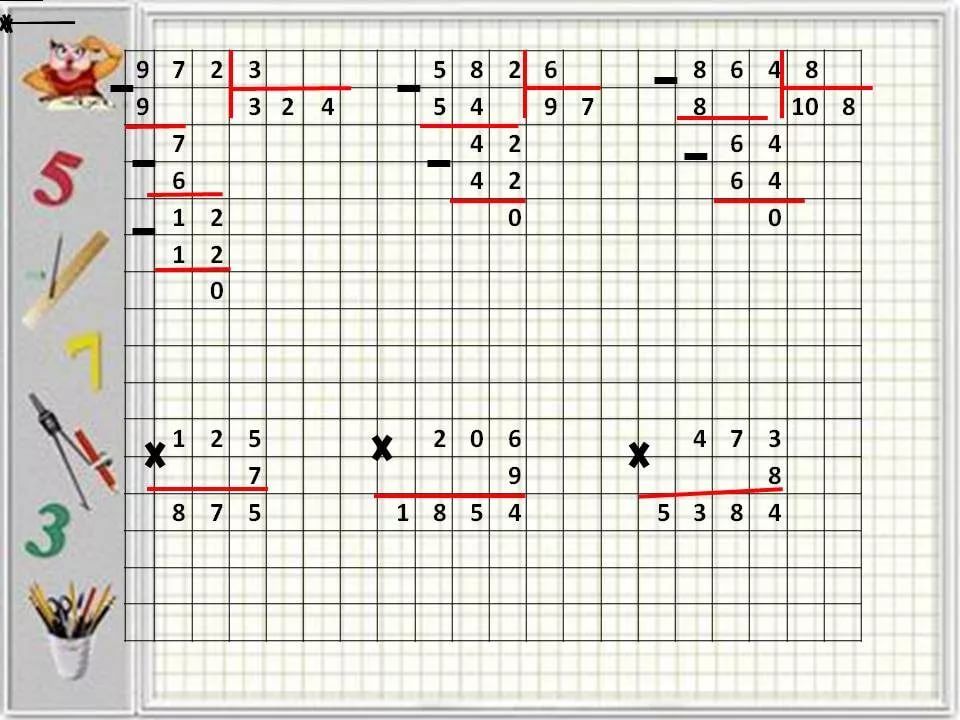


 Это была бы хорошая возможность взглянуть на любую школьную ткань тапа или панели тукутуку. Кроме того, используйте PowerPoint 1, чтобы показать изображения подходящих стеганых одеял или ткани тапа. Например:
Это была бы хорошая возможность взглянуть на любую школьную ткань тапа или панели тукутуку. Кроме того, используйте PowerPoint 1, чтобы показать изображения подходящих стеганых одеял или ткани тапа. Например: 

 выше), выделяя и записывая словами эти идеи:
выше), выделяя и записывая словами эти идеи: Выделите мультипликативные представления, такие как «9 равно 3 x 3, поэтому 9 + 9 равно 6 x 3».
Выделите мультипликативные представления, такие как «9 равно 3 x 3, поэтому 9 + 9 равно 6 x 3». Когда учащиеся будут делиться идеями, попросите их назвать конкретные числа. Запишите эти истории, используя схемы и слова.
Когда учащиеся будут делиться идеями, попросите их назвать конкретные числа. Запишите эти истории, используя схемы и слова. 
 У вас есть время до конца сегодняшней сессии, чтобы спланировать свой дизайн и то, как вы будете располагать свои «квадратные лоскуты» . Где-то в проблеме может быть вызов. Вы выбираете лучший способ решить эту проблему для вашего дизайна стеганого одеяла.
У вас есть время до конца сегодняшней сессии, чтобы спланировать свой дизайн и то, как вы будете располагать свои «квадратные лоскуты» . Где-то в проблеме может быть вызов. Вы выбираете лучший способ решить эту проблему для вашего дизайна стеганого одеяла.  )
)
 Особое внимание обратите на деление. Например, 36 ÷ 4 = 9дает количество строк, созданных из 36 патчей (площадь), если каждый ряд состоит из четырех патчей.
Особое внимание обратите на деление. Например, 36 ÷ 4 = 9дает количество строк, созданных из 36 патчей (площадь), если каждый ряд состоит из четырех патчей.
 Они могут быть написаны с использованием цифровых инструментов и могут быть смоделированы с использованием материалов (например, счетчиков). Это не обязательно должны быть сценарии квилтинга.
Они могут быть написаны с использованием цифровых инструментов и могут быть смоделированы с использованием материалов (например, счетчиков). Это не обязательно должны быть сценарии квилтинга.  Пусть пары учеников возьмут по 48 кубиков. Спросите, какие множители могут составить 48. Запишите возможности, используя умножение; 1 х 48, 2 х 24, 3 х 16 и т. д.
Пусть пары учеников возьмут по 48 кубиков. Спросите, какие множители могут составить 48. Запишите возможности, используя умножение; 1 х 48, 2 х 24, 3 х 16 и т. д. 48 не делится на 5 и 7).
48 не делится на 5 и 7). 
 (Это немного сложнее увидеть, потому что этот массив физически нельзя «отменить». Однако вы можете составить ряды из шести кубиков и показать 5 x 6, расположив пять рядов по вертикали Сколько у меня лоскутов? Что произойдет, если я теперь разделю на пять? )
(Это немного сложнее увидеть, потому что этот массив физически нельзя «отменить». Однако вы можете составить ряды из шести кубиков и показать 5 x 6, расположив пять рядов по вертикали Сколько у меня лоскутов? Что произойдет, если я теперь разделю на пять? ) Связывают ли они деление с вопросом «Сколько столбцов одного патча составляет в общей сложности 16, 30 или 45 патчей?»
Связывают ли они деление с вопросом «Сколько столбцов одного патча составляет в общей сложности 16, 30 или 45 патчей?»