Примеры на умножение в столбик 4 класс: 4 класс. Примеры на умножение многозначных чисел в столбик. Примеры с ответами. Скачать pdf или jpg.

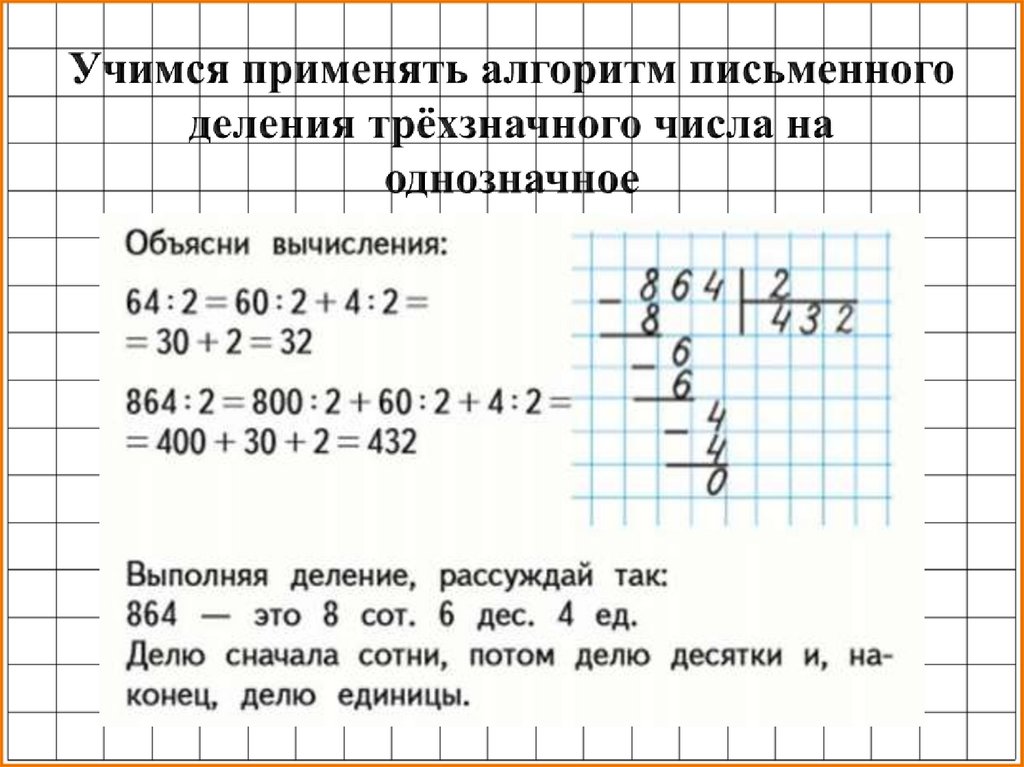
Умножение в 4 классе

Народ, ваши дети-4 клашки умножают в столбик 4-5 значные числа? Наша учительница постоянно дает задания на перемножение больших чисел. Не 5значное на однозначное, а 5значное на 4значное, или даже на 5значное…
Не пойму, к чему это … Отработать навык умножения вполне можно на трехзначных числах. Или кто-то в ходе вычислений в средней школе будет такие числа считать не на калькуляторе??
Огромный столбик с кучей приписанных промежуточных цифр, дети путаются…
Или сейчас везде такое??

На уроках математики калькулятора нет никогда. Так что будут считать в столбик до выпуска. Молодец ваша учитель.

Мой сын учится в 7 классе. Ни разу еще такие числа не понадобилось перемножать.. ни на математике/алгебре, ни на физике… Лицей, если что.

разницы нет умножать трёхзначные или 10 значные-правило одно и то же, а учитель молодец-заставляет детей руку набивать.

регионы я так понимаю?

Нужды в таком умножении может и нет (гляну в тетрадку ребенка, посмотрю), но вот научиться концентрироваться, не путаться, очень важно.

Хотя в четвертом классе может быть это слишком жестко, не знаю. Наших четвероклашек больше учат устному счету на скорость. Умножать четырехзначные в столбик пока не заставляют.

Москва.

Скажите, вы в принципе рассуждаете, или у вас дети-школьники, которые так же постоянно решают такие примеры?
В учебных программах примеры максимум 3 значные.

Хотелось бы увидеть ответы мам 4 клашек)
Потому что я тоже могу рассуждать о том, как это классно, перемножать миллиарды, учить 15 стихотворений каждую неделю, сдавать нормы ГТО на каждой физре, пересказывать 20страничные тексты итд))
Нуачё такоВа. Это ж полезные навыки!)))
Хочу понять, в других классах это то же считают, или ограничиваются более простыми вариантами.

ах-ха, в столбик только в Маскве умножают, да, особенно если больше 3-значных

У нас считали, а еще цифровые цепочки с определенной последовательность в 12-18 действий.

Это супер автоматизирует навыки счета и развивает внимательность.
Сейчас, в 6 классе, огромное отличие от ученика , который только пришел в класс. Ему за моим в счете ( и в минимуме ошибок) никак не угнаться, хотя у меня абсолютно нематематический ребенок.

Я мамам 4-клашки. Второй ребенок сейчас в 6-м классе.
Миллиарды не перемножаем, по 15 стихотворений не учим, нормы ГТО не сдаем (но дополнительно футбол, пионербол и другие подвижные игры каждую неделю), большие тексты не пересказываем. Зачем утрировать?
Пятизначные на пятизначные мои перемножают и перемножали. Считаю это нормальным.

конечно нормально. А что вас удивляет?

То есть у вас тоже на постоянной основе такие большие примеры? Не в целом, иногда взять и перемножить, а реально почти каждый день?
Я полагаю, гораздо полезнее было бы тренировать перевод единиц, к примеру скорости из км/ч в м/с и так далее.

Потому что вот это уж точно потом часто нужно будет на той же физике. И надо быстро ориентироваться…
Или, опять же, часто требуется быстро считать проценты и доли, вот это тоже нужно тренировать. ..

Меня удивляет то, что в программе 4класса таких примеров не предусмотрено. Вроде, если это так нормально, то и в заданиях это должно быть, в рабочей те ради, в учебнике, нет?
В мое время мы точно никогда 5значные на 5 значные не множили.да, я умела это делать. Но мы не решали эти примеры по полурока каждый день.

Честно говоря, в этой четверти я ребенковые уроки отдала полностью под ее ответственность, не знаю что проходят по матике.
В конце октября умножали и делили многозначные числа на однозначные. Ну или на 100 типа.
У моей математика Моро, довольно просто все.
Как умножить 54876 на 4978 мой ребенок не в курсе.

Что полезнее решает учитель
На проценты их в 5-6-м классе будут хорошо гонять. И перевод единиц там же.

Программы есть разные. В Вашей не предусмотрено, в других предусмотрено. Учитель молодец, что не зацикливается на одной программе, а дополняет уроки упражнениями из других программ.

Мы считаем такое в 3 классе (умножение).
Деление многозначных на двузначные.
Раскрываем скобки и ты пы.
Навык, я считаю, полезный.

Ну а что вы страдаете? Неужели в вашей школе не найдётся класса с учителем-пофигистом и программой уровня «не бей лежачего»?
А учитель молодец. Таких сейчас очень мало.

Вы в 3 классе решаете примеры по типу 12345*12345? Позвольте Вам не поверить))

Ваш учитель дает более сложные задания, это факт. Тем не менее они на материал, который в 4 классе знают. И это очень полезные задания.

Что еще вам добавить?
Считаете нужным заниматься чем-то другим? Подойдите к учителю с этим предложением. А, кстати, чем? что они не проходят, занимаясь этим?

да же не знаю что это за программа.. В обычном учебнике Моро, Гейдмана, и в той же Петерсон, такие примеры предусмотренны.
Мымножили, причем и в 5 классе помню были. Длинные примерыв несколько действий.. ненавидела жуть.

Если математика по Петерсон то очень может быть, мне кажется у сына чуть ли не со второго класса огромные примеры были с огромными числами.

Нет такого в Петерсоне в 3м классе. Есть длинные примеры, но никаких умножений 6и значных чисел нет. И в 4м тоже.

В Петерсоне может быть и нет, а в учебнике Петерсон было.

конечно умножали
какая разница сколько разрядов, если приемом владеешь
именно и важно научиться аккуратно расписывать большие столбики, этому и учат

калькуляторы разрешены только на физике
умножение — фигня, потом корни начнутся и не только простые квадратные
и без калькулятора )))

Есть такие

Вам до физики еще 2 года, если конечно класс не углубленный будет, сто раз еще все забудется)))

у других мам дети уже уравнения высших степеней решают
и с радикалами
не к ночи Безу с Фалесами будь помянуты
и это только кажется, что до них от 4 класса еще далеко
на их фоне умножение хоть бы и 10значного — как веселый отдых в переменку
кстати в столбик еще и делят и не только простые во всех смыслах числа, а целые уравнения
так что не жалуйтесь на прыжки со скакалкой перед прыжками с парашютом
тренировочная рутина не развлекательна, но необходима для следующего уровня

наверняка есть, там умножение очень рано начинается и в конце второго — умножение трехзначных (смотрела учебник за 2 класс — впечатлилась)

Гейдман помедленнее примерно на полгода

Я , наоборот, даю сыну такие примеры, хотя в учебнике их нет.
Да, в 5-6 классах они понадобятся.

Ну и не верьте. Ваше право.
У Петерсон это есть. Кроме того, похожие примеры встречаются в разного рода тренажерах.

Это класс?

Вы задание то прочитайте.. Там дано произведение, через которое ответ находится. Тут нет умножения в столбик многозначных чисел. Это примеры на сложение и вычитание.

Там ниже посмотрите и вот тут целая тема

Есть, решаем

+100. Добавлю ещё (ну у меня свой шкурный интерес), что практически на всех вступительных экзаменах в 5 класс более-менее сильных школ по математике такие примеры были, есть и, если верить демоверсиям и рекомендациям с сайтов школ, будут.

Посмотрела ниже. И там нет умножения многозначных на многозначные в столбик. А урок 21 — это ПОСЛЕДНИЙ урок З класса.

Не все идут линейно по учебнику. У Петерсон очень скачут темы. Понятие многозначных чисел вводится примерно в октябре — это уроки 18-30 части 1. У нас решили продолжить эту тему, усложнить для закрепления принципа, а потом уже переходить к другим.

И что вы уперлись…

Ну а если бы вы только решали примеры и все? Максимум- простейшие задачи на скорость.. тогда вас тоже бы устраивали эти ежедневные тренировки «калькуляции»? Я реально не понимаю, в 4 классе ничего больше не надо? Считать, считать и считать?

что не мешает умножать столбиком двух и более значные числа уже раньше. И что последнию тему уже не надо делать? Хотя вы правы, учителя часто не успевают пройти учебники целиком.. и половина остается непройденной.

У меня двое детей закончили началку по Петерсон. Это прекрасный учебник, я его хорошо знаю. Сейчас у меня есть третьеклассник, который учится по Ивановой. Они прошли умножение трехназначных чисел на трехзначные в столбик. Но пятизначные на пятизначные не умножают. И уж конечно не тратят по полурока на один такой пример.

На это просто нет времени. И если учитель из стартового поста занимается такой ерундой, значит дети пропускают более важные темы.

Моро очень простенький учебник,неолимпиалного уровня.

Нет, почему полурока на один пример. На уроке примера четыре таких решается, плюс пара задачек

а что надо ?дифференцировать?

Решать разные типы задач, не?

а что одно другому мешает? Там я дала фото из учебника, посмотрите, там очень разнэ задания, естественно все учат щхитать. Потому я и люблю этот учебник Хотя конечно уже в 8 классе ох уж эти стобики примеров и примеров)) правда уже не прсото умножениие и деление

А я вам отвечаю, что у нас на уроках дети в основном ТОЛЬКО перемножают!!! Вот я и задаюсь вопросом. Зачем это в таких количествах. И так ли это и в других 4 классах

Я в курсе)

Ну я то причем, вы выбрали школу. Можете дома заниматься, все в ваших руках. Ктото школу меняет.

длинные примеры обычно идут в дз. Ну и произволительность труда у всех коннчно разная , однако мало кто из детей, идущих по петерсон , делает пример один полчаса. . такие дети подобные примеры в 5-6 классе решают, а не в 3 и 4. В среднем длинный пример загимает не более 5 минут. И все оавно у хорршего учителя это не классная работа.

Ну менять школу за полгода до окончания началки бессмысленно… Когда выбирали, ожидали другого)))

Вот лучше бы они длинными примерами занимались. Или уравенениями сложными с раскрытием скобок и всеми изученными арифметическими действиями. Задачами сложными….чем просто перемножать числа.

Откуда вы знаете, что на уроках в основном только перемножают? Вы были на нескольких уроках? Не надо говорить, что это говорит так ваш ребенок. Дети скажут то, что вам хочется услышать. Если ребенку лень перемножать, то можно маме сказать и мама будет негодовать о правильности преподавания. Главное, стрелки перевести на другого.

Если знаете, что и как преподавать, идите в школу работать. У вас будет самое эффективное преподавание.

Не надо так нервничать. Откуда я знаю? Потому что я вижу тетради с классными работами, я вижу постоянные самостоятельные и контролтные на эту тему.
Где я писала о том, что моему ребенку лень умножать?

3 месяца только перемножают? Значит уже должны были научиться)))

О чем и речь))))

А зачем оно в 3 классе то?
Началка ка раз время отработки для более простых навыков

Петерсон?
Там такое делают…заглядываю и закрываю.
Если ребёнок тянет, как мой, ну…пусть решает.

у вас деточка считать не умеет, и поэтому вы беспокоитесь? учите считать. на огэ и егэ калькуляторов нет, а числа могут попасться любые

Моя деточка считает на 4 и 5, не переживайте.

+ бывают в ВПР+ вообще полезно в уме многоходовые операции совершать.

В Впр перемножение 5значных чисел???
Вы давно вариант Впр смотрели?)))

У нас и умножают и деление сейчас началось. Есть кстати тренажер Узоровой/Нефедовой. У меня от старших остался. С большими числами. Мой практикуется еще и там

ВПР вообще неизвестно на кого рассчитаны. После Петерсон за полурока в прошлом году весь класс сделал

Противоречие. В начале топа вы пишите, что дети путаются.

так в чём тогда проблема? умножение больших чисел тренирует мозги, так же как и сложение нескольких чисел в уме. учит держать в уме не одно действие, а несколько. ну и внимательность тоже развивает

Я про 5 класс, в прошлом году и во входной работе МЦКО было.
Весь 4 класс- это 1 четверть 5, там важно все хорошо отработать.

неважно, сколькизначное число… я так понимаю, учитель доводит до автоматизма сам принцип перемножения. мне кажется, наоборот, это хорошо… мне бы понравилось. в 4 классе тоже умножала дочь, не помню, правда, какие цифры, но точно помню, что столбик присутствовал

Ну вряд ли бы вам понравились сплошняком перемножение 5значных чисел на большинстве уроков))
А то, что в 4 классе умножают в «какой-то столбик»- это конечно хорошо, и никто и не спорит!

10 математических секретов, которые научат легко считать в уме

Те, кто в школе относился к урокам математики с пренебрежением, наверняка хотя бы несколько раз в жизни бывали в неловкой ситуации.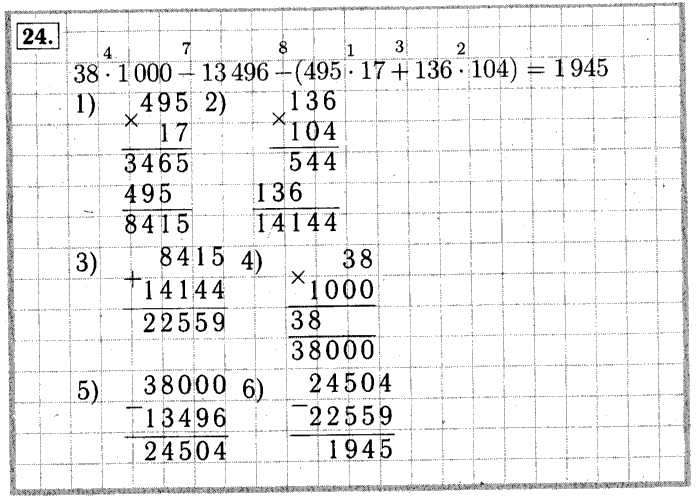 Как посчитать, сколько оставить на чай или сумму коммунального платежа? Если знать пару простых приёмов, это займёт у вас буквально секунду. А уж во время экзамена знание правил умножения больших чисел может помочь сэкономить критически недостающее время. «Мел» совместно с Creu делится простыми секретами вычислений.

1. Умножение на 11

Все мы знаем, что при умножении на десять к числу добавляется ноль, а знаете ли вы, что существует такой же простой способ умножения двузначного числа на 11? Вот он:

Возьмите исходное число и представьте промежуток между двумя знаками (в этом примере мы используем число 52): 5_2

Теперь сложите два числа и запишите их посередине: 5_(5+2)_2.

Таким образом, ваш ответ: 572.Если при сложении чисел в скобках получается двузначное число, просто запомните вторую цифру, а единицу прибавьте к первому числу: 9_(9+9)_9 (9+1)_8_9 10_8_9 1089. Это срабатывает всегда.

2. Быстрое возведение в квадрат

Этот приём поможет быстро возвести в квадрат двузначное число, которое заканчивается на пять. Умножьте первую цифру саму на себя +1, а в конце допишите 25. Вот и всё! 252 = (2x(2+1)) & 25

2×3 = 6

625

3. Умножение на пять

Большинству очень просто даётся таблица умножения на пять, но когда приходится иметь дело с большими числами, сделать это становится сложнее.

Этот приём невероятно прост. Возьмите любое число и поделите пополам. Если в результате получилось целое число, припишите ноль в конце. Если нет, не обращайте внимание на запятую и в конце добавьте пять. Это срабатывает всегда:

2682×5 = (2682 / 2) & 5 или 0

2682 / 2 = 1341 (целое число, поэтому добавьте 0)

13410

Давайте попробуем другой пример:

5887×5

2943,5 (дробное число, пропустите запятую, добавьте 5)

29435

4. Умножение на девять

Это просто. Чтобы умножить любое число от одного до девяти на девять, посмотрите на руки. Загните палец, который соответствует умножаемому числу (например, 9×3 — загните третий палец), посчитайте пальцы до загнутого пальца (в случае 9×3 — это два), затем посчитайте после загнутого пальца (в нашем случае — семь).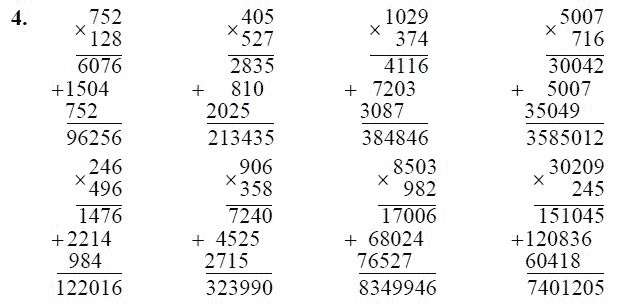 Ответ — 27.

5. Умножение на четыре

Это очень простой приём, хотя очевидный лишь для некоторых. Хитрость в том, что нужно просто умножить на два, а затем опять умножить на два: 58×4 = (58×2) + (58×2) = (116) + (116) = 232.

6. Подсчёт чаевых

Если вам нужно оставить 15% чаевых, есть простой способ сделать это. Высчитайте 10% (разделите число на десять), а потом добавьте получившееся число к его половине и получите ответ:

15% от $25 = (10% от 25) + ((10% от 25) / 2)

$2.50 + $1.25 = $3.75

7. Сложное умножение

Если вам нужно умножать большие числа, причём одно из них — чётное, вы можете просто перегруппировать их, чтобы получить ответ:

32×125 всё равно что:

16×250 всё равно что:

8×500 всё равно что:

4×1000 = 4,000

8. Деление на пять

На самом деле делить большие числа на пять очень просто. Нужно просто умножить на два и перенести запятую:

195 / 5

1. 195 * 2 = 390

2. Переносим запятую: 39,0 или просто 39.

2978 / 5

1. 2978 * 2 = 5956

2. 595,6

9. Вычитание из 1000

Чтобы выполнить вычитание из 1000, можете пользоваться этим простым правилом. Отнимите от девяти все цифры, кроме последней. А последнюю цифру отнимите от десяти:

1000-648

1. От 9 отнимите 6 = 3

2. От 9 отнимите 4 = 5

3. От 10 отнимите 8 = 2

Ответ: 352

10. Систематизированные правила умножения

Умножение на 5: Умножьте на 10 и разделите на 2.

Умножение на 6: Иногда проще умножить на 3, а потом на 2.

Умножение на 9: Умножьте на 10 и отнимите исходное число.

Умножение на 12: Умножьте на 10 и дважды прибавьте исходное число.

Умножение на 13: Умножьте на 3 и 10 раз прибавьте исходное число.

Умножение на 14: Умножьте на 7, а затем на 2.

Умножение на 15: Умножьте на 10 и 5 раз прибавьте исходное число, как в предыдущем примере.

Умножение на 16: Если хотите, 4 раза умножьте на 2. Или умножить на 8, а потом на 2.

Умножение на 17: Умножьте на 7 и 10 раз прибавьте исходное число.

Умножение на 18: Умножьте на 20 и дважды отнимите исходное число.

Умножение на 19: Умножьте на 20 и отнимите исходное число.

Умножение на 24: Умножьте на 8, а потом на 3.

Умножение на 27: Умножьте на 30 и 3 раза отнимите исходное число.

Умножение на 45: Умножьте на 50 и 5 раз отнимите исходное число.

Умножение на 90: Умножьте на 9 и припишите 0.

Умножение на 98: Умножьте на 100 и дважды отнимите исходное число.

Умножение на 99: Умножьте на 100 и отнимите исходное число.

БОНУС: проценты

Вычислить 7% от 300.

Сперва нужно понять значение слова «процент» (percent). Первая часть слова — про (per). Per = для каждого. Вторая часть — цент (cent), это как 100. Например, столетие = 100 лет. 100 центов в одном долларе и так далее. Итак, процент = для каждой сотни.

Итак, получается, что 7% от 100 будет семь. (Семь для каждой сотни, только одной сотни).

8% от 100 = 8.

35,73% от 100 = 35,73

Но как это может быть полезным? Вернёмся к задачке 7% от 300.

7% от первой сотни равно 7. 7% от второй сотни — то же 7, и 7% от третьей сотни — все те же 7. Итак, 7 + 7 + 7 = 21. Если 8% от 100 = 8, то 8% от 50 = 4 (половина от 8).

Дробите каждое число, если нужно вычислить проценты из 100, если же число меньше 100, просто перенесите запятую влево.

Примеры:

8%200 =? 8 + 8 = 16.

8%250 =? 8 + 8 + 4 = 20,

8%25 = 2,0 (Передвигаем запятую влево).

15%300 = 15+15+15 =45

15%350 = 15+15+15+7,5 = 52,5

Также полезно знать, что вы всегда можете поменять числа местами: 3% от 100 — то же самое, что 100% от 3. А 35% от 8 — то же самое, что и 8% от 35.

Источник: Creu

---

What?, Methods, Long, Properties & Examples

Процесс нахождения произведения двух или более чисел называется умножением. Полученный таким образом результат называется продуктом . Предположим, вы купили 6 ручек в один день и 6 ручек на следующий день. Всего ручек, которые вы купили, теперь 2 умножить на 6 или 6 + 6 = 12.

Это также можно записать как 2 x 6 = 12

Не тот символ, который используется для умножения. Символ (x) обычно используется для обозначения умножения. Другими распространенными символами, которые используются для умножения, являются звездочка (*) и точка (.) 

Важные термины при умножении

Некоторые важные термины, используемые при умножении:

Множимое — Число, которое нужно умножить, называется множимым.

Множитель — Число, на которое мы умножаем, называется множителем.

Произведение – Результат, полученный после умножения множителя на множимое, называется произведением.

Связь между множителем, множимым и произведением может быть выражена как:

Множитель  ×  Множитель = Произведение

Разберем это на примере.

Предположим, у нас есть два числа 9 и 5. Мы хотим умножить 9 на 5.

Итак, мы выражаем это как 9 x 5, что дает нам 45.

Следовательно, 9 x 5 = 45

Здесь 9 равно множимое, 5 — множитель, 45 — произведение.

Существует два метода умножения чисел, а именно метод расширенной записи и метод столбца.

Метод расширенной записи

В методе расширенной записи мы расширяем множимое в соответствии со значениями разряда, а затем умножаем каждое число на множитель. Затем мы суммируем все полученные результаты, чтобы получить окончательный ответ. Давайте разберемся на примере.

Например, умножьте 1235 на 4

Решение

Мы решим это шаг за шагом.

Шаг 1. Запишите число (множимое) в развернутой форме. Получаем,

1235 = 1000 + 200 + 30 + 5

Шаг 2. Умножьте каждое число на заданное число (множитель) по одному. Получаем,

1000 х 4 + 200 х 4 + 30 х 4 + 5 х 4

= 4000 + 800 + 120 + 20

Шаг 3 — Складываем полученные результаты.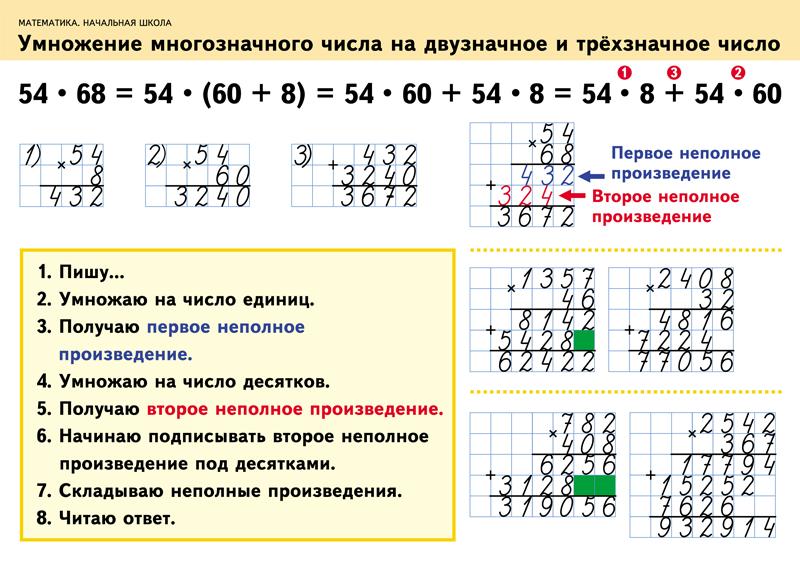 Мы получаем

4000 + 800 + 120 + 20 = 4940, что является нашим окончательным результатом

Следовательно, 1235 x 4 = 4940

Этот метод, хотя и простой, может не подходить для больших чисел. Но он используется для понимания основных понятий умножения.

Колоночный метод

В этом методе мы разбиваем числа на столбцы и умножаем числа на множимое одно за другим. Есть два сценария использования этого метода.

Давайте разберемся с ними один за другим

Умножение без перегруппировки

Этот метод вступает в силу, когда у нас есть меньшие числа, которые не требуют переноса каких-либо чисел на разряд следующего разряда. Давайте разберемся на примере.

Например, умножить 1021 на 3

 Решение

Мы будем использовать следующие шаги, чтобы получить наш результат.

Шаг 1. Сначала мы записываем множимое и множитель в столбцах.

Шаг 2. Теперь умножаем число, стоящее в разряде единиц, на 3.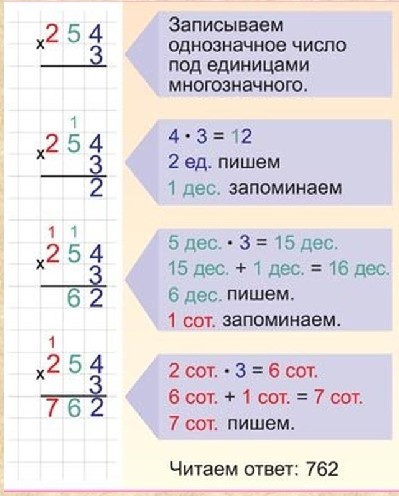 Получаем

Шаг 3. Теперь умножаем число в разряде десятков на 3. Получаем

. Шаг 4. Далее умножаем число в разряде сотен на 3. Получаем

Шаг 5 – Наконец, умножаем число в разряде тысяч на 3. Получаем

Следовательно, 1021 x 3 = 3063

Умножение с перегруппировкой

В приведенном выше случае у нас есть небольшие умножения, которые ни на одном шаге не давали двузначных результатов. Но в случае больших чисел потребуется перенести число на число со следующим значением разряда. Это называется умножением с перегруппировкой. Давайте разберемся на примере.

Например, умножить 5092 на 5

Решение

Мы будем использовать следующие шаги, чтобы получить наш результат.

Шаг 1. Сначала мы записываем множимое и множитель в столбцах.

Шаг 2. Умножьте цифру единиц на 5. У нас 2 x 5 = 10. Запишите 0 в колонке единиц и перенесите 1 в колонку десятков.

Шаг 3 – Умножьте цифру десятков на 5. Получаем 9 x 5 = 45. Добавьте к ней 1, которая была перенесена, чтобы получить 45 + 1 = 46. Теперь запишите 6 в столбце десятков и перенесите 4 в сотню. столбец.

Шаг 4 – Умножаем цифру сотен на 5. Получаем 0 x 5 = 5. Теперь прибавляем к ней перенесенное 4 и получаем 4. Записываем 4 в столбец сотен.

Шаг 5 – Умножьте 5 на цифру тысячи. Получаем 5 x  = 25. Запишите 5 в столбце тысяч и 2 в столбце десятков тысяч.

Следовательно, конечный продукт равен 25460.

Длинное умножение похоже на метод столбца, за исключением того факта, что здесь мы умножаем большие числа. Этот метод используется, когда множимое больше 9, т. е. множимое больше однозначного числа. Этот метод включает следующие шаги –

1. Сначала мы записываем множимое и множитель в столбцах.
2. Сначала умножьте число, стоящее на месте единицы множителя, на все числа множимого и запишите их горизонтально.
3. Убедитесь, что вы записываете числа справа налево и каждое число находится под соответствующим разрядом множимого.
4. Теперь перейдите к следующей строке.
5. Поставьте 0 на месте единицы в этой строке.
6. Теперь найдите цифру в разряде десятков множителя. Умножьте число, стоящее в десятом разряде множителя, на все числа множимого и запишите их горизонтально в той строке, где вы отметили 0,9.0136
7. Снова перейти на следующую строку.
8. Поставьте 0 на месте единиц и десятков в этой строке.
9. Теперь найдите цифру в разряде сотен множителя. Умножьте число, стоящее в сотенном разряде множителя, на все числа множимого и запишите их горизонтально в той строке, где вы отметили два нуля.
10. Продолжайте в том же духе, добавляя дополнительный ноль в каждую строку, пока не дойдете до конца множителя
11. Сложите числа по вертикали в соответствии с их разрядностью.
12. Полученное таким образом число и есть ваш результат.

Давайте разберем это на примере

Например, Умножьте 132 на 13

Решение

1. Сначала мы запишем множимое и множитель в столбцах.

2. Сначала умножьте число, стоящее на месте единицы множителя, на все числа множимого и запишите их горизонтально.

3. Поставьте 0 на месте единицы следующей строки

4. Теперь найдите цифру в разряде десятков множителя. Умножьте число в десятом разряде множителя на все числа множимого и запишите их горизонтально в строке, где вы отметили 0.

5. В множимом больше нет числа. Теперь сложите числа по вертикали в соответствии с их разрядностью.

6. Окончательный ответ 1716. Следовательно, 132 x 13 = 1716

Давайте посмотрим на другой пример, где мы 3 цифры в множимом.

Например, Умножьте 364 на 123

Решение

1. Сначала запишем множимое и множитель в столбцы

2. Сначала умножим число, стоящее на месте единицы, на все числа множителя множимое и запишем их горизонтально.

3. Поставьте 0 на месте единицы следующей строки

4. Теперь найдите цифру в разряде десятков множителя. Умножьте число, стоящее в десятом разряде множителя, на все числа множимого и запишите их горизонтально в той строке, где вы отметили 0,9.0005

5. Поставьте 0 на месте единиц и десятков в следующей строке.

6. Теперь найдите цифру в разряде сотен множителя. Умножьте число, стоящее в сотенном разряде множителя, на все числа множимого и запишите их горизонтально в той строке, где вы отметили два нуля.

7. В множимом больше нет числа. Теперь сложите числа по вертикали в соответствии с их разрядностью.

8. Следовательно, конечный продукт равен 44 772. Мы можем сказать, что 364 х 123 = 44772

• Чтобы умножить число на 10, поставьте 0 справа от числа. Например, 435 х 10 = 4350
• Чтобы умножить число на 100, нужно поставить два нуля справа от числа. Например, 435 х 100 = 43500
• Чтобы умножить число на 1000, поставьте справа от числа три нуля. Например, 435 x 1000 = 435000
• Чтобы умножить число на произведение 10, 100 и 1000 на счетные числа, умножьте числа на ненулевые числа, а затем добавьте к результату количество нулей. Например, умножьте 45 на 200. Чтобы решить это, мы сначала умножим 45 на 200. Получаем 45 х 2 = 90. Теперь мы добавляем 2 нуля (поскольку 200 имеет 2 нуля) справа от 90. Получаем 9000.
• Следовательно, 45 x 20 = 9000

Переместительное свойство

Переместительное свойство утверждает, что при выполнении операции над два числа, порядок расположения чисел не имеет значения. Это означает, что если одно число умножается на другое, не имеет значения, какое число помечено как множитель, а какое число помечено как множимое. Справедливо ли это для умножения? Давайте узнаем.

Возьмем два числа 8 и 5.

Сначала отметим 8 как множитель и 5 как множимое.

Получаем, 8 х 5 = 40.

Теперь обратим порядок, т.е. 5 станет множителем, а 8 станет множимым.

Теперь мы получаем 5 x 8 = 40.

Оба процесса дают нам один и тот же ответ.

Следовательно, мы можем сказать, что умножение удовлетворяет коммуникативному свойству. Получаем

a x b = b x a

Следовательно, умножение коммуникативно.

Ассоциативное свойство

Ассоциативное свойство указывает, что при выполнении операции над более чем двумя числами порядок, в котором расположены числа, не имеет значения. В случае умножения это означает, что если мы хотим умножить 3 числа, сначала можно выбрать два из них, одно как множитель, а второе как множимое. Результат умножения будет служить множителем, а третье число — множителем для получения окончательного ответа. Является ли умножение ассоциативным? Давайте узнаем.

Возьмем 3 числа, 8, 5 и 2.

Возьмем сначала 8 и 5.

Сначала мы помечаем 8 как множитель и 5 как множимое.

Получаем, 8 х 5 = 40.

Теперь умножаем 40 на 2, получаем 40 х 2 = 80

Теперь обратим порядок и сначала выберем 5 и 2.

Получаем, 5 х 2 = 10

Теперь умножаем этот результат на 8, получаем 10 х 8 = 80

Оба процесса дают нам одинаковый ответ.

Следовательно, мы можем сказать, что умножение удовлетворяет ассоциативному свойству. мы получаем

(a x b) x c =  a x (b x c)

Следовательно, умножение ассоциативно.

Мультипликативное свойство «0»

Произведение числа на 0 всегда равно 0. Например,

45 x 0 = 0 x 45 = 0 умножение, если число, умноженное на это тождественное число, дает само число. Здесь 1 является элементом идентичности для умножения . Давайте посмотрим, почему?

4 x 1 = 4

15 x 1 = 15

20 x 1 = 20

Следовательно, любое число при умножении на 1 дает само число. Это тождественное свойство умножения.

Мультипликативное обратное

Число называется мультипликативным обратным, если число умножается на мультипликативное обратное, полученный результат является тождеством операции, в данном случае 1 (1 — мультипликативное тождество всех чисел).

Это означает, что для всех ненулевых чисел числа, умноженные на их обратные числа, дадут ответ как 1, т.е.

4 x 1/4 = 1

Следовательно, 1/a , которое также записывается как ^-1 , является мультипликативной инверсией a.

Распределительное свойство умножения на сложение/вычитание

Когда два числа складывают или вычитают, а результат умножают на другое число, их можно умножать отдельно.

Следовательно, для любых трех чисел, a, b и c, распределительное свойство умножения над сложением утверждает, что

a x ( b + c) = (a x b) + (a x c) 9Например, пусть сначала рассмотрим 10 x (18 + 12)

Есть два способа решить эту проблему.

Первый способ

Сначала складываем 18 и 12, получаем 30. Теперь умножаем 30 на 10, получаем 10 х 30 = 300

  Второй способ

Теперь мы используем распределительное свойство умножения вместо сложения.

Имеем 10 х (18 + 12)

 = (10 х 18) + (10 х 12)

 = 180 + 120

 = 300

Оба метода дают одинаковый ответ. Следовательно,

10 х (18 + 12) = (10 х 18) + (10 х 12)

Теперь давайте рассмотрим 10 х (18 – 12)

Снова давайте решим это обоими методами.

Первый способ

Находим разницу между 18 и 12. Имеем 18 – 12 = 6

Теперь мы умножаем 10 на 6. Получаем 10 x 6 = 60.

Второй метод

Теперь мы используем распределительное свойство умножения вместо вычитания.

Имеем 10 х (18 – 12)

 = (10 х 18) – (10 х 12)

 = 180 – 120

 = 60

Оба метода дают одинаковый ответ. Следовательно,

10 х (18 – 12) = (10 х 18) – (10 х 12)

Мы используем умножение при решении наших повседневных задач. Давайте посмотрим на некоторые примеры.

Пример 1 : На стадионе 287 рядов. Сколько студентов можно разместить на этом стадионе, если в каждом ряду 165 мест?

Решение

Нам известно, что

Количество рядов на стадионе = 287

Количество мест в каждом ряду = 165

Общее количество студентов, которые могут сидеть на стадионе = 287 x 165 = 47335.

Пример 2 : Генри купил 15 упаковок печенья. Каждый пакет содержит 35 файлов cookie. Сколько всего печенья у Генри?

Решение

Нам дано, что

Количество пакетов печенья, купленных Генри = 15

Количество печенья в каждом пакете = 35

Общее количество печенья, которое есть у Генри = 15 x 35 = 525

5

5

5 Умножение и решение задач на деление (на тему Хэллоуина) Рабочие листы по математике
Умножение рациональных алгебраических выражений с одинаковыми знаменателями (на тему аптеки) Рабочие листы
Умножение целых чисел с разными знаками (на тему банковского дела и финансов) Рабочие листы

Мы тратим много времени на изучение и сбор информации на этом сайте. Если вы сочтете это полезным в своем исследовании, используйте приведенный ниже инструмент, чтобы правильно указать ссылку Helping with Math в качестве источника. Мы ценим вашу поддержку!

Схемы умножения Факты в пределах 100

Ключевые понятия

Мы можем умножать в пределах 100, используя различные методы
Таблица умножения
Схема в таблице умножения.
Распределительное свойство умножения
Свойство идентичности
Свойство нуля

1.1 Что такое таблица умножения

• Таблица умножения — это таблица, которая показывает произведение двух чисел 
• Обычно один набор чисел записывается в левом столбце, а другой набор записывается как Верхний ряд. Продукты перечислены в виде прямоугольного массива чисел.
• Таблица умножения помогает нам видеть множество произведений одновременно.
• Например, таблицу умножения 10 можно записать так: 

Умножение повторяющееся сложение

Есть 3 группы по 4 леденца в каждой. То есть общее количество леденцов равно 3, умноженному на 4, или 4+4+4, или 12.

Простым способом ежедневных вычислений является использование таблицы умножения.

• Шаг 1 : Выберите первое число из чисел, перечисленных в крайнем левом столбце, и второе число из верхнего ряда.
• Шаг 2 : Начиная с первого числа двигаться вправо и начиная со второго числа двигаться вниз. Квадрат, в котором встречаются два числа, дает произведение.
• Например  5 × 4 

1.2 Шаблоны в умножении 

Свойства можно использовать для понимания шаблона.

Например, 4×6 вдвое больше 2×6

Решение:

2×6=12

4×6=12+12

4×6=24

900 2, произведение любого числа, умноженного на 4, будет в два раза больше произведения того же числа, умноженного на 2 .  

• Мы можем заштриховать столбцы для 0,2,4,6,8 и 10. 
• Мы видим, что все произведения в этих столбцах заканчиваются на 0,2,4,6,8.
• Все продукты четные числа.
• Все произведения числа 4 в два раза больше произведения числа 2
• Все произведения числа 6 в два раза больше произведения числа 3
• Это работает для произведений чисел 8 и 4, а также для произведений чисел 10 и 5.

1.3 Распределительное свойство: 

• Если мы посмотрим на столбцы 2, 4 и 6, мы увидим, что произведения для 6 представляют собой сумму произведений для 2 и 4.  
• 2+4=6 
• Эта закономерность возникла из-за того, что Распределительное свойство утверждает, что умножение суммы на число равносильно умножению каждого слагаемого на число с последующим сложением произведений.

Это работает для столбцов для 2,4 и 6, потому что

2+4 = 6

Например:

3 × 6 = 3 × (2+4)

= (3×2) +(3×4) 

         = 6+12 

         = 18 

Это также будет работать для столбцов 

1,2 и 3             1+2=3 

1,3 и 4             1+3=4 

И многих других.

Пример:  

Для одной игрушечной собаки требуется 4 батарейки. Сколько батареек нужно для 6 игрушечных собак?

мы можем описать шаблон в таблице.

Ищем шаблон для заполнения таблицы. Мы можем просмотреть ряды и увидеть, что количество батареек увеличивается на 4 для каждой игрушечной собачки.

Сравнивая столбцы в таблице, мы можем умножить количество игрушечных собак на 4, чтобы найти количество необходимых батареек.