примеры столбиком 2 класс | Картотека по математике (2 класс):
2 класс
Письменное сложение двузначных чисел без перехода через десяток.
В-1 +34 +42 +76 +84 +52 +27 + 63 23 37 12 14 35 52 26 + 26 +57 +88 +65 + 75 +44 +36 31 22 11 23 23 35 53 |
В-2 +25 + 46 +51 +34 +62 +77 + 84 +14 34 22 36 54 27 21 13 73 +32 +64 +15 +43 +26 + 12 + 48 +37 43 24 63 45 72 84 31 41 |
В-3 +45 + 36 +24 +13 +51 +62 +72 +84 53 42 65 76 28 27 25 13 +35 + 63 +56 +67 +82 + 72 +53 +31 23 36 22 12 17 26 34 58 |
2 класс
Письменное сложение двузначных чисел без перехода через десяток.
В-1 _98 _65 _74 _86 _59 _48 _34 _48 35 34 51 63 47 26 13 25 _89 _56 _47 _68 _95 _84 _43 _97 76 23 36 45 73 53 22 64 |
В-2 _85 _76 _65 _98 _54 _49 _63 _96 54 43 33 75 32 27 41 64 _58 _67 _56 _89 _45 _94 _36 _69 37 46 35 67 34 72 14 37 |
В-3 _74 _96 _85 _69 _48 _37 _58 _99 43 65 52 36 24 15 36 78 _47 _69 _58 _96 _84 _73 _85 _98 36 46 26 63 61 52 64 74 |
2 класс
Письменное сложение и вычитание двузначных чисел без перехода через десяток.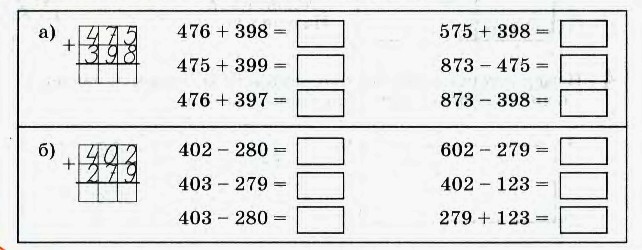
В1 +24 _56 +75 _98 + 32 _87 +15 54 23 12 76 56 75 73 _97 +32 _78 +47 _ 69 +53 _88 +64 85 24 56 52 37 36 56 23
|
В-2 +45 _42 +57 _89 + 65 _78 _37 +37 42 21 32 77 34 56 16 31 +47 _87 +31 _98 +56 _87 +26 _75 32 45 48 76 32 43 43 51 |
В-3 +36 _86 +31 _93 +32 _56 +75 _64 43 52 37 62 47 33 22 42 +77 _25 +52 _48 +43 _76 +53 _86 21 13 36 27 56 44 26 63 |
2 класс
Письменное сложение и вычитание двузначных чисел без перехода через десяток.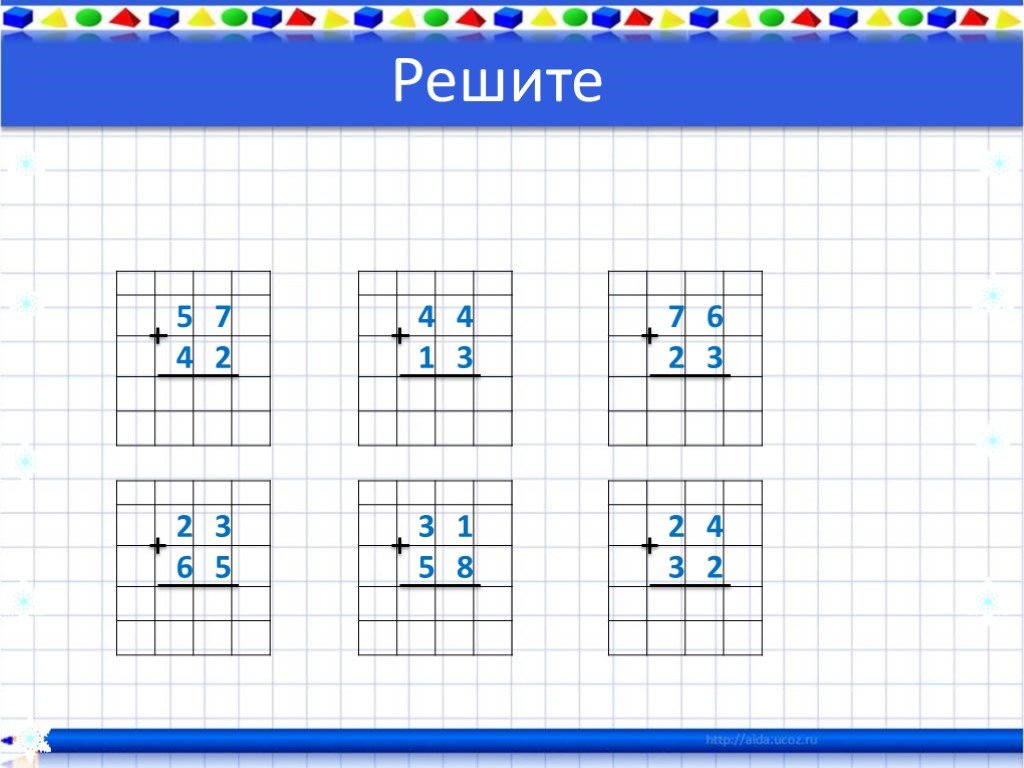
В-4 +36 _85 _97 +54 _48 +73 _84 +37 52 63 74 42 16 24 53 62
_67 +63 _96 +45 _83 +27 _69 +13 25 16 53 22 41 41 36 84 |
В-5 +45 _94 +32 _86 +63 _78 +41 -57 33 73 57 52 31 26 38 34 +62 _85 +41 _97 +36 _76 +54 _95 23 54 37 75 33 32 15 63 |
В-6 +31 _67 +54 _97 +45 _86 +23 _76 24 34 35 64 34 53 46 33 +64 _ 75 +31 _68 +23 _96 +14 23 43 37 27 56 74 84 |
2 класс
Письменное сложение двузначных чисел с переходом через десяток.
В-1 +25 + 46 +53 +34 +62 +77 + 74 +14 47 39 28 57 19 14 18 79 + 26 +57 +78 +65 + 65 +44 +36 37 24 15 28 27 38 56 |
В-2 +45 +36 +24 +16 +53 +68 +69 +74 46 48 69 76 28 27 25 17 +35 + 58 +56 +67 +77 + 66 +59 +34 29 36 29 16 17 26 34 58 |
В-3 +34 +44 +76 +79 +56 +27 + 67 29 37 15 14 35 56 26 + 26 +57 +78 +65 + 65 +49 +36 38 24 13 29 28 35 57 |
2 класс
Письменное вычитание двузначных чисел с переходом через десяток.
В-1 _93 _61 _74 _86 _51 _48 _32 _44 35 34 57 68 37 29 13 25 _81 _56 _47 _63 _95 _84 _43 _97 76 29 19 45 77 58 25 69 |
В-2 _85 _76 _65 _91 _54 _41 _63 _96 57 49 36 75 36 27 34 69 _58 _67 _53 _84 _45 _94 _36 _63 39 48 25 57 18 66 18 37 |
В-3 _74 _96 _85 _61 _48 _32 _54 _91 48 69 57 36 29 15 36 78 _47 _63 _58 _96 _84 _73 _85 _93 18 36 29 68 57 2 8 57 74 |
2 класс
Письменное сложение двузначных чисел вида 37+53
В-1 +34 +42 +76 +84 +52 +27 +63 26 38 14 16 38 53 27 + 26 +57 +88 +65 + 75 +44 +36 34 23 12 25 25 36 54 |
В-2 +25 + 46 +51 +34 +62 +77 + 84 +14 35 24 39 56 28 23 16 76 +32 +64 +15 +43 +26 + 12 + 48 +37 48 26 65 47 74 88 32 43 |
В-3 +45 + 36 +24 +13 +51 +62 +72 +84 55 44 66 77 29 28 28 16 +35 + 63 +56 +67 +82 + 72 +53 +31 25 37 24 13 18 28 37 59 |
2 класс
Вычитание из круглого числа двузначного.
В-1 _40 _60 _80 _90 _30 _100 _70 23 17 46 58 13 89 35 _50 _90 _60 _80 _100 _70 _30 32 48 25 41 57 38 16 |
В-2 _50 _90 _60 _100 _40 _80 _30 27 74 38 69 22 56 17 _70 _60 _80 _40 _100 _50 _90 43 19 48 24 79 36 67
|
В-3
_90 _40 _80 _30 _100 _60 _50 67 18 39 19 48 32 27 _70 _90 _60 _100 _80 _50 _40 24 53 48 75 39 21 19 |
2 класс
Письменные случаи сложения и вычитания двузначных чисел в пределах ста.
В-1 +34 _45 +67 +72 +54 _90 -72 23 14 23 28 27 67 45 +42 _95 +54 +63 +75 _60 _85 44 62 16 37 18 31 58 |
В-2 +56 _66 +47 +53 +27 _80 _61 23 24 33 47 64 56 18 +63 _78 +27 +86 +65 _70 _45 25 43 53 14 26 34 27 |
В-3 +36 _87 + 58 +49 +66 _60 _84 52 36 22 51 17 25 48
+47 _89 +68 +77 +56 -90 _85 52 36 12 23 36 43 58 |
Урок «Вычитание столбиком, проверка вычитания, таблица вычитания, примеры», математика для 2 класса
Дата публикации: .
Дополнительные материалы
Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания. Все материалы проверены антивирусной программой.
Скачать:Вычитание столбиком. Таблицы вычитания (PDF)
Обучающие пособия и тренажеры в интернет-магазине «Интеграл» для 2 класса
Электронный репетитор по математике к учебнику Л.Г. Петерсон для 2 класса
Электронный репетитор по математике к учебнику М.И. Моро, 2 класс
Ребята, давайте поговорим о вычитании двузначных чисел.
В первом классе вы проходили арифметические действия: сложение и вычитание. Давайте вмести с Дейлом вспомним, как называются числа при сложении.
Правильно, для этого в математике нужно использовать операцию вычитания.
Вычитание – это арифметическая операция, обратная сложению.
Давайте вместе с Вжиком научимся вычитать двузначные числа столбиком.
Пример вычитания 1
Вжику задали домашнее задание, ему надо решить пример.
Для этого:
1. Расположим числа друг под другом, знак «–» расположим слева между числами, а снизу проведём черту, как показано на рисунке. Это стандартная запись для вычитания столбиком.
2. Начнем вычитать с правого столбца.
Из числа 7 вычитаем число 4 и разность – число 3 записываем в столбик внизу после черточки.
3. Затем мы переходим ко второму столбцу.
Из числа 5 вычитаем число 3 и разность – число 2 записываем в столбик слева от числа 3.
Вот и всё. Мы из числа 57 отняли число 34 столбиком и получили число 23.
Пример вычитания 2
Чипу задали пример сложнее. Ему необходимо из числа 62 отнять число 48. Давайте поможем ему решить этот пример.
1. Запишем числа друг под другом, как в предыдущем примере.
2. Приступим к вычитанию с правого столбца и сразу сталкиваемся с проблемой!!!
Из числа 2 нельзя вычесть число 8.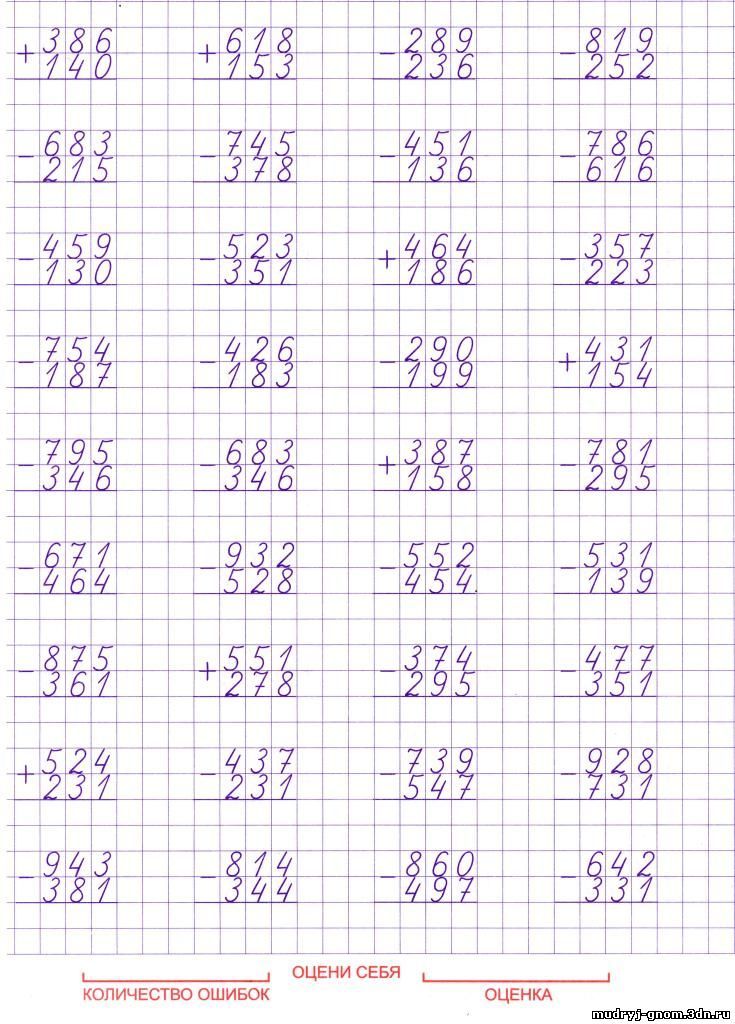
Поэтому, займем десять единиц у соседнего числа слева. А над самим числом поставим точку, чтобы не забыть.
Что мы сделали.
Первый шаг: 2 + 10 = 12 (заняли 10 у соседнего числа).
Второй шаг: 12 – 8 = 4
Число 4 запишем в крайний правый столбик под чертой.
3. Переходим к соседнему столбцу слева. Помните, мы заняли один десяток у числа 60, значит уменьшаем число 60 на 10.
Что мы сделали.
Первый шаг: 60 – 10 = 50.
В итоге мы получили вот такой результат.
Вычитание столбиком – очень полезный навык. Он позволяет правильно выполнять арифметические операции при работе с большими числами.
Проверка вычитания сложением
Вычитание – это действие, обратное сложению. Поэтому результат вычитания можно проверить сложением.
Рокфор хочет проверить, правильно ли Чип выполнил вычитание?
Для этого ему нужно сложить разность и вычитаемое. Давайте и ему поможем.
1. Начинаем с крайнего правого столбца.
4 + 8 = 12
Число 2 записываем под чертой в крайнем правом столбце, дополнительные 10 единиц запоминаем.
2. Переходим к левому столбцу. 1 + 4 = 5. Мы помним, что у нас есть лишняя десятка с предыдущего суммирования (4 + 8 = 12).
Мы добавляем эти десять единиц к сумме: 50 + 10 = 60
Вычитание вместе с Чипом было выполнено правильно.
Таблица вычитания
Чтобы научиться быстро вычитать, можно воспользоваться таблицой вычитания. Ниже приведена таблица вычитания для 2 класса (до 10).
Потренироваться Вы можете в теме, которая называется»Вычитание столбиком». Вычитание двузначных чисел». «Текстовые задачи». «Проверка вычитания сложением»
Column Matrix — определение, формула, свойства, примеры.
Матрица-столбец — это матрица, все элементы которой находятся в одном столбце. Элементы расположены вертикально, а порядок матрицы столбцов равен n x 1. Матрица столбцов имеет только один столбец и может иметь множество строк, равное количеству элементов в столбце.
Давайте узнаем больше о свойствах матрицы-столбца, матричных операциях над матрицей-столбцом, на примерах, в часто задаваемых вопросах.
| 1. | Что такое матрица столбцов? |
| 2. | Свойства матрицы столбцов |
| 3. | Операции над матрицей столбцов |
| 4. | Примеры на матрице столбцов |
| 5. | Практические вопросы |
| 6. | Часто задаваемые вопросы о столбцовой матрице |
Что такое матрица столбцов?
Матрица-столбец — это матрица, в которой все элементы находятся в одном столбце. Матрица столбцов имеет только один столбец и несколько строк. Порядок матрицы-столбца равен n × 1, и она состоит из n элементов. Элементы расположены вертикально, при этом количество элементов равно количеству строк в матрице-столбце.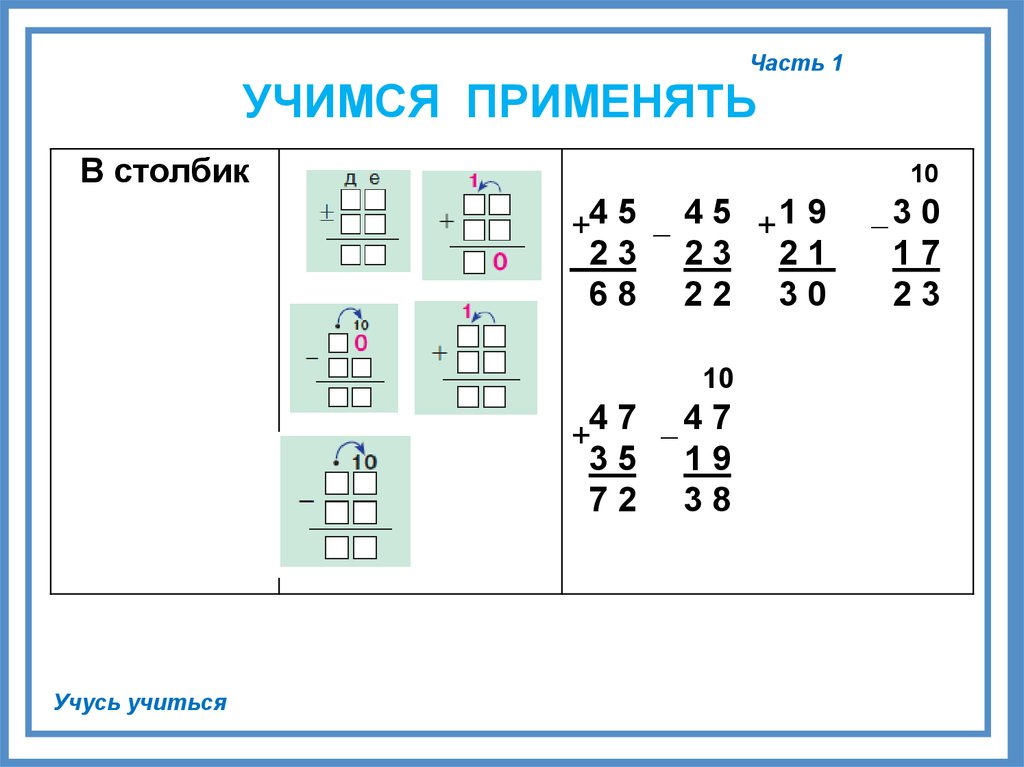
Общая форма матрицы-столбца выглядит следующим образом.
Примеры матрицы столбцов
Давайте посмотрим на три примера матриц столбцов ниже.
B = \(\begin{bmatrix}4\\5\end{bmatrix}_{2×1}\)
C = \(\begin{bmatrix}a\\b\\c\end{bmatrix }_{3×1}\)
D = \(\begin{bmatrix}8\\-2\\4\\1\end{bmatrix}_{4×1}\)
Свойства матрицы столбцов
Следующие свойства матрицы-столбца помогают глубже понять матрицу-столбец.
- Матрица столбцов имеет только один столбец.
- Матрица-столбец имеет множество строк.
- Количество элементов в матрице-столбце равно количеству строк в матрице.
- Матрица-столбец также является прямоугольной матрицей.
- Транспонирование матрицы-столбца является матрицей-строкой.
- Матрица-столбец может быть добавлена или вычтена только из матрицы-столбца того же порядка.
- Матрица-столбец может быть умножена только на матрицу-строку
- Произведение матрицы-столбца на матрицу-строку дает одноэлементную матрицу.
Операции над матрицей столбцов
Над матрицами-столбцами можно выполнять следующие алгебраические операции сложения, вычитания, умножения и деления. Операции сложения и вычитания над матрицами-столбцами можно выполнять так же, как и над любыми другими матрицами. Матрица-столбец может быть добавлена или вычтена только из любой другой матрицы-столбца. Здесь порядок двух матриц должен быть одинаковым.
A = \(\begin{bmatrix}7\\-3\\4\\5\end{bmatrix}\), B = \(\begin{bmatrix}3\\8\\2\\-7 \end{bmatrix}\)
A + B = \(\begin{bmatrix}7+3\\(-3)+8\\4+2\\5+(-7)\end{bmatrix}\) = \(\begin{ bmatrix}10\\5\\6\\-2\end{bmatrix}\)
Умножение матрицы-столбца возможно на матрицу-строку. При выполнении условия умножения матриц количество столбцов в первой матрице должно быть равно количеству строк во второй матрице. То есть количество столбцов в матрице столбцов для умножения равно количеству строк в столбце строки.
A = \(\begin{bmatrix}4\\2\\3\\1\end{bmatrix}\), B = \(\begin{bmatrix}7&4&6&5\end{bmatrix}\)
A × B = \(\begin{bmatrix}4\\2\\3\\1\end{bmatrix}\), × \(\begin{bmatrix}7&4&6&5\end{bmatrix}\)= \(\begin{bmatrix}4×7&4×4&4×6&4×5\\2×7&2×4&2×6&2×5\\3×7&3×4&3×6&3×5\\1×7&1×4&1×6&1×5\ end{bmatrix}\)
= \(\begin{bmatrix}28&16&24&20\\14&8&12&10\\21&12&18&15\\7&4&6&5\end{bmatrix}\)
Умножение матрицы-столбца на матрицу-строку приводит к квадратной матрице .
Кроме того, матрицу-столбец нельзя использовать для деления, поскольку обратной матрицы-столбца не существует.
Связанные темы
Следующие темы помогают лучше понять матрицу столбцов.
- Операции с матрицами
- Матрица трансформации
- Несингулярная матрица
- Эрмитова матрица
- Нильпотентная матрица
Примеры на матрице столбцов
Пример 1: Найти транспонирование матрицы-столбца \(\begin{bmatrix}5\\11\\4\\3\end{bmatrix}\).
Решение:
Дана матрица A = \(\begin{bmatrix}5\\11\\4\\3\end{bmatrix}\)
Чтобы найти транспонирование этой матрицы-столбца, элементы столбца записываются как элементы строки.
A T = \(\begin{bmatrix}5&11&4&3\end{bmatrix}\)
Следовательно, транспонирование матрицы-столбца является матрицей-строкой.
Пример 2: Найдите произведение матрицы-столбца \(\begin{bmatrix}4 \\5\\3\end{bmatrix}\) и матрицы-строки \(\begin{bmatrix}2&6&9\end{bmatrix}\).
Решение:
Даны матрицы A = \(\begin{bmatrix}4 \\5\\3\end{bmatrix}\) и B = \(\begin{bmatrix}2&6&9\end{ bматрица}\).
A × B = \(\begin{bmatrix}4 \\5\\3\end{bmatrix}\) × \(\begin{bmatrix}2&6&9\end{bmatrix}\)
= \(\begin {bmatrix}4×2&4×6&4×9\\5×2&5×6&5×9\\3×2&3×6&3×9\\\end{bmatrix}\)= \(\begin{bmatrix}8&24&36\\ 10&30&45\\6&18&27\\\конец{bmatrix}\)
Таким образом, произведение матрицы-столбца и матрицы-строки является одноэлементной матрицей.
перейти к слайдуперейти к слайду
Есть вопросы по основным математическим понятиям?
Станьте чемпионом по решению проблем, используя логику, а не правила. Узнайте, что стоит за математикой, с нашими сертифицированными экспертами
Запишитесь на бесплатный пробный урок
Практические вопросы по матрице столбцов
перейти к слайдуперейти к слайду
Часто задаваемые вопросы о матрице столбцов
Что такое матрица столбцов?
Матрица-столбец — это матрица только с одним столбцом, все элементы которой расположены друг под другом по вертикальной линии.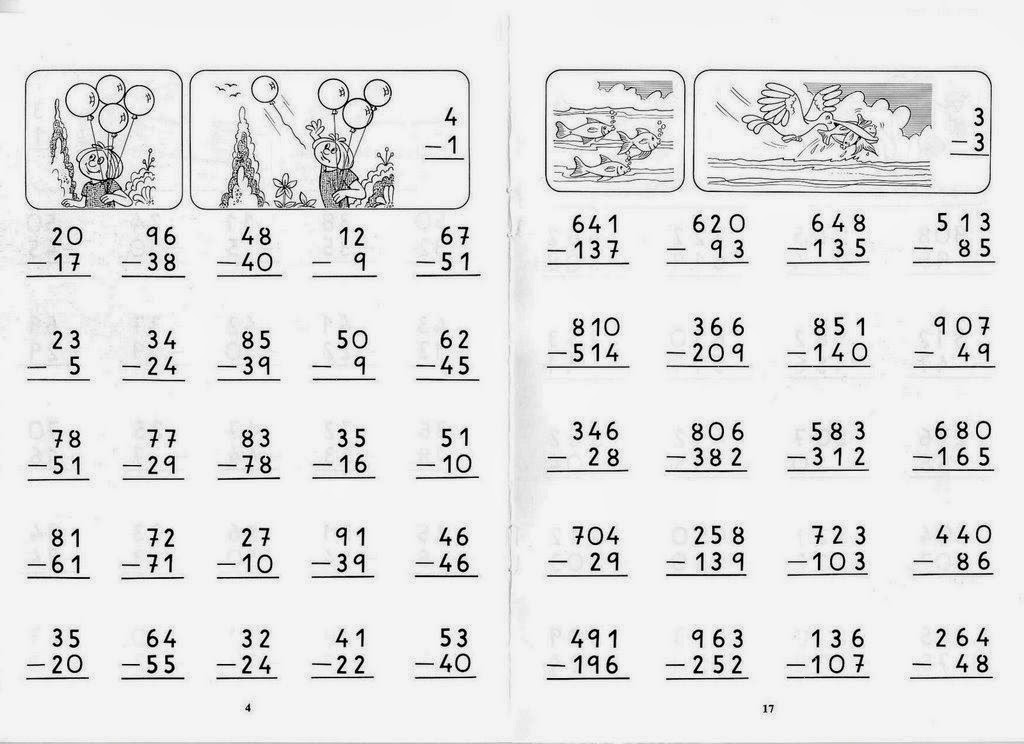
В матрице столбцов A = \(\begin{bmatrix}a\\b\\c\\d\end{bmatrix}\) четыре элемента размещены в одном столбце. Матрица столбцов имеет только один столбец и множество строк. Порядок матрицы-столбца равен n × 1.
Каков порядок матрицы-столбца?
Порядок матрицы-столбца равен n × 1. Матрица-столбец состоит из одного столбца и n строк. Количество строк в матрице-столбце равно количеству элементов.
Какой тип матрицы является матрицей-столбцом?
Матрица-столбец представляет собой прямоугольную матрицу. Он имеет неравное количество строк и столбцов. Матрица столбцов имеет один столбец и множество строк в зависимости от количества элементов в матрице.
Что такое транспонирование матрицы столбцов?
Транспонирование матрицы-столбца дает матрицу-строку. Матрица-столбец порядка n × 1 имеет транспонированную матрицу, которая представляет собой матрицу-строку порядка 1 × n. В матрице столбцов элементы расположены вертикально, а в матрице строк элементы расположены вертикально.
Какие операции выполняются над матрицей-столбцом?
Матричные операции сложения, вычитания и умножения можно выполнять с помощью матрицы-столбца. Обратная матрица-столбец невозможна, так как это не квадратная матрица. Сложение или вычитание матриц возможно между двумя матрицами-столбцами одного порядка. Умножение матрицы-столбца возможно на матрицу-строку. При выполнении условия умножения матриц количество столбцов в матрице-столбце должно быть равно количеству строк матрицы-строки.
В чем разница между матрицей столбцов и матрицей строк?
В матрице столбцов элементы расположены вертикально, а в матрице строк элементы расположены горизонтально. Порядок матрицы-столбца равен n × 1, а порядок матрицы-строки — 1 × n. Матрица-столбец или матрица-строка имеют одинаковое количество элементов. А произведение матрицы-столбца и матрицы-строки дает одноэлементную матрицу.
Доказательство в два столбца по геометрии (определение, примеры и видео)
Написано
Малкольм МакКинси
. Проверясь по фактам
Пол Маццола
Двухцветное определение
Двух Костоловое. истинность некоторого математического утверждения. Тем не менее, это один из самых надежных методов, поскольку он заставляет геометра или, по крайней мере, изучающего геометрию подкреплять каждое утверждение реальными доказательствами.
Среди многих методов, доступных математикам, есть доказательства , или логические аргументы, которые начинаются с предпосылки и приходят к заключению путем очерчивания фактов.
Написание доказательства — непростая задача, потому что вам нужно расставить все части в правильном порядке. Большая часть геометрии работает около трех типов доказательств:
Параграф. , но по чистоте и ясности ничто не сравнится с доказательством в два столбца.
Доказательство с двумя столбцами использует таблицу для представления логического аргумента и назначает каждому столбцу одну работу, а затем два столбца работают синхронно, чтобы провести читателя от предпосылки к заключению.
Структура корректуры в два столбца
Корректура абзаца рассказывает историю, где каждый факт и причина изложены в хронологическом порядке. Это означает, что вы должны быть чрезвычайно организованы и, возможно, несколько раз переписать абзац, прежде чем сделать все правильно. Доказательство блок-схемы может быть трудным для понимания, но, по крайней мере, оно четко отделяет математику от рассуждений.
Только доказательство с двумя столбцами явно помещает математику с одной стороны (первый столбец), а рассуждения с другой стороны (второй или правый столбец). Пока вы держите две стороны на одной линии, вы не можете не подвести читателя от одной предпосылки к другой и, наконец, к заключению.
Структура доказательства в два столбца должна следовать четырем основным принципам:
Структура доказательства в два столбцаПервый или левый столбец содержит только математические выражения, такие как «четырехугольник 9».0243 РОЗОВЫЙ является параллелограммом» или « сторона PI = сторона NK ».
если четырехугольники имеют одинаковую длину, то фигура является параллелограммом». конец, когда вы доказали свою концепцию.0005
Как решать двухколоночные доказательства
Двухколоночное доказательство — это только структура, подобная скелету. У вас должно быть под рукой пять инструментов, чтобы пройти путь от предпосылки к заключению и завершить проверку в два столбца:
Как решать доказательства в два столбцаГивены — Укажите, что дано вам и читателю на диаграмме или схеме. задачи
Диаграмма – Диаграмма пояснит, что такое геометрическая фигура; если диаграммы нет, нарисуйте ее!
Основополагающие знания – Вы должны иметь глубокое понимание теорем и постулатов, чтобы применять их быстро и логично; без понимания определений, словарного запаса и взаимосвязей между геометрическими фигурами вы не можете переходить от аргумента к аргументу
Способность рассуждать и мыслить – Это не царская дорога; вы можете начать, столкнуться с ментальной стеной, и вам придется начинать заново; логическое мышление — это сложный и сложный навык, поэтому наберитесь терпения и дайте себе время подумать
Заказать – Корректура в два столбца логично, ясно и лаконично переходит от одной идеи к другой, делая вывод и затем останавливаясь
Как писать корректуру в два столбца двухколоночное доказательство путем проведения горизонтальной линии вверху листа бумаги и вертикальной линии посередине.
Назовите левую сторону «Утверждение», а правую — «Причина». Скажем, вас попросили доказать теорему о равнобедренном треугольнике, которая утверждает, что если две стороны треугольника конгруэнтны, то и их противоположные углы конгруэнтны.Вам будет предоставлена некоторая информация, например, △WHZ имеет Сторона HW ≅ Сторона HZ , что делает его равнобедренным треугольником.
Вас просят доказать ∠W ≅ ∠Z .
Как писать корректуры в два столбцаПример корректуры в два столбца Заявления Причины ГШ ≅ ГЦ Дано Построить биссектрису ∠H к точке I на стороне WZ Каждая внутренность ∠ имеет ровно одну биссектрису ∠ ∠WHI ≅ ∠ZHI Определение, ∠ биссектриса HI ≅ HI Рефлексивное свойство равенства △HWI ≅ △ HZI Постулат стороны-угла-стороны ∠W ≅ ∠Z Соответствующие части конгруэнтных треугольников конгруэнтны (CPCTC) Это было доказательство из пяти шагов.
Большинство доказательств геометрии можно выполнить менее чем за 10 шагов. Если вы обнаружите, что проходите, скажем, семь или восемь шагов, возможно, вы идете по неэффективному или неправильному пути. Как вы можете себе помочь?Доказательства и рассуждения в два столбца
Одна из стратегий работы над доказательством в два столбца состоит в том, чтобы сначала рассмотреть конец: что вас просят доказать? Не рассматривая пронумерованный элемент, запишите его как утверждение для последней позиции. Подумайте о причине этого утверждения; что вам нужно, чтобы доказать это?
Еще одна важная деталь — нарисовать схему или картинку, точно соответствующую предоставленной информации. Посмотрите, что еще раскрывает данная информация, например, дополнительные или дополнительные углы, прямые углы, которые вы, возможно, не заметили, или равенство углов или сторон.
Держите свои доводы под рукой, особенно если вы не выучили наизусть огромное собрание аксиом и теорем. Это могут быть постулаты, другие теоремы, определения или свойства.
если четырехугольники имеют одинаковую длину, то фигура является параллелограммом». конец, когда вы доказали свою концепцию.0005
Назовите левую сторону «Утверждение», а правую — «Причина». Скажем, вас попросили доказать теорему о равнобедренном треугольнике, которая утверждает, что если две стороны треугольника конгруэнтны, то и их противоположные углы конгруэнтны.
Большинство доказательств геометрии можно выполнить менее чем за 10 шагов. Если вы обнаружите, что проходите, скажем, семь или восемь шагов, возможно, вы идете по неэффективному или неправильному пути. Как вы можете себе помочь?