Примеры решить 1 класс: Тренажеры по математике 1 класс. Примеры на сложение и вычитание, задачи

Математика 1 класс «Решение задач и числовых выражений»

Урок 45. Математика 1 класс

Тема: «Решение задач и числовых выражений».

Цели урока: в ходе выполнения различных заданий закреплять умение выполнять вычисления вида + 2; -2, развивать умение решать простые задачи, провести проверку знаний. воспитывать внимательность, интерес к урокам математики.

Планируемые результаты: обучающиеся повторят присчитывание и отсчитывание по 2; составлять задачи на сложение и вычитание; оценивать себя и товарищей.

Оборудование: презентация, мультимедийный проектор, экран, индивидуальный раздаточный материал,

1. Организационный момент: Слайд №2

Ну-ка, проверь, дружок,
Ты готов начать урок?
Всё ль на месте, всё в порядке
Ручка, книжка и тетрадка?
Все ли правильно сидят?
Все ль внимательно глядят?
Ждут нас интересные задачи,
Я желаю всем удачи!
2. Актуализация знаний.

– Урок у нас необычный,
В гости ждём животных различных.
Им мы будем помогать,
Задачи и примеры вместе решать.

Тема нашего урока решение задач и примеров.

3.Устный счёт. Слайд №3, 4

1) СКОЛЬКО? Покажи нужную цифру. (4, 9)

2) Состав числа. (дифференцированный подход)

Работа у доски и индивидуально

Хворых Д. и Бургонов Д. -5

Мамацев и Перелыгина – 9, 10

Девочки 7, мальчики 6

Самопроверка по слайду (светофоры) Слайд №5

Работу у доски проверяем все. (За правильную работу – печатку.)

3) Присчитывание по2 Слайд №6-9

–Какое время года вы видете? (золотая осень)

– Сейчас уже поздняя осень и для птиц самое трудное время.

– Как вы, думаете, почему?

(Ответы детей)

– Не забывайте и подкармливайте птичек, чтобы они пережили холодную зиму и весной запели свои радостные песни.

4 Работа в проверочной тетради с.20 № 3, 2

Самостоятельная работа №3 и 2

5.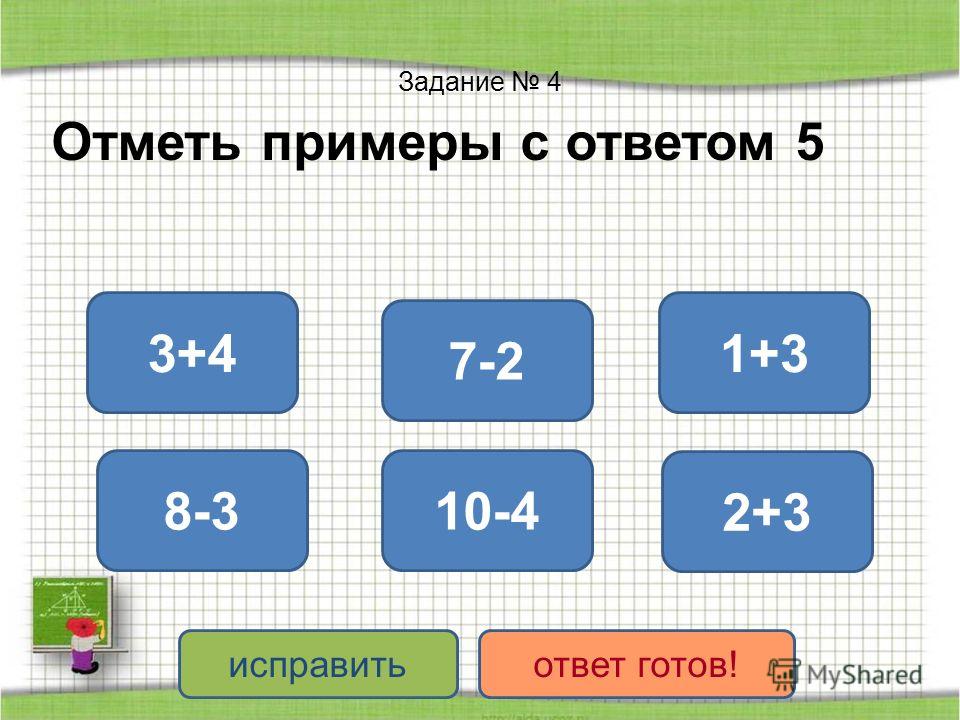 Физкультминутка (цыпленок)

6. Решение примеров +, — 1, 2

Помоги героям сказок найти свой вагон

-Как прочитать по разному пример 6+2=8

7. Проверочная работа №1 (решение примеров)

Пальчиковая гимнастика Слайд №14

8. Работа над задачей

1) Задачи в стихах. Слайд №15

-Из чего состоит задача? ( условие, вопрос, решение, ответ)

2) Составление задач по слайду № 16 (дети работают с аббаками)

9. Работа с учебником с.100 №3 Слайд №17

Работа у доски и в тетрадях

5+2=7 (п.)

Ответ: 7 приседаний.

Сдать тетради .

10. Физкультминутка для глаз. Слайд №18

11. Геометрический материал.

Как можно одним словом назвать все эти фигуры? Слайд №19

Какая фигура лишняя?

Продолжи цепочку. Слайд № 20

12. Сравни Слайд №21

На доске дети вставляют знаки сравнения.

Повторяем равенства и неравенства.

. Итог урока:

– Что понравилось на уроке?

– Что не понравилось?

– Какие задания были для вас сложными?

– Спасибо всем за активную работу на уроке.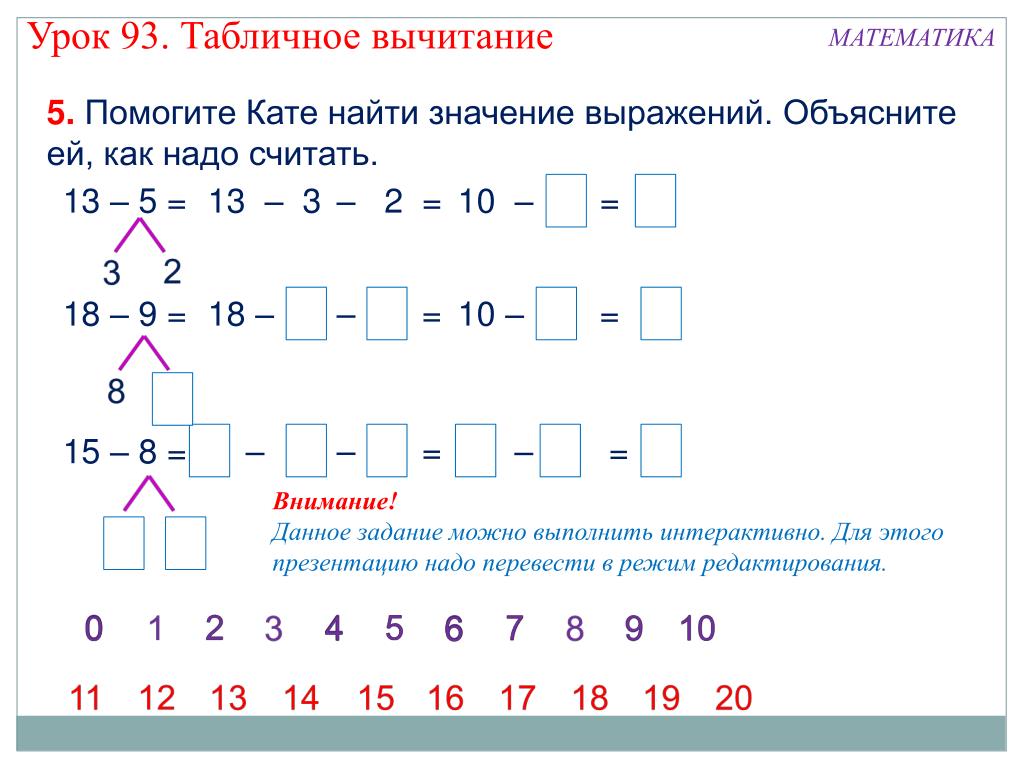 (Учитель раздаёт подарки детям)

Урок математики 1 класс тема: «Составление и решение задач»

Тема: «Составление и решение задач»

Цели:

• создать содержательные и организационные условия для развития у учащихся умений анализировать задачу и выделять в ней составные части;
• способствовать формированию у учащихся вычислительных навыков и умения решать задачи;
• создать условия для развития мыслительных операций, творческих способностей, речи учащихся.

Задачи:

1. Образовательные:

• учить составлять задачи по модели, схеме её решения;
• совершенствовать навык решения задачи с опорой на рисунок и часть условия;
• закреплять умения выполнять арифметические действия с числами; 

2. Развивающие:

• развивать речь учащихся;
• развивать познавательную активность;
• совершенствовать мыслительные операции;
• развивать психические процессы: память, мышление, воображение, внимание; эмоции;
• развивать навык самооценивания.

3. Воспитательные:

• воспитывать активности, усидчивости, прилежания в процессе учения;
• воспитывать уважение к товарищам.

Планируемые результаты образования:

Предметные: умеют устанавливать различия между задачей и математическим рассказом, составляют числовые выражения на увеличение\уменьшение чисел, считают в пределах первого десятка.

Метапредметные:

Познавательные: — общеучебные — составление вопроса в соответствии с записью и сюжетной ситуацией, моделирование сюжетной ситуации, формирование навыка счета в пределах первого десятка; — логические — формировать умения анализировать объекты с целью выделения признаков;

Регулятивные: принимать и сохранять учебную задачу; определять и формулировать цель на уроке, оценивать правильность выполнения действий, вносить необходимые коррективы на основе учета характера сделанных ошибок, высказывать свое предположение.

Коммуникативные: уметь формировать коммуникативно-речевые действия, конструктивные способы взаимодействия с окружающими (учителем, сверстниками), понимать возможность различных позиций других людей, отличных от собственной, и ориентироваться на позицию партнера в общении и взаимодействии.

Личностные: высказывают свое мнение, подтверждая собственными аргументами и другим авторитетным мнением; уважают мнения других.

Ход занятия

1. Организационный этап.

– Давайте улыбнемся друг другу.

Пожелаем друг другу успехов в учении и произнесем наш девиз урока.

Мы умные, мы дружные

Мы — внимательные, мы — старательные

Мы в первом классе учимся

Всё у нас получится!

II. Этап актуализации субъектного опыта учащихся

1. Сообщение темы урока.

— Посмотрите на доску — перед вами вселенная Математики (слайд 1). Это необычная вселенная, с множеством математических планет, далеких и близких. Сегодня мы с вами побываем на одной из них.

2.-Давайте подготовимся к полету.

Чтобы взлететь нам нужно сделать обратный отсчет.

А вот какие цифры мы будем использовать для отсчета вы сейчас отгадаете.

Загадки про цифры.

1).Смотрит мама с нетерпеньем

На страницы дневника.

Ждет заветную оценку 

У сынка-озорника.

Но опять одни четверки.

Нет красавицы…

Ответ: Пятерки

2)Я у бабушки была, — 

У нее во всей квартире 

Три огромные стола, 

Ног у каждого — … 

Ответ: Четыре

3) Необычна цифра эта,
Круглолица, так и знай.
И на букву З похожа,
Что за цифра? Отгадай!

Ответ: Три

4)Гибко шейку изгибает,
И красива, и стройна,
Ловко хвостик поднимает,
Что за цифра? Цифра. ..

Ответ: Два

5) На стебелёк она похожа,
Стоит почтенно, как вельможа.
Прямая, ровная всегда,
После нуля идёт она.

Ответ: Один

_Откройте тетради, отступите 4 клетки и запишите цифры, которые у нас получились

3) устный счет

Разложите цифры от 0 до 9

Покажите соседей числа 6, 3, 8.

Покажите число, следующее за числом 5, 7, 2.

Покажите предыдущее число 5, 9, 4.

— Итак, к полету готовы!

-Но куда мы полетим? Об этом вы мне скажете, выполнив задание.

4) Работа в группе. Повторяем состав чисел в пределах 10. На доске таблица:

6	8	9	7	5	10

Вам необходимо расшифровать слово. Каждая группа получает звездочку. На его лучиках написаны примеры. Необходимо решить примеры, вписать число в круг и отгадать букву, которая входит в название планеты.

2+6

4+4

3+5

1+7

6+2

Как же называется планета? Правильно, Задача.

Молодцы. Ну, что же приготовились. Ведем отсчет-5,4,3,2,1. — полетели! (слайд 2).

III. Сообщение темы урока.

1.– Рассмотрите рисунки на доске. (слайд 3).

– По каким рисункам можно составить и решить задачи? Как вы думаете, какая тема урока?

– Тема урока «Составляем и решаем задачи».

Чем мы будем заниматься на этой планете? Поставим перед собой задачи.

Давайте вспомним, что мы уже знаем о задаче (слайд 3).

— И так самая большая планета математической вселенной -Задача (слайд 4).

— На этой планете нас ожидает очень умный мальчик — Знайка, он приготовил для вас задания.

Но сначала давайте настроим на работу глазки. Посмотрите на звездное небо и понаблюдайте за космическими объектами.

Физкультминутка для глаз. (слайд 5).

А теперь приступаем к работе по теме.

2. Составление задачи.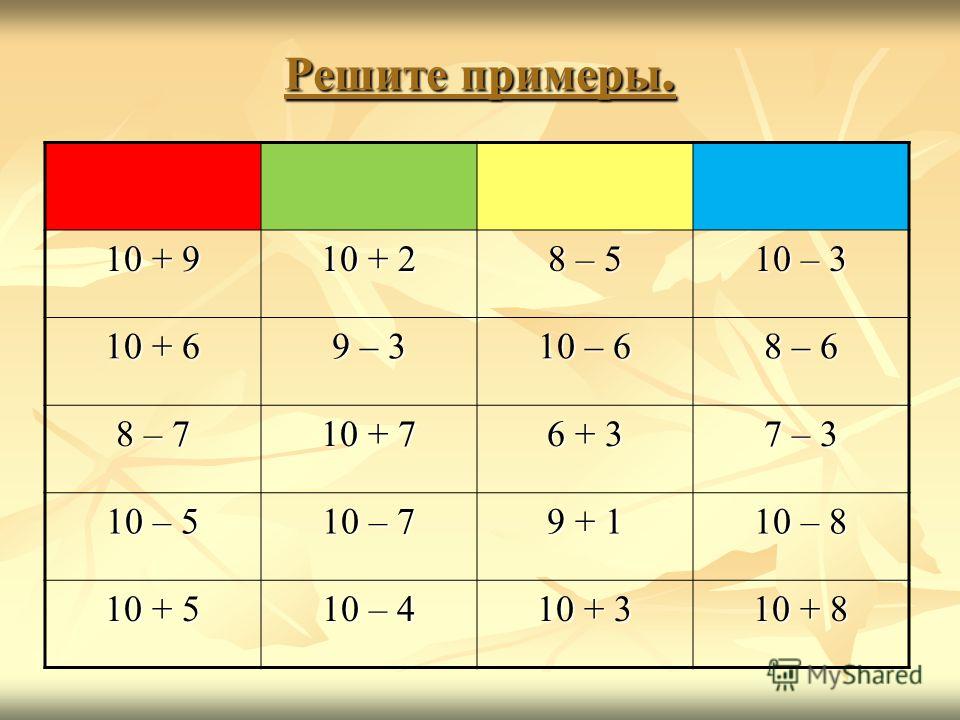 Работа по учебнику. (слайд 6).

а) Коллективно. Посмотрите на экран. Кого вы видите на картинке? Составьте задачу. Ваня поймал 6 рыбок. Вдруг кот утащил 1 рыбку. Сколько рыбок осталось?

Докажите, что это задача. Назовите условие, вопрос.

Кто запишет решение? (Один ученик у доски, остальные в тетради)

Решение:

6 – 1 = 5.

Прочитайте решение. Назовите ответ.

б) Работа в паре. (слайд 7).В домике живут семеро козлят. Три козленка ушли на луг. Сколько козлят осталось в домике?

Решение:

7 – 3 = 4.

Из чего состоит задача? Что мы можем сказать о вопросе и условии задачи?

Физкультминутка

3. Работа по учебнику. Самостоятельная работа

Стр.89 №3 — по выбору (слайд 8).

Вывод: Какую задачу ставили перед собой? (Научиться составлять задачи)

IV. Этап применения изученных знаний и способов действий

1. Работа в паре. Стр. 88 №2

2. Наше путешествие подходит к концу.

.- Мы покидаем планету Задача. Знайка и его друг приготовили вам подарки

Составь и реши задачу. слайд 11

V. Этап подведения итогов

Мы возвращаемся на Землю. Пристегните ремни, полетели! (слайды 12).

VI. Этап рефлексии.

— Давайте вспомним, на какой планете мы сегодня побывали

-Какие задачи ставили перед собой?

Ребята, мы побывали на прекрасной математической планете. Давайте оставим жителям этой планеты свои звездочки.

_Если на уроке у вас все получилось, работать было легко и интересно прикрепите зеленую звездочку.

— Если у вас что-то немного не получалось- были затруднения –прикрепите желтую звездочку.

— Ну а кому было трудно, нужна помощь , прикрепите красную. Звездочку.

— Сегодня наше путешествие подошло к концу, но путешествие во вселенную Математики только начинается и впереди у нас еще множество неизведанных планет и открытий.

Урок окончен.

Решите задачи, приведенные в примере 1

Решение:

Задача в примере 1 была следующей:

Математически представить следующие ситуации:

(i) Джон и Дживанти вместе имеют 45 шариков. Оба они потеряли по 5 шариков каждый, и произведение количества шариков, которое у них теперь есть, равно 124. Мы хотели бы узнать, сколько шариков у них было в начале.

(ii) Кустарное производство производит определенное количество игрушек в день. Себестоимость производства каждой игрушки (в рупиях) составила 55 минус количество игрушек, произведенных за день. В конкретный день общая стоимость производства составила 750 ₹. Мы хотели бы узнать количество игрушек, произведенных в этот день.

Дано:

(i) Пусть у Джона было x шариков.

Количество шариков у Дживанти будет = 45 — x

Оба потеряли по 5 шариков каждый:

Шарики с Джоном = x — 5

Шарики с Дживанти = 45 — x — 5 = 40 — x

Произведение текущего количества шариков = 124

Используем это условие, чтобы составить квадратное уравнение.

(x — 5) (40 — x) = 124

(i) (x — 5) (40 — x) = 124

⇒ 40x — x ² — 200 + 5x = 124

⇒ -x ² + 45x — 200 -124 = 0

⇒ -x ² + 45x — 324 = 0

получаем

⇒ х ² — 45х + 324 = 0

⇒ х ² — 36х — 9х + 324 = 0

⇒ х(х — 36) — 6 = 9 (х — 0

⇒ (x — 36) (x — 9) = 0

⇒ x — 36 = 0 и x — 9 = 0

⇒ x = 36 и x = 9

Джон и Дживанти начали с 36 и 9мраморы.

(ii) Пусть количество игрушек, произведенных за день, равно x.

Стоимость каждой игрушки = (55 — x) рупий

Общая стоимость производства = стоимость каждой игрушки × общее количество игрушек

⇒ (55 — x) (x) = 750

⇒ 55x — x ² = 750

⇒ 55x — x ² — 750 = 0

⇒ x

2 — 25x — 30x + 750 = 0

⇒ (x — 25) (x — 30) = 0

x — 25 = 0 и x — 30 = 0

x = 25 и x = 30

Количество игрушек, произведенных в этот день, равно 25 или 30.

☛ Проверка: NCERT Solutions Class 10 Maths Глава 4

---

Видео Решение:

класс 10 Математика NCERT Solutions Глава 4 Упражнение 4.2 Вопрос 2

. имеют 45 шариков, и каждый из них потерял по 5 шариков, а произведение количества шариков, которое у них теперь есть, равно 124, тогда количество шариков, с которыми они должны были начать, равно 9 и 36.

Если кустарное производство производит определенное количество игрушек в день, а стоимость производства каждой игрушки (в рупиях) составила 55 минус количество игрушек, произведенных за день, где в конкретный день общая стоимость производства составляла 750 фунтов стерлингов, количество игрушек, произведенных в этот день, 25 или 30.

---

☛ Похожие вопросы:

• Найдите два числа, сумма которых равна 27, а произведение равно 182.
• Найдите два последовательных натуральных числа, сумма квадратов которых равна 365.
• Высота прямоугольного треугольника на 7 см меньше его основания. Найдите две другие стороны, если гипотенуза равна 13 см.
• Кустарное производство производит определенное количество гончарных изделий в день. Было замечено, что в определенный день стоимость производства каждого изделия (в рупиях) в 3 раза превышала количество изделий, произведенных в этот день. Если общая стоимость производства в этот день составляла 9 рупий0, найти количество произведенных изделий и стоимость каждого изделия

Решение словесных вопросов

МНОГО примеров!

В алгебре у нас часто возникают словесные вопросы, например:

Пример: Сэм и Алекс играют в теннис.

В выходные Сэм сыграл на 4 игры больше, чем Алекс, а вместе они сыграли 12 игр.

Сколько игр сыграл Алекс?

Как их решить?

Хитрость заключается в том, чтобы разбить решение на две части:

Превратите английский в алгебру.

Затем используйте алгебру для решения.

Превращение английского языка в алгебру

Превратить английский в алгебру поможет:

• Сначала прочитайте все
• Сделайте эскиз если возможно
• Назначить букв для значений
• Найдите или разработайте формулы

Вы также должны записать то, что на самом деле запрашивается , чтобы вы знали, куда вы идете и когда вы прибыли!

Также ищите ключевые слова:

Когда увидишь		Подумай
добавить, итого, сумма, увеличить, больше, вместе, вместе, плюс, более		+
минус, меньше, разность, меньше, меньше, меньше		—
умножить, раз, произведение, коэффициент		×
разделить, частное, на, вне, отношение, отношение, процент, скорость		÷
увеличить или уменьшить		геометрия формулы
Скорость, скорость		расстояние формулы
Как долго, дни, часы, минуты, секунды		время

Мыслить ясно

Некоторые формулировки могут быть сложными, из-за чего трудно думать «правильно», например:

$

Пример: У Сэма на 2 доллара меньше, чем у Алекса.

Как мы запишем это в виде уравнения?

• Пусть S = доллары У Сэма есть
• Пусть A = долларов У Алекса есть

Теперь … это: S − 2 = A

или должно быть: S = A − 2

или должно быть: S = 2 − A

 

Правильный ответ S = A − 2

( S − 2 = A — распространенная ошибка, так как вопрос написан «Сэм… на 2 меньше… Алекс»)

Пример: на нашей улице собак вдвое больше, чем кошек. Как мы запишем это в виде уравнения?

• Пусть D = количество собак
• Пусть C = количество кошек

Теперь… это: 2D = C

или должно быть: D = 2C

Теперь хорошенько подумайте!

Правильный ответ D = 2C

( 2D = C — распространенная ошибка, так как вопрос пишется «дважды… собаки… кошки»)

Примеры

Давайте начнем с очень простого примера , чтобы мы увидели, как это делается:

Пример: прямоугольный сад размером 12 м на 5 м, какова его площадь?

 

Превратите английский в алгебру:

Эскиз:

Буквы:

• Используйте w для ширины прямоугольника: w = 12 м
• Используйте h для высоты прямоугольника: h = 5 м

Формула для площади прямоугольника: A = w × h

Нас спрашивают о площади.

 

Решите:

A = w × h = 12 × 5 = 60 м ²

Площадь 60 квадратных метров .

Теперь давайте попробуем пример из верхней части страницы:

Пример: Сэм и Алекс играют в теннис. В выходные Сэм сыграл на 4 игры больше, чем Алекс, а вместе они сыграли 12 игр. Сколько игр сыграл Алексей?

 

Превратите английский в алгебру:

Буквы:

• Используйте S для того, сколько игр Сэм сыграл
• Используйте A для того, сколько игр сыграл Алекс

Мы знаем, что Сэм сыграл на 4 игры больше, чем Алекс, поэтому: S = A + 4

И мы знаем, что вместе они сыграли 12 игр:

S + A = 12

Нас спрашивают, сколько игр, в которые играл Алекс: A

 

Решите:

Начните с: S + A = 12

S = A + 4 , поэтому мы можем
заменить «A + 4» на S: (A + 4) + A = 12

Упростить: 2A + 4 = 12

Вычесть 4 из обеих частей: 2A = 12 − 4

Упростить: 2A = 8

Разделить обе части на 2: A = 4

Это означает, что Алекс сыграл 4 игры в теннис.

 

Проверка: Сэм сыграл на 4 игры больше, чем Алекс, поэтому Сэм сыграл 8 игр. Вместе они сыграли 8 + 4 = 12 игр. Да!

Более сложный пример:

Пример: Алекс и Сэм тоже строят столы.

Вместе они делают 10 столов за 12 дней.

Алекс, работая в одиночку, может сделать 10 штук за 30 дней.

Сколько времени потребуется Сэму, работающему одному, чтобы сделать 10 столов?

 

Превратите английский в алгебру:

Буквы:

• Используйте a для скорости работы Алекса
• Используйте s для скорости работы Сэма

12 дней Алекса и Сэма — это 10 столов, поэтому: 12a + 12s = 10

30 дней одного Алекса — это тоже 10 столов: 30a = 10

Нас спрашивают, сколько времени займет Сэм сделать 10 столов.

Решите:

30a = 10 , значит, ставка Алекса (столов в день): a = 10/30 = 1/3

Начнем с: 12a + 12s = 10

52

61 /3″ для a: 12(1/3) + 12s = 10

Упрощение: 4 + 12S = 10

Вычитание 4 с обеих сторон: 12S = 6

Разделите обе стороны на 12: S = 6/12

, что упрощает: с = 1/2 9

, что означает с = 1/2 99000

. что скорость Сэма составляет полстола в день (быстрее, чем у Алекса!)

Таким образом, 10 столов займут у Сэма всего 20 дней.

Интересно, Сэму нужно платить больше?

И еще пример «замены»:

Пример: Дженна усердно тренируется, чтобы пройти отбор на Национальные игры.

У нее регулярный еженедельный распорядок: в некоторые дни она тренируется по пять часов в день, а в другие дни — по 3 часа.

Всего она тренируется 27 часов в неделю. Сколько дней она тренируется по пять часов?

Буквы:

• Количество «5-часовых» дней: д
• Количество «3-х часовых» дней: e

Мы знаем, что в неделе семь дней, поэтому: d + e = 7

И она тренируется 27 часов в неделю, из них d 5-часовой день и e 3-часовой день: 5d + 3e = 27

Нас спрашивают, сколько дней она тренируется по 5 часов: d

 

Решите:

6

5

= 7

Итак: e = 7 − d

Поместите это в 5d + 3e = 27 5d + 3(7−d) = 27

2

= 1 − 7 d = 1 − 7 d 5 901

Вычесть 21 с обеих сторон: 5d − 3d = 6

Упростить: 2d = 6

Разделите обе части на 2: d = 3

Число «5-часовых» дней равно 3

Проверка : Она тренируется по 5 часов 3 дня в неделю, поэтому тренироваться по 3 часа в день в остальные 4 дня недели.

3 × 5 часов = 15 часов плюс 4 × 3 часа = 12 часов дает в сумме 27 часов

Несколько примеров из геометрии:

Пример: Круг имеет площадь 12 мм

² , каков его радиус?

Буквы:

• Используйте A для площади: A = 12 мм ²
• Используйте r для радиуса

И формула для площади: A = π r ²

Нас спрашивают о радиусе.

Решите:

Нам нужно изменить формулу, чтобы найти площадь

Начните с: A = π r ²

Поменяйте местами стороны: π r ²

= A 0005

Разделение обеих сторон на π : R ² = A / π

Квадратный корень с обеих сторон: R = √ (A / π)

69 формула: r = √(12 / π)

И получаем: r = 1,954 (на 3 знака)

Пример: куб имеет объем 125 мм

³ , какова площадь его поверхности?

Сделать быстрый набросок:

Буквы:

• Используйте V для тома
• Используйте A для Зоны
• Используйте s для длины стороны куба

Формулы:

• Объем куба: V = s ³
• Площадь поверхности куба: A = 6s ²

Нас спрашивают о площади поверхности.

Решите:

Сначала вычислите с по формуле объема:

Начните с: V = S ³

СОЗДАЯ СЛАДКИ: S ³ = V

Корень куба с обеих сторон: S = ∛ (V )

и We Get: )

и We Get: )

и We Get: ) (125 ) = 5

Now we can calculate surface area:

Start with: A = 6s ²

And we get: A = 6(5) ²

  А = 6 × 25 = 150 мм ²

Пример про Деньги:

Пример: Джоэл работает в местной пиццерии. Когда он работает сверхурочно, он зарабатывает в 1¼ раза больше обычной ставки.

Одну неделю Джоэл отработал 40 часов по обычной ставке оплаты, а также отработал 12 часов сверхурочно. Если Джоэл в общей сложности заработал 660 долларов за эту неделю, какова его нормальная ставка?

 

Письма:

• Обычная ставка Джоэла: N долларов в час

Формулы:

• Джоэл работает 40 часов при N$ в час = 40N$
• Когда Джоэл работает сверхурочно, он зарабатывает в 1¼ раза больше обычной ставки = 1,25 N долларов в час
• Джоэл работает 12 часов по цене 1,25 н. долл. в час = (12 × 1¼ Н) = 15 н. долл.
• А вместе он заработал 660 долларов, значит:

$40N + $(12 × 1¼N) = $660

Нас спрашивают об обычной ставке Джоэла в $N.

 

Решите:

Начните с 40N $ + (12 × 1¼N) = 660 $

Упростите: 40N $ + 15N = 660 $

Упростить больше: $ ​​55N = 660 долл. США

Разделите обе стороны на 55: $ ​​n = 12 долларов

, так что нормальная ставка Джоэла — 12 долларов США в час

. составляет 12 долларов в час, поэтому его ставка сверхурочных составляет 1¼ × 12 долларов в час = 15 долларов в час. Таким образом, его обычная заработная плата 40 × 12 = 480 долларов плюс оплата за сверхурочную работу 12 × 15 = 180 долларов дает нам в сумме 660

долларов.

Подробнее о деньгах, с этими двумя примерами, связанными со сложными процентами

Пример: Алекс кладет в банк 2000 долларов под сложные проценты в размере 11% годовых.

Сколько он будет стоить через 3 года?

Это формула сложных процентов:

Поэтому мы будем использовать эти буквы:

• Приведенная стоимость PV = 2000 долларов США
• Процентная ставка (в десятичном виде): r = 0,11
• Количество периодов: n = 3
• Будущая стоимость (значение, которое мы хотим): FV

Нас спрашивают о будущем значении: FV

 

Решите:

Начните с: FV = PV × (1+r) ⁿ

FV9 = 106 9000 что мы знаем: 2000 долл. США × (1+0,11) ³

Расчет: FV = 2000 долл. США × 1,367631

Расчет: FV = 2735,26 долл. США (с точностью до ближайшего цента) 900

Пример: Роджер положил 1000 долларов на сберегательный счет. Начисленные проценты начислялись ежегодно по той же ставке. Через девять лет депозит Роджера вырос до 1551,33 доллара 9.0139

Какова была годовая процентная ставка по сберегательному счету?

Формула сложных процентов:

С:

• Текущая стоимость PV = $1,000
• Процентная ставка (значение, которое мы хотим): r
• Количество периодов: n = 9
• Будущая стоимость: FV = 1 551,33 доллара США

Нас спрашивают о процентной ставке: r

 

Решите:

Начните с: FV = PV × (1+r) ⁿ

Put in what we know: $1,551. 33 = $1000 × (1+r) ⁹

Swap sides: $1000 × (1+r) ⁹ = $1,551.33

Divide both sides by 1000 : (1+r) = 1 551,33 долл. США / 1 000 долл. США

Упрощение: (1+R) ⁹ = 1,55133

9 -й корень: 1+R = 1,5513 3 ^{9135 (}

913513591359135 (19/

359135.9003 (9016.9003 (3913913913913 (1903

( 1 *

Рассчитать: 1+r = 1,05

Рассчитать: r = 0,05 = 5%

Таким образом, годовая процентная ставка составляет 5%

Чек : 1000 долл. США × (1,05) ⁹ = 1000 долл. США × 1,55133 = 1551,33 долл. США

И пример вопроса о соотношении:

Пример: В начале года соотношение мальчиков и девочек в классе 2 : 1

Но сейчас, спустя полгода, из класса ушли четыре мальчика и две новые девочки. Соотношение мальчиков и девочек теперь 4 : 3

Сколько сейчас всего учеников?

Письма:

• Количество мальчиков сейчас: b
• Количество девушек сейчас: г

Коэффициент тока составляет 4: 3

B G = 4 3

, который может быть перестроен до 3B = 4G

В начале года. 4) мальчиков и (г — 2) девочек, а соотношение было 2 : 1

б + 4 г — 2 = 2 1

Которое можно преобразовать в b + 4 = 2(g − 2)

Нас спрашивают, сколько всего учеников сейчас: b + g

1 9000 Решите :

Начало с: B + 4 = 2 (g — 2)

Упрощение: B + 4 = 2G — 4

Подряд 4 с обеих сторон: B =

. 8

Умножаем обе части на 3 (получаем 3b): 3B = 6G — 24

Помните 3B = 4G : 4G = 6G — 24

Сборник 6G От обоих С. ​​С. С. С. С. СИДЕР 9016: 0101616. 9010. 9010. 9010. 9010. 010101616.6.6.6.6.6.6.6.6.6. 6. Разделите обе части на −2: г = 12

Есть 12 девочек !

И 3b = 4g , поэтому b = 4g/3 = 4 × 12/3 = 16 , значит, 16 мальчиков

Итак, теперь в классе 12 девочек и 16 мальчиков, что составляет Всего 28 учащихся .

Чек

Сейчас 16 мальчиков и 12 девочек, поэтому соотношение мальчиков и девочек 16 : 12 = 4 : 3
В начале года было 20 мальчиков и 10 девочек, поэтому соотношение было 20 : 10 = 2 : 1

А теперь немного квадратных уравнений:

Пример: Произведение двух последовательных четных целых чисел равно 168. Что это за целые числа?

Последовательный означает один за другим. А их даже , так что они могут быть 2 и 4, или 4 и 6, и т. д.

Мы назовем меньшее целое число n , поэтому большее целое число должно быть n+2

И нам говорят, что произведение ( то, что мы получаем после умножения) равно 168, поэтому мы знаем:

n(n + 2) = 168

Нас просят ввести целые числа

Решите:

Начните с: n(n + 2) = 168

Развернуть: n ² + 2n = 168

Вычесть 168 с обеих сторон: n ² + 2n − 168 = 0

Это квадратное уравнение, и есть много способов его решения. Используя Решатель квадратных уравнений, мы получаем -14 и 12.

Проверка -14: -14(-14 + 2) = (-14)×(-12) = 168 ДА

Проверка 12: 12( 12 + 2) = 12×14 = 168 ДА

Итак, есть два решения: −14 и −12 — одно, 12 и 14 — другое.

 

Примечание: мы могли бы также попробовать «угадать и проверить»:

• Мы могли бы попробовать, скажем, n=10: 10(12) = 120 НЕТ (слишком маленький)
• Далее мы можем попробовать n=12: 12(14) = 168 ДА

Но если мы не будем помнить, что умножение двух отрицательных чисел дает положительное, мы можем упустить из виду другое решение (−14)×(−12).

А:

Пример: Вы архитектор. Ваш клиент хочет, чтобы комната была в два раза длиннее, чем ее ширина. Они также хотят веранду шириной 3 метра вдоль длинной стороны.

У вашего клиента есть 56 квадратных метров красивой мраморной плитки, чтобы покрыть всю площадь.

Какой длины должна быть комната?

Давайте сначала сделаем эскиз, чтобы все получилось правильно!:

Буквы:

• длина комнаты: L
• ширина комнаты: Ш
• Площадь общая включая веранду: А

Мы знаем:

• ширина комнаты равна половине ее длины: Ш = ½Д
• общая площадь равна (ширине комнаты + 3), умноженной на длину: А = (Ш+3) × Д = 56

Нас спрашивают о длине комнаты: Д

Решите:

Начните с: (Ш + 3) × Д = 56

Замените Ш = ½ Д : (½ Д + 6 1) × L = 56

Simplify: ½L ² + 3L = 56

Multiply all terms by 2: L ² + 6L = 112

Subtract 112 from both sides : л ² + 6 л — 112 = 0

Это квадратное уравнение , есть много способов решить его, на этот раз давайте воспользуемся факторингом:

Начнем с: L ² + 6L − 112 = 0

Два числа, которые умножаются, чтобы получить ас=-112,
и прибавьте к b=6 14 и −8: L ² + 14L − 8L − 112 = 0

Группа: L(L +14) − 8(L + 14) = 0

Группа : (L − 8)(L + 14) = 0

Итак, L = 8 или −14

Есть два решения квадратного уравнения, но возможно только одно из них, так как длина комнаты не может быть отрицательной!

Итак, длина комнаты 8 м

Чек

L = 8, поэтому W = ½L = 4

Итак, площадь прямоугольника = (W+3) × L = 7 × 8 = 56

Вот и мы.