Задачи по математике 3 класс.
| Страница | 1, | 2, | 3 |
Задача 1.
Для приготовления обеда повару понадобилось 24 кг картошки, свеклы в 3 раза меньше, а лука в 2 раза меньше чем свеклы. Сколько килограмм лука потратил повар?
Решение:
- 1) 24 : 3 = 8
- 2) 8 : 2 = 4
- Выражение: 24 : 8 : 2 = 4
- Ответ: 4 кг.
Задача 2
Оля вырезала из бумаги 5 квадратов, 7 треугольников, а кругов в 2 раза больше чем треугольников. Сколько всего Оля вырезала фигур?
Решение:
- 1) 7 * 2 = 14
- 2) 5 + 7 + 14 = 26
- Ответ: 26 фигур.
Задача 3
Первое число 12, второе в 3 раза меньше, а третье в 4 раза больше чем второе. Вычисли сумму этих трех чисел.
Решение:
- 1) 12 : 3 = 4 (второе число)
2) 4 * 4 = 16 (третье число) - 3) 12 + 4 = 16 (сумма первого и второго чисел)
- 4) 16 + 16 = 32 (сумма трех чисел)
- Выражение: 12 : 3 * 4 + 4 + 12 = 32
- Ответ: 32
Задача 4
В школьную столовую привезли 6 кг, лимонов, яблок на 24 кг больше чем лимонов, а груш на 12 кг меньше чем яблок.
Сколько килограмм груш привезли в школьную столовую?
Решение:
- 1) 6 + 24 = 30 (в столовую привезли яблок)
- 2) 30 — 12 = 18 (привезли груш)
- Выражение: (6 + 24) — 12 = 18
- Ответ: 18 кг груш привезли в столовую.
Задача 5
Для приготовления обеда повару понадобилось 24 кг картошки, свеклы в 3 раза меньше, а лука в 2 раза меньше чем свеклы. Сколько килограмм лука потратил повар?
Решение:
- 1) 24 : 3 = 8 (понадобилось свеклы)
- 2) 8 : 2 = 4 (понадобилось лука)
- Выражение: 24 : 3 : 2 = 4
- Ответ: 4 кг лука понадобилось повару.
Задача 6
Для приготовления крахмала требуется 6 кг картошки. Сколько крахмала получится из 36 кг картофеля?
Решение:
- 1) 36 : 6 = 6
- Ответ: 6 кг крахмала.
Задача 7
В поход пошли 24 мальчика, а девочек в 3 раза меньше, чем мальчиков.
Сколько всего детей пошло в поход?
Решение:
- 1) 24 : 3 = 8 (девочек пошло в поход)
- 2) 24 + 8 = 32
- Выражение: 24 : 3 + 8 = 32
- Ответ: 32.
Задача 8
Ящик с виноградом и три одинаковых ящика с яблоками весят 45 кг. Сколько весит один ящик с яблоками, если ящик с виноградом весит 15 кг.
Решение:
- 1) 45 — 15 = 30 (весят 3 ящика с яблоками)
- 2) 30 : 3 = 10 (весит один ящик с яблоками)
- Выражение: (45 — 10) : 3 = 10
- Ответ: 10 кг.
Задача 9
На детской площадке катались дети на двух и трехколесных велосипедах. Сколько и каких велосипедов было на площадке, если всего было 21 колесо и 8 велосипедов?
Решение:
- 1) 8 * 2 = 16 (было бы колес, если бы все велосипеды были двухколесными)
- 2) 21 — 16 = 5
- 2) 8 — 5 = 3
- Ответ: на площадке было 5 трехколесных велосипедов и 3 двухколесных.
Задача 10
В парке выкорчевали 6 орешников, а вместо них посадили 18 орешников. Во сколько раз больше посадили орешников, чем выкорчевали?
Решение:
- 1) 18 : 6 = 3
- Ответ: в 3 раза больше орешников посадили.
Задача 11
Отцу 36 лет, а сыну 9. Во сколько раз отец старше сына и на сколько лет сын моложе отца?
Решение:
- 1) 36 : 9 = 4
- 2) 36 — 9 = 27
- Ответ: в 4 раза сын моложе отца; на 27 лет отец старше сына.
Задача 12
Автобус за 8 часов работы расходует 48 литров топлива. Сколько литров топлива израсходует автобус за 6 часов работы?
Решение:
- 1) 48 : 8 = 6 (литров топлива автобус расходует за 1 час)
- 2) 6 * 6 = 36 (литров автобус расходует за 6 часов)
- Выражение: 48 : 8 * 6 = 36
- Ответ: 36 литров.
Задача 13
В столовую привезли абрикосы. Из них на компот взяли 3 килограмма, а на варенье в 3 раза больше. Сколько всего абрикос привезли в столовую?
Решение:
- 1) 3 * 3 = 9 (взяли абрикос на варенье)
- 2) 3 + 9 = 12 (всего в столовую привезли абрикос)
- Выражение: 3 * 3 + 3 = 9
- Ответ: 9 кг абрикос.
| Страница | 1, | 2, | 3 |
Задачи в два действия: математика 2, 3 класс
Занимательная математика / 2 класс / Задачи в два действия
Поделитесь с друзьями:
Решение задач в несколько действий помогает развивать навыки анализа условий математических задач и текстовой информации вообще.
Образовательный проект ЛогикЛайк помогает детям научиться решать любые задачи по методике «от простого к сложному».
Типовые составные задачи для 1-2 класса
Простая с точки зрения математики задача решается в одно арифметическое действие. Чтобы решить составную задачу, ее нужно разложить на две или более простые или составные задачи.
Типовые задания на сложение и вычитание
Маша съела 4 мандарина, а Саша съел на 2 мандарина меньше Маши.
Сколько всего мандаринов съели ребята?
Решение:
4−2=2; 4+2=6.
Сравни выражения:
10 + 25 ? 15 + 20.
Решение:
10 + 25 = 35; 15 + 20 = 35.
Следовательно: 10 + 25 = 15 + 20.
Это довольно скучные задачи, решать которые захочется не каждому ребенку. Есть и другой подход.
Интересные составные задачи для 2-3 класса
Задача 1. Арифметический ребус
В математических ребусах одинаковые картинки скрывают одинаковые цифры. Подобные задания вызывают интерес к математике даже у дошкольников.
Показать решение
Гриб повторяется в обоих примерах. Чтобы узнать, какое число спрятано за звездой:
1. Решим пример 10-3. За грибом прячется 7.
2. Заменим гриб семеркой и решим пример 7+1.
Ответ: 8.
Задача 2. Что тяжелее, а что легче?
Фрукты взвесили 2 раза. Определи какой из наборов фруктов самый легкий.
Показать решение
Для решения задачи мы выполняем два действия:
1. Описываем неравенства из условий задачи: виноград легче ананаса, апельсин легче винограда.
2. Делаем вывод: апельсин легче, чем ананас. Итоговое неравенство:
Масса апельсина < масса винограда < масса ананаса.
Ответ: апельсин.
Задача 3. Кто больше съел?
Фиолетовый монстрик съел 4 целых апельсина, а Красный — 7 половинок таких же апельсинов. Кто съел больше?
Показать решение
1.
4 целых апельсина = 2 + 2 + 2 + 2 = 8 половинок.
2. Сравниваем количество частей апельсинов, которые съели монстрики: 8 > 7.
Ответ: фиолетовый монстрик.
Задача 4. Кто что выбрал?
На отдыхе семья взяла напрокат 2 скутера и 3 велосипеда. Папа и мама выбрали разные транспортные средства, а папа и дочка — одинаковые. У мамы и сына оказался разный транспорт. На чем поехала бабушка?
Показать решение
Подобные задачи начинают решать с группировки объектов.
1. Из условий задачи видно, что в одну группу попадают папа и дочка. Из условий про пары папа-мама, мама-сын можно сделать вывод, что сын и папа — в одной группе. С ними и дочка.
2. 3 человека, 3 транспортных средства — велосипеды. Следовательно, маме и бабушке достаются 2 скутера.
Ответ: Бабушка поехала на скутере.
Более 100 000 ребят уже занимаются логикой на ЛогикЛайк – присоединяйтесь!
Начать обучение
17 категорий, 5 уровней сложности, более 2500 заданий
Двухшаговые уравнения — определение, этапы решения, примеры, часто задаваемые вопросы
Двухшаговые уравнения — это уравнения, которые можно решить ровно за два шага. Двухшаговые уравнения чрезвычайно легко решить. Как следует из названия, для решения двухшаговых уравнений требуется всего два шага. Эти уравнения немного сложнее, чем одношаговые уравнения. При решении двухэтапного уравнения нам нужно выполнить операцию с обеих сторон знака равенства.
В этой статье мы поймем значение двухшаговых уравнений с целыми, десятичными и дробными числами, как их решить, золотое правило решения двухэтапных уравнений, а также несколько примеров для лучшего понимания.
| 1. | Что такое двухшаговые уравнения? |
2. | Решение двухшаговых уравнений |
| 3. | Двухшаговые уравнения с десятичными дробями и дробями |
| 4. | Золотое правило решения двухшаговых уравнений |
| 5. | Часто задаваемые вопросы о двухшаговых уравнениях |
Что такое двухшаговые уравнения?
Двухшаговые уравнения — это алгебраические задачи, для решения которых требуется всего два шага. Двухшаговое уравнение представляет собой линейное уравнение с одной переменной. При выполнении операции для решения двухэтапного уравнения нам необходимо выполнить одну и ту же операцию с обеих сторон уравнения. Мы изолируем переменную на одной стороне уравнения, чтобы определить ее значение.
Двухшаговые уравнения Определение
Двухшаговые уравнения — это алгебраические уравнения, которые можно решить ровно за два шага и получить окончательное значение переменной за два шага. Как правило, двухшаговые уравнения имеют вид ax + b = c, где a, b, c — действительные числа.
- 2x + 3 = 7
- 0,3 года + 5 = 1
- (2/3)г — 12 = 10
Решение двухшаговых уравнений
Двухшаговые уравнения очень легко решить. Он включает всего один дополнительный шаг по сравнению с одношаговыми уравнениями для решения. Мы можем решить двухэтапное уравнение, изолируя переменную (обычно представленную буквой или алфавитом) в одной части уравнения и все остальные значения в другой части. Общие два шага для решения двухшаговых уравнений:
- Шаг 1. Сложение и вычитание, чтобы изолировать переменную.
- Шаг 2. Умножение или деление для определения значения переменной.
Давайте рассмотрим несколько примеров и решим двухэтапные уравнения, чтобы понять концепцию решения двухэтапных уравнений.
Пример 1: Решите уравнение 2x + 6 = 12.
Чтобы решить двухшаговое уравнение 2x + 6 = 12, нам нужно определить значение x.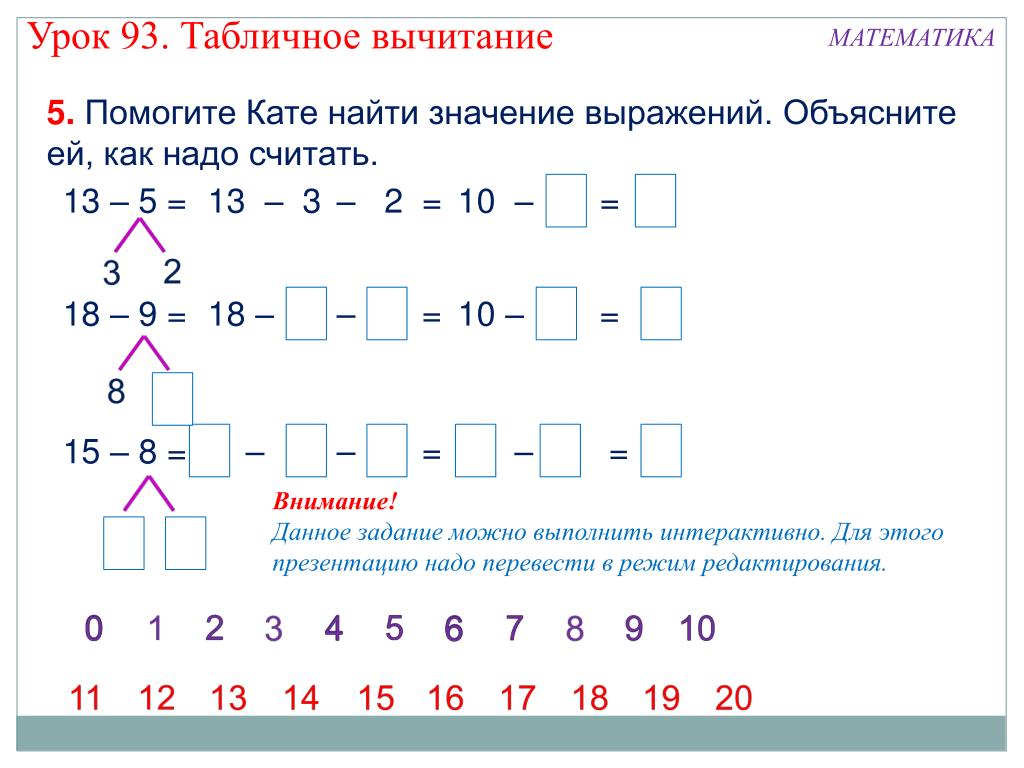
Давайте решим ее поэтапно.
Шаг 1: Вычтите -6 из обеих частей уравнения, чтобы выделить переменную x.
2x + 6 — 6 = 12 — 6
⇒ 2x = 6
Шаг 2: Разделите обе части уравнения на 2, чтобы найти x.
2x/2 = 6/2
⇒ x = 3
Следовательно, мы решили уравнение 2x + 3 = 12 всего за два шага.
Таким образом, двухэтапное уравнение может быть легко решено в виде последовательности шагов, представленной выше.
Двухшаговые уравнения с десятичными дробями и дробями
Двухшаговые уравнения, в которых десятичные дроби и дроби используются в качестве коэффициента при переменной и постоянном члене, называются двухшаговыми уравнениями с десятичными дробями и дробями. Вот несколько примеров двухэтапных уравнений с дробями и десятичными знаками:
- 0,3 x + 2/3 = 1
- 3x — 0,5 = 1,2
- (1/3) х + 4/5 = 3/4
Эти уравнения решаются таким же образом, как и общие двухшаговые уравнения, и те же шаги выполняются для определения значения переменной.
Золотое правило решения двухшаговых уравнений
Золотое правило решения двухшаговых уравнений — выполнять все операции одновременно с обеих сторон уравнения. Чтобы изолировать переменную с одной стороны уравнения и определить ее значение, мы сначала складываем или вычитаем с обеих сторон уравнения, а затем умножаем или делим с обеих сторон, чтобы получить окончательное решение двухшагового уравнения.
Важные примечания о двухшаговых уравнениях
- Удалите круглые скобки и объедините одинаковые члены, чтобы упростить каждую часть двухэтапного уравнения.
- Всегда сначала удаляйте константу, добавляя или вычитая соответствующее число.
- Всегда проверяйте решение в конце.
Темы, относящиеся к двухшаговым уравнениям
- Уравнения в математике
- Простые уравнения
- Алгебраические формулы
Часто задаваемые вопросы о двухшаговых уравнениях
Что такое двухшаговые уравнения в алгебре?
Двухшаговые уравнения — это алгебраические уравнения, для решения которых требуется всего два шага.
Во-первых, переменная изолируется путем добавления или вычитания числового значения с обеих сторон уравнения. Во-вторых, значение переменной вычисляется путем умножения или деления переменной на соответствующее число.
Каковы шаги для решения двухшаговых уравнений?
Общие два шага для решения двухшаговых уравнений:
- Шаг 1: Упростите данное уравнение, удалив все скобки и круглые скобки:
- Шаг 2: сложите или вычтите, чтобы изолировать переменную.
- Шаг 2: Умножьте или разделите, чтобы определить значение переменной.
- Шаг: Проверьте ответ, подставив его в данное уравнение.
Как решить двухшаговые уравнения?
Уравнения в два шага можно решить, выполнив два быстрых шага:
- Шаг 1: сложите или вычтите числа с обеих сторон, чтобы изолировать переменную.
- Шаг 2: Умножьте или разделите, чтобы определить значение переменной.
ЯВЛЯЕТСЯ ЛИ двухшаговое уравнение таким же, как и многошаговое уравнение?
Двухшаговое уравнение также можно назвать многошаговым уравнением, поскольку оно включает более одного шага.
А многоэтапное уравнение может состоять из двух или более шагов в процессе решения уравнения.
В чем разница между одношаговыми и двухшаговыми уравнениями?
Для решения одношаговых уравнений требуется всего один шаг, тогда как для решения двухшаговых уравнений требуется два шага. Двухшаговые уравнения включают только один дополнительный шаг по сравнению с одношаговыми уравнениями, которые необходимо решить.
Какова цель решения двухшаговых уравнений?
Целью решения двухэтапных уравнений является выделение переменной и определение ее значения. И, наконец, переменная должна удовлетворять заданному двухэтапному уравнению.
Решение многошаговых уравнений: обзор и примеры
Независимо от того, являетесь ли вы новичком в решении многошаговых уравнений или просто изучаете перед большим тестом главы, Альберт поможет вам!
Эта запись блога поможет вам определить многошаговые уравнения, примеры многошаговых уравнений и способы решения многошаговых уравнений (включая задачи с дробями и словами).
Пойдем!
Вернуться к оглавлению
Что мы рассматриваем
Что такое многошаговое уравнение?
Помните, уравнение — это математическое предложение, в котором используется знак равенства = , чтобы показать, что два выражения равны.
Мы начали изучение решения уравнений с одношаговых уравнений, затем перешли к двухшаговым уравнениям. (Проверьте эти ссылки, если вам нужно быстро освежить в памяти!)
Теперь мы переходим к многошаговым уравнениям . Многошаговое уравнение — это уравнение, для решения которого требуется два или более шагов. Эти задачи могут включать сложение, вычитание, умножение или деление. Нам также, возможно, придется комбинировать одинаковые термины или использовать свойство дистрибутивности, чтобы правильно решить наши уравнения.
Так что доставай свои математические инструменты! Вы никогда не знаете, что вы можете увидеть в многоступенчатом уравнении!
Примеры многошаговых уравнений
Многошаговые уравнения представляют собой широкую категорию уравнений.
Некоторые могут быть очень простыми, а другие становятся более сложными. Не бойся! Мы собираемся показать вам много примеров многошаговых уравнений и способы решения этих важных аспектов Алгебры 1.
Вот несколько примеров многошаговых уравнений:
5x + 10 = 3x + 12
8 лет — 3 — 2 года = 5
4(3м — 2) = 16
5х — 10 + 5 = 20 — 5х
Вернуться к оглавлению
Как решать многошаговые уравнения
Помните, уравнение решено, когда мы выделили переменную и нашли значение, которое делает уравнение верным. Чтобы решить уравнения, мы используем обратные операции, чтобы помочь нам изолировать переменную.
\text{Сложение} \leftrightarrow \text{Вычитание}
\text{Умножение} \leftrightarrow \text{Деление}
Порядок операций
Еще одна математическая концепция, которая поможет при решении многоэтапных уравнений, — это Порядок операций . Чтобы использовать порядок операций, мы должны сначала выполнить любые операции внутри группирующих символов (скобки, квадратные скобки и т.
д.), затем возвести в степень, затем умножить или разделить (что наступит раньше, слева направо), затем, наконец, сложение или вычитание (что наступит раньше). , слева направо). Вы можете запомнить это по аббревиатуре PEMDAS .
Кроме того, нам может понадобиться объединить одинаковые члены с обеих сторон уравнения, чтобы решить эти уравнения. В конце концов, вы создадите одно- или двухэтапное уравнение, которое сможете решить так же, как и предыдущие задачи!
Начните заниматься алгеброй 1 на Альберте прямо сейчас!
Вот пример многошагового уравнения с переменными с обеих сторон:
Найдите x в следующем уравнении:
| 8x — 10 = 4x + 2 | Исходное уравнение |
Поскольку переменные есть с обеих сторон, мы должны сначала исключить переменную с одной стороны. Я предлагаю сначала переместить 4x, чтобы не создавать негатив.
| 8x — 4x — 10 = 4x — 4x + 2 | Вычеркивание 4x с каждой стороны |
| 4x — 10 = 2 | Упрощенный |
Теперь. уравнение.
| 4x — 10 + 10 = 2 + 10 | Добавить 10 с каждой стороны | |||||
| 4x = 12 | Упрощение | |||||
| \ DFRAC {4x} {4} = \ DFRAC {12} {4} | DIDIDE CANIE SIDE на 4 | 9 | 111111115 | 1111111115 | 111111111115 | |
| Упростить |
Чтобы проверить свой ответ, вы можете упростить подстановку 3 в переменную, чтобы проверить, верно ли уравнение:
Вернуться к оглавлению
Ниже приведено короткое видео Майка ДеВора, показывающее другие примеры решения многошаговых уравнений: движение и посмотрите на некоторые более сложные примеры!
Многоступенчатые уравнения с дробями
При работе с уравнением, содержащим более одной дроби, проще всего решить уравнение, найдя наименьший общий знаменатель . Наименьший общий знаменатель — это наименьшее число, которое может быть общим знаменателем для набора дробей.
Как только мы найдем наименьший общий знаменатель, мы умножим каждый член на это значение, чтобы исключить дробь. Вот пример многошагового уравнения с дробями:
Ознакомьтесь с лицензиями школы Альберта !
Найдите y в следующем уравнении:
\dfrac{5y}{6} — \dfrac{1}{4} = \dfrac{3y}{4} + \dfrac{1}{2}
Знаменатели выше равны 2, 4, 6 , поэтому наименьший общий знаменатель для этих чисел равен 12 . Таким образом, мы умножим каждое слагаемое на 12.
| 12 \cdot \dfrac{5y}{6} — 12 \cdot \dfrac{1}{4} = 12 \cdot \dfrac{3y}{4} + 12 \cdot \dfrac{1}{ 2} | Умножить каждое слагаемое на 12 | |
| \dfrac{60y}{6} — \dfrac{12}{4} = \dfrac{36y}{4} + \dfrac{12}{2} | Результат умножения | |
| 10y — 3 = 9y + 6 | Упрощайте | |
| 10y — 9y — 3 = 9y — 9y + 6 | Вычитание 9y с каждой стороны | |
| y — 3 = 6 | . 3 = 6 + 3 | Добавить по 3 с каждой стороны |
| y = 9 | Упростить |
Чтобы проверить свой ответ, вы можете подставить 9 в переменную, чтобы проверить, верно ли уравнение:
| \dfrac{5y}{6} — \dfrac{1}{4} = \dfrac {3y}{4} + \dfrac{1}{2} | Исходное уравнение |
| 10y — 3 = 9y + 6 | Упрощенное уравнение (все члены умножаются на 12 ) |
| 9 -\cdot 3 = 9 \cdot 9 + 6 | Замена |
| 90 — 3 = 81 + 6 | Упростить |
| 87 = 87 \checkmark | Ответ подтвержден |
Следовательно, y = 9 является правильным решением.
Вернуться к оглавлению
Многошаговые уравнения с дистрибутивным свойством
Пример 1
Решите для z в следующем уравнении:
уравнение верно:
| 2(3z — 4) = 10 | Original equation |
| 2(3 \cdot 3 — 4) = 10 | Substitute |
| 2(9 — 4) = 10 | Simplify |
| 2(5) = 10 | Упростить |
| 10 = 10 \checkmark | Ответ подтвержден |
Таким образом, z = 3 является правильным решением.
Ознакомьтесь с лицензиями школы Альберта !
Пример 2
Решите для m в следующем уравнении:
| 3(m + 3) — 4 = 2(m — 2) | Исходное уравнение | |
| 3(m) + 3(3) — 4 = 2 (M) — 2 (2) | Распределительное свойство | |
| 3M + 9 — 4 = 2m — 4 | Упрощение | |
| 3M + 5 = 2M — 4 | , такие — 2 м + 5 = 2 м — 2 м — 4 | Вычесть по 2 м с каждой стороны |
| M + 5 = — 4 | Упрощение | |
| M + 5 — 5 = — 4 — 5 | Вычитание 5 с каждой стороны | |
| M = -9 | Спроф | M = -9 | M = -9 | Вы отвечаете, вы можете упростить подстановку -9 в переменную, чтобы увидеть, верно ли уравнение:
Таким образом, m = -9 является правильным решением. Вернуться к оглавлению Многошаговые задачи с уравнениямиПример 1
Solution First, let’s create an equation for the situation:
Чтобы проверить свой ответ, вы можете упростить, подставив 15 в переменную, чтобы убедиться, что уравнение верно: |
| 5 (15) + 10 = 2 (15) + 1 (15) + 40 | Заменитель | |
| 75 + 10 = 30 + 15 + 40 | Упростить | |
| 85 = 85 \ Checkmark | Ответ. подтверждено |
подтверждено
Таким образом, точка безубыточности для дистрибьютора А и дистрибьютора Б будет составлять 15 фунтов.
Начните заниматься алгеброй 1 на Альберте прямо сейчас!
Пример 2
Сэм идет в книжный магазин с купоном на 5 долларов на книгу. Купон можно использовать столько раз, сколько Сэм захочет. В конце концов он покупает три книги, которые стоят одинаковую сумму денег. Общая стоимость книг составила 45 долларов. Сколько стоила каждая книга c до применения купона? |
Решение
Сначала составим уравнение, моделирующее ситуацию:
3(c — 5) = 45
Поскольку каждая книга стоит одинаковую сумму, мы обозначаем эту сумму переменной c . Затем мы применили купон на $5 к каждой книге и, наконец, умножим стоимость каждой книги после купона на 3 .
Теперь просто решите для c, как любое другое многошаговое уравнение:
| 3(c) — 3(5) = 45 | Distribute the 3 |
| 3c — 15 = 45 | Simplify |
| 3c — 15 + 15 = 45 + 15 | Add 15 to both sides |
| 3c = 60 | Simplify |
| \dfrac{3c}{3} = \dfrac{60}{3} | Разделите обе части на 3 |
| c = 20 | Решено |
Таким образом, каждая книга стоила \$20 до того, как купон был использован.