Решить пример в столбик на умножение: Онлайн калькулятор. Умножение столбиком

Home -Photomath

Математика еще никогда не была такой увлекательной

Наши пошаговые объяснения помогут вам освоить многие разделы математики, от арифметики и до анализа, благодаря чему вы станете увереннее в своих силах.

С чем мы можем помочь?

• Математический анализ
• Деление в столбик
• Алгебра
• Геометрия
• Сложение и вычитание
• Функции
• Тригонометрия
• Умножение
• Дроби
• Пределы и интегралы
• Текстовые задачи
• Элементарная математика
• Статистика
• и многое другое!

Начать обучение

Решение задач с основ

Один отец хотел помочь своим детям с домашней работой по математике. Теперь его творение помогает уже миллионам учеников по всему миру.

Родителям

Damir Sabol

основатель

Нечто большее, чем приложение

Один школьный учитель должен уделять внимание многим ученикам. В приложении Photomath, напротив, одному ученику предоставляется множество учителей.

Photomath для обучения

Более 300 млн

скачиваний

4.7

Рейтинг приложения

ОБОЖАЮ это приложение. Каждый раз, когда я использую его в классе, мы с учениками поражаемся его способностям. Приложение демонстрирует несколько вариантов решения тех или иных уравнений, что дает ученикам благоприятные возможности для обучения, которые порой отсутствуют на обычном уроке.

Прекрасное приложение для решения математических задач, часто выручает в самый нужный момент! 

Благодаря Photomath моего 8-летнего сына будто бы осенило: он понял, как в его случае получается правильный ответ.

Большое спасибо! Я в математическом классе, и мне это очень полезно, спасибо!

О нас пишут

Страница 88 — ГДЗ по Математике 3 класс Моро, Волкова 2 часть

---

• Тип: ГДЗ, Решебник.
• Автор: Моро М. И., Волкова С. И., Бантова М. А.
• Год: 2020.
• Серия: Школа России (ФГОС).
• Издательство: Просвещение.

❤️️Ответ к странице 88. Математика 3 класс учебник 2 часть. Автор: М.И. Моро.

Решебник — страница 88

Готовое домашнее задание

Номер 1.

Запиши решение столбиком и выполни умножение с объяснением.

Ответ:

Номер 2.

Ответ:

Номер 3.

Купили 5 рулонов пленки, по 20 м в каждом. Хватит ли этой пленки на 4 теплицы, если на каждую идет 16 м пленки? 25 м пленки?

Ответ:

Количество рулонов — 5 шт. Плёнки в 1 рулоне — 20 м 1) 5 ∙ 20 = 100 (м) – плёнки было. 2) 4 ∙ 16 = 64 (м) – плёнки по 16 м надо на 4 теплицы. 3) 4 ∙ 25 = 100 (м) – плёнки по 25 м надо на 4 теплицы.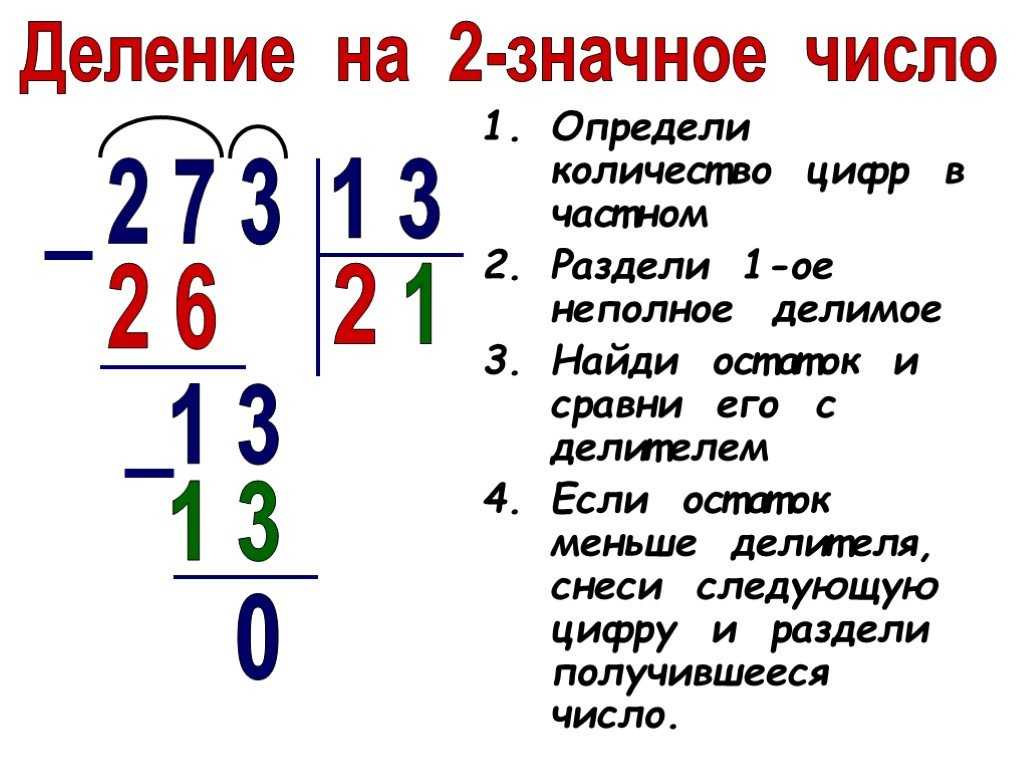 Ответ: плёнки хватит.

Номер 4.

Вставь пропущенные знаки действий, чтобы выражение имело указанное значение.

Ответ:

75 : 15 – 5 = 0      72 : 9 + 2 = 10 48 – 48 : 6 = 40    64 + 17 ∙ 2 = 98 36 : 6 : 6 = 1         56 – 9 ∙ 6 = 2

Номер 5.

Как можно взвесить:
1) 800 г масла, если есть по одной гире в 1 кг, 500 г и 200 г?
2) 3 кг черешни, если есть по одной гире в 5 кг и 2 кг; одна гиря в 2 кг?

Ответ:

1) С одной стороны весов – гиря в 1 кг, а с другой – 200 г и масло 800 г. 2) С одной стороны весов – гиря в 5 кг, а с другой – гиря 2 кг и черешня 3 кг.

Задание внизу страницы

Вычисли.

Ответ:

Задание на полях страницы

Цепочка:

Ответ:

90 : 6 = 15 15 ∙ 4 = 60 60 : 3 = 20 20 + 80 = 100

Рейтинг

Выберите другую страницу

1 часть

Учебник Моро	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	21	22	23	24	25	26	27	28	29	30	31	32	33	34	35	36	37	38	39	40	41	42	43	44	45	46	47	48	49	50	51	52	53	54	55	56	57	58	59	60	61	62	63	64	65	66	67	68	69	70	71	72	73	74	75	76	77	78	79	80	81	82	83	84	85	86	87	88	89	90	91	92	93	94	95	96	97	98	99	100	101	102	103	104	105	106	107	108	109	110	111

2 часть

4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	21	22	23	24	25	26	27	28	29	30	31	32	33	34	35	36	37	38	39	40	41	42	43	44	45	46	47	48	49	50	51	52	53	54	55	56	57	58	59	60	61	62	63	64	65	66	67	68	69	70	71	72	73	74	75	76	77	78	79	80	81	82	83	84	85	86	87	88	89	90	91	92	93	94	95	96	97	98	99	100	101	102	103	104	105	106	107	108	109	110	111

4.

Умножение матриц

Важно: Мы можем перемножать матрицы, только если количество столбцов в первой матрице совпадает с количеством строк во второй матрице.

Пример 1

а) Умножение матрицы 2 × 3 на матрицу 3 × 4 возможно и дает в качестве ответа матрицу 2 × 4.

b) Умножение матрицы 7 × 1 на матрицу 1 × 2 допустимо; это дает матрицу 7 × 2

c) Матрица 4 × 3, умноженная на матрицу 2 × 3, НЕвозможна.

Как умножить 2 матрицы

Сначала мы используем буквы, чтобы понять, что происходит. После этого мы увидим пример с числами.

В качестве примера возьмем обычную матрицу 2 × 3, умноженную на матрицу 3 × 2.

`[(a,b,c),(d,e,f)][(u,v),(w,x),(y,z)]`

Ответом будет матрица 2 × 2.

Умножаем и складываем элементы следующим образом. Мы работаем через 1-й строки первой матрицы, умножая на 1-й столбец второй матрицы, элемент за элементом. Мы добавить полученных продуктов. Наш ответ занимает позицию a ₁₁ (вверху слева) матрицы ответов.

Проделываем аналогичный процесс для 1-й строки первой матрицы и 2-го столбца второй матрицы. Результат помещается в позицию a ₁₂ .

Теперь о 2-й -й строке первой матрицы и 1-м -м столбце второй матрицы. Результат помещается в позицию а ₂₁ .

Наконец, делаем 2-ю строку первой матрицы и 2-й столбец второй матрицы. Результат помещается в позицию a ₂₂ .

Таким образом, результат умножения двух наших матриц выглядит следующим образом:

`[(a,b,c),(d,e,f)][(u,v),(w,x),(y,z)]` `=[(au+bw+cy,av +bx+cz),(du+ew+fy,dv+ex+fz)]`

Теперь давайте рассмотрим числовой пример.

Пользователи телефона

ПРИМЕЧАНИЕ. Если вы разговариваете по телефону, вы можете прокручивать любые широкие матрицы на этой странице вправо или влево, чтобы увидеть все выражение.

Пример 2

Умножить:

`((0,-1,2),(4,11,2))((3,-1),(1,2),(6,1))`

Ответить

Это 2×3 умножить на 3×2, что даст нам 2×2 отвечать.

`((0,-1,2),(4,11,2)) ((3,-1),(1,2),(6,1))`

`=((0xx3+ — 1xx1 + 2xx6,0xx-1+ -1xx2 + 2xx1), (4xx3+11xx1+2xx6,4xx -1 + 11xx2 + 2xx1))`

` = ((0-1+12,0-2+2), (12+11+12,-4+22+2))`

` = ((11,0),(35,20)) `

Наш ответ — матрица 2×2.

Умножение матриц 2 × 2

Процесс одинаков для матрицы любого размера. Мы умножаем на строк первой матрицы и на столбцов второй матрицы, элемент за элементом. Затем мы добавляем продукты:

`((a,b),(c,d))((e,f),(g,h))` `=((ae+bg,af+bh),(ce+dg,cf+dh ))`

В этом случае мы умножаем матрицу 2 × 2 на матрицу 2 × 2 и в результате получаем матрицу 2 × 2.

Пример 3

Умножить:

`((8,9),(5,-1))((-2,3),(4,0))`

Ответить

` ((8,9),(5,-1))((-2,3),(4,0)) `

`= ((8 xx -2+9xx4,8xx3+9xx0),( 5xx-2+ -1xx4,5xx3 + -1xx0))`

` = ((-16+36,24+0),(-10+ -4,15 + 0)) `

` = ((20 ,24),(-14,15)) `

Матрицы и системы одновременных линейных уравнений

Теперь мы видим, как написать систему линейных уравнений, используя матричное умножение.

Пример 4

Система уравнений

−3 х + y = 1

6 х — 3 у = -4

можно записать как:

`((-3,1),(6,-3))((x),(y))=((1),(-4))`

Матрицы идеально подходят для компьютерного решения задач, потому что компьютеры легко формируют массивы . Мы можем опустить алгебраические символы. Компьютеру для решения системы требуются только первая и последняя матрицы, как мы увидим в разделе «Матрицы и линейные уравнения».

Примечание 1 — Обозначение

Уход с записью умножение матриц.

Следующие выражения имеют различных значения:

AB это умножение матриц

A × B является произведением перекрестного , которое возвращает вектор

A * B используется в компьютерной записи, но не на бумаге

А • B Произведение точек , которое возвращает скаляр .

[Дополнительную информацию о векторных и скалярных величинах см. в главе «Вектор».]

Примечание 2. Коммутативность умножения матриц

`AB = BA`?

Давайте посмотрим, так ли это на примере.

Пример 5

Если

`А=((0,-1,2),(4,11,2))`

и

`В=((3,-1),(1,2),(6,1))`

найти AB и ВА.

Ответить

Мы выполнили AB выше, и ответ был:

`AB = ((0,-1,2),(4,11,2)) ((3,-1),(1,2), (6,1))`

` = ( (11,0),(35,20) )`

Теперь BA равно (3 × 2)(2 × 3), что даст 3 × 3:

`BA= ((3,-1),(1,2),(6,1))((0,-1,2),(4,11,2))`

`= ((0 -4,-3-11,6-2),(0+8,-1+22,2+4),(0+4,-6+11,12+2))`

` = (( -4,-14,4),(8,21,6),(4,5,14)) `

Итак, в этом случае AB НЕ равно BA.

На самом деле, для большинства матриц нельзя изменить порядок умножения и получить тот же результат.

В общем случае при перемножении матриц перестановочный закон не выполняется, т.е. AB ≠ BA . Есть два общих исключения из этого:

• Матрица идентичности: IA = AI = A .
• обратная матрица: A ^-1 А = АА ^-1 = I.

В следующем разделе мы узнаем, как найти обратную матрицу.

Пример 6. Умножение на матрицу идентичности

Учитывая, что

`А=((-3,1,6),(3,-1,0),(4,2,5))`

найти AI .

Ответить

`AI = ((-3,1,6),(3,-1,0),(4,2,5)) ((1,0,0),(0,1,0),(0 ,0,1))`

`=((-3+0+0,0+1+0,0+0+6),(3+0+0,0+ -1+0,0+0 +0),(4+0+0,0+2+0,0+0+5))`

`=((-3,1,6),(3,-1,0),(4,2,5))`

`=A`

Мы видим, что умножение на единичную матрицу не изменить значение исходной матрицы.

То есть

АИ = А

Упражнения

1. Если возможно, найдите BA и AB .

`А=((-2,1,7),(3,-1,0),(0,2,-1))`

`В=(4\\-1\\\5)`

Ответить

`BA=(4\ \ -1\ \ \ 5)((-2,1,7),(3,-1,0),(0,2,-1))`

`=(-8+(-3)+0\ \ \ 4+1+10\ \ \ 28+0+(-5))`

`=(-11\ \ 15\ \ 23)`

AB невозможно. (3 × 3) × (1 × 3).

2. Определить, если B = A ^-1 , учитывая:

`А=((3,-4),(5,-7))`

`В=((7,4),(5,3))`

Ответить

Если B = A ^-1 , то `AB = I`.

`AB=((3,-4),(5,-7))((7,4),(5,3))`

`=((21-20,12-12),( 35-35,20-21))`

`=((1,0),(0,-1))`

` !=I`

Итак, B НЕ является обратным A.

3. При изучении движения электронов, одна из спиновых матриц Паули равна

`s=((0,-j),(j,0))`

где

`j=sqrt(-1)`

Покажите, что с ² = I.

[Если вы никогда раньше не видели j , перейдите в раздел, посвященный комплексным числам].

92+0))`

`= ((1,0),(0,1))`

`=I`

4. Оцените следующее матричное умножение, которое используется при управлении движением роботизированного механизма .

`( (cos\ 60° ,-sin\ 60° ,0),(sin\ 60°, cos\ 60°,0),(0,0,1))((2),(4),( 0))`

Ответить

`( (cos\ 60° ,-sin\ 60° ,0),(sin\ 60°, cos\ 60°,0),(0,0,1))((2),(4),( 0))`

`=((2(0,5)-4(0,866)+0),(2(0,866)+4(0,5)+0),(0+0+0))`

`= ((-2.464),(3.732),(0))`

Интерпретация этого заключается в том, что рука робота перемещается из позиции (2, 4, 0) в позицию (-2,46, 3,73, 0). То есть это движется в x-y плоскость, но ее высота остается равной z = 0 . Матрица 3 × 3, содержащая sin и Значения cos говорят ему, на сколько градусов двигаться.

Интерактивы Matrix Multiplication

• Другие примеры умножения матриц
• Интерактивные операции с матрицами

6.

2 — Операции с матрицами 6.2 — Операции с матрицами

Равенство

Две матрицы равны тогда и только тогда, когда

• Порядок матриц одинаковый
• Соответствующие элементы матриц совпадают

Дополнение

• Порядок матриц должен быть одинаковым
• Сложить соответствующие элементы вместе
• Сложение матриц коммутативно
• Сложение матриц ассоциативно

Вычитание

• Порядок матриц должен быть одинаковым
• Вычесть соответствующие элементы
• Вычитание матриц не является коммутативным (как и вычитание действительных чисел)
• Вычитание матриц не является ассоциативным (как и вычитание действительных чисел)

Скалярное умножение

Скаляр — это число, а не матрица.

• Матрица может быть любого порядка
• Умножить все элементы матрицы на скаляр
• Скалярное умножение коммутативно
• Скалярное умножение ассоциативно

Нулевая матрица

• Матрица любого порядка
• Состоит из всех нулей
• Обозначается заглавной буквой O
• Аддитивная идентичность для матриц
• Любая матрица плюс нулевая матрица является исходной матрицей

Умножение матриц

A _m×n × B _n×p = C _m×p

• Количество столбцов в первой матрице должно быть равно количество строк во второй матрице. То есть внутренние размеры должны быть одинаковыми.
• Порядок произведения равен количеству строк в первой матрице на количество столбцов в вторая матрица. То есть размеры изделия – это наружные габариты.
• Так как количество столбцов в первой матрице равно количеству строк во второй матрица, вы можете спаривать записи.
• Каждый элемент в строке i из первой матрицы соединяется с элементом в столбце j из вторая матрица.
• Элемент в строке i , столбце j произведения образован путем умножения этих парных элементов и их суммирование.
• Каждый элемент произведения представляет собой сумму произведений элементов из ряд i первой матрицы и столбец j второй матрицы.
• Будет n произведений, которые суммируются для каждого элемента произведения.

См. полный пример умножения матриц.

Умножение матриц не является коммутативным

• Умножение действительных чисел.
• Внутренние размеры могут не совпадать при изменении порядка матриц.

Нельзя просто перемножать соответствующие элементы

• Поскольку порядок (размеры) матриц не обязательно должен быть одинаковым, может не быть соответствующие элементы, чтобы умножить вместе.
• Умножить строки первого на столбцы второго и сложить.

Нет деления матрицы

• Не существует определенного процесса деления матрицы на другую матрицу.
• Матрицу можно разделить на скаляр.

Идентификационная матрица

• Квадратная матрица
• Единицы по главной диагонали
• Нули везде
• Обозначается I. Если индекс включен, это порядок единичной матрицы.
• I — мультипликативная идентичность для матриц
• Любая матрица, умноженная на единичную матрицу, является исходной матрицей.
• Умножение на единичную матрицу является коммутативным, хотя порядок изменить

Идентификационная матрица размера 2

I 2 =		1	0
		0	1

Идентификационная матрица размера 3

I 3 =		1	0	0
		0	1	0
		0	0	1

Свойства матриц

Собственность	Пример
Коммутативность сложения	А + В = В + А
Ассоциативность сложения	А + (В + С) = (А + В) + С
Ассоциативность скалярного умножения	(кд) А = с (дА)
Скалярная идентичность	1А = А(1) = А
Распределительный	с (А + В) = сА + сВ
Распределительный	(с + г) А = сА + дА
Дополнительный идентификатор	А + О = О + А = А
Ассоциативность умножения	А (ВС) = (АВ) С
Распределительный левый	А (В + С) = АВ + АС
Правый распределитель	( А + В ) С = АС + ВС
Скалярная ассоциативность/коммутативность	с (АВ) = (сА) В = А (сВ) = (АВ) с
Мультипликативная идентичность	ИА = АИ = А

Свойства действительных чисел, которые не являются свойствами матриц

Коммутативность умножения

• Вы не можете изменить порядок задачи на умножение и ожидать чтобы получить то же самое продукт. АБ≠БА
• Вы должны быть осторожны при факторизации общих факторов, чтобы убедиться, что они находятся на такой же сторона. AX+BX = (A+B)X и XA+XB = X(A+B), но AX+XB не учитывается.

Свойство нулевого продукта

• Тот факт, что произведение двух матриц является нулевой матрицей, не означает, что одна из им была нулевая матрица.

Мультипликативное свойство равенства

• Если A=B, то AC = BC. Это свойство остается верным, но обратное не обязательно верно. Тот факт, что AC = BC, не означает, что A = B.
• Поскольку умножение матриц не является коммутативным, вы должны предварительно умножить или постумножить на обеих сторонах уравнения. То есть, если A=B, тогда AC = BC или CA = CB, но AC≠CB.

Нет деления матрицы

• Вы должны умножить на обратную матрицу

Вычисление функции с использованием матрицы

Рассмотрим функцию f(x) = x ² — 4x + 3 и матрицу A

А =		1	2
		3	4

Первоначальная попытка вычислить f(A) состояла бы в замене каждого x с A, чтобы получить f(A) = A ² — 4A + 3. Есть одно небольшое проблема однако. Константа 3 не матрица, и сложить нельзя матрицы и скаляры вместе. Итак, мы умножаем постоянная по матрице идентичности.

f(A) = A ² — 4A + 3I.

Вычислите каждый член функции, а затем сложите их вместе.

А 2 =		1	2		*		1	2		=		7	10
		3	4				3	4				15	22

-4 А = -4		1	2		=		-4	-8
		3	4				-12	-16

3И = 3		1	0		=		3	0
		0	1				0	3

ф(А) =		7	10		+		-4	-8		+		3	0		=		6	2
		15	22				-12	-16				0	3				3	9

Факторинг выражений

Показаны некоторые примеры факторинга.