Сложение и вычитание обыкновенных и десятичных дробей. смотреть онлайн видео от Математика от Баканчиковой в хорошем качестве.
12+
6 месяцев назад
Математика от Баканчиковой286 подписчиков
Математика 5 класс. Продолжая тему «Десятичные дроби», сегодня мы расскажем Вам о том, как обращать обыкновенную дробь в десятичную. А начнём мы с объяснения для чего обращают обыкновенную дробь в десятичную. Оказывается это нужно для того, чтобы выполнить сложение или вычитание обыкновенной дроби и десятичной, т.к. не существует правил сложения и вычитания таких дробей. Мы дадим Вам и на конкретных примерах пошагово разберём правило обращения обыкновенной дроби в десятичную дробь. Затем поспорим с авторами современных учебников математики 5 класса о том, что при делении одного натурального числа на другое натуральное число получается обыкновенная дробь. А для обращения обыкновенной дроби в десятичную, числитель необходимо представить сначала в виде десятичной дроби, а затем уже десятичную дробь разделить на знаменатель, потому что при делении десятичной дроби на натуральное число получается десятичная дробь.
 Равные десятичные дроби. Правило нулей. Математика 5 класс. https://rutube.ru/video/73e724f37977aeb256ba64ecb7932f54/
Округление десятичных дробей. Разряды и классы десятичной дроби. Математика 5 класс.
https://rutube.ru/video/27b315e7f6947dcede06cf447ae5e949/
Сложение и вычитание десятичных дробей. Математика 5 класс. https://rutube.ru/video/fde1d5a21516a66460a9744103adeb91/
Решение уравнений на сложение и вычитание десятичных дробей в 5 классе. Примеры решения уравнений. https://rutube.ru/video/14bfaafb1c6047388e14c264284db257/
Умножение десятичных дробей. Математика 5 класс. https://rutube.ru/video/d10e83ffbc0994bff4cc8c131e834c81/
#ДесятичныеДроби #ОбыкновеннуюДробьВДесятичную #СложениеДесятичнойДробиИОбыкновеннойДроби #МатематикаОтБаканчиковой
математика 5 класс, десятичные дроби, как обратить обыкновенную дробь в десятичную, обыкновенную дробь в десятичную, сложение и вычитание обыкновенной и десятичной дроби, сложение и вычитание десятичной и обыкновенной дроби, правило обращения обыкновенной дробь в десятичную
Равные десятичные дроби. Правило нулей. Математика 5 класс. https://rutube.ru/video/73e724f37977aeb256ba64ecb7932f54/
Округление десятичных дробей. Разряды и классы десятичной дроби. Математика 5 класс.
https://rutube.ru/video/27b315e7f6947dcede06cf447ae5e949/
Сложение и вычитание десятичных дробей. Математика 5 класс. https://rutube.ru/video/fde1d5a21516a66460a9744103adeb91/
Решение уравнений на сложение и вычитание десятичных дробей в 5 классе. Примеры решения уравнений. https://rutube.ru/video/14bfaafb1c6047388e14c264284db257/
Умножение десятичных дробей. Математика 5 класс. https://rutube.ru/video/d10e83ffbc0994bff4cc8c131e834c81/
#ДесятичныеДроби #ОбыкновеннуюДробьВДесятичную #СложениеДесятичнойДробиИОбыкновеннойДроби #МатематикаОтБаканчиковой
математика 5 класс, десятичные дроби, как обратить обыкновенную дробь в десятичную, обыкновенную дробь в десятичную, сложение и вычитание обыкновенной и десятичной дроби, сложение и вычитание десятичной и обыкновенной дроби, правило обращения обыкновенной дробь в десятичнуюс другой дробью, целым натуральным числом
Sign in
Password recovery
Восстановите свой пароль
Ваш адрес электронной почты
MicroExcel. ru Математика Алгебра Сложение десятичных дробей: правила, примеры
ru Математика Алгебра Сложение десятичных дробей: правила, примеры
В данной публикации мы рассмотрим, каким образом десятичную дробь можно сложить с другой дробью (десятичной и обыкновенной) или целым натуральным числом. Также разберем примеры для лучшего понимания представленного материала.
- Правило сложения десятичных дробей
- Примеры
Правило сложения десятичных дробей
Сумма десятичных дробей находится путем их сложения столбиком. Порядок действий следующий:
1. Одноименные разряды пишем друг под другом: десятые под десятыми, сотые под сотыми, тысячные под тысячными и т.д.
Примечание: При необходимости (если количество цифр после запятой у суммируемых дробей разное), в конце более “короткой” дроби с меньшим количеством знаков после запятой добавляем нули, чтобы выровнять ее с более “длинной”. Согласно основному свойству десятичной дроби, это никоим образом не отразится на ее величине.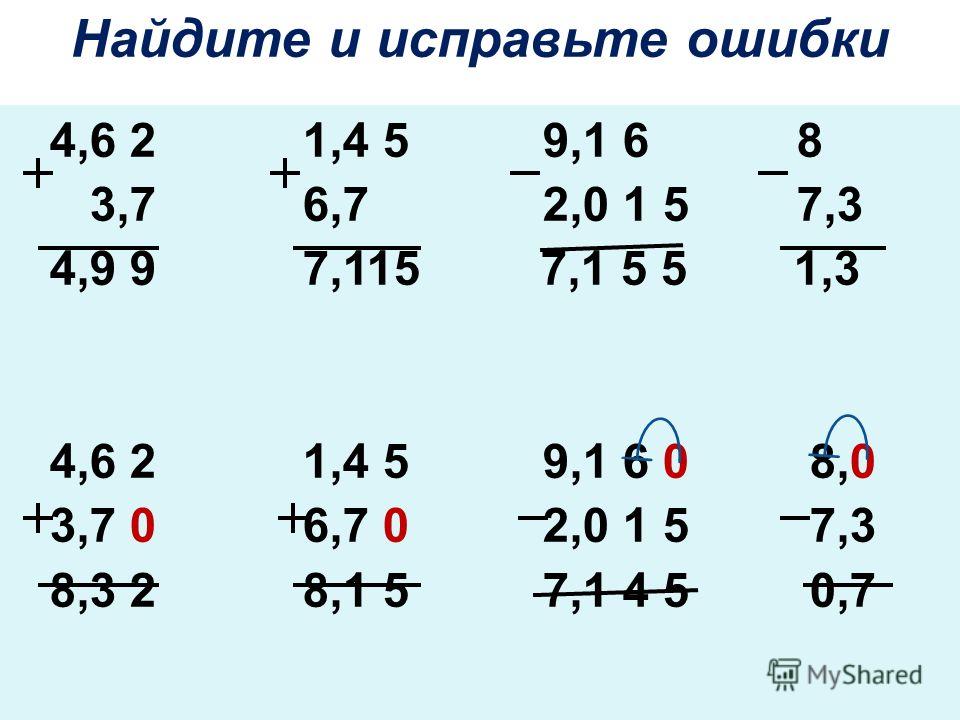 Когда процесс доведен до автоматизма, нули можно просто держать в уме.
Когда процесс доведен до автоматизма, нули можно просто держать в уме.
2. Десятичные разделители (запятые), также, должны находится строго друг под другом.
Примеры неправильной записи слагаемых:
Примеры правильной записи слагаемых:
3. Складываем дроби, как будто имеем дело с целыми натуральными числами. Т.е. на запятые внимания не обращаем.
4. В полученном результате ставим запятую строго там же, где она стояла в суммируемых дробях.
Сумма десятичной дроби и целого натурального числа
Если к десятичной дроби требуется прибавить целое натуральное число, то в конце последнего ставим запятую, после которой добавляем столько нулей, сколько цифр содержится в дробной части десятичной дроби. Затем вычисляем сумму слагаемых.
Сложение десятичной и обыкновенной дробей
Чтобы найти сумму десятичной и обыкновенной дробей, последнюю переводим в десятичную. После этого выполняем сложение.
Можно поступить наоборот – десятичную дробь преобразовать в обыкновенную. В этом случае уже складываем обыкновенные дроби.
Примеры
Давайте найдем сумму десятичных дробей, рассмотренных выше:
Примечание: если сумма десятых в дробной части результата больше 10, то единицу держим в уме и переносим ее в целую часть.
И, напоследок, вычислим сумму десятичной дроби и целого числа:
ЧАЩЕ ВСЕГО ЗАПРАШИВАЮТ
Таблица знаков зодиака
Нахождение площади трапеции: формула и примеры
Нахождение длины окружности: формула и задачи
Римские цифры: таблицы
Таблица синусов
Тригонометрическая функция: Тангенс угла (tg)
Нахождение площади ромба: формула и примеры
Нахождение объема цилиндра: формула и задачи
Тригонометрическая функция: Синус угла (sin)
Геометрическая фигура: треугольник
Нахождение объема шара: формула и задачи
Тригонометрическая функция: Косинус угла (cos)
Нахождение объема конуса: формула и задачи
Таблица сложения чисел
Нахождение площади квадрата: формула и примеры
Что такое тетраэдр: определение, виды, формулы площади и объема
Нахождение объема пирамиды: формула и задачи
Признаки подобия треугольников
Нахождение периметра прямоугольника: формула и задачи
Формула Герона для треугольника
Что такое средняя линия треугольника
Нахождение площади треугольника: формула и примеры
Нахождение площади поверхности конуса: формула и задачи
Что такое прямоугольник: определение, свойства, признаки, формулы
Разность кубов: формула и примеры
Степени натуральных чисел
Нахождение площади правильного шестиугольника: формула и примеры
Тригонометрические значения углов: sin, cos, tg, ctg
Нахождение периметра квадрата: формула и задачи
Теорема Фалеса: формулировка и пример решения задачи
Сумма кубов: формула и примеры
Нахождение объема куба: формула и задачи
Куб разности: формула и примеры
Нахождение площади шарового сегмента
Что такое окружность: определение, свойства, формулы
Объединение десятичных дробей и дробей.
 Элементарная математика
Элементарная математикаПредставьте, что вам нужно решить следующую задачу на сложение, состоящую в том, что объединяет десятичные и дробные числа:
Не так-то просто сложить дробь к десятичной дроби, верно? Намного проще складывать дроби к дробям или десятичные дроби к десятичным дробям. Итак, мы можем сделать это двумя способами:
- Изменить десятичную дробь на дробь .
- Изменить дробь на десятичный.
Сегодня мы научимся делать первый вариант: превращать десятичные дроби в дроби . Для того, чтобы начать, вам сначала нужно знать, как найти эквивалентные дроби.
В любом случае, в этом посте мы сделаем краткий обзор по нахождению равных дробей:
Нахождение равных дробей
Пример: Вот наша дробь…
И мы хотим сделать ее знаменатель числом 6, или другими словами:
Вы должны спросить себя, на какое число можно умножить 3 (знаменатель), чтобы получить 6… вот и все! Его умножили на 2.
Итак, числитель тоже надо умножить на 2.
Если мы умножим 2 на 2, мы получим 4.
Итак, теперь, когда вы знаете, как найти эквивалент дроби, мы собираемся преобразовать десятичную дробь в дробь.
Замена десятичной дроби
Предположим, у нас есть число…
Как мы можем изменить это на дробь? Здесь мы будем следовать этой стратегии, но сначала нам нужно спросить себя, какой знаменатель у числа… какой знаменатель может быть у любого числа, чтобы оно оставалось неизменным?… Вот и все! Число 1.
Теперь мы должны спросить себя, какое число нам нужно подставить в знаменатель эквивалентной дроби? Хитрость заключается в том, чтобы использовать 1 и ставить нули после нее. Итак, первое, что мы сделаем, это попробуем с одним нулем, 10.
Так как мы должны умножить 1 на 10, чтобы получить 10, мы также должны умножить 0,25 (числитель) на 10.
И у нас осталось….
Мы еще не избавились от всех десятичных знаков, верно? Тогда давайте продолжим добавлять нули!
Если мы умножим на 100, у нас останется:
Хорошо, помните, что дроби можно упростить. Если мы упростим эту дробь, у нас останется
Итак…
И все! Мы преобразовали десятичную дробь в дробь благодаря эквивалентным дробям.
Обзор
Подводя итог, когда мы хотим преобразовать десятичную дробь в дробь, мы должны:
- Измените десятичную дробь на дробь больше 1. Таким образом, десятичная дробь будет числителем, а 1 — знаменателем.
- Найдите эквивалентную дробь.
 Знаменатель этой дроби будет иметь 1, за которой следует столько нулей, сколько десятичных знаков в преобразуемом числе.
Знаменатель этой дроби будет иметь 1, за которой следует столько нулей, сколько десятичных знаков в преобразуемом числе. - Умножьте десятичную дробь на знаменатель эквивалентной дроби.
- Просто дробь.
Теперь вернемся к проблеме, которую мы видели в начале этого поста!
Затем,
Далее,
Теперь упростим,
Теперь проблема решена!
Я оставлю вам несколько ресурсов, которые вы можете использовать для ознакомления и практики:
- Повторить, как складывать дроби
- Практика с некоторыми упражнениями на эквивалентные дроби
- Обзор Как складывать десятичные дроби
В Smartick вы найдете еще много упражнений.
Подробнее:
- Автор
- Последние сообщения
Smartick
Команда создания контента.
Мультидисциплинарная и мультикультурная команда, состоящая из математиков, учителей, профессоров и других специалистов в области образования!
Они стремятся создать наилучший математический контент.
Последние сообщения Smartick (посмотреть все)
дроби, обыкновенные и десятичные — Студенты | Britannica Kids
Введение
Есть много способов получить сдачу за доллар: два полдоллара, четыре четверти, десять десятицентовиков, 20 пятицентовых монет или 100 пенни. Независимо от того, как производится сдача, доллар разбивается — «раскалывается» — на несколько частей. Эти части называются дробями, от того же латинского слова ( fractus, означает «сломанный»), из-за которого происходит перелом.
Все дроби представляют собой части целого. Давно удобно и принято делить вещи на сегменты. Часы делятся на 60 минут каждый. Сутки делятся на 24 часа, а годы на 12 месяцев. Мили делятся на футы, а километры на метры. Каждый из этих сегментов может быть представлен в виде дроби. Один дюйм составляет одну двенадцатую часть или одну двенадцатую фута. Дроби очень полезны, потому что они позволяют измерять не только целые числа, такие как 1, 2 или 5. Измерения с помощью дробей часто могут быть более точными: точнее сказать «четыре и одна десятая галлона», чем «немного». более четырех галлонов».
Измерения с помощью дробей часто могут быть более точными: точнее сказать «четыре и одна десятая галлона», чем «немного». более четырех галлонов».
Типы дробей
В повседневной математике есть два типа дробей: обыкновенные и десятичные. Единственная разница между ними заключается в том, как они написаны. Все дроби записываются с использованием тех же символов, которые используются для записи целых чисел, но символы используются по-другому. Простые дроби записываются как 4 / 10 или 7 / 100 : четыре больше десяти и семь больше ста. Одни и те же числа, представленные в виде десятичных дробей, будут 0,4 и 0,07. Обычно их читали как «четыре точки» и «ноль семь». Они выражают одинаковые суммы.
В обыкновенной дроби число под чертой является знаменателем, а число над чертой — числителем. При чтении обыкновенной дроби первым ставится числитель. Таким образом, 2 / 3 читается как две трети. Любое число, кроме нуля, может быть как знаменателем, так и числителем.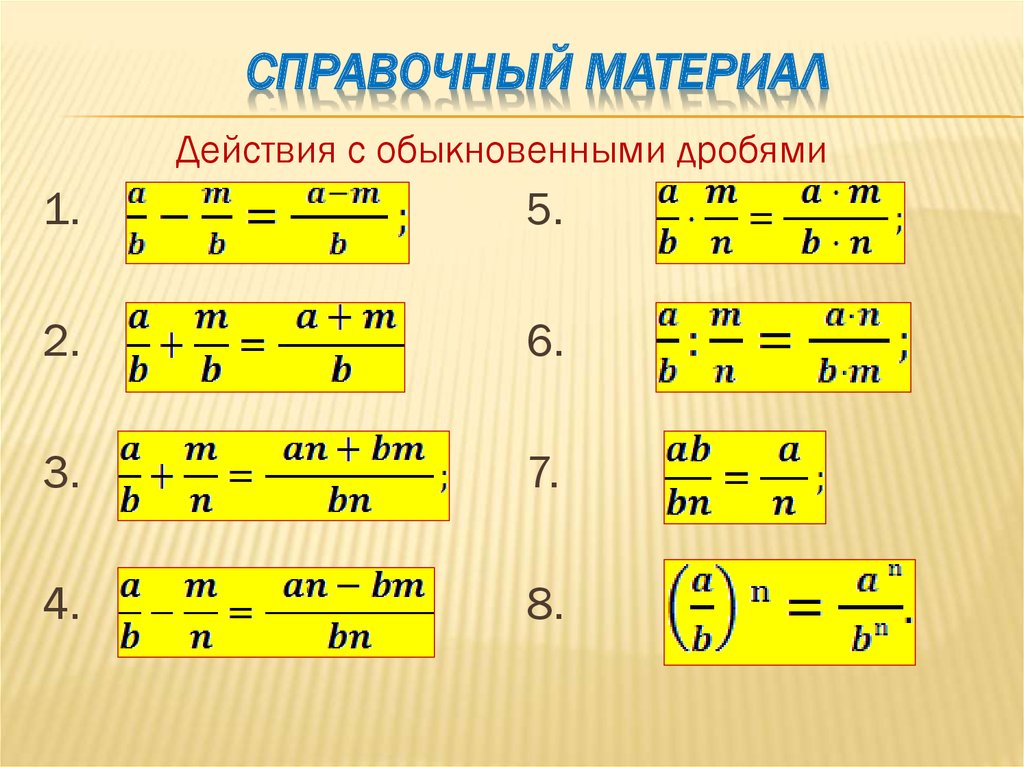 В обыкновенной дроби выражается не только количество, но и отношение: отношение одной величины к другой. Например, дробь 1 / 2 выражает отношение один к двум: Отношение один к двум состоит в том, что один равен половине двух. Использование коэффициента довольно распространено. Когда пекарь делает пирог, он может использовать две чашки сахара на каждые три чашки муки: соотношение два к трем, и оно может быть выражено дробью, 2 / 3 .
В обыкновенной дроби выражается не только количество, но и отношение: отношение одной величины к другой. Например, дробь 1 / 2 выражает отношение один к двум: Отношение один к двум состоит в том, что один равен половине двух. Использование коэффициента довольно распространено. Когда пекарь делает пирог, он может использовать две чашки сахара на каждые три чашки муки: соотношение два к трем, и оно может быть выражено дробью, 2 / 3 .
Десятичные дроби называются так потому, что они основаны на десятичной или десятичной системе счисления (см. Системы счисления и числа). Иногда называемые просто «десятичными», все десятичные дроби состоят из одного или нескольких чисел, которым предшествует точка, называемая десятичной запятой: например, 0,4 читается как четыре десятых. Если справа от запятой стоит только одна цифра, дробь всегда читается как «десятые». При наличии двух цифр дробь читается как «сотые», а при наличии трех – как «тысячные». Другими словами, десятичные дроби следуют той же последовательности, что и целые числа, где первая цифра находится в столбце «десятки», вторая — в «сотнях» и так далее (см. Арифметика). Например, десятичная дробь 0,075 читается как «семьдесят пять тысячных», а дробь 0,3852 — как «три тысячи восемьсот пятьдесят две десятитысячных».
Другими словами, десятичные дроби следуют той же последовательности, что и целые числа, где первая цифра находится в столбце «десятки», вторая — в «сотнях» и так далее (см. Арифметика). Например, десятичная дробь 0,075 читается как «семьдесят пять тысячных», а дробь 0,3852 — как «три тысячи восемьсот пятьдесят две десятитысячных».
В обыкновенных дробях любое число может быть знаменателем. Но в десятичных дробях неписаный знаменатель всегда равен 10 или некоторой степени 10, такой как 100, 1000, 10000 и так далее. Это означает, что преобразовать десятичную дробь в обыкновенную просто, поставив правильный знаменатель под числом справа от десятичной точки. Таким образом, 0,85 становится обыкновенной дробью 85 / 100 .
Чтобы превратить обыкновенную дробь в десятичную, надо числитель разделить на знаменатель. Таким образом, 3 / 4 можно изменить на десятичное число 0,75. Однако не все обыкновенные дроби можно преобразовать в такие точные десятичные дроби: 2 / 3 , поскольку десятичная дробь представляет собой бесконечный ряд шестерок справа от запятой.
Обыкновенные дроби.
Обыкновенные дроби бывают четырех видов: правильные, неправильные, смешанные и сложные. У правильной дроби числитель меньше знаменателя, например 3 / 4 . Поэтому значение правильной дроби всегда меньше единицы. В неправильных дробях числитель больше или равен знаменателю, как 4 / 4 или 6 / 5 . Таким образом, все неправильные дроби равны или больше единицы.
Смешанная дробь, также называемая смешанным числом, состоит из целого числа и дроби, например 2 1 / 3 . Любую смешанную дробь можно превратить в неправильную, умножив целое число на знаменатель, прибавив результат к числителю и поместив сумму над исходным знаменателем. Таким образом 2 1 / 3 можно заменить на 7 / 3 .
Сложные дроби, используемые в высшей математике, не состоят из натуральных чисел. Например, квадратный корень из двух на квадратный корень из пяти считается сложной дробью:
Точно так же использование смешанных дробей как для числителя, так и для знаменателя создаст сложную дробь:
Десятичные дроби .

Смешанные десятичные числа, известные как смешанные десятичные числа, возникают, если в числе есть цифры как слева, так и справа от десятичной точки. Примером может служить число 2,38: оно читается как «две и тридцать восемь сотых». Слово «и» используется только там, где стоит десятичная точка, чтобы отделить целое число от десятичной дроби. Во избежание путаницы при чтении десятичных дробей обычно говорят «точка» вместо «и». Число 2,38 будет читаться как «два целых три десятых восемь».
Неправильных десятичных дробей быть не может, потому что ни один числитель (десятичное число) никогда не может превышать понятный знаменатель (десятые, сотые и т. д.). Все, что больше десятичной дроби, будет смешанным или целым числом. Также было бы невозможно выразить сложную дробь в виде десятичной с какой-либо точностью.
Вычисления с десятичными дробями
Дроби можно складывать, вычитать, умножать и делить так же, как и целые числа. Эти операции легче выполнять с десятичными дробями, потому что процедуры очень похожи на использование целых чисел. Разница заключается в запоминании правильного размещения десятичной точки. Необходимо также отметить, что при сложении или вычитании каждое из чисел должно иметь одинаковое количество знаков после запятой. Чтобы добавить или вычесть нечетные десятичные дроби, возможно, придется добавить нули к одному из чисел. Например, чтобы прибавить 3,68 к 7,5, необходимо поставить ноль в конце второго десятичного знака, чтобы получилось 7,50. А при сложении или вычитании десятичные запятые всегда должны стоять в прямой колонке. Для выполнения этого сложения цифры должны быть записаны так:
Разница заключается в запоминании правильного размещения десятичной точки. Необходимо также отметить, что при сложении или вычитании каждое из чисел должно иметь одинаковое количество знаков после запятой. Чтобы добавить или вычесть нечетные десятичные дроби, возможно, придется добавить нули к одному из чисел. Например, чтобы прибавить 3,68 к 7,5, необходимо поставить ноль в конце второго десятичного знака, чтобы получилось 7,50. А при сложении или вычитании десятичные запятые всегда должны стоять в прямой колонке. Для выполнения этого сложения цифры должны быть записаны так:
Те же самые принципы применяются при вычитании десятичных дробей, и операция идентична вычитанию целых чисел, за исключением наличия десятичной точки. Если бы вышеупомянутую задачу нужно было решить как вычитание, она выглядела бы точно так же; только результат будет другим:
Обратите внимание, что ноль должен быть помещен в конце 7,5, чтобы было из чего вычесть 8.
Умножать десятичные дроби не сложнее, чем целые числа, за исключением того, что нужно помнить о правильном расположении десятичной точки. Основное отличие от сложения и вычитания состоит в том, что для заполнения десятичной дроби не нужно добавлять нули. Это связано с тем, что добавление нулей может привести к путанице в расположении десятичной точки.
Существуют определенные правила умножения с десятичными дробями, которые помогают правильно расставить десятичную точку.
Правило 1. Если десятичная дробь умножается на целое число, количество знаков после запятой в произведении равно количеству знаков после запятой в умножаемом числе.
Задача умножения десятичных шестидесятых (0,6) на четыре (4) выглядит следующим образом:
Обратите внимание, что десятичная точка ставится перед 4 в произведении, потому что в произведении был только один десятичный знак. число умножается (0,6).
Правило 2. Если целое число умножается на десятичную, количество знаков после запятой в произведении равно количеству знаков после запятой в множителе. (Обратите внимание, что это противоположно правилу 1, но принцип тот же.) Чтобы умножить 32 на 2,5, задача ставится следующим образом:
(Обратите внимание, что это противоположно правилу 1, но принцип тот же.) Чтобы умножить 32 на 2,5, задача ставится следующим образом:
Еще раз обратите внимание на размещение десятичной дроби. В множителе (2,5) был только один десятичный знак, поэтому в произведении (80,0) появляется только один. Однако в этом случае десятичную дробь можно исключить, поскольку 80 — это целое число. Если бы множитель был равен 2,6, произведение было бы 83,2, смешанное десятичное число, и десятичная точка была бы сохранена.
Правило 3. Если десятичная дробь умножается на десятичную, количество знаков после запятой в произведении равно количеству знаков после запятой в множителе плюс количество знаков после запятой в умножаемом числе. Если множитель и число, умноженные вместе, имеют в общей сложности четыре знака после запятой, в произведении будет четыре знака после запятой. (Любые нули в конце можно, конечно, исключить.) Задача умножения 0,56 на 0,44 ставится следующим образом:
Сумма показывает четыре десятичных знака, потому что множитель и число, умноженные вместе, имеют четыре десятичных знака. При умножении смешанных десятичных дробей применяется тот же принцип. Произведение 33,5 × 6,055 равно 202,8425 с четырьмя знаками после запятой.
При умножении смешанных десятичных дробей применяется тот же принцип. Произведение 33,5 × 6,055 равно 202,8425 с четырьмя знаками после запятой.
Процесс деления десятичных дробей такой же, как и целых чисел, но необходимо соблюдать особую осторожность при расстановке десятичной точки. При делении следует помнить один главный момент: положение запятой в ответе определяется положением запятой в делимом числе. Как и в умножении, здесь могут помочь определенные правила.
Правило 1. Если десятичная дробь делится на целое число, количество знаков после запятой в ответе равно количеству знаков после запятой в делимом десятичном числе.
Таким образом, если 0,06 разделить на 2, ответ будет 0,03.
Правило 2. При делении целого числа на десятичную дробь необходимо сначала преобразовать десятичную дробь в целое путем перемещения запятой вправо. Затем десятичная точка в делимом числе должна быть перемещена на такое же количество знаков вправо и при необходимости добавлены нули. Затем десятичная точка в ответе ставится непосредственно над десятичной точкой в делимом числе:
Затем десятичная точка в ответе ставится непосредственно над десятичной точкой в делимом числе:
Правило 3. При делении десятичного числа на десятичное число снова преобразуется в целое число, при этом десятичная точка в числе делится, а десятичная точка в ответе перемещается соответственно. Следовательно, ответ, полученный при делении 6,816 на 2,13, равен 3,2 с одним десятичным знаком, полученным по этому правилу.
Вычисления с обыкновенными дробями
Эта процедура несколько сложнее, чем с десятичными дробями. Но его можно упростить, если не забыть сделать так, чтобы все дроби имели одинаковый знаменатель. Это легко сделать, потому что деление или умножение обоих членов дроби на одно и то же число не меняет его значения. Поэтому добавить 2 / 3 и 3 / 4 , необходимо найти общий знаменатель. В данном случае это 12. Задача принимает вид 8 / 12 + 9 / 12 . Результат находится путем сложения числителей (8 + 9), чтобы получить 17 / 12 . Этот ответ можно изменить на смешанную дробь или десятичную.
Результат находится путем сложения числителей (8 + 9), чтобы получить 17 / 12 . Этот ответ можно изменить на смешанную дробь или десятичную.
Процесс вычитания аналогичен. Найдите общий знаменатель, затем вычтите один числитель из другого:
When dealing with mixed fractions, such as 2 1 / 3 + 3 3 / 4 , change them into improper fractions:
Then find the common denominator:
Это можно изменить обратно на смешанную или десятичную дробь (6 1 / 12 или немного больше 6,08).
При умножении дробей умножаются и числитель, и знаменатель. Но не обязательно находить общий знаменатель. Чтобы умножить 3 / 5 на 2 / 3 , умножьте два числителя (3 и 2), чтобы получить 6, затем два знаменателя (5 и 3), чтобы получить 15. Ответ: 6 / 15 .
 Знаменатель этой дроби будет иметь 1, за которой следует столько нулей, сколько десятичных знаков в преобразуемом числе.
Знаменатель этой дроби будет иметь 1, за которой следует столько нулей, сколько десятичных знаков в преобразуемом числе.