Сложные примеры 1 класс: Тренажеры по математике 1 класс. Примеры на сложение и вычитание, задачи

Примеры по математике на деление для 3 класса | контрольные, примеры для детей

Учим детей » Математика

Не все дети 3 класса хорошо понимают тему деления числа. Для того, чтобы ребенок лучше усвоил материал, нужно постоянно решать примеры на деление. Так он повторит правила на умножение и деление, а также приобретет навыки решения подобных примеров. На нашем сайте можно распечатать примеры на деления для 3 класса бесплатно.

Тема: Деление двухзначного числа на однозначное

1. Реши примеры на деление (для детей 3 класса)

28 : 7 =	27 : 9 =	28 : 4 =
54 : 9 =	56 : 7 =	56 : 8 =
36 : 6 =	64 : 8 =	63 : 9 =
45 : 5 =	42 : 6 =	25 : 5 =

примеры деление 3 класс

36 : 4 =	27 : 9 =	72 : 9 =
18 : 6 =	36 : 3 =	91 : 7 =
15 : 3 =	10 : 10 =	10 : 5 =
81 : 9 =	9 : 3 =	50 : 5 =

примеры деление 3 класс

2. Выполни деление и проверь результат умножением.

12 : 6 =	24 : 4 =	14 : 2 =
20 : 10 =	60 : 15 =	40 : 8 =

примеры деление 3 класс

2. Реши примеры. Внимательно выполняй последовательность действий.

72 : 9 + 22 * 5 — 28 : 7 =
36 — 81 : 9 + 12 : 2 * 7 =
20 + 7 * 5 — 48 : 12 =
90 : 30 — 34 + 11 * 4 =

3. Реши примеры на деление (для детей 3 класса)

90:3=
76:2=
46:3=
81:4=
100:25=
54:3=
74:2=
66:33=
90:30=
66:22=
36:2=
46:3=
99:11=
80:2=
88:4=
84:2=
100:20=
56:2=

4. Примеры с элементами деления. Запиши заданные предложения в виде примеров и реши их.

1. К числу 34 прибавь частное чисел 40 и 5.
3.2. К числу 33 прибавь частное чисел 33 и 11.
3.3. Из числа 42 вычти частное чисел 54 и 5.
3.3. Из числа 90 вычти частное чисел 64 и 8.

5. Сравни выражения и поставь знак >, < или = :

7 * 3 + 7 (?) 7 * 5

3 * 5 — 5 (?) 3 * 4

8 * 4 — 8 (?) 8 * 3

3 * 6 + 6 (?) 3 * 5

6 * 5 — 6 (?) 6 * 4

7 * 2 + 7 (?) 7 * 4

6.

Реши сложные примеры на деление (тренажер деления)

40:20=
96:8=
46:2=
75:25=
80:2=
100:2=
78:6=
90:18=
34:17=
85:17=

85:17=
80:16=
84:7=
32:4=
99:9=
48:4=
72:3=
96:6=
26:2=
84:6=

7. Примеры для распечатки для урока 3 класса

Порядок действий в примерах со скобками: попробуйте решить простой пример

Англоязычный Twitter облетела старая задачка по математике, которая разделила пользователей на несколько враждующих лагерей. Однако, ничего удивительного здесь нет, ведь правильное решение примеров по действиям со скобками всегда непросто отыскать, особенно если вы давно закончили школу.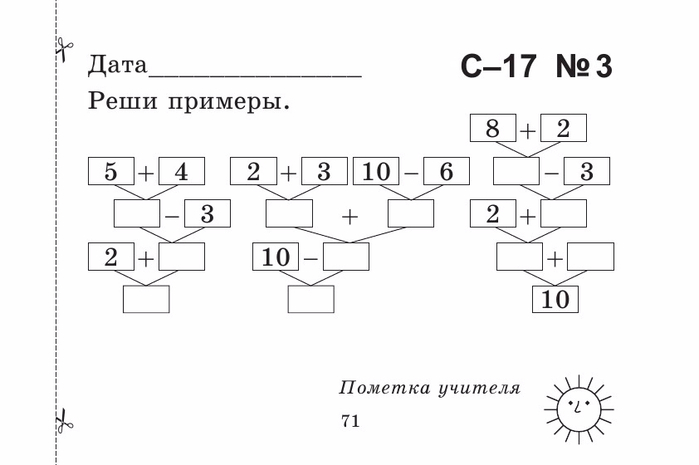 Хватит ли у вас смекалки и знаний базовой математики, чтобы пройти это испытание, посильное для младшеклассника, но непреодолимое для взрослого?

Юлиана Качанова Отвечаю за тесты

Twitter: 1RealMir

Решить пример со скобками по действиям пытались многие комментаторы твиттера, при этом используя самые разные, в том числе и несуществующие, математические приемы.

Известный новозеландский актёр Тайка Вайтити, знакомый отечественным кинозрителям по фильму «Реальные упыри», принял участие в данном интернет-споре, но к сожалению, не стал «отличником», решившим задачу правильно. Его, как и большинство других участников, подвело знание порядка действий сложных примеров со скобками.

Если вы считаете что хорошо помните последовательность действий в примерах со скобками, то попробуйте дать правильный ответ:

Не торопитесь давать ответ: правила хотя бы вспомните!

ВОПРОС 1 ИЗ 1

3

17

21

Главное – не торопитесь! В математике порядок действий примеров со скобками имеет огромное значение. «Дорожная карта» для того, чтобы правильно решить тот, или иной пример выглядит следующим образом:

• Внимательно посмотрите на пример и сначала произведите действие, которое указано в скобках.
• Запомните: порядок выполнения действий в примерах со скобками отдаёт предпочтение умножению и делению. Их называют действиями первой ступени.
• Последними выполняются сложение и вычитание. Это действия второй ступени.

Такая последовательность действий в примере со скобками выбрана не случайно и позволяет без особых затруднений получить правильный ответ.

Для закрепления рассмотрим следующий пример действия со скобками:

5+(7−2⋅3)⋅(6−4):2

В этом сложном примере со скобками порядок действий будет точно таким же.

Сначала мы вычислим значение первой скобки. Для этого сначала нужно выполнить умножение 2 на 3, как действие первой ступени, а затем вычесть из 7 полученное произведение. Получится 7-6=1
После этого мы переходим ко второй скобке. Если в первой скобке у нас был пример с умножением и вычитанием в ней, то здесь у нас только вычитание: 6-4=2

Давайте подставим решение примеров в скобках в первоначальное выражение:

5+(1)⋅(2):2 . 

Здесь уже сложных примеров со скобками нет, мы оставили их просто для визуального понимания, какое число по итогам наших манипуляций получилось.

Порядок действий в примерах со скобками (как впрочем и без них) требует от нас сначала выполнения умножения и деления, а затем сложения и вычитания. Продолжаем соблюдать его и получаем что сначала мы должны умножить 1 на 2, а затем поделив её на 2 прибавить разность к 5:

5+1⋅2:2=6

Таким образом первоначальный пример со скобками также будет равняться 6

5+(7−2⋅3)⋅(6−4):2=6.

ENG 1001: Предложения: простые, составные и сложные

Общим недостатком письменной речи является отсутствие разнообразных предложений. Осознание из трех основных типов предложений — простых, составных и сложных — может помочь вам варьировать предложения в вашем письме.

Самое эффективное письмо использует Разновидность типы предложений, описанные ниже.

1. Простые предложения

Простое предложение содержит самые основные элементы, которые делают его предложение: подлежащее, глагол и законченная мысль.

Примеры простых предложений включают следующее:

1. Джо ждал поезда.
   «Джо» = подлежащее, «ждал» = глагол
    
2. Поезд опоздал.
   «Поезд» = подлежащее, «был» = глагол
    
3. Мэри и Саманта сели на автобус.
   «Мэри и Саманта» = составное подлежащее, «брал» = глагол
    
4. Я искал Мэри и Саманту на автобусной остановке.
   «Я» = подлежащее, «посмотрел» = глагол
    
5. Мэри и Саманта прибыли на автобусную станцию ​​рано, но ждали до полудня на автобусе.
   «Мэри и Саманта» = составное подлежащее, «прибыл» и «waited» = составной глагол  

Совет . Если вы используете много простых предложений в эссе, подумайте над тем, чтобы пересмотреть некоторые из них. предложений в составные или сложные предложения (поясняется ниже).

использование составных подлежащих, составных глаголов, предложных фраз (таких как «на автовокзале») и другие элементы помогают удлинить простой предложения, но простые предложения часто бывают короткими. Использование слишком большого количества простых предложения могут сделать письмо «прерывистым» и могут помешать письму течет плавно.

Простое предложение может также называться самостоятельным предложением . Это называется «независимым», потому что, хотя он может быть частью составное или сложное предложение, оно также может стоять само по себе как полное предложение.
 

2. Составные предложения

Составное предложение относится к предложению, состоящему из двух независимых предложения (или полные предложения), связанные друг с другом с помощью

координирующего соединение . Сочинительные союзы легко запомнить, если подумать о слова «FAN BOYS»:

• Ф или
• А и
• N или
• Б ут
• О р
• Y и
• С или

Примеры составных предложений включают следующее:

1. Джо ждал поезд, но поезд опоздал.
    
2. Я искал Мэри и Саманту на автовокзале, но они прибыли на вокзал раньше полдень и ушел на автобус до моего приезда.
    
3. Мэри и Саманта прибыли на автовокзал до полудня, и они уехали на автобус до моего приезда.
    
4. Мэри и Саманта ушли на автобус до моего приезда, так
   я их на автовокзале не видел.

Совет : Если в эссе вы часто используете сложные предложения, вам следует подумать о том, чтобы преобразовать некоторые из них в сложные предложения (поясняется ниже).

Сочинительные союзы полезны для соединения предложений, но составные предложения часто злоупотребляют. В то время как сочинительные союзы могут указывать на некоторые тип отношения между двумя независимыми частями в предложении, они иногда не указывают на большую часть отношений. Слово «и» для например, только добавляет одно независимое предложение к другому, не указывая, как две части предложения логически связаны. Слишком много сложных предложений, которые использование «и» может ослабить написание.

Более четкие и конкретные отношения могут быть установлены с помощью сложные предложения.
 

3. Сложные предложения

Сложное предложение

состоит из независимого предложения и одного или нескольких связанных с ним зависимых пунктов . А зависимое предложение похоже на независимое предложение или полное предложение, но в нем отсутствует один из элементов, которые сделали бы его законченным предложением.

Примеры зависимых статей включают следующее:

• , потому что Мэри и Саманта прибыли на автовокзал до полудня
• пока он ждал на вокзале
• после того, как они уехали на автобусе

Зависимые предложения, подобные приведенным выше , не могут стоять отдельно как предложение, но их можно добавлять к независимое предложение, образующее сложное предложение.

Зависимые предложения начинаются с подчинительных союзов . Ниже приведены некоторые из наиболее распространенных подчинительных союзов:

• после
• хотя
• как
• потому что
• до
• хотя
• если
• с
• хотя
• кроме
• до
• когда
• всякий раз, когда
• тогда как
• где
• , а

Сложное предложение объединяет независимое предложение с одним или несколькими зависимыми предложениями.

Зависимое предложение может идти первым в предложении, за которым следует независимое предложение, как в следующем:

Совет : Когда зависимое предложение идет первым, для разделения двух предложений следует использовать запятую.

1. Поскольку Мэри и Саманта прибыли на автовокзал до полудня, я не увидел их на вокзале.
2. Ожидая на вокзале, Джо понял, что поезд опаздывает.
3. Выехав на автобусе, Мэри и Саманта поняли, что Джо ждет их на вокзале.

И наоборот, независимые предложения могут идти первыми в предложении, а за ними — зависимое предложение, как в следующем примере:

Совет : Когда независимое предложение стоит первым, для разделения двух предложений следует использовать запятую , а не .

1. Я не видел их на вокзале, потому что Мэри и Саманта прибыли на автовокзал до полудня.
2. Джо понял, что поезд опаздывает, пока он ждал на вокзале.
3. Мэри и Саманта поняли, что Джо ждал на вокзале после того, как они уехали в автобусе.

Сложные предложения часто более эффективны, чем сложные предложения, потому что сложное предложение указывает на более четкие и конкретные отношения между главными частями предложения. Слово «прежде» например, сообщает читателям, что одно происходит раньше другого. Такое слово, как «хотя» передает более сложные отношения, чем такое слово, как «и».

Термин периодическое предложение используется для обозначения сложного предложения, начинающегося с зависимого предложения и заканчивающийся независимым предложением, например: «Пока он ждал на вокзале, Джо понял, что поезд опаздывает».

Периодические предложения могут быть особенно эффективными, потому что завершенная мысль возникает в конец этому, так что первая часть предложения может доходить до значения, которое приходит в конце.

Предложения, начинающиеся с «И» или «Потому что»

Следует ли начинать предложение с «и» или «но» (или с одной из других координирующих союзы)?

Короткий ответ — «нет». Вы должны избегать начала предложения с «и», «или», «но» или другого сочинительные союзы. Эти слова обычно используются для соединения частей предложения, а не начинать новое предложение.

Однако такие предложения можно эффективно использовать. Поскольку предложения, начинающиеся с этих слов, выделяются, они иногда используются для выделения. Если вы используете предложения, начинающиеся с одного из сочинительных союзов, вы должны использовать эти предложения экономно и осторожно.

Следует ли начинать предложение со слова «потому что»?

Нет ничего плохого в том, чтобы начинать предложение со слова «потому что».

Возможно, некоторым учащимся говорят не начинать предложение со слова «потому что», чтобы избежать фрагментов предложения. (что-то вроде «Потому что Мэри и Саманта приехали на автовокзал до полудня» — это фрагмент предложения), но это совершенно верно. допустимо начинать предложение со слова «потому что», если предложение завершено (например, «Потому что Мэри и Саманта прибыли в автовокзала до полудня, я их на вокзале не видел».)

Смотри!

Комплексное число — определение, формула, свойства, примеры

Комплексные числа помогают найти квадратный корень из отрицательных чисел. Концепция комплексных чисел была впервые упомянута в I веке греческим математиком Героем Александрийским, когда он пытался найти квадратный корень из отрицательного числа. Но он просто изменил отрицательное значение на положительное и просто взял числовой корень. Кроме того, реальная идентичность комплексного числа была определена в 16 веке итальянским математиком Джероламо Кардано в процессе нахождения отрицательных корней кубических и квадратичных полиномиальных выражений.

Комплексные числа находят применение во многих научных исследованиях, обработке сигналов, электромагнетизме, гидродинамике, квантовой механике и анализе вибрации. Здесь мы можем понять определение, терминологию, визуализацию комплексных чисел, свойства и операции с комплексными числами.

1.	Что такое комплексные числа?
2.	График комплексных чисел
3.	Свойства комплексных чисел
4.	Операции над комплексными числами
5.	Алгебраические тождества комплексных чисел
6.	Решенные примеры
7.	Практические вопросы
8.	Часто задаваемые вопросы о комплексных числах

Что такое комплексные числа?

Комплексное число – это сумма действительного числа и мнимого числа. Комплексное число имеет вид a + ib и обычно обозначается буквой z. Здесь и a, и b – действительные числа. Величина «а» называется действительной частью, которая обозначается Re(z), а «b» называется мнимой частью Im(z). Также ib называют мнимым числом.

 

 

 

 

 

 

 

 

Примеры комплексных чисел: \(2+3i, -2-5i, \,\,\dfrac 1 2 + i\dfrac 3 2\) и т. д.

Степень of i

Алфавит i называется йотой и полезен для представления мнимой части комплексного числа. Кроме того, йота (i) очень полезна для нахождения квадратного корня из отрицательных чисел. У нас есть значение i ²  = -1, и оно используется для нахождения значения √-4 = √i ² 4 = 9. 0337 + 2i Значение i ²  = -1 является основным аспектом комплексного числа. Давайте попробуем понять больше о возрастающих силах i.

• я = √-1
• я ²  = -1
• i ³   = i.i ²  = i(-1) = -i
• i ⁴  = (i ² ) ²  = (-1) ²  = 1
• i ⁴ⁿ  = 1
• я ^{4n + 1}  = я
• i ^{4n + 2}  = -1
• i ^{4n + 3}  = -i

Графики комплексных чисел

Комплексное число состоит из действительной и мнимой частей, которые можно рассматривать как упорядоченную пару (Re(z), Im(z)) и представлять в виде точек координат на евклидовой плоскости. Евклидова плоскость применительно к комплексным числам называется комплексной плоскостью или Плоскостью Аргана, названной в честь Жана-Роберта Аргана. Комплексное число z = a + ib представлено действительной частью — a относительно оси x и мнимой частью -ib относительно оси y. {-1}\frac{b}{a}\). 9{-1}\frac{b}{a}\)).

Свойства комплексного числа

Следующие свойства комплексных чисел помогают лучше понять комплексные числа, а также выполнять различные арифметические операции над комплексными числами.

Сопряжение комплексного числа

Сопряжение комплексного числа образуется путем взятия той же действительной части комплексного числа и замены мнимой части комплексного числа на ее аддитивную обратную. Если сумма и произведение двух комплексных чисел являются действительными числами, то они называются сопряженными комплексными числами. Для комплексного числа z = a + ib его сопряженным является \(\bar z\) = a — ib.

Сумма комплексного числа и его сопряженного равна \(z + \bar z\)  = (a + ib) + (a — ib) = 2a, а произведение этих комплексных чисел \(z.\bar z \) = (a + ib) × (a — ib) = a ²  + b ² .

Обратная величина комплексного числа

Обратная величина комплексных чисел полезна в процессе деления одного комплексного числа на другое комплексное число. {-1}\).

Равенство комплексных чисел

Равенство комплексных чисел аналогично равенству действительных чисел. Два комплексных числа \(z_1 = a_1 + ib_1\) и \(z_2 = a_2 + ib_2 \) называются равными, если относительная часть обоих комплексных чисел равна \(a_1 = a_2\),  и мнимая части обоих комплексных чисел равны \(b_1 = b_2 \). Кроме того, два комплексных числа в полярной форме равны тогда и только тогда, когда они имеют одинаковую величину, а их аргумент (угол) отличается на целое кратное 2π.

Упорядочивание комплексных чисел

Упорядочивание комплексных чисел невозможно. Действительные числа и другие связанные системы счисления можно упорядочить, но нельзя упорядочить комплексные числа. Комплексные числа не имеют структуры упорядоченного поля, и нет упорядоченности комплексных чисел, совместимой со сложением и умножением. Также нетривиальная сумма квадратов в упорядоченном поле есть число \(\neq 0\), а в комплексном числе нетривиальная сумма квадратов равна i ²  + 1 ²  = 0. Комплексные числа можно измерить и представить на двумерной арграндовой плоскости по их величине, которая является расстоянием от начала координат.

Формула Эйлера: В соответствии с формулой Эйлера для любого действительного значения θ мы имеем e ^iθ  = Cosθ + iSinθ, и оно представляет комплексное число в координатной плоскости, где Cosθ – действительная часть, представленная относительно ось x, Sinθ – мнимая часть, представленная относительно оси y, θ – угол, образованный по отношению к оси x и воображаемой линии, соединяющей начало координат и комплексное число. Согласно формуле Эйлера и функциональному представлению x и y имеем e ^{x + iy}  = e ^x (уютный + isiny) = e ^x уютный + т.е. ^x Siny. Это разлагает экспоненциальную функцию на ее действительную и мнимую части.

Операции над комплексными числами

Различные операции сложения, вычитания, умножения, деления натуральных чисел можно выполнять и для комплексных чисел. Детали различных арифметических операций с комплексными числами заключаются в следующем.

Сложение комплексных чисел

Сложение комплексных чисел аналогично сложению натуральных чисел. Здесь в комплексных числах действительная часть добавляется к действительной части, а мнимая часть добавляется к мнимой части. Для двух комплексных чисел вида \(z_1 = a + id\) и \(z_2 = c + id\) сумма комплексных чисел \(z_1 + z_2 = (a + c) + i(b + d) \). Комплексные числа следуют всем следующим свойствам сложения.

• Закон замыкания: Сумма двух комплексных чисел также является комплексным числом. Для двух комплексных чисел \(z_1\) и \(z_2\) сумма \(z_1 + z_2\) также является комплексным числом.
• Коммутативный закон: Для двух комплексных чисел \(z_1\), \(z_2\) имеем \(z_1 + z_2 = z_2 + z_1\).
• Ассоциативный закон: Для данных трех комплексных чисел \(z_1, z_2, z_3\) имеем \(z_1 + (z_2 + z_3) = (z_1 + z_2)+z_3 \). 2 = -1\). Для двух комплексных чисел \(z_1\) = a + ib, \(z_2\) = c + id произведение равно \(z_1.z_2\) = (ca — bd) + i(ad + bc).

  Умножение комплексных чисел в полярной форме немного отличается от упомянутой выше формы умножения. Здесь абсолютные значения двух комплексных чисел перемножаются, а их аргументы складываются для получения произведения комплексных чисел. Для комплексных чисел \(z_1 = r_1(Cos\theta_1 + iSin\theta_1)\) и  z ₂  = \(z_2 = r_1(Cos\theta_2 + iSin\theta_2)\) произведение комплексные числа \(z_1.z_2 = r_1.r_2(Cos(\theta_1 + \theta_2) + iSin(\theta_1 + \theta_2))\). 92 + 2z_1z_2 +2z_2z_3 +2z_3z_1\)

Связанные темы:

• Комплексное сопряжение
• Калькулятор комплексных чисел
• Тригонометрия
• Координатная плоскость
• Координатная геометрия

Комплексные числа Советы и подсказки:

• Все действительные числа являются комплексными числами, но все комплексные числа не обязательно должны быть действительными числами.
• Все мнимые числа являются комплексными числами, но все комплексные числа не обязательно должны быть мнимыми числами. 9{2}-4(1)(1)}}{2(1)} \\[0,2 см]
  &=\frac{-1 \pm \sqrt{-3}}{2}\\[0,2 см]
  \text{Здесь } &\sqrt{-3} = \sqrt{-1} \times \sqrt{3} = i \sqrt{3}\\[0,2 см]
  x&= \frac{-1 \pm i\sqrt{3}}{2}\\[0,2 см]
  \end{align} \]

  Таким образом, корнями данного квадратного уравнения являются: \(\frac{-1}{2}+ i\frac{\sqrt{3}}{2};\,\,\ , \frac{-1}{2}- i\frac{\sqrt{3}}{2}\)

• Пример 2: Выразите сумму, разность, произведение и частное следующих комплексных чисел в виде комплексного числа.

  \[\begin{align} z_1&=-2+i\\[0.2cm]z_2&= 1-2i \end{align} \]

  Решение:

  Сумма:

  \[ \begin{ выровнять} z_1+z_2&= (-2+i)+(1-2i)\\[0,2 см] &=(-2+1)+ (i-2i)\\[0,2 см] &= -1-i \end{align}\]

  Разница:

  \[ \begin{align} z_1-z_2&= (-2+i)-(1-2i)\\[0,2 см] &=(-2-1) + (i+2i)\\[0,2 см] &= -3+3i \end{align}\]

  Продукт:

  \[ \begin{align} z_1\cdot z_2&= (-2+i)( 1-2i)\\[0,2см] &=-2+4i+i-2i^2\\[0,2см] &=-2+4i+i+2 \,\,\, [\потому что i^2 =-1]\\[0,2 см] &=5i \end{выравнивание}\] 92=-1]\\[0,2 см] &= \dfrac{-4-3i}{5}\\[0,2 см] &=- \dfrac{4}{5}- i \dfrac{3}{5 }\end{align}\]

  Следовательно, имеем:

  Сумма = -1 — i
  Разница = -3 + 3i
  Продукт = 5i
  Деление = -4/5 — 3i/5

перейти к слайдуперейти к слайду

Разбивайте сложные концепции с помощью простых визуальных средств.

Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций.

Записаться на бесплатный пробный урок

перейти к слайдуперейти к слайду

 

Часто задаваемые вопросы о комплексных числах

Что такое комплексные числа в математике?

Комплексное число представляет собой комбинацию действительных и мнимых значений. Обозначается z = a + ib, где a, b — действительные числа, а i — мнимое число. i = \(\sqrt{-1}\) и никакое действительное значение не удовлетворяет уравнению i ²  = -1, поэтому I называется мнимым числом.

Для чего используются комплексные числа?

Комплексное число используется для простого нахождения квадратного корня из отрицательного числа. Здесь мы используем значение i ²  = -1 для представления отрицательного знака числа, что помогает легко находить квадратный корень. Здесь мы имеем √-4 = √i ² 4 = + 2i. {-1}\frac{b}{a} \)).

Что такое действительные и комплексные числа?

Комплексные числа являются частью действительных чисел. Некоторые действительные числа с отрицательным знаком трудно вычислить, и мы представляем отрицательный знак с помощью йоты «i», и такое представление чисел вместе с «i» называется комплексным числом. Дополнительные комплексные числа полезны для нахождения квадратного корня из отрицательного числа, а также для нахождения отрицательных корней квадратного или полиномиального выражения.

Как делить комплексные числа? 92)}\).

Как строить графики комплексных чисел?

Комплексное число вида z = a + ib может быть представлено в плоскости арганда. Комплексное число z = a + ib может быть представлено в виде координат точки как (Re(z), Im(z)) = (a, ib). Здесь действительная часть представлена ​​относительно оси x, а мнимая часть представлена ​​относительно оси y.

Как преобразовать комплексные числа в полярную форму?

Комплексное число может быть легко преобразовано в полярную форму.