Сначала плюс или умножение: Что идёт первым плюс минус умножить или делить

Содержание

Порядок выполнения математических действий

Contents

Порядок выполнения действий:
38 – (10 + 6) = 22;
10 ÷ 2 × 4 = 20;
18 ÷ 2 – 2 × 3 + 12 ÷ 3 = 7
30 + 6 × (13 – 9) = 54 , т.е.:
Отзывов (58)

Читаем выражение слева направо и выбираем порядок действий по приоритету. Сначала выполняем действия в скобках. Затем умножение и/или деление. Далее складываем и вычитаем.

Если скобки имеют несколько вложений, то есть если внутри скобок есть ещё скобки, то сначала выполняем действия во внутренних скобках. Для простоты понимания, выражение в скобках можно воспринимать как самостоятельное выражение, то есть как отдельный пример, который надо решить. Внутри скобок действия выполняются согласно тому же порядку: Действия в скобках, затем умножение/деление, затем сложение/вычитание.

Умножение и деление не имеет между собой приоритета и выполняются слева направо, также как и сложение с вычитанием.

38 – (10 + 6) = 22;

Итак, вспомним о том, что сначала вычисляются выражения в скобках

1) в скобках: 10 + 6 = 16 ;

2) вычитание: 38 – 16 = 22 .

Если в выражение без скобок входит только сложение и вычитание, или только умножение и деление, то действия выполняются по порядку слева направо.

10 ÷ 2 × 4 = 20;

Порядок выполнения действий:

1) слева направо, сначала деление: 10 ÷ 2 = 5 ;

2) умножение: 5 × 4 = 20 ;

10 + 4 – 3 = 11 , т.е.:

Если в выражении без скобок есть не только сложение и вычитание, но и умножение или деление, то действия выполняются по порядку слева направо, но преимущество имеет умножение и деление, их выполняют в первую очередь, а за ними и сложение с вычитанием.

18 ÷ 2 – 2 × 3 + 12 ÷ 3 = 7

Порядок выполнения действий:

4) 9 – 6 = 3 ; т.е. слева направо – результат первого действия минус результат второго;

5) 3 + 4 = 7 ; т.е. результат четвертого действия плюс результат третьего;

Если в выражении есть скобки, то сначала выполняются выражения в скобках, затем умножение и деление, а уж потом сложение с вычитанием.

30 + 6 × (13 – 9) = 54 , т.е.:

1) выражение в скобках: 13 – 9 = 4 ;

2) умножение: 6 × 4 = 24 ;

3) сложение: 30 + 24 = 54 ;

Итак, подведем итоги. Прежде чем приступить к вычислению, надо проанализировать выражение: есть ли в нем скобки и какие действия в нем имеются. После этого приступать к вычислениям в следующем порядке:

1) действия, заключенные в скобках;

2) умножение и деление;

3) сложение и вычитание.

Если вы хотите получать анонсы наших статей подпишитесь на рассылку “Новости сайта“.

Продолжаем рубрику «основные содержательные линии курса математики начальной школы». В.

Продолжаем тему «основные содержательные линии курса математики начальной школы». В.

Продолжим изучение предметов, которые изучают наши дети в начальной школе.

Продолжим изучение программы математики в начальной школе и на этот.

Одним из простых арифметических действий является деление.

Мы знаем, что.

Понравилась статья – поделитесь с друзьями:

Оставляйте пожалуйста комментарии в форме ниже

Отзывов (58)

Полезная статья. Спасибо!

Очень все понятно. Для детей важна такая разъяснительная работа. Где Вы были, когда я пошла в школу?

)) Покажу сыну, пусть изучает. Я это вроде все помню. Спасибо )

Спасибо, сайт нужный. Честно говоря, уже кое – что подзабыла, а уроки с внучкой делаем. Вот, вспомнилось…

Очень необычная тематика сайта. Но тем, наверное, он и интересен. Иногда не знаешь, как объяснить ребенку тот или иной материал школьной программы.

Какое подспорье для родителей. И полезности для деток. Не всегда они материал усваивают в школе.

Сам учитель. Сайт очень полезный. Детям и родителям – хорошее подспорье

Вы взяли пример из головы, в начальной школе не изучают отрицательных чисел, а также не оперируют такими большими числами. Результат пятого действия будет отрицательным.
Но попробуем решить данный пример:
1) Выражение в скобках: 64385 – 39288 = 25097
Далее умножение:
2) 4217 * 4 = 16868
3) 25097 * 3 = 75291
4) 321 * 1000 = 321000
Теперь слева на право
5) 16868 – 75291 = -58423 (. )
Это уже шестой класс, тема “Сложение положительных и отрицательных чисел”
6) -58423 + 321000
От перемены мест слагаемых сумма не меняется:
321000 + (-58423) = 321000 – 58423 = 262577

Помогите люди добрые.
Я тут читал кое где в иностранной литературе, что если в выражении есть действия двух уроовней 1(сложение и вычитание) и 2 (умножение и деление)
к примеру 20-6:3х2+2=
то в первую очередь должно выполнятся действия 2-ого уровня, потом 1-го. Но загвоздка с тем, что говорится – надо выполнить сперва умножение а потом деление, а не как нас учили по правилу слева направо.
Объясните плз.

Обязательно слева на право, так как умножение и деление равноценны. Но, если представить умножение в виде дроби:

тогда 2 перенесется в числитель и первым выполняется умножение
(6 * 2)/3 = (6:3)*2 = 4.
То есть порядок выполнения важен!

Помогите решить пример у всех расходятся ответы
6/2*(1+2)
ответь пожалуйста

Если 6 : 2 * (1 + 2) =
1) 1 + 2 = 3
2) 6 : 2 = 3
3) 3 * 3 = 9

Если
6
———-
2 * (1 + 2)
то есть 6 : (2 * (1 + 2))
1) 1 + 2 = 3
2) 2 * 3 = 6
3) 6 : 6 = 1

Это два разных примера.
Если

6 * (1 + 2)
———–
2
1) 1 + 2 = 3
2) 6 * 3 = 18
3) 18 : 2 = 9
Это тот же первый вариант

Если Вы правильно написали, то это первый вариант и ответ 9

Очень жаль, если вы этому детей учите.. Примеры 6:2*(1+2) и 6/2*(1+2) одинаковые… никогда не было такого, чтобы черта дроби и двоеточие означали разные действия или определяли порядок действий.
В данном случае необходимо также учесть правило раскрытия скобок:
6:2*(1+2) = 6:(2*1 + 2*2) = 6:(2+4) = 6:6 = 1 – единственный верный ответ.

6:2*(1+2) и 6/2*(1+2) это абсолютно эквивалентные записи (то есть одинаковые).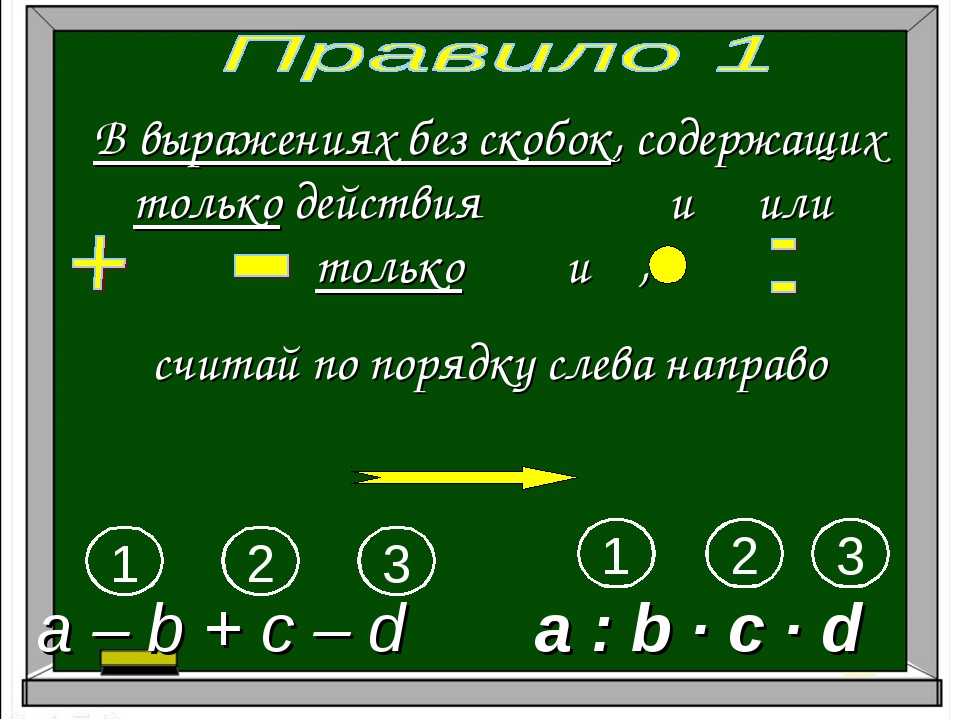

Порядок действий следующий:
1) 1+2 = 3
2) 6:2 = 3
3) 3*3 = 9

Ваш вариант с раскрытием скобок будет верен, если запись выражения будет следующей:
6:(2*(1+2)) = 1;

Ваше недоумение понятно, оно имеет глубокие исторические корни, в старых учебниках по алгебре можно встретить упоминание о именно такой последовательности действий, как предлагаете вы. Это связанно с неоднозначностью интерпретации записи. Но в наше время это разночтение устранено. Так что не надо забивать людям голову неверной информацией, а тем более забивать этими пережитками прошлого головы детей.
Простой пример. Ребенок на уроке информатики на языке Паскаль запишет y:=6:2*(1+2) и, поверьте мне, получит y=9. Не ломайте детскую психику.
В связи с порядком действий бывают забавные ситуации когда человеку в руки попадает калькулятор с обратной польской записью, а он и понятия не имеет об этом. И начинается “Святая Война за Истину”. Будьте проще, меньше пафоса, мы все люди и нам свойственно ошибаться. Добра Вам.

§ Порядок действий в решении примеров по математике

Похоже, вы используете блокировщик рекламы. Наш сайт существует и развивается только за счет дохода от рекламы.

Пожалуйста, добавьте нас в исключения блокировщика.

Скрыть меню

На главную страницу

Войти при помощи

Темы уроков

Начальная школа

Геометрия: начальная школа
Действия в столбик
Деление с остатком
Законы арифметики
Периметр
Порядок действий
Разряды и классы. Разрядные слагаемые
Счет в пределах 10 и 20

Математика 5 класс

Взаимно обратные числа и дроби
Десятичные дроби
Натуральные числа
Нахождение НОД и НОК
Обыкновенные дроби
Округление чисел
Перевод обыкновенной дроби в десятичную
Площадь
Проценты
Свойства сложения, вычитания, умножения и деления
Среднее арифметическое
Упрощение выражений
Уравнения 5 класс
Числовые и буквенные выражения

Математика 6 класс

Масштаб
Модуль числа
Окружность. Площадь круга
Отношение чисел
Отрицательные и положительные числа
Периодическая дробь
Признаки делимости
Пропорции
Рациональные числа
Система координат
Целые числа

Алгебра 7 класс

Алгебраические дроби
Как применять формулы сокращённого умножения
Многочлены
Одночлены
Системы уравнений
Степени
Уравнения
Формулы сокращённого умножения
Функция в математике

Геометрия 7 класс

Точка, прямая и отрезок
Что такое аксиома и теорема

Алгебра 8 класс

Квадратичная функция. Парабола
Квадратные неравенства
Квадратные уравнения
Квадратный корень
Неравенства
Системы неравенств
Стандартный вид числа
Теорема Виета

Алгебра 9 класс

Возрастание и убывание функции
Нули функции
Область определения функции
Отрицательная степень
Среднее
геометрическое

Алгебра 10 класс

Иррациональные числа

Алгебра 11 класс

Факториал

Не пером пишут, а умом. В.И. Даль

на главную

Введите тему

Русский язык Поддержать сайт

При расчётах примеров нужно соблюдать определённый порядок действий. С помощью правил ниже, мы разберёмся в каком порядке выполняются действия и для чего нужны скобки.

Если в выражении скобок нет, то:

сначала выполняем слева направо все действия умножения и деления;
а потом слева направо все действия сложения и вычитания.

Рассмотрим порядок действий в следующем примере.

Напоминаем вам, что порядок действий в математике расставляется слева направо (от начала к концу примера).

При вычислении значения выражения можно вести запись двумя способами.

Первый способ

Каждое действие записывается отдельно со своим номером под примером.
После выполнения последнего действия ответ обязательно записывается в исходный пример.

Запомните!

При расчёте результатов действий с двузначными и/или трёхзначными числами обязательно приводите свои расчёты в столбик.

Второй способ

Второй способ называется запись «цепочкой». Все вычисления проводятся в точно таком же порядке действий, но результаты записываются сразу после знака равно.

Запомните!

Если выражение содержит скобки, то сначала выполняют действия в скобках.

Внутри самих скобок действует правило порядка действий как в выражениях без скобок.

Если внутри скобок находятся ещё одни скобки, то сначала выполняются действия внутри вложенных (внутренних) скобок.

Порядок действий и возведение в степень

Если в примере содержится числовое или буквенное выражение в скобках, которое надо возвести в степень, то:

Сначала выполняем все действия внутри скобок
Затем возводим в степень все скобки и числа, стоящие в степени, слева направо (от начала к концу примера).
Выполняем оставшиеся действия в обычном порядке

Термины для уравнений сложения, вычитания, умножения и деления — 3-й класс математики

Итак, вы узнали, как решать уравнения сложения, вычитания, умножения и деления. 👏

Давайте рассмотрим терминов для каждого из них.

Совет: Термины — это имен различных частей уравнения.

Условия добавления

Сложения — это числа, которые складываются вместе.

Сумма — это ответ, который вы получите, если сложите числа.

Мы пишем плюс знак ( +) между двумя слагаемыми, а равно знак перед суммой.

Подсказка: Знак равно (=) означает, что элементы слева и справа от него равны.

Условия вычитания

Уменьшаемое — это число, из которого вычитается. Это большее число.

Вычитаемое — это число, которое вычитается из уменьшаемого. Это меньшее число.

Уменьшаемое всегда идет перед вычитаемым.

Совет вместо запоминание:

Разница — это ответ, который мы получаем в уравнении вычитания.

Мы используем минус знак (-) между уменьшаемым и вычитаемым.

Условия умножения

Числа, которые мы перемножаем вместе, называются множителями .

Иногда люди называют их множимым и множителем и .

Множимое часто пишется первым, но порядок множителей на самом деле не имеет значения. Это называется коммутативным свойством умножения.

Ответ в уравнении умножения называется произведением .

A умножение знак ( ×) записывается между двумя факторами. Его также называют знаком умножить на .

Условия деления

Дивиденд — это число, которое делится.

Делитель — это число, указывающее, сколько раз нужно разделить делимое. Он отвечает на вопрос «На сколько равных групп делится число?».

Ответ, который мы получаем в уравнении деления, называется частным .

А отдел Знак (÷) ставится между делимым и делителем. Это короткая горизонтальная линия с точками над и под ней.

Совет: Вы также можете увидеть / в качестве знака деления. То же, что и ÷.

Подсказка: Вы также много формируете длинное деление!

Отличная работа по изучению этих терминов. 👏

Думаете, вы их запомнили? Попробуйте практику, чтобы увидеть.

Что такое BODMAS, BIDMAS и PEMDAS?

Если вам нужна PDF-версия этой страницы, просто нажмите Bodmas PDF

BODMAS объясняет «Порядок операций» в математике, а BIDMAS и PEMDAS делают то же самое, но используют немного разные слова. Если вышеизложенное звучит для вас как абракадабра, посмотрите наше короткое видео ниже, где Али объясняет, как все это работает.

Что такое аббревиатура?

Акроним — это слово, состоящее из начальных букв слов в фразе. Аббревиатуры могут произноситься как отдельные слова.

Подумайте о НАСА и часто задаваемых вопросах. Оба они произносятся так, как если бы они были самостоятельным словом. Тем не менее, НАСА означает N National A Aeronautics и S темп A администрация, а FAQ означает F часто A sked Q вопросы.

Аналогичным образом буквы в BODMAS, BIDMAS и PEMDAS обозначают слова.

BODMAS, BIDMAS и PEMDAS — это аббревиатуры для запоминания порядка операций в математике.

Что означают буквы в BODMAS, BIDMAS и PEMDAS?

В случае математических сокращений BODMAS, BIDMAS и PEMDAS все они означают одно и то же и служат одной и той же цели. Вот что означают буквы:

Кронштейны
Заказов
Подразделение
Умножение
Дополнение
Вычитание

Скобки
Индексы
Подразделение
Умножение
Дополнение
Вычитание

Скобки
Экспоненты
Умножение
Подразделение
Дополнение
Вычитание

Третья серия выше наиболее часто используется в США, в то время как школы Великобритании почти всегда принимают серию 1 или серию 2 выше. Когда ваш ребенок впервые столкнется с одним из них, вам следует запомнить, какой именно, потому что в разных школах используются разные.

Придерживаясь того же, который используется в вашей школе, вы, по крайней мере, избежите одного уровня сложности.

Что такое ордера, индексы и экспоненты?

Порядки, индексы и экспоненты — это маленькие надстрочные числа, которые представляют степени в математике.

Скобки, Деление, Умножение, Сложение и Вычитание — все это слова, с которыми мы знакомы, но что насчет второго элемента акронимов — Порядков, Индексов или Экспонентов? Это «числа половинного размера», которые часто встречаются в математических выражениях. В следующем примере 2 является индексом (единственное число множественного числа индексы ):

3 ² = 3 х 3

Что такое математические операции?

Математическая операция может рассматриваться как один из символов, который заставляет что-то происходить в математике. Знак умножения (х) означает, что нужно умножить два числа, а знак сложения (+) означает, что нужно сложить два числа.

Это операции .

Каков правильный порядок операций в математике?

Правильный порядок действий в математике: B ракетки, O ряды, D провидение, M умножение, A сложение и S вычитание.

Если вы используете BIDMAS, замените O заказов на I индексов.

Весь смысл BIDMAS и BODMAS в том, чтобы помочь вам запомнить, какие операции выполнять в каком порядке. К сожалению, математика подсказывает, что это не порядок слева направо, как можно было бы ожидать: давайте рассмотрим типичный пример и посмотрим, получите ли вы правильный ответ:

2 + 3 х 4

Вы пришли к выводу, что ответ равен 20? Если да, то вы произвели вычисления слева направо и сказали, что 2 плюс 3 равно 5

, а затем умножить на 4, чтобы получить 20 . К сожалению, с математической точки зрения это неверно!

Если вы посмотрите на правила BIDMAS/BODMAS, вы увидите, что умножение предшествует сложению (две операции, с которыми мы имеем дело), и поэтому вы должны были иметь дело с умножением ДО вы имели дело с Дополнением. Следовательно, правильная логика такова: 3 умножить на 4, получится 12 , а затем добавить к 2, чтобы получить 14 . 14 это правильный ответ.

Я уже сбился со счета, сколько раз мне звонил родитель, который говорил: «Ты просто ошибаешься. Смотри, я сделал это на своем калькуляторе и набрал 2 + 3 x 4, и это всегда, но всегда дает мне ответ 20».

Среди многих тысяч вопросов на сайте Education Quizzes именно этот выпуск Порядка операций чаще всего вызывает вопросы у наших учителей — и когда кажется, что у родителей есть калькуляторы на их стороне, неудивительно, почему!

Порядки, индексы и экспоненты — это маленькие надстрочные числа, которые представляют степени в математике.

Используются ли на экзамене 11-Plus BODMAS или BIDMAS?

Вообще говоря, нет. В это может потребоваться некоторое доверие, но на экзамене 11-Plus неправильный ответ часто помечается как правильный, а правильный ответ занижается! Это связано с тем, что некоторые авторитетные лица считают, что дети в возрасте до 11 лет не должны знать порядок операций, определенный BIDMAS / BODMAS, и поэтому они ожидают, что учащиеся ошибочно будут выполнять вычисления слева направо.

Во избежание возможного понижения кандидата 11+ за правильный ответ (!) обязательно уточните в школе, следует ли применять правила порядка действий в математических вопросах.

Каковы правила BODMAS или BIDMAS?

Чтобы увидеть, как правила BIDMAS (или BODMAS) применяются в более сложных сценариях, нам нужно проанализировать математическое выражение, содержащее все различные элементы. Если вы готовы, то давайте начнем!

2 x 20 ÷ 2 + (3+4) x 3 ² – 6 + 15

Этап 1

Разберитесь со скобами, чтобы получить:

2 х 20 ÷ 2 + 7 х 3 ² – 6 + 15

Этап 2

Сделка с индексами (если вы думаете о BIDMAS) или с ордерами (если вы думаете о BODMAS), чтобы получить:

2 х 20 ÷ 2 + 7 х 9 – 6 + 15

Этап 3

Деление и умножение имеют одинаковый ранг, поэтому действуйте вместе слева направо, чтобы получить:

20 + 63 – 6 + 15

Этап 4

Сложение и вычитание имеют одинаковый ранг, поэтому решите их вместе слева направо, чтобы получить:

СОВЕТ.