Выполнение действий со скобками, примеры по математике со скобками от Skills4u
Зарегистрируйся и получи 7 дней бесплатного доступа к тренажерам и персональный план прокачки знаний до 100%!
Вопросов в тесте: 25
Среднее время прохождения: ~10:00
Зарегистрируйся и получи персональный план прокачки знаний до 100%!
Как работает платформа Skills4u
Тестирование по предмету за класс
Платформа определит, какие темы сформированы слабо и составит индивидуальный план обучения
Персональный план обучения
План обучения и повторений поможет ученику в закреплении всех необходимых тем по предмету
Закрепление темы на 100%
Платформа напомнит и проконтролирует все повторения для закрепления каждой темы на 100%
Проработка слабых тем с предыдущих классов
Чтобы идеально овладеть предметом, рекомендуем закрепить пробелы, начиная с самых простых тем
Почему нужно пройти общее тестирование по математике за 3 класс, а не по отдельной теме «Порядок выполнения действий (сложение, вычитание, умножение, деление) со скобками»
Пройдя тестирование за класс вы получите ПОЛНУЮ КАРТИНУ ЗНАНИЙ ПО ВСЕМ ТЕМАМ.
Такой подход позволит глубинно проанализировать знания, вывести успеваемость и понимание предмета на качественно новый уровень.
Пройдя тестирование по одной теме вы получите РЕЗУЛЬТАТ ЗНАНИЙ ТОЛЬКО ЭТОЙ ТЕМЫ, которая, возможно, плохо изучена. Такой метод не является комплексным и дает лишь точечное понимание знаний по предмету.
Зарегистрироваться и пройти тестирование
В начальной школе действия со скобками изучают в 3 классе на уроках математики. Для некоторых учеников они представляют затруднение, поэтому мы рекомендуем пройти проверочный тест, чтобы определить, насколько ваш ребенок усвоил эту тему.
Наш интерактивный тест на выполнение действий со скобками состоит из 25 заданий, в каждом из которых вам предстоит выполнить несложные вычисления и записать ответ в отведенную графу. Если ответ указан верно, загорается зеленый свет, и сразу появляется очередной вопрос. Если же допущена ошибка, результат вычислений подсвечивается красным, но обязательно указывается и правильное решение.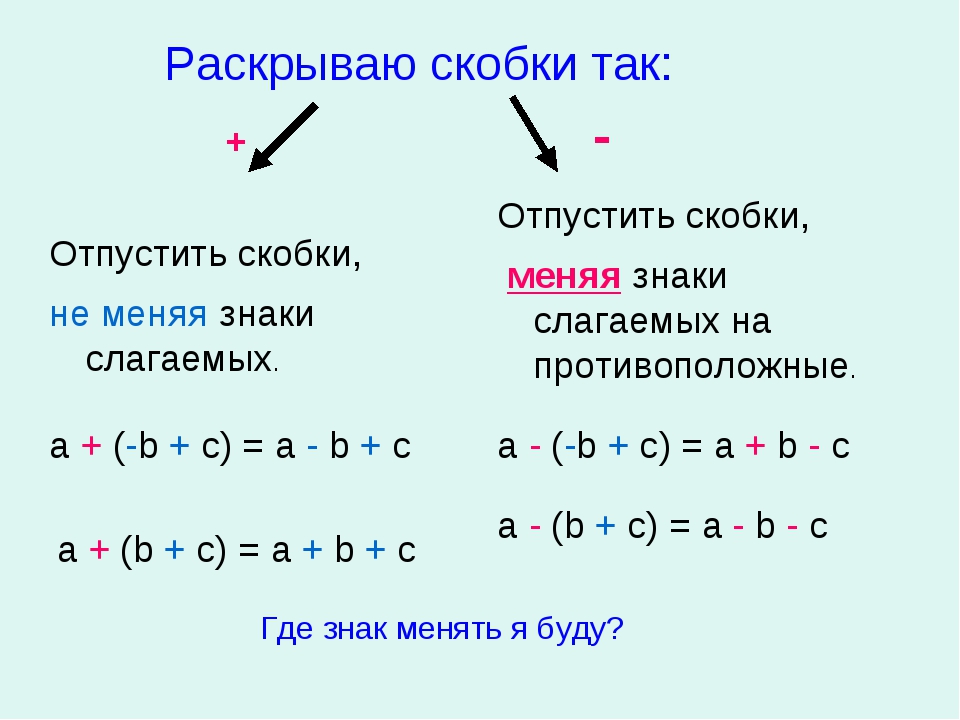
Самое главное, когда вы решаете примеры, это соблюдать правильный порядок действий со скобками. Для этого необходимо определить, что выполнять сначала: умножение или вычитание. Если вы хорошо изучили правила, сомнений не возникнет. В начальной школе порядок действий в математике со скобками изучают уже в 3 классе. Наш тест будет полезен как третьеклассникам, так и ученикам старших классов, которые хотят проверить, насколько хорошо они запомнили правила. Мы рекомендуем проверить знания перед важной контрольной или проверочной работой, в начале учебного года после каникул.
Немного интересной статистики, или почему важно проходить общее тестирование и закрывать пробелы в знаниях за текущие и предыдущие классы
- 60% пятиклассников не могут быстро выполнять базовые математические действия, такие как вычитание и сложение.
- 70% пятиклассников часто делают ошибки в таких действиях как умножение и деление.
- Более 75% девятиклассников не могут решить системы из двух уравнений.
- До 20% выпускников школы реально обладают математическими познаниями на уровне 6-8 класса. До 40% — не выше 9 класса.
- От 5 к 7 классу возникает четко выраженная тенденция ухудшения математической подготовки, а доля троечников увеличивается с 20-25% до 40-45%.
Основано на результатах учеников нашей платформы и исследованиях журнала «Коммерсант»
Каждый желающий может пройти тест на действия со скобками за 3 класс совершенно бесплатно. По итогам тестирования формируется рейтинг ученика и даются рекомендации по дальнейшему продолжению занятий. Система сама напомнит, когда пора приступить к упражнениям.
Для того чтобы получить устойчивый учебный навык по указанной теме и всегда выбирать правильный порядок действий в примерах со скобками, нужно зарегистрироваться на сайте образовательной платформы Skills4u и оформить доступ к тренажерам по различным предметам школьной программы. Существуют варианты доступа на месяц, полугодие и полный учебный год.
Вы также можете выбирать, какой навык нужно прокачать в данный момент: нужна ли вся математика, действие со скобками или другие темы за 3 класс начальной школы. Стоимость подписки варьируется в зависимости от выбранного уровня доступа, но всегда остается чисто символической. Это один из самых выгодных способов подтянуть успеваемость и получить индивидуальный подход к изучению и независимую оценку знаний.
Как растут результаты учеников
после занятий на тренажерах Skills4u
Занятия
на Skills4u
Занятия
с учебником
Успеваемость
Мотивация
Внимательность
Скорость
Самостоятельность
Запоминание
Первичный Тест «Порядок выполнения действий (сложение, вычитание, умножение, деление) со скобками» по математике за 3 класс онлайн и бесплатно предоставляется всем желающим.
Советуем пройти тестирование за весь 3 класс по математике, чтобы узнать пробелы в знаниях по всем темам и получить индивидуальный план обучения.
После регистрации вы получите 7 дней бесплатного доступа, чтобы увидеть первые результаты занятий и оценить эффективность тренажеров.
Зарегистрироваться и пройти тестирование
Регистрируйтесь на сайте образовательной платформы Skills4u и решайте примеры действий со скобками в удобное для вас время. Родители могут быть спокойны – им не понадобится листать учебник. Достаточно будет только напомнить ребенку, что наступило время занятий. Система сама пришлет напоминание и познакомит с результатом. Желаем успеха!
А для комплексного результата пройдите общее тестирование за
класс! Узнайте пробелы в знаниях по всем темам
Ученик
Занимайся 20 минут в день и прокачай знания по школьной программе за месяц!
Родитель
Наслаждайтесь прогрессом вашего ребенка в школе и на платформе
Учитель/
репетитор
Зарегистрироваться и пройти тестирование
67640
учеников уже занимаются с нами
Урок математики по теме «Порядок выполнения действий в выражениях без скобок и со скобками».
3-й классХод урока
I. Оргмомент (звучит песня “Дважды два четыре”). СЛАЙД
Презентация.
— Ребята, кто из вас любит математику? Почему вы её любите? Математику любят наши знакомые Миша и Маша, ученики 3 класса. Сегодня они как всегда с нами на уроке.
“Кто с детских лет занимается математикой, тот развивает внимание, тренирует свой мозг, свою волю, воспитывает настойчивость и упорство в достижении цели.” (А. Маркушевич)
СЛАЙД “Математику уже затем изучать нужно, что она ум в порядок приводит”
Михаил Васильевич Ломоносов, русский учёный, энциклопедист, поэт.
II. Устная работа.
1. Повторение табличных случаев умножения и деления. Работа в группах с использованием ноутбуков.
— Как вы считаете, какое задание, выполняемое нами на каждом уроке приводит наш ум в порядок? (повторение таблицы умножения и деления)
— Проверим, чья группа первая справится с этим
заданием.
Если вы ошибаетесь в ответе, вас
компьютер возвращает к началу теста, и вы
выполняете задание заново.
— Прекрасное начало урока! Рада, что вы все справились с заданием!
2. Игра “Да или нет”
— Поиграем в игру “Да или нет”. Если вы согласны с моим высказыванием, то показываете “Да” (скрещенные пальчики), если не согласны – “Нет” ( один указательный пальчик). Договорились?
— При умножении любого числа на 1 получается 1 (да).
— При умножении любого числа на 1, получается 1 (да).
— Чтобы разделить на 10, достаточно дописать 0 (нет, отбросить).
— Умножать на 0 нельзя (нет, можно).
— Чтобы найти делимое, нужно значение частного умножить на делитель (да).
— Чтобы найти неизвестный множитель, нужно значение произведения умножить на известный множитель (нет, разделить).
— В выражениях без скобок все действия
выполняются по порядку слева направо (нет,
сначала умножение и деление, потом вычитание и
сложение).
— С каждым уроком у вас получается всё лучше! Просто замечательно!
3. Логические упражнения.
Предмет математики столь серьезен, что не следует упускать ни одной возможности сделать его более занимательным. (Б. Паскаль) Предлагаю выполнить логические задания. Вы готовы?
— Какие два числа, если их перемножить, дают такой же результат, что и при их сложении? (2 и 2)
— Из-под забора видно 6 пар лошадиных ног. Сколько этих животных во дворе? (3)
— Петух, стоя на одной ноге весит 5кг. Сколько он будет весить, стоя на двух ногах? (5кг)
— На руках 10 пальцев. Сколько пальцев на 6 руках? (30)
— У родителей 6 сыновей. Каждый имеет сестру. Сколько всего детей в семье? (7)
— Сколько хвостов у семи котов?
— Сколько носов у двух псов?
— Сколько ушей у 5 малышей?
— Ребята, именно такой работы я и ждала от вас: вы
были активны, внимательны, сообразительны.
III. Актуализация знаний.
“Чтобы переварить знания, надо поглощать их с аппетитом.” (А.Франц)
— Вы готовы поглощать их с аппетитом? Тогда внимание!
— Посмотрите, пожалуйста, внимательно на доску. Как вы считаете, какое задание предполагается? (Указать арифметические действия, которые выполняются в заданном порядке)
— Проговорите правило, которое подходит к данной схеме.
В выражениях без скобок, содержащих только сложение и вычитание – действия I ступени, или умножение и вычитание – действия II ступени, действия выполняются в том порядке, как они записаны : слева направо.
В выражениях без скобок сначала выполняются по порядку слева направо умножение или деление, а потом сложение или вычитание.
В выражениях со скобками сначала вычисляют
значения выражений в скобках. Затем по порядку
слева направо выполняется умножение или деление.
— Озвучьте тему нашего урока. (“Порядок выполнения действий в выражениях со скобками и без скобок”)
— Просто умницы, ловко справились, умело.
VI. Целеполагание.
— Ребята, как вы считаете, достаточно ли хорошо отработана нами тема “Порядок выполнения действий в выражениях”?
— На что нам сегодня необходимо обратить внимание? Над чем поработать? (Упражняться в нахождении значений выражений, содержащий действия разных ступеней со скобками и без них. Познакомиться с видами выражений, в которых можно допустить ошибки)
— И в этом разобрались. Я думаю, достаточно поставленных задач на сегодняшний урок.
V. Постановка проблемной ситуации. Работа в группах. (карточки)
— Ребята, послушайте, пожалуйста, что говорил французский математик Д.Пойя: “Лучший способ изучить что-либо — это открыть самому”. Вы готовы к открытиям?
СЛАЙД- Даны выражения, посмотрите, как
справились с заданием Маша и Миша.
— Кто выполнил задание верно: Маша или Миша? (ответы детей)
— К кому из наших друзей можно отнести следующее высказывание Р. Декарта “Мало иметь хороший ум, главное – хорошо его применять? (К Мише, потому что он ошибся)
— Какие ошибки допущены Мишей?
СЛАЙД — Давайте проверим!
— Я знала, что это задание вам было под силу!
VII. Разрешение проблемной ситуации.
СЛАЙД — В данной ситуации кто является КП – “кислой парочкой”? (Миша и выражения)
— Как разрешить проблему?
(Миша должен САМ найти значения выражений
— Какие у него есть для этого ресурсы? (Память, чтобы запомнить правило, старание, тренировка, учебник,
Выражения САМИ должны быть решены, для этого ресурсы: Маша, учитель, родители)
— Какое ИКР вы бы выбрали? Почему?
— А если Миша воспользуется ИКР2? Это будет хорошо или плохо, давайте поиграем!
Игра “Хорошо-плохо”
— Если за него выполнят задание, то будет
хорошо, потому что.
..(ему не нужно будет долго
сидеть за уроками, не нужно будет думать, у него
появится свободное время…)
— Если за него выполнят задание, то будет плохо…(сам не научится решать, не будет трудолюбивым, не усвоит тему, будут проблемы в учёбе…)
“Величие человека — в его способности мыслить.” (Б. Паскаль)
— Ребята, у вас получилось лучше, чем я могла бы подумать!
— А ещё вам предлагается новый способ записи решения. В чём он заключается? (Нужно выписывать все действия ниже данного выражения)
— Вот в этом мы сейчас с вами и поупражняемся.
VIII. Нахождение значений выражений. (№228) – у доски 3 выражения.
“Счет и вычисления — основа порядка в голове.” (Песталоцци)
IX. Самостоятельная работа № 228, 3 выражения.
— Я горжусь вами, что вам удалось выполнить задание почти без ошибок.
X. Решение задачи №227.
“Если вы хотите научиться плавать, то смело входите в воду, а если хотите научиться решать задачи, то решайте их.” (Д.Пойа)
| У всех учащихся второго класса 39 ручек.
У шести учеников по одной ручке, у пяти по три, а у
остальных по две. Сколько учеников имеют по две
ручки? Маша записала решение этой задачи выраженим так: 39-1 * 6+3 * 5. Миша – так: 39-(1 * 6+3 * 5) Кто прав: Миша или Маша? |
— Прочитайте установку и ответьте на вопрос. Кто прав Миша или Маша?
— Самостоятельно запишите решение задачи и ответ.
— Назовите ответ.
СЛАЙД — Давайте проверим!
— Поздравляю, это правильный ответ!
XI. Работа по алгоритму.
— Что такое алгоритм? (Порядок выполнения действий)
СЛАЙД — Выполните действия по алгоритму.
— “Много из математики не остается в памяти, но когда поймешь ее, тогда легко при случае вспомнить забытое.”, говорил М.В. Остроградский. Вот и мы сейчас вспомним то, что изучали на уроках информатики.
— Какая фигура получилась? (прямоугольник)
— Ниже начертите фигуру, площадь которой в 6 раз больше.
— Что примите за единичный отрезок? (2 клетки)
— Вы на верном пути!
СЛАЙД — Из скольких мерок состоит ваша фигура?
— Внимание на слайд! Вас ждёт сюрприз, если правильно найдёте значения выражений.
XII. Нахождение значений выражений. (СЛАЙД)
— Именно этого мы с вами и ждали! (на слайде появляется фото класса)
XIII. Итог урока.
— Выполнили ли мы поставленные цели урока? Что планировали? Всё ли у нас получилось? Над чем необходимо поработать?
— Вы сегодня просто умнички, много сделали.
Работать с вами просто радость!
XIV. Рефлексия.
— Оцените работу вашей группы, насколько успешно работали, аргументируйте свой выбор (карточки с цифрами).
XV. Домашнее задание.
— Что необходимо закрепить дома? (порядок выполнения действий в сложных выражениях) № 234 (1 столбик), №230.
— “Если вы хотите участвовать в большой жизни, то наполняйте свою голову математикой, пока есть к тому возможность. Она окажет вам потом огромную помощь во всей вашей работе.” (М.И. Калинин)
- Приложение 1
- Приложение 2
- Приложение 3
- Приложение 4
- Приложение 5
3.3 Порядок действий — Современная математика
Рисунок
3.19
Калькуляторы могут автоматически применять порядок операций к вычислениям. (кредит: «Точность», Леонид Мамченков/Flickr, CC BY 2.
0)
После завершения этого модуля вы сможете:
- Упростите выражения, используя порядок операций.
- Упростите выражения, используя порядок операций, включающих группировку символов.
Вычисляет еще, что кто-то должен знать, что правила ожидают явного определения того, что нужно сделать, мы им, что нужно вычислить, чтобы вычислить сначала.
Вероятно, вы прочитали это предложение и не смогли его разобрать. Кажется, это может быть связано с расчетами, но, может быть, это касается потребностей? Возможно, вы даже пытаетесь расшифровать предложение по мере его чтения, расставляя слова в том порядке, в котором вы ожидаете их появления. Причина, по которой предложение не имеет смысла, заключается в том, что слова не следуют порядку, в котором вы ожидаете их следовать. . В расшифрованном виде это предложение должно было звучать так: «Чтобы быть уверенным, что кто-то другой вычислит, когда мы ожидаем, что он вычислит, нам нужны правила, которые четко определяют, что нужно вычислить в первую очередь».
Точно так же при работе с математическими выражениями и уравнениями, если мы не следуем правилам порядка операций, арифметические выражения теряют смысл. Простое выражение было бы проблематичным, если бы у нас не было некоторых правил, говорящих нам, что вычислять в первую очередь. Например, 4×22+3+524×22+3+52 можно вычислить разными способами. Вы можете получить 5184. Или вы можете получить 80. Или 96. Проблема в том, что без соблюдения набора правил расчета одно и то же выражение будет давать разные результаты. Если вам интересно, используя соответствующий порядок операций, мы находим 4×22+3+52=444×22+3+52=44.
Упростить выражения, используя порядок операций
Порядок, в котором выполняются математические операции, является соглашением, облегчающим правильное вычисление. Они следуют аббревиатуре EMDAS:
.| Е | Экспоненты |
| М/Д | Умножение и деление |
| А/С | Сложение и вычитание |
Итак, что нам говорит EMDAS? В уравнении, двигаясь слева направо, мы начинаем с вычисления всех показателей степени.
Как только показатели степени были вычислены, мы снова двигаемся слева направо, вычисляя умножения и деления по одному. Умножение и деление занимают одно и то же место в упорядочении, поэтому, когда вы столкнетесь с одним или другим на этом шаге, сделайте это. Как только умножение и деление были вычислены, мы снова двигаемся слева направо, вычисляя сложения и вычитания, по одному. Сложения и вычитания занимают одно и то же место в порядке, поэтому, когда вы сталкиваетесь с одним или другим на этом шаге, сделайте это. (Возможно, вы уже изучили порядок операций в PEMDAS, сначала со скобками; мы добавим этот аспект позже.) Мы изучим это, работая на примере.
Пример 3,43
Используя два порядка операций
Вычислить 21−4×1321−4×13.
Решение
В этом выражении нет показателей степени, поэтому следующие операции для проверки — умножение и деление.
Шаг 1: Двигаясь слева направо, первое умножение, которое встретится, равно 4, умноженному на 13.
Сначала мы выполняем эту операцию.
21−4×13=21−5221−4×13=21−52
Шаг 2: Единственная оставшаяся операция — вычитание.
21-52=-3121-52=-31.
Итак, 21−4×13=−3121−4×13=−31.
Твой ход 3,43
1.
Вычислить 43+18\умножить на 15.
Пример 3,44
Используя два порядка операций
Вычислить 4×834×83.
Решение
Шаг 1: Двигаясь слева направо, мы видим, что есть показатель степени. Сначала вычисляем показатель степени.
4×83=4×(8×8×8)=4×5124×83=4×(8×8×8)=4×512 92}/50.
Пример 3,45
Используя три порядка операций
Вычислить 2+32×42+32×4.
Решение
Шаг 1: Чтобы вычислить это, двигайтесь слева направо и сначала вычислите все показатели степени.
Единственная экспонента, которую мы видим, — это возведение в квадрат числа 3, поэтому оно вычисляется первым.
2+32×4=2+(3×3)×4=2+9×42+32×4=2+(3×3)×4=2+9×4
Шаг 2: Поскольку все показатели степени вычислены, теперь вычислите все умножения и деления слева направо. Единственное присутствующее умножение или деление — 93}-18.
Даже если вычисляемое выражение усложняется, выполняем операции в следующем порядке: EMDAS.
Пример 3,46
Используя восьмеричный порядок операций
Правильно примените порядок операций для вычисления следующего:
4−25×6/10×32+7×234−25×6/10×32+7×23.
Решение
Шаг 1: Для этого сначала вычислите показатели степени, двигаясь слева направо. В выражении есть два вхождения показателей степени: 3 в квадрате и 2 в кубе.
4−25×6/10×32+7×23=4−25×6/10×9+7×84−25×6/10×32+7×23=4−25×6/10×9+ 7×8
Шаг 2: Теперь, когда показатели степени вычислены, выполните умножение и деление, двигаясь слева направо.
Первый — произведение 25 и 6.
4−25×6/10×9+7×8=4−150/10×9+7×84−25×6/10×9+7×8=4−150/10×9+7×8
Шаг 3: Затем 150 разделить на 10.
4−150/10×9+7×8=4−15×9+7×84−150/10×9+7×8=4−15×9+7×8
Шаг 4: Далее 15 умножить на 9.
4−15×9+7×8=4−135+7×84−15×9+7×8=4−135+7×8
Шаг 5: Наконец, умножьте 7 на 8.
4−135+7×8=4−135+564−135+7×8=4−135+56
После вычисления всех умножений и делений выполняются сложения и вычитания слева направо.
4−135+56=−131+56=−131+56=−754−135+56=−131+56=−131+56=−75
Вычисленное значение равно −75.
Твой ход 3,46
1.
92}-3\х4.Пример 3,47
Использование шести порядков операций
Правильно примените правила порядка операций, чтобы точно вычислить следующее:
10−3×53/15+56/410−3×53/15+56/4.
Решение
Шаг 1: Сначала вычислить показатели степени, двигаясь слева направо:
10−3×53/15+56/4=10−3×125/15+56/410−3×53/15+56/4=10−3×125/15+56/4
Шаг 2 : Умножение и деление слева направо: 93}-24\х25/10.
Пример 3,48
Использование порядка операций
Правильно применяйте правила порядка операций для точного вычисления следующего: (-8)/2×3-9×24/12+9×(-4)2/23(-8)/2×3-9×24/12+9×(-4)2/23.
Решение
Шаг 1: Сначала вычислите показатели степени, двигаясь слева направо:
(−8)/2×3−9×24/12+9×(−4)2/23=(−8)/2×3−9×16/12+9×122/23=(−8) /2×3−9×16/12+9×144/23=(−8)/2×3−9×16/12+9×144/8(−8)/2×3−9×24/12+9×(−4)2/23=(−8)/2×3−9×16/12+9×122/23=(−8)/2×3−9×16/12 +9×144/23=(−8)/2×3−9×16/12+9×144/8
Шаг 2: Умножить и разделить, двигаясь слева направо:
=(−8)/2×3−9×16/12+9×144/8=(−4)×3−9×16/12+9×144/8=(−12)−9×16/ 12+9×144/8=(−12)−144/12+9×144/8=(−12)−12+9×144/8=(−12)−12+1296/8=(−12 )−12+162=(−8)/2×3−9×16/12+9×144/8=(−4)×3−9×16/12+9×144/8=(−12) −9×16/12+9×144/8=(−12)−144/12+9×144/8=(−12)−12+9×144/8=(−12)−12+1296/ 8=(−12)−12+162
Шаг 3: Сложение и вычитание слева направо: 92}-9/3\х8.
Использование порядка операций, связанных с группировкой символов
Мы рассмотрели, как использовать порядок операций, обозначенный EMDAS, для правильного вычисления выражений. Однако могут быть выражения, в которых умножение должно происходить перед показателем степени или вычитание перед делением. Чтобы указать, что операция должна выполняться не по порядку, операция помещается в круглые скобки. При наличии круглых скобок в первую очередь выполняются операции внутри круглых скобок. Добавив скобки к нашему списку, мы получили PEMDAS, как показано ниже.
| П | Скобки | |
| Е | Экспоненты | |
| М/Д | Умножение и деление | (деление это просто умножение на обратное) |
| А/С | Сложение и вычитание | (вычитание — это просто сложение минуса) |
Как было сказано ранее, круглые скобки указывают, что некоторая операция или операции будут выполняться вне стандартного порядка правил операций.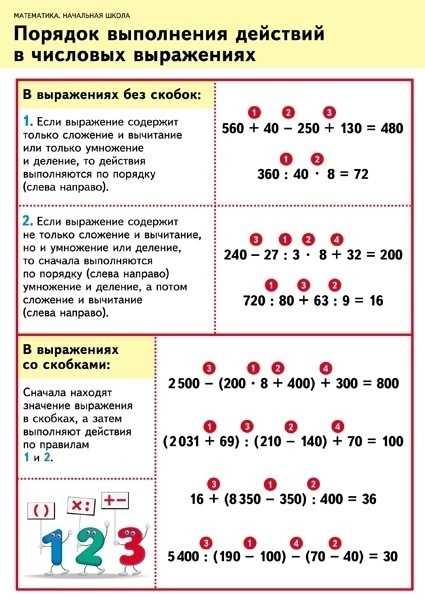
Например, возможно, вы хотите умножить 4 и 7 перед возведением в квадрат. Чтобы указать, что умножение происходит перед показателем степени, умножение помещается в круглые скобки: (4×7)2(4×7)2.
Это означает, что операции внутри круглых скобок имеют приоритет или выполняются раньше других операций. Теперь первым шагом в вычислении арифметических выражений с использованием порядка операций является выполнение сначала операций внутри круглых скобок. Внутри скобок вы соблюдаете порядок работы правил EMDAS.
Пример 3,49
Приоритизация скобок в порядке операций
Правильно примените правила порядка операций, чтобы точно вычислить следующее:
(10−3)×53(10−3)×53.
Решение
Шаг 1: Выполните все вычисления в скобках перед всеми другими операциями.
(10−3)×53=7×53(10−3)×53=7×53
Шаг 2: Поскольку все скобки сняты, двигайтесь слева направо и затем вычисляйте все показатели степени.
92})/7.
Имейте в виду, что может быть несколько наборов скобок и скобок внутри скобок. Когда один набор скобок находится внутри другого набора, сначала сделайте самый внутренний набор, а затем работайте снаружи.
Пример 3,50
Работа с самыми внутренними скобками в порядке операций
Правильно применять правила порядка операций для точного вычисления следующего:
4+2×(32−(2+5)2×4)/(3+8) 4+2×(32−(2+5)2×4)/(3+8).
Решение
Шаг 1: Выполнить все вычисления в скобках перед другими операциями. Сначала оцените самые внутренние скобки. Мы можем работать с отдельными выражениями в скобках одновременно. Самый внутренний набор скобок содержит 2 + 5 внутри. 3 + 8 находится в отдельном наборе круглых скобок, так что сложение может происходить одновременно с 2 + 5.
4+2×(32−(2+5)2×4)/(3+8)=4+2×(32−(7)2×4)/(11)4+2×(32−(2) +5)2×4)/(3+8)=4+2×(32−(7)2×4)/(11)
Шаг 2: Теперь, когда эти скобки обработаны, перейдите к следующему набору скобок.
Применяя правила порядка операций внутри этого набора скобок, сначала вычисляется показатель степени, затем умножение, а затем сложение.
4+2×(32−72×4)/11=4+2×(32−49×4)/11=4+2×(−187)/114+2×(32−72×4)/11 =4+2×(32−49×4)/11=4+2×(−187)/11
Шаг 3: Поскольку все круглые скобки сняты, примените правила EMDAS, чтобы завершить вычисления. 92}.
Раздел 3.3 Упражнения
1.
Какие операции имеют самый низкий приоритет в порядке операций?
2.
Если несколько операций имеют одинаковый приоритет в выражении, в каком порядке должны выполняться операции?
3.
Какие операции имеют одинаковый приоритет в порядке операций?
4.
После того, как все операции в скобках выполнены, какие операции следует выполнить дальше? 92}
38.
9 \раз (13-12 \раз (41-32))-8 \раз 45
39.
21-3 \раз (5 \раз (2+6)-3 \раз (18-11)+25) \дел 2
40.
48-6 \times (10 \times (18+12)-25 \times (16-9)+19) \div 4
Типы чисел Порядок действий
Сложение, вычитание, умножение, деление и возведение в степень — это все операции над действительными числами, то есть то, что вы делаете с действительными числами. Для сложных арифметических выражений важно выполнять операции в правильном порядке. Так что тактика «в каком порядке я хочу» не сработает для вас.
Этот правильный порядок задается волшебной фразой «Пожалуйста, извините, моя дорогая тетя Салли» (PEMDAS). О, бедная, дорогая тетя Салли; иногда она немного запутывается, и ей нужны аббревиатуры, чтобы напомнить ей, как решать ее любимые математические уравнения.
Буквы обозначают P арентезы, E xponents, M умножение и D ivision, A дополнение и S вычитание, в том порядке, в котором мы хотим их делать.
Обратите внимание, что «Умножение и деление» и «Сложение и вычитание» сгруппированы вместе. Это потому, что умножение не обязательно должно быть выполнено перед делением — вам просто нужно, чтобы все ваши умножения и деление завершено, прежде чем вы начнете сложение и вычитание. Не расстраивайтесь, если вы не поняли этого сначала. Тетя Салли 40 лет пытается понять эту концепцию, но она все еще ускользает от нее.
Пример задачи
Сначала мы оцениваем значения в скобках. Мм, мы не можем упростить (4) больше, чем это уже есть, так что давайте перейдем к показателям степени.
Затем умножение и деление:
6 – 1
И, наконец, сложение и вычитание:
5
При сложении и вычитании мы работаем слева направо. Проверьте, на подошве какой из ваших туфель написана большая буква «L», если вы не уверены.
Пример задачи
Сколько будет 4–6–2?
У нас нет круглых скобок, показателей степени, умножения, деления или сложения, поэтому мы сразу переходим к вычитанию.
Однако, как обычно, мы должны двигаться слева направо.
4 – 6 – 2 =
(4 – 6) – 2 =
-2 – 2 = -4
Обратите внимание, что если бы мы сначала вычли 6 – 2, мы получили бы совершенно другое (и неправильное) ответ:
4 – (6 – 2) =
4 – 4 = 0
Мы также работаем слева направо при оценке умножения и деления.
Пример задачи
Что такое 3 × 4 ÷ 2 ÷ 6?
Здесь у нас есть только умножение и деление, так что давайте пролистнем слева направо.
3 × 4 ÷ 2 ÷ 6 =
12 ÷ 2 ÷ 6 =
6 ÷ 6 = 1
Если бы мы работали справа налево, мы бы получили другой ответ: ваша работа состоит в том, чтобы разбить задачу на части, разделенные знаками сложения или вычитания. Каменный молоток или ступка и пестик должны помочь.
Пример задачи
Теперь вычислите каждую из частей:
=
6 + 2 – 0 – 4
Затем соедините ответы по частям:
6 + 2 – 0 – 4 = 4
3 Пример задачи
Ой, какой зверь.
Давайте разобьем его на более мелкие части, каждая из которых будет разделена знаком плюс или минус (поскольку сложение и вычитание идут последними).
=
3 + 6 × 16 – 6 × 1
Теперь займемся этим умножением.
3 + 6 × 16 – 6 × 1 =
3 + 96 – 6
И, наконец, качаем сложение и вычитание слева направо.
3 + 96 – 6 = 93
Хорошо, но, пожалуйста, извините, моя дорогая тетя Салли, это очень долгая вещь для запоминания. И мы уже потратили последние 10 лет, пытаясь заблокировать ее. Здесь, в Shmoop, мы любим все упрощать («Shmoop» на самом деле является сокращением от «Shmoopalumpagus»).
Мы видели, что вычитание можно заменить добавлением отрицательного числа, а деление можно заменить умножением обратного числа. Так что все мы действительно нужно помнить, пожалуйста, извините мою тетю. Сначала сделайте то, что находится внутри скобок, затем возьмите все экспоненты, затем умножьте, затем добавьте. Только помните, что деление = умножение на обратное, а вычитание = прибавление минуса.