Сначала умножение потом деление: Выполни сначала умножение или деление затем сложение или вычитание: 70-50:2=,39+18:2=?

Share on telegram

Telegram

Порядок выполнения действий.

Содержание

1. Сложение и вычитание
2. Умножение
3. Деление
4. Почему умножение первое?
5. Порядок действий в выражениях без скобок
6. Первый способ
7. Второй способ
8. Задания для самостоятельного решения
9. Дополнительные примеры

Сложение и вычитание

Какие же действия можно произвести с числами? Есть два базовых. Это сложение и вычитание. Все остальные действия построены на этих двух.

Самое простое действие: взять две кучки камней и смешать их в одну. Это и есть сложение. Для того чтобы получить результат такого действия, можно даже не знать, что такое сложение. Достаточно просто взять кучку камней у Пети и кучку камней у Васи. Сложить все вместе, посчитать все заново. Новый результат последовательного счета камней из новой кучки − это и есть сумма.

Точно так же можно не знать, что такое вычитание, просто взять и разделить кучу камней на две части или забрать из кучи какое-то количество камней. Вот и останется в куче то, что называется разностью. Забрать можно только то, что есть в куче. Кредит и прочие экономические термины в данной статье не рассматриваются.

Чтобы не пересчитывать каждый раз камни, ведь бывает, что их много и они тяжелые, придумали математические действия: сложение и вычитание. И для этих действий придумали технику вычислений.

Сумма двух любых цифр тупо заучиваются без всякой техники. 2 плюс 5 равно 7. Посчитать можно на счетных палочках, камнях, яблоках– результат одинаковый. Положить сначала 2 палочки, потом 5, а потом посчитать все вместе. Другого способа нет.

Те, кто поумнее, обычно это кассиры и студенты, заучивают больше, не только сумму двух цифр, но и суммы чисел. Но самое главное, они могут складывать числа в уме, используя разные методики. Это называется навыком устного счета.

Для сложения чисел, состоящих из десятков, сотен, тысяч и еще больших разрядов, используют специальные техники − сложение столбиком или калькулятор.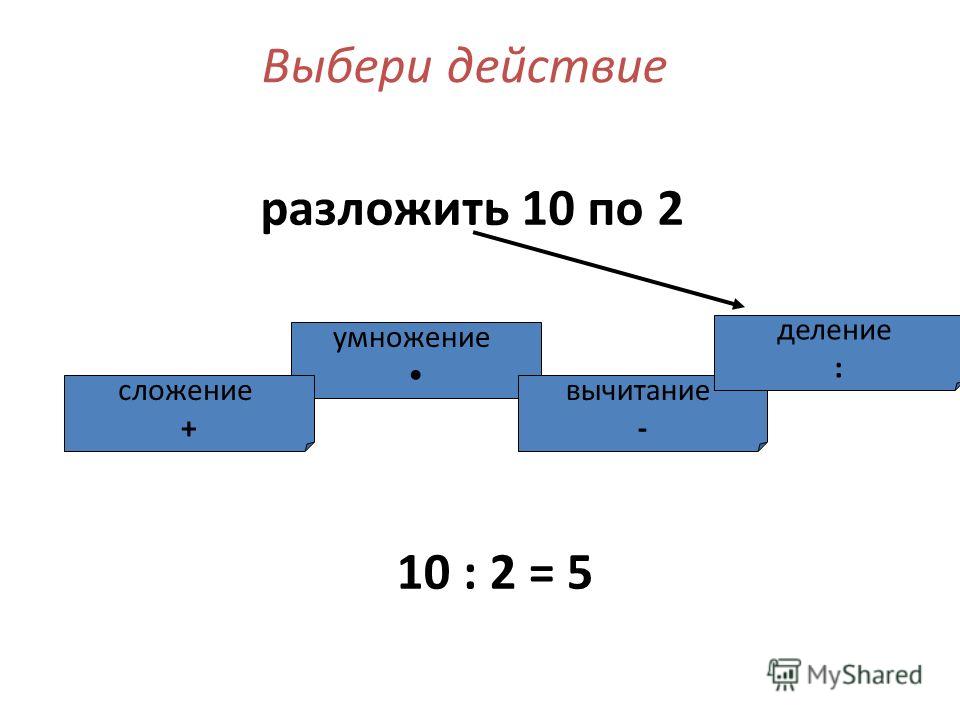 С калькулятором можно не уметь складывать даже цифры, да и читать дальше не нужно.

Сложение столбиком −­­­­­­ это метод, который позволяет складывать большие (многоразрядные) числа, выучив только результаты сложения цифр. При сложении столбиком последовательно складываются соответствующие десятичные разряды двух чисел (то есть фактически две цифры), если результат сложения двух цифр превышает 10, то учитывается только последний разряд этой суммы – единицы числа, а к сумме следующих разрядов добавляется 1.

Умножение

Математики любят группировать похожие действия для упрощения расчетов. Так и операция умножения является группировкой одинаковых действий – сложения одинаковых чисел. Любое произведение N x M − есть N операций сложения чисел M. Это всего лишь форма записи сложения одинаковых слагаемых.

Для вычисления произведения используется такой же метод – сначала тупо заучивается таблица умножения цифр друг на друга, а потом применяется метод поразрядного умножения, что называется «в столбик».

Деление

Операция деления отдельно не рассматривается, она обратная умножению. Нужно что-то распределить по коробкам, так, чтобы во всех коробках было одинаковое заданное количество предметов. Самый прямой аналог в жизни – это фасовка.

Почему умножение первое?

Разберем математические действия на примере. Давайте собирать яблоки у бабушки на даче:

• Мама, папа и дедушка собрали по 50 яблок каждый и выполнили норму.
• Катя и Даша не ходили на уроки математики и помогали взрослым: собрали по 5 ядблок, норму не выполнили, съели 3 яблок, надкусили и испортили еще 6 яблок, 7 яблок было изъято из карманов помощников. Зачем брали с собой их в поле – непонятно.

Все яблоки приностили бабушке, она укладывала их по кучкам.

Запишем результат «сбора» урожая в виде выражения:

• 50 + 50 + 50 – это кучки взрослых работников;
• 5 + 5 – это кучки девочек;
• 7 – изъято из карманов
• !!!! испорченное и надкусанное в зачет результата не идет.

Получаем пример для школы, запись учетчика результатов работы:

50 + 50 + 50 + 5 + 5 + 7 =?;

Здесь можно применить группировку: 3 кучки по 50 яблок − это можно записать через операцию умножения: 3 ∙ 50.

Две кучки по 5 – это тоже можно записать через умножение.

И одна кучка 7 яблок.

3 ∙ 50 + 2 ∙ 5 + 1 ∙ 7 =?

И что делать в примере сначала − умножение или сложение? Так вот, складывать можно только яблоки. Нельзя сложить 50 яблок и 2 кучки. Они не складываются. Поэтому сначала нужно всегда все записи привести к базовым операциям сложения, то есть в первую очередь вычислить все операции группировки – умножения. Совсем простыми словами – сначала выполняется умножение, а сложение уже потом. Если умножить 3кучки по 50 яблок каждая, то получится 150 яблок. А дальше их уже можно складывать с яблоками из других кучек.

250 + 10 + 7 = 267

При изучении ребенком математики нужно донести до него, что это инструмент, используемый в повседневной жизни. Математические выражения являются, по сути (в самом простом варианте начальной школы), складскими записями о количестве товаров, денег (очень легко воспринимается школьниками), других предметов.

Соответственно, любое произведение – это сумма содержимого некоторого количества одинаковых емкостей, ящиков, кучек, содержащих одинаковое количество предметов. И что сначала умножение, а сложение потом, то есть сначала начала вычислить общее количество предметов, а затем уже складывать их между собой.

Порядок действий в выражениях без скобок

Для правильного вычисления выражений, в которых нужно произвести более одного действия, нужно знать порядок выполнения арифметических действий. Арифметические действия в выражении без скобок условились выполнять в следующем порядке:

1. Если в выражении присутствует возведение в степень, то сначала выполняется это действие в порядке следования, т. е. слева направо.
2. Затем (при наличии в выражении) выполняются действия умножения и деления в порядке их следования.
3. Последними (при наличии в выражении) выполняются действия сложения и вычитания в порядке их следования.

В качестве примера рассмотрим следующее выражение:

3 · 42 – 23 : 2 + 20

Сначала необходимо выполнить возведение в степень (число 4 возвести в квадрат и число 2 в куб):

3 · 16 – 8 : 2 + 20

Затем выполняются умножение и деление (3 умножить на 16 и 8 разделить на 2):

48 – 4 + 20

И в самом конце, выполняются вычитание и сложение (из 48 вычесть 4 и к результату прибавить 20):

48 – 4 + 20 = 44 + 20 = 64

Первый способ

• Каждое действие записывается отдельно со своим номером под примером.
• После выполнения последнего действия ответ обязательно записывается в исходный пример.

Запомните!

При расчёте результатов действий с двузначными и/или трёхзначными числами обязательно приводите свои расчёты в столбик.

Второй способ

• Второй способ называется запись “цепочкой”. Все вычисления проводятся в точно таком же порядке действий, но результаты записываются сразу после знака равно.

Запомните!

Если выражение содержит скобки, то сначала выполняют действия в скобках.

Внутри самих скобок действует правило порядка действий как в выражениях без скобок.

Если внутри скобок находятся ещё одни скобки, то сначала выполняются действия внутри вложенных (внутренних) скобок.

Задания для самостоятельного решения

Задание 1. Найдите значение выражения: 5 + 2 − 2 − 1 Решение

Показать решение Задание 2. Найдите значение выражения: 14 + (6 + 2 × 3) − 6 Решение

Показать решение Задание 3. Найдите значение выражения: 486 : 9 − 288 : 9 Решение

Показать решение Задание 4. Найдите значение выражения: 756 : 3 : 4 × 28 Решение

Показать решение Задание 5. Найдите значение выражения: 807 : 3 − (500 − 58 × 4) Решение

Дополнительные примеры

В данном разделе мы познакомимся с порядком действий, с выражениями со скобками и без них.

1) Если тебе нужно выполнить только сложение и вычитание или только умножение и деление, то все действия выполняют по порядку слева направо.

Например, 

В числовом выражении 3 арифметических действия: сложение, вычитание и вычитание.

Определим порядок действий и запишем их над арифметическими знаками: так как нет ни умножения ни деления, действия выполняют по порядку слева направо:

Вычисляем:

1) 10 + 15 = 25

2) 25 – 6 = 19

3) 19 – 8 = 11

Полностью пример записываем так:

10 + 15 – 6 – 8 = 25 – 6 – 8 = 19 – 8 = 11

Например, 

В числовом выражении 3 арифметических действия: деление, умножение и деление.

Определим порядок действий и запишем их над арифметическими знаками: так как нет ни сложения ни вычитания, действия выполняют по порядку слева направо:

Вычисляем:

1) 15 : 5 = 3

2) 3 • 4 = 12

3) 12 : 6 = 2

Полностью пример записываем так:

15 : 5 • 4 : 6 = 3 • 4 : 6 = 12 : 6 = 2

2) Если тебе нужно выполнить несколько арифметических действий (сложение, вычитание, умножение и деление), то сначала выполняют умножение и деление по порядку слева направо, а затем сложение и вычитание по порядку слева направо.

Например, 

В числовом выражении 4 арифметических действия: вычитание, деление, сложение и умножение.

Определим порядок действий и запишем их над арифметическими знаками: сначала производим деление, потом умножение, затем вычитание и сложение.

1)15 : 3 = 5

2) 6 • 8 = 48

3) 10 – 5 = 5

4) 5 + 48 = 53

Полностью пример записываем так:

10 – 15 : 3 + 6 • 8 = 10 – 5 + 6 • 8 = 10 – 5 + 48 = 5 + 48 = 53

3) Если в выражении есть скобки, то сначала выполняют действия в скобках, но обязательно учитывать первое и второе правила.

Например,

В числовом выражении 4 арифметических действия: вычитание, деление, сложение и умножение.

Определим порядок действий и запишем их над арифметическими знаками: сначала производим вычитание в скобках, затем деление, потом умножение и сложение.

1) 25 – 10 = 15

2) 15 : 3 = 5

3) 6 • 8 = 48

4) 5 + 48 = 53

Полностью пример записываем так:

(25 – 10) : 3 + 6 • 8 = 15 : 3 + 6 • 8 = 5 + 6 • 8 = 5 + 48 = 53

Например, 

В числовом выражении 4 арифметических действия: сложение, деление, сложение и деление.

Определим порядок действий и запишем их над арифметическими знаками: сначала производим действия в скобках (деление, затем сложение), затем деление, потом сложение.

1) 12 : 4 = 3

2) 6 + 3 = 9

3) 18 : 9 = 2

4) 42 + 2 = 44

Полностью пример записываем так:

42 + 18 : (6 + 12 : 4) = 42 + 18 : (6 + 3) = 42 + 18 : 9 = 42 + 2 = 44

Источники

• https://FB.ru/article/463522/chto-snachala—slojenie-ili-umnojenie-pravila-poryadok-vyipolneniya-deystviya-i-rekomendatsii
• http://www.webstaratel.ru/2012/03/pochemu-umnozhenie-pervoe.html
• https://naobumium.info/arifmetika/poryadok_deistviy.php
• http://math-prosto.ru/?page=pages/order_of_action/order_of_action.php
• http://math-prosto.ru/?page=pages%2Forder_of_action%2Forder_of_action.php
• https://budu5.com/manual/chapter/1172
• http://spacemath.xyz/poryadok_deistviy/
• https://vashurok.ru/questions/8×12-3-chto-snachala-delaem-delenie-ili-umnozhenie

Объяснение правила PEMDAS! (Примеры включены) — Mashup Math

Сообщение от Энтони Персико

Каково правило PEMDAS для математического порядка операций и решения задач? Изучая математику, вы узнаете о процессе, называемом порядком операций .

Существует множество приемов для запоминания математического порядка операций в правильном порядке, но самым популярным является правило PEMDAS.

P: Круженное заключение

E: Экспоненты

M: Умножение

D: Разделение

A: Добавление

S = Suptracting

. в правиле PEMDAS выполняются слева направо.

Кроме того, правило PEMDAS для запоминания математического порядка операций имеет несколько важных подправил, которые также необходимо соблюдать, если вы хотите правильно использовать PEMDAS (и получать правильные ответы на математические задачи). Эти важные подправила относятся к отношениям между умножением/делением и сложением/вычитанием.

Эти важные подправила правила PEMDAS подробно объясняются в следующем разделе:

Правило PEMDAS существует уже несколько десятилетий как инструмент, помогающий учащимся запомнить математический порядок операций. . Многие предпочитают просто запоминать мнемоническое слово PEMDAS (произносится как PEM-DAHS), в то время как другие предпочитают запоминать фразу , пожалуйста, извините, моя дорогая тетя Салли.

Однако вы предпочитаете помнить, что правило PEMDAS не так важно, как запоминание ранее упомянутых подправил? Почему подправила правила PEMDAS так важны? Потому что подправила часто определяют правильный или неправильный ответ на математическую задачу.

Правило PEMDAS может быть несовершенным, но если вы помните подправила, оно может быть полезным инструментом, помогающим вам правильно применять математический порядок операций и получать правильные ответы как на простые, так и на сложные математические задачи при условии, что вы знаете важных подправила.

1.) P: Выполняйте операции внутри круглых скобок или групп, прежде чем делать что-либо еще (если нет групп или круглых скобок, вы можете пропустить этот шаг) .

2.) E: Далее, после выполнения операций внутри круглых скобок и группировок (если они есть), примените любые степени (если степеней нет, то этот шаг можно пропустить).

3.) M/D: Далее, после круглых скобок, групп и показателей степени, выполните умножение/деление слева направо в зависимости от того, какая операция будет первой).

★ Тот факт, что М стоит перед D в правиле PEMDAS, не означает, что вы всегда будете выполнять умножение перед делением.

4.) A/S: Наконец, после умножения и/или деления выполните сложение/вычитание слева направо в зависимости от того, какая операция была первой).

★ Тот факт, что A стоит перед S в правиле PEMDAS, не означает, что вы всегда будете выполнять сложение перед вычитанием

★ = Чрезвычайно важно

Теперь, когда вы знаете, что означает правило PEMDAS для запоминания математического порядка операций, пришло время узнать, как использовать это правило для решения математических задач и получения правильных ответов.

Почему? Потому что знание того, что означает правило PEMDAS, не имеет никакой образовательной ценности, если вы понятия не имеете, как применить его к математическому порядку операций.

Помните, что правило PEMDAS полезно только в том случае, если вы помните ключевые подправила, показанные в предыдущем разделе.

Имея в виду подправила, в следующем разделе будет рассмотрено несколько примеров того, как правильно применять правило PEMDAS, когда речь идет о математическом порядке операций и решении задач. 92=9

Последний шаг — разделить: 27÷9 = 3

Окончательный ответ: 3

Обратите внимание, что в этом примере не используются группировки или экспоненты. Поэтому вы можете пропустить P и E в правиле PEMDAS и начать с M/D.

Поскольку умножение/деление предшествует сложению/вычитанию, вы можете решить эту задачу, двигаясь слева направо следующим образом:

 10×6 = 60

60 + 1 = 61

Окончательный ответ: 61

Правило PEMDAS Пример. 4:

Правило PEMDAS требует сначала умножить, а затем выполнить вычитание следующим образом:

10 x 5 = 50

75 – 50 = 25

Окончательный ответ: 25

Вы готовы применить важные подправила?

Обратите внимание, что в этом математическом примере есть только две операции: умножение и деление.

Прежде чем двигаться дальше, давайте вернемся к подправилу №3:

3.) M/D: Затем, после круглых скобок, групп и показателей степени, выполните умножение/деление слева направо в зависимости от того, какая операция будет первой).

★ Тот факт, что М стоит перед D в правиле PEMDAS, не означает, что вы всегда будете выполнять умножение перед делением.

Эту задачу можно решить, выполнив сначала умножение (крайняя левая операция), а затем деление второго следующим образом:

8 x 8 = 64.

64 ÷ 16 = 4

Окончательный ответ: 4

Примечание: Если бы вы строго следовали правилу PEMDAS и решали слева направо, вы все равно могли бы получить 4 как правильный ответ. Однако так будет не всегда, как в следующем примере.

Начнем с того, что многие люди неправильно решают эту простую задачу, потому что забывают ключевые подправила правила PEMDAS. Они совершат ошибку, строго следуя правилу PEMDAS и выполняя умножение перед делением (поскольку M стоит перед D в PEMDAS).

Не делайте этой ошибки!

Помните, что ★ Тот факт, что М стоит перед D в правиле PEMDAS, не означает, что вы всегда будете выполнять умножение перед делением.

В этом случае единственными операциями являются умножение и деление. На этот раз деление на первом месте, и это нормально. Вы по-прежнему решаете задачу, двигаясь слева направо следующим образом:

42 ÷ 7=6

6×3=18

Окончательный ответ: 18

Почему 2 не является окончательным ответом? Если вам не удалось правильно применить правило PEMDAS, возможно, вы допустили ошибку, выполнив умножение перед делением следующим образом:

7 x 3 = 21

42 / 21 = 2 (ЭТОТ ОТВЕТ НЕВЕРНЫЙ!)

( Совет профессионала: Если бы это был вопрос с несколькими вариантами ответов, то оба варианта были бы вариантами 18 и 2. Так что будьте осторожны!) (как простые, так и сложные) без понимания того, как применять математический порядок операций, а PEMDAS — эффективный инструмент для их запоминания в правильной последовательности — при условии, что вы также помните важные подправила, описанные выше.

 Правило PEMDAS и математический порядок операций привлекли огромное внимание в последние годы из-за вирусных сообщений в социальных сетях, в которых сообщаются, казалось бы, простые математические задачи, которые собирают тысячи ответов (и неправильных ответов) из-за того, что многие взрослые могут помните «PEMDAS», но не то, как применять фактическое правило PEMDAS (и соответствующие подправила).

Поскольку многие люди не могут найти правильный ответ на эти простые вопросы, они склонны оставлять комментарии и отмечать друзей, что только делает самых популярных в социальных сетях.

Правило PEMDAS для математического порядка операций: Заключение

Правило PEMDAS — популярный инструмент памяти для запоминания математического порядка операций. Правило означает P: скобки, E: экспоненты, M: умножение, D: деление, A: сложение, S = вычитание.

Как правило, операции выполняются слева направо, но есть очень важные ключевые подправила, а именно (1) выполнять умножение/деление слева направо в зависимости от того, какая операция выполняется первой) и выполнять сложение/вычитание слева вправо в зависимости от того, какая операция была первой).

Без понимания этих подправил правило PEMDAS становится крайне ненадежным и может привести к неправильным ответам на простые математические задачи (см. правило PEMDAS, пример 6 выше).

PEMDAS, возможно, не лучший способ запомнить, как правильно применять математический порядок операций, но он может быть надежным инструментом тогда и только тогда, когда вы также помните ключевые подправила.

6 комментариев

— можете ли вы опровергнуть это правило PEDMSA? — (деление перед умножением, вычитание перед сложением)

Чтобы расширить ответ Losethegame

Losethegame ответил: «Я попал сюда, погуглив тот же вопрос, хотя я не уверен, что (m) любой из комментаторов ответил на него конкретно. Я думаю, вы правы в том, что ваше правило нельзя нарушать. Вероятно, это можно доказать алгебраически, потому что a * (b / c) = (a / c) * b и a + (b-c) =(а-в)+б…?»

Я согласен, что это, вероятно, может быть доказано алгебраически с помощью методов, подобных тому, что упоминает LosetheGame (хотя пример с LosetheGame может быть ошибочным, поскольку, как указывает user21280, Losethegame меняет операнды местами). Но развивая идею алгебраического доказательства (и без замены операндов!), я могу придумать какую-нибудь алгебру, которая могла бы это доказать. (Предоставленный пользователь 21280 считает, что мои примеры не учитывают все возможности. Его ответ с использованием логических формул мог бы).

Дано уравнение, в котором умножение предшествует делению, например. 3*4/2 неважно, что вы сделаете первым. Так что буквальный PEMDAS или PEDMAS подойдет. Принимая во внимание уравнение, в котором деление идет текстуально перед умножением, например. 6/2*3 тогда имеет значение, что вы сделаете первым. Традиционное прочтение PEMDAS или PEDMAS делает это правильно (потому что они сказали бы сначала сделать первое, а это деление), буквальное PEDMSA делает это правильно. Буквальное прочтение PEMDAS может привести к ошибкам.

Вычитание и деление разделяют это свойство. Допустим, мы составим небольшое уравнение из той части уравнения, в которой операторы конкурируют друг с другом. Если вычитание конкурирует со сложением, и вычитание происходит первым (текстуально, в уравнении), оно должно быть выполнено первым. Если деление конкурирует с умножением, а деление идет первым, деление должно быть выполнено первым. В то время как если бы сложение конкурировало с вычитанием, то независимо от того, происходит ли оно первым текстуально или нет, не имеет значения, выполняется ли сначала сложение или вычитание. Точно так же, если умножение конкурирует с делением, если умножение идет первым текстуально, то не имеет значения, выполняется ли сначала деление или умножение. Таким образом, литерал PEDMSA всегда работает (т. е. строго выполняет деление перед умножением, вычитание перед сложением). Как и традиционное/правильное прочтение PEMDAS/PEDMAS, то есть чтение, в котором говорится, что умножение и деление имеют одинаковый приоритет и сначала выполняют первое, аналогично сложению и вычитанию.

Так, например.

Взятие 1*2/3 so a*b/c
Следование PEDMSA буквально дает 1*(2/3) so a(b/c) Следование PEDMSA традиционно дает (1 * 2)/3 , поэтому (ab)/c

И мы знаем алгебраически, что a(b/c) = (ab)/c

 1*2/ 3 а* б/к
знак равно
1*2/3 сб/с
 

Принимая 1/2*3 так a/b*c Это оценивается одинаково независимо от того, следуете ли вы строго упорядоченному PEDMSA или традиционному PEMDAS, т. Е. Делаете ли вы сначала деление, как правило, или сначала вы выполняете первое из умножения и деления, это (a/b)*c в обоих случаях так явно одно и то же.

 1/2*3 (а/б)*в
знак равно
1/2*3 (а/б)*в
 

С 1+2-3 , если мы делаем a+ b-c , который заказан PEDMSA, т.е. a+(b-c) , это тот же результат, что и при традиционном PEMDAS (a+b)-c. Мы знаем алгебраически a+(b-c)=a+b-c=(a+b)-c

Я помню, как мой учитель математики указал, что одна вещь, которую вы хотите остерегаться / знать, это -(a+b) , которое мы просверлили, было -a-b настолько сильно отличается от -а+б . Вычитания всегда должны выполняться первыми и по порядку… и если сначала выполняется вычитание или сначала сложение и вычитание, то мы сохраняем это правило.

 1+2-3 а+(б-в)
знак равно
1+2-3 (а+б)-в
 

И для этого тоже самое. алгебраически

 1-2+3 (1-2)+3 (a-b)+c
знак равно
1-2+3 (1-2)+3 (а-б)+в
 

И, наверное, наконец. 1-2-3 и 1/2/3 И независимо от того, делаете ли вы строго упорядоченный PEDMSA или традиционный PEMDAS, это (1-2)-c и (1/2)/3 так же есть.