Полезно знать об АЛЛЕРГИИ НА СОЮ (soya)
АЛЛЕРГИЯ НА СОЮ (soya)
Полезная информация об аллергии на сою – Информационный лист Норвежского союза астматиков и аллергиков
Что такое пищевая аллергия?
Аллергическая реакция на продукты питания возникает из-за того, что организм реагирует на некоторые виды протеинов, содержащиеся в пище. У некоторых людей возникает сильная реакция даже на минимальные количества пищевых продуктов, которые они не переносят. У других реакция выражается в недомогании, которое проходит без драматических последствий. Пищевая аллергия более распространена среди детей, чем среди взрослых. У большинства пищевая аллергия проходит с возрастом. Реакция на несколько продуктов не является необычной. В том случае, если из рациона удаляются продукты, являющиеся важными источниками питательных веществ, необходимо подобрать хорошие альтернативы, которые позволят сохранить здоровый и разнообразный рацион.
Что такое аллергия на сою?
Аллергия на сою означает, что организм реагирует на один или несколько видов протеинов, находящихся в соевых бобах.
Соевые бобы относятся к стручковым растениям. Из плодов стручковых растений можно получать протеин, крахмал, растительное масло и клетчатку, которые затем можно применять для приготовления пищи.
При соевой аллергии обычно проявляется реакция на пробу Пирке, а также она проявляется в анализе крове (антитела иммуноглобулина). Следует отметить, что бывают случае позитивного анализа крови и пробы Пирке на соевую аллергию, в то время как организм на самом деле переносит сою. Это происходит из-за перекрёстной чувствительности к другим видам стручковых или к пыльце берёзы. Некоторые аллергики на пыльцу берёзы отмечают, что они переносят наличие соли в обработанной пище, но реагируют на холодные продукты из сои, как например соевый напиток и соевый йогурт.
Где содержится соевый протеин?
Соевый протеин, обладающий высокой питательной ценностью и многочисленными функциональными свойствами, используется в качестве компонента во многих продуктах питания. Например, соевый протеин содержится гамбургерах, рыбных котлетах, пицце, хлебе и других выпечных изделиях.
Многие продукты-заменители для страдающих молочной аллергией и целиакией имеют в своей основе сою. Причиной этому служит то, что соевый протеин является хорошей альтернативой (благодаря питательной ценности и физиологическим качествам) для молочного протеина и глютена. Соя также является основным ингридиентом для соевого соуса и таких продуктов, как мисо, тофу и темпе.
Какие реакции возникают при аллергии на сою?
Реакция аллергика, употребившего продукт питания с содержанием сои, может быть различной. В качестве примеров можно назвать жидкий стул, боли в животе, приступ астмы, обострение экземы, затруднение дыхания и анафилактический шок. Аллергики на пыльцу берёзы, которые реагируют на холодные продукты из сои, чаще всего испытывают желудочно-кишечные симптомы.
Как лечить аллергию на сою?
Единственным способом борьбы с аллергией на сою является полное исключение из рациона питания продуктов, содержащих соевый протеин. Те из аллергиков, кто реагирует только на холодные соевые напитки и соевый йогурт, как правило могут не принимать во внимание наличие сои в смешанных продуктах, так как большинство продуктов выпечки, мясных и прочих продуктов с соей, употребляются в подогретом виде.
Что можно есть при аллергии на сою?
Соевый протеин отсутствует в продуктах из чистого молока, яиц, мяса, рыбы, ракообразных и моллюсков, фруктов, орехов, растительного масла или овощей. Тем не менее, у некоторых могут возникать реакции на другие стручковые растения, как горох, бобы, чечевица и арахис, которых следует избегать. В сладостях и чипсах соевый протеин встречается редко. Вегетарианские и иностранные блюда, а также продукты для здорового питания, содержат соевый протеин чаще, чем типичные норвежские продукты. По причине все более частого использования соевого протеина в различных продуктах питания, важно тщательно читать перечень ингредиентов на товарных упаковках. Согласно предписанию о маркировке, все продукты, содержащие сою, должны быть чётко помечены.
О соевом масле
Соевое масло В процессе производства масла исчезают протеины, т.е. вещества, вызывающие аллергические реакции. Результаты зарубежных анализов масел показывают отсутствие в некоторых из них соевого протеина.
Некоторые крупные норвежские производители осуществляют регулярные анализы на предмет обнаружения остатков соевого протеина в растительном масле или маргарине.
О соевом лецитине
Соевый лецитин также является жировым продуктом, получаемым из соевых бобов. Соевый лецитин может в отдельных случаях содержать следы соевого протеина, но в этом случае речь идёт об очень небольшом количестве вещества. Именно поэтому, нет особой необходимости предостерегать аллергиков от употребления продуктов питания с содержанием соевого лецитина.
Теннис – запредельно быстрая игра, для реакции на удар есть всего секунда. Как мозг игроков адаптируется под темп? — С миру по Нитке — Блоги
Все о языке тела и обманках.
Когда смотришь профессиональный теннис с трибун, сразу же бросается в глаза, что игра на самом деле намного быстрее, чем кажется по телевизору. Скорость, с которой летит мяч и двигаются игроки, поражает каждый раз.
Замедление игры в трансляциях происходит по двум причинам.
Во-первых, из-за угла, с которого теннис снимают. В основном картинка идет с камеры, установленной высоко и за задней линией. В итоге мы смотрим на корт по диагонали, из-за чего он сжимается. Поэтому кажется, что мяч пролетает меньшее расстояние.
Например, во время трансляций с итогового турнира ATP всегда кажется, что корт там очень короткий. Хотя на самом деле он такой же, как везде.
Слева – корт итогового турнир ATP. Справа – точно такой же корт в Индиан-Уэллс. Но поскольку в Лондоне камера, как кажется, стоит дальше и ниже, корт сжимается сильнее.
Во-вторых, на восприятие скорости мяча влияют особенности человеческого мозга. По телевизору расстояние от зрителя до мяча никогда не меняется. А когда мы смотрим матч с трибун, мозг более точно оценивает скорость, потому что у него появляется еще один вспомогательный фактор – еще одно измерение.
Поэтому по телевизору теннис может казаться медленным. Но на самом деле скорости там нереальные.
Мы рассказывали, что мужские подачи летят так быстро, что среагировать на них невозможно.
Игроки и тренеры, естественно, понимают, насколько это выгодно с игровой точки зрения, – поэтому мужской теннис постепенно становится все более подачецентричным.
Исследование показателей 50 лучших подающих выявило, что с 1991 года каждые 10 лет:
• Количество очков, выигранных на первой подаче, растет на 0,4%, а на второй – на 0,9%;
• Количество эйсов растет на 0,7%;
• Количество выигранных геймов на подаче растет на 1,4%.
Так что подача постепенно становится эффективнее.
А вот прием – наоборот. Даже у 50 лучших принимающих показатели стабильно падают. Каждые 10 лет:
• Количество очков, выигранных на приеме и первой, и второй подачи снижается на 0,8%;
• Реализация брейк-пойнтов ухудшается на 0,7%;
• Количество выигранных геймов на приеме снижается на 1,9%.
Поскольку скорость женской подачи в целом ниже, в WTA теннис все еще строится на розыгрышах. Но в них времени на размышления тоже не очень много.
Удары сейчас такие сильные, что мозгу приходится много считать, чтобы жить в настоящем
Средняя скорость мужского форхенда составляет от 115 до 130 км/ч.
У женщин цифры ненамного ниже – от 112 до 127 км/ч (но у мужских ударов намного более сильное вращение, поэтому в целом они наносят больший урон). Усредним еще дальше, и получится примерно 120 км/ч – или же 33 метра в секунду.
Средний бэкхенд летит медленнее, со скоростью 105 км/ч – или же 28 метров в секунду. Но длина корта – всего 23,8 метра. Если принять во внимание замедление мяча после отскока, выйдет, что у игроков в среднем две секунды на то, чтобы нанести свой удар, подготовиться к ответу соперника и добежать до мяча.
Ситуация только усугубляется тем, что при восприятии движущихся предметов мозг немного отстает от настоящего времени – потому что в процессе существует задержка. Она возникает из-за того, что дополнительное время требуется на три процесса: движение глаз, поступление зрительного сигнала и обработку этого сигнала мозгом.
Эта задержка может составлять до 0,5 секунды. За это время мяч в среднем пролетает 16,5 метра – 2/3 длины корта. Ученые из Мельбурнского университета в исследовании 2018 года писали: «Для эффективного действия в настоящем необходимо, чтобы мозг компенсировал не только время, потраченное на передачу и обработку информации, но и время, которое будет потрачено на подготовку и выполнение движения.
Если мозг не учтет эти задержки, то возникнут ошибки при локализации движущихся предметов».
В теннисе это приведет к тому, что игрок неправильно подойдет к мячу (или не подойдет вообще) и допустит ошибку. К счастью, у мозга есть механизмы предсказывания, способные компенсировать эти задержки.
Например, в 2018-м специалисты из Массачусетского технологического института провели эксперимент. Они показывали испытуемым полет мяча по прямой линии, но после какого-то времени тот исчезал за препятствием. Испытуемые должны были нажать на кнопку в тот момент, когда мяч, по их мнению, должен был появиться из-за препятствия.
Оказалось, что точность ответа зависит того, как много информации получил мозг. Например, она снижалась, если полет мяча до препятствия был не очень длинным.
В целом уже доказано, что мозг всегда стремится получить и использовать как можно больше информации. Например, при восприятии речи мы не только слушаем звук слов, но и смотрим на губы собеседника.
Размер предмета точнее всего определяется, когда мы можем его не только увидеть, но и потрогать.
Лучшие теннисисты – мастера сбора информации: смотрят на мяч, соперника и слушают вращение. Но реакцию тоже тренируют
Теннис тоже иллюстрирует этот тезис, потому что ученые доказали: наиболее успешно положение мяча предсказывают те, кто сосредотачивается не только на нем, но и на сопернике. Точность увеличивается, потому что мозг считывает дополнительную информацию с подхода к мячу, движений плеч, бедер и рук, положения ракетки, замаха – и даже звука, с которым мяч отлетает от струн.
Поэтому теннисисты много работают над маскировкой ударов. Например, Роджер Федерер в этой ситуации мог играть как по линии, так и по диагонали, и не давал Агасси вообще никаких подсказок, чтобы считать направление – оставалось только гадать.
Еще от теннисистов требуется хорошо маскировать укороченные удары – особенно с учетом того, что очень часто для их выполнения требуется поменять хват ракетки.
Это делается в самый последний момент, чтобы соперник не заметил и не рванул вперед.
Хотя Бернарду Томичу ничего менять не надо, и он может вот так обманывать. Этот удар особенно эффективен, потому что мозг теннисистов заточен на то, что с таким замахом и в такой ситуации мяч полетит глубоко.
Еще один классический обман – удар вслепую, когда соперника заставляют дернуться не в ту сторону одним движением головы. Вот Федерер, например, взглядом показал Гулбису, чтобы будет играть по диагонали, а сам положил по линии.
И на противника смотрит не только тот, кто ждет удара, но и тот, кто его наносит. Например, Рафаэль Надаль в финале «Уимблдона»-2008 показывает: если мяч прилетел достаточно мягко и ты можешь послать его куда угодно, можно просто чуть подождать, пока соперник дернется в какую-нибудь сторону.
Но вообще ученые проводили эксперименты с бейсболистами и теннисистами, и оказалось, что они могут точно предсказать направление броска или удара, даже если видео обрывается до того, как они будут сделаны – исключительно по движениям питчера или соперника.
Теннисный тренер Томас Мензингер утверждает, что реакцию можно тренировать сколько угодно, но его опыт указывает, что лучше сосредотачиваться на умении читать игру. Но Хинце Хогендоорн из Мельбурнского университета не может точно сказать, результатом чего становится наблюдательность профессионалов, позволяющая им это делать – врожденной способности быстрее и точнее обрабатывать информацию или многочасовых тренировок, или сочетания обоих объяснений.
Исследования все же показывают, что спортсмены в целом быстрее реагируют на визуальные стимулы – и чем больше у них опыта, тем лучше их результаты. Так что теннис сам по себе может быть отличным упражнением. Потому что лучший способ подготовить мозг – это постоянно заставлять его что-то делать.
Например, про трехкратного чемпиона «Больших шлемов» Артура Эша рассказывали, что он тренировал реакцию для игры у сетки простым упражнением: выходил вперед и просил спарринга выполнять мощные подачи в полную силу. Поскольку подача – самый сильный удар в теннисе, действовать приходилось быстро. У сетки Эш был хорош.
Но есть и более щадящие упражнения.
Для некоторых потребуется специальная техника. Например, в 2018-м ATP во время итогового турнира поставила установку для измерения скорости реакции. Лучший результат на ней показал 37-летний Роджер Федерер, во время упражнения сказавший, что оно может стать для него хорошей разминкой.
Такая хорошая реакция помогает Федереру у сетки вытаскивать даже самые мощные удары.
На отметке 10:09 Роджер разобрался с шлепком от Кириоса – и австралиец не мог в это поверить.
Новак Джокович использовал похожую систему для игры с сыном.
Посмотреть эту публикацию в Instagram
Публикация от Novak Djokovic (@djokernole)
И подобные тренировки полезны не только для теннисистов. Например, гонщик «Формулы-1» Ромен Грожан показывал, как отрабатывает реакцию.
Но иногда достаточно просто мяча.
Это может быть как специальный тренировочный мяч с непредсказуемым отскоком, так и обычный теннисный. Например, Мария Шарапова в 2017-м показала, как во время разминки одним упражнением включает не только ноги, но и мозг.
Посмотреть эту публикацию в Instagram
Публикация от Maria Sharapova (@mariasharapova)
В целом в подтрибунных помещениях перед матчами можно часто увидеть подобные упражнения, суть которых в том, что игрок ловит мячи, которые ему неожиданно бросает тренер. Опять же, гонщики «Формулы-1» ими тоже пользуются. Вот, например, француз Пьер Гасли.
Reaction test on a F1 driver 🏎
pic.twitter.com/4tx1BjVayj
— World of Engineering (@engineers_feed) August 11, 2020
Для теннисистов тренировки с мячом предпочтительнее.
Ведь, как уже было показано, для мозга очень важны детали. Реакция на мяч ближе к игровым ситуациям, чем реакция на что-нибудь другое, и это повышает качество подсознательных расчетов.
Тот же принцип действует и в обратную сторону. Да, теннис поможет в целом улучшить реакцию и способность воспринимать движущиеся объекты. Но для успеха в других видах спорта лучше сосредоточиться на специальных упражнениях, симулирующих ситуации из этих видов.
Фото: Gettyimages.ru/Dean Mouhtaropoulos, Cameron Spencer, Daniel Pockett / Stringer; REUTERS/Paul Childs
Лучшие мужские кроссовки для бега в 2020 году. Купить сейчас
2.5: Скорость реакции — Химия LibreTexts
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 1438
В ходе реакции, показанной ниже, расходуются реагенты A и B, а концентрация продукта AB увеличивается.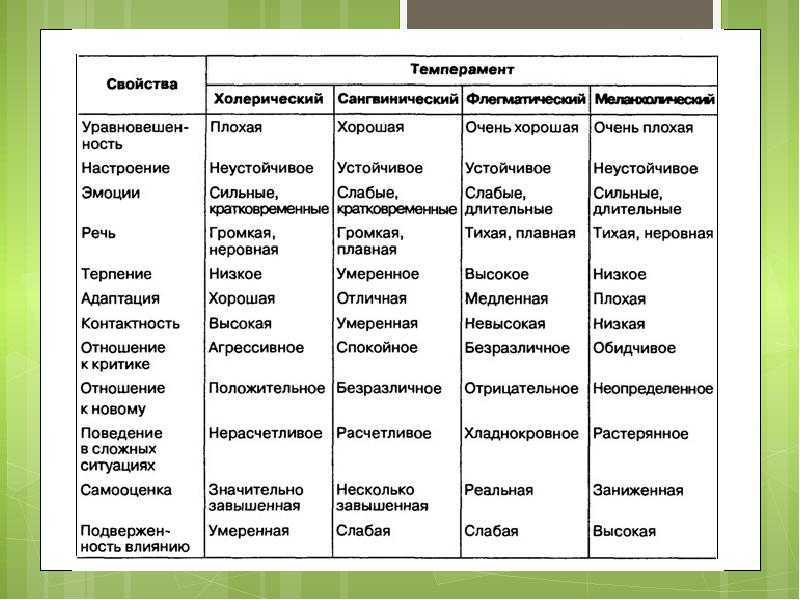
\[ \ A + B \ longrightarrow AB \]
Рисунок \(\PageIndex{1}\): На приведенном выше рисунке показан гипотетический профиль реакции, в котором концентрация реагентов (красный цвет) уменьшается по мере увеличения концентрации продуктов (синий цвет).Для стехиометрически сложной реакции:
\[ aA + bB \longrightarrow cC + dD \label{1} \]
\[ \text{Скорость} = \dfrac{-1}{a}\dfrac{d[A]}{dt} = \dfrac{-1}{b} \dfrac{d[B]}{dt} = \dfrac{1}{c}\dfrac{d[C]}{dt} = \dfrac{1}{d}\dfrac{d[D]}{dt} \]
Глядя на рисунок \(\PageIndex{1}\) выше, мы видим, что скорость может быть измерена либо по реагенту (A или B), либо по любому продукту (C или D). Не все переменные необходимы для определения скорости. Следовательно, если у вас есть значение «А», а также значение «а», вы можете найти скорость реакции.
Вы также можете заметить из уравнения \ref{1}, что изменение реагентов по сравнению с изменением во времени должно стоять перед ними со знаком минус.
Причина этого в том, что количество реагентов уменьшается с течением времени, поэтому скорость будет отрицательной (потому что это обратная скорость). Таким образом, если перед переменной поставить знак минус, решение будет иметь положительную скорость.
Химические реакции сильно различаются по скорости, с которой они происходят. Некоторые из них сверхбыстрые, в то время как другим могут потребоваться миллионы лет, чтобы достичь равновесия.
Определение скорости реакции
Скорость реакции для данной химической реакции является мерой изменения концентрации реагентов или изменения концентрации продуктов в единицу времени. Скорость химической реакции можно определить как изменение концентрации вещества, деленное на интервал времени, в течение которого наблюдается это изменение:
\[ \text{скорость}=\dfrac{\Delta \text{концентрация}}{\Delta \text{время}} \label{2-1}\]
Для реакции вида \(A + B \rightarrow C\), скорость может быть выражена через изменение концентрации любого из ее компонентов
\[\text{rate}=-\dfrac{\Delta [A]}{\Delta t} \]
\[\text{rate}=-\dfrac{\Delta [B]}{\Delta t}\]
\[\text{rate}=\dfrac{\Delta [C]}{\ Delta t}\]
где \(Δ[A]\) — разница между концентрациями \(A\) за интервал времени \(t_2 – t_1\):
\[ \Delta [A] = [A]_2 – [A]_1 \label{2-2}\]
Обратите внимание на знаки минус в первых двух примерах выше.
Концентрация реагента всегда уменьшается со временем, поэтому \(\Delta [A]\) и \(\Delta [A]\) оба отрицательны. Поскольку отрицательные скорости не имеют особого смысла, скорости, выраженные в терминах концентрации реагента, равны
Рассмотрим теперь реакцию, в которой коэффициенты различны:
\[A + 3B \rightarrow 2D\]
Понятно, что \([B]\) убывает в три раза быстрее, чем \([A]\), поэтому во избежание двусмысленности при выражении скорости в по разным компонентам принято делить каждое изменение концентрации на соответствующий коэффициент:
\[\text{rate}= -\dfrac{\Delta [A]}{\Delta t} = -\dfrac{\ Delta [B]}{3\Delta t} = \dfrac{\Delta [D]}{2\Delta t} \label{2-3}\]
Пример \(\PageIndex{1}\): Окисление аммиака
При окислении аммиака
\[\ce{4 Nh4 + 3O2 -> 2 N2 + 6 h3O}\]
установлено, что скорость образования N 2 составляет 0,27 моль л –1 с –1 .
- С какой скоростью образовывалась вода?
- С какой скоростью расходовался аммиак?
Раствор
а) Из уравнения стехиометрии Δ[H 2 O] = 6/2 Δ[N 2 ], поэтому скорость образования H 2 O is
3 × (0,27 моль л –1 с –1 ) = 0,81 моль л –1 с –1 .
б) на каждые 2 моля образовавшегося N 2 расходуется 4 моля NH 3 , поэтому скорость исчезновения аммиака составляет = 0,54 моль л –1 с –1 .
Комментарий : Из-за того, как сформулирован этот вопрос, было бы приемлемо выразить это последнее значение как отрицательное число.
Мгновенные скорости
Большинство реакций замедляются по мере расходования реагентов. Следовательно, скорости, даваемые приведенными выше выражениями, имеют тенденцию терять свое значение при измерении на более длительных интервалах времени Δ t .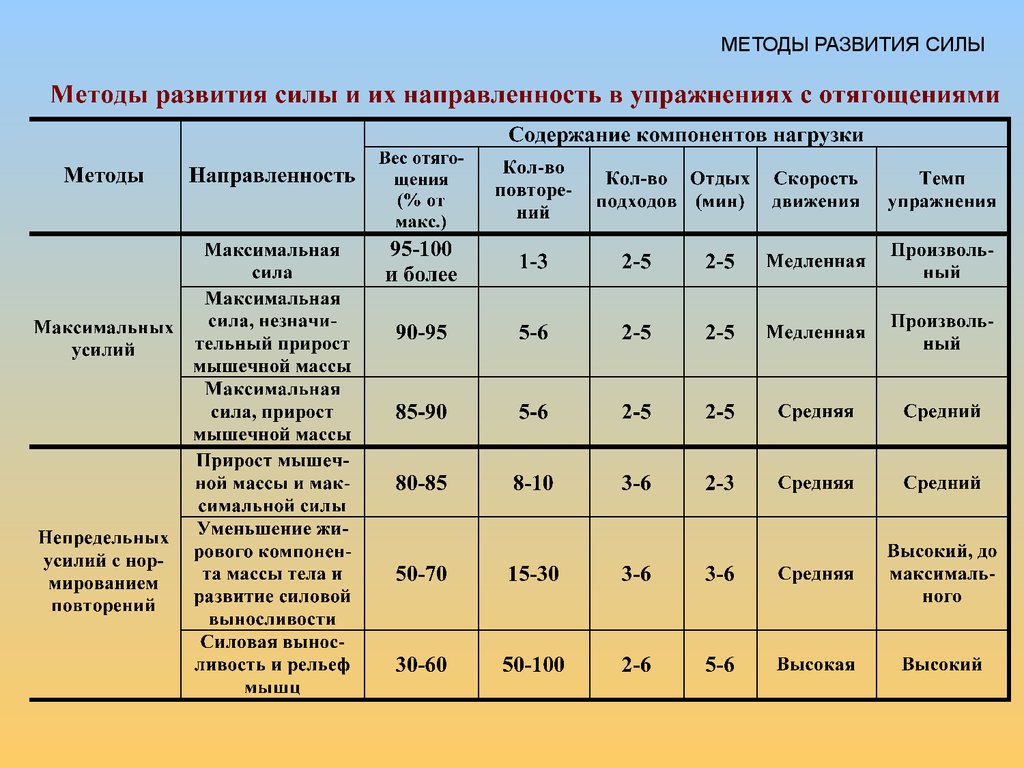
Примечание. Мгновенные ставки также известны как дифференциальные ставки.
Таким образом, для реакции, протекание которой показано здесь, фактическая скорость (измеряемая увеличением концентрации продукта) постоянно меняется, достигая наибольшего значения в нулевой момент времени. мгновенная скорость реакции определяется наклоном касательной к кривой зависимости концентрации от времени.
Мгновенная скорость, полученная в начале реакции (t = 0), известна как начальная скорость (метка (1) здесь). Как мы вскоре увидим, начальные скорости играют важную роль в изучении кинетики реакций. Если вы изучали дифференциальное исчисление, то знаете, что эти наклоны касательных представляют собой 90 130 производных 90 131, значения которых могут различаться в каждой точке кривой, так что эти мгновенные скорости на самом деле равны предельные скорости определяются как
\[ \text{rate} = \lim_{\Delta t \rightarrow 0} \dfrac{-[A]}{\Delta T}\]
Если вы не знаете исчисления, иметь в виду, что чем больше временной интервал Δ t , тем меньшей будет точность мгновенной скорости.
Законы скорости и константы скорости
Закон скорости – это выражение, связывающее скорость реакции с константой скорости и концентрациями реагентов. Константа скорости \(k\) является константой пропорциональности для данной реакции. Общий закон скорости обычно выражается как: 9t \label{2}\]
Как видно из уравнения \ref{2} выше, скорость реакции зависит от концентрации реагентов, а также от константы скорости. Однако есть и другие факторы, влияющие на скорость реакции. Эти факторы включают температуру и катализаторы. Когда вы можете написать уравнение закона скорости для определенной реакции, вы можете определить порядок реакции на основе значений s и t.
Порядок реакции
Скорость реакции для данной реакции является важным инструментом, который позволяет нам рассчитать конкретный порядок реакции. Порядок реакции важен, поскольку он позволяет нам легко и эффективно классифицировать конкретные химические реакции. Знание порядка реакции позволяет быстро понять многочисленные факторы реакции, включая закон скорости, единицы константы скорости, период полураспада и многое другое.
Порядок реакции можно рассчитать из закона скорости, добавив экспоненциальные значения реагентов в закон скорости. 9t \label{4}\]
\[ \text{Порядок реакции} = s + t \label{5}\]
Важно отметить, что хотя порядок реакции можно определить из закона скорости, существует в общем, нет связи между порядком реакции и стехиометрическими коэффициентами в химическом уравнении.
ПРИМЕЧАНИЕ. Скорость реакции должна быть неотрицательной. Он может быть равен нулю и не обязательно должен быть целым числом.
Как показано в уравнении \ref{5}, полный порядок реакции равен сумме «s» и «t». Но что означает каждая из этих переменных? Каждая переменная представляет порядок реакции по отношению к реагенту, к которому она относится. В этой конкретной ситуации s — это порядок реакции по [A], а t — порядок реакции по [B].
Вот пример того, как вы можете посмотреть на это : Если порядок реакции по отношению к [A] равен 2 (s = 2), а [B] равен 1 (t = 1), то это в основном означает, что концентрация реагента A уменьшается в 2 раза, а концентрация [B] уменьшается в 1 раз.
Итак, если у вас нулевой порядок реакции (т. ), это в основном означает, что концентрация реагентов не влияет на скорость реакции. Вы можете удалить или добавить реагенты в смесь, но скорость не изменится.
Список различных уравнений скорости реакции для реакций нулевого, первого и второго порядка можно увидеть в таблице \(\PageIndex{1}\). Эта таблица также включает дополнительные уравнения, которые можно определить с помощью этого уравнения, если известен порядок реакции (период полураспада, интегральный закон скорости и т. д.).
| Закон об интегрированных ставках | \(\ {[A]_t} = \ {-kt + [A]_0}\) | \(\ {ln[A]_t} = \ {-kt + ln[A]_0}\) | \(\dfrac{1}{[A]_t} = +kt + \dfrac{1}{[A]_0} \) |
| Единицы постоянной скорости (k): | \(\ {моль л^{-1} с^{-1}}\) 9{-1}}\) | ||
| Линейный график для определения (k): | \([A] \) в зависимости от времени | \(\ln [A] \) в зависимости от времени | \(\dfrac{1}{[A]}\) в зависимости от времени |
| Отношение постоянной скорости к наклону прямой: | \(\ {наклон} = \ {-k}\) | \(\ {наклон} = \ {-k}\) | \(\ {наклон} = \ {k}\) |
| Период полураспада: | \(\dfrac{[A]_0}{2k}\) | \(\dfrac{\ln2}{k}\) | \(\dfrac{1}{k[A]_0}\) |
Примеры задач
1.
Определите скорость реакции
2. ВЕРНО или НЕВЕРНО: изменения температуры или введение катализатора повлияют на константу скорости реакции
Для примеров задач 3-6 используйте Формула 6 для ответов на вопросы
\[ H_2O \longrightarrow 2H_2+ O_2 \label{6} \]
* Предположим, что реакция протекает при постоянной температуре
3. Для приведенной выше реакции сформулируйте закон скорости.
4. Укажите общий порядок реакции.
5. Найдите скорость, если k = 1,14 x 10 -2 и [H 2 O] = 2,04M
6. Найдите период полураспада реакции.
Ответы
1. Скорость реакции является мерой изменения концентрации исчезновения реагентов или изменения концентрации появления продуктов в единицу времени.
2. НЕВЕРНО. Константа скорости не зависит от присутствия катализатора. Однако катализаторы могут влиять на общую скорость реакции.
3. \(\ {Скорость} = \ {k[H_2O]}\)
4.
Первый порядок
5. 2,33 x 10 -2 с -1
6,60,8 с (t1/2 = ln 2 / k = ln 2 / 1,14 x 10 -2 = 60,8 с). CA: Университетские научные книги,
Авторы и авторство
2.
5: Reaction Rate распространяется по незаявленной лицензии и был создан, изменен и/или курирован LibreTexts.
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или Страница
- Показать страницу TOC
- № на стр.
- Теги
12.1 Скорости химических реакций — химия 2e
Цели обучения
К концу этого раздела вы сможете:
- Определение скорости химической реакции
- Вывести выражение скорости из сбалансированного уравнения для данной химической реакции
- Рассчитать скорость реакции на основе экспериментальных данных
Коэффициент является мерой того, как некоторое свойство изменяется во времени.
Скорость — это известная скорость, которая выражает расстояние, пройденное объектом за заданный промежуток времени. Заработная плата – это ставка, которая представляет собой сумму денег, заработанную человеком, работающим в течение определенного периода времени. Точно так же скорость химической реакции является мерой того, сколько реагента потребляется или сколько продукта образуется в результате реакции за данный промежуток времени.
Скорость реакции – это изменение количества реагента или продукта в единицу времени. Таким образом, скорость реакции определяется путем измерения временной зависимости некоторого свойства, которое может быть связано с количеством реагента или продукта. Скорости реакций, которые потребляют или производят газообразные вещества, например, удобно определять путем измерения изменений объема или давления. Для реакций с участием одного или нескольких окрашенных веществ скорость можно контролировать с помощью измерений поглощения света. Для реакций с участием водных электролитов скорость можно измерить по изменению проводимости раствора.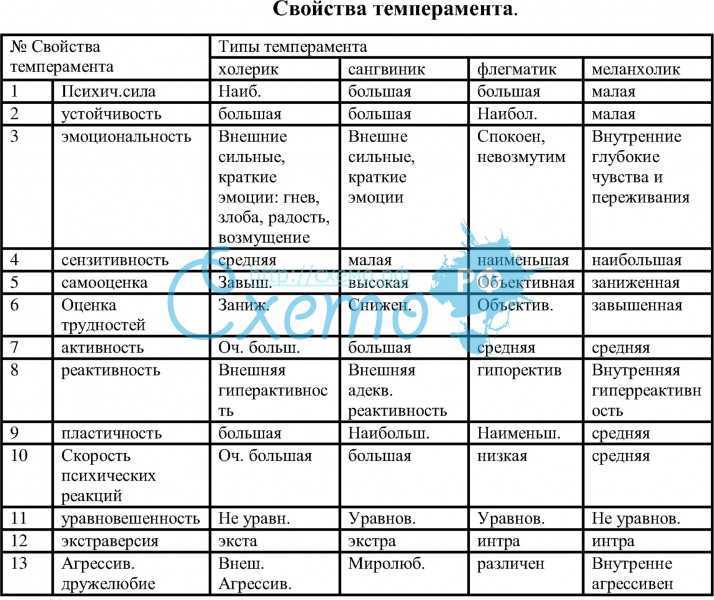
Для реагентов и продуктов в растворе их относительные количества (концентрации) удобно использовать для целей выражения скорости реакции. Например, концентрация перекиси водорода, H 2 O 2 , в водном растворе медленно меняется с течением времени по мере его разложения в соответствии с уравнением:
2h3O2(aq)⟶2h3O(l)+O2(g) 2h3O2(водн.)⟶2h3O(ж)+O2(г)
Скорость разложения пероксида водорода можно выразить через скорость изменения его концентрации, как показано здесь:
скорость разложения h3O2=-изменение концентрации реагентавременной интервал=-[h3O2]t2-[h3O2]t1t2-t1=-Δ[h3O2]Δскорость разложения h3O2=-изменение концентрации реагентавременной интервал=-[h3O2] t2-[h3O2]t1t2-t1=-Δ[h3O2]Δt
Это математическое представление изменения концентрации частиц с течением времени является выражением скорости реакции. В скобках указаны молярные концентрации, а символ дельта (Δ) указывает на «изменение». Таким образом, [h3O2]t1[h3O2]t1 представляет собой молярную концентрацию перекиси водорода в некоторый момент времени т 1 ; аналогично [h3O2]t2[h3O2]t2 представляет собой молярную концентрацию перекиси водорода в более позднее время t 2 ; Δ[H 2 O 2 ] представляет собой изменение молярной концентрации пероксида водорода за интервал времени Δ t (то есть t 2 − 909754 1
).
Поскольку концентрация реагента уменьшается по мере протекания реакции, Δ[H 2 O 2 ] является отрицательной величиной. По соглашению скорость реакции является положительной величиной, поэтому это отрицательное изменение концентрации умножается на -1. На рис. 12.2 представлен пример данных, собранных во время разложения H 2 О 2 .Рисунок 12.2 Скорость разложения H 2 O 2 в водном растворе снижается по мере уменьшения концентрации H 2 O 2 .
Для получения табличных результатов этого разложения концентрацию перекиси водорода измеряли каждые 6 часов в течение дня при постоянной температуре 40 °C. Скорость реакции рассчитывали для каждого временного интервала путем деления изменения концентрации на соответствующее приращение времени, как показано здесь для первого 6-часового периода:
-Δ[h3O2]Δt=-(0,500 моль/л-1,000 моль/л)(6,00 ч-0,00 ч)=0,0833 мольл-1ч-1-Δ[h3O2]Δt=-(0,500 моль/л-1,000 моль/л)(6,00 ч-0,00 ч)=0,0833 мольл-1ч-1
Обратите внимание, что скорости реакции меняются со временем, уменьшаясь по мере протекания реакции.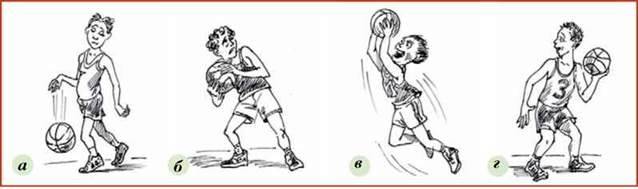
Результаты за последние 6 часов дают скорость реакции:
-Δ[h3O2]Δt=-(0,0625моль/л-0,125моль/л)(24,00ч-18,00ч)=0,010мольл-1ч-1- Δ[h3O2]Δt=-(0,0625моль/л-0,125моль/л)(24,00ч-18,00ч)=0,010мольл-1ч-1
Такое поведение указывает на то, что реакция постоянно замедляется со временем. Использование концентраций в начале и в конце периода времени, в течение которого скорость реакции изменяется, приводит к расчету средней скорости реакции за этот интервал времени. В любой конкретный момент времени скорость, с которой протекает реакция, называется ее мгновенной скоростью. Мгновенная скорость реакции в «нулевой момент времени», когда реакция начинается, является ее начальной скоростью. Возьмем аналогию с автомобилем, замедляющимся по мере приближения к знаку «стоп». Начальная скорость автомобиля — аналогичная началу химической реакции — будет показанием спидометра в момент, когда водитель начинает нажимать на тормоза (9).0454 т 0 ). Несколько мгновений спустя мгновенная скорость в конкретный момент — назовем ее t 1 — будет несколько меньше, о чем свидетельствуют показания спидометра в этот момент времени.
Со временем мгновенная скорость будет продолжать падать, пока не достигнет нуля, когда машина (или реакция) остановится. В отличие от мгновенной скорости, средняя скорость автомобиля не указывается спидометром; но его можно рассчитать как отношение пройденного пути ко времени, необходимому для полной остановки автомобиля (Δ т ). Как и в случае с замедляющимся автомобилем, средняя скорость химической реакции находится где-то между начальной и конечной скоростями.
Мгновенная скорость реакции может быть определена одним из двух способов. Если экспериментальные условия позволяют измерять изменения концентрации за очень короткие промежутки времени, то средние скорости, рассчитанные, как описано выше, обеспечивают достаточно хорошее приближение к мгновенным скоростям. В качестве альтернативы можно использовать графическую процедуру, которая, по сути, дает результаты, которые были бы получены, если бы были возможны измерения с короткими временными интервалами.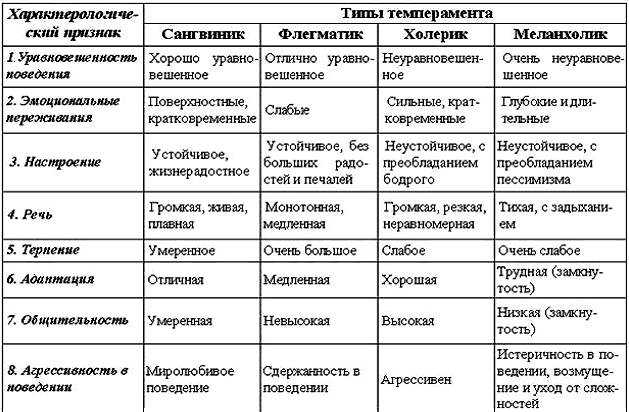
На графике зависимости концентрации перекиси водорода от времени мгновенная скорость разложения H 2 O 2 в любое время t задается наклоном прямой линии, касательной к кривой в этот момент времени (рис. 12.3). Эти наклоны касательной могут быть оценены с помощью исчисления, но процедура для этого выходит за рамки этой главы.
Рисунок 12.3 На этом графике показан график зависимости концентрации от времени для 1,000 M раствора H 2 O 2 . Скорость в любой момент времени равна минусу наклона линии, касательной к кривой в этот момент времени. Касательные показаны на t = 0 ч («начальная скорость») и at t = 12 ч («мгновенная скорость» на 12 ч).
Химия в повседневной жизни
Скорость реакции в анализе: тест-полоски для анализа мочи
Врачи часто используют одноразовые тест-полоски для измерения количества различных веществ в моче пациента (рис.
12.4). Эти тест-полоски содержат различные химические реагенты, встроенные в небольшие подушечки в различных местах вдоль полоски, которые изменяют цвет при воздействии достаточных концентраций конкретных веществ. В инструкциях по применению тест-полосок часто подчеркивается, что правильное время считывания имеет решающее значение для получения оптимальных результатов. Этот акцент на времени считывания предполагает, что кинетические аспекты химических реакций, происходящих на тест-полоске, являются важными факторами.
Тест на глюкозу в моче основан на двухэтапном процессе, представленном химическими уравнениями, показанными здесь: 2I−→катализаторI2+2h3O+O2
Первое уравнение описывает окисление глюкозы в моче с образованием глюколактона и перекиси водорода. Полученная перекись водорода впоследствии окисляет бесцветный йодид-ион с образованием коричневого йода, который можно обнаружить визуально. Некоторые полоски содержат дополнительное вещество, которое вступает в реакцию с йодом, вызывая более отчетливое изменение цвета.
Две показанные выше тестовые реакции по своей природе очень медленные, но их скорость увеличивается за счет специальных ферментов, встроенных в прокладку тест-полоски. Это пример катализа , тема, обсуждаемая далее в этой главе. Обычной тест-полоске на глюкозу для использования с мочой требуется около 30 секунд для завершения реакции цветообразования. Слишком раннее прочтение результата может привести к заключению, что концентрация глюкозы в образце мочи ниже, чем она есть на самом деле (9).0454 ложноотрицательный результат ). Слишком долгое ожидание оценки изменения цвета может привести к ложноположительному результату из-за более медленного (не катализируемого) окисления йодид-иона другими веществами, обнаруженными в моче.
Рисунок
12,4
Тест-полоски обычно используются для определения наличия определенных веществ в моче человека. Многие тест-полоски имеют несколько прокладок, содержащих различные реагенты, что позволяет обнаруживать несколько веществ на одной полоске.
(кредит: Икбал Осман)
Относительные скорости реакции
Скорость реакции может быть выражена как изменение концентрации любого реагента или продукта. Для любой данной реакции все эти выражения скорости просто связаны друг с другом в соответствии со стехиометрией реакции. Скорость общей реакции
аА⟶бБаА⟶бБ
можно выразить через уменьшение концентрации А или увеличение концентрации В. Эти два выражения скорости связаны стехиометрией реакции:
скорость =-(1a)(ΔAΔt)=(1b)(ΔBΔt) скорость=-(1a)(ΔAΔt)=(1b)(ΔBΔt)
Рассмотрим реакцию, представленную следующим уравнением:
2Nh4(g)⟶N2(g)+3h3(g)2Nh4(g)⟶N2(g)+3h3(g)
Соотношение между скоростями реакции, выраженными через образование азота и потребление аммиака, например, таково:
Это может быть представлено в сокращенном формате, опуская единицы стехиометрического коэффициента:
−12∆мольNh4∆t=∆мольN2∆t−12∆мольNh4∆t=∆мольN2∆t
Обратите внимание, что отрицательный знак был включен в качестве коэффициента для учета противоположных знаков двух изменений количества (количество реагента уменьшается, а количество продукта увеличивается).
Для гомогенных реакций как реагенты, так и продукты находятся в одном и том же растворе и, таким образом, занимают один и тот же объем, поэтому молярные количества можно заменить молярными концентрациями:
−12Δ[Nh4]Δt=Δ[N2]Δt−12Δ[Nh4]Δt=Δ[N2]Δt
Точно так же скорость образования H 2 в три раза превышает скорость образования N 2 , потому что на каждый моль произведенного N 2 приходится три моля H 2 .
13Δ[h3]Δt=Δ[N2]Δt13Δ[h3]Δt=Δ[N2]Δt
На рис. 12.5 показано изменение концентрации во времени при разложении аммиака на азот и водород при 1100 °C. Наклоны касательных линий при t = 500 с показывают, что мгновенные скорости, полученные для всех трех частиц, участвующих в реакции, связаны их стехиометрическими факторами. Скорость производства водорода, например, наблюдается в три раза выше, чем скорость производства азота:
2,91×10-6М/с9,70×10-7М/с≈32,91×10-6М/с9,70×10-7М/с≈3
Рисунок
12,5
Изменение концентраций реагента и продуктов реакции 2Nh4⟶N2+3h3.
2Nh4⟶N2+3h3. Скорости изменения трех концентраций связаны стехиометрией реакции, о чем свидетельствуют различные наклоны тангенсов при t = 500 с.
Пример 12.1
Выражения для относительных скоростей реакций
Первым этапом производства азотной кислоты является сжигание аммиака:
4Nh4(г)+5O2(г)⟶4NO(г)+6h3O(г)4Nh4(г)+5O2(г)⟶4NO(г)+6h3O(г)
Напишите уравнения, связывающие скорости расход реагентов и скорость образования продуктов.
Раствор
С учетом стехиометрии этой гомогенной реакции скорости расходования реагентов и образования продуктов составляют:
−14Δ[Nh4]Δt=−15Δ[O2]Δt=14Δ[NO]Δt=16Δ[h3O]Δt−14Δ[Nh4]Δt=−15Δ[O2]Δt=14Δ[NO]Δt=16Δ[h3O ]Δt
Проверьте свои знания
Скорость образования Br 2 составляет 6,0 × × 10 -6 моль/л/с в реакции, описываемой следующим суммарным ионным уравнением:
5Br-+BrO3-+6H+⟶3Br2+3h3O5Br-+BrO3-+6H+⟶3Br2+3h3O
Напишите уравнения, связывающие скорости расходования реагентов и скорости образования продуктов.