4 класс. Математика. Умножение на двузначное и трехзначное число. — Умножение на двузначное и трехзначное число.
Комментарии преподавателяНа этом уроке мы рассмотрим письменное умножение на двузначное и трехзначное число. Решим несколько примеров на письменное умножение в столбик и сформулируем общее правило записи подобных примеров.
Рассмотрим произведение чисел 54 и 32.
Чтобы умножить число 54 на двузначное число 32, заменим второй множитель 32 на сумму разрядных слагаемых 30 и 2.
Воспользуемся правилом умножения числа на сумму. То есть можно умножить число 54 на каждое слагаемое и полученные результаты сложить. Умножим 54 на три десятка.
Умножим 54 на две единицы.
Сложим полученные результаты.
Эти вычисления удобно записать столбиком.
Умножим 54 на количество единиц второго множителя.
То есть на 2. . .
Получили первое неполное произведение – 108 единиц. Умножим 54 на количество десятков второго множителя. То есть на 3. При умножении на десятки мы получим десятки. Поэтому удобно записать второе неполное произведение под десятками. . Два пишем, один запоминаем. . И единица, которую запоминали, . Итак, второе неполное произведение – 162 десятка.
Сложим полученные результаты.
Переписываем 8.
, , переписываем.
Ответ: .
Выполним умножение чисел 245 и 24.
Умножим число 245 на количество единиц второго множителя, то есть на 4. . 0 записываем, 2 запоминаем.
. И еще 2, . 8 записываем, 1 запоминаем.
. И еще 1, . Мы получили первое неполное произведение – единиц.
Умножим число 245 на число десятков второго множителя, то есть на 2.
Так как мы умножаем на десятки, то и получим в результате десятки. Удобно записать второе неполное произведение под десятками. Итак, . 0 записываем под десятками, а 1 запоминаем.
. И 1, .
. Мы получили второе неполное произведение – десятков.
Сложим два неполных произведения.
0 переписываем.
.
, 8 записываем, 1 запоминаем.
.
Ответ: .
Рассмотрим еще один случай умножения. Найдем значение произведения чисел и . — это десятков. Запишем второй множитель 43 под десятками.
Умножим на не обращая внимания на . Умножим сначала на число единиц второго множителя. То есть на . , 5 записываем, запоминаем.
, и , .
.
Мы получили первое неполное произведение – .
Теперь умножим число 705 на число десятков второго множителя, то есть на 4.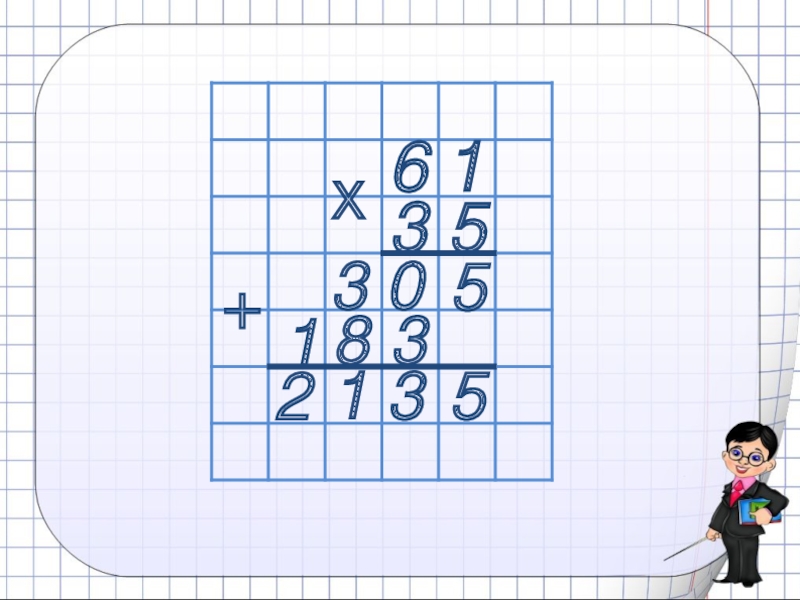
, плюс , .
.
Мы получили второе неполное произведение – десятков.
Важно помнить, что, когда мы умножали на десятка, результат нужно записывать под десятками.
Теперь сложим два неполных произведения.
5 переписываем.
.
.
0 записываем, 1 запоминаем.
.
Мы получили . Но помните, что мы умножали десятков, значит, число показывает количество десятков. Приписываем .
Ответ: .
Подведем итог. Чтобы выполнить умножение письменно на двузначное число, нужно первый множитель умножить сначала на единицы второго множителя, получится первое неполное произведение. Затем умножить число на количество десятков второго множителя. Помните: при умножении на десятки получатся десятки. Поэтому второе неполное произведение нужно начинать записывать под десятками.
Вы уже умеете выполнять письменно умножение на однозначное число и на двузначное число. При умножении на двузначное число мы первый множитель умножаем на число единиц второго множителя.
В примере мы число 534 умножаем сначала на 6, число единиц числа 26.
Затем первый множитель умножаем на число десятков второго множителя.
Получаем два неполных произведения, которые нужно сложить.
Важно помнить, что при умножении на десятки мы получаем десятки, потому запись второго неполного произведения следует начинать под разрядами десятков.
Сравним два столбика решений:
Мы видим: в первом столбике при умножении на двузначное число получают два неполных произведения.
Во втором столбике при умножении на трехзначное число получают три неполных произведения. Почему? Вы, наверное, догадались. Во втором столбике в состав второго множителя, кроме единиц и десятков, входят еще и сотни. Поэтому первый множитель надо умножить на число единиц второго множителя, получим первое неполное произведение.
Затем первый множитель надо умножить на число десятков второго множителя, получим второе неполное произведение, которое начинают записывать под разрядом десятков.
И затем первый множитель надо умножить на количество сотен второго множителя, получим третье неполное произведение. Обратите внимание: при умножении на сотни, получим сотни, поэтому третье неполное произведение нужно начинать записывать под разрядом сотен.
Остается сложить три неполных произведения, и получим результат умножения.
Найти значение произведения чисел.
Умножим первый множитель 624 на число единиц второго множителя, то есть на 3.
, 2 пишем, а 1 запоминаем.
, и еще 1, будет 7.
Мы получили первое неполное произведение.
Теперь перейдем к умножению на десятки. 624 нужно умножить на ноль. Но мы знаем, что при умножении любого числа на ноль получится ноль, потому можем сразу перейти к умножению числа на сотни.
Умножим первый множитель 624 на число сотен второго множителя, то есть на 4. Результат начнем записывать под разрядом сотен.
, 6 пишем под сотнями, 1 запоминаем.
, и еще 1, будет 9.
, запишем 24.
Получили следующее неполное произведение – 2496 сотен. Теперь сложим полученные результаты.
2 переписываем.
7 также переписываем.
, 4 пишем, 1 запоминаем.
, и еще 1, будет 11. 1 пишем, 1 запоминаем.
4 и 1 будет 5.
2 записываем.
Значение произведения – 251 472.
При письменном умножении на трехзначное число первый множитель надо умножить на число единиц второго множителя, затем первый множитель надо умножить на число десятков второго множителя и затем первый множитель умножить на число сотен второго множителя. Мы получим три неполных произведения. Важно помнить: при умножении на десятки получатся десятки, потому результат нужно начинать записывать под разрядом десятков. При умножении на сотни мы получим сотни, поэтому результат надо начинать записывать под разрядом сотен. Остается сложить три неполных произведения.
Источник конспекта: http://interneturok.ru/ru/school/matematika/4-klass/umnozhenie-na-dvuznachnoe-i-trehznachnoe-chislo/pismennoe-umnozhenie-na-dvuznachnoe-chislo?konspekt
http://interneturok.
ru/ru/school/matematika/4-klass/umnozhenie-na-dvuznachnoe-i-trehznachnoe-chislo/pismennoe-umnozhenie-na-tryohznachnoe-chislo?konspekt
Источник видео: http://www.youtube.com/watch?v=rWxllUMMu-I
«Умножение двузначного числа на однозначное в столбик» | План-конспект занятия по математике (3 класс):
Урок математики в 3 классе
Тема: «Умножение двузначного числа на однозначное в столбик»
Цель урока: познакомить с алгоритмом умножения двузначного числа на однозначное в столбик; повторить распределительное свойство умножения и свойство умножения суммы на число; закреплять умения решать задачи, находить площадь прямоугольника.
Задачи урока:
Личностные:
— прививать интерес к математике;
— уметь находить выход из спорных ситуаций при объяснении алгоритма умножения двузначного числа на однозначное в столбик;
— развитие способности к рефлексивной оценке собственных действий.
Предметные:
— уметь пользоваться: устной и письменной речью при объяснении алгоритма умножения двузначного числа на однозначное в столбик, основами логического мышления, исполнения алгоритмов при вычислении выражений;
— составлять последовательности (цепочки) предметов, чисел, фигур по заданному правилу;
— выполнять перебор всех возможных вариантов объектов и комбинаций, удовлетворяющих заданным условиям.
Метапредметные:
— умение выполнять заданное учебное действие, в случае неуспеха грамотно фиксировать своё затруднение, анализировать ситуацию, устранять причины затруднения;
— формирование специфических для математики логических операций (сравнение, анализ, аналогия).
Ход урока
I. Организационный момент.
— Здравствуйте, дети! Я очень рада вас видеть, начинаем наш урок!
Математика – королева наук!
Без нее не летят корабли,
Без нее не поделишь ни акра земли,
Даже хлеба не купишь, рубля не сочтешь,
Что почем, не узнаешь,
А узнав, не поймешь!
II. Устный счет, актуализация знаний:
— умножьте 78 на 8;
— умножьте 32 на 3;
— умножьте 14 на 6;
— умножьте 28 на 2.
— Удобно ли было умножать устно?
— Что нужно помнить, когда мы устно умножаем двузначное число на однозначное?
III. Открытие новых знаний. (Презентация.)
— Рассмотрим графическую модель распределительного свойства умножения – нахождение площади прямоугольника по известным его сторонам:
(a + b) ∙ c = a ∙ c + b ∙ c
— Как же можно выполнить умножение 24 на 8?
(Дети решают.
Ответы фиксируются на доске.)
24 х 8 = (20+4) х 8 = 20 х 8 + 4 х 8 = 160 + 32 = 192
Постановка проблемы:
— Запись решения громоздкая, неудобная. Существует ли другой способ умножения таких чисел? Сформулируйте задачи урока: (придумать более компактную, удобную запись по аналогии записи сложения в столбик).
Логика рассуждений:
— Произведение 24 и 8 равно площади прямоугольника со сторонами 24 ед. и 8 ед. Разбив большую сторону на части 20 ед. и 4 ед., видим, что вся площадь равна сумме площадей получившихся прямоугольников: 32 и 160 кв. ед. Записав сумму в столбик, приходим к более удобной записи умножения:
24
8
32
160
192
— Эту запись можно еще упростить, вычисляя число десятков «в уме». Тогда число десятков первого произведения удобно писать для памяти над числом десятков первого множителя.
3
24
8
192
Знакомство с алгоритмом:
— Чему мы будем учиться на уроке? (Выполнять умножение, записывая числа в столбик).
IV. Первичное закрепление знаний.
Работа по учебнику — № 2- 3 на странице 36.
(Коллективное выполнение с комментированием у доски).
14х2 21х4 32х3
11х9 13х3 42х3
VI. Самостоятельная работа.
Решение примеров:
26 х 3 44 х 5 73 х 4
(Самопроверка по образцу).
VII. Физкультминутка.
VIII. Закрепление изученного материала.
Работа по учебнику — №4, с.36 (самопроверка), №6, с.37 (работа в парах).
IX. Подведение итогов урока.
— Все ли было понятно сегодня на уроке?
— Кому было трудно?
— Расскажите алгоритм умножения двузначного числа на однозначное в столбик.
— Где можно применить полученные знания?
Х. Рефлексия.
— Кто доволен своей работой?
— Кому еще нужна помощь?
XI. Домашнее задание
№9, с.37, №15, 16, с.38
Выучить алгоритм умножения в столбик.
— Спасибо за работу! До свидания!
Выучить определение, факты и примеры
Умножение — одна из самых простых математических операций, которая заключается в объединении чисел или других величин по определенным правилам для получения их произведения.
Это процесс многократного сложения числа по отношению к другому числу. Например, 6X5 означает, что мы прибавляем 6, 5 раз; 6+6+6+6+6=30. Этот процесс сложения очень сложен, и поэтому эти методы умножения пригодятся.
Прежде чем мы начнем, мы должны хотя бы знать основы умножения, а именно
Множитель (первое число) X Множитель (второе число) = Произведение
Любое число, умноженное на 0, дает произведение, равное 0. Например, 5×0=0
Любое число, умноженное на 1 равно тот же номер. например, 5×1=5
Три простых метода умножения двузначных чисел
Существует 3 основных метода умножения двухзначного числа на двузначное, которые обсуждаются ниже.
Традиционный метод
Метод окна/ящика
Метод решетки
1.
Использование традиционного метода25X42=?
Шаг 1: Установите проблему. Итак, нам придется выровнять их в соответствии с их значением места.
Шаг 2: Умножение числа в разряде единиц и разряде десятков множителя на все множимое отдельно.
Примечание: Нам нужно поставить 0, прежде чем мы сделаем вторую цифру множителя.
Шаг 3: Сложите оба значения, которые мы получили в результате умножения по отдельности.
перенесено = 5
Шаг 1 умножения
5X2 = 10, 1 будет перенесено вперед до разряда десятков X5 = 20, 2 переноса вперед
4X2 = 8 и +2 (перенос) = 10. Мы также опускаем 1, потому что больше нет доступных для переноса номеров.
Шаг 3 умножения
Шаг 4 умножения
50+1000 получаем 1050, это наш конечный продукт.
2. Метод окна/окна
32X34=?
Шаг 1: Создайте таблицу или сетку 2X2, поскольку мы делаем уравнение умножения 2-значного числа.
Шаг 2: Разложение этих факторов на их расширенные формы. Итак, 32 становится 30 и 2; 34 становится 30 и 4.
Примечание. Обозначьте расширенную форму множимого сверху и расширенную форму множителя слева от сетки.
Шаг 3: Мы умножаем числа, которые встречаются в каждом месте на коробке. Следуйте изображению выше.
Шаг 4: Добавьте все те мелкие продукты, которые у нас получились, чтобы получить конечный продукт.
Расширенные формы Факторов
Шаг 2 стандартного метода
900+60+120+8=1088 -> Конечный продукт
3. Решетчатый метод
25X42=?
Шаг 1: Создайте сетку, соответствующую требуемому количеству цифр. В этом случае нам нужна сетка 2X2, так как мы выполняем умножение двух цифр.
Примечание. Расширять множители нет необходимости, поэтому мы непосредственно помечаем множимое в верхней части сетки, а множитель — в правой части сетки.
Шаг 2: Перемножьте числа, которые встречаются в каждой клетке, и запишите значение продукта в разряде десятков в верхней части коробки, а значение в разряде единиц — в нижней части коробки.
Шаг 3: Добавление номеров, находящихся на одной полосе.
Шаг 1 решетчатого метода
5X4=20
2X4=08 (мы ставим 0 в разряде десятков)
5X2=10
2X2=04
Шаги метода решетки
Мы ставим 0 как есть, потому что нет другого числа, с которым его можно было бы добавить.
4+1+0=5
0+8+2=10 (1 было непосредственно поставлено в разряд тысяч)
Таким образом, наш конечный результат равен 1050.
Решаемые примеры
Ниже приведены некоторые из Задачи на умножение двух цифр на две цифры:
Q1. 98X66=?
Решение:
Решение Q 1
Q2.
75X39=?
Решение:
Решение вопроса 2
Самостоятельная практика
Q1. 62X70=
Ответ: 4340
Q2. 49X10=
Ответ: 490
Q3. 27X19=
Ответ: 513
Итог
В этой статье мы смогли понять 3 основных метода, которые можно использовать для умножения двузначных чисел. Как мы видим, традиционный метод более удобен и очень легко умножает числа, которые также состоят из более чем двух цифр. Мы также поняли шаги, связанные со всеми тремя методами, с помощью изображений, на которых были проиллюстрированы процедуры. Вы можете посетить наш веб-сайт, чтобы загрузить и попрактиковаться в умножении двузначных чисел для лучшего понимания.
Рабочие листы по умножению однозначных и двузначных чисел
Все мы знаем, что умножение не такое уж сложное дело. Но знаете ли вы, что это значит? Умножение связано со сложением.
Это означает добавление чисел к определенному времени. Чтобы облегчить умножение, большинство из нас заучивают таблицу умножения наизусть. Эти таблицы умножения помогают нам решать многие суммы умножения двух чисел и приносят пользу при умножении больших чисел. Например, вы можете легко ответить 3×3=9, но для умножения 14×34 или 234×44 нужен другой подход. Давайте посмотрим, как можно умножать однозначные и двузначные числа.
Сначала напишите большее число над меньшим числом. Убедитесь, что столбцы десятков и единиц обоих чисел совпадают. Например, вам дано разложить 56 на 9.. Вы пишете 6 вместо 9.
Начните умножать единицы меньшего числа на большее число. В этом случае умножьте 9 на разряд единиц 56. Продолжите тот же метод с десятым разрядом двузначного числа.
Помните, что при умножении на десятый разряд меньшего числа начинайте умножение с нуля.
После того, как вы умножили однозначную цифру на двузначную, добавьте свои ответы. В этом случае дополнение работает так же. Начинайте складывать цифры с разряда единицы и переходите к десятому.
Вы сделали!Учащиеся в этом разделе найдут произведение однозначного и двузначного числа. Это часто помогает научить студентов разбивать двузначное число на десятки и единицы. Это делает их гораздо более опытными в выполнении задач на умножение. В качестве примера рассмотрим умножение 6 и 58. Начнем с того, что разобьем 58 на 50 и 8. Мы умножим 6 на оба этих числа, а затем сложим их. 6 х 50 = 300, 6 х 8 = 48. Произведение будет 348 (300 + 48). Эти рабочие листы дают учащимся возможность попрактиковаться в умножении однозначных и двузначных чисел. Студенты также узнают, как использовать столбцы для умножения двузначных чисел.
Получите бесплатные рабочие листы в свой почтовый ящик!
Нажмите кнопки, чтобы распечатать каждый рабочий лист и ключ ответа.
Учащиеся будут решать задачи на умножение между однозначными и двузначными числами.
Очень похоже на последний лист. Мы обязательно используем весь спектр вариантов множимого.
Дано десять задач.
Учащиеся укрепят свои навыки запоминания основных таблиц умножения, умножая однозначные и двузначные числа. Вы найдете десять оценок для работы.
Это хороший лист, который поможет вам увидеть, где вы находитесь с этим навыком. Дано десять задач.
Мы немного усложняем задачу и начинаем переходить к навыкам умножения двузначных чисел. Вы найдете десять оценок для работы.
Здесь мы сосредоточимся исключительно на проблемах с двузначными числами. Дано десять задач.
Мы помогаем учащимся найти произведение 36 и 7. Умножить единицы. 6 х 7 = 42. Переименуйте 42 в 40 +2. Поставьте ноль в столбце единиц. Умножьте десятки. Завершите добавлением отдельно. Решается примерная задача и предлагаются две практические задачи.
Учащиеся решают задачи на быстрое умножение. Вы найдете десять оценок для работы.
SМы получаем больше работы с теми же навыками и концепциями. У вас будет десять возможностей их проработать.
Пересматривается концепция решения проблем и их постановки. Примерная задача решена. Предлагаются шесть практических задач.
Учащиеся продемонстрируют свое мастерство в использовании этого набора навыков. Дано десять задач.
Краткий обзор нахождения произведений однозначных и двузначных значений. Предлагаются три задачи, а также место, где учащиеся могут скопировать правильный ответ, когда он будет дан.
Умножить 3 на 4. 3 х 4 = 12 Напишите 2 под единицами столбец и перенести 1 на столбец десятков. Умножьте 6 на 4. 6 х 4 = 24 Добавьте перенос вперед 24 + 1 = 25. Результат запишите под десятки место, и мы получаем ответьте как 252.
Учащиеся повторят, как выполнять эти типы упражнений плавно и быстро. Решается примерная задача и предлагаются две практические задачи.
Учащиеся научатся обрабатывать эти вычисления с помощью быстрой серии упражнений. У вас будет десять возможностей их проработать.
Учащиеся будут практиковаться в быстром умножении.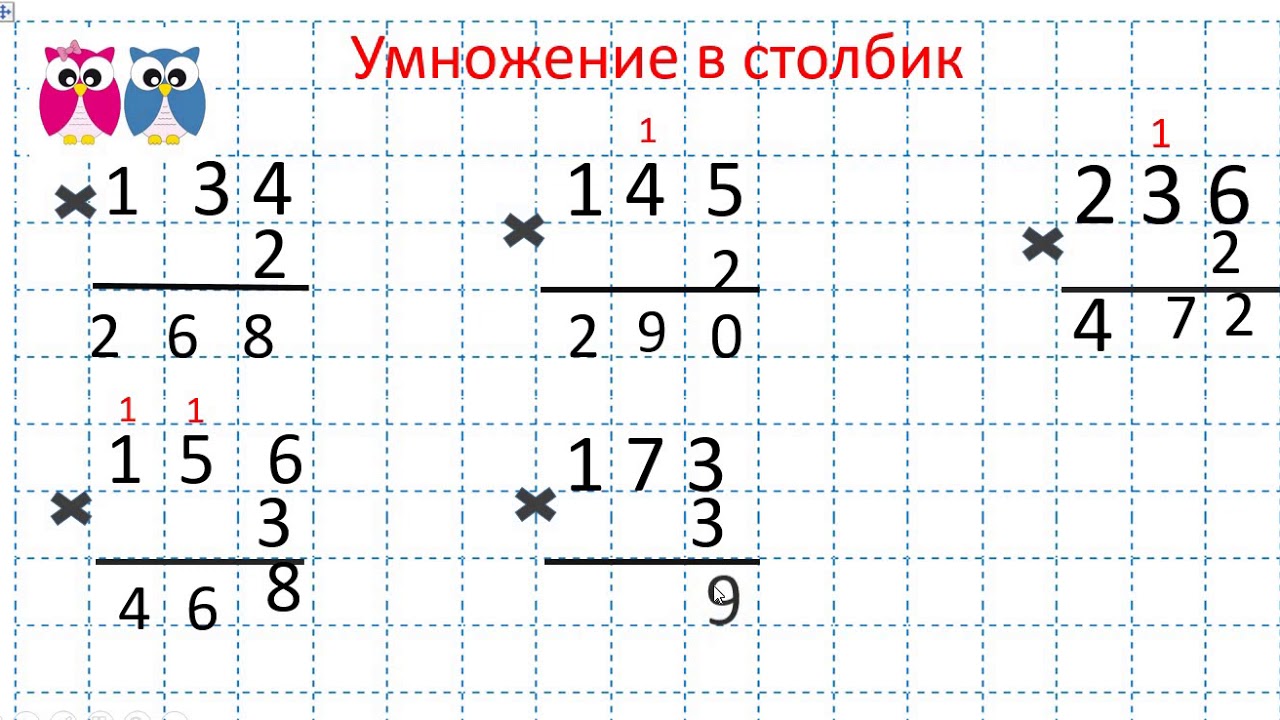
Дано десять задач.
Учащиеся продемонстрируют свою способность работать с этими однозначными и двузначными задачами на быстрое умножение. Предлагается восемь задач.
Предоставляет вам хороший конструктор классовых навыков.
В этом листе объясняется, как найти произведение 73 и 8. A. Умножить 3 на 8. B. 3 x 8 = 24 C. Запишите произведение 4 под разрядом единиц и перенесите 2 в разряд десятков. Пример задачи решен , и две практические задачи предоставляются.
Прямые практические упражнения для вас. У вас будет десять возможностей их проработать.
У тебя может быть прекрасный набор задач для себя. Есть десять упражнений.
Пересматривается концепция решения более сложных упражнений по продукту. Примерная задача решена. Предлагаются шесть практических задач.
Учащиеся продемонстрируют свои навыки работы с однозначными и двузначными числами. Дано десять задач.
Это отличный лист для ознакомления или повторения этих навыков.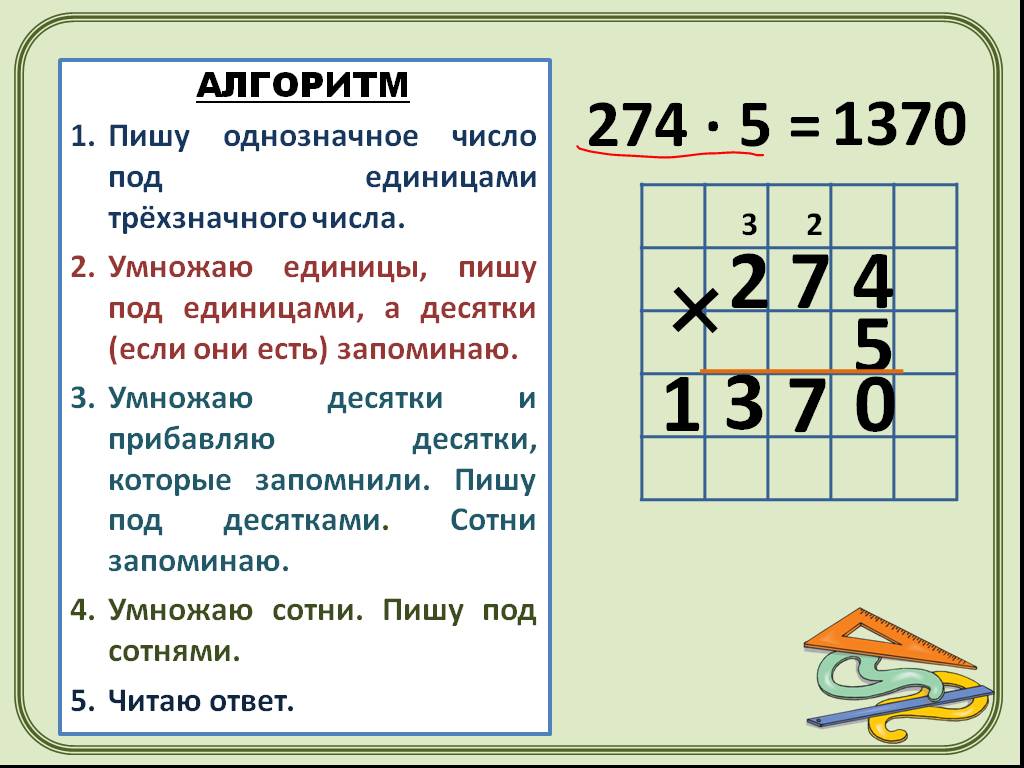
Предлагаются три задачи, а также место, где учащиеся могут скопировать правильный ответ, когда он будет дан.
В этом листе объясняется, как найти произведение 85 и 4. Поместите 0 под чертой у единиц место, но десятки (2) написаны выше десятки столбцов. Как маленькое воспоминание обратите внимание, что это называется переносом на десятки. Умножьте десятки и добавьте 2 десятки что было перенесено. Примерная задача решена.
Учащиеся повторят, как решать больше таких упражнений. Решается примерная задача и предлагаются две практические задачи.
Между двузначными числами намеренно сделан пробел, чтобы увидеть, как вы выстраиваете свою перегруппировку. Есть десять упражнений.
Учащиеся будут больше работать над этими формами умножения. Дано десять задач.
Учащиеся продемонстрируют свои способности к умножению, используя стандартный метод. Предлагается восемь задач.
Отличный способ проверить эти навыки. Предлагаются три задачи.
Этот рабочий лист объясняет четырехэтапный подход, который мы будем использовать для решения этих проблем. Решается примерная задача и предлагаются две практические задачи.
Учащиеся умножают двузначные числа на однозначные и двузначные. Есть десять упражнений.
Учащиеся будут практиковаться в умножении смешанных цифр и находить их конечный продукт. Дано десять задач.
Концепция того, как подходить к этим типам проблем, связанных с продуктом, пересмотрена и перенесена на следующий уровень. Примерная задача решена. Предлагаются шесть практических задач.
Учащиеся продемонстрируют свои навыки работы с двузначными произведениями с однозначными и двузначными числами. Дано десять задач.
Это очень полезно для учителей. Предлагаются три задачи, а также место, где учащиеся могут скопировать правильный ответ, когда он будет дан.
Этот рабочий лист показывает, как найти произведение однозначных и двузначных чисел.
Примерная задача решена.
Учащиеся повторят, как решать задачи на умножение двузначных чисел. Решается примерная задача и предлагаются две практические задачи.
Ученики будут решать смешанные задачи на умножение цифр. Всего таких парней десять.
Мы будем работать над этими десятью упражнениями, которые заставят нас работать с этими двузначными продуктами.
Учащиеся продемонстрируют свои навыки умножения, решая эти двузначные задачи. Предлагается восемь задач.
Учащиеся решают задачи на умножение с двумя цифрами. Дано двадцать пять задач.
Студенты решат эти задачи, требующие от вас глубокого мышления. Предлагаются три задачи.
В этом листе объясняется, как найти произведение значений с помощью метода столбцов. Примерная задача решена.
Этот метод очень полезен для учащихся. Решается примерная задача и предлагаются две практические задачи.
Запишите каждую цифру произведения
начиная с самой верхней строки в
Таблица.