Умножение дробей.Законы умножения
Дорогу осилит идущий, математику – мыслящий
«Счет и вычисления – основа порядка в голове» Песталоцци И
- Как умножить на 5,15, 25 и на 11
- 2405 = ; 96 5 = ; 32 5 = ;
- 18 15 = ; 44 15 = ; 26 15 = .
- 16 25 = ; 8 25 = ; 24 25 = .
- 26 ∙ 11 = ; 43∙11 = ; 84 ∙11 = ;
- 18 ∙ 11 = ; 47 ∙11 = .
1) 308 • 4
2) половина 2500
3) ( 3964 + 378 ) – 2964
4) 64056 : 8
5) 25 • 27 • 4
6) 6060 • 100
7) 6536 + 3464
8) 3807 – 3007
9) 4596 – ( 550 + 596)
10) 20100 — 1
Помогите Винни — Пуху
Самопроверка:
Винни– Пух и яблоки
- Винни–Пух пошёл в гости к Пятачку.
Пятачок поставил на стол две тарелки с яблоками. В одной тарелке – 3 целых яблока, а в другой -5 половинок. - “ Выбирай,” – говорит Пятачок.
- Винни–Пух любит хорошо поесть. Ему захотелось выбрать тарелку, в которой яблок побольше, но он никак не может понять , что больше: 3 целых яблок или 5 половинок.
- Помогите Винни – Пуху выбрать нужную тарелку
Пятачок поставил на стол две тарелки с яблоками. В одной тарелке – 3 целых яблока, а в другой -5 половинок.Запишите дробью, какая часть фигуры, изображённой на рисунке , заштрихована
в)
б)
а)
д)
е)
г)
Решение упражнений
30
- Найдите от числа 120
- Найдите от числа 120
- Найдите число, если
от него равно 35?
80
- Найдите число, если
от него равно 20?
36
63
Задача
На столе лежат 18 шариков.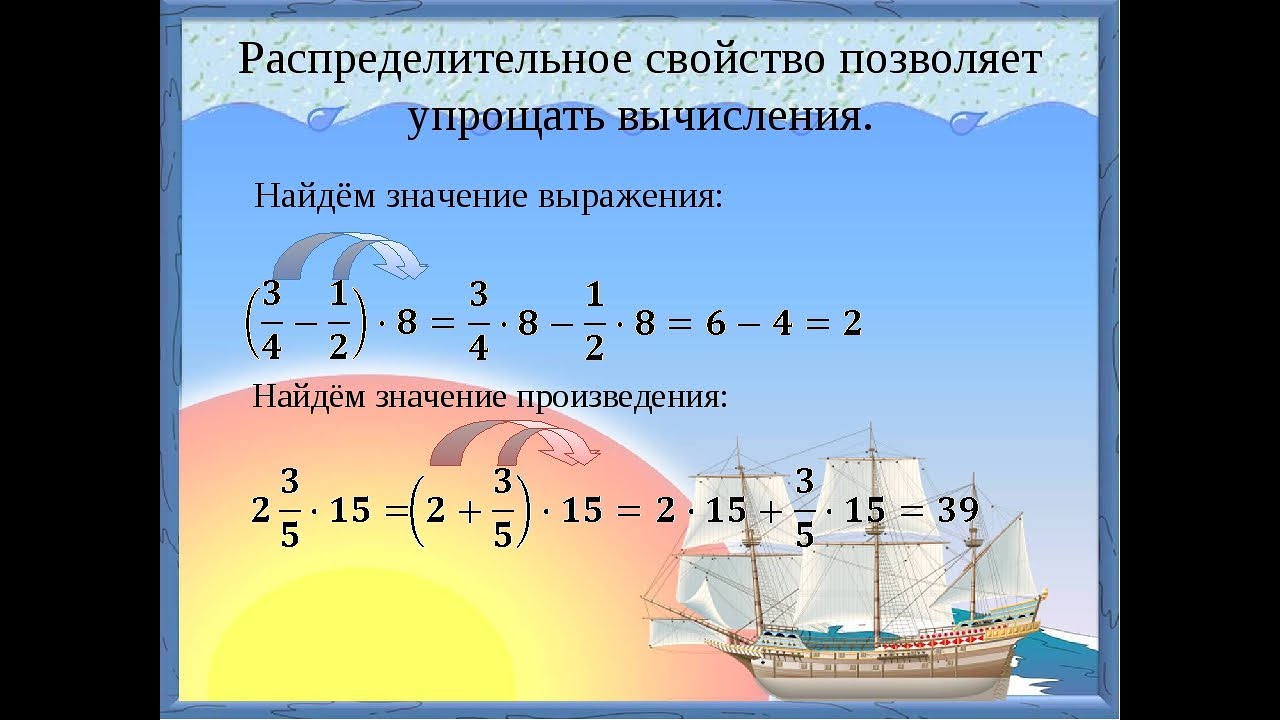
Одна вторая — синие, одна третья – жёлтые, остальные – зеленые.
Сколько шариков каждого цвета?
1.Как умножить две дроби? ( произведение двух дробей есть дробь , числитель которой равен произведению числителей , а знаменатель – произведению знаменателей этих дробей: )
2.Как умножить натуральное число на дробь? (чтобы умножить натуральное число на дробь , можно числитель дроби умножить на это натуральное число, а знаменатель оставить тот же = )
3.Какую дробь называют обратной? (дробь называют обратной для дроби ( ).
4.Какие дроби называются взаимно обратными?
5.Чему равно произведение взаимно обратных чисел? (произведение взаимно обратных чисел равно 1 )
6.Сформулируйте и запишите переместительный закон умножения (от перестановки множителей произведение не меняется )
7.
Сформулируйте и запишите сочетательный закон умножения (чтобы произведение двух чисел умножить на третье число, можно первое число умножить на произведение второго и третьего чисел ) = )).
8. Сформулируйте и запишите распределительный закон умножения относительно сложения ( чтобы число умножить на сумму двух чисел, можно это число умножить на каждое слагаемое и полученные произведения сложить + = + )
9. Сформулируйте и запишите распределительный закон умножения относительно вычитания ( чтобы число умножить на разность двух чисел, можно это число умножить на уменьшаемое и вычитаемое и от первого произведения вычесть второе произведение, и если — = — )
1 . Если произведение чисел равно______, то такие числа называют взаимно простыми.
А) 0; В) 1; С) натуральному числу.
2. Чтобы умножить обыкновенную дробь на _____________, надо числитель этой дроби умножить на это число, а знаменатель оставить тот же.
А) натуральное число; В)смешанное число; С) обратное число.
3. Чтобы найти дробь от числа, надо это число умножить на ______________.
А) 1; В) обратную ей дробь; С) данную дробь.
4.Запишите алгоритм умножения обыкновенных дробей.
Чтобы умножить обыкновенные дроби,надо:
1. Числитель первой дроби умножить на ____________________ ,
2. _____________________ умножить на знаменатель второй,
3. если можно ____________________,
4. выполнить _________________ в числителе и в знаменателе
5. Запишите это правило на математическом языке (формулой).
5. Запишите переместительный закон умножения
6. Запишите сочетательный закон умножения
7.Запишите распределительный закон умножения относительно сложения
8. Запишите распределительный закон умножения относительно вычитания
. Если произведение чисел равно ___1___ , то такие числа называют взаимно простыми.
А) 0; В) 1; С) натуральному числу.
2. Чтобы умножить обыкновенную дробь на _натуральное_ надо числитель этой дроби умножить на это число, а знаменатель оставить тот же.
А) натуральное число; В)смешанное число; С) обратное число.
3. Чтобы найти дробь от числа, надо это число умножить на _данную дробь__
А) умножить на 1; В) на обратную ей дробь; С) на данную дробь.
4.Запишите алгоритм умножения обыкновенных дробей.
Чтобы умножить обыкновенные дроби надо:
1. Числитель первой дроби умножить на _числитель второй _
2. _знаменатель первой _ умножить на знаменатель второй,
3. если можно _сократить числитель и знаменатель на общий делитель
4. выполнить __умножение_ в числителе и в знаменателе
5. Запишите это правило на математическом языке (формулой)
6.
7. ) = ).
8 + = +
9. если , то — = —
Творческое задание :
Как разрезать головку сыра на 8 равных частей, выполнив всего лишь три разреза
18 слайд
Решение :
19 слайд
2
8
4
части
частей
16
Великий русский писатель Л.
Н.Толстой писал, что человека можно оценивать дробью, знаменатель которой составляет то хорошее, что думает о себе человек, а числитель – то хорошее, что думают о нём другие люди. А как вы считаете? Правильно ли это ?
Успехов Вам, дорогие ребята и уважаемые коллеги , и, дай вам Бог, мудрости научиться заботиться о своём здоровье и здоровье своих учеников , потому что счастья человека — это здоровье .
Математика, 6 класс: 13-18. Умножение десятичных дробей
13-18. Умножение десятичных дробей
Устный счет
Это надо знать
Умножение десятичной дроби на 10; 100; 1000 и так далее
При умножении десятичной дроби на 10; 100; 1000 и так далее запятую надо перенести вправо на столько знаков, сколько нулей в числе на которое умножаем.Примеры:
5,13 ∙ 10 = 51,3
1,235 ∙ 100 = 123,5
0,56 ∙ 1000 = 560
Умножение десятичной дроби на 0,1; 0,01; 0,001 и так далее
При умножении десятичной дроби на 0,1; 0,01; 0,001и так далее запятую надо перенести влево на столько знаков, сколько цифр после запятой в числе на которое умножаем.
Примеры:
5,13 ∙ 0,1 = 0,513
123,5 ∙ 0,01 = 1,235
0,56 ∙ 0,001 = 0,00056
Умножение десятичных дробей
1. Перемножить десятичные дроби как натуральные числа, не обращая внимание на запятые;
2. В полученном произведении отделить запятой справа столько десятичных знаков, сколько их содержится в обоих множителях вместе;
3. Отбросить нули в конце дробной части (если они есть).
Пример:
5,25 ∙ 0,4 = 2,1
Законы умножения
Переместительный закон умножения
a ∙ b = b ∙ a
Сочетательный закон умножения
a ∙ (b ∙ c) = (a ∙ b) ∙ c
Распределительный закон умножения
a ∙ (b + c) = a ∙ b + a ∙ c
a ∙ (b — c) = a ∙ b — a ∙ c
Видеоурок
youtube.com/embed/rZoA7HjgiE0″ frameborder=»0″ allow=»accelerometer; autoplay; encrypted-media; gyroscope; picture-in-picture» allowfullscreen=»»> Домашнее задание
К уроку 13 (на 20.09)
П. 3.1
1 уровень (учебник)
№ 3.3
№ 3.7
2 уровень (сборник)
№ 1.41 стр. 11
Найдите произведение 1,20689 и числа:
1) 10; 2) 1000; 3) 10 000; 4) 100;
5) 100 000; 6) 100 000 000; 7) 1 000 000 000;
8) 1 000 000; 9) 10 000 000 000.
№ 1.44 стр. 12
На какое число была умножена десятичная дробь 17, 29, если в результате получилось число:
1) 1 729 000; 2) 1 729 000 000; 3) 172 900 000 000?
№ 5.
Периметр треугольника равен 14,4 дм. Длина одной из его сторон на 1 дм больше длины другой и на 1,6 дм меньше третьей стороны. Найдите длины сторон треугольника.
К уроку 14 (на 21.09)
П. 3.2
1 уровень (учебник)
№ 3.18
№ 3.20
2 уровень (сборник)
№ 1.45 стр. 12
На какое число была умножена десятичная дробь 916,1, если в результате получилось число:
1) 0,09161; 2) 0,9161; 3) 0,0009161?
№ 1.47 стр. 13
Найдите произведение 804 и десятичной дроби:
1) 0,001; 2) 0,01; 3) 0,000001; 4) 0,1; 5) 0,0001; 6) 0,00000001.
№ 5.19 стр. 121
Сумма двух чисел равна 124. При делении большего числа на меньшее получается в частном 3 и в остатке 4.
Найдите эти числа.
К уроку 15 (на 22.09)
П. 3.3
1 уровень (учебник)
№ 3.31
№ 3.35
2 уровень (сборник)
№ 1.56 стр. 14
Найдите произведение чисел:
1) 4,8 ∙ 12,9; 2) 90,8 ∙ 0,15; 3) 62,07 ∙ 2,48.
№ 1.60 стр. 15
Используя верное равенство 612 ∙ 78 = 47 736, найдите значение выражения:
1) 6,12 ∙ 7,8; 2) 0,612 ∙ 7,8; 3) 0,0612 ∙ 0,78; 4) 0,00612 ∙ 7,8;
5) 0,000612 ∙ 0,078; 6) 0,00612 ∙ 0,00078.
№ 5.4 стр. 118
Во время ремонта планируется выложить кафельной плиткой пол на кухне. Для этого куплено 150 штук кафельной плитки для пола размером 25 см на 25 см каждая. Хватит ли этой плитки, чтобы выстелить пол на кухне площадью 9,35 м2
К уроку 16 (на 23.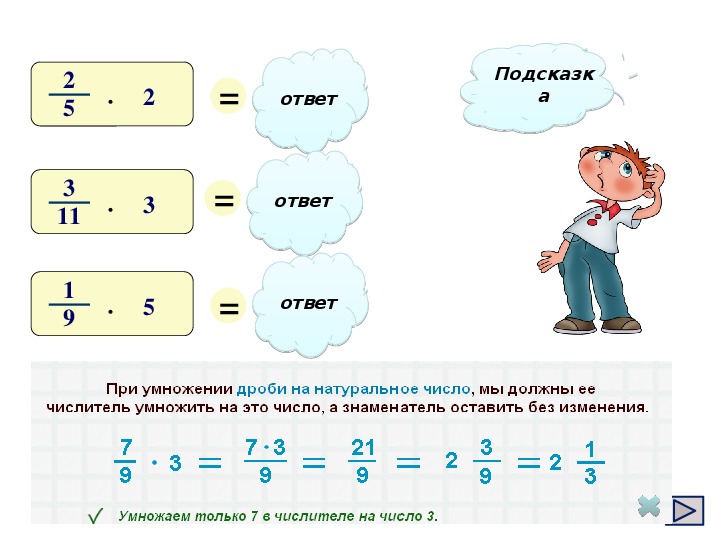
09)
П. 3.3
1 уровень (учебник)
№ 3.37 (1-4)
№ 3.39
2 уровень (сборник)
№ 1.59 стр. 15
Вычислите:
1) 1,23 ∙ 5,7; 2) 0,43 ∙ 4,91; 3) 15,74 ∙ 0,035; 4) 7,64 ∙ 22,3;
5) 0,0801 ∙ 14,35; 6) 9,041 ∙ 0,0042.
№ 5.48 стр. 126
Два комбайна, работая вместе, могут выполнить задание за 6 часов. Первый комбайн, работая один, может выполнить задание за 10 часов. За сколько часов может выполнить это задание второй комбайн, работая один?
К уроку 17 (на 26.09)
П. 3.3
1 уровень (учебник)
№ 3.53 (1-4)
№ 3.55
2 уровень (сборник)
№ 1.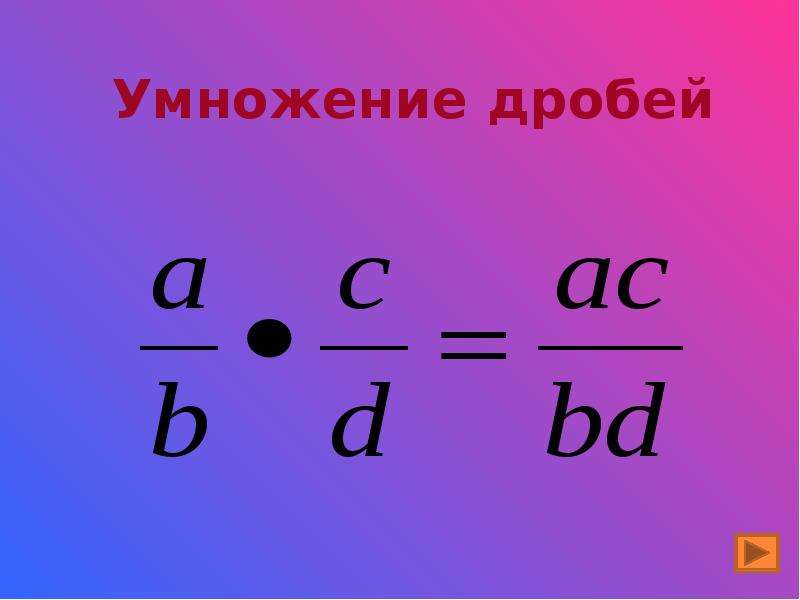
63 стр. 15
Найдите 0,15 от числа:
1) 23; 2) 8; 3) 4,2; 4) 0,76; 5) 105,22; 6) 6045,38.
№ 5.58 стр. 127
На одну чашу весов положили кусок хозяйственного мыла, на другую — 0,6 такого же куска и, чтобы уравновесить весы, гири массой 0,6 кг. Найдите массу одного куска хозяйственного мыла.
К уроку 18 (на 27.09)
П. 3.4
1 уровень (учебник)
№ 3.63
№ 3.73 (1-4)
2 уровень (сборник)
№ 1.58 стр. 14
Выполните действия:
1) 6,482 ∙ 10 ∙ 3,05; 2) 0,001 ∙ 4,28 ∙ 35; 3) 5,094 ∙ 100 ∙ 0,401; 4) 10 000 ∙ 0,0519 ∙ 0,034.
№ 5.60 стр. 128
На вопрос, сколько у него учеников, Пифагор ответил: «Половина моих учеников изучает математику, четверть — изучает природу, восьмая часть — проводит время в молчаливом размышлении, остальную часть составляют три девы».
Сколько учеников было у Пифагора?
Подписаться на: Сообщения (Atom)
Умножение дробей — УРОКИ МАТЕМАТИИ КЕЙТ
Сопутствующие ресурсы: Boom Cards (цифровые карточки с заданиями), Что означает умножение на дробь?Когда вы умножаете число на дробь, вы находите часть этого числа. Например, если вы умножите 6 на 1/2, вы найдете 1/2 от 6. | Добро пожаловать на уроки математики Кейт! |
Мы можем сделать это, проведя горизонтальную линию посередине прямоугольника. 1/2 от 1/4 составляет половину заштрихованной части.
Вы видите ярлык, который мы могли бы использовать? Чтобы найти ответ без диаграммы, мы можем перемножить числители вместе (1 x 1 = 1) и умножить вместе знаменатели (2 x 4 = 8), чтобы получить ответ.
Давайте рассмотрим еще один пример, чтобы увидеть, применимо ли это сокращение. Допустим, у нас есть 2/3 умножить на 4/5. Это означает, что нам нужно 2/3 дроби 4/5. Начнем с картинки 4/5. 4/5 означает, что целое было разделено на 5 равных частей, и у нас есть 4 из 5 равных частей.
Если мы хотим найти 2/3 от 4/5, это означает, что нам нужно найти 2/3 заштрихованной части выше. Для этого мы можем разбить прямоугольник на 3 равные строки. Чтобы найти 2/3, нам нужны 2 строки из 3.
Так что же такое 2/3 от 4/5? Когда мы разделили коробку на 3 ряда, мы образовали прямоугольник размером 5 х 3. Это дает нам в общей сложности 15 равных частей. Нам нужны только 2/3 заштрихованной части, поэтому нам нужно подсчитать только то, что заштриховано в 2 из 3 рядов (внутри фиолетового прямоугольника, показанного выше). Мы видим, что это дает нам 8 одинаковых частей из 15: 8/15.
Вы видите ярлык? Чтобы найти ответ, мы можем перемножить числители вместе (2 х 4 = 8) и умножить знаменатели вместе (3 х 5 = 15).
Как умножать дроби
Вам не нужно рисовать каждый раз, когда вы перемножаете две дроби. Вместо этого используйте ярлык. Чтобы умножить дроби вместе, вы просто умножаете прямо. Перемножьте числители вместе.
Затем умножьте знаменатели вместе. Наконец, упростите свой ответ, если это необходимо.
15 и 56 не имеют общих делителей, кроме 1, поэтому дробь не нужно упрощать. Вот пример, где дробь можно упростить:
Есть еще один вариант, который может быть проще. Вместо упрощения в конце можно упростить в начале. Если вы сначала упростите, может быть легче увидеть общие факторы с меньшими числами в начале.
Не имеет значения, упростите ли вы первое или последнее, вы получите один и тот же ответ. Выберите способ, который кажется вам самым простым.
Умножение дробей на целые числа
Что делать, если только одно число является дробью, а другое — целым числом? Превратите целое число в дробь, используя 1 в качестве знаменателя. Деление на 1 не меняет числа, поэтому любое целое число можно переписать с 1 в знаменателе. После того, как вы записали целое число в виде дроби, вы можете выполнить шаги по умножению дробей.
Умножение на смешанное число
Одно или оба числа, которые вы умножаете, могут быть смешанными числами.
Прежде чем умножать, запишите смешанное число как неправильную дробь. Остальные шаги будут такими же.
Видео
Хотите увидеть еще один пример? Посмотрите короткое видео ниже.
Практика
Готовы решить некоторые задачи самостоятельно? Нажмите кнопку СТАРТ ниже, чтобы пройти пробный тест.
Работает на Interact |
Хотите научиться складывать дроби?
Что такое правило умножения вероятности? (Видео и практика)
TranscriptPractice
Привет! Добро пожаловать в это видео о правиле умножения вероятности!
Чтобы освежить вашу память, вероятность — это мера того, насколько вероятно, что данное событие произойдет.
Осознаете вы это или нет, но каждый божий день вы используете вероятность, чтобы делать выбор и принимать решения в своей повседневной жизни.
Например, если вы просыпаетесь с 80-процентной вероятностью дождя, вы, скорее всего, возьмете с собой на работу зонтик. Питчер, столкнувшийся с отбивающим со средним показателем 0,347, скорее всего, будет подавать осторожно и стратегически.
«Вероятность дождя 80 %» — это еще один способ сказать, что из 100 дней с такой конкретной погодой 80 дней, скорее всего, будут идти с дождем. Среднее количество ударов 0,347 указывает на то, что отбивающий в среднем наносит 347 ударов из 1000 ударов летучими мышами.
Это просто вероятности одного события. Чтобы определить вероятность возникновения нескольких событий, нам нужно использовать правило умножения вероятности. Чтобы понять это правило, нам нужно глубже погрузиться в область вероятностей.
Независимые и зависимые события
Во-первых, важно различать независимые и зависимые события.
Два события независимы друг от друга, если появление первого не влияет на второе. Например, монету можно подбросить дважды, но независимо от того, какая сторона выпадет после первого подбрасывания, при втором подбрасывании шанс выпадения орла или решки составляет 50/50.
В отличие от этого, предположим, что вы делаете два выбора из стандартной колоды карт и выбираете туза при первом выборе, не возвращая его обратно в колоду. Вероятность вашего второго выбора изменилась, потому что теперь у вас на одну карту меньше в колоде. Эти два выбора будут зависимыми, поскольку первый из них оказывает влияние и влияет на вероятность второго выбора.
Исходя из этого, давайте копнем глубже и исследуем еще один элемент вероятности — что, если вы хотите определить вероятность двух событий, происходящих в последовательности?
Определение вероятности нескольких событий
Пример 1
В качестве примера предположим, что у вас есть традиционный шестигранный кубик и вы хотите определить вероятность выпадения 2 при первом броске И 3 при втором броске.
Поскольку каждое число появляется на кубике только один раз, мы знаем, что вероятность выпадения 2 равна 1 из 6. Помните, что, поскольку числа на кубике не меняются независимо от того, сколько раз его бросают, выпадение кости будут считаться независимыми событиями.
Следовательно, вероятность выпадения 3 при втором броске также равна 1 из 6.
Но как вычислить вероятность ОБОИХ событий? Чтобы ответить на этот вопрос, воспользуемся правилом умножения вероятности.
Это правило гласит, что если вы хотите найти вероятность того, что произойдут как событие A, так и событие B, вы должны умножить вероятность события A на вероятность события B.
В нашем примере событие A будет вероятностью выпадение 2 при первом броске, то есть \(\frac{1}{6}\). Событие B будет выбрасывать 3 при втором броске, вероятность которого также равна \(\frac{1}{6}\).
Следовательно, чтобы найти вероятность того, что произойдут оба этих события, мы возьмем вероятность события A и умножим ее на вероятность события B.
\(\frac{1}{6} \times \frac {1}{6}\)
Умножение числителей даст нам 1, а умножение знаменателей даст нам 36, что даст нам ответ 1 на 36.
\(\frac{1}{ 6} \times \frac{1}{6}= \frac{1}{36}\)
Это означает, что, по всей вероятности, человек будет выбрасывать 2, а затем 3 один раз в каждые 36 попытки.
Пример 2
Рассмотрим другой пример.
Допустим, у вас есть стандартная колода карт, и вы хотите определить вероятность того, что сначала выпадет король червей, а затем любая карта червовой масти.
Давайте рассмотрим эту задачу по одному событию за раз.
Первое событие — розыгрыш червового короля. Мы знаем, что в стандартной колоде 52 карты, и в каждой колоде есть только один король червей. Следовательно, вероятность вытянуть короля червей равна \(\frac{1}{52}\).
Теперь давайте рассмотрим второе событие — вытягивание одной из оставшихся карт червовой масти. Помните, что второе событие является зависимым событием. Это означает, что он должен отражать изменения обстоятельств, вызванные первым событием.
Вот что я имею в виду: Обычно в колоде 13 карт каждой масти. Но так как червового короля мы уже вытащили, то в червовой масти осталось всего 12 карт. Если мы запишем нашу вероятность в виде дроби, это даст нам 12 в нашем числителе для 12 оставшихся червей.
И хотя в стандартной колоде обычно 52 карты, поскольку мы уже вынули одну карту, осталась только 51 карта. Это дает нам 51 в нашем знаменателе и вероятность \(\frac{12}{51}\) для второго события.
Следуя правилу умножения, мы должны умножить \(\frac{1}{52}\) и \(\frac{12}{51}\).
\(\frac{1}{52} \times \frac{12}{51}\)
Умножение числителей даст нам 12, а умножение знаменателей, 52 и 51, даст нам 2652, что дает нам вероятность \(\frac{12}{2652}\). Поскольку и числитель, и знаменатель являются четными числами, мы знаем, что их можно упростить, по крайней мере, разделив оба на 2. В этом случае мы действительно можем разделить оба на 12, что даст нам окончательный ответ \(\frac{1} {221}\). Это означает, что вероятность вытянуть короля червей, за которым следует еще одна карта червовой масти, будет один раз на каждые 221 попытку.
Итак, помните, чтобы определить вероятность возникновения нескольких событий, просто умножьте вероятность события A на вероятность события B, по возможности упрощая дроби.
Надеюсь отзыв был полезен! Спасибо за просмотр и удачной учебы!
Таблица умножения и печатные формы
Практические вопросы
Вопрос №1:
Какой сценарий описывает два независимых события?
Неоплата счета за электроэнергию, а затем отключение электричества.
Незаконная парковка, а затем получение парковочного талона.
Сначала посадка в самолет, а потом поиск хорошего места.
Завести собаку, а потом посадить цветник.
Показать Ответ
Ответ:
Зависимые события описывают ситуации, когда первое событие оказывает прямое влияние на второе событие. Например, если вы припарковались неправильно, в результате вы, скорее всего, получите штраф. Первое событие влияет на второе событие. Только один предоставленный сценарий является примером независимых событий.
Посадка цветника не зависит от того, есть ли у вас собака. Два события независимы друг от друга.
Скрыть ответ
Вопрос №2:
Определите вероятность того, что на обычном игральном кубике выпадет шестерка, а затем пятерка.
\(\frac{1}{6}\)
\(\frac{2}{6}\)
\(\frac{1}{36}\)
\(\frac{2 }{36}\)
Показать ответ
Ответ:
При определении вероятности двух или более событий вероятность первого события можно умножить на второе событие. В этом примере вероятность выпадения шестерки равна \(\frac{1}{6}\), а вероятность выпадения пятерки также равна \(\frac{1}{6}\). Правило умножения вероятности гласит, что \(\frac{1}{6}\times\frac{1}{6}\) будет вероятностью того, что произойдут оба события: \(\frac{1}{6}\times \frac{1}{6}=\frac{1}{36}\)
Скрыть ответ
Вопрос №3:
Определите вероятность того, что выпадет нечетное число, а затем число больше семи.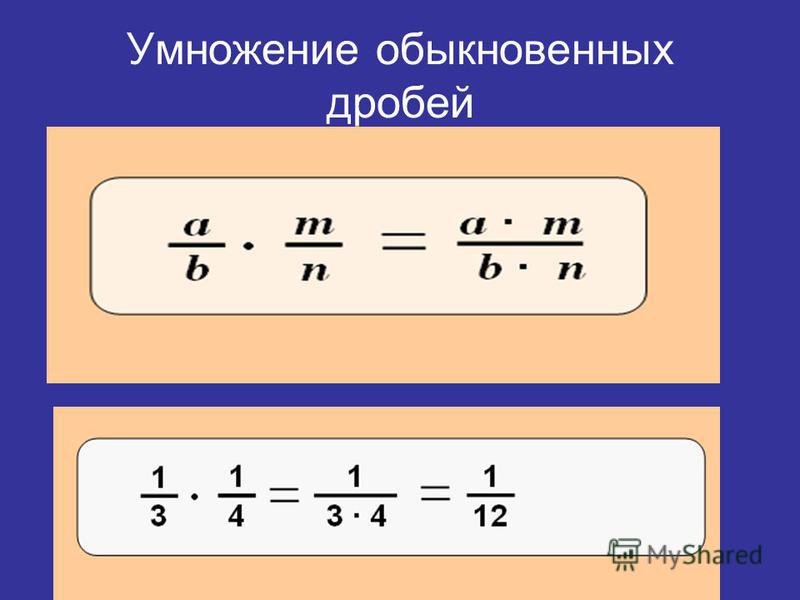
\(\frac{1}{10}\)
\(\frac{2}{10}\)
\(\frac{1}{9}\)
\(\frac{ 3}{3}\)
Показать ответ
Ответ:
Для решения этой задачи можно использовать правило умножения вероятности. Вероятность выпадения нечетного числа равна \(\frac{5}{10}\), а вероятность выпадения числа больше семи равна \(\frac{2}{10}\). Когда эти две вероятности перемножаются, мы видим, что наш ответ равен \(\frac{10}{100}\), или в простейшей форме \(\frac{1}{10}\).
Скрыть ответ
Вопрос № 4:
В классе из 30 учеников 8 учеников занимаются в кружке искусств, 12 учеников в драматическом кружке и 17 учеников в футбольном клубе. Какова вероятность случайного выбора студента, который участвует в драматическом кружке?
\(\frac{2}{5}\)
\(\frac{15}{6}\)
\(\frac{5}{3}\)
\(\frac{12 }{35}\)
Показать Ответ
Ответ:
В драмкружке 12 учеников, всего 30 учеников.