1 класс математика примеры: Тренажеры по математике 1 класс. Примеры на сложение и вычитание, задачи

5000 заданий по математике. 1 класс

Электронная библиотека

Воспитывая детей, нынешние родители воспитывают будущую историю нашей страны, а значит и историю мира.

— А.С. Макаренко

---

	Авторы: Л.П. Николаева, И.В. Иванова
	Название: 5000 заданий по математике. 1 класс
	Формат: PDF (в zip-архиве)
	Размер: 31,7 Мб
	Объём: 25 стр.
	Аннотация:
Выработка чёткого алгоритма вычислений Создание условий успешного усвоения материала Устойчивость навыка решения задач и уравнений Совершенствование техники вычислений Базовый уровень умений и навыков Быстрота принятия решения Развитие внимания и памяти Самостоятельность

Просмотров: 168762

Говорят Дети

«Для организма нужны белки, жиры, углеводы и обнимашки» — Катя, 7 лет

Рекомендуем

Прописи для детей

	Подготовка к школе
	Развитие моторики рук
	Обучение письму
	Интересные задания
	Современные методики

Новинки

• Речевые игры с лего
• Нейрологопедические прописи. Учимся читать и развиваем речь
• Стань буквой! Динамические паузы при обучении грамоте дошкольников и младших школьников
• Скорочтение для детей и не только
• Вся базовая английская лексика. Справочник в виде карт памяти

---

 

Политика конфиденциальности

Тренажеры по математике 1 класс. Примеры на сложение и вычитание, задачи — «Семья и Школа»

Содержание

Примеры по математике на деление для 3 класса | контрольные, примеры для детей

Учим детей » Математика

Не все дети 3 класса хорошо понимают тему деления числа. Для того, чтобы ребенок лучше усвоил материал, нужно постоянно решать примеры на деление. Так он повторит правила на умножение и деление, а также приобретет навыки решения подобных примеров. На нашем сайте можно распечатать примеры на деления для 3 класса бесплатно.

Тема: Деление двухзначного числа на однозначное

1. Реши примеры на деление (для детей 3 класса)

28 : 7 =	27 : 9 =	28 : 4 =
54 : 9 =	56 : 7 =	56 : 8 =
36 : 6 =	64 : 8 =	63 : 9 =
45 : 5 =	42 : 6 =	25 : 5 =

примеры деление 3 класс

36 : 4 =	27 : 9 =	72 : 9 =
18 : 6 =	36 : 3 =	91 : 7 =
15 : 3 =	10 : 10 =	10 : 5 =
81 : 9 =	9 : 3 =	50 : 5 =

примеры деление 3 класс

2. Выполни деление и проверь результат умножением.

12 : 6 =	24 : 4 =	14 : 2 =
20 : 10 =	60 : 15 =	40 : 8 =

примеры деление 3 класс

2.

Реши примеры. Внимательно выполняй последовательность действий.

72 : 9 + 22 * 5 — 28 : 7 =
36 — 81 : 9 + 12 : 2 * 7 =
20 + 7 * 5 — 48 : 12 =
90 : 30 — 34 + 11 * 4 =

3. Реши примеры на деление (для детей 3 класса)

90:3=
76:2=
46:3=
81:4=
100:25=
54:3=
74:2=
66:33=
90:30=
66:22=
36:2=
46:3=
99:11=
80:2=
88:4=
84:2=
100:20=
56:2=

4. Примеры с элементами деления. Запиши заданные предложения в виде примеров и реши их.

1. К числу 34 прибавь частное чисел 40 и 5.
3.2. К числу 33 прибавь частное чисел 33 и 11.
3.3. Из числа 42 вычти частное чисел 54 и 5.
3.3. Из числа 90 вычти частное чисел 64 и 8.

5. Сравни выражения и поставь знак >, < или = :

7 * 3 + 7 (?) 7 * 5

3 * 5 — 5 (?) 3 * 4

8 * 4 — 8 (?) 8 * 3

3 * 6 + 6 (?) 3 * 5

6 * 5 — 6 (?) 6 * 4

7 * 2 + 7 (?) 7 * 4

6.

Реши сложные примеры на деление (тренажер деления)

40:20=
96:8=
46:2=
75:25=
80:2=
100:2=
78:6=
90:18=
34:17=
85:17=

85:17=
80:16=
84:7=
32:4=
99:9=
48:4=
72:3=
96:6=
26:2=
84:6=

7. Примеры для распечатки для урока 3 класса

Порядок действий в примерах со скобками: попробуйте решить простой пример

Англоязычный Twitter облетела старая задачка по математике, которая разделила пользователей на несколько враждующих лагерей. Однако, ничего удивительного здесь нет, ведь правильное решение примеров по действиям со скобками всегда непросто отыскать, особенно если вы давно закончили школу. Хватит ли у вас смекалки и знаний базовой математики, чтобы пройти это испытание, посильное для младшеклассника, но непреодолимое для взрослого?

Юлиана Качанова Отвечаю за тесты

Twitter: 1RealMir

Решить пример со скобками по действиям пытались многие комментаторы твиттера, при этом используя самые разные, в том числе и несуществующие, математические приемы.

Известный новозеландский актёр Тайка Вайтити, знакомый отечественным кинозрителям по фильму «Реальные упыри», принял участие в данном интернет-споре, но к сожалению, не стал «отличником», решившим задачу правильно. Его, как и большинство других участников, подвело знание порядка действий сложных примеров со скобками.

Если вы считаете что хорошо помните последовательность действий в примерах со скобками, то попробуйте дать правильный ответ:

Не торопитесь давать ответ: правила хотя бы вспомните!

ВОПРОС 1 ИЗ 1

3

17

21

Главное – не торопитесь! В математике порядок действий примеров со скобками имеет огромное значение. «Дорожная карта» для того, чтобы правильно решить тот, или иной пример выглядит следующим образом:

• Внимательно посмотрите на пример и сначала произведите действие, которое указано в скобках.
• Запомните: порядок выполнения действий в примерах со скобками отдаёт предпочтение умножению и делению. Их называют действиями первой ступени.
• Последними выполняются сложение и вычитание. Это действия второй ступени.

Такая последовательность действий в примере со скобками выбрана не случайно и позволяет без особых затруднений получить правильный ответ.

Для закрепления рассмотрим следующий пример действия со скобками:

5+(7−2⋅3)⋅(6−4):2

В этом сложном примере со скобками порядок действий будет точно таким же.

Сначала мы вычислим значение первой скобки. Для этого сначала нужно выполнить умножение 2 на 3, как действие первой ступени, а затем вычесть из 7 полученное произведение. Получится 7-6=1
После этого мы переходим ко второй скобке. Если в первой скобке у нас был пример с умножением и вычитанием в ней, то здесь у нас только вычитание: 6-4=2

Давайте подставим решение примеров в скобках в первоначальное выражение:

5+(1)⋅(2):2 . 

Здесь уже сложных примеров со скобками нет, мы оставили их просто для визуального понимания, какое число по итогам наших манипуляций получилось.

Порядок действий в примерах со скобками (как впрочем и без них) требует от нас сначала выполнения умножения и деления, а затем сложения и вычитания. Продолжаем соблюдать его и получаем что сначала мы должны умножить 1 на 2, а затем поделив её на 2 прибавить разность к 5:

5+1⋅2:2=6

Таким образом первоначальный пример со скобками также будет равняться 6

5+(7−2⋅3)⋅(6−4):2=6.

ENG 1001: Предложения: простые, составные и сложные

Общим недостатком письменной речи является отсутствие разнообразных предложений. Осознание из трех основных типов предложений — простых, составных и сложных — может помочь вам варьировать предложения в вашем письме.

Самое эффективное письмо использует Разновидность типы предложений, описанные ниже.

1. Простые предложения

Простое предложение содержит самые основные элементы, которые делают его предложение: подлежащее, глагол и законченная мысль.

Примеры простых предложений включают следующее:

1. Джо ждал поезда.
   «Джо» = подлежащее, «ждал» = глагол
    
2. Поезд опоздал.
   «Поезд» = подлежащее, «был» = глагол
    
3. Мэри и Саманта сели на автобус.
   «Мэри и Саманта» = составное подлежащее, «брал» = глагол
    
4. Я искал Мэри и Саманту на автобусной остановке.
   «Я» = подлежащее, «посмотрел» = глагол
    
5. Мэри и Саманта прибыли на автобусную станцию ​​рано, но ждали до полудня на автобусе.
   «Мэри и Саманта» = составное подлежащее, «прибыл» и «waited» = составной глагол  

Совет

. Если вы используете много простых предложений в эссе, подумайте над тем, чтобы пересмотреть некоторые из них. предложений в составные или сложные предложения (поясняется ниже).

использование составных подлежащих, составных глаголов, предложных фраз (таких как «на автовокзале») и другие элементы помогают удлинить простой предложения, но простые предложения часто бывают короткими. Использование слишком большого количества простых предложения могут сделать письмо «прерывистым» и могут помешать письму течет плавно.

Простое предложение может также называться самостоятельным предложением . Это называется «независимым», потому что, хотя он может быть частью составное или сложное предложение, оно также может стоять само по себе как полное предложение.
 

2. Составные предложения

Составное предложение относится к предложению, состоящему из двух независимых предложения (или полные предложения), связанные друг с другом с помощью

координирующего соединение . Сочинительные союзы легко запомнить, если подумать о слова «FAN BOYS»:

• Ф или
• А и
• N или
• Б ут
• О р
• Y и
• С или

Примеры составных предложений включают следующее:

1. Джо ждал поезд, но поезд опоздал.
    
2. Я искал Мэри и Саманту на автовокзале, но они прибыли на вокзал раньше полдень и ушел на автобус до моего приезда.
    
3. Мэри и Саманта прибыли на автовокзал до полудня, и они уехали на автобус до моего приезда.
    
4. Мэри и Саманта ушли на автобус до моего приезда, так я их на автовокзале не видел.

Совет : Если в эссе вы часто используете сложные предложения, вам следует подумать о том, чтобы преобразовать некоторые из них в сложные предложения (поясняется ниже).

Сочинительные союзы полезны для соединения предложений, но составные предложения часто злоупотребляют. В то время как сочинительные союзы могут указывать на некоторые тип отношения между двумя независимыми частями в предложении, они иногда не указывают на большую часть отношений. Слово «и» для например, только добавляет одно независимое предложение к другому, не указывая, как две части предложения логически связаны. Слишком много сложных предложений, которые использование «и» может ослабить написание.

Более четкие и конкретные отношения могут быть установлены с помощью сложные предложения.
 

3. Сложные предложения

Сложное предложение состоит из независимого предложения и одного или нескольких

связанных с ним зависимых пунктов . А зависимое предложение похоже на независимое предложение или полное предложение, но в нем отсутствует один из элементов, которые сделали бы его законченным предложением.

Примеры зависимых статей включают следующее:

• , потому что Мэри и Саманта прибыли на автовокзал до полудня
• пока он ждал на вокзале
• после того, как они уехали на автобусе

Зависимые предложения, подобные приведенным выше , не могут стоять отдельно как предложение, но их можно добавлять к независимое предложение, образующее сложное предложение.

Зависимые предложения начинаются с подчинительных союзов . Ниже приведены некоторые из наиболее распространенных подчинительных союзов:

• после
• хотя
• как
• потому что
• до
• хотя
• если
• с
• хотя
• кроме
• до
• когда
• всякий раз, когда
• тогда как
• где
• , а

Сложное предложение объединяет независимое предложение с одним или несколькими зависимыми предложениями.

Зависимое предложение может идти первым в предложении, за которым следует независимое предложение, как в следующем:

Совет : Когда зависимое предложение идет первым, для разделения двух предложений следует использовать запятую.

1. Поскольку Мэри и Саманта прибыли на автовокзал до полудня, я не увидел их на вокзале.
2. Ожидая на вокзале, Джо понял, что поезд опаздывает.
3. Выехав на автобусе, Мэри и Саманта поняли, что Джо ждет их на вокзале.

И наоборот, независимые предложения могут идти первыми в предложении, а за ними — зависимое предложение, как в следующем примере:

Совет : Когда независимое предложение стоит первым, для разделения двух предложений следует использовать запятую , а не .

1. Я не видел их на вокзале, потому что Мэри и Саманта прибыли на автовокзал до полудня.
2. Джо понял, что поезд опаздывает, пока он ждал на вокзале.
3. Мэри и Саманта поняли, что Джо ждал на вокзале после того, как они уехали в автобусе.

Сложные предложения часто более эффективны, чем сложные предложения, потому что сложное предложение указывает на более четкие и конкретные отношения между главными частями предложения. Слово «прежде» например, сообщает читателям, что одно происходит раньше другого. Такое слово, как «хотя» передает более сложные отношения, чем такое слово, как «и».

Термин периодическое предложение используется для обозначения сложного предложения, начинающегося с зависимого предложения и заканчивающийся независимым предложением, например: «Пока он ждал на вокзале, Джо понял, что поезд опаздывает».

Периодические предложения могут быть особенно эффективными, потому что завершенная мысль возникает в конец этому, так что первая часть предложения может доходить до значения, которое приходит в конце.

Предложения, начинающиеся с «И» или «Потому что»

Следует ли начинать предложение с «и» или «но» (или с одной из других координирующих союзы)?

Короткий ответ — «нет». Вы должны избегать начала предложения с «и», «или», «но» или другого сочинительные союзы. Эти слова обычно используются для соединения частей предложения, а не начинать новое предложение.

Однако такие предложения можно эффективно использовать. Поскольку предложения, начинающиеся с этих слов, выделяются, они иногда используются для выделения. Если вы используете предложения, начинающиеся с одного из сочинительных союзов, вы должны использовать эти предложения экономно и осторожно.

Следует ли начинать предложение со слова «потому что»?

Нет ничего плохого в том, чтобы начинать предложение со слова «потому что».

Возможно, некоторым учащимся говорят не начинать предложение со слова «потому что», чтобы избежать фрагментов предложения. (что-то вроде «Потому что Мэри и Саманта приехали на автовокзал до полудня» — это фрагмент предложения), но это совершенно верно. допустимо начинать предложение со слова «потому что», если предложение завершено (например, «Потому что Мэри и Саманта прибыли в автовокзала до полудня, я их на вокзале не видел».)

Смотри!

Комплексное число — определение, формула, свойства, примеры

Комплексные числа помогают найти квадратный корень из отрицательных чисел. Концепция комплексных чисел была впервые упомянута в I веке греческим математиком Героем Александрийским, когда он пытался найти квадратный корень из отрицательного числа. Но он просто изменил отрицательное значение на положительное и просто взял числовой корень. Кроме того, реальная идентичность комплексного числа была определена в 16 веке итальянским математиком Джероламо Кардано в процессе нахождения отрицательных корней кубических и квадратичных полиномиальных выражений.

Комплексные числа находят применение во многих научных исследованиях, обработке сигналов, электромагнетизме, гидродинамике, квантовой механике и анализе вибрации. Здесь мы можем понять определение, терминологию, визуализацию комплексных чисел, свойства и операции с комплексными числами.

1.	Что такое комплексные числа?
2.	График комплексных чисел
3.	Свойства комплексных чисел
4.	Операции над комплексными числами
5.	Алгебраические тождества комплексных чисел
6.	Решенные примеры
7.	Практические вопросы
8.	Часто задаваемые вопросы о комплексных числах

Что такое комплексные числа?

Комплексное число – это сумма действительного числа и мнимого числа. Комплексное число имеет вид a + ib и обычно обозначается буквой z. Здесь и a, и b – действительные числа. Величина «а» называется действительной частью, которая обозначается Re(z), а «b» называется мнимой частью Im(z). Также ib называют мнимым числом.

 

 

 

 

 

 

 

 

Примеры комплексных чисел: \(2+3i, -2-5i, \,\,\dfrac 1 2 + i\dfrac 3 2\) и т. д.

Степень of i

Алфавит i называется йотой и полезен для представления мнимой части комплексного числа. Кроме того, йота (i) очень полезна для нахождения квадратного корня из отрицательных чисел. У нас есть значение i ²  = -1, и оно используется для нахождения значения √-4 = √i ² 4 = 9. 0337 + 2i Значение i ²  = -1 является основным аспектом комплексного числа. Давайте попробуем понять больше о возрастающих силах i.

• я = √-1
• я ²  = -1
• i ³   = i.i ²  = i(-1) = -i
• i ⁴  = (i ² ) ²  = (-1) ²  = 1
• i ⁴ⁿ  = 1
• я ^{4n + 1}  = я
• i ^{4n + 2}  = -1
• i ^{4n + 3}  = -i

Графики комплексных чисел

Комплексное число состоит из действительной и мнимой частей, которые можно рассматривать как упорядоченную пару (Re(z), Im(z)) и представлять в виде точек координат на евклидовой плоскости. Евклидова плоскость применительно к комплексным числам называется комплексной плоскостью или Плоскостью Аргана, названной в честь Жана-Роберта Аргана. Комплексное число z = a + ib представлено действительной частью — a относительно оси x и мнимой частью -ib относительно оси y. {-1}\frac{b}{a}\). 9{-1}\frac{b}{a}\)).

Свойства комплексного числа

Следующие свойства комплексных чисел помогают лучше понять комплексные числа, а также выполнять различные арифметические операции над комплексными числами.

Сопряжение комплексного числа

Сопряжение комплексного числа образуется путем взятия той же действительной части комплексного числа и замены мнимой части комплексного числа на ее аддитивную обратную. Если сумма и произведение двух комплексных чисел являются действительными числами, то они называются сопряженными комплексными числами. Для комплексного числа z = a + ib его сопряженным является \(\bar z\) = a — ib.

Сумма комплексного числа и его сопряженного равна \(z + \bar z\)  = (a + ib) + (a — ib) = 2a, а произведение этих комплексных чисел \(z.\bar z \) = (a + ib) × (a — ib) = a ²  + b ² .

Обратная величина комплексного числа

Обратная величина комплексных чисел полезна в процессе деления одного комплексного числа на другое комплексное число. {-1}\).

Равенство комплексных чисел

Равенство комплексных чисел аналогично равенству действительных чисел. Два комплексных числа \(z_1 = a_1 + ib_1\) и \(z_2 = a_2 + ib_2 \) называются равными, если относительная часть обоих комплексных чисел равна \(a_1 = a_2\),  и мнимая части обоих комплексных чисел равны \(b_1 = b_2 \). Кроме того, два комплексных числа в полярной форме равны тогда и только тогда, когда они имеют одинаковую величину, а их аргумент (угол) отличается на целое кратное 2π.

Упорядочивание комплексных чисел

Упорядочивание комплексных чисел невозможно. Действительные числа и другие связанные системы счисления можно упорядочить, но нельзя упорядочить комплексные числа. Комплексные числа не имеют структуры упорядоченного поля, и нет упорядоченности комплексных чисел, совместимой со сложением и умножением. Также нетривиальная сумма квадратов в упорядоченном поле есть число \(\neq 0\), а в комплексном числе нетривиальная сумма квадратов равна i ²  + 1 ²  = 0. Комплексные числа можно измерить и представить на двумерной арграндовой плоскости по их величине, которая является расстоянием от начала координат.

Формула Эйлера: В соответствии с формулой Эйлера для любого действительного значения θ мы имеем e ^iθ  = Cosθ + iSinθ, и оно представляет комплексное число в координатной плоскости, где Cosθ – действительная часть, представленная относительно ось x, Sinθ – мнимая часть, представленная относительно оси y, θ – угол, образованный по отношению к оси x и воображаемой линии, соединяющей начало координат и комплексное число. Согласно формуле Эйлера и функциональному представлению x и y имеем e ^{x + iy}  = e ^x (уютный + isiny) = e ^x уютный + т.е. ^x Siny. Это разлагает экспоненциальную функцию на ее действительную и мнимую части.

Операции над комплексными числами

Различные операции сложения, вычитания, умножения, деления натуральных чисел можно выполнять и для комплексных чисел.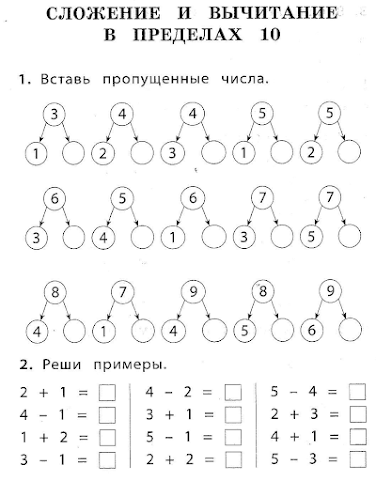 Детали различных арифметических операций с комплексными числами заключаются в следующем.

Сложение комплексных чисел

Сложение комплексных чисел аналогично сложению натуральных чисел. Здесь в комплексных числах действительная часть добавляется к действительной части, а мнимая часть добавляется к мнимой части. Для двух комплексных чисел вида \(z_1 = a + id\) и \(z_2 = c + id\) сумма комплексных чисел \(z_1 + z_2 = (a + c) + i(b + d) \). Комплексные числа следуют всем следующим свойствам сложения.

• Закон замыкания: Сумма двух комплексных чисел также является комплексным числом. Для двух комплексных чисел \(z_1\) и \(z_2\) сумма \(z_1 + z_2\) также является комплексным числом.
• Коммутативный закон: Для двух комплексных чисел \(z_1\), \(z_2\) имеем \(z_1 + z_2 = z_2 + z_1\).
• Ассоциативный закон: Для данных трех комплексных чисел \(z_1, z_2, z_3\) имеем \(z_1 + (z_2 + z_3) = (z_1 + z_2)+z_3 \). 2 = -1\). Для двух комплексных чисел \(z_1\) = a + ib, \(z_2\) = c + id произведение равно \(z_1.z_2\) = (ca — bd) + i(ad + bc).

  Умножение комплексных чисел в полярной форме немного отличается от упомянутой выше формы умножения. Здесь абсолютные значения двух комплексных чисел перемножаются, а их аргументы складываются для получения произведения комплексных чисел. Для комплексных чисел \(z_1 = r_1(Cos\theta_1 + iSin\theta_1)\) и  z ₂  = \(z_2 = r_1(Cos\theta_2 + iSin\theta_2)\) произведение комплексные числа \(z_1.z_2 = r_1.r_2(Cos(\theta_1 + \theta_2) + iSin(\theta_1 + \theta_2))\). 92 + 2z_1z_2 +2z_2z_3 +2z_3z_1\)

Связанные темы:

• Комплексное сопряжение
• Калькулятор комплексных чисел
• Тригонометрия
• Координатная плоскость
• Координатная геометрия

Комплексные числа Советы и подсказки:

• Все действительные числа являются комплексными числами, но все комплексные числа не обязательно должны быть действительными числами.
• Все мнимые числа являются комплексными числами, но все комплексные числа не обязательно должны быть мнимыми числами. 9{2}-4(1)(1)}}{2(1)} \\[0,2 см]
  &=\frac{-1 \pm \sqrt{-3}}{2}\\[0,2 см]
  \text{Здесь } &\sqrt{-3} = \sqrt{-1} \times \sqrt{3} = i \sqrt{3}\\[0,2 см]
  x&= \frac{-1 \pm i\sqrt{3}}{2}\\[0,2 см]
  \end{align} \]

  Таким образом, корнями данного квадратного уравнения являются: \(\frac{-1}{2}+ i\frac{\sqrt{3}}{2};\,\,\ , \frac{-1}{2}- i\frac{\sqrt{3}}{2}\)

• Пример 2: Выразите сумму, разность, произведение и частное следующих комплексных чисел в виде комплексного числа.

  \[\begin{align} z_1&=-2+i\\[0.2cm]z_2&= 1-2i \end{align} \]

  Решение:

  Сумма:

  \[ \begin{ выровнять} z_1+z_2&= (-2+i)+(1-2i)\\[0,2 см] &=(-2+1)+ (i-2i)\\[0,2 см] &= -1-i \end{align}\]

  Разница:

  \[ \begin{align} z_1-z_2&= (-2+i)-(1-2i)\\[0,2 см] &=(-2-1) + (i+2i)\\[0,2 см] &= -3+3i \end{align}\]

  Продукт:

  \[ \begin{align} z_1\cdot z_2&= (-2+i)( 1-2i)\\[0,2см] &=-2+4i+i-2i^2\\[0,2см] &=-2+4i+i+2 \,\,\, [\потому что i^2 =-1]\\[0,2 см] &=5i \end{выравнивание}\] 92=-1]\\[0,2 см] &= \dfrac{-4-3i}{5}\\[0,2 см] &=- \dfrac{4}{5}- i \dfrac{3}{5 }\end{align}\]

  Следовательно, имеем:

  Сумма = -1 — i
  Разница = -3 + 3i
  Продукт = 5i
  Деление = -4/5 — 3i/5

перейти к слайдуперейти к слайду

Разбивайте сложные концепции с помощью простых визуальных средств.

Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций.

Записаться на бесплатный пробный урок

перейти к слайдуперейти к слайду

 

Часто задаваемые вопросы о комплексных числах

Что такое комплексные числа в математике?

Комплексное число представляет собой комбинацию действительных и мнимых значений. Обозначается z = a + ib, где a, b — действительные числа, а i — мнимое число. i = \(\sqrt{-1}\) и никакое действительное значение не удовлетворяет уравнению i ²  = -1, поэтому I называется мнимым числом.

Для чего используются комплексные числа?

Комплексное число используется для простого нахождения квадратного корня из отрицательного числа. Здесь мы используем значение i ²  = -1 для представления отрицательного знака числа, что помогает легко находить квадратный корень. Здесь мы имеем √-4 = √i ² 4 = + 2i. {-1}\frac{b}{a} \)).

Что такое действительные и комплексные числа?

Комплексные числа являются частью действительных чисел. Некоторые действительные числа с отрицательным знаком трудно вычислить, и мы представляем отрицательный знак с помощью йоты «i», и такое представление чисел вместе с «i» называется комплексным числом. Дополнительные комплексные числа полезны для нахождения квадратного корня из отрицательного числа, а также для нахождения отрицательных корней квадратного или полиномиального выражения.

Как делить комплексные числа? 92)}\).

Как строить графики комплексных чисел?

Комплексное число вида z = a + ib может быть представлено в плоскости арганда. Комплексное число z = a + ib может быть представлено в виде координат точки как (Re(z), Im(z)) = (a, ib). Здесь действительная часть представлена ​​относительно оси x, а мнимая часть представлена ​​относительно оси y.

Как преобразовать комплексные числа в полярную форму?

Комплексное число может быть легко преобразовано в полярную форму.

Визуальные модели для решения задач в 1-м классе

Когда учащиеся поступают в 1-й класс, они продолжают работать над пониманием математики, используя ранние структуры, такие как журнал «Детский сад», который мы представили на прошлой неделе, но теперь мы начинаем добавлять в смесь визуальные модели!

Давайте подытожим путь развития ребенка через решение задач:

1. В раннем детстве ребенку требуется много соответствующего развитию опыта взаимодействия с реальными объектами в физическом мире.
2. Физический мир запечатлен в количественной картине, которую маленькие дети наблюдают и используют как плацдарм для математических бесед.
3. Мы переходим к более структурированному математическому рабочему коврику, чтобы помочь учащимся связывать числа со словами и слова с числами, используя знакомые ситуации из реальной жизни.
4. Рабочий коврик по математике уступает место официальному математическому журналу в детском саду, в котором используются навыки понимания математики. Он предоставляет учащимся структуру для объяснения своего понимания чисел в реальных ситуациях, которые будут использоваться в начальной школе.

Каждый этап развития основывается на навыках, полученных на предыдущем этапе, поэтому важно, чтобы учащиеся не торопились пройти эти этапы. Цель состоит в том, чтобы научить учащихся почему позади как , чтобы они не просто запоминали процедуры, но и действительно понимали, что происходит при решении задач.

По моему мнению, этот 1-й класс является последним этапом в развитии Math5Littles. После этого не так много строительных лесов, поэтому мы действительно хотим тщательно реализовать все предыдущие этапы решения задач, прежде чем отпустить студентов, потому что мы не хотим, чтобы они начали гадать и проверять. Отправляя учащихся на этот путь развития, мы пытаемся создать прочную основу для визуальных моделей, которые помогут им понять решение проблем.

Как мы учили решать задачи

Когда я преподавал в первом классе, я помню стратегию, которую мы использовали для решения задач, называемую CUBS.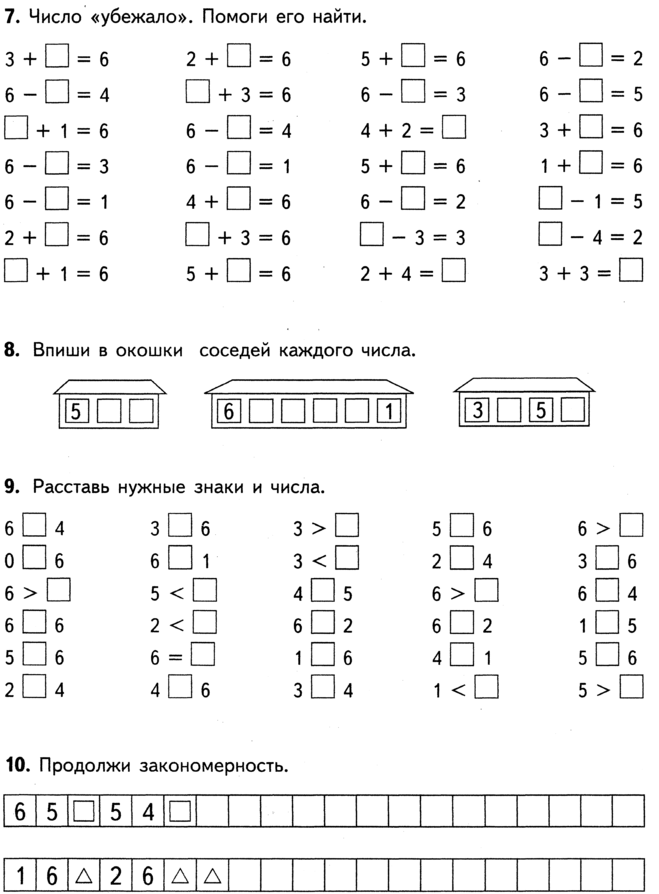 метод. Каждая из этих букв обозначала шаг в процессе решения задачи, чтобы учащиеся могли запомнить, что нужно делать: C — обвести цифры, U — подчеркнуть слово, B — выделить операцию, S — решить задачу. Кажется, это простой процесс, который дает детям действительно отличную структуру, чтобы начать понимать, какие слова задают задачи, верно? Но я понял, что эта стратегия не работает в долгосрочной перспективе.

Когда ребенок читал историю о сложении части-целого или вычитании части-целого, бокс и подчеркивание работали отлично. Но когда мы добрались до задач сравнения, все развалилось.

«У Шеннон 5 леденцов, а у Скотта на 4 леденца больше, чем у Шеннон. Сколько их всего вместе?»

Я наблюдал, как студенты следовали этой процедуре с этим типом задач. Они обвели 4 и 5, подчеркнули важную информацию и обвели рамкой слова вместе , что означает добавить, потому что мы все видели T-диаграммы словаря сложения/вычитания – там написано разница , это означает, что мы собираемся вычесть, если вы видите все вместе , мы собираемся добавить . Но эта стратегия дает мне 4, 5 и вместе . Если вы вернетесь к вопросу, то поймете, что ответ не 9.

Как я часто делаю, я спросил себя почему ? Почему не 9? Чтобы расшифровать этот ответ, требуется немного больше понимания прочитанного. Проблема говорит, что у меня было 5 леденцов на палочке. У Скотта было 4 больше, чем меня, а это значит, что у него тоже было 5. Сложив это, у него было 9, а у меня было 5, так что всего было 14.

Почему мы учим детей процедурам, которые они не понимают? Иногда стратегии, которым мы обучаем в математике, являются условными, то есть они работают только для определенного количества детей или определенного периода времени. Затем вы должны беспокоиться об обучении их тому, как применять это и правилам его применения, и то, что должно было облегчить ученикам, в конечном итоге становится более сложным.

Когда мы начнем работать со стратегиями, я хочу иметь возможность найти эту вертикальную молнию, то есть, если я покажу вам, как эта стратегия может работать в первом классе, она должна работать и по мере того, как ребенок становится старше, чтобы он не каждый год приходится изучать совершенно новый набор стратегий, потому что каждый учитель преподает его по-своему.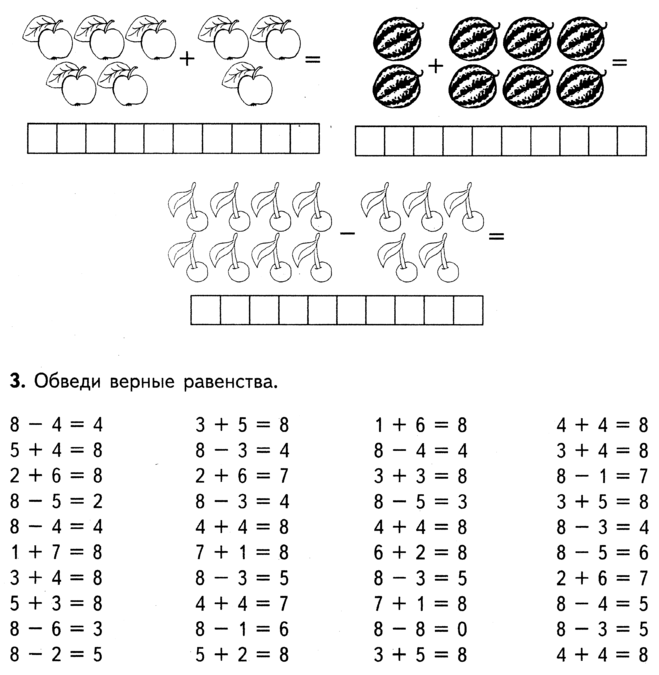 Честно говоря, метод CUBS, вероятно, сработает для 75% задач в первом классе. Учащиеся решают более сложные задачи на сложение часть-целое, вычитание часть-целое, отсутствующие слагаемые часть-целое, и они начинают решать несколько многошаговых задач, каждая из которых подходит к семейству задач часть-целое, для которых CUBS метод работает хорошо. Но когда вы выходите из этого жанра проблем, он разваливается.

Вот почему даже в журнале «Детский сад» мы используем систему кодирования для наших задач. Учителя и ученики должны начать изучать различные характеристики существующих типов сюжетных задач, что продвинет их вперед.

В журнале Kindergarten мы описали сложение часть-целое, вычитание части-целого, недостающее сложение часть-целое, несколько задач с числами для подростков и смешанный обзор. Дневник очень структурирован, потому что он предназначен для того, чтобы учащиеся думали о том, что они читают в задаче на рассказ: у нас есть рассказ, форма предложения, область быстрого рисования, числовая связь, 10-кадр и вычисление. площадь. Когда они переходят в 1-й класс, как мы можем убрать некоторые из этих строительных лесов, сохраняя при этом их соответствие уровню развития?

Мы должны быть очень осторожны с тем, как мы совершаем этот переход, потому что очень быстро учащиеся могут перейти к стратегии «обведи числа, вставь слово в рамку», и много раз они просто обращаются к нам, потому что они не знают, что делать. Это проблема со словами, и это сбивает с толку, поэтому они просто добавляют, потому что мы говорим о добавлении этой недели.

Аддитивные задачи на сравнение 

Аддитивные задачи на сравнение, где у меня есть сумма, а у вас та же сумма, но у вас может быть больше или меньше, чем у меня, вводятся после того, как учащиеся потратили некоторое время на работу над многошаговой частью. целые проблемы.

По моему мнению, этот тип задач представляет собой языковую игру, из-за которой дети сбиваются с толку, пытаясь точно понять, о чем они спрашивают. Итак, мы действительно хотим, чтобы дети сделали шаг назад, чтобы понять проблемы аддитивного сравнения, которые в наших журналах обозначаются кодом AC. Я считаю, что построение этих проблем с помощью кубов unfix — хороший способ начать.

Давайте возьмем такую ​​задачу: у Шеннон есть 10 ручных камней, а у Шерри 4 ручных камня. На сколько камней у Шеннон больше, чем у Шерри?

В некотором смысле может показаться, что это может быть проблема с отсутствующими слагаемыми, но на самом деле мы сравниваем мои любимые камни с любимыми камнями Шерри и спрашиваем, на сколько больше у одного больше, чем у другого. Это действительно требует, чтобы студенты подняли его на конкретный уровень и сделали модель бара с кубами unifix.

Я положил 10 кубиков, чтобы обозначить любимые камни Шеннон, а затем я использую кубики разного цвета, чтобы показать 4 камня Шерри. Затем я хочу сравнить длины этих двух полос и выяснить, в чем на самом деле заключается проблема, а именно в том, промежуток между местом остановки бара Шерри и баром Шеннон. Знак вопроса просит сколько еще у Шеннон?

Иногда язык задачи аддитивного сравнения может быть изменен на противоположный и сказать, на сколько меньше у Шерри? Поскольку это игра слов, которая иногда сбивает учащихся с толку, нам действительно нужно подумать о том, как мы будем учить детей решать подобные задачи.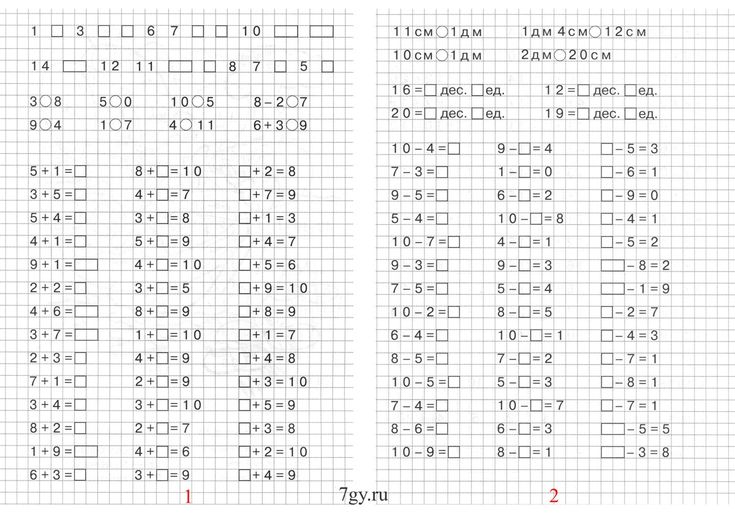

Визуальные модели для аддитивных задач сравнения

Если бы я выстроил в ряд все программы, с которыми мы работаем, каждая из них имеет немного другое название для визуальных моделей: чертежи моделей, диаграммы лент, модели стержней, единичные стержни. . Мы собираемся называть их визуальными моделями для текстовых задач.

Это не те маленькие быстрые рисунки, которые мы делали в детском саду, потому что по мере взросления учеников и усложнения задач я не смогу нарисовать 13 уточек, а затем еще 9, потому что это займет слишком долго! Вместо этого я хочу поместить его в визуальную модель, в которой есть эти единицы.

Этот первый год обучения является переходным периодом, когда дети переходят от быстрого розыгрыша к тому, что я буду называть пропорциональными полосами, длина отдельных кубов которых представляет величины, о которых мы говорим в задаче. .

Допустим, у Эрин есть 4 книги, но потом она идет в библиотеку и берет еще 3. Каждый куб или квадрат представляет собой книгу, которая помогает детям перейти от быстрого рисования, которое они делали в детском саду, к более формальной структуре. Мы по-прежнему могли поставить крестик в ячейке, чтобы обозначить книги, которые были у Эрин, и кружок в ячейках, чтобы обозначить книги, которые она получила в библиотеке, просто чтобы различать их. Рисунок — это инструмент понимания, и мы действительно меньше сосредотачиваемся на ответе на вопрос, чем на выяснении того, как его решить. Я думаю, что это самая непонятная часть визуальных моделей.

На прошлой неделе я работал с первоклассником по телефону Zoom, и этот учитель не смог посетить наш семинар в своем кампусе по визуальным моделям. Она, как и большинство учителей, с которыми я работаю, не понимала, почему визуальные модели так важны. Она считала, что ее ученики должны уметь быстро рисовать, и не понимала, зачем им нужно делать коробки. Она сказала мне, что была ярым сторонником поощрения студентов решать задачи разными способами, так зачем ей учить студентов такой процедуре и заставлять их решать текстовые задачи таким образом.

После того, как я показал ей ту же последовательность решения проблем, которую мы проходили в нашем блоге последние несколько недель, она была продана! Я провел ее по пятому классу, чтобы помочь ей понять, почему в 1-м классе мы просим учеников перестать делать быстрые зарисовки и начать использовать визуальную модель, которая имеет линейку единиц измерения с различными частями. Эта пропорциональная модель также является отличным переходом к использованию непропорциональной планки.

Допустим, у меня было 92 драгоценных камня, а у Шерри 45 драгоценных камней. Быстрое рисование явно не сработает для этой задачи, и у меня недостаточно места на бумаге, чтобы нарисовать пропорциональную модель для этих чисел. Но я могу нарисовать более длинную полосу, обозначающую скалы Шеннона, напишите через 92 камня и нарисуйте более короткую полосу, чтобы показать 45 камней Шерри, чтобы я мог видеть пропорциональность.

Когда мы создаем визуальные модели для текстовых задач, самое сложное помнить, что на самом деле это не имеет ничего общего с математикой! На самом деле мы не решаем проблему на модели; мы используем исключительно стратегию понимания прочитанного.

Одно из самых больших заблуждений, с которыми мы столкнулись, когда приступили к развертыванию образцов журналов для 1-го класса, которые я буду использовать в этом видео, заключалось в том, что в строке не указывается итоговая сумма. Если задача требует итоговой суммы, мы представляем ее в визуальной модели знаком вопроса.

Мы также хотим пометить визуальную модель. Например, поставив букву Б над книгами, которые были у Эрин, и буквой Л над книгами, которые она получила в библиотеке.

Весь смысл этого процесса в том, чтобы предоставить учащимся систематический способ решения задач, который не перестает работать после 1-го класса или когда вы начинаете работать над задачами другого типа. На самом деле, эта стратегия распространяется на задачи мультипликативного сравнения и дроби вплоть до соотношений и пропорций в средней школе.

Пошаговое решение проблем

Этот пошаговый контрольный список, который мы используем, помогает учащимся стать более независимыми в этом процессе по мере их продвижения. Мы немного вводим его в детский сад как процесс, в большей степени управляемый учителем, но он также интегрирован в классную комнату первого класса, где дети должны решать пошаговый процесс визуальной модели. Как вы можете видеть в примерах, у нас есть профессор Барбл, объясняющий шаги.

Прочитайте задачу. Затем попросите кого-нибудь прочитать и повторить, и каждый раз, когда будет представлена ​​новая часть математической информации, мы будем вставлять часть. Итак, когда дети читают задачу, они начинают учиться анализировать то, о чем их спрашивают.

Не все первоклассники смогут прочитать задачу-рассказ, но этот процесс моделируется изо дня в день в классе первого класса, так что со временем ребенок станет самостоятельным.

Я буду читать задачку: у Марка 9клубники, 6 из них мелкие. Остальные большие. Сколько клубники крупной?

 

Тогда я вернусь и прочитаю по частям: У Марка 9 клубник . Это новая часть математической информации, поэтому учащиеся будут повторять это утверждение и выделять его или зачеркивать. Студенты также любят говорить кусков! Тогда продолжим чтение: Шесть из них были маленькими. Я остановлюсь, повторю, а ученики говорят кусок! , поскольку они отмечают этот фрагмент в своих журналах. Теперь у нас есть две части математической информации. Продолжим: Остальные были большими . Повторите, а затем кусков! Итак, у нас есть три раздела информации, которую нам дала проблема, которую нам нужно воспроизвести в нашей визуальной модели. Наконец, Сколько ягод клубники больших? Повторите это, а затем кусок!

Медленно и методично решая задачу, учащиеся могут действительно увидеть те разделы, которые они читают, и, переходя к последующим шагам решения задачи, они могут фактически отметить, что они включили все куски информации в свою визуальную модель.

Создать форму предложения. Что такое форма предложения? Проще говоря, это формулировка проблемы в полном предложении. Я не могу вам передать, сколько раз я видел, как ученики решали задачки на истории и на самом деле забывали, о чем их спрашивают, потому что они так увлеклись арифметикой и выяснили, что они делают! Таким образом, этот шаг удерживает их внимание на том, что на самом деле задает проблема.

В нашей задаче меня спросили, сколько ягод клубники больших? Чтобы выразить это в форме предложения, я бы сказал: У Марка есть ____ большая клубника. я люблю говорить Хмм для ____ , пока мы читаем это вслух.

В детском саду мы предоставляем предложение для учащихся, оставляя пустое место для их ответа. Но в 1-м классе мы убираем часть строительных лесов. Может быть сказано: «Было _____ больших ____», и учащиеся должны заполнить пропуски.

Форма предложения — отличный способ убедиться, что дети понимают то, что читают. Как правило, ученикам первого класса трудно составить предложение, потому что они еще не готовы в своем развитии дать вам полный ответ при чтении. Но учащиеся должны будут составлять предложения со 2-го по 5-й класс, чтобы мы могли быть уверены, что они понимают поставленные задачи, поэтому это действительно отличная практика, чтобы начать в 1-м классе с строительных лесов.

Пропорциональная модель. Начинаем 1 класс с пропорциональной модели. Мы можем построить здесь «кто» или «что», и ученики в конце концов начнут изучать, что входит в эту визуальную модель. В данном случае мы говорим обо всей клубнике Марка, хотя сам вопрос заключается только в том, сколько из них крупных.

В пропорциональной модели вы можете увидеть 9 квадратов. Это проблема с отсутствующим дополнением, поэтому в заголовке будет PWMA вверху, и будет ровно девять квадратов. Некоторые люди могут подумать, что это выдает себя, но помните цель визуальных моделей? Задача состоит не в том, чтобы решить задачу, а в том, чтобы понять, что в ней происходит, поэтому нас больше волнует, сможет ли ученик правильно обозначить рисунок.

В этом примере учащийся подсчитывает 9 и отмечает первую часть задачи, которую мы читали ранее — У Марка девять ягод клубники.

В следующей части говорится: «6 из них маленькие». В шести полях я поставлю шесть крестиков или маленькие кружочки, а вверху напишу маленькими буквами или сокращу s .

Потом написано «остальные большие». Я мог бы пометить эту другую часть ящиков буквой B как большую или написать все слово, если бы захотел. Затем мне нужно поставить вопросительный знак над этим разделом между 9(общее количество ягод клубники) и 6 (количество мелких ягод клубники). Этот раздел представляет собой большую клубнику, и это то, что моя форма предложения напоминает мне, что я ищу.

Технически ученик может просто посмотреть на эту простую пропорциональную модель и сказать: есть 3 большие клубники , потому что она прямо перед ним. Таким образом, некоторые люди могут подумать, что этот дневник слишком прост, но в конце концов студенты укрепляют этот процесс. Они возвращаются к задаче и ставят галочку, когда добавляют крестики или кружочки для шести маленьких ягод клубники. Они выставляют чек, когда говорят о том, чтобы положить большую клубнику. Затем они ставят знак вопроса, чтобы показать, что мы ищем. Есть много деталей, которые мы ищем, чтобы дети взаимодействовали с текстом по математике, чтобы показать понимание.

В некоторых наших школах мы поместим панель единиц внизу страницы. В журнале для 1-го класса, который мы создали для Math5Littles, мы не будем использовать планку и введем непропорциональную планку чуть позже в этом году. Нет ничего плохого в том, чтобы иметь модель пропорционального стержня, а затем под ним иметь непропорциональный стержень. В нашем дневнике мы планируем показать пропорциональную полосу, а затем ввести оба типа полос, чтобы дети могли видеть взаимосвязь между ними. Если где насчет этой непропорциональной полосы, куда мне ее нарезать, чтобы вставить девятку? И где тогда мой вопросительный знак? он помечен? и т. д.

Неотъемлемыми частями визуальных моделей являются: маркировка кто или что, взятие планки и корректировка ее на основе предоставленной информации, а также запись вопросительного знака. Тогда пора решать!

Расчет. Хотя этот шаг может показаться необязательным, потому что наша примерная задача очень проста, и первоклассникам, после того как они решат так много, она кажется простой, и как учителя, так и учащиеся могут задаться вопросом, зачем они вообще это делают, но я могу обещать, что эти проблемы станут более сложными, очень быстро. В нашем журнале для 1-го класса мы представим этот взгляд на пропорциональную полосу, а затем перейдем к пропорциональным и непропорциональным моделям, а затем, в конце концов, просто оставим ее пустой и попросим ученика ввести непропорциональную полосу, чтобы увидеть, что они могут развить. эта прогрессия.

Цели для 1-го класса

Цель состоит в том, чтобы к концу первого года обучения учащиеся могли решать задачи с большими числами и непропорциональной планкой. Вы, конечно, не хотите торопиться с этим прогрессом. 1-й класс — это действительно хорошая опора для учеников, чтобы они достигли этой точки независимости, потому что, когда мы добираемся до 2-го класса, мы не делаем много строительных лесов. В предложениях больше открытых окончаний, больше пропусков, и студенты выполняют больше работы.

Кроме того, мы хотим смешать типы задач, которые мы решаем, чтобы дать учащимся время понять их. Вы можете сделать три дня сложения части-целого, чтобы увидеть, смогут ли они получить это под своим поясом. Затем сделайте некоторое вычитание часть-целое, а затем смешайте их, чтобы увидеть, просто ли учащиеся следуют шаблону, где мы сегодня прибавляем или вычитаем сегодня. Мы хотим знать, что они действительно могут применить то, что изучают. Далее следуют многошаговые задачи, где учащиеся должны складывать, а затем вычитать или наоборот. Дайте учащимся много хорошей практики, а затем снова перемешайте, чтобы увидеть, действительно ли они следуют словам или просто изучают процедуру. Последний тип задач, которые мы будем интегрировать в первый класс, — это аддитивные сравнения.

Видеоуроки

В видеоуроках вы увидите аспекты четырех различных проблем. У некоторых будет полоса пропорциональности, у некоторых будет пропорциональная и непропорциональная, а у некоторых просто ее не будет, чтобы вы могли получить общее представление о том, как это выглядит по ходу дела.

[yotuwp type=”playlist” id=”PL76vNL0J-a405ysBIwEwXfaMp5883yGh5″ ]

Пока вы смотрите видео, подумайте, как вы могли бы настроить это в своем классе, начиная с некоторых примеров задач, которые мы предлагаем в качестве бесплатно скачать сегодня. Скоро мы выпустим полный журнал для 1-го класса, так что следите за обновлениями!

Присоединяйтесь к нам на следующей неделе для решения задач во 2-м классе: С какими проблемами предстоит столкнуться во 2-м классе? Как журналы кодируются? По мере того, как мы начинаем смотреть на то, как кодируются журналы, вы, безусловно, можете использовать эти обучающие видеоролики прямо сейчас в своем классе или на дистанционном обучении, думая о проблемах истории по-другому.

Утверждение «Я умею» — 1 класс

Математика 1 класса

Я умею складывать и вычитать, чтобы понять математику

• Я могу использовать стратегии для решения задач на сложение и вычитание в пределах 20. 1.OA.1
• Я могу решать текстовые задачи, складывая 3 целых числа, меньших или равных 20. 1.OA.2
• Я могу использовать коммутативное свойство сложения. 1.OA.3 (8+3=11 аналогично 3+8=11)
• Я могу использовать ассоциативное свойство сложения. 1.OA.3 (2+6+4=12 аналогично 2+10=12)
• Я могу использовать факт сложения, чтобы решить задачу на вычитание. 1.ОА.4
• Я умею считать, чтобы складывать и вычитать. 1.ОА.5
• Я могу складывать и вычитать факты в пределах 20. 1.OA.6
• Я знаю, что означает знак равенства. 1.ОА.7
• Я могу сказать, верны ли уравнения сложения и вычитания. 1.ОА.8
• Я могу назвать пропущенное число в задаче на сложение или вычитание. 1.ОА.8

Я могу использовать чувство числа и значение места, чтобы понять математику

• Я умею считать до 120. 1.NBT.1
• Я могу сказать, сколько десятков и сколько единиц в числе. 1.НБТ.2
• Я могу сравнивать двузначные числа, используя <, = и >. 1.НБТ.3
• Я могу использовать манипулятивные приемы, изображения или стратегии для решения проблем в пределах 100. 1.NBT.4
• Я могу найти в голове на 10 больше или 10 меньше. 1.НБТ.5
• Я могу вычесть кратные 10 из числа 100 и объяснить, что я сделал. 1.НБТ.6

Я могу использовать измерения и данные для понимания математики

• Я могу расположить три объекта в порядке от самого длинного к самому короткому. 1.MD.1
• Я могу определить длину объекта, используя целые числа. 1.MD.2
• Я могу сказать и записать время в часах и получасах, используя часы. 1.MD.3
• Я могу понять, организовать или ответить на вопросы о данных. 1.MD.4

Я могу использовать геометрию, чтобы понять математику

• Я умею называть, строить и рисовать фигуры. 1.G.1
• Я могу создавать двухмерные или трехмерные фигуры и использовать их для создания новых фигур. 1.Г.2
• Я могу делить фигуры на части. 1.G.3

Чтение в 1-м классе

Я умею читать художественную литературу

• Я могу задавать и отвечать на вопросы о ключевых деталях текста. РЛ.1.1
• Я могу пересказать историю. РЛ.1.2
• Я могу рассказать персонажей, обстановку и то, что происходит в истории. РЛ.1.3
• Я могу использовать стратегии понимания. IA.1

Я умею читать документальную литературу

• Я могу задавать и отвечать на вопросы о ключевых деталях текста. РИ.1.1
• Я могу найти основную тему и детали. РИ.1.2
• Я могу определить связь между двумя людьми, событиями или идеями. РИ.1.3
• Я могу использовать стратегии понимания. IA.1

Я могу понять художественную литературу

• Я понимаю, как слова в рассказе могут рассказать о чувствах и ощущениях. РЛ.1.4
• Я могу отличить художественную литературу от документальной. РЛ.1.5
• Я могу говорить о том, кто рассказывает историю. РЛ.1.6

Я могу понять документальную литературу

• Я могу задавать вопросы и отвечать на них, чтобы помочь понять новые слова. РИ.1.4
• Я могу использовать функции текста, чтобы находить ключевые факты или информацию в тексте. РИ.1.5
• Я могу использовать слова и изображения, чтобы понять документальную литературу. РИ.1.6

Я могу использовать то, что знаю, чтобы понять художественную литературу

• Я могу использовать слова и изображения, чтобы рассказать о персонажах, обстановке или событиях. РЛ.1.7
• Я могу сравнивать и противопоставлять действия персонажей в рассказе. РЛ.1.9

Я могу использовать то, что знаю, чтобы понять документальную литературу

• Я могу использовать слова и изображения для описания ключевых идей. РИ.1.7
• Я могу найти доводы в поддержку основной идеи документальной литературы. РИ.1.8
• Я могу сравнить и противопоставить основную мысль двух научно-популярных текстов. РИ.1.9

Я умею читать и понимать художественную литературу для первого класса RL. 1.10

Я могу читать и понимать документальную литературу для первого класса RI.1.10

Я могу использовать основные функции работы с текстом, чтобы помочь себе в чтении RF.1.1

8

8 (найти первое слово, заглавные буквы, знаки препинания в конце)

Я могу использовать навыки фонетики, чтобы читать

• Я могу определить количество слогов в словах. РФ.1.2
• Я могу рассказать о разных звуках в слове. РФ.1.2
• Я могу использовать диграфы, чтобы читать. РФ.1.3
• Я могу читать односложные слова. РФ.1.3
• Умею читать команды гласных (магические е, еа, ау, оа) RF.1.3
• Я могу читать двухсложные слова. РФ.1.3
• Я умею читать слова первого класса. РФ.1.3

Я могу бегло читать

• Я могу читать с выражением. РФ.1.4
• Я могу читать точно. РФ.1.4
• Я могу перечитать, чтобы понять, что означают слова. РФ.1.4

1-й класс Письмо

Я умею писать разными способами

• Я умею писать свое мнение. W.1.1
• Могу писать информативные тексты по теме. W.1.2
• Я могу написать, чтобы рассказать историю. W.1.3

Я могу улучшить свои записи

• Я могу пересматривать и редактировать свои записи. W.1.5
• Я могу опубликовать свое письмо. W.1.6

Я могу использовать исследования, чтобы помочь моему письму

• Я могу помочь моему классу в исследованиях. W.1.7
• Я могу помочь моему классу писать. W.1.7
• Я могу вспомнить, чему меня учили, чтобы ответить на вопрос. W.1.8

Язык 1-го класса

Я умею правильно писать и говорить по-английски

• Я могу печатать прописные и строчные буквы. Л.1.1
• Я могу использовать нарицательные, собственные и притяжательные существительные. Л.1.1
• Я могу использовать существительные в единственном и множественном числе с нужным глаголом. Л.1.1
• Я могу использовать местоимения. Л.1.1 (я, мне, мой, они, их, их)
• Я могу правильно использовать прилагательные. Л.1.1
• Я умею использовать союзы. Л.1.1 (и, но, или, так, потому что)
• Я могу использовать определители. Л.1.1 (а, тот, этот, тот, мой, много, мало)
• Я могу составлять простые и сложные предложения. Л.1.1
• Я могу составлять говорящие и спрашивающие предложения. Л.1.1
• Я могу писать даты и имена людей с большой буквы. Л.1.2
• Я умею ставить знаки препинания. Л.1.2
• Я могу использовать запятые в датах. Л.1.2
• Я могу использовать запятые при написании групп по 3. L.1.2
• Я могу писать слова первого класса. Л.1.2
• Я могу использовать свои знания о фонетике для написания новых слов. Л.1.2

Я могу понять, что означают слова, и использовать их в различных ситуациях

• Я могу сортировать слова по категориям.