Что первое умножение или деление в примерах без скобок: Выражения без скобок — урок. Математика, 2 класс.

Порядок выполнения действий в выражениях без скобок

Цели:

• Предметные: организовать деятельность учащихся по изучению порядка действий в выражениях.
• Познавательные — развивать умение самостоятельно находить и извлекать нужную информацию, осуществлять для решения учебных задач операции анализа, синтеза, сравнения, классификации, устанавливать причинно-следственные связи, делать обобщения, выводы.
• Регулятивные — развивать умение планировать необходимые действия; контролировать процесс и результат деятельности, вносить необходимые коррективы; осознавать возникшие трудности, искать их причину и пути преодоления.
• Коммуникативные — развивать умение вступать в диалог с учителем, сверстниками, участвовать в беседе, соблюдая правила речевого поведения; формулировать собственные мысли, высказывать и обосновывать свою точку зрения, осуществлять совместную деятельность в парах с учетом конкретных учебно-познавательных задач.
• Личностные: формирование положительного отношения к познавательной деятельности, желание приобретать новые знания, проявлять интерес к предмету.

Тип занятия: учебное занятие по изучению и первичному закреплению нового материала

Оборудование:

• проектор, компьютер,
• для каждого ученика — учебник, учебные принадлежности, тетрадь, карточки с заданиями

Задачи:

• формировать способности к практическому использованию правила;
• развивать умение анализировать и обобщать;
• учить учебному сотрудничеству.

Ход урока

I. Организационный момент

II. Мотивация к учебной деятельности

— В природе есть солнце. Оно светит и греет.

А кого в нашем родном крае называют солнцем Осетии?

(Основоположника осетинской литературы Коста Левановича Хетагурова).

— Да, Коста-солнце Осетии…

Так пусть же сегодня каждый лучик солнца доберётся до вас и не только согреет своим теплом, но и придаст вам сил и уверенности в своих знаниях.

Это отрывок из стихотворения К.Хетагурова…

Учись, дружок, с охотой,
Чтоб мудрость всю познать,
И с радостью работай,
Чтоб человеком стать!

— Прочитайте на доске высказывание всемирно известного ученого, физика, математика, филолога Михаила Ломоносова.

(Высказывание)

«Математику уже затем учить следует, что она ум в порядок приводит».
М.Ломоносов

— Как вы понимаете это высказывание?

(Математика точная наука, она учит терпению, раскладывает всё по полочкам, дисциплинирует мозг)

— Да, математика, большая любительница порядка. Где в математике вы имели дело с порядком? (В числовой последовательности; порядок действий в выражениях…)

— Наш урок сегодня будет посвящен открытию нового знания

III. Актуализация и фиксирование индивидуального затруднения в пробном учебном действии

Цели:

• организовать актуализацию умений;
• организует выполнение учащимися пробного учебного действия;
• организовать фиксирования учащимися индивидуального затруднения;
• уточнить следующий шаг учебной деятельности.

— Посмотрите внимательно на выражения, разделите их на группы и запишите в 2 столбика

(Буквенные и числовые)

(a — b )+ с	(a — b )+ с	(6 ∙ 3) : 2= 9
(6 ∙ 3) : 2 =	(а : b) + c	40 : 5 ∙ 2 = 16?
40 : 5 ∙ 3 =
(а : b) + c

— Найдите значение числовых выражений.

IV. Выявление места и причины затруднения

Цели:

• выявить место (шаг, операция) затруднения;
• зафиксировать во внешней речи причину затруднения.

Учащиеся выявляют затруднение при определении порядка действий в выражении, содержащем скобки

Проверка.

— Кто справился без ошибок? У кого есть ошибки?

— В каком месте возникло затруднение? (В выражении без скобок)

— Почему возникло затруднение? (Из-за разного порядка действий)

Построение выхода из затруднения.

— Какую цель вы поставите перед собой? (Научиться решать выражения без скобок)

— Попробуйте сформулировать тему нашего урока. (Порядок выполнения действий в выражениях без скобок)

— Посмотрите еще раз на данное выражение 40 : 5 ∙ 2 = 16 (На доске) и давайте составим план наших действий

Составление плана действий

1.

Из каких арифметических действий составлено выражение ?

2. В каком направлении считать?

3. Какое действие выполнять первым?

4. Какое действие выполнять вторым?

5. Сделать вывод.

V. Реализация построенного проекта

— Предлагаю поработать в парах. 20: 4 ∙ 5 =25

Карточка № 1 и опорная картинка «Волк и Заяц»

— Исследуйте с помощью плана и опорной картинки «Волк и Заяц» последовательность выполнения действий в данном выражении и найдите значение выражения.

— Проверим 20: 4 ∙ 5 =25

— Как решали выражение? (1 ученик)

(Выражение не содержит скобок, из арифметических действий только умножение и деление, считали слева направо по порядку)

— Какой вывод сделали?

(Если выражение содержит только умножение и деление и нет скобок, то выполнять надо по порядку)

— Сравните вывод, который вы сделали с эталоном в учебнике с. 107 (читает ученик)

VI. Первичное закрепление с проговариванием во внешней речи

— Можно ли сказать, что вы уже все сделали на уроке? (Нет)

— Какую цель вы поставите на оставшиеся этапы? (Научиться применять эталон)

— Что для этого надо сделать? (Потренироваться в использовании нового эталона)

с. 108 № 2 — с комментированием у доски

(Это выражение без скобок, содержит только деление, буду выполнять действия по порядку, ….)

16 : 4 : 2 = 2
72 : 9 ∙ 8 = 64
5 ∙1 ∙ 9 = 45
6 ∙ 4 : 8 : 3 = 1

ФИЗМИНУТКА

№ 3 с. 108 устно

— Какое правило нарушил Волк? (

Правило порядка действий в примерах без скобок)

— Как нужно было решить? (Сначала выполнить деление 12:3, а затем умножение)

Каким правилом воспользоваться? Проговорите его. (Проговаривают правило и решают пример устно)

(Если выражение без скобок содержит из действий только умножение, только деление или умножение и деление, то принято выполнять их по порядку слева направо)

VII. Самостоятельная работа с самопроверкой по эталону

Цели:

• организовать выполнение учащимися самостоятельной работы на новое знание;
• организовать самопроверку по эталону;
• организовать выявление места и причины затруднений, работу над ошибками.

— Вы поработали вместе, в парах, а теперь необходимо поработать самостоятельно.

— Выполните задание самостоятельно, карточка №2

• 18 : 2 ∙ 3
• 7 ∙ 6 : 6
• 4 ∙ 2 ∙ 9
• 2 ∙ 9 : 3 : 2
• 56 : 7 : 4

10 СЛАЙД

— Проверьте решение по эталону для самопроверки.

Подробный образец	Эталон
18 : 2 ∙ 3 =27 7 ∙ 6 : 6 = 7 4 ∙ 2 ∙ 9 = 72 2 ∙ 9 : 3 : 2 = 3 56 : 7 : 4= 2	Выражение без скобок и содержит только умножение и деление. Выполняем действия по порядку слева направо

— У кого получился другой ответ — поставьте «?».

— В каком месте вы допустили ошибку.

— Почему у вас возникло затруднение? (В расстановке порядка действий (применение нового правила), знание таблицы умножения и деления)

— Что необходимо сделать, чтобы такие ошибки не допускать? (Проговаривают правило, необходимо повторить таблицу умножения и деления, порядок действий в выражениях)

— Кто справился с заданием без ошибок?

— Поставьте себе «+». Замечательно.

VIII. Рефлексия учебной деятельности на уроке (итог)

Цели:

• зафиксировать новое содержание, изученное на уроке;
• организовать рефлексию и самооценку учениками собственной учебной деятельности.
• соотнести ее цель и результаты, зафиксировать степень их соответствия, и наметить дальнейшие цели деятельности.

— Вернёмся к выражению, которое мы в начале урока на доске разбирали.

40 : 5 ∙ 2 = 16

— Почему были разные ответы? (Не знали порядок действий в выражениях на умножение и деление без скобок)

— Какие шаги выполняли? (Когда возникло затруднение, составили план, нашли решение и пришли к выводу)

— Какой сделали вывод? (Если выражение из скобок содержит из действий только умножение, только деление или умножение и деление, то принято выполнять их по порядку)

— Сегодня вы ещё на один шаг продвинулись в своём обучении.

Теперь я предлагаю вам оценить свою работу на уроке. Положите перед собой «лестницу успеха». Покажите, на какой ступеньке вы находитесь в конце урока. Если вы выполнили самостоятельную работу без ошибок, и у вас нет вопросов, то поставьте себя на верхнюю ступеньку. Если вы выполнили самостоятельную работу, но у вас остались вопросы, поставьте себя на среднюю ступеньку. Если вы ошиблись в самостоятельной работе, у вас остались вопросы, поставьте себя на нижнюю ступеньку.

IX. Домашнее задание

Р. т. стр. 53, № 187, 188.

— Спасибо за урок!

Порядок выполнения действий в числовых выражениях

Ничего не понимаю. Вчера Плюс с Минусом и Умножение с Делением решали примеры. Вот посмотрите. Это решал Плюс и Минус.

Числа одни и те же, знаки одни и те же, а ответы разные! И точно так же с примерами, которые решали Умножение и Деление.

Так-так-так. Надо разобраться.

Ах я растяпа! Ведь тут стоят скобки! А ведь скобки, они такие важные! То действие, которое они окружают, будет обязательно выполняться первым. Вот и в этих числовых выражениях. Возьмём первое из них.

Шестьдесят семь минус двенадцать и плюс пять. Сначала выполняю вычитание. Из шестидесяти семи вычитаю двенадцать, получается пятьдесят пять. К пятидесяти пяти прибавляю пять получается шестьдесят.

А вот точно такое же выражение, точнее почти такое. Потому что в нём стоят скобки. И вот они, окружив числа двенадцать и пять и знак плюс между ними, молчаливо, но настойчиво предлагают сначала выполнить именно сложение! И не смотрите на то, что это действие записано не первым. Закон есть закон – раз в скобках, значит выполняем первым. Сложили числа двенадцать и пять. Получилось семнадцать. Ну а уж теперь надо вычитать. И вычитать надо не число двенадцать, а результат действия в скобках, то есть семнадцать. Шестьдесят семь минус семнадцать равно пятидесяти. О как!

Теперь решаем следующую парочку примеров.

Восемнадцать разделить на два и умножить на три. При делении числа восемнадцать на два получается девять, и девять умножить на три – двадцать семь.

А во втором примере сначала два умножаем на три. Это шесть. И восемнадцать делим на результат действия в скобках, то есть на шесть. Получается три.

Да, но в этих примерах всё просто – два действия. Одно в скобках выполняется первым, а после него – второе.

А вот если в примере несколько различных действий? Например, вот в этом примере.

56 – (35 – 29) ∙ 3

Конечно, сначала выполняем действие в скобках. А что потом? Вычитание или умножение? Ну конечно же умножение. Хоть вычитание записано первым, но умножение, как и деление, выполняются раньше сложения и вычитания. Ну а уж третьим действием будем выполнять вычитание.

Разность чисел тридцать пять и двадцать девять равна шести. Заменяем её результатом. Пишем пятьдесят шесть минус произведение чисел шесть и три. Произведение чисел шесть и три равно восемнадцати. Заменяем это произведение его результатом. Пишем: пятьдесят шесть минус восемнадцать равно тридцати восьми.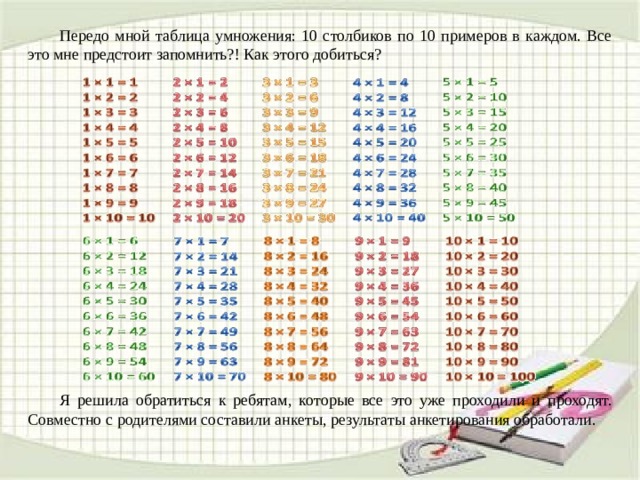

А вот в этом числовом выражении ещё больше действий:

38 + 60 : (14 – 4) – 14

И первым в нем выполняется вычитание в скобках, затем – деление. А что третьим? Сложение или вычитание? А вот сложение и вычитание между собой вполне равноправные. Что записано первым в направлении слева направо, то и выполняется первым. В нашем примере сначала выполняем сложение, а потом – вычитание.

Четырнадцать минус четыре – десять. Шестьдесят разделить на десять – шесть. Тридцать восемь плюс шесть – сорок четыре. Сорок четыре минус четырнадцать – тридцать.

Да, вот это решение получилось! Даже на строке целиком не поместилось. Но это не беда. Часть длинной записи можно переносить ниже. Только место переноса может быть там, где стоит знак – плюс или минус, умножить или разделить… или знак равно. Просто этот знак записывается два раза – один раз в конце верхней строчки, а второй раз – в начале следующей строки. И в тетради между этими строчками вниз пропускается, как обычно, одна клеточка.

Но вернёмся к нашим числовым выражениям. А вот посмотрите на это выражение. В нём нет скобок.

6 ∙ 3 + 24 : 3 – 5 ∙ 2 =

Как вы думаете, решаем, как обычно, слева направо? Конечно нет. Сначала выполняем умножение и деление. По порядку слева направо. А уж потом сложение и вычитание тоже по порядку слева направо. Шестью три – восемнадцать. Двадцать четыре разделить на три – восемь. Пятью два – десять. Ставлю знаки плюс и минус. Считаю. Ответ – шестнадцать.

Ну что, всем все понятно?

Самое главное – не забывать.

Если в выражении несколько действий, но это только действия сложения и вычитания, или только умножение и деление, то действия выполняются по порядку слева направо.

25 – 14 + 7 + 12 – 6 = 24

3 ∙ 4 : 2 ∙ 3 = 18

Если в выражении несколько действий, но там есть не только сложение и вычитание, но и умножение и деление, то сначала выполняется умножение и деление по порядку слева направо, а потом в таком же порядке – сложение и вычитание.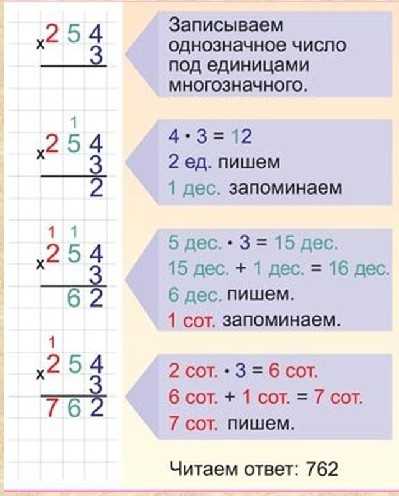

6 ∙ 3 + 24 : 3 – 5 ∙ 2 = 16

Если в выражении несколько разных действий и есть скобки, первыми выполняется действия в скобках, затем – умножение и деление по порядку слева направо, а потом в таком же порядке – сложение и вычитание.

14 + 8 : (15 – 11) – (5 + 2) ∙ 2 = 2

Ну, а если сказать коротко, то получится вот такая памятка:

Порядок действий в числовых выражениях:

1) действия, записанные в скобках;

2) умножение и деление по порядку слева направо;

3) сложение и вычитание по порядку слева направо.

Не забывайте это правило!

Ну а мне пора спать – на улице день, а я тут с вами разговариваю. Вам хорошего дня, а мне – хорошего отдыха. Пока, ребята!

Правило BODMAS: практические вопросы с использованием формулы

• Автор Шротасвини Мохапатра
• Последнее изменение 25-01-2023

Правило БОДМА:  Правило БОДМА – важный математический метод, который используется для решения математических задач. Это метод выполнения арифметического выражения для решения математических уравнений. BODMAS — это аббревиатура от B — скобки, O — порядок степеней или корней, D — деление и M — умножение. A означает сложение, а S означает вычитание.

Это правило упрощает решение выражений с несколькими операторами. Решения должны быть упрощены только в этой последовательности, слева направо. BODMAS используется, когда имеется множество выражений по математической задаче. Студенты должны следовать набору правил при использовании подхода BODMAS. Прочтите следующую статью, чтобы узнать больше о правиле BODMAS и вопросах BODMAS.

Правило BODMAS, также известное как порядок операций, представляет собой последовательность операций в арифметическом выражении.

BODMAS — это аббревиатура, используемая для скобок, порядка, деления, умножения, сложения и вычитания. В некоторых регионах люди/учащиеся используют PEMDAS (круглые скобки, экспоненты, умножение, деление, сложение и вычитание), которое является синонимом или эквивалентом правила BODMAS и может использоваться взаимозаменяемо.

Изучение концепций экзамена на Embibe

В нем объясняются математические операции, которые необходимо выполнять при решении математического выражения. В соответствии с этим правилом, если в выражении есть несколько квадратных скобок \(\left({{\rm{vinculum}}, +, \times, \div } \right)\), начните решение внутри vinculum, или черты, или строки сначала квадратная скобка, затем круглая скобка, затем фигурная скобка, затем квадратная скобка, а затем решите порядок (означает степень и корни и т. д.), затем деление, умножение, сложение и затем вычитание.

Таким образом, правило BODMAS используется для оценки математических выражений и выполнения сложных вычислений гораздо проще и правильнее.

Определение правила BODMAS

Согласно правилу, чтобы решить любое математическое выражение, сначала решают члены, написанные в скобках, затем упрощают экспоненциальные члены и переходят к операциям деления и умножения, затем, наконец, к сложению и вычитанию.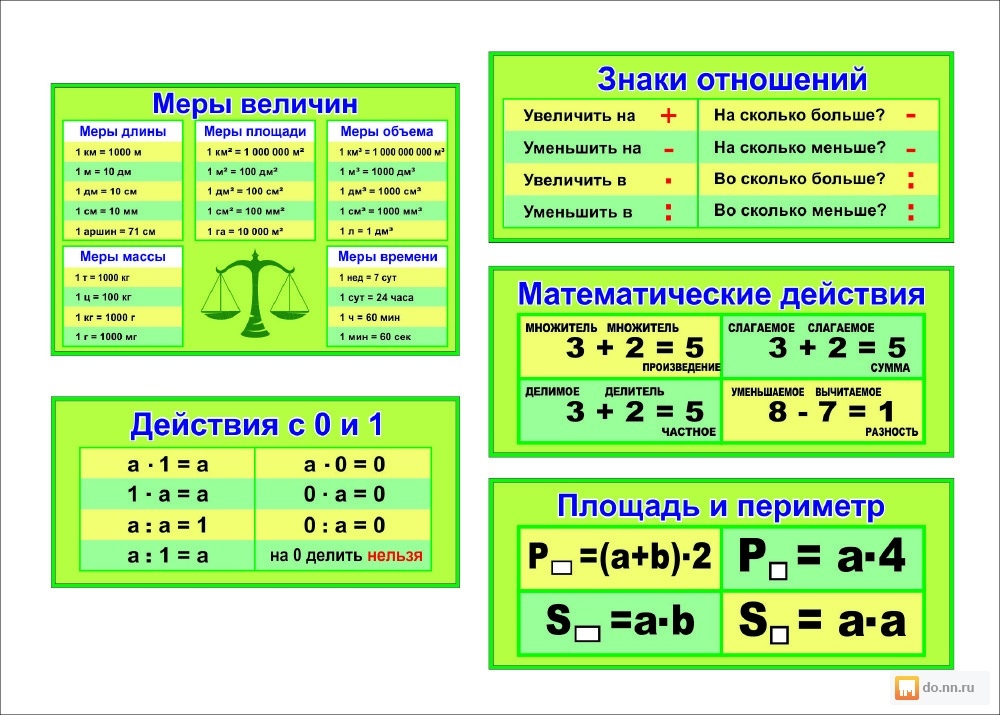

Здесь умножение и деление можно считать операциями первого уровня, поскольку они должны быть решены в первую очередь, а сложение и вычитание можно считать операциями второго уровня.

Упрощение терминов в скобках можно сделать напрямую. Это означает, что мы можем выполнять операции внутри скобок деления, умножения, сложения и вычитания.

Соблюдение этого порядка операций в правиле BODMAS всегда дает правильный ответ. Если в выражении несколько скобок, все одинаковые скобки могут быть решены одновременно.

Пример, \((31+2)÷(13-2) = 33 ÷ 11 = 3\)

Посмотрите на приведенную ниже диаграмму, чтобы понять термины и операции, обозначаемые аббревиатурой BODMAS, в правильном порядке.

BODMAS против PEMDAS

BODMAS и PEMDAS — это две аббревиатуры, используемые для запоминания порядка выполнения операций при решении математического выражения. BODMAS является синонимом PEMDAS.

Правило PEMDAS почти аналогично правилу BODMAS.

Аббревиатура несколько отличается, поскольку некоторые термины известны под разными названиями в разных регионах.

BODMAS Примеры с условием

Существует несколько условий и правил для общего упрощения, как указано ниже:

Условие	Правило
\(p + (q + r) \Rightarrow p + q + r\)	Откройте скобки.
\(p – (q + r) \Стрелка вправо p – q – r\)	Раскройте скобку и умножьте знак минус на каждое слагаемое внутри скобки. (Все положительные члены будут отрицательными, а отрицательные будут положительными)
\(p(q + r) \Rightarrow pq + pr\)	Умножьте внешний член на каждый член в круглой скобке

Давайте решим некоторые вопросы БОДМАС или примеры БОДМАС, следуя приведенным выше правилам:

Пример \(1:\,3 + \left( {6 + 7 } \right) = 3 + 6 + 7 = 16\)

Пример \({\rm{2: 15 — }}\left( {\rm{3 + 2}}} \right){\rm{ = 15 – 3 – 2 = 15 – 5 = 10}}\)

Пример \(2 \times \left( {3 \times 8} \right) = \left( {2 \times 3} \right) + \влево({2\умножить на 8}\вправо) = 6 + 16 = 22\)

Простые способы запомнить правило BODMAS

Во-первых, упростите выражение внутри скобок.

Затем решите все экспоненциальные члены.

Затем выполните деление или умножение (слева направо).

Затем выполните сложение или вычитание (слева направо).

Формула BODMAS

Способ определения приоритетности математических операций, которые должны выполняться первыми по порядку, называется формулой BODMAS. Сначала решите выражение в скобках, затем выполните порядок или из, затем деление, затем умножение, затем сложение и затем вычитание.

Как решить суммы BODMAS, связанные с реальной жизнью?

Во время сегодняшней бури с дерева в нашем саду упало несколько манго. Мой брат подобрал в корзине. Я посчитал, что в корзине 50 манго. Оттуда я взял 2 манго, а мой брат взял 3 манго.

Через некоторое время мама нашла в саду еще 15 манго. Она разделила все манго поровну между 12 соседскими девочками и мальчиками. Сколько манго получил каждый?

Первое задание: Сколько манго взяли я и мой брат?

\((2+3) [() ставится в первую скобку ]

Второе задание: Сколько манго осталось в корзине после того, как мы взяли?

\(\{ 50 – (2 + 3 )\} [ \left\{ {} \right\}\) во второй скобке ]

Если мама оставила еще 15 манго, общее количество манго будет \(\left\{ {50 – \left( {2 + 3} \right) + 15} \right\}\)

У нас осталось больше работы. Итак, нам нужна еще одна скобка. Мы назовем эту скобку квадратной скобкой. 

Третье задание: \(\left\{ {50 – \left( {2 + 3} \right) + 15} \right\}\) Разделить поровну между 12 людьми, каждому достанется,

Далее Задача: 
\(\left[ {\left\{ {50 – \left( {2 + 3} \right)} \right\} + 15} \right] \div 12\)
\(= \left [ {\left\{ {50 – 5} \right\} + 15} \right] \div 12\) (упрощение внутри круглых скобок)
\(= \left[ {45 + 15} \right] \div 12 \) (Упростить внутри фигурной скобки)
\(= 60 \div 12\) (Упростить внутри квадратной скобки)
\(= 5\) (Разделить)
Следовательно, каждый получит по 5 манго.

Распространенные ошибки при использовании правила BODMAS

Кто-то может допустить некоторые распространенные ошибки при применении правила BODMAS для решения выражения, и эти ошибки приведены ниже:

1. Наличие нескольких квадратных скобок может вызвать путаницу, и мы можем получить неправильный ответ .
2. Ошибки возникают из-за отсутствия правильного понимания сложения и вычитания целых чисел.
   Например: \(2-5+6=-3+6=3\).
   Но если мы упростим \(2-5+6=2-11=-9\), то получим неверный ответ.
3. Предполагая, что деление имеет более высокий приоритет, чем умножение, а сложение имеет более высокий приоритет, чем вычитание.

Умножение и деление являются операциями одного уровня и должны выполняться слева направо (в зависимости от того, что идет первым в выражении) и то же самое со сложением и вычитанием, которые являются операциями одного уровня, которые должны выполняться после умножения и деления.

Если сначала решить деление перед умножением (которое находится в левой части операции деления), поскольку D стоит перед M в BODMAS, они могут получить неправильный ответ.

Вопросы BODMAS

Кандидаты, которым нужны вопросы BODMAS для 8-го класса, или вопросы BODMAS для 7-го класса, или вопросы BODMAS для 5-го класса, могут проверить несколько примеров ниже:

Q. 1. Решите \(8+9÷9+5×2-7\).
Ответ:
Данное выражение равно \(8+9÷9+5×2-7\) .
Сначала выполните операцию деления, т.е. \(9÷9=1\)
Таким образом, \(8+1+5×2-7\)
Затем умножение, т.е. \(5×2=10\) 
Теперь , \(8+1+10-7\)
Затем выполнить сложение, т.е. \(8+1+10=19\)
Теперь, \(19-7=12\) (вычесть)
Следовательно, требуемый ответ равно \(12\).

Q.2. Упростить \(\left[ {25 – 3\left( {6 + 1} \right)} \right] \div 4 + 9.\)
Ответ:
Данное выражение равно \(\left[ {25 – 3\left( {6 + 1} \right)} \right] \div 4 + 9.\)
Начнем решать внутри круглой скобки, т.е. \(\left( {6 + 1} \right) = 7\)
Затем умножьте \(3\left( 7 \right)\;\) или \(3×7=21\)
Теперь \(\left[ {25 – 21} \right] \div 4 + 9\ )
Осталась одна скобка, т.е. \(\left[ {25 – 21} \right] = 4\)
После \(B\) и \(O,D\) идет.
Следовательно, \(4÷4=1\)
Наконец, \(1+9=10\)
Следовательно, требуемый ответ равен \(10\) после упрощения выражения.

Q.3. Решите \ (\ влево ( {\ гидроразрыва {1} {4} + \ гидроразрыва {1} {8}} \ справа) \) из \ (64 \).
Ответ:
Сначала решите выражение в скобках, т.е. \(\left( {\frac{1}{4} + \frac{1}{8}} \right) = \frac{{2 + 1} {8} = \frac{3}{8}\)
Теперь выражение принимает вид \(\frac{3}{8}\) of \(64\)
«Of» означает умножение. Итак, \(\frac{3}{8} \times 64\)
Следовательно, искомый ответ равен \(24\).

Q.4. Упростите \(180 \div 15\{ (12 – 6) – (14 – 12)\} \).
Ответ:
Данное выражение равно \(180 \div 15\{ (12 – 6) – (14 – 12)\} \)
Сначала упростим члены внутри \(()\), а затем \({} \).
Теперь,\(180 \div 15\{ (12 – 6) – (14 – 12)\} \)
\(=180÷156-2\) (Решение внутри круглых скобок) 94} = 2 \times 2 \times 2 \times 2 = 16\)
Затем, \(16×5=80\)
Наконец, выполните сложение, \(3+80=83\)
Следовательно, искомое ответ \(83\).

Q.6. Решите \(16[8 – \{ 5 – 2(\overline {2 – 1} + 1)\} ]\), используя правило BODMAS.
Ответ:
Данное выражение равно \(16[8 – \{ 5 – 2(\overline {2 – 1} + 1)\} ].\)
Сначала решите винкулум или квадратную скобку
Теперь, \( 16\влево[ {8 – \влево\{ {5 – 2\влево( {1 + 1} \вправо)} \вправо\}} \вправо]\)
\(= 16\влево[ {8 – \влево \{ {5 – 2 \times 2} \right\}} \right]\) (решается внутри фигурной скобки)
\(= 16\left[ {8 – \left\{ {5 – 4} \right\}} \right]\) (умноженное внутри фигурной скобки)
\(= 16\left[ {8 – 1} \right]\) (Решается внутри фигурной скобки)
\(=16×7\) (Решается внутри квадратной скобки)
\(=112\) (умножается)
Следовательно, искомый ответ равен \(112\) .

Резюме

В этой статье мы изучили правило BODMAS, которое играет очень важную роль при простом и правильном решении математических/арифметических выражений.

Мы рассмотрели полную форму правила БОДМАС, что такое правило БОДМАС, его применение, как правильно упростить большие математические выражения. Это очень поможет учащимся в математических расчетах.

Часто задаваемые вопросы о правиле BODMAS

Ниже приведены часто задаваемые вопросы о BODMAS:

Q.1: Используете ли вы BODMAS, когда нет скобок?
Ответ:  Да, мы используем правило BODMAS, чтобы получить правильный ответ, даже если скобок нет. Если скобок нет, начните решение с «порядка» или «из», за которыми следует деление или умножение (то, что идет первым слева направо), а затем сложение или вычитание (то, что идет первым слева направо).

Q.2: Правильно ли правило BODMAS?
Ответ:  Да, правило BODMAS (порядок скобок или деления, умножения, сложения, вычитания) верно. Но в некоторых регионах люди также используют PEMDAS (круглые скобки, умножение, умножение, деление, вычитание) или BIDMAS (скобки, индексы, деление, умножение, сложение, вычитание). Кстати, все три аббревиатуры правильные.

Q.3: Что такое правило BODMAS в математике?
Ответ:  BODMAS – это аббревиатура, используемая для запоминания порядка операций, которым необходимо следовать при решении математических выражений. В соответствии с этим правилом сначала решите выражение в скобках (vinculum,(),{},[])(vinculum,(),{},[]), затем решите порядок или (степень или корни), затем деление или умножение (поскольку деление и умножение имеют одинаковый приоритет, выполняйте то, что идет первым слева направо), затем решите сложение или вычитание (поскольку сложение и вычитание имеют одинаковый приоритет, выполняйте то, что идет первым слева направо).

Q.4: Вы умножаете сначала, если нет скобок?
Ответ:  да, мы умножаем сначала, если скобки нет (при условии, что умножение идет первым в выражении слева направо). Потому что, по правилу БОДМАСА, внутри скобки нужно решить сначала. Если скобки нет, то следующим приоритетом будет деление или умножение (поскольку и деление, и умножение имеют одинаковый порядок предпочтения), и если умножение идет первым в математическом выражении слева направо.

Q.5: Что означает O в правиле BODMAS?
Ответ:  Значение O  в BODMAS означает «порядок» или «из».

Q.6: Что такое полная форма BODMAS?
Ответ:  Полная форма BODMAS: скобки, порядок или деление, умножение, сложение, вычитание.

Q.7: Вы сначала складываете или умножаете?
Ответ:  Сначала умножаем. Поскольку правило BODMAS говорит, какую операцию следует выполнить первой при решении математической операции. Согласно правилу БОДМАС, мы должны сначала умножить, а затем сложить.

Теперь у вас есть вся необходимая информация о правиле BODMAS. Мы надеемся, что эта подробная статья поможет вам.

Если у вас есть какие-либо вопросы относительно этой статьи о правиле BODMAS, оставьте свои вопросы в поле для комментариев ниже. Мы свяжемся с вами как можно скорее.

Оставайтесь с нами на Embibe, чтобы быть в курсе последних новостей и обновлений.

БОДМАС Правила | Определение, примеры, как использовать, удаление скобок

Введение

При упрощении математических выражений, состоящих из операций одного типа, мы выполняем одну операцию за раз, как правило, начиная слева направо. Если выражение имеет более одной основной операции, вы не можете выполнять операции в том порядке, в котором они указаны. Некоторые операции должны быть выполнены раньше, чем другие. Это каждая операция имеет свой приоритет. Как правило, порядок, в котором мы последовательно выполняем операции слева направо, таков: деление, умножение, сложение, вычитание. Но когда в выражениях также используются скобки, у нас есть набор правил, определяющих приоритет операций. Давайте узнаем, как определяется это правило.

Давайте разберемся с этим на примере.

Предположим, мы хотим найти значение 2 + 3 x 5

Есть два способа найти значение приведенного выше выражения.

В первом методе будем двигаться слева направо, решая выражение в указанном порядке. Это означает, что сначала мы найдем сумму 2 и 3. Мы получим, 2 + 3 = 5.

Теперь у нас есть 2 + 3 x 5 = 5 x 5

Теперь мы найдем произведение 5 на 5 чтобы получить ответ как 25. Следовательно, мы имеем

2 + 3 x 5 = 25 …………………………………. . ( 1 )

Теперь найдем значение этого выражения другим методом.

Сначала мы найдем значение 3 x 5 и добавим это произведение к 2. Таким образом, мы получим

3 x 5 = 15 и 15 + 2 = 17

Следовательно, теперь у нас есть

2 + 3 x 5 = 17 ………………………… ( 2 )

Из ( 1 ) и ( 2 ) мы видим, что оба полученных результата не совпадают. Это подтверждает необходимость наличия приоритета операторов, чтобы получить один и тот же ответ на данное алгебраическое выражение. Этот приоритет известен как порядок операций.

Определение

BODMAS можно определить как стандартную процедуру, которая указывает, какие вычисления следует начинать в выражении с несколькими арифметическими операциями. Без последовательного порядка операций можно допустить большие ошибки во время вычислений. Существует ряд правил, определяющих порядок операций в зависимости от задействования операторов, скобок, показателей степени и других математических символов для операций. Это правило известно как БОДМАС, где

B означает скобки

O означает Of

D означает деление (÷)

M означает умножение (x)

A означает сложение (+)

S означает вычитание (–)

1

1

Понимание BODMAS

Понимание BODMAS является неотъемлемой частью понимания использования группирующих символов в выражениях. Это связано с тем, что именно правило BODMAS определяет порядок, в котором должны выполняться операции в случае математических выражений. Другими словами, он определяет порядок, в котором должны выполняться операции над числами, когда возникают ситуации, когда в выражении имеется на две операции больше, чем две.

Рассмотрим пример. Предположим, мы хотим найти значение 3 + 5 x 2.

Здесь у нас есть два оператора, а именно ( x ) и ( + ). Мы знаем, что в математике мы можем выполнять операции между двумя числами только за один раз. Если у нас есть более 2 чисел, результат первой операции используется для выполнения следующей операции. Итак, в приведенном выше примере необходимо выполнить две операции: (3 + 5) и (5 x 2). Нам нужно решить, с какой из них начать. Здесь вступает в действие правило MDAS.

Из этого правила видно, что умножение предшествует сложению. Поэтому сначала выполним операцию умножения. Полученный таким образом результат будет добавлен к 3. Шаги, связанные с этим процессом, будут – 

3 + 5 x 2

 = 3 + 10

 = 13

Следовательно, 3 + 5 x 2 = 13

Как использовать БОДМАС в арифметических выражениях

Важно отметить, что при отсутствии специальных символов группировки математические задачи решаются слева направо. Однако, когда у вас задействованы группирующие символы, нам нужно следовать порядку операций, как мы обсуждали выше. Мы только что узнали о приоритете основных операций сложения, вычитания, умножения и деления. В соответствии с ним порядок, в котором должны выполняться операции, — это сначала деление, затем умножение, после чего сложение и, наконец, вычитание, но иногда в сложных операциях требуется, чтобы набор операций выполнялся до другого. Например, если мы хотим, чтобы сложение выполнялось перед делением или умножением, нам нужно использовать скобки.

BODMAS используется, чтобы прояснить порядок операций, порядок, в котором несколько операций должны выполняться в математическом выражении. Скобка указывает, что операции внутри нее должны выполняться до операций вне ее. Например, выражение 24 ÷ 3 x 4 обычно решается как –

24 ÷ 3 x 4

= 8 x 4 = 32

Однако, если мы хотим сначала умножить 3 и 4, а затем разделить 24 на получившееся число запишем выражение как

24 ÷ ( 3 x 4 )

Теперь, в соответствии с порядком действий, сначала разгадаем скобки, чтобы получить,

 24 ÷ ( 3 x 4 )

= 24 ÷ 12

 = 1 2

В сложных выражениях иногда необходимо иметь (внутри) в одно и то же время (одно внутри другого может сбивать с толку, потому что чаще всего используются разные типы скобок)

Скобки Имя

( ) Круглые скобки

{ } Скобки или фигурные скобки

[ ] Скобки или квадратные скобки

Здесь важно отметить, что левая часть каждого символа скобки указывает на начало скобки, а правая часть указывает на конец скобки. При написании математических выражений, состоящих более чем из одной скобки, в самой внутренней части используются круглые скобки, за которыми следуют фигурные скобки, и эти две скобки заключаются в квадратные скобки.

Некоторые другие важные моменты, на которые следует обратить внимание: – 

1. Скобки используются в математике, чтобы показать часть математического выражения или уравнения, которое должно быть решено до того, как будут выполнены какие-либо другие вычисления. Часть между двумя круглыми скобками обрабатывается как одно число; ответ заменяет выражение в большем математическом уравнении.
2. В сложных задачах квадратные скобки можно использовать для заключения разделов задачи, которые уже содержат круглые скобки для дальнейшего разделения разделов.
3. В очень сложных задачах фигурные скобки можно использовать для заключения разделов, которые уже содержат квадратные и круглые скобки.

Удаление скобок

Чтобы упростить выражения, включающие более одного символа группировки, мы будем использовать шаги, описанные ниже:

1. Посмотрите, содержит ли данное выражение винкулум или нет. Если винкулум присутствует, выполните операции с красным цветом, в противном случае перейдите к следующему шагу. Винкулум — это горизонтальная линия, расположенная над выражением, чтобы показать, что все, что ниже линии, является одной группой, например, $\overline{2 x 3}$.
2. Теперь найдите самую внутреннюю скобку и выполните в ней операции.
3. Удалите самую внутреннюю скобку, выполнив следующие действия: 
   • Если скобке предшествует знак плюс, удалите ее, записав ее термины как есть.
   • Если скобке предшествует знак минус, измените положительный знак внутри нее на отрицательный и наоборот.
   • Если между числом и символом группировки нет знака, то это означает умножение.
   • Если перед некоторыми скобками стоит число, то мы умножаем число внутри скобок на число вне скобок.
4. Найдите следующую самую внутреннюю скобку и выполните в ней операции. Удалите второй в направлении, используя правила, указанные в предыдущих шагах. Продолжайте этот процесс, пока не будут удалены все скобки.

Давайте разберем приведенные выше шаги на примере.

Пример

Упростим: 37 – [ 5 + { 28 – ( 19 – 7 ) } ]

Решение

Нам дано выражение, 37 – [ 5 + { 9 – 28 – ( 1 9 – 28 – ( 1 ) } ]

Мы будем использовать порядок операций для решения данного выражения.

Сначала мы удалим самую внутреннюю скобку, чтобы получить

37 – [ 5 + { 28 – 12 } ] …………………… [ Удаление самой внутренней скобки ( ) ]

Далее мы удалим фигурные скобки, чтобы получить

37 – [ 5 + 16 ] …………………………. [ Удаление фигурных скобок ]

Теперь мы удалим квадратные скобки, чтобы получить

37 – 21 ………………………… [удаление квадратных скобок ]

Наконец, мы найдем разницу между 37 и 21, чтобы получить 16.

Следовательно, упрощение 37 – [ 5 + { 28 – 12 } ] приведет к 16.

Использование правил BODMAS для упрощения математических выражений выражения позволяют нам узнать о шагах, связанных с решением математических выражений, включающих БОДМАС. Необходимые шаги: 

1. Всегда начинайте с вычисления всех выражений в круглых скобках

Прежде всего, мы должны искать удаление любых символов группировки в алгебраическом выражении. Это означает, что в верхней части списка всегда помните 9 0009   упростите все внутри символов группировки. Примерами символов группировки являются круглые скобки ( ), скобки и фигурные скобки { }. Для вложенных символов группировки проработайте их изнутри и снаружи.

2. Упростить все показатели степени, такие как квадратные корни, квадраты, кубы и кубические корни

После удаления круглых скобок мы переходим к следующему шагу решения всех экспоненциальных значений в алгебраическом выражении. Экспоненциальные выражения, которые могут включать корневые значения, такие как квадратные корни, квадраты, кубы, кубические корни и т. д., сначала вычисляются или оцениваются перед выполнением любой из четырех основных арифметических операций, а именно: сложения, вычитания, умножения и деления.

3. Выполните умножение и деление, начиная слева направо

Затем умножьте и/или разделите слева направо перед выполнением сложения и вычитания. Это говорит нам о том, что умножение и деление имеют более высокий уровень важности, чем сложение и вычитание.

4. Наконец, аналогично выполните сложение и вычитание, начиная слева направо.

Давайте разберемся на примере.

Пример Упростить 95 – [ 144 ÷ ( 12 x 12 ) – ( ​​-4 ) – { 3 – $\overline{17-10}$ } ]

Решение Нам дано выражение

95 – [ 144 ÷ ( 12 x 12 ) – ( ​​-4 ) – { 3 – $\overline{17-10 }$} ]

Мы будем использовать PEMDAS для решения приведенного выше выражения.

Обратите внимание, мы видим наличие vinculum в выражении, поэтому его нужно сначала решить.

Решив винкулум, получим,

95 – [ 144 ÷ ( 12 x 12 ) – ( ​​– 4 ) – { 3 – 7 } ]

Далее мы удалим самую внутреннюю скобку, чтобы получить

95 — [ 144 ÷ 144 + 4 — { 3 — 7 } ]

Теперь мы удалим фигурные скобки, чтобы получить

95 — [ 144 ÷ 144 + 4  + 4 ]

Теперь важно увидеть, что в квадратных скобках мы должны выполнить две операции: деление и сложение. Итак, следуя правилу PEMDAS, мы сначала выполним деление, чтобы получить

95 – [ 1 + 4  + 4 ]

. Затем мы удалим квадратные скобки, чтобы получить 9.0011

95 – 9

= 86

Следовательно, упрощение 95 – [ 144 ÷ ( 12 x 12 ) – (-4 ) – { 3 –  $\overline{17-10}$} ] = 86

Рассмотрим другой пример.

Пример Найдите значение выражения 4 [ 10 + 15 ÷ 5 × 4 – 2 × 2 ) 

Решение Шаги, использованные для решения данного выражения, можно представить в виде таблицы

5 Скобки 9 9585 4 (10 + 3 × 2)99

4 ( 10 + 15 ÷ 5 × 4 – 2 × 2 )
Дивизион	4 (10 + 15 ÷ 5 x 4 — 2 × 2)
Умножение	4 (10 + 3 × 2) 9		4 (10 + 3 × 2)
Addition	4 ( 10 + 12 – 4 )
Subtraction	4 ( 22 – 4 )
Answer	= 4 x 18
	72

Решенные примеры

Пример 1 Упрощайте: 197 — [1/9 {42 +(56 — $ \ aupline {8 +9 $) at108 at18.

Решение Нам дано алгебраическое выражение,

197 – [1/9 { 42 + (56 – $\overline{8+9}$ ) } +108 ]

Мы будем использовать PEMDAS для решения выше выражение.

Обратите внимание, в выражении мы видим наличие винкулума; следовательно, ее нужно решить в первую очередь.

Решив винкулум, получим,

197 – [1/9 { 42 + (56 – 17 ) } +108 ]

Далее удалим самую внутреннюю скобку, чтобы получить,

197 – [1/ 9 { 42 + 39 } +108 ]

Теперь мы удалим фигурные скобки, чтобы получить

197 – [81 / 9  +108 ]

Теперь важно видеть, что в квадратных скобках у нас есть две операции выполняться, деление и сложение. Итак, следуя правилу PEMDAS, мы сначала выполним деление, чтобы получить

197 – [9  + 108 ]

Далее мы удалим квадратные скобки, чтобы получить

197 – 117

Наконец, нам просто нужно найти разницу двух оставшихся значений, чтобы получить

80.

Следовательно, упрощение 197 – [1/9 { 42 + (56 –  $\overline{8+9}$ ) } +108 ] = 80.

Пример 2 Упростить 15 – ( – 5) { 4 – $\overline{7-3}$ } ÷ [ 3 { 5 + ( -3 ) x ( -6 ) } ]

Решение Нам дано выражение

15 – ( – 5) { 4 – $\overline{7-3}$ } ÷ [ 3 { 5 + ( -3 ) x ( -6 ) } ]

Мы будем использовать PEMDAS для решения приведенного выше выражения.

Обратите внимание, мы видим наличие vinculum в выражении, поэтому его нужно сначала решить.

Решив винкулум, получим,

15 – ( – 5) { 4 – 4 } ÷ [ 3 { 5 + ( -3 ) x ( -6 ) } ]

Далее удалим самую внутреннюю скобку чтобы получить,

15 + 5 x 0  ÷ [ 3 { 5 + 18 } ]

Теперь мы удалим фигурные скобки, чтобы получить

15 + 0  ÷ [ 3  x 23 ]

Далее мы удалим квадратные скобки, чтобы получить

15 + 0  ÷ 69

Теперь важно видеть, что нам нужно выполнить две операции: деление. и дополнение. Итак, следуя правилу PEMDAS, мы сначала выполним деление, чтобы получить

15 + 0

 = 15

Следовательно, упрощение 15 – ( – 5) { 4 – $\overline{7-3} $ } ÷ [ 3 { 5 + ( -3 ) x ( -6 ) } ] = 15

Ключевые факты и резюме

1. Порядок работы можно определить как стандартную процедуру, которая указывает, какие вычисления следует начинать в выражении с несколькими арифметическими операциями.
2. BODMAS — это базовый порядок операций, где B означает скобки, O — Of, D — деление (÷), M — умножение (x), A — сложение (+), S — вычитание (–) .
3. BODMAS используются, чтобы прояснить порядок операций, порядок, в котором несколько операций должны выполняться в математическом выражении.
4. Правила использования BODMAS для упрощения арифметических выражений – 
   1. Всегда начинайте с вычисления всех выражений в скобках
   2. Упростите все показатели степени, такие как квадратные корни, квадраты, куб и кубические корни.
   3. Выполните умножение и деление, начиная слева направо
   4. Наконец, аналогично выполните сложение и вычитание, начиная слева направо.
5. Скобки используются для ясности в порядке операций, в котором должны выполняться несколько операций в математическом выражении.
6. При написании математических выражений, состоящих более чем из одной скобки, в самой внутренней части используются круглые скобки, за которыми следуют фигурные скобки, и эти две скобки заключаются в квадратные скобки.