Что такое переместительное и сочетательное свойство сложения: Свойства сложения: переместительное и сочетательное

Переместительное и сочетательное свойства сложения

Похожие презентации:

Элементы комбинаторики ( 9-11 классы)

Применение производной в науке и в жизни

Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»

Знакомство детей с математическими знаками и монетами

Тренажёр по математике «Собираем урожай». Счет в пределах 10

Методы обработки экспериментальных данных

Лекция 6. Корреляционный и регрессионный анализ

Решение задач обязательной части ОГЭ по геометрии

Дифференциальные уравнения

Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи

Переместительное
и сочетательное
свойства сложения

2. 6+7+8+9+3+4+1+2=

Найди значение выражения удобным
(рациональным) способом
6+7+8+9+3+4+1+2=
6+7+8+9+3+4+1+2=40
6+7+8+9+3+4+1+2=40
(6+4)+(7+3)+(8+2)+(9+1)=40
6+7+8+9+3+4+1+2=40
(6+4)+(7+3)+(8+2)+(9+1)=40
Переместительное свойство
сложения
(Мы перемещаем удобные слагаемые и
забираем из в скобки)

6.

Слагаемые можно менять местами. От перестановки слагаемых сумма не меняется.(5+3)+2

7. Слагаемые можно менять местами. От перестановки слагаемых сумма не меняется.

5+(3+2)
Найди значение выражения
(запиши в тетрадь).
50+6+30=
Найди значение выражения
(запиши в тетрадь).
50+6+30= (50+30) +6=
Найди значение выражения
(запиши в тетрадь).
50+6+30= (50+30) +6= 86
3+6+7=
Найди значение выражения
(запиши в тетрадь).
50+6+30= (50+30) +6= 86
3+6+7= (3+7) +6=
Найди значение выражения
(запиши в тетрадь).
50+6+30= (50+30) +6= 86
3+6+7= (3+7) +6= 16
Найди значение выражения
(запиши в тетрадь).
50+6+30= (50+30) +6= 86
3+6+7= (3+7) +6= 16
7+20+3+70=
Найди значение выражения
(запиши в тетрадь).
50+6+30= (50+30) +6= 86
3+6+7= (3+7) +6= 16
7+20+3+70= (7+3) + (20+70)
Найди значение выражения
(запиши в тетрадь).
50+6+30= (50+30) +6= 86
3+6+7= (3+7) +6= 16
7+20+3+70= (7+3) + (20+70) =100

16.

Переместительное свойство сложенияa+b=b+a
Переместительное свойство
сложения
ВЫВОД:
Результат сложения
не изменится, если соседние слагаемые
заменить их суммой.

17. (14+67)+3=

Найди значение выражения удобным
(рациональным) способом
(14+67)+3=

18. (14+67)+3=

Найди значение выражения удобным
(рациональным) способом
(14+67)+3= 14+(67+3)=

19. (14+67)+3=

Найди значение выражения удобным
(рациональным) способом
(14+67)+3= 14+(67+3)=
=14+(70)=

20. (14+67)+3=

Найди значение выражения удобным
(рациональным) способом
(14+67)+3= 14+(67+3)=
=14+(70)= 84

21. (14+67)+3=

Найди значение выражения удобным
(рациональным) способом
(14+67)+3= 14+(67+3)=
=14+(70)= 84
Сочетательное свойство
сложения

22. Из учебника с. 24 № 4 (2 столбик).

(25+136)+75=

23. Из учебника с. 24 № 4 (2 столбик).

(25+136)+75= (25+75)+136=

24. Из учебника с.

24 № 4 (2 столбик).(25+136)+75= (25+75)+136= 236

25. Из учебника с. 24 № 4 (2 столбик).

(25+136)+75= (25+75)+136= 236
592+(85+108)=

26. Из учебника с. 24 № 4 (2 столбик).

(25+136)+75= (25+75)+136= 236
592+(85+108)= 85+(592+108) =

27. Из учебника с. 24 № 4 (2 столбик).

(25+136)+75= (25+75)+136= 236
592+(85+108)= 85+(592+108) = 785

28. Из учебника с. 24 № 4 (2 столбик).

(25+136)+75= (25+75)+136= 236
592+(85+108)= 85+(592+108) = 785
(37+207)+463=

29. Из учебника с. 24 № 4 (2 столбик).

(25+136)+75= (25+75)+136= 236
592+(85+108)= 85+(592+108) = 785
(37+207)+463= (37+463)+207=

30. Из учебника с. 24 № 4 (2 столбик).

(25+136)+75= (25+75)+136= 236
592+(85+108)= 85+(592+108) = 785
(37+207)+463= (37+463)+207= 707
(a+ b) + c = a+ (b+ c)
Сочетательное свойство
сложения
Вывод:
значение суммы не зависит от
порядка действий.

English     Русский Правила

Свойства сложения.

Законы сложения

ГДЗ 1 класс

ГДЗ 10 класс

  

Категория: Математика

Прибавить одно число к другому довольно просто. Рассмотрим пример, 6+3=9. Это выражение означает, что к шести единицам добавили три единицы и в итоге получили девять единиц. Или, если рассмотреть числовой отрезок: сначала по нему передвинулись на 6 единиц, а затем на 3, и оказались в точке 9. Числа 6 и 3, которые мы сложили, называются слагаемыми. А результат сложения — число 9 —  называется суммой. В виде буквенного выражения этот пример будет выглядеть так: a+b=c, где a — слагаемое, b — слагаемые, c – сумма.
Если мы к 3 единицам добавим 6 единиц, то в результате сложения получим тот же результат, он будет равен 9. Из этого примера делаем вывод, что как бы мы не меняли местами слагаемые, ответ остается неизменным: 6+3=3+6=9

Называется такое свойство слагаемых переместительным законом сложения.

Переместительный (коммуникативный) закон сложения:

a + b = b + a.

От перемены мест слагаемых сумма не меняется.

Примеры:

55 + 21 = 21 + 55 = 76
108 + 2 = 2 + 108 = 110

Если же мы рассмотрим три слагаемых, например, возьмем числа 1, 2 и 6 и выполним сложение в таком порядке, сначала прибавим 1+2, а потом прибавим к получившейся сумме 6, то получим выражение: (1+2)+6=9
Можем сделать наоборот, сначала сложить 2+6, а потом к полученной сумме прибавить 1. У нас пример будет выглядеть так: 1+(2+6)=9
Ответ остался прежним. У обоих видов сложения одного и того же примера ответ одинаковый. Делаем вывод: (1+2)+6=1+(2+6)

Это свойство сложения называется сочетательным законом сложения.

Сочетательный (ассоциативный) закон сложения:

a + b + c = a + (b + c).

Сумма не меняется, если какую-нибудь группу рядом стоящих слагаемых заменить их суммой.

Пример:

197 + 23 + 77 = 197 + (23 + 77) = 197 + 100 = 297.

 

Примечание от 7 гуру: оба закона справедливы для любого количества слагаемых. Переместительный и сочетательный законы сложения работают для всех неотрицательных чисел.

Переместительное и сочетательное свойства используются для удобства и упрощения вычислений при сложении.

Пример:

Нужно найти сумму 23 + 9 + 7
Пользуясь переместительным законом, поменяем местами слагаемые 9 и 7, получим 23 + 7 + 9,
теперь, пользуясь сочетательным свойством, объединяем 23 и 7, так как они дают круглое число: (23 + 7) + 9,
Сначала складываем 23 и 7, их сумма равна 30.
Затем прибавляем девять:       30 + 9 = 39.
Итак:  23 + 9 + 7 = (23 + 7) + 9 = 36

Свойство сложения с нулем.

Прибавление к числу нуля не изменяет этого числа: a + 0 = 0 + a = 0.

Пример:

99 + 0 = 0 + 99 = 99

 

• Назад
• Вперед

 
умножить наподелить на

 

org/BreadcrumbList»>
• Уроки
• Математика

Вам может пригодиться:

Ассоциативное свойство сложения — примеры, определение, формула

LearnPracticeDownload

Ассоциативное свойство сложения — это свойство чисел, которое гласит, что способ группировки трех или более чисел не меняет суммы этих чисел. Это означает, что сумма трех или более чисел остается неизменной независимо от того, как они сгруппированы. Давайте узнаем больше об ассоциативном свойстве сложения в этой статье.

1.	Что такое ассоциативное свойство сложения?
2.	Ассоциативное свойство формулы сложения
3.	Ассоциативное свойство сложения и умножения
4.	Часто задаваемые вопросы по ассоциативному свойству дополнения

Что такое ассоциативное свойство сложения?

Ассоциативное свойство сложения — это правило, которое гласит, что при сложении трех или более чисел мы можем сгруппировать их в любую комбинацию, и полученная сумма останется неизменной независимо от того, каким образом они сгруппированы. В этом случае группировка относится к размещению скобок. Например, на приведенном ниже рисунке видно, что сумма чисел не меняется независимо от того, как сгруппированы слагаемые.

Ассоциативное свойство формулы сложения

Формула ассоциативности сложения показывает, что группировка чисел другим способом не влияет на сумму. Скобки, которые группируют числа, помогают упростить процесс сложения. Обратите внимание на следующую формулу для ассоциативного свойства сложения.

Давайте рассмотрим пример, чтобы понять и доказать формулу. Сгруппируем 13 + 7 + 3 тремя способами.

• Шаг 1: Мы можем сгруппировать набор чисел как (13 + 7) + 3, 13 + (7 + 3) и (13 + 3) + 7.
• Шаг 2: Сложите первый набор чисел, то есть (13 + 7) + 3. Далее это можно решить как 20 + 3 = 23.
• Шаг 3: Добавьте второй набор, т. е. 13 + (7 + 3) = 13 + 10 = 23.
• Шаг 4: Теперь решите третий набор, то есть (13 + 3) + 7 = 16 + 7 = 23.
• Шаг 5: Сумма всех трех выражений равна 23. Это показывает, что как бы мы ни группировали числа с помощью скобок, сумма остается неизменной.

Ассоциативное свойство сложения и умножения

Ассоциативное свойство применимо к сложению и умножению, но не существует к вычитанию и делению. Мы знаем, что ассоциативное свойство сложения говорит о том, что группировка чисел не меняет суммы данного набора чисел. Это означает, что (7 + 4) + 2 = 7 + (4 + 2) = 13. Точно так же ассоциативное свойство умножения говорит о том, что группировка чисел не меняет произведения данного набора чисел. Эта формула выражается как (a × b) × c = a × (b × c). Например, (2 × 3) × 4 = 2 × (3 × 4) = 24,9.0003

Важные примечания:

• Ассоциативность применима только к сложению и умножению.
• Ассоциативные свойства соответствуют возможности связывать или группировать числа, что невозможно в случае вычитания и деления.
• Ассоциативное свойство входит в список математических свойств, полезных при работе с математическими уравнениями и их решениями.

☛ Похожие темы

• Свойства дополнения
• Коммутативное свойство сложения
• Нулевое свойство умножения
• Свойство мультипликативной идентичности
• Распределительная собственность
• Коммутативное свойство
• Аддитивная идентичность против мультипликативной идентичности
• Распределительная собственность
• Ассоциативное свойство дополнительных рабочих листов

 

Ассоциативное свойство примеров сложения

1. Пример 1: Следует ли данное уравнение ассоциативному свойству сложения?
   (25 + 2) + 8 = 25 + (2 + 8)

   Решение: Следующие шаги помогут выяснить, следует ли данное уравнение ассоциативному свойству сложения или нет:

   • Шаг 1: Складываем набор чисел, указанный в левой части, то есть (25 + 2) + 8 = 27 + 8 = 35,
   • Шаг 2: Теперь сложите набор чисел, указанный в правой части, то есть 25 + (2 + 8) = 25 + 10 = 35.
   • Мы видим, что сумма, полученная из левой части уравнения, равна сумме, полученной из правой части. Итак, уравнение следует ассоциативному свойству сложения.

2. Пример 2: Вставьте пропущенное число и напишите сумму:

   7 + (10 + 6) = (7 + 10) + ___ = ___

   Решение: Согласно ассоциативному свойству формулы сложения, a + (b + c) = (a + b) + c. Если мы подставим значения в эту формулу, мы получим 6 как пропущенное число, то есть 7 + (10 + 6) = (7 + 10) + 6 , а сумма равна 23.

3. Пример 3: Выберите правильный вариант для отсутствующего номера.

   8 + (4 + 2) = (8 + ___) + 2

   а) 4

   б) 7

   в) 6

   Решение:

   По ассоциативному свойству сложения: а + (b + c) = (a + b) + c. Подставляя значения в формулу: 8 + (4 + 2) = (8 + 4 ) + 2,

   Следовательно, пропущенное число равно 4, потому что сумма обоих выражений равна 14,

   Следовательно, правильный вариант (а).

перейти к слайдуперейти к слайдуперейти к слайду

Разбивайте сложные концепции с помощью простых визуальных средств.

Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций с помощью Cuemath.

Записаться на бесплатный пробный урок

Практические вопросы по ассоциативному свойству сложения

 

перейти к слайдуперейти к слайду

Часто задаваемые вопросы по ассоциативному свойству дополнения

Что такое ассоциативное свойство сложения?

Ассоциативное свойство сложения гласит, что независимо от того, как набор из трех или более чисел сгруппирован вместе, сумма остается неизменной. Группировка чисел осуществляется с помощью скобок. Формула для этого свойства выражается как, a + (b + c) = (a + b) + c = (a + c) + b. Например, если мы сгруппируем числа 3 + 4 + 5 как 3 + (4 + 5) или (3 + 4) + 5, сумма, которую мы получим из обоих наборов, равна 12.

Что является примером ассоциативного свойства сложения?

Ассоциативное свойство сложения гласит, что группировка чисел не меняет их суммы. Например, (75 + 81) + 34 = 156 + 34 = 190; и 75 + (81 + 34) = 75 + 115 = 190. Сумма обеих сторон равна 190.

В чем преимущество использования ассоциативного свойства сложения?

Преимущество ассоциативного свойства сложения заключается в том, что оно помогает формировать более мелкие компоненты, что упрощает вычисление сложения. Группировка чисел с помощью скобок облегчает процесс упрощения выражения.

Как проверить ассоциативность сложения?

Ассоциативность сложения легко проверить, сложив заданный набор чисел. Например, сгруппируем 6 + 7 + 8 двумя способами.

• Шаг 1: Мы можем сгруппировать данный набор чисел как (6 + 7) + 8 и 6 + (7 + 8).
• Шаг 2: Теперь давайте сложим первый набор чисел, то есть (6 + 7) + 8. В результате получится 13 + 8 = 21.
• Шаг 3: Теперь добавим второй набор, т. е. 6 + (7 + 8) = 6 + 15 = 21,
• Шаг 4: Сумма обоих выражений равна 21. Это доказывает ассоциативное свойство сложения, которое показывает, что независимо от того, как мы группируем числа с помощью скобок, сумма остается неизменной.

Всегда ли ассоциативное свойство сложения включает 3 или более чисел?

Да, ассоциативное свойство сложения всегда включает 3 или более чисел, потому что правило свойства гласит, что изменение группировки слагаемых не меняет суммы, а в случае только двух чисел мы не можем создавать группы.

Какова формула ассоциативного свойства сложения?

Формула ассоциативного свойства сложения утверждает, что сумма трех или более чисел остается неизменной независимо от того, как эти числа сгруппированы. Это выражается как, a + (b + c) = (a + b) + c = (a + c) + b.

В чем разница между коммутативным и ассоциативным свойством сложения?

Следующие пункты показывают разницу между коммутативным и ассоциативным свойством сложения:

• Переместительное свойство сложения утверждает, что изменение порядка слагаемых не меняет сумму. Например, 4 + 6 = 6 + 4 = 10. Ассоциативное свойство сложения утверждает, что группировка чисел не меняет сумму. Например, 8 + (2 + 3) = (8 + 2) + 3 = 13.
• Переместительное свойство сложения можно применять к двум числам, а ассоциативное свойство применимо к трем и более числам.
• В коммутативном свойстве сложения порядок слагаемых не имеет значения, а в ассоциативном свойстве сложения не имеет значения группировка слагаемых.

Как ассоциативное свойство сложения используется в повседневной жизни?

Есть много мест, где мы можем применить ассоциативное свойство сложения. Например, если мы тратим 3 доллара на кекс, 6 долларов на мороженое и 2 доллара на конфеты, мы можем сложить стоимость предметов в любом порядке как 3 + (6 + 2) или (3 + 6). + 2. Оба выражения дают одну и ту же сумму, то есть 11. Это показывает ассоциативное свойство сложения, которое гласит, что независимо от того, как мы группируем 3 или более чисел, сумма остается неизменной.

Загрузить БЕСПЛАТНЫЕ учебные материалы

Ассоциативное свойство сложения Рабочий лист

Рабочие листы по математике и
наглядный учебный план

Ассоциативное свойство сложения — определение, формула, примеры

Определение:

«ассоциировать» означает соединять или соединять .

Согласно ассоциативному свойству сложения сумма трех и более чисел остается неизменной независимо от того, как эти числа сгруппированы.

Вот пример того, как сумма НЕ меняется независимо от того, как сгруппированы слагаемые.

Как видно из приведенного выше примера, группировка определяется скобками. Группируем ли мы 5 и 3 или 3 и 4 в круглых скобках, окончательная сумма равна 12. Вы можете проверить окончательный результат, проверив цветные блоки, которые остаются одинаковыми в обоих случаях.

Общий случай:

Для любых трех чисел a,b и c

a + (b + c) = (a + b) + c  

т.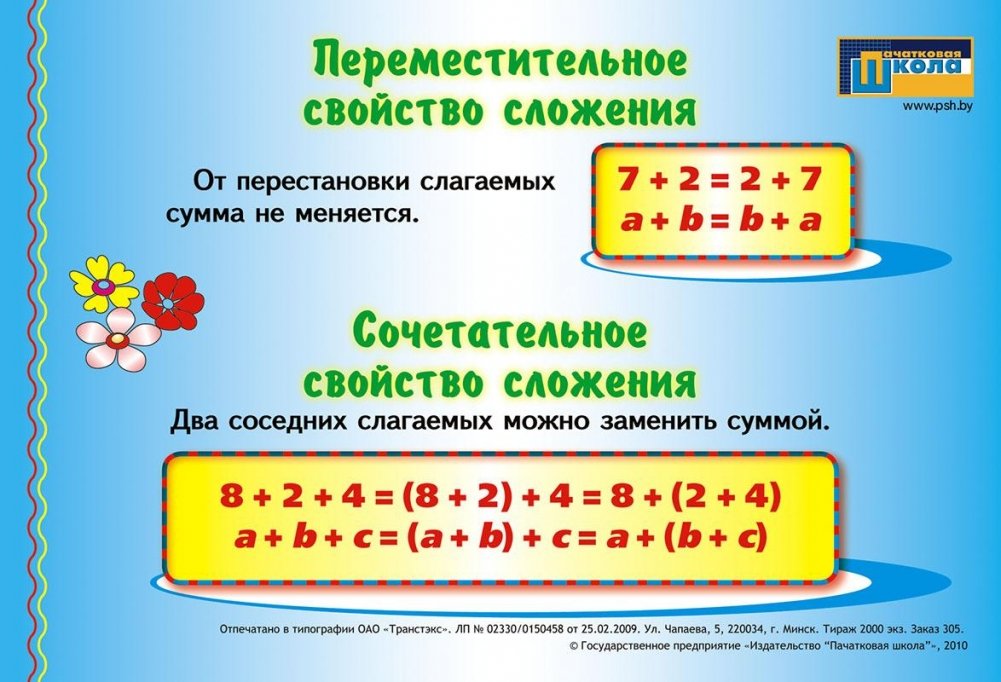 е. при сложении можно группировать числа в любой комбинации.

Возьмем другой пример, чтобы понять и доказать формулу.

Сгруппируем 14 + 7 + 5 двумя способами.

• Шаг 1. Мы можем сгруппировать набор чисел двумя способами: (14 + 7) + 5 или 14 + (7 + 5).
• Шаг 2: Сложите первый набор чисел, то есть (14 + 7) + 5. Далее это можно решить как 21 + 5 = 26.
• Шаг 3: Добавьте второй набор, т. е. 14 + (7 + 5) = 14 + 12 = 26.
• Шаг 4. Сумма обоих выражений равна 26. 

Это показывает, что сумма остается неизменной независимо от того, как мы группируем числа с помощью скобок.

Минимальные числа, требуемые для ассоциативного свойства сложения, равны 3. Однако ассоциативное свойство сложения справедливо и для более чем трех чисел.

Ассоциативное свойство наряду с другими свойствами в математике полезно при работе с уравнениями и их решениями.

• Ассоциативность сохраняется и для умножения, т.е. для любых трех чисел a, b и c a $\times$ (b $\times$ c) = (a $\times$ b) $\times$ c

Пусть a = 2, b = 3, c = 4

a $\times$ (b $\times$ c) = 2 $\times$ (3 $\times$ 4) = 2 $\times$ 12 = 24

(a $\times$ b) $\times$ c = (2 $\times$ 3) $\times$ 4 = 6 $\times$ 4 = 24

Следовательно, a $\times$ ( b $\times$ c) = (a $\times$ b) $\times$ c 

• Ассоциативность для вычитания не выполняется. Давайте посмотрим на пример

Пусть a = 2, b = 3, c = 4

a- (b – c) = 2 – (3 – 4) = 3

(a – b) -c = (2 – 3) – 4 = -53

Следовательно, свойство ассоциативности для вычитания не выполняется.

• Ассоциативность не годится для деления. Давайте посмотрим на пример

a $\div$ (b $\div$ c) = 2 $\div$ (3 $\div$ 4) = 2,67

(a $\div$ b) $\div$ c = (2 $ \div$ 3) $\div$ 4 = 5,97 $\neq$ 2,67

Следовательно, для деления свойство ассоциативности не выполняется.

Решенные примеры

1. Является ли (5 + 10) + 4 тем же, что и 5 + (10 + 4)?

Ответ: Да. Решим и проверим:

(5 + 10) + 4 = 15 + 4 = 19

И, 5 + (10 + 4) = 5 + 14 = 19

Если сгруппировать эти три числа по-разному, то получим те же ответы.

2. Вставьте пропущенные числа:

21 + (45 + 36) = (21 + 45) + _ = _

Ответ. (45 + 36) = (21 + 45) + 36 = 102

3. Найдите x, используя формулу ассоциативного свойства: (2 + 3) + x = 2 + (3 + 6)

Ответ: Дано,   (2 + 3) + x = 2 + (3 + 6)

По свойству ассоциативности Кроме того, LHS = RHS,

Следовательно, 5 + x = 2 + 9

Или 5 + x = 11

Или x = 6

Практические задачи

1

Выберите правильный вариант, чтобы заполнить пропуск: 20 долларов + (7 + 4) = (20 + \underline{} ) + 4$

27

11

7

4

Правильный ответ: 7
Используя ассоциативное свойство сложения,
$20 + (7 + 4) = (20 + 7) + 4$

2

Какое из этих уравнений верно?

12$ + (18 + 16) = (12 + 18) + 16$

11$ — 2 + 1 = 11 — (2 + 1)$

2$ + 3 + 1 = 2 + 3 — 1$

78$ — 70 + 1 = 78 + 70 — 1$

Правильный ответ: 12$ + (18 + 16) = (12 + 18) + 16$
Ассоциативность справедлива только для сложения и умножения.
Это свойство неприменимо к вычитанию, поэтому остальные уравнения неверны.

3

Что из следующего является примером ассоциативного свойства сложения?

$(2 + 3) + 5 = (2 + 3) * 5$

$(2 + 3) + 5 = 2 x (3 + 5)$

$(4 — 5) — 6 = 4 — (5 — 6)$

$(9 + 10) + 11 = 9 + (10 + 11)$

Правильный ответ: $(9 + 10) + 11 = 9 + (10 + 11)$
Ассоциативность актуальна только для сложения и умножения.
Это свойство неприменимо к вычитанию, поэтому остальные уравнения неверны.

4

Какое из этих уравнений верно?

$(2 + 3) + 6 = 2 * (3 + 6)$

$(2 + 3) + 6 = 2 + (3 + 6)$

$(7 — 10) — 15 = 7 — (10 — 15)$

$(9 ÷ 3) ÷ 3 = 9 ÷ (3 ÷ 3)$

Правильный ответ: $(2 + 3) + 6 = 2 + (3 + 6)$
Ассоциативность актуальна только для сложения и умножения. Это свойство неприменимо к вычитанию, поэтому остальные уравнения неверны.

Заключение

Вы родитель или учитель? Хотите превратить изучение математики в увлекательное занятие для ваших детей? Присоединяйтесь к SplashLearn, творческой и полноценной обучающей платформе бесплатно!

Часто задаваемые вопросы

Сколько чисел требуется для применения ассоциативного свойства сложения?

Для применения ассоциативного свойства сложения требуется минимум три числа.