Как объяснить ребенку деление и умножение чисел
Искусство учиться
Как объяснить ребенку деление и умножение чисел
3 апреля 2018 89 569 просмотров
Лиана Хазиахметова
Далеко не все дети понимают деление и умножение с первого раза, поэтому родителям приходится дома подробнее разбирать эти процессы. Сегодня расскажем, как это сделать проще для ребенка. В книге «Как объяснить ребенку математику» объяснения строятся на визуальных принципах. Так школьнику будет понятнее, а родителю легче построить общение.
Умножение чисел
При умножении второе число показывает, сколько раз нужно сложить первое число с самим собой. На рисунке ниже в каждой шеренге стоят 13 человек, а всего шеренг 9. Чтобы подсчитать общее количество людей, нужно число 13 сложить само с собой 9 раз. Это и будет произведением чисел 13 на 9.
Иллюстрация из книги «Как объяснить ребенку математику»
Количество людей в шеренге (13) умножается на количество шеренг (9). Общее количество людей равно 117.
Общее количество людей равно 117.
Не имеет значения, в каком порядке перемножаются числа: ответ будет одинаковым. Ниже показаны два способа, как можно вычислить произведение.
Некоторые числа легко умножать, зная особые приемы. Вот они.
Таблица из книги «Как объяснить ребенку математику»
В таблице показаны приемы быстрого умножения на 2, 5, 6, 9, 12 и 20.
Деление чисел
Деление позволяет найти, сколько раз одно число содержится в другом. Процесс деления можно представить, например, так: если 10 монет раздать 2 людям, то каждый получит по 5 монет. Или так: 10 монет, разложенные в стопки по 2 монеты, дадут 5 стопок.
Деление одного числа (делимого) на другое (делитель) показывает, сколько делителей содержится в делимом. Например, при делении 10 на 2 мы находим, сколько чисел 2 содержится в числе 10. Результат деления называется частным.
Деление как распределение. Из книги «Как объяснить ребенку математику»
Распределение чего-либо — это, по сути, операция деления. Так, если поровну распределить четыре конфеты между двумя людьми, у каждого из них будет по две конфеты.
Так, если поровну распределить четыре конфеты между двумя людьми, у каждого из них будет по две конфеты.
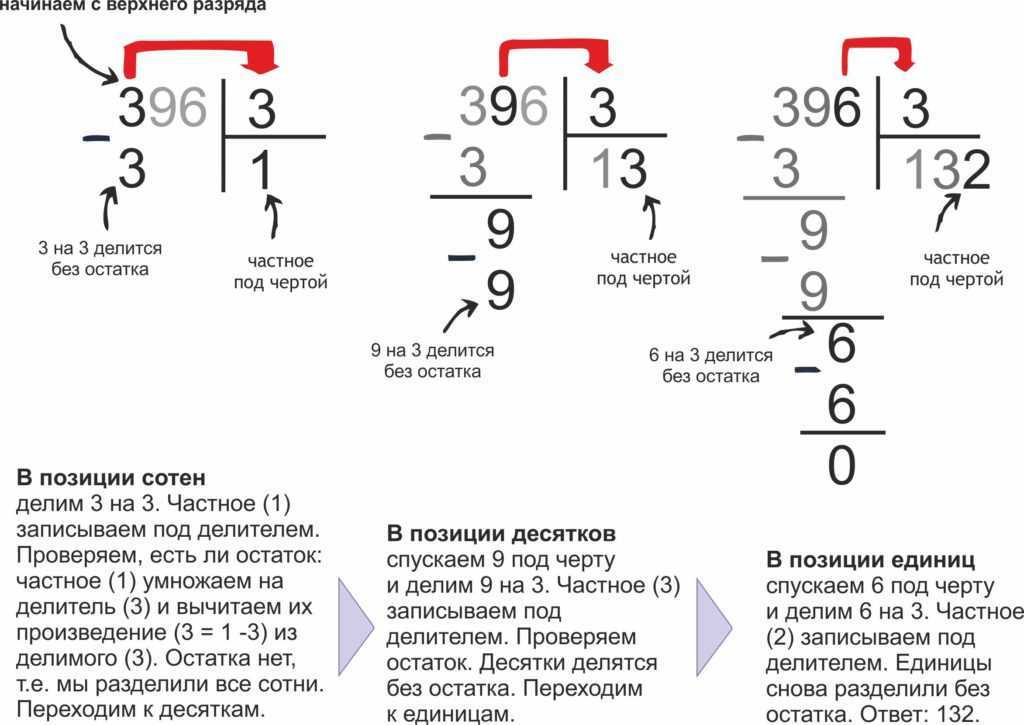
Деление и умножение лучше рассматривать параллельно, чтобы ребенок увидел взаимосвязь. В книге «Как объяснить ребенку математику» есть объяснения более сложных операций, например, деления с остатком, умножения в столбик и так далее. Если визуально показать, как это делается, ребенку легче будет усвоить материал.
Рабочие тетради на деление и умножение
Если ваш ребенок освоил азы деления и умножения, то сейчас ему нужна практика. Японская система Kumon предлагает рабочие тетради «Математика. Деление. Уровень 4»
и «Математика. Умножение. Уровень 4». Постепенно, решая все более сложные задачи, ребенок научится работать с большими цифрами. Ниже — пример одного из последних заданий тетради с делениями.
Пример из тетради «Математика. Деление. Уровень 4»
Такие примеры ребенок научится решать легко и быстро, если тренироваться регулярно и по принципу от простого к сложному. Задания нужно усложнять постепенно, тогда школьник будет учиться с чувством «я могу!».
Задания нужно усложнять постепенно, тогда школьник будет учиться с чувством «я могу!».
По материалам книги «Как объяснить ребенку математику», рабочих тетрадей «Математика. Деление. Уровень 4» и «Математика. Умножение. Уровень 4».
Обложка поста: pixabay.com
Конспект урока математики «Деление с 0 и 1» УМК «Перспектива» 2 класс. | План-конспект урока по математике (2 класс):
Дата: 28.02.2020 ФИО учителя: Балдина Н. А..
Школа: МАОУ СОШ № 104 ФИ студента: Шестакова Татьяна
Класс: 2 «А» ФИО методиста: Серебренникова С. В.
Кабинет: 209
КОНСПЕКТ УРОКА ПО МАТЕМАТИКЕ
Тема: Деление с 0 и 1.
Цели деятельности учителя: Формирование умения деления с 0 и 1; углубление знаний о смысле деления.
Планируемые результаты
Предметные:
Знать – частные случаи деления с 0 и 1, понимать названия компонентов деления
Уметь – делить с 0 и 1
Личностные:
принимать и осваивать социальную роль обучающегося;
проявлять мотивы к учебной деятельности, навыки сотрудничества со взрослыми и сверстниками в разных социальных ситуациях;
осознавать личностный смысл учения
Тип урока: открытие нового знания;
Оборудование: УМК «Перспектива» Л. Г. Петерсон. 2 класс, раздаточный материал, учебная презентация.
Этап урока Методы и приемы | Хроно- метраж | Содержание урока | Формируемые УУД | |
Деятельность учителя | Деятельность ученика | |||
I. Этап самоопределения к деятельности Словесный (слово учителя) | 1 мин | Здравствуйте ребята! — Сегодня урок математики проведу я, меня зовут Татьяна Викторовна. Сегодня мы отправимся в путешествие в страну Математики, но нам нужно найти наших помощников, помогите мне: Он похож на колобок,
Ответы на слайде | Предполагаемые правильные ответы детей. Прямая речь. Ноль Единица | Волевая саморегуляция (Р) Самоопределение (Л) Планирование учебного сотрудничества с учителем и сверстниками (К) |
II. Актуализация знаний и мотивация Словесный (беседа) Практический (выполнение упражнений) | 6 мин | Ребята, с какими числами мы отправимся в путешествие? Какую тему вы изучали на прошлом уроке? Сегодня мы продолжим изучать эту тему. Решите первое задание: 7•0= 2•1= 2•2= 1•6= 4•2= Что общего между этими примерами? Найдите значения выражений, проверка по эталону (на слайде) Какое правило вы использовали в первом примере? Какое правило помогло вам найти произведение во втором и четвертом примере? Чем вы воспользовались при нахождении других произведений? Посмотрите на ответы примеров, что вы заметили? Продолжите ряд чисел еще на 2 числа Теперь давайте решим другие примеры 18:2 = 14:7 = 6:2= Что общего в этих выражениях? Что вы знаете об этом действии? Что вам поможет при нахождении частного? Найдите значения выражений по цепочке Что мы повторили? А теперь решите вот этот пример 8:8= Что нового в это задании? Попробуйте его выполнить Объясните, как вы решили задание В чем у вас затруднение? Чем вы попробовали воспользоваться? Что же вас затруднило? | С 0 и 1 Деление Это примеры на умножение 0; 2; 4; 6; 8 При умножении числа на ноль, получится ноль При умножении числа на 1 и при умножении 1 на число получается то же самое число Знания таблицы умножения на 2 Они увеличиваются на 2 10; 12 Во всех примерах действие деление Деление обратно умножению, чтобы разделить число a на число b, надо найти такое число с, чтобы при умножении числа b на число c, получилось число a Таблица умножения 18 разделить на 2, будет 9, так как 9 умножить на 2, будет 18 и т. Правила умножения на 0 и 1, таблицу умножения на 2, повторили действие деления Нужно число разделить само на себя Не можем объяснить почему именно так Таблицей умножения В таблице нет такого случая. Нет правила, для выполнения этого деления | Общеучебные умения структурировать знания, контроль и оценка процесса и результатов деятельности (П) Самоконтроль (Л) Волевая саморегуляция в ситуации затрудения(Р) |
III. Постановка учебной задачи Словесный (беседа) | 1-2 мин | Какую цель вы поставите перед собой? Что нам в этом поможет? Давайте узнаем тему нашего урока, для этого откроем страницу 95 в учебнике. Какая у нас тема? | Узнать об особых случаях деления, «открыть» правило, которое поможет нам решать такие примеры Знания смысла действия деления, правила умножения на 0 и 1. Деление с 0 и 1 | Подведение под понятие (П) |
IV. Открытие нового знания Словесный (объяснение) Наглядный (иллюстрация) | 7 мин | И так давайте вернемся к примеру 8:8 Вспомним смысл деления Что значит 8:8? Что это за число? Почему? Какой можно сделать вывод? Ребята, давайте вспомним, кто же наш помощник на нашем уроке? Чему посвящен наш урок? Дальше, вам нужно «открыть» знание самим Какие можно еще составить случаи деления на 0 и 1? Послушайте задание: Вам нужно вывести правило со случаем, который вам попадется, с помощью смысла деления, как мы сделали с вами только что. Сейчас вы должны разбиться на группы, для этого на ваших партах лежат цветные карточки, вам нужно найти одноклассников, у которых такой же цвет карточки. Жеребьевка Представители групп возьмите случай деления Давайте проверять Первая группа: а : 1 Вторая группа: 0 : а Третья группа: а : 0 Молодцы, вы хорошо поработали Ребята, а где можно проверить свое открытие? Кто прочитает правило? Сделайте вывод Сможете вы решать примеры с этими случаями? Для этого мы закрепим эти правила на упражнениях. | Это значит нужно найти такое число, чтобы при умножении этого числа на 8 даст 8 1 При умножении на 1 получается то же самое число При делении числа на себя, будет 1 а:а=1 0 и 1 Деление с 0 и 1 а:1; 0:а; а:0 Не шуметь, выделить лидера, слушать и слышать друг друга Мы должны были открыть правило как делить число на 1. Мы привели пример этого случая с помощью примера 7:1. По правилу смысла деления, чтобы 7 разделить на 1, нужно найти такое число, которое при умножении числа на 1 получалось 7. Мы должны были открыть правило как 0 делить на число. Мы взяли как пример выражение 0 : 8. По смыслу деления, чтобы разделить 0 на 8, нужно получить такое число, которое при умножении на число будет давать 0. Это число 0, т.к. при умножении числа на 0, будет получаться 0. Значит, делая вывод, при делении 0 на число, получается 0. Мы должны были открыть правило, как делить число на 0. Мы привели пример это случая и записали выражение 0 : 6. По смыслу деления, чтобы разделить 6 на 0, нужно найти такое число, которое при умножении на 0 даст 6. Такого числа нет, т.к. при умножении числа на 0 будет получаться 0. Значит, на 0 делить нельзя. В учебнике Мы все «открыли» правильно да | Определение основной и второстепенной информации (П) Структурирование знаний (П) Аргументация своего мнения и ответа (К) Учет разных мнений в работе с коллективом (К) |
V. Словесный (беседа) Практический (выполнение упражнений) | 13 мин | Выполните номер 3 на странице 95, по цепочке Упражнение 4, по одному у доски Упражнение 5 первое решим вместе, остальное сами Упражнение 7, устно Блиц игра на слайде | 52 : 52= 1 94 : 1 = 94 975 : 975=1 0 : 48= 0 24 : 0 0 : 732= 0 16 : 16=1 56 : 1 = 56 0 : 294 = 0 Придумывают свои примеры Х : 9 Х = 9 72 : 9 = 8(р) в каждом пучке 32 : 8 = 4 (см) длина каждой части 35 : 5 =7 (дм2) площадь каждой части а:m (тет) у каждого ученика | умение контролировать процесс и результаты своей деятельности (проверка вычислений)(Р) Установление причинно-следственных связей (П) |
VI. Практический (выполнение упржнений) | 7 мин | Выполняем сейчас №9 самостоятельно. 1 вариант выполняет 1 сточку, а 2 вариант – 2 строчку. -Закончили, а теперь смотрим на экран. Сверьте свои ответы. — Кто сделал ошибки? В чем у вас было затруднение? надо быть внимательными. — Теперь выполним задание № 10. Прочитайте задание про себя. Выполняем у себя в тетради А) периметр = 12 см, площадь = 8 см2 Б) 2•4 = 8; 8: 4= 2; 8:2 = 4 ; 4•2 = 8 Ответ на доске, у кого так же? | Решают примеры Отвечают на вопрос Выполняют задание | Выполнение действий по алгоритму (П) Контроль (Р) Оценка(Р) Использование критериев для обоснования своего суждения (К) |
VII. Включение в систему знаний Словесный (беседа) | 2 мин | Как звучала тема урока? | Деление с 0 и 1 Ответы детей Ответы детей | Установление причинно-следственный связей (П) Построение логической цепи рассуждений (П |
VIII. Практический (анкетирование) | 2 мин | Школьникам предлагается небольшая анкета, наполнение которой можно менять, дополнять в зависимости от того, на какие элементы урока обращается особое внимание. 1. На уроке я работал 2. Своей работой на уроке я 3. Урок для меня показался 4. За урок я 5. Мое настроение 6. Материал урока мне был 7. Домашнее задание | мне кажется активно / пассивно доволен / не доволен коротким / длинным не устал / устал стало лучше / стало хуже понятен / не понятен полезен / бесполезен интересен / скучен легким / трудным интересным / неинтересным | Адекватное понимание причин успеха и неуспеха в учебной деятельности (Л) Выражение своих мыслей с достаточной полнотой и точностью (К) |
Правила деления в математике
Предоставление учащимся инструментов для решения деления с помощью этих сокращений не только делает деление менее сложным, но и делает его похожим на забавную головоломку. Для многих наличие четкого набора правил и структуры помогает прояснить концепцию и помогает учащимся решать уравнения и манипулировать выражениями. Возможность проверки делимости может помочь во многих математических настройках, таких как возможность проверить решение, уменьшить дроби или проверить правильность вычисления.
Для многих наличие четкого набора правил и структуры помогает прояснить концепцию и помогает учащимся решать уравнения и манипулировать выражениями. Возможность проверки делимости может помочь во многих математических настройках, таких как возможность проверить решение, уменьшить дроби или проверить правильность вычисления.
Каковы правила разделения?
Приступая к разделу о делении, обязательно поделитесь этими правилами с классом и обсудите их во время выступления по математике:
ДЕЛИМОСТЬ НА 2
Число, которое делится на 2, называется четным. Когда последняя цифра в числе равна 0 или даже четной, то есть 2, 4, 6 или 8, то число делится на 2. Например, 20 оканчивается на 0, поэтому оно делится на 2. Число 936 заканчивается в 6, а 6 четно. Значит, 936 делится на 2,9.0003
ДЕЛИМОСТЬ НА 3 Число делится на 3, если сумма цифр делится на 3. Чтобы использовать этот прием, учащиеся должны уметь делить, но проверка меньших чисел менее сложна, чем проверка больших. . Например, если вы спросите учащихся, делится ли 168 на 3, они должны ответить следующим образом:
. Например, если вы спросите учащихся, делится ли 168 на 3, они должны ответить следующим образом:
1 + 6 + 8 = 15
15/3 = 5
Следовательно, 168 делится на 3.
ДЕЛИМОСТЬ НА 4
Если последние две цифры числа делятся на 4, то делится и все число. Например, в 1012 12 делится на 4. Однако в 1013 13 не делится. Следовательно, 1012 делится на 4, а 1013 — нет.
ДЕЛИМОСТЬ НА 5Когда последняя цифра числа 0 или 5, число можно разделить на 5 без остатка. Таким образом, 5, 10, 15, 20, 25 и т. д. можно разделить на 5. Учащиеся могут посмотреть на большие числа и сразу сказать, можно ли их поровну разделить на пять частей.
ДЕЛИМОСТЬ НА 6
Числа, которые делятся на 6, также можно разделить на как на 3, так и на 2. Учащиеся должны проверить число с обоими правилами для 3 и 2. Если число проходит оба теста, его можно разделить на 6. Если он провалит хотя бы один тест, он не сможет. Например:
308 оканчивается на четную цифру, поэтому оно делится на 2. Однако 3 + 0 + 8 = 11, что не может делиться на 3 без остатка. Таким образом, 308 не делится на 6.
Однако 3 + 0 + 8 = 11, что не может делиться на 3 без остатка. Таким образом, 308 не делится на 6.
Большое число делится на 8, если последние три цифры также делятся на 8 или равны 000. В числе 7120 120 можно разделить на 8 без остатка, поэтому 7120 также делится на 8.
ДЕЛИМОСТЬ НА 9
Правило делимости 9 такое же, как и 3. Если сумма цифр числа делится на 9, так же как и весь номер. Например:
В числе 549 5 + 4 + 9 = 18
18/9 = 2
Итак, 549 делится на 9.
ДЕЛИМОСТЬ НА 10
Если последняя цифра может быть 0, то число разделить поровну на 10.
Почему правила помогают и как их использовать Эти правила позволяют учащимся рассматривать большие числа в менее сложном контексте. Правила делимости также позволяют им многое узнать о числе, просто взглянув на его цифры. Таким образом, вы должны поощрять учащихся использовать все правила при изучении числа. Глядя на что-то вроде 1159,350, учащиеся могут пройтись по списку делимости, отметив, на какие числа можно разделить большее число.
Глядя на что-то вроде 1159,350, учащиеся могут пройтись по списку делимости, отметив, на какие числа можно разделить большее число.
Конечно, на уроках математики вы будете говорить не только о четных делениях. Некоторые числа будут иметь остатки. Вы все еще можете использовать правила, чтобы говорить об этих числах. Предложите учащимся определить, будет ли у определенного числа остаток при делении на 2, 3, 4, 5, 6, 8 или 10. это вдохновляет учащихся увидеть ценность и цель математики в их повседневной жизни через полезные, реальные действия и уроки.
Как использовать MDAS (Видео с практическими вопросами)
ОбзорТранскриптПрактика
Что такое MDAS?
MDAS означает умножение, деление, сложение и вычитание. Он является частью Порядка операций, набора правил, который определяет последовательность упрощения математических операций . Он используется, когда выражение или уравнение имеют более одной операции. Согласно Порядку операций , любое умножение или деление должно выполняться до сложения или вычитания. Например, выражение \(6+4×5\) включает сложение и умножение. Согласно MDAS, перед сложением упростите часть выражения, связанную с умножением. Поскольку \(4×5\) равно \(20\), перепишем выражение как \(6+20\), что равно \(26\).
Согласно Порядку операций , любое умножение или деление должно выполняться до сложения или вычитания. Например, выражение \(6+4×5\) включает сложение и умножение. Согласно MDAS, перед сложением упростите часть выражения, связанную с умножением. Поскольку \(4×5\) равно \(20\), перепишем выражение как \(6+20\), что равно \(26\).
Почему мы используем эту систему?
Вспомним, что умножение — это многократное сложение, а это значит, что умножение более эффективно, чем сложение. А деление — это многократное вычитание, а это значит, что деление сильнее вычитания. Математики разработали порядок операций, чтобы упростить несколько операций в порядке их относительной силы. Как упростить выражения MDAS: Поскольку умножение и деление одинаково эффективны, вычисляйте эти две операции одновременно, работая слева направо. Как только все операции умножения и деления будут упрощены, оцените сложение и вычитание. Поскольку сложение и вычитание одинаково эффективны, оценивайте эти две операции одновременно, работая слева направо. Примеры:
Примеры:
- \(7-3+8\times5\)
| \(7-3+\mathbf{8\times5})\(7-3+\mathbf{8\times5})\ сложение и умножение. Согласно MDAS, упрощайте все операции умножения или деления перед сложением или вычитанием. Поэтому начните с упрощения \(8×5\). | |
| \(\mathbf{7-3}+40\) | Поскольку \(8×5=40\), перепишите выражение, используя \(40\). В выражении остаются две операции: вычитание и сложение. Поскольку эти операции равны по мощности, прочитайте выражение слева направо и упростите первую операцию, то есть \(7-3\). |
| \(\mathbf{4+40}\) | Поскольку \(7-3=4\), перепишите выражение, используя \(4\). Далее решите \(4+40\). |
| \(44\) | \(4+40=44\). Следовательно, \(7-3+8×5\) можно упростить до \(44\). |
- \(24\div4\times3\)
\(\mathbf{24\div4}\times3\) деление 6. Поскольку обе операции имеют одинаковую мощность, прочитайте выражение слева направо и упростите первую операцию, то есть \(24÷4\). Поскольку обе операции имеют одинаковую мощность, прочитайте выражение слева направо и упростите первую операцию, то есть \(24÷4\). | |
| \(\mathbf{6\times3}\) | Поскольку \(24÷4=6\), перепишите выражение, используя \(6\). Далее решите \(6×3\). |
| \(\mathbf{18}\) | \(6×3=18\). Следовательно, \(24÷4×3\) можно упростить до \(18\). |
- \(6+10×2÷4\)
| \(6+\mathbf{10\times2}\div4\) 901 разделение. Согласно MDAS, упрощайте все операции умножения или деления перед сложением или вычитанием. Читая выражение слева направо, начните с умножения \(10×2\). | |
| \(6+\mathbf{20\div4}\) | Поскольку \(10×2=20\), перепишите выражение, используя \(20\). В выражении остаются две операции — сложение и деление. Согласно MDAS, упрощайте все операции умножения или деления перед сложением или вычитанием. Поэтому упростите \(20÷4\). |
| \(\mathbf{6+5}\) | Поскольку \(20÷4=5\), перепишите выражение, используя \(5\).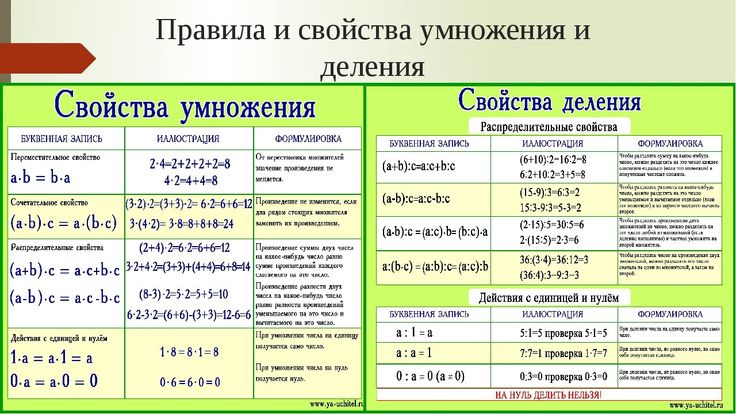 Далее решите \(6+5\). Далее решите \(6+5\). |
| \(11\) | \(6+5=11\). Следовательно, \(6+10×2÷4\) можно упростить до \(11\). 99010 , деление, умножение и вычитание. Согласно MDAS, упрощайте все операции умножения или деления перед сложением или вычитанием. Читая выражение слева направо, начните с упрощения \(81÷9\). |
| \(5+\mathbf{9×3}-7\) | Поскольку \(81÷9=9\), перепишите выражение, используя \(9\). В выражении остаются три операции: сложение, умножение и вычитание. Согласно MDAS, упрощайте все операции умножения или деления перед сложением или вычитанием. Поэтому упростите \(9×3\). |
| \(\mathbf{5+27} -7\) | Поскольку \(9×3=27\), перепишите выражение, используя \(27\). В выражении остаются две операции: сложение и вычитание. Поскольку обе операции имеют одинаковую мощность, прочитайте выражение слева направо и упростите первую операцию, то есть \(5+27\). |
| \(\mathbf{32-7}\) | Поскольку \(5+27=32\), перепишите выражение, используя \(32\). Далее решите \(32-7\). Далее решите \(32-7\). |
| \(25\) | \(32-7=25\). Следовательно, \(5+81÷9×3-7\) можно упростить до \(25\). |
Здравствуйте! Сегодня мы поговорим о MDAS . Эта аббревиатура может показаться немного знакомой, потому что она является частью порядка операций (PEMDAS). Таким образом, PEMDAS означает: круглые скобки, показатели степени, умножение, деление, сложение и вычитание. Итак, MDAS — это последняя часть. Он сообщает вам, в каком порядке выполнять операции в выражении. Итак, сначала у нас есть M и D, а затем у нас есть A и S. Сложение и вычитание, когда вы упрощаете выражение. Итак, мы хотим выполнить все операции умножения и деления слева направо, а затем все операции сложения и вычитания слева направо. Важно сгруппировать умножение и деление вместе, а также сложение и вычитание вместе, потому что вы можете умножать и делить в любом порядке, если они предшествуют сложению и вычитанию. И то же самое с этим — вы можете складывать и вычитать в любом порядке (обычно вы идете слева направо).
Давайте рассмотрим несколько примеров.
\(84-8\дел 2\умножить на 3\)
Сначала найдите любое умножение или деление. Здесь у нас есть оба, поэтому нам нужно упростить их слева направо. Начните с деления 8 на 2.
\(84-4\умножить на 3\)
Затем умножьте 4 на 3.
\(84-12\)
. Вычтите 12 из 84.
\(84-12=72\)
Таким образом, это выражение упрощается до 72,
Давайте попробуем еще раз!
\(16+8\умножить на 4-9\дел 3\)
Начните с упрощения любого умножения или деления в порядке слева направо. Сначала умножьте 8 на 4.
\(16+32-9\дел 3\)
Затем разделите 9 на 3.
\(16+32-3\)
Отсюда, упростить сложение и вычитание слева направо. Сложите 16 и 32.
\(48-3\)
Наконец, вычтите 3 из 48.
\(48-3=45\)
Таким образом, ответ равен 45.
Давайте решим вместе последнюю задачу перед тем, как идти.
\(18\дел 3-2+4\умножить на 9-11\)
Начните с упрощения любого умножения или деления в порядке слева направо. Сначала разделите 18 на 3.
\(6-2+4\умножить на 9-11\)
Затем умножьте 4 на 9.
\(6-2+36-11\)
Отсюда упростите сложение и вычитание слева направо. Вычтите 2 из 6.
\(4+36-11\)
Затем прибавьте 4 и 36.
\(40-11\)
29\)
Вот и все! Я надеюсь, что это видео о MDAS было полезным. Спасибо за просмотр и удачной учебы!
Вопрос №1:
Упростите с помощью MDAS следующее: 12\)
\(13\)
Show Answer
Answer:
MDAS is part of the Order of Operations (PEMDAS):
Parentheses
Exponents
Multiply
Divide
Add
Subtract
Перед сложением и вычитанием необходимо выполнить умножение и деление. В этом примере первый шаг равен \(3×1\).
В этом примере первый шаг равен \(3×1\).
\(4+3+6-1\)
Отсюда остаются только сложение и вычитание, так что просто двигайтесь слева направо. Это упрощается до \(12\).
Скрыть ответ
Вопрос №2:
Упростите следующее с помощью MDAS:
\(60×2+5-3+8×6-1\)
\(169\)
3 (170\)
\(171\)
\(172\)
Показать Ответ
Ответ:
Перед сложением и вычитанием необходимо выполнить умножение и деление. В этом примере первый шаг равен \(60×2\), затем \(8×6\). Это оставляет \(120+5-3+48-1\). Отсюда остаются только сложение и вычитание, поэтому действуйте слева направо. Это упрощается до \(169\).
Скрыть ответ
Вопрос №3:
Упростите с помощью MDAS:
\(16÷2÷4+4×2-16×4\)
\(46\)
0 (-54\)
\(-46\)
\(81\)
Показать ответ
Ответ:
Перед сложением и вычитанием необходимо выполнить умножение и деление. В этом примере первый шаг равен \(16÷2÷4\). Работая слева направо для этого раздела, у вас останется \(2\). Теперь упростите \(4×2\) и \(16×4\). Теперь этап умножения и деления завершен.
В этом примере первый шаг равен \(16÷2÷4\). Работая слева направо для этого раздела, у вас останется \(2\). Теперь упростите \(4×2\) и \(16×4\). Теперь этап умножения и деления завершен.
Отсюда переходим к сложению и вычитанию. Упрощение слева направо дает \(-54\).
Скрыть ответ
Вопрос №4:
Упростите с помощью MDAS следующее:
\(24÷6+1+8+3×(-4)-11\)
\(8\)
\(-10\)
\(10\)
\(-8\)
Показать ответ
Ответ:
Перед сложением и вычитанием необходимо выполнить умножение и деление. В этом примере первый шаг равен \(24÷6\) и \(3×-4\). Теперь у нас есть \(4+1+8+(-12)-11\), что упрощается до \(-10\).
Скрыть ответ
Вопрос № 5:
\(7+3-2,5×(-3)-0,5+3\)
\(
\) \(5.
 Красиво встали, посмотрели друг на друга, улыбнулись и тихонечко сели.
Красиво встали, посмотрели друг на друга, улыбнулись и тихонечко сели.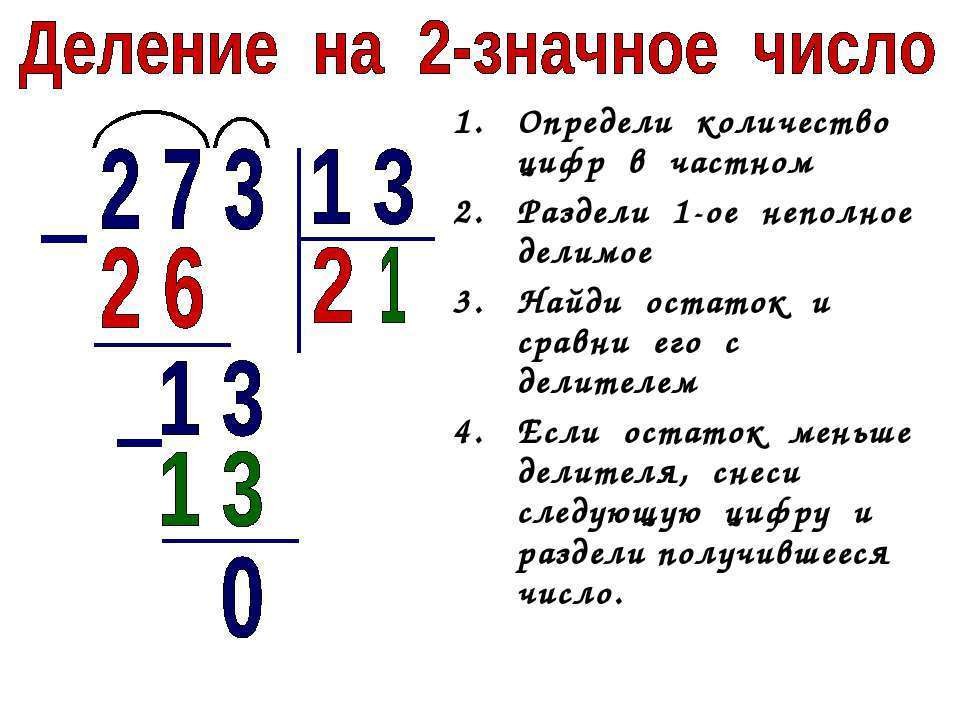 Только сегодня вы узнаете кое-что новое о делении. Вам нужно будет самим открыть новое знание
Только сегодня вы узнаете кое-что новое о делении. Вам нужно будет самим открыть новое знание д.
д.

 Это число 7, т.к. при умножении числа на 1, будет получаться то же самое число. Поэтому 7:1 = 7. Значит, можно сделать вывод. При делении числа на 1, будет получаться то же самое число
Это число 7, т.к. при умножении числа на 1, будет получаться то же самое число. Поэтому 7:1 = 7. Значит, можно сделать вывод. При делении числа на 1, будет получаться то же самое число Первичное закрепление во внешней речи
Первичное закрепление во внешней речи Самостоятельная работа с самопроверкой
Самостоятельная работа с самопроверкой Рефлексия деятельности
Рефлексия деятельности