Алгоритмы письменного умножения и деления многозначных чисел
Алгоритмы письменного умножения и деления многозначных чисел.
Этапы изучения темы:
умножение и деление на однозначное число;
умножение и деление на двузначные и трехзначные разрядные числа;
умножение и деление на двухзначные и трехзначные числа.
Умножение и деление изучаются одновременно на каждом этапе, но сначала – умножение, затем – деление.
На каждом этапе наряду с умножением и делением натуральных чисел изучается умножение и деление величин на число.
Частные случаи:
Умножение
-первый и второй множитель оканчиваются нулями 87600*4,376*240
-нули в середине второго множителя 875*304
-различные сочетания этих случаев 170*230, 1630*103
Деление:
-частное оканчивается нулями 227200:4=56800
-нули в середине частного 72450:7=10350.
Умножение многозначных чисел на однозначное число
К письменному приему обращаемся только тогда, когда устно решить трудно.
54879*5
А лгоритм:
-записать числа в столбик (однозначное число под единицами многозначного)
-умножить единицы I множителя на II множитель, результат записать по единицами;
-умножить десятки I множителя на II, результат записать под десятками;
-аналогичные действия проделать со всеми основными разрядами I множителя;
-прочитать полученный результат.
Далее, опираясь на алгоритм, дети решают аналогичные выражения, при этом фиксируют словами каждую операцию (комментируют). Выражения подбираются в усложняющейся последовательности:
-увеличивается I множитель 284*3 2934*5 28751*7
-I множитель содержит нули (частный случай).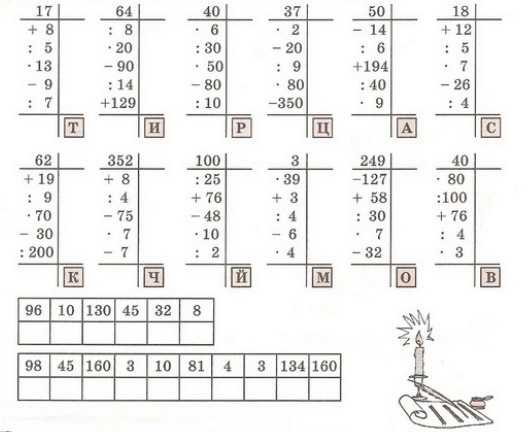
На освоение алгоритма умножения – задания на нахождение преднамеренно допущенных ошибок.
Например: 7056 8539 5700
8 2 9
56408
II этап умножение на двузначные и трехзначные разрядные числа
621*30. Используя свойство а*(в*с), показываем детям целесообразность записи 621*(3*10) 621
30
Особое внимание заслуживают выражения, где оба множителя заканчиваются нулями.
Устно: 300*50 (3 сот * 5)*10=15 сот*10=150 сот=15000.
Письменно: аналогично вышеприведенному случаю 7800
30
234000
Вывод: сначала решать без нулей, затем посчитать сколько их и приписать.
7тыс*30=~210000= в ответе не меньше 6 цифр.
При выполнении умножения «в столбик» обязательно делать прикидку.
III этап умножения на двухзначное и трехзначное число
87*64, 286*374
А лгоритм:
1.Записать числа в столбик, единицы под единицами; десятки под десятками.
2.Умножить I множитель на единицы II множителя – получится I неполное произведение, результат записать под единицами.
3.Умножить I множитель на десяток II множителя – получится II полное произведение, записать результат на один разряд влево, под десятки.
4.Далее действия повторяются.
5.Сложить все неполные произведения.
6.Записать и прочитать полученный результат.
Новое понятие «неполное произведение».
Закрепление:
-расписать 286*374
-по плану решения составить пример 84*6+84*30
-сравнить 138*14 и 138*40 алгоритмы.
-376*4+376*10 на какое число умножаем?
-решить удобным способом:
32*2*50= 73*6*3+73*2=
54*80+54*20= 83*16+17*16=
Частные случаи умножения чисел, содержащих нули.
Умножение чисел, оканчивающихся нулями, знакомы детям =больше самостоятельности.
158
4003
Эти виды выражений трудны для детей. (Сдвиг цифр на 2 или 3 цифры влево). Использовать «нерациональный» способ! Пока слабые дети не будут ориентированы.
158
4003
474
000 000
000
63648 632
632474
После вводится умножение величин выражений в 2 наименованиях.
Закрепление: аналогично.
Деление многозначных чисел.
I этап – деление на однозначное число.
Алгоритм:
1.Записать пример в столбик.
2.Выбрать первое неполное делимое. Определить количество цифр в частном.
3.Методом подбора найти первую цифру частного.
4.Проверить правильность выбора первой цифры частного, умножив её на делитель.
5.Полученное число сравнить с I неполным делимым (с помощью вычитания).
6.Получившийся остаток сравнить с делителем:
а)если остаток
б)если остаток = делимому, то допущена ошибка при подборе цифры частного (цифру увеличить)
в)остаток = 0, деление закончено (в одном случае)
г)(в другом) 0 является промежуточным результатом, надо снести цифру исходного делимого и получить II неполное делимое.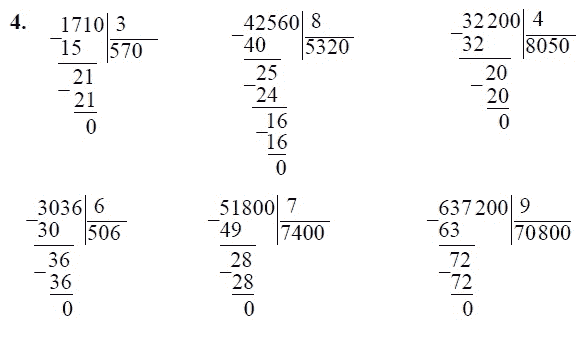
7.II неполное делимое сравнить с делимым:
а)если оно = делителя, то произвести подбор второй цифры частного
б)если оно
8.Аналогично подбираются следующие цифры частного.
9.Записать и назвать полученный результат.
Постепенно примеры усложняются: увеличивается число разрядов в делимом (3,4,5,6 значные числа)
Частные случаи: (в записи частного встречается 0)
22720:4=5680 – полностью весь алгоритм и последнее 0:4=0. Частное…
4254:6=709 – дети часто пропускают 0.
Для предупреждения ошибок:
-определить количество цифр в частном;
-проверка умножением;
-проверка неправильным решением примеров.
На этом же этапе решаем примеры на деление с остатком и деление однородных величин.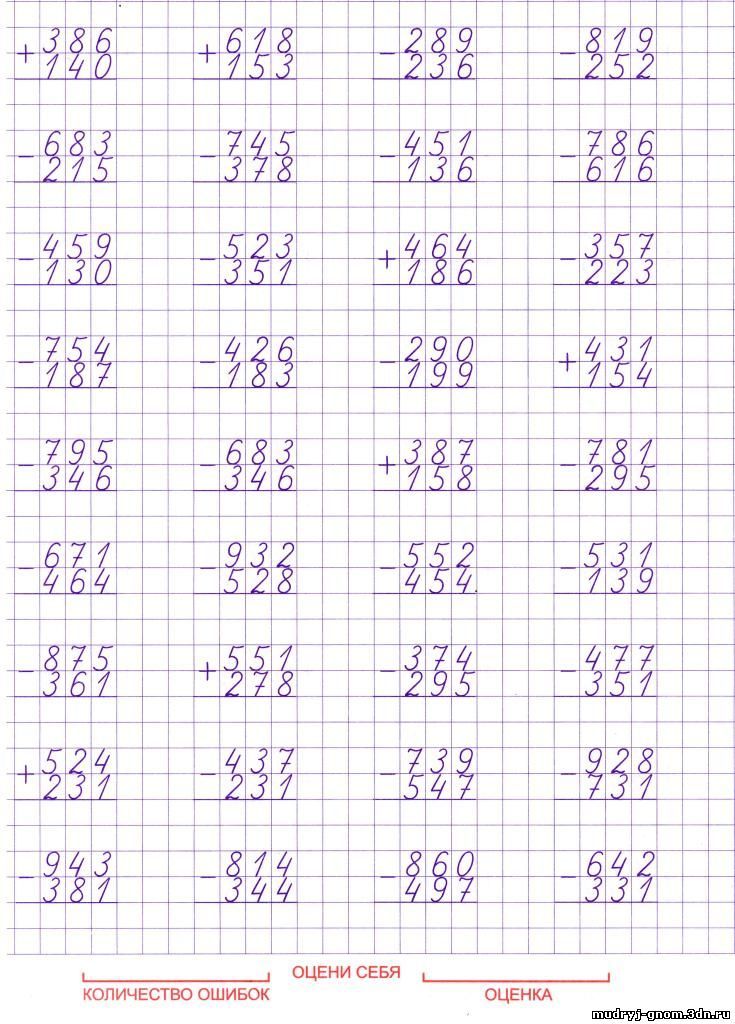
II этап. Деление на двухзначные и трехзначные разрядные числа
Письменные приемы:
4980:60
480
180
180
Делимое 498 десятков =в частном 2 цифры. Здесь перемешивать деление с остатком и без остатка.
Частные случаи: Дети могут разобрать аналогично предыдущему. Так же и деление на разрядные трехзначные числа.
III этап. Деление на двухзначное и трехзначное число.
а)деление трехзначного числа на двухзначное, цифра после одной пробы, в частном однозначное число
315 : 63=5
Чтобы найти цифру частного округлим делитель ближайшим разрядным числом (60)=31:6…
б)деление четырех, пяти, шестизначных чисел на двухзначное, цифра частного после одной пробы
3456:54=64
в)деление трехзначного числа на двухзначное = однозначное (несколько проб) 464:58=8 (9 много)
г)деление четырехзначного, пятизначного, шестизначного числа без остатка и с остатком 4042:47=
делитель округлять в меньшую сторону!
Прием деления на трехзначное число аналогично.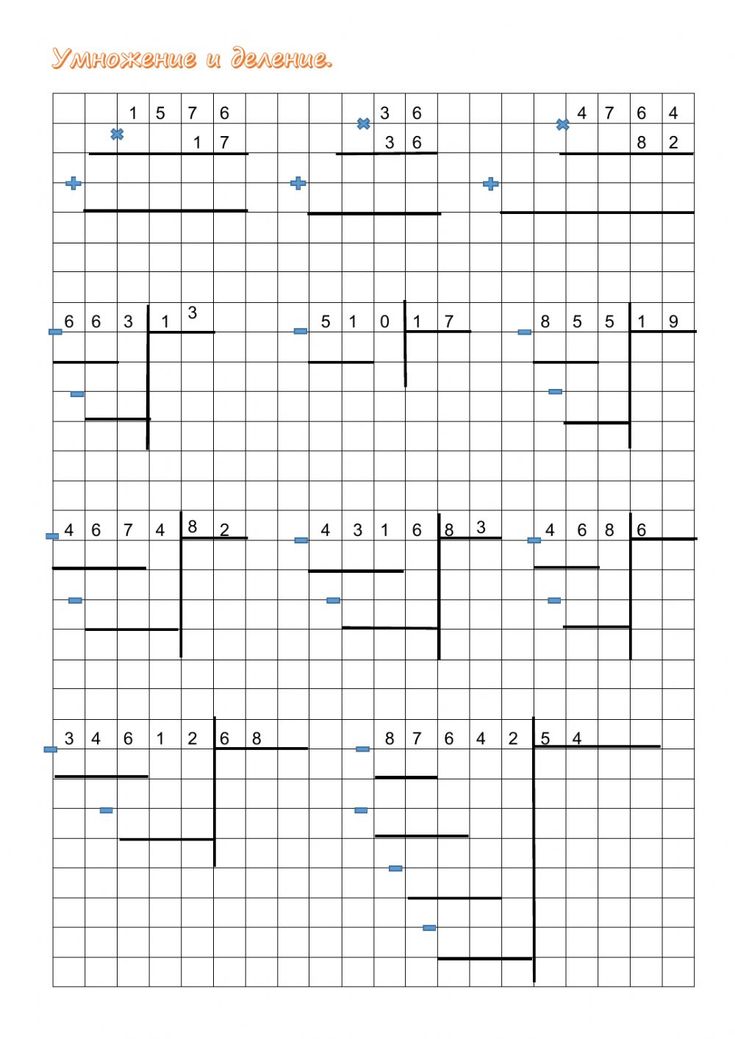
Математика 4 класс — Kid-mama
[spacer height=»5px» id=»2″]Перейти в каталог тренажёров с изображениями[spacer height=»5px» id=»2″]
- Числа больше 1000. Разрядный состав числа. (8)
- Действия с большими числами (12)
- Деньги (2)
- Меры длины, площади, веса, объема, времени (9)
[su_label type=»important»]mobil[/su_label] — работает на мобильных устройствах
[su_table][ps2id id=’ss1′ target=»/]
| Числа больше 1000 | ||
| [su_dropcap style=»flat» size=»2″ class=»ared1″]1.1[/su_dropcap] | Числа от 1 до 1000 (тест, 17 разных заданий) | Тест [su_label type=»important»]mobil[/su_label] |
| [su_dropcap style=»flat» size=»2″ class=»ared1″]1.2[/su_dropcap] | Запиши число. Числа больше 1000 записаны словами, а вам нужно записать их цифрами. | Тренажер [su_label type=»important»]mobil[/su_label] |
| [su_dropcap style=»flat» size=»2″ class=»ared1″]1.3[/su_dropcap] | Напиши соседей числа больше 1000. | Тренажер [su_label type=»important»]mobil[/su_label] |
| [su_dropcap style=»flat» size=»2″ class=»ared1″]1.4[/su_dropcap] | Сравни числа больше 1000. | Тренажер [su_label type=»important»]mobil[/su_label] |
| [su_dropcap style=»flat» size=»2″ class=»ared1″]1.5[/su_dropcap] | Сколько в числе всего десятков (сотен, единиц тысяч и т.д.) | Тренажер [su_label type=»important»]mobil[/su_label] |
| [su_dropcap style=»flat» size=»2″ class=»ared1″]1.6[/su_dropcap] | Запиши число, в котором 3 ед. III класса, 2 ед I класса. | Статья + Тренажер [su_label type=»important»]mobil[/su_label] |
| [su_dropcap style=»flat» size=»2″ class=»ared1″]1.7[/su_dropcap] | Запиши число, в котором 5 ед. 6 разряда, 4 ед. 2 разряда 6 разряда, 4 ед. 2 разряда | Тренажер [su_label type=»important»]mobil[/su_label] |
| [su_dropcap style=»flat» size=»2″ class=»ared1″]1.8[/su_dropcap] | Числа больше 1000. Нумерация. Тест (разные задания)[ps2id id=’ss2′ target=»/] | Тест [su_label type=»important»]mobil[/su_label] |
| [showads ad=adapt1] | ||
| Действия с большими числами | ||
| [su_dropcap style=»flat» size=»2″ class=»ablow1″]2.1[/su_dropcap] | Действия с большими числами. № 1 (устный счет) | Тренажер [su_label type=»important»]mobil[/su_label] |
| [su_dropcap style=»flat» size=»2″ class=»ablow1″]2.2[/su_dropcap] | Действия с большими числами №2 (устный счет) | Тренажер [su_label type=»important»]mobil[/su_label] |
| [su_dropcap style=»flat» size=»2″ class=»ablow1″]2.3[/su_dropcap] | Умножение и деление на 10, 100, 1000 Деление на 10, 100, 1000 с остатком | Тренажёр [su_label type=»important»]mobil[/su_label] |
[su_dropcap style=»flat» size=»2″ class=»ablow1″]2. 4[/su_dropcap] 4[/su_dropcap] | Сложение столбиком | Тренажер [su_label type=»important»]mobil[/su_label] |
| [su_dropcap style=»flat» size=»2″ class=»ablow1″]2.5[/su_dropcap] | Вычитание столбиком | Тренажер [su_label type=»important»]mobil[/su_label] |
| [su_dropcap style=»flat» size=»2″ class=»ablow1″]2.6[/su_dropcap] | Вычитание столбиком из чисел с нулями | Тренажер [su_label type=»important»]mobil[/su_label] |
| [su_dropcap style=»flat» size=»2″ class=»ablow1″]2.7[/su_dropcap] | Умножение столбиком на однозначное число | Тренажер [su_label type=»important»]mobil[/su_label] |
| [su_dropcap style=»flat» size=»2″ class=»ablow1″]2.8[/su_dropcap] | Умножение столбиком чисел с нулями на конце | Тренажер [su_label type=»important»]mobil[/su_label] |
| [su_dropcap style=»flat» size=»2″ class=»ablow1″]2.9[/su_dropcap] | Деление столбиком на однозначное число | Тренажёр [su_label type=»important»]mobil[/su_label] |
[su_dropcap style=»flat» size=»2″ class=»ablow1″]2. 10[/su_dropcap] 10[/su_dropcap] | Деление столбиком на двузначное число | Тренажёр [su_label type=»important»]mobil[/su_label] |
| [su_dropcap style=»flat» size=»2″ class=»ablow1″]2.11[/su_dropcap] | Умножение столбиком на двузначное число | Тренажер [su_label type=»important»]mobil[/su_label] |
| [su_dropcap style=»flat» size=»2″ class=»ablow1″]2.12[/su_dropcap] | Проверь себя. Сложение, вычитание, умножение в столбик. [ps2id id=’ss3′ target=»/] | Тренажёр [su_label type=»important»]mobil[/su_label] |
| Деньги | ||
| [su_dropcap style=»flat» size=»2″ class=»agreen1″]3.1[/su_dropcap] | «Денежный счет» — считаем купюры и монеты. | Игра — тренажер [su_label type=»important»]mobil[/su_label] |
| [su_dropcap style=»flat» size=»2″ class=»agreen1″]3.2[/su_dropcap] | Набери нужную сумму денег при помощи купюр и монет. [ps2id id=’ss4′ target=»/] | Игра — тренажер [su_label type=»important»]mobil[/su_label] |
| Меры длины, площади, веса, объема, времени | ||
| [su_dropcap style=»flat» size=»2″ class=»ared1″]4.1[/su_dropcap] | Сантиметр и миллиметр | Тренажер [su_label type=»important»]mobil[/su_label] |
| [su_dropcap style=»flat» size=»2″ class=»ared1″]4.2[/su_dropcap] | Дециметр, сантиметр, миллиметр | Тренажер [su_label type=»important»]mobil[/su_label] |
| [su_dropcap style=»flat» size=»2″ class=»ared1″]4.3[/su_dropcap] | Метр, дециметр, сантиметр | Тренажер [su_label type=»important»]mobil[/su_label] |
| [su_dropcap style=»flat» size=»2″ class=»ared1″]4.4[/su_dropcap] | Километры и метры | Тренажер [su_label type=»important»]mobil[/su_label] |
| [su_dropcap style=»flat» size=»2″ class=»ared1″]4.5[/su_dropcap] | Меры площади: км2, м | Тренажер [su_label type=»important»]mobil[/su_label] |
| [su_dropcap style=»flat» size=»2″ class=»ared1″]4.6[/su_dropcap] | Ар, гектар | Тренажер [su_label type=»important»]mobil[/su_label] |
| [su_dropcap style=»flat» size=»2″ class=»ared1″]4.7[/su_dropcap] | Единицы массы : г, кг, ц, т | Тренажер [su_label type=»important»]mobil[/su_label] |
| [su_dropcap style=»flat» size=»2″ class=»ared1″]4.8[/su_dropcap] | Час, минута, секунда. | Тренажер [su_label type=»important»]mobil[/su_label] |
| [su_dropcap style=»flat» size=»2″ class=»ared1″]4.9[/su_dropcap] | Измерение углов транспортиром — обучающая онлайн игра | Обучающая онлайн игра |
[/su_table]
Миссис Рейндель — Могучее умножение
Могучее умножение и доминантное деление
Если бы мне просто захотелось узнать, сколько полос или столбцов было, я мог бы сосчитать количество полос (14) и умножьте это число на 1 (потому что есть один набор столбцов), чтобы узнать, сколько существует полос или столбцов. 14×1= 14.
14×1= 14.
Если по какой-то причудливой причине я хочу знать, сколько разделов во всем заголовке, мне нужно взять количество столбцов (14), а затем подсчитать количество штук в одном разделе. (Я насчитал 26.) Затем я умножал столбцы на количество разделов в каждом столбце. 1 4 х 2 6 =
14 столбцов x 26 штук
Вышеприведенный заголовок является хорошей моделью для 14×26.
Итак, что такое 14×26?
Я могу решить эту проблему, используя модель области.
Я также могу решить эту проблему, разделив числа 14 и 26 на их позиционные значения.
2 6 = 20 + 6 и 1 4 = 10 + 4
Здесь происходит следующее:
2 0 x 10 + 20 x 4 и 6 x 10 + 6 x 4
20 x 10 = 200 + 20 x 4 = 80 и 6 x 10 = 60 + 6 x 4 = 24
200+80 = 280 и 60 + 24 = 84
сложите оба произведения вместе: 280 + 84 = 364
Итак, 26 x 14 = 364
В заголовке баннера выше 364 раздела.
В четвертом классе учащиеся могут использовать стандартный алгоритм для решения 26x 14
2 Вы видите, как работает разложение чисел на разряды
2 6 чтобы получить такой же ответ на 26×14 как стандартный алгоритм?
x 1 4
——————
1 0 4 Здесь я показал 2 разных метода.
+ 2 6 0 для решения той же задачи 26×14
——————- Математика такая классная.
3 6 4 Есть несколько способов решить проблему!
Этот клип представляет собой разговор о числах умножения. Это отлично.
Трехзначное умножение 4 класс, 5 класс
В видеоролике ниже показаны 2 примера.
Нажмите на синюю ссылку ниже.
В этом примере показана модель области и стандартный алгоритм
, чтобы найти решение для:
3 5 2 x 4 8 1
(Это полный адрес, вы можете вырезать и вставить его в браузер.)
https://www.khanacademy.org/math/arithmetic/arith-review-multiply-divide/arith-review-place-value-area-models/v/multiplying-using-area-models-and-the-standard- алгоритм
Полезно помнить, как разбивать числа на их разрядные значения.
352= 300+50+2 481= 400+80+1
Теперь вы можете себе представить, где бы вы нарисовали линии, чтобы создать модель области? Объясните, как решить эту проблему?
400 80 1
300
50
2
Обратите внимание, что на этот раз я показал 352 как 300+50+2. В модели площади в ролике 352 записывается как 2+50+300.
Это свидетельствует о распределительном свойстве.
Какой ответ вы получили? Так же, как в видеоклипе?
Можете ли вы придумать другой способ решения 352×481?
многократное сложение или умножение ?
3+3+3=9 или, 3×3=9
Видеоклип внизу слева — хорошее введение в умножение.
Видеоклип ниже справа помогает показать, как связаны умножение и деление.
youtube.com/embed/dPksJHBZs4Q» allowfullscreen=»»/>Когда вы умножаете, подумайте: сколько групп из скольких вещей или сколько вещей в скольких группах. Когда мы умножаем, мы находим общее количество групп или вещей.
Берем 2 части и умножаем, чтобы найти целое.
Да, когда мы делим, мы берем целое и разделяем ~ или делим это целое на группы.
8 разделить на 2
Всего у меня 8 штук. * * * * * * * *
* * * * * * * *
Я разделяю их или делю 8 на 2 группы. * * * * l * * * *
В каждой группе по 4 элемента * * * * * * * *
Итак, 8 разделить на 2 равно 4
Ниже представлен забавный ролик, который помогает объяснить деление. Наслаждаться! (Ты будешь танцевать в такт?) 4 9 класс0005
класс 4,5
В Фейрпорте мы начинаем с метода деления, используя частичные частные, чтобы помочь нашим ученикам понять операцию с точки зрения разрядного значения. Посмотрите видеоклип ниже в качестве еще одной демонстрации.
Математика есть математика, это просто другой способ решения с упором на понимание разрядного значения.
класс (4)5
В приведенном выше примере показан другой способ деления. Это называется длинным делением.
5 класс
Ого! Это длинное деление с БОЛЬШИМИ числами.
Расслабьтесь, дети. Процесс такой же, как в примере выше.
Осталось совсем немного номеров! Дыши, ты понял!
Снимок выше был сделан в магазине домашних сладостей в Техасе.
Вы видите целых 5 лотков с конфетами.
Вам нужно знать, сколько конфет в одном полном лотке.
Можете ли вы оценить (т.е. не считая единиц), сколько конфет на этой картинке?
Будете ли вы использовать умножение, деление, сложение или вычитание, чтобы помочь вам?
Как знание числа в целом лотке поможет вам узнать, сколько их в 5 полных лотках?
Что делать с пропавшими конфетами? Они добавляются или вычитаются?
Если бы все подносы были полны, сколько было бы конфет?
Какой вкус должен быть внутри шоколада?
Когда дети изучают умножение и деление
Из всех математических операций умножение и деление могут быть самыми трудными для изучения детьми. Овладение этими навыками — логичный следующий шаг после сложения и вычитания. Но на самом деле это скорее скачок для большинства детей. Узнайте, когда дети учатся умножать и делить.
Но на самом деле это скорее скачок для большинства детей. Узнайте, когда дети учатся умножать и делить.
Когда дети обычно изучают умножение
Обучение умножению можно начинать уже во втором классе. Дети обычно начинают с объединения равных групп (3 + 3 + 3 = 9)., что соответствует 3 × 3 = 9). Это называется повторным добавлением.
Вот как и когда дети учатся умножать:
Исследуйте темы, выбранные нашими экспертами
Математика
- Во втором классе дети учатся визуализировать повторяющееся сложение. (Это похоже на рисование квадрата с пятью строками и пятью столбцами для представления 5 × 5 = 25.)
- В третьем классе дети начинают понимать связь между умножением и делением. (Это как знать, что 3 × 4 = 12, а 12 ÷ 4 = 3.)
- В четвертом классе детей начинают умножать двузначные числа на двузначные числа.
Чтобы научиться умножению, дети используют практические материалы и наглядные модели, чтобы разбить числа и построить концепцию.
К концу пятого класса большинство детей знают, как использовать распространенную процедуру умножения больших чисел. Некоторым нужно немного больше времени и практики, чтобы полностью понять концепцию.
Когда дети обычно изучают деление
Деление обычно является самым сложным математическим понятием для детей. Уравнение деления состоит из трех частей:
- Делимое — это число, которое нужно разделить (первое число в задаче).
- Делитель — это число, на которое делится делимое (второе число в задаче).
Обучение делению начинается в третьем классе. Дети знакомятся с понятием, выполняя многократное вычитание. (Например, 20 – 5, затем еще 5, и еще 5, и еще один 5. Это то же самое, что 20 ÷ 4.)
Вот как и когда дети учатся делить:
- В третьем классе детей начинают делить путем многократного вычитания. Они учатся делить две цифры на однозначные числа с решениями больше 10.
- В четвертом классе дети начинают учиться делить четырехзначные числа на однозначные числа.
 (Например, 4000 ÷ 2.)
(Например, 4000 ÷ 2.) - В пятом классе детей начинают делить четырехзначные числа на четырехзначные числа. (Например, 8 000 ÷ 4 000.) Кроме того, большинство детей знакомятся с десятичными дробями в пятом классе.
Ожидается, что дети полностью поймут, как умножать и делить, прежде чем перейдут в среднюю школу. Но это не значит, что каждый ребенок это поймет. Некоторым детям нужно больше времени и практики.
Почему у некоторых детей возникают проблемы с умножением и делением
У детей нередко возникают проблемы с математикой, особенно с умножением и делением. Для этого есть много причин и много способов помочь. Поддержка, такая как отдельное обучение или обучение в небольшой группе, может со временем иметь большое значение.
Например, у некоторых детей возникают проблемы с пониманием основных математических понятий, известных как чувство числа. Проблемы с концентрацией внимания или памятью могут повлиять на изучение математики.
 (Например, 4000 ÷ 2.)
(Например, 4000 ÷ 2.)