Деление столбиком 2 класс объяснение: Как объяснить ребенку деление столбиком — «Семья и Школа»

Содержание

Как объяснить ребенку деление столбиком — «Семья и Школа»

Содержание

Деление в столбик — объяснение и примеры…

Привет, мой друг, тебе интересно узнать все про деление в столбик — объяснение , тогда с вдохновением прочти до конца. Для того чтобы лучше понимать что такое деление в столбик — объяснение , настоятельно рекомендую прочитать все из категории Арифметика.

Деление — Арифметическое действие, по к-оторому узнается, сколько раз одно число содержится в другом.

Если вы родитель , то объясните ребенку, что, в математике, действие, противоположное умножению, называется «деление».

Оперируя таблицей умножения, продемонстрируйте ученику на любом примере взаимосвязь между умножением и делением.

Пример: 3х4=12. результатом умножения является произведение двух чисел. После этого объясните, что операция деления, является обратной операции умножения и проиллюстрируйте это наглядно.

В нашем пример разделите получившееся произведение «12» – на любой из множителей – «3» или «4», и результатом всегда будет другой, не использовавшийся в операции множитель, то есть «4» или «3».

Также нужно знать термины, используемые в операции деления – «делимое», «делитель» и «частное».

Для деления чисел из двух и более цифр (знаков) применяют деление в столбик.

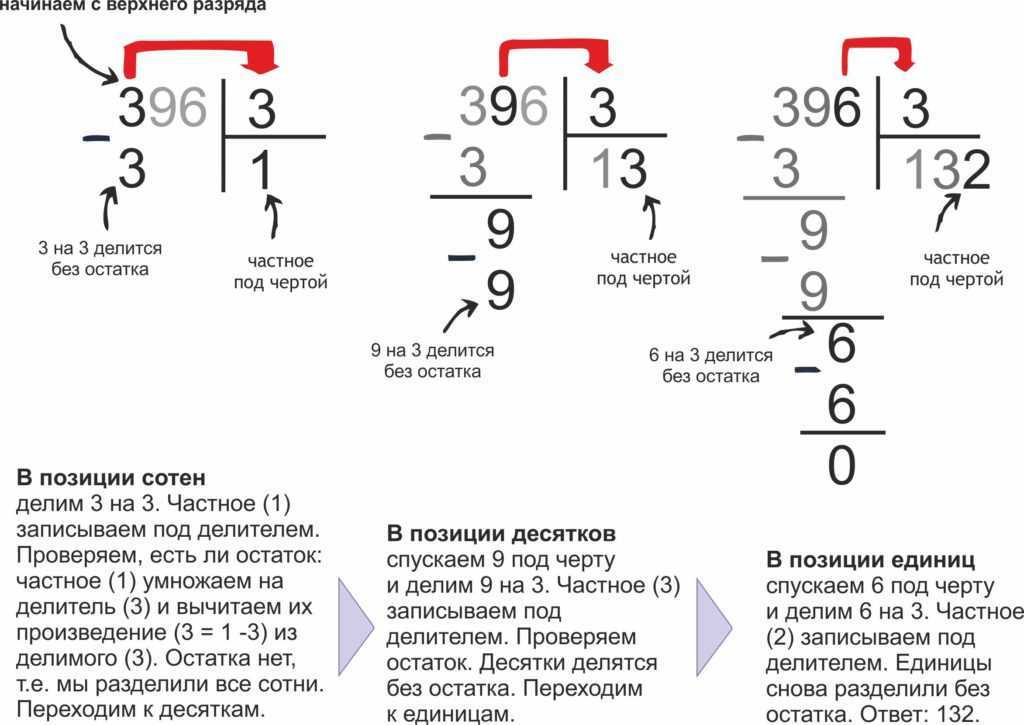
Посмотрим на примере как делить столбиком.

Вычислить:

Для начала запишем делимое и делитель в столбик . Об этом говорит сайт https://intellect.icu . Выглядеть это будет так:

Их частное (результат) будем записывать под делителем. У нас это цифра 8.

Начинаем делить 512 на 8 следующим образом:

Определяем неполное частное. Для этого слева направосравниваем цифры делимого и делитель.
Берем 5. Цифра 5 меньше 8, значит нужно взять еще одну цифру из делимого.
51 больше 8. Значит это неполное частное. Ставим точку в частном (под уголком делителя). Для того, чтобы избежать ошибок, не забывайте определять количество цифр в частном.
Для этого посчитаем сколько цифр осталось в делимом, после неполного частного. У нас после 51 стоит только одно цифра 2. Значит и добавляем в результат еще одну точку.
Приступаем к делению. Вспоминая таблицу умножения на 8, находим ближайшее к 51 произведение.
6 x 8 = 48
Записываем цифру 6 в частное.
Записываем 48 под 51.

При записи под неполном частным самая правая цифра неполного частного должна стоять над самой правой цифрой произведения.

Между 51 и 48 слева поставим «-» (минус). Вычтем по правилам вычитания в столбик 48 и под чертой запишем результат.
В остатке получилось 3. Сравним остаток с делителем. 3 меньше 8.
Если остаток получился больше делителя, значит мы ошиблись в расчете и есть произведение более близкое, чем то, которое взяли мы.

Спишем из делимого 512 цифру 2 к 3.

Число 32 больше 8. И опять по таблице умножения на 8, найдем ближайшее произведение.
8 x 4 = 32

В остатке получился ноль. Значит числа разделились нацело (без остатка).

Как ты считаеешь, будет ли теория про деление в столбик — объяснение улучшена в обозримом будующем? Надеюсь, что теперь ты понял что такое деление в столбик — объяснение и для чего все это нужно, а если не понял, или есть замечания, то нестесняся пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Арифметика

Из статьи мы узнали кратко, но емко про деление в столбик — объяснение

Деление столбиком. Онлайн калькулятор | Математика

Как записывать деление в столбик
Как делить столбиком
Деление столбиком с остатком
Калькулятор деления столбиком

Как записывать деление в столбик

Деление многозначных чисел легче всего выполнять столбиком. Деление столбиком иначе называют деление уголком.

Перед тем как начать выполнение деления столбиком, рассмотрим подробно саму форму записи деления столбиком. Сначала записываем делимое и справа от него ставим вертикальную черту:

За вертикальной чертой, напротив делимого, пишем делитель и под ним проводим горизонтальную черту:

Под горизонтальной чертой поэтапно будет записываться получающееся в результате вычислений частное:

Под делимым будут записываться промежуточные вычисления:

Полностью форма записи деления столбиком выглядит следующим образом:

Как делить столбиком

Допустим, нам нужно разделить 780 на 12, записываем действие в столбик и приступаем к делению:

Деление столбиком выполняется поэтапно. Первое, что нам требуется сделать, это определить неполное делимое. Смотрим на первую цифру делимого:

это число 7, так как оно меньше делителя, то мы не можем начать деление с него, значит нужно взять ещё одну цифру из делимого, число 78 больше делителя, поэтому мы начинаем деление с него:

В нашем случае число 78 будет неполным делимым, неполным оно называется потому, что является всего лишь частью делимого.

Определив неполное делимое, мы можем узнать сколько цифр будет в частном, для этого нам нужно посчитать, сколько цифр осталось в делимом после неполного делимого, в нашем случае всего одна цифра — 0, это значит, что частное будет состоять из 2 цифр.

Узнав количество цифр, которое должно получиться в частном, на его месте можно поставить точки. Если при завершении деления количество цифр получилось больше или меньше, чем указано точек, значит где-то была допущена ошибка:

Приступаем к делению. Нам нужно определить сколько раз 12 содержится в числе 78. Для этого мы последовательно умножаем делитель на натуральные числа 1, 2, 3, …, пока не получится число максимально близкое к неполному делимому или равное ему, но не превышающее его. Таким образом мы получаем число 6, записываем его под делитель, а из 78 (по правилам вычитания столбиком) вычитаем 72 (12 · 6 = 72). После того, как мы вычли 72 из 78, получился остаток 6:

Обратите внимание, что остаток от деления показывает нам, правильно ли мы подобрали число. Если остаток равен делителю или больше него, то мы не правильно подобрали число и нам нужно взять число побольше.

К получившемуся остатку — 6, сносим следующую цифру делимого — 0. В результате, получилось неполное делимое — 60. Определяем, сколько раз 12 содержится в числе 60. Получаем число 5, записываем его в частное после цифры 6, а из 60 вычитаем 60 (12 · 5 = 60). В остатке получился нуль:

Так как в делимом больше не осталось цифр, значит 780 разделилось на 12 нацело. В результате выполнения деления столбиком мы нашли частное — оно записано под делителем:

780 : 12 = 65.

Рассмотрим пример, когда в частном получаются нули. Допустим нам нужно разделить 9027 на 9.

Определяем неполное делимое — это число 9. Записываем в частное 1 и из 9 вычитаем 9. В остатке получился нуль. Обычно, если в промежуточных вычислениях в остатке получается нуль, его не записывают:

Сносим следующую цифру делимого — 0. Вспоминаем, что при делении нуля на любое число будет нуль. Записываем в частное нуль (0 : 9 = 0) и в промежуточных вычислениях из 0 вычитаем 0. Обычно, чтобы не нагромождать промежуточные вычисления, вычисление с нулём не записывают:

Сносим следующую цифру делимого — 2. В промежуточных вычислениях вышло так, что неполное делимое (2) меньше, чем делитель (9). В этом случае в частное записывают нуль и сносят следующую цифру делимого:

Определяем, сколько раз 9 содержится в числе 27. Получаем число 3, записываем его в частное, а из 27 вычитаем 27. В остатке получился нуль:

Так как в делимом больше не осталось цифр, значит число 9027 разделилось на 9 нацело:

9027 : 9 = 1003.

Рассмотрим пример, когда делимое оканчивается нулями. Пусть нам требуется разделить 3000 на 6.

Определяем неполное делимое — это число 30. Записываем в частное 5 и из 30 вычитаем 30. В остатке получился нуль. Как уже было сказано, нуль в остатке в промежуточных вычислениях записывать не обязательно:

Сносим следующую цифру делимого — 0. Так как при делении нуля на любое число будет нуль, записываем в частное нуль и в промежуточных вычислениях из 0 вычитаем 0:

Сносим следующую цифру делимого — 0. Записываем в частное ещё один нуль и в промежуточных вычислениях из 0 вычитаем 0. Так как в промежуточных вычислениях, вычисление с нулём обычно не записывают, то запись можно сократить, оставив только остаток — 0. Нуль в остатке в самом конце вычислений обычно записывают для того, чтобы показать, что деление выполнено нацело:

Так как в делимом больше не осталось цифр, значит 3000 разделилось на 6 нацело:

3000 : 6 = 500.

Деление столбиком с остатком

Пусть нам требуется разделить 1340 на 23.

Определяем неполное делимое — это число 134. Записываем в частное 5 и из 134 вычитаем 115. В остатке получилось 19:

Сносим следующую цифру делимого — 0. Определяем, сколько раз 23 содержится в числе 190. Получаем число 8, записываем его в частное, а из 190 вычитаем 184.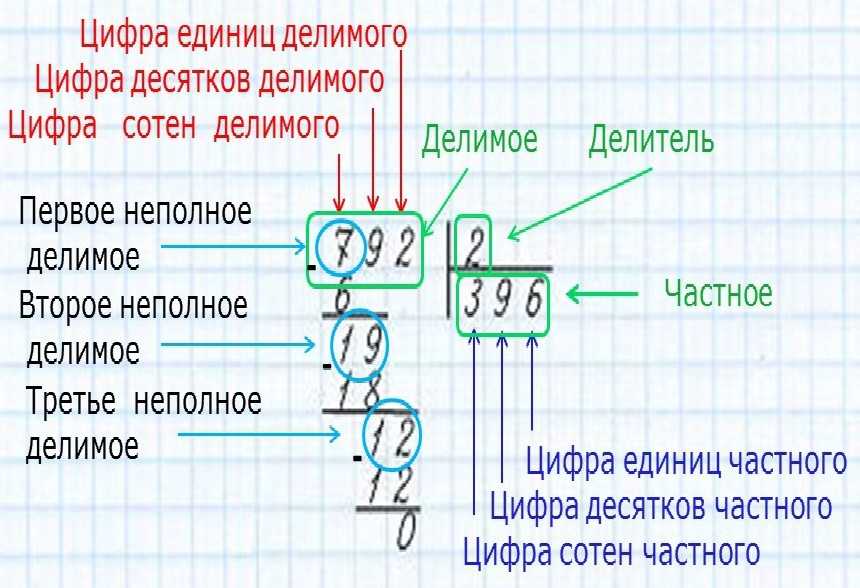 Получаем остаток 6:

Так как в делимом больше не осталось цифр, деление закончилось. В результате получилось неполное частное 58 и остаток 6:

1340 : 23 = 58 (остаток 6).

Осталось рассмотреть пример деления с остатком, когда делимое меньше делителя. Пусть нам требуется разделить 3 на 10. Мы видим, что 10 ни разу не содержится в числе 3, поэтому записываем в частное 0 и из 3 вычитаем 0 (10 · 0 = 0). Проводим горизонтальную черту и записываем остаток — 3:

3 : 10 = 0 (остаток 3).

Калькулятор деления столбиком

Данный калькулятор поможет вам выполнить деление столбиком. Просто введите делимое и делитель и нажмите кнопку Вычислить.

длинная дивизия

Показать рекламу

Скрыть рекламу
О рекламе

Ниже Процесс выписан полностью.
Вы часто будете видеть другие версии, которые, как правило, являются просто укороченной версией процесса ниже .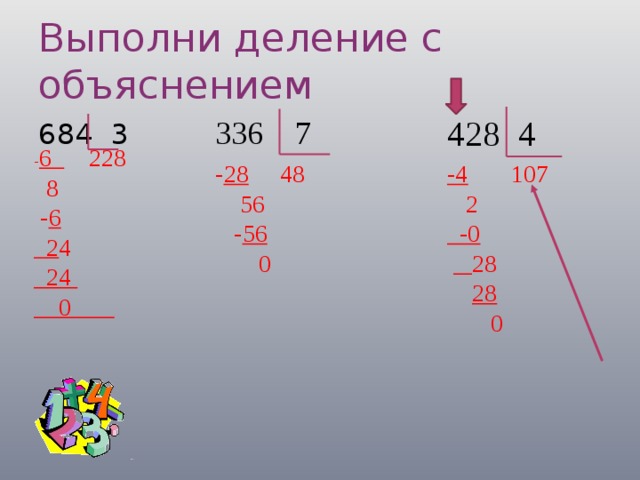
Вы также можете увидеть это в Long Division Animation.

Посмотрим как это делается с помощью:

число, на которое нужно разделить, называется делимое
Число, на которое делится другое число, называется делителем

И вот:

	4 ÷ 25 = 0 остаток 4	Первая цифра делимого (4) делится на делитель.
		Целое число помещается вверху. Любые остатки в этот момент игнорируются.
	25 × 0 = 0	Ответ из первой операции: умножить на делитель. Результат помещается под числом, разделенным на.
	4 − 0 = 4	Теперь мы вычитаем нижнее число из верхнего числа.
		Сократите следующую цифру делимого.
	42 ÷ 25 = 1 остаток 17	Разделите это число на делитель.
		Целое число помещается вверху. Любые остатки в этот момент игнорируются.
	25 × 1 = 25	Результатом вышеописанной операции является , умноженное на на делитель. Результат помещается под последним числом, на которое делится.
	42 − 25 = 17	Теперь мы вычитаем нижнее число из верхнего числа.
		Сократите следующую цифру делимого.
	175 ÷ 25 = 7 остатка 0	Разделите это число на делитель.
		Целое число помещается вверху. Любые остатки в этот момент игнорируются.
	25 × 7 = 175	Результатом вышеописанной операции является , умноженное на на делитель. Результат помещается под числом, разделенным на.
	175 — 175 = 0	Теперь мы вычитаем нижнее число из верхнего числа.
		Больше нет цифр для записи. Ответ должен быть 17

Рабочие листы длинного деления

Как сделать длинное деление с 2 цифрами + Пример

В сегодняшней статье мы собираемся объяснить

как решать двузначное деление.

Перед тем, как начать учиться решать двузначное деление, важно, чтобы вы ознакомились с этими терминами, потому что мы будем использовать их позже.

Дивиденд: число, которое делится.

Делитель: число, на которое делится делимое.

Частное: результат деления.

Остаток: сумма, оставшаяся после деления.

Увидев это, вы знаете, где разместить каждую цифру в дивизионе. Теперь нам нужно выполнить следующие шаги:

Возьмите первые цифры делимого, столько же цифр, сколько и у делителя. Если число, взятое из делимого, меньше делителя, нужно взять следующую цифру делимого.
Разделите первое число делимого (или два первых числа, если на предыдущем шаге была другая цифра) на первую цифру делителя. Запишите результат этого деления в пространстве частного.
Умножьте цифру частного на делитель, запишите результат под делимым и вычтите его. Если вы не можете, потому что делимое меньше, вам придется выбирать меньшее число в частном, пока оно не сможет вычитаться.
После вычитания отбросить следующую цифру делимого и повторять с шага 2 до тех пор, пока в делимом не останется оставшихся чисел.
Это концепция, но мы рассмотрим ее на примере.

Мы собираемся решить следующее двузначное деление:
Возьмем первые цифры делимого: в данном случае 57. Но так как 57 меньше 73, вы должны взять еще одну цифру: 573.
Чтобы разделить 573 на 73, берем первые две цифры делимого: 57 и делим их на первую цифру делителя:
57 ÷ 7 = 8
Запишите 8 в частном и умножьте на делитель:
8 x 73 = 584
Но 584 больше, чем 573; следовательно, 8 «не подходит». Вы должны выбрать предыдущее число и снова умножить:
7 x 73 = 511
511 меньше, чем делимое; поэтому 7 «подходит». Мы пишем 511 под цифрами делимого, а затем делим и вычитаем:
Отбросьте следующую цифру делимого, то есть 8. Теперь вам нужно разделить 628 на 73. Повторите предыдущие шаги:
Разделите первые две цифры делимого на первую цифру делителя и запишите это в месте частного:

62 ÷ 7 = 8
Умножьте эту цифру на делитель:
8 x 73 = 584
584 меньше 628; следовательно, мы можем вычесть:
628 – 584 = 44
Результат этого деления 78 и остаток 44.
Как объяснить ребёнку деление в столбик
Один из важных этапов в обучении ребёнка математическим действиям – обучение операции деления простых чисел. Как объяснить ребёнку деление, когда можно приступать к освоению этой темы?
СодержаниеРаскрыть
Осваиваем операцию разделения (деления) на части в игровой форме
Умножаем и делим, используя таблицу умножения
Делим столбиком – приведем пример
Объясняем наглядно
Как научить ребенка делению – закрепляем навык
Для того чтобы научить ребёнка делению, необходимо, чтобы он к моменту обучения уже освоил такие математические операции, как сложение, вычитание, а также имел чёткое представление о самой сущности действий умножения и деления. То есть, он должен понимать, что деление – это разделение чего-либо на равные части. Также необходимо научить операции умножения и выучить таблицу умножения.

Я уже писала о том, как запомнить таблицу умножения легко и быстро. Эта статья может стать для вас полезной.
Осваиваем операцию разделения (деления) на части в игровой форме
На этом этапе необходимо сформировать у ребёнка понимание того, что деление – это разделение чего-либо на равные части. Самый просто способ научить ребёнка этому – предложить ему разделить некоторое количество предметов между ним его друзьями или членами семьи.
Допустим, возьмите 8 одинаковых кубиков и предложите ребёнку разделить на две равные части – для него и другого человека. Варьируйте и усложняйте задание, предложите ребёнку разделить 8 кубиков не на двоих, а на четырёх человек. Проанализируйте вместе с ним результат. Меняйте составляющие, пробуйте с другим количеством предметов и людей, на которые нужно разделить эти предметы.
Важно: Следите, чтобы вначале ребёнок оперировал с чётным количеством предметов, для того, чтобы результатом деления было одинаковое количество частей. Это окажется полезным на следующем этапе, когда ребёнку будет нужно понять, что деление – это операция обратная умножению.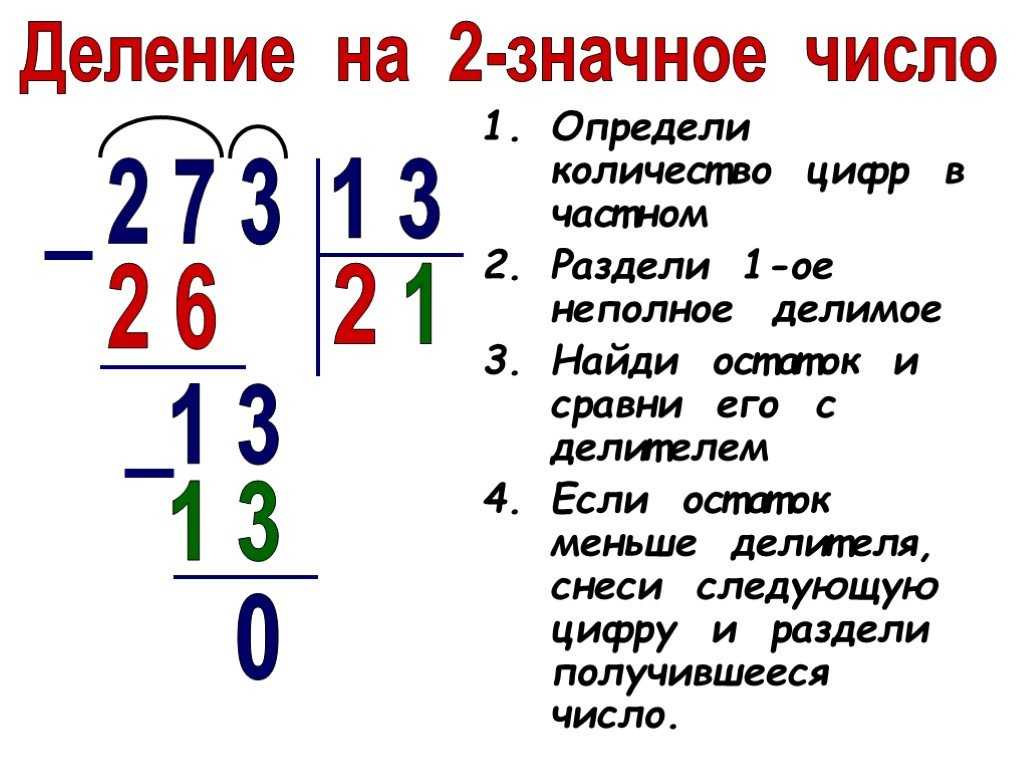
Умножаем и делим, используя таблицу умножения
Объясните ребёнку, что, в математике, действие, противоположное умножению, называется «деление». Оперируя таблицей умножения, продемонстрируйте ученику на любом примере взаимосвязь между умножением и делением.
Пример: 4х2=8. Напомните ребёнку, что результатом умножения является произведение двух чисел. После этого объясните, что операция деления, является обратной операции умножения и проиллюстрируйте это наглядно.
Разделите получившееся произведение «8» из примера – на любой из множителей – «2» или «4», и результатом всегда будет другой, не использовавшийся в операции множитель.
Также нужно научить юного ученика, тому, как называются категории, описывающие операцию деления – «делимое», «делитель» и «частное». На примере покажите, какие цифры являются делимым, делителем и частным. Закрепите эти знания, они необходимы для дальнейшего обучения!
Двигайтесь дальше, разбирая другие примеры из таблицы умножения.
По сути, вам нужно научить ребёнка таблице умножения «наоборот», и запомнить её необходимо так же хорошо, как и саму таблицу умножения, ведь это будет необходимым, когда вы начнёте обучение делению в столбик.
Делим столбиком – приведем пример
Перед началом занятия вспомните вместе с ребёнком, как называются цифры в процессе операции деления. Что является «делителем», «делимым», «частным»? Научите безошибочно и быстро определять эти категории. Это будет очень полезным во время обучения ребёнка делению простых чисел.
Объясняем наглядно
Давайте разделим 938 на 7. В данном примере 938 – это делимое, 7 – делитель. Результатом будет частное, его то и нужно вычислить.
Шаг 1. Записываем числа, разделив их «уголком».
Шаг 2. Покажите ученику числа делимого и предложите ему, выбрать из них то наименьшее число, которое окажется больше делителя. Из трёх цифр 9, 3 и 8, этим числом будет 9. Предложите ребёнку проанализировать, сколько раз число 7 может содержаться в числе 9? Правильно, только один раз. Поэтому первым записанными нами результатом будет 1.
Шаг 3. Переходим к оформлению деления столбиком:
Умножаем делитель 7х1 и получаем 7. Полученный результат записываем под первым числом нашего делимого 938 и вычитаем, как обычно, в столбик. То есть из 9 мы вычитаем 7 и получаем 2.
Записываем результат.
Шаг 4. Число, которое мы видим, меньше делителя, поэтому необходимо его надо увеличить. Для этого объединим его со следующим неиспользованным числом нашего делимого – это будет 3. Приписываем 3 к полученному числу 2.
Шаг 5. Далее действуем по уже известному алгоритму. Анализируем, сколько раз наш делитель 7 содержится в полученном числе 23? Правильно, три раза. Фиксируем число 3 в частном. А результат произведения – 21 (7*3) записываем внизу под числом 23 в столбик.
Шаг.6 Теперь осталось найти последнее число нашего частного. Используя уже знакомый алгоритм, продолжаем делать вычисления в столбике. Путём вычитания в столбике (23-21) получаем разницу. Она равняется 2.
Из делимого у нас осталась неиспользованным одно число – 8. Объединяем его с полученным в результате вычитания числом 2, получаем – 28.
Шаг.7 Анализируем, сколько раз наш делитель 7 содержится в полученном числе? Правильно, 4 раза. Записываем полученную цифру в результат. Итак, мы полученное в результате деления столбиком частное= 134.
Как научить ребенка делению – закрепляем навык
Главное из-за чего у многих школьников возникает проблема с математикой — это неумение быстро делать простые арифметические расчеты. А на этой основе построена вся математика в начальной школе. Особенно часто проблема именно в умножении и делении.
Чтобы ребенок научился быстро и качественно проводить расчеты деления в уме — необходима правильная методика обучения и закрепление навыка. Для этого мы советуем воспользоваться популярными на сегодня пособиями в усвоение навыка деления. Одни предназначены для занятий детей с родителями, другие для самостоятельной работы.
«Деление. Уровень 3. Рабочая тетрадь» от крупнейшего международного центра дополнительного образования Kumon
«Деление. Уровень 4. Рабочая тетрадь» от Kumon
«Не Ментальная арифметика. Система обучения ребенка быстрому умножению и делению. За 21 день. Блокнот-тренажёр.» от Ш. Ахмадулина — автора обучающих книг-бестселлеров
Самым главным, когда вы учите ребёнка делению в столбик, является усвоение алгоритма, который, в общем-то, достаточно прост.
Если ребёнок хорошо оперирует таблицей умножения и «обратным» делением, у него не возникнет трудностей. Тем не менее очень важно постоянно тренировать полученный навык. Не останавливайтесь на достигнутом, как только вы поймёте, что ребёнок уловил суть метода.
Для того чтобы легко научить ребёнка операции деления нужно:
Чтобы в возрасте двух–трех лет он освоил отношения «целое – часть». У него должно сложиться понимание целого, как неразделимой категории и восприятие отдельной части целого как самостоятельного объекта. Например – игрушечный грузовик – целое, а его кузов, колеса, дверцы – части этого целого.
Чтобы в младшем школьном возрасте ребенок свободно оперировал действиями по сложению и вычитанию чисел, понимал суть процессов умножения и деления.
Для того чтобы занятия математикой доставляли ребёнку удовольствие, необходимо возбуждать его интерес к математике и математическим действиям, не только во время обучения, но и в бытовых ситуациях.
Поэтому поощряйте и развивайте наблюдательность у ребёнка, проводите аналогии с математическими действиями (операции на счёт и деление, анализ отношений «часть-целое» и т.д.) во время конструирования, игр и наблюдений за природой.
Преподаватель, специалист детского развивающего центра
Дружинина Елена
специально для проекта marypop.ru
Видео сюжет для родителей, как правильно объяснить ребенку деление в столбик:

Дивизион для 2 класса: определение, факты и примеры
Что такое Дивизион?
Дата последнего обновления: 20 апр 2023
•
Всего просмотров: 74.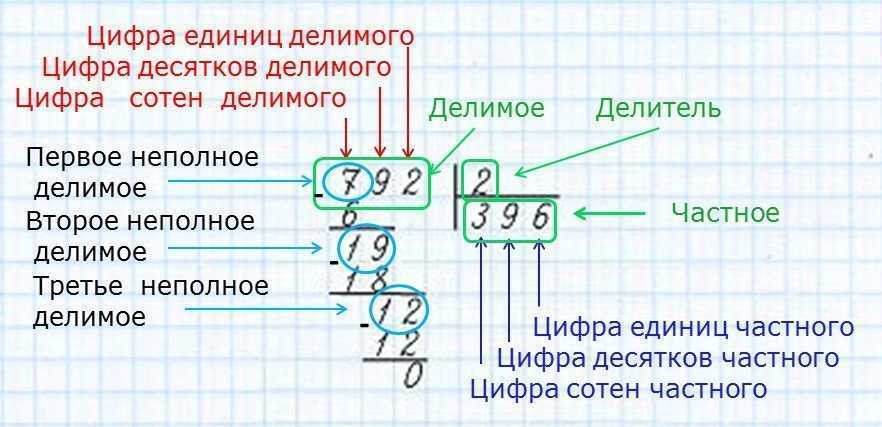 4k
•
Просмотров сегодня: 0.43k
В основном дети начинают изучать деление углубленно в третьем классе; однако в первый и второй годы дети познакомятся с понятиями, которые ведут к делению в полных формах и простому делению с использованием методов и игр. Ожидается, что дети будут работать с числами, намного большими, чем те, которые они могут физически сосчитать, поскольку математические концепции становятся более сложными. Понимание деления будет проще, если изучать его на примерах из реальной жизни. Давайте рассмотрим деление для детей 2 года в этой статье.
Что такое определение подразделения?
Деление — это процесс многократного вычитания. Это действие, обратное умножению. Считается формированием равных групп. Когда мы делим числа, мы разбиваем их на меньшие числа, так что умножение этих меньших чисел равняется взятому большему числу.
Примеры из повседневной жизни
1. У Нирмала есть 12 сладостей, и он хочет разделить их поровну между тремя своими друзьями. Давайте начнем с создания трех групп, затем добавляйте по одной сладости в каждую группу, пока все двенадцать сладостей не будут разделены поровну. Подсчитаем, сколько конфет в каждой группе, чтобы получить ответ: Двенадцать конфет, разделенных поровну между друзьями, равны 4.
Деление обозначается математическим символом, состоящим из небольшой горизонтальной линии с точками над и под линией. Есть два основных символа деления, которые обозначают деление двух чисел.
Условные обозначения раздела
Другими словами для обозначения раздела являются «разделить между» и «разделить». Наш решенный пример можно записать так: 12 разделить на 3 равно 4.
Изображение показывает деление 12/3
2. У Махимы 16 яблок, и она хочет разделить их поровну между своими 4 друзьями. Это можно записать как 16 разделить на 4.
Изображение показывает деление 16/4
Чтобы найти ответ, нам нужно разделить 16 поровну между 4 группами. Давайте посчитаем, сколько яблок в каждой группе, чтобы получить ответ.
На изображении показано, что 16 яблок делятся поровну между 4 людьми с делением 16/4
Таким образом, 16 яблок, разделенных поровну между друзьями, равно 4.
3. Мы можем разделить, разделив предметы на равные группы. Итак, если мы произведем расчет для 10, разделенного на 2, мы можем получить ответ, разделив десять предметов поровну на две группы.
На изображении показана группа из 10 объектов
В каждой из двух групп по пять шариков.
На изображении показаны 10 объектов, которые поровну разделены на 2 группы. Каждая из 5 объектов
Итак, десять разделить на два равно пяти.
Деление на группировку
Деление на группировку показывает, сколько одинаковых групп содержится в числе. Итак, если мы возьмем вычисление, как в примере истории 3,
10 разделить на 2.
Мы можем посмотреть на это как на то, сколько групп по 2 есть в 10.
На изображении показаны 10 объектов, которые поровну разделены на 5 групп. Каждый из 2 объектов
Равные группы по 2 из 10 равны 5 (см. изображение выше). Таким образом, 10, деленное на 2, равно 5.
Важные термины деления
Число, на которое делится сумма деления, называется делимым.
Делитель — это число, на которое мы делим.
Результат деления называется частным.
Изображение показывает условия деления на примере
Умножение и деление
На приведенном ниже рисунке показаны 12 конфет, сгруппированных по 4.
Изображение показывает три группы, каждая из четырех конфет
показывает факт умножения: 3 x 4 = 12, а также факт деления: 12 ÷ 4 = 3. 12 конфет также можно расположить группами по 3. Это показано ниже.
На изображении показаны четыре группы по три конфеты
Здесь мы имеем факт умножения: 4 x 3 = 12 и факт деления: 12 ÷ 3 = 4.
Таким образом, мы можем заметить, что,
Помощь детям с делением дома
Игрушки, немного винограда, бумага зажимы и пуговицы — отличные предметы для практики. Попросите ребенка сосчитать количество предметов для начала. Могут ли они поровну распределить предметы между вами двумя? Помогите им по очереди делиться предметами между двумя группами. Когда все предметы будут разделены, спросите ребенка, сколько их в каждой группе. Если у вас одинаковые числа, объясните, что ваш ребенок разделил предметы поровну на две группы, что равносильно делению на два.
Заключение
Деление — это разделение большой группы на более мелкие таким образом, чтобы в каждой группе было равное количество вещей. В математике это операция, используемая для равного группирования и равного распределения. В этой статье мы подробно обсудили процесс деления в математике с некоторыми примерами.
Недавно обновленные страницы
Числа на английском языке — Произношение, чтение и примеры
Числа от 1 до 10 для печати — Изучайте с примерами для детей
Расширенная форма десятичных знаков и система стоимостных значений – определение, примеры и использование
Что такое половинки? — Изучите определение и примеры
Nonagon: изучите определение, типы, свойства и формулы
Unit Cubes: изучите определение, факты и примеры
Числа на английском языке — Произношение, чтение и примеры
Печатные числа от 1 до 10 — Изучите с помощью Примеры для детей
Расширенная форма десятичных знаков и разрядная система значений — определение, примеры и использование
Что такое половинки? — Изучите определение и примеры
Nonagon: изучите определение, типы, свойства и формулы
Кубы единиц: изучите определение, факты и примеры
Эффективные альтернативы делению в длину
Деление в длину часто называют самым сложным математическая концепция для обучения. Если мы, как учителя, боремся с обучением делению в длину, то и наши ученики, несомненно, будут бороться с этим.
Одна из основных причин того, что традиционное деление в длинных числах так трудно освоить, заключается в том, что правильный ответ зависит от заученной серии шагов — деление, умножение, вычитание, уменьшение. Если учащийся забывает, какой шаг и когда делать, очень высока вероятность того, что он получит неверный ответ.
Вот почему НЕОБХОДИМО обучать стратегиям, а не шагам.
Стратегии поощряют НАСТОЯЩЕЕ ПОНИМАНИЕ. Это такая важная часть математики. Мы хотим, чтобы наши ученики действительно понимали, что они делают, и знали, что есть разные способы найти правильный ответ.
В этой статье я расскажу о трех различных альтернативах традиционному делению в длинную сторону. Я призываю вас сосредоточиться на первых двух, так как они очень сосредоточены на умственной математике.
Готовы серьезно заняться обучением многозначному делению? Проверьте станцию длинного дивизиона ЗДЕСЬ.

Метод прямоугольника/площади
Метод квадрата или модель площади представляет собой подход, основанный на ментальной математике, который улучшает понимание числа. Если вы планируете обучать стратегии Частных Частных (о которой я расскажу далее), это отличный способ представить ее.
Учащиеся решают уравнение, вычитая множители, пока не получат 0 или как можно ближе к 0. Например, в приведенном ниже примере мы убрали 100 групп по 3, затем 50 групп по 3, а затем еще 1 группу по 3, чтобы получить в общей сложности 151 группу по 3, взятых из делимого. Пожалуйста, перейдите к ЭТОМУ ПОСТУ, чтобы получить очень подробное объяснение этой стратегии с картинками.

Частичные частные
Частичные частные — это стратегия, которую необходимо выучить для многозначного деления. Если вы сначала обучаете методу «Ящик/Площадь», это будет очень естественным прогрессом.
Когда мы используем стратегию частичных частных, мы составляем уравнение аналогично тому, как составляется традиционное уравнение деления в длинную сторону. Разница здесь в том, что мы убираем кратные делителю, пока не дойдем до 0 или как можно ближе к 0. Пожалуйста, смотрите ЭТУ СТАТЬЮ для очень подробного объяснения этой стратегии, дополненной множеством изображений.

Метод сетки
Метод сетки НЕ основан на вычислениях в уме. Это означает, что если у вас есть ученики, которые борются с многозначным делением, вам следует сосредоточиться на двух предыдущих стратегиях, которые я описал, а не переходить к этой. Метод сетки можно использовать для студентов, которые готовы к сложной задаче, или в качестве введения, если вы планируете преподавать традиционное деление на две части. Некоторым учащимся эта сетка покажется очень полезной для организации их мышления.
Когда мы используем метод сетки, мы просто организуем цифры из уравнения в сетку. Полное и подробное объяснение того, как использовать метод сетки, а также множество изображений см. в ЭТОЙ СТАТЬЕ В БЛОГЕ.

СЛЕДУЮЩИЕ ШАГИ:
Используйте в классе карточки с заданиями «Длинное деление», чтобы закрепить стратегии в изоляции.