Как число умножить на дробь правило: Как умножить дробь на натуральное число?

Как умножать дроби

Пожаловаться

Шпак Юлия

, автор статей | Создано 24 дек 2022

Содержание:

Виды дробей

Умножение дробей

Умножение десятичных дробей

Как умножить дробь на натуральное число

Умножение трёх и более дробей

Дробь в математике – это результат деления меньшего числа a на большее число b.

Часто в жизни нам приходится вспоминать правила математики

Существует две формы записи дробей:

• В столбик через черту: a/b, где а – делимое или числитель, b – делитель или знаменатель.
• Одним числом через «,» после ноля: 0,5. Такие дроби называют десятичными.

В обычной жизни редко встречаются случаи, когда меньшее число делится на большее красиво. Легко разделить в уме на 2, 4, 5, 8, 10. А вот деление на 3, 7, 11, 13 и кратные им числа представляет сложность в виде бесконечного ряда цифр после запятой. Поэтому такие числа легче и проще записывать дробями.

Виды дробей

По содержанию дроби делятся на:

• математические, то есть записанные цифрами – 5/6;
• алгебраические, то есть записанные буквами или буквенными выражениями – a/(a—b).

По свойствам дроби бывают:

• правильными – числитель меньше знаменателя (5/6);
• неправильными – числитель больше знаменателя (
  6/5).

В неправильной дроби сначала находят целое, а после выделяют дробный остаток

6/5=1 1/5 (одна целая и одна пятая часть числа). Иначе такое число называют смешанным.

Это базовые знания о дробях, которые помогут вам справиться с их умножением.

Умножение дробей

Главное правило: произведение двух дробей равно отношению произведения их числителей на произведение их знаменателей.

В теории всё просто: чтобы перемножить дроби, умножьте числитель первой дроби на числитель второй, аналогично поступите со знаменателями:

a/b * c/

d = a * c/b * d

С математическими дробями работать интереснее. Вот простой пример:

½ * 3/5 = 1 * 3/2 * 5 =3/10

Если есть числа второго и более порядка, попробуйте до умножения сократить дроби. Например:

30/40 * 21/70

Первую дробь сократите на 10. Получится 3/4.

Вторую дробь сократите на 7. Получится 3/7.

С учётом сокращений пример изменится:

¾ * 3/7 = 3 * ¾ * 7 = 9/28

Когда требуется умножить смешанное число на дробь, перед умножением нужно привести смешанное число к дроби.

1 1/5  * 2/3 = 6/5 * 2/3 = 6 * 2/5 * 3 (можно провести сокращение на 3) = 2 * 2/5 * 1 = 4/5

Умножение десятичных дробей

В обычной жизни редко встречаются случаи, когда меньшее число делится на большее красиво

Десятичные дроби умножают в столбик, как и любые многозначные числа. Выглядит это так:

3,12 * 0,02

_х 3,12

   0,02

_______

   624

Теперь нужно понять, где ставить 0 и запятые. После запятых будет столько знаков, сколько их суммарно в двух множителях, то есть в нашем примере –

4. Ответ будет выглядеть так: 0,0624.

Как умножить дробь на натуральное число

Правило: произведение дроби на натуральное число равно отношению произведения числителя дроби на натуральное число к знаменателю дроби.

При умножении обычной дроби на натуральное число, нужно умножить только числитель:

2/3 * 4 = 8/3

С полученным результатом можно работать дальше, например, выделить целую часть числа: 2 2/3.

Другой пример:

2/4  *5 = 10/4

Такую дробь можно сократить на 2. Получим

5/2 или 2 ½.

Иногда в результате умножения дроби на натуральное число удаётся сократить дробь до натурального числа. Этим активно пользуются в математике.

2/3 * 6 = 12/3 = 4

Умножение десятичной дроби на натуральное число производят в столбик.

1,324 * 3

Сначала перемножают числа, не обращая внимания на запятые:

_х1,324

         3

_______

   3972

После запятой должно остаться столько же цифр, как и в дроби. В нашем примере их три.

Ответ:

3,972.

Умножение трёх и более дробей

Когда требуется умножить между собой 3 и более дроби, вспомните главное правило умножения. Оно будет распространяться и на умножение дробей.

Правило: от перемены мест множителей произведение не меняется.

Как это выглядит на примере? Умножим четыре дроби:

2/3 *4/7 * 3/8 * 12/20 = 2 * 4 * 3 * 12/3 * 7 * 8 * 20

Для начала сократим дробь. Для удобства запишем:

2 * 3 * 4 * 12 / 20 * 3 * 8 * 7

В результате сокращения получим:

1 * 1 * 1 * 3/5*1*1*7

Ответ: 3/35.

Знание правил умножения дробей может оказаться полезным, когда нет под рукой калькулятора. К тому же обычный калькулятор не умеет умножать обычные дроби, для этого есть специальные программы.

Фото: © Shutterstock.com

24 декабря 2022 16:00 | Отредактировано: 24 декабря 2022 22:55

РубрикаОбучение

В жизни пригодится: основы финансовой грамотности для детей

Славянский календарь: удивительные факты из жизни наших предков

Ваша любовь помогает ребенку больше всего

Комментарии

‘ + ‘

‘ + tooltips[tooltip][0] + ‘

‘ + » + tooltips[tooltip][1] + » + ‘

‘ + ‘

Узнавай и участвуй

Клубы на Бэби.ру — это кладезь полезной информации

Кто такие Коробыши? Давайте знакомиться!Проблемы у родителей: кто поможет?Зимний отдых: что выбрать?Есть ли альтернатива школе?Речевое развитие детей: когда начинать?

6 класс. Математика. Нахождение дроби от числа — Нахождение дроби от числа

Комментарии преподавателя

Нам часто в жизни при­хо­дит­ся на­хо­дить дробь от числа.

Чет­верть часа – это что такое? Это  от 60 минут. Это будет 15 минут.

А три чет­вер­ти часа? Это в 3 раза боль­ше, чем одна чет­верть. 3 раза по 15 минут, 45 минут.

 по­лу­то­ра­лит­ро­вой бу­тыл­ки мо­ло­ка – сколь­ко это? Одна треть – пол-лит­ра, 2 трети – литр.

Ни­че­го но­во­го нам на этом уроке изу­чать не нужно. Чтобы найти дробь от числа, нужно умно­жить эту дробь на это число.

Число, ко­то­рое мы умно­жа­ем на дробь, само может быть целым или дроб­ным. Раз­ни­ца несу­ще­ствен­на, но рас­смот­рим по от­дель­но­сти оба слу­чая.

1. Найти  от 63

Умно­жить на  – озна­ча­ет раз­де­лить на 7.

2. Най­дем  от 63.

Надо умно­жить 63 на .

Здесь очень много ва­ри­ан­тов, как можно рас­суж­дать.

Ва­ри­ант 1.

Можно вспом­нить, что  – это 5 раз по , то есть .

Ва­ри­ант 2.

Можно вспом­нить фор­маль­ное пра­ви­ло. Чтобы дробь умно­жить на число, надо чис­ли­тель умно­жить на это число.

Ва­ри­ант 3.

Можно пред­ста­вить 63 в эк­ви­ва­лент­ном виде как дробь и уже поль­зо­вать­ся пра­ви­лом умно­же­ния дро­бей. Чис­ли­тель умно­жить на чис­ли­тель, зна­ме­на­тель – на зна­ме­на­тель.

Ва­ри­ант 4

Самая ко­рот­кая за­пись по­лу­чит­ся, если вспом­нить, что число, ко­то­рое мы умно­жа­ем на дробь, можно со­кра­щать со зна­ме­на­те­лем.

Все это одно и то же. По­сту­пай­те так, как вам удоб­нее.

Най­дем те­перь дробь от дроб­но­го числа, то есть от дру­гой дроби.

1. Найти  от 

Умно­жа­ем:

Оче­вид­но, что  от  и  от  равны друг другу. Ведь это про­из­ве­де­ние двух этих чисел, ко­то­рое не за­ви­сит от по­ряд­ка мно­жи­те­лей.

Най­дем 0,03 от 45.

0,03 мы можем за­пи­сать в эк­ви­ва­лент­ном виде как обык­но­вен­ную дробь и вы­пол­нить умно­же­ние.

Но де­ся­тич­ная за­пись удоб­на сама по себе, и вы­пол­нить дей­ствия можно сразу.

45 умно­жа­ем на 3 и за­пя­той от­де­ля­ем две цифры:

Это дело вкуса и кон­крет­ных чисел. Ино­гда удоб­нее одна за­пись, ино­гда дру­гая.

Мы знаем еще одно обо­зна­че­ние дро­бей, про­цен­ты.

Кто хочет на­пом­нить себе, что такое про­цен­ты, прой­ди­те по ссыл­ке.

1. Найти 35 % от 400.

1 % – это 1 сотая, 35 % – это 35 сотых.

Эти сотые мы можем за­пи­сать обык­но­вен­ной дро­бью или де­ся­тич­ной.

Са­мо­сто­я­тель­но вы­пол­ни­те сле­ду­ю­щие за­да­ния:

Найти:

1)  от 12

2)  от 

3) 0,2 от 0,8

4) 30 % от 50

5) 65 % от 

Про­ве­ря­ем:

1) 

2) 

3) 

4) 

5) 

Итак, чтобы найти дробь от числа, це­ло­го или тоже дроб­но­го, нужно это число умно­жить на дробь.

 

источник видео — http://www.youtube.com/watch?v=pIM_k14jZac

источник видео — http://www.youtube.com/watch?v=bqAxzVFTeoU

источник конспекта — http://interneturok.ru/ru/school/matematika/6-klass/umnozhenie-i-delenie-obyknovennyh-drobej/nahozhdenie-drobi-ot-chisla

источник презентации — http://ppt4web. ru/matematika/nakhozhdenie-drobi-ot-chisla1.html

источник теста — http://testedu.ru/test/matematika/6-klass/test-10-naxozhdenie-drobi-ot-chisla-variant-1.html

источник презентации — http://www.myshared.ru/slide/download/

Как умножить дробь на целое число

Как умножить дробь на целое число

Чтобы умножить дробь на целое число:

1. Умножить числитель дроби на целое число.
2. Оставьте знаменатель прежним.
3. Упростите дробь, если это возможно.

Например, умножьте 5 × ² / ₇ .

Числитель дроби — число сверху, равное 2.

Мы умножаем 2 на 5, но сохраняем знаменатель 7 равным 7.

5 × ² / ₇ = ¹⁰ / ₇ .

Упрощаем, если это возможно. Поскольку дробь неправильная, мы можем преобразовать ее в смешанное число.

¹⁰ / ₇   означает 10 ÷ 7, что составляет 1 остаток 3. Следовательно, дробь может быть записана как 1   ³ / ₇ .

Альтернативный метод умножения дроби на целое число

Чтобы умножить дробь на целое число:

1. Запишите целое число как дробь от 1.
2. Умножить числители.
3. Умножить знаменатели..
4. Упростите, если возможно.

Например, умножьте 4 ×   ¹ / ₂ .

Первый шаг — записать 4 как ⁴ / ₁ .

Второй шаг — умножить числители: 4 × 1 = 4. Числитель ответа равен 4.

Третий шаг — умножить знаменатели: 1 × 2 = 2. Знаменатель ответа равен 2.

Следовательно, 4 × ¹ / ₂ = ⁴ / ₂ .

Наконец, упростите дробь, разделив и числитель, и знаменатель на одно и то же значение. Мы можем разделить 4 и 2 на 2, поэтому ⁴ / ₂ упрощается до ² / ₁ . ² / ₁  то же, что и 2.

Следовательно, 4 × ¹ / ₂

  = 2.

Мы также знаем, что половина 4 равна 2.

Как умножить дробь на целое число в простейшей форме

Чтобы умножить дробь на целое число, умножьте числитель на целое число. Чтобы записать этот ответ в простейшей форме, разделите числитель и знаменатель на наибольшее число, которое точно делится на оба.

Например, вычислите 2 × ³ / ₁₀ в простейшей форме.

Первый шаг — умножить числитель дроби на целое число. 2 × 3 = 6 и, следовательно, 2 × ³ / ₁₀ = ⁶ / ₁₀ .

Второй шаг — упростить дробь, разделив числитель и знаменатель на наибольшее число, которое делится на оба.

И 6, и 10 можно разделить на 2. ⁶ / ₁₀ упрощается до ³ / ₅ .

Следовательно, 2 × ³ / ₁₀  в простейшей форме:   ³ / ₅ .

Умножение дроби на целое число можно также рассчитать, разделив знаменатель на целое число.

10 — знаменатель, а 10 ÷ 2 = 5 — новый знаменатель. Это работает только в том случае, если знаменатель дроби можно разделить на целое число.

Как умножить смешанное число на целое

Чтобы умножить смешанное число на целое число:

1. Преобразуйте смешанное число в неправильную дробь.
2. Умножить числитель неправильной дроби на целое число.
3. Упростите, если возможно, и преобразуйте обратно в смешанное число.

Например, умножьте 2 × 1   ² / ₃ .

Шаг 1. Превратите смешанное число в неправильную дробь.

Оставьте знаменатель прежним.

Чтобы найти новый числитель, умножьте целое число смешанного числа на знаменатель, а затем добавьте числитель.

Знаменатель равен 3. Числитель находится путем умножения 1 и 3, чтобы получить 3, а затем прибавления 2, чтобы получить 5.

1   ² / ₃   =   ⁵ / ₃ .

Шаг 2. Умножьте числитель неправильной дроби на целое число.

Мы умножаем 2 × 5 = 10 и, таким образом, 2 × ⁵ / ₃ = ¹⁰ / ₃ .

Последний шаг — упростить и снова записать смешанное число.

¹⁰ / ₃ = 3 ¹ / ₃ .

Следовательно, 2 × 1   ² / ₃   = 3   ¹ / ₃

Умножение дроби на целое число с использованием числовой строки

Отметьте дробь на числовой прямой. Чтобы умножить его на целое число, прибавьте к той же дроби столько раз, сколько требуется для умножения.

Например, вот 5 ×   ¹ / ₈   в числовой строке.

Разбиваем каждое целое число на восьмые и считаем пять из них.

5 × ¹ / ₈ = ⁵ / ₈ .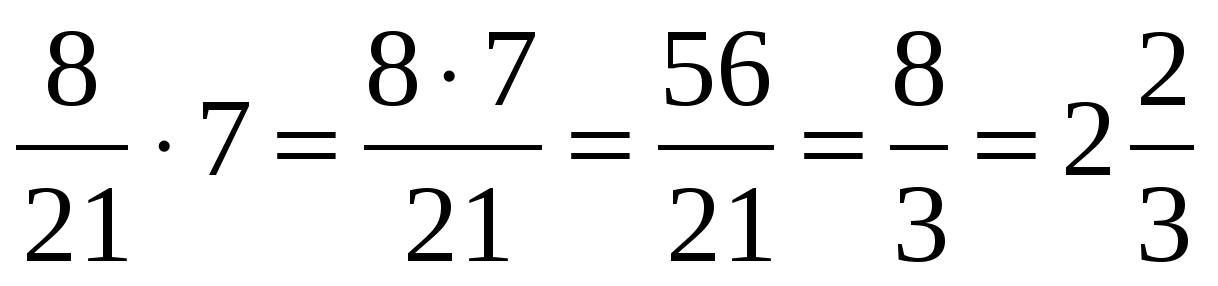

Вот еще один пример с неправильной дробью или смешанным числом.

Вычислите 5 × ¹ / ₃ , используя числовую прямую.

Разобьем каждое целое число на трети. Затем мы отсчитываем пять таких прыжков на нашей числовой прямой.

5 × ¹ / ₃ = ⁵ / ₃ .

В качестве смешанного числа это 1   ² / ₃ .

Умножение дроби на целое число с использованием моделей

Модели можно использовать для обучения процессу умножения дробей на целые числа.

Вот модель дроби ¹ / ₃ . Чтобы умножить его на 2, мы имеем в два раза больше частей.

Мы видим, что теперь у нас есть   ² / ₃   заштриховано.

Вот еще один пример использования модели для умножения ¹ / ₄ на 3.

Если мы умножим ¹ / ₄ на 3, то получим ³ / ₄ .

Модели полезны при умножении дробей и целых чисел, потому что мы видим, что знаменатель дроби не меняется, потому что количество частей в модели остается прежним.

Словесные задачи на умножение дробей и целых чисел

Вот несколько примеров текстовых задач на умножение дробей и целых чисел.

Q1. Я проезжаю ¹ / ₃ километр каждый день. Сколько километров я проеду за 5 дней?

Ответ: ¹ / ₃ × 5 = ⁵ / ₃ .

Q2. На вечеринку каждому человеку нужно   ³ / ₄   литра напитка. Всего приходит 10 человек. Сколько литров напитка нужно купить?

Ответ: ³ / ₄ × 10 = ³⁰ / ₄ .

Q3. Аккумулятор моего телефона заряжается на     ³ / ₁₀₀   каждую минуту. Какую долю он зарядит за 7 минут?

Ответ: ³ / ₁₀₀ × 7 = ²¹ / ₁₀₀ .

Умножение дробей на целые числа

Для умножение дробей на целые числа, целое число записывается в виде дроби, а затем умножается на данную дробь по правилам умножения дробей. При умножении дробей на целые числа следует также помнить, что данные дроби должны быть в виде правильной дроби или неправильной дроби. Давайте узнаем больше об умножении дробей на целые числа вместе с некоторыми примерами.

1.	Что такое умножение дробей на целые числа?
2.	Как умножать дроби на целые числа?
3.	Как умножать смешанные дроби на целые числа?
4.	Часто задаваемые вопросы об умножении дробей на целые числа

Что такое умножение дробей на целые числа?

Умножение дробей на целые числа аналогично многократному сложению, когда дробь прибавляется столько же раз, сколько и целое число. Для умножения дробей мы сначала умножаем числители, затем умножаем знаменатели и, наконец, приводим полученную дробь к наименьшему порядку. Однако, когда нам нужно умножить дроби на целые числа, мы записываем целое число в виде дроби, записывая 1 в качестве ее знаменателя. После этого шага мы можем умножить его, используя те же правила. Например, когда мы умножаем дробь a/b × c/d, мы получаем (a × c)/(b × d). Это правило применимо и при умножении дробей на целые числа.

Как умножать дроби на целые числа?

Умножение дробей на целые числа — простая идея. Нам просто нужно преобразовать целое число в дробь, написав 1 в качестве знаменателя и написав целое число в качестве числителя. Затем оно умножается на заданную дробь. После их умножения окончательный результат должен быть в виде правильной дроби или смешанной дроби. Если в результате получается неправильная дробь, преобразуем ее в смешанную дробь. Давайте разберемся с шагами на примере.

Пример: Умножить 1/8 × 5

Решение: Здесь 1/8 — дробь, а 5 — целое число.

• Шаг 1: Преобразуйте целое число в дробь, написав 1 в качестве знаменателя. Это означает, что 5 записывается как 5/1
.
• Шаг 2: Умножьте числители. Здесь 1 × 5 = 5
• Шаг 3: Умножьте знаменатели. Здесь 8 × 1 = 8
• Шаг 4: При необходимости упростите и сократите продукт. Если в результате получится неправильная дробь, мы преобразуем ее в смешанную дробь. Итак, товар 5/8

Давайте посмотрим на другой пример, чтобы лучше понять это.

Пример 2: Умножьте 5 × 3/10.

Решение: Здесь 5 — целое число, а 3/10 — правильная дробь.

• Шаг 1: Преобразуем целое число 5 в дробь, написав 1 в знаменателе. Это означает, что 5 записывается как 5/1.
• Шаг 2: Умножьте числители обеих дробей. 5/1 × 3/10 = 5 × 3 = 15,
• Шаг 3: Умножьте знаменатели обеих дробей. 5/1 × 3/10 = 1 × 10 = 10,
• Шаг 4: Упростите дроби. 5/1 × 3/10 = 15/10. Мы можем еще упростить это, так как и 15, и 10 можно разделить на 5. Это означает, что (15 ÷ 5) / (10 ÷ 5) = 3/2. Следовательно, 5 × 3/10 = 3/2 = \(1\dfrac{1}{2}\)

Как умножать смешанные дроби на целые числа?

Чтобы умножать смешанные дроби на целые числа, мы преобразуем смешанную дробь в неправильную дробь, а затем умножаем ее на целое число.

Пример: Умножить \(1\dfrac{2}{5}\) на 10.

Решение: Посмотрим, как умножить заданную смешанную дробь на целое число.

• Шаг 1: Сначала преобразуем смешанную дробь в неправильную. Это означает, что \(1\dfrac{2}{5}\) = 7/5.
• Шаг 2: Затем преобразуйте целое число 10 в дробь. Это означает, что 10 = 10/1. Это составляет 7/5 × 10/1
.
• Шаг 3: Умножьте числители обеих дробей. 7 × 10 = 70. Перемножьте знаменатели обеих дробей. Это означает, что 5 × 1 = 5,
.
• Шаг 4: Упростите и сократите дробь, то есть 70/5 = (70 ÷ 5) / (5 ÷ 5) = 14/1. Следовательно, \(1\dfrac{2}{5}\) × 10 = 14,

☛ Похожие статьи

• Умножение смешанных дробей
• Деление дробей
• Сокращение дробей
• Сложение и вычитание дробей
• Формула фракций

 

Примеры умножения дробей на целые числа

1. Пример 1: Умножьте дробь на целое число: 1/3 × 15

   Решение:

   Умножим дробь на целое число,

   1/3 × 15 = 1/3 × 15/1 = (1 × 15) / (3 × 1) = 15/3 = 5.

   Следовательно, 1/3 × 15 = 5

2. Пример 2: Найдите произведение после умножения дроби на целое число: 3/4 × 4

   Решение:

   Для умножения дробей на целые числа нам нужно преобразовать целое число в дробь, написав 1 в качестве ее знаменателя.

   3/4 × 4 = 3/4 × 4/1 = (3 × 4) / (4 × 1) = 12/4 = 3.

   Следовательно, 3/4 × 4 = 3

3. Пример 3: Найдите произведение целого числа 6 и смешанной дроби \(3\dfrac{4}{7}\)

   Решение:

   Сначала преобразуем смешанную дробь в правильную дробь .

   \(3\dfrac{4}{7}\) = [(7 × 3) + 4] / 7 = 25/7

   Преобразуем целое число в дробь,

   6 = 6/1

   Теперь давайте умножим дробь на целое число,

   6/1 × 25/7 = (6 × 25) / (1 × 7) = 150/7

   Получив результат, мы преобразуем его в смешанная фракция.

   150/7 = \(21\dfrac{3}{7}\).

перейти к слайдуперейти к слайдуперейти к слайду

Есть вопросы по основным математическим понятиям?

Станьте чемпионом по решению проблем, используя логику, а не правила. Узнайте, что стоит за математикой, с нашими сертифицированными экспертами

Записаться на бесплатный пробный урок

Практические вопросы по умножению дробей на целые числа

 

перейти к слайдуперейти к слайду

Часто задаваемые вопросы об умножении дробей на целые числа

Что означает умножение дробей на целые числа?

Умножение дробей на целые числа считается повторным сложением, когда дробь прибавляется столько же раз, сколько и целое число. Умножение дробей с целыми числами выполняется по тем же правилам умножения, где числители умножаются вместе, затем знаменатели умножаются вместе, а затем они уменьшаются, чтобы получить произведение.

Как умножать дроби на целые числа?

Чтобы умножать дроби на целые числа, мы используем следующие шаги.

• Шаг 1: Преобразуйте целое число в дробь, написав 1 в качестве знаменателя.
• Шаг 2: После этого нам нужно умножить две дроби. Итак, мы используем правило умножения дробей, чтобы умножить дроби.
• Шаг 3: Это означает, что сначала перемножаются числители, а затем перемножаются знаменатели.
• Шаг 4: Наконец, продукт упрощается или сокращается, если это необходимо.

Как умножать смешанные дроби на целые числа?

Следующие шаги показывают, как умножать смешанные дроби на целые числа:

• Шаг 1: Преобразуйте смешанную дробь в неправильную дробь.
• Шаг 2: Преобразуйте целое число в дробь со знаменателем 1.
• Шаг 3: Умножьте числители.
• Шаг 4: Умножьте знаменатели.
• Шаг 5: Упростите окончательный результат до минимума.

Как умножать неправильные дроби на целые числа?

Для умножения неправильных дробей на целые числа используются те же правила умножения. Это означает, что целое число записывается в виде дроби, а затем умножается на неправильную дробь. Числители перемножаются, затем знаменатели перемножаются, а затем при необходимости упрощаются.

Как умножить 3 дроби на целые числа?

Чтобы умножить 3 дроби на целые числа, мы используем следующие шаги. Умножим 4/5 × 10/6 × 1/4 × 25.

• Шаг 1: Здесь 25 — целое число, а остальные дроби, поэтому мы преобразуем целое число в дробь, написав его знаменатель равен 1. Это означает, что 25 записывается как 25/1
.
• Шаг 2: Теперь у нас есть 4 дроби для умножения. Итак, мы используем правило умножения дробей, чтобы умножить все эти дроби. 4/5 × 10/6 × 1/4 × 25/1
• Шаг 3: Это означает, что сначала перемножаются числители, а затем перемножаются знаменатели. Здесь произведение числителей будет 4 × 10 × 1 × 25 = 1000. Произведение знаменателей будет 5 × 6 × 4 × 1 = 120.
• Шаг 4: Дробь, которую мы получаем в результате произведения, равна 1000/120. Наконец, произведение упрощается или сокращается, это означает, что 1000/120 = 25/3 = \(8\dfrac{1}{3}\)

Как умножать отрицательные дроби на целые числа?

Для умножения отрицательных дробей на целые числа используются те же правила умножения. Это означает, что целое число записывается в виде дроби, а затем умножается на отрицательную дробь. Числители перемножаются, затем знаменатели перемножаются, а затем при необходимости упрощаются. Однако следует помнить, что произведение будет иметь знак, соответствующий знаку, данному в дроби. Это означает, что если отрицательную дробь умножить на целое положительное число, произведение будет иметь отрицательный знак. Например, -6/4 × 5 = -6/4 × 5/1. Теперь мы можем перемножить числители и знаменатели, чтобы получить -30/4, что в дальнейшем будет уменьшено до -15/2.