Сложение десятичных дробей: правила и примеры
- Сложение путём перевода в обыкновенные дроби
- Сложение десятичных дробей столбиком
- Сложение десятичной дроби с натуральным числом
- Сложение десятичной дроби с обыкновенной дробью
Сложение десятичных дробей можно выполнить двумя способами:
- Представить десятичные дроби в виде обыкновенных дробей и выполнить их сложение.
- Выполнить сложение десятичных дробей столбиком.
Сложение путём перевода в обыкновенные дроби
При сложении десятичных дробей путём их перевода в обыкновенные дроби следует руководствоваться следующим правилом:
- Нужно сравнить количество десятичных знаков у десятичных дробей.
- Если количество десятичных знаков одинаково, то переводим десятичные дроби в обыкновенные и складываем их.
- Если количество десятичных знаков различно, то сначала нужно уравнять их количество, приписав справа к десятичной дроби с меньшим количеством знаков необходимое число нулей.

Пример 1. Выполнить сложение чисел 3,1 и 4,7.
Решение. Так как количество десятичных знаков одинаково, то просто переводим десятичные дроби в обыкновенные и складываем. Десятичной дроби 3,1 соответствует обыкновенная дробь , а десятичной дроби 4,7 — обыкновенная дробь , значит:
Пример 2. Сложить числа 3,45 и 7,368.
Решение. Так как количество десятичных знаков различно, то сначала уравняем их количество, приписав справа к дроби 3,45 цифру 0. Десятичной дроби 3,450 соответствует обыкновенная дробь , а десятичной дроби 7,368 — обыкновенная дробь , значит:
Сложение десятичных дробей столбиком
Десятичные дроби можно складывать столбиком.
При сложении десятичных дробей столбиком следует руководствоваться следующим правилом:
- Записать десятичные дроби в столбик так, чтобы цифры одинаковых разрядов стояли друг под другом. Запятые десятичных дробей так же должны стоять друг под другом.

- Если количество десятичных знаков у дробей различно, для удобства можно уравнять их число, приписав справа к десятичной дроби с меньшим количеством десятичных знаков необходимое число нулей.
- Не обращая внимание на запятые, выполнить сложение так, как выполняется сложение столбиком натуральных чисел.
- В полученной сумме поставить запятую так, чтобы она стояла под запятыми слагаемых.
Пример 1. Сложить числа 3,1 и 4,7.
Решение. Выполняем сложение так, как выполняется сложение столбиком натуральных чисел, не обращая внимание на запятые:
Пример 2. Сложить 3,45 и 7,368.
Решение. Выполняем сложение так, как выполняется сложение столбиком натуральных чисел. Для удобства, можно уравнять количество десятичных знаков в складываемых дробях:
Сложение десятичной дроби с натуральным числом
Правило сложения десятичных дробей с натуральными числами:
Чтобы сложить десятичную дробь и натуральное число, нужно данное натуральное число прибавить к целой части десятичной дроби, а дробную часть оставить без изменений.
Пример. Вычислить сумму 14,3 и 29.
Решение. Для удобства сложения, любое натуральное число можно представить в виде десятичной дроби. Для этого нужно поставить запятую после разряда единиц и приписать после запятой нужное количество нулей. Сложение выполняется по правилу сложения десятичных дробей столбиком:
Сложение десятичной дроби с обыкновенной дробью
Правило сложения десятичных дробей с обыкновенной дробью:
Сложение десятичной дроби с обыкновенной дробью сводится к сложению обыкновенных дробей. Для этого десятичная дробь переводится в обыкновенную дробь.
Пример. Выполнить сложение десятичной дроби 0,28 и обыкновенной дроби .
Решение. Переводим десятичную дробь 0,28 в обыкновенную: . И далее выполняем уже сложение обыкновенных дробей и :
§ Смешанные числа. Целая часть дроби. Правильные и неправильные дроби
Похоже, вы используете блокировщик рекламы. Наш сайт существует и развивается
только за счет дохода от рекламы.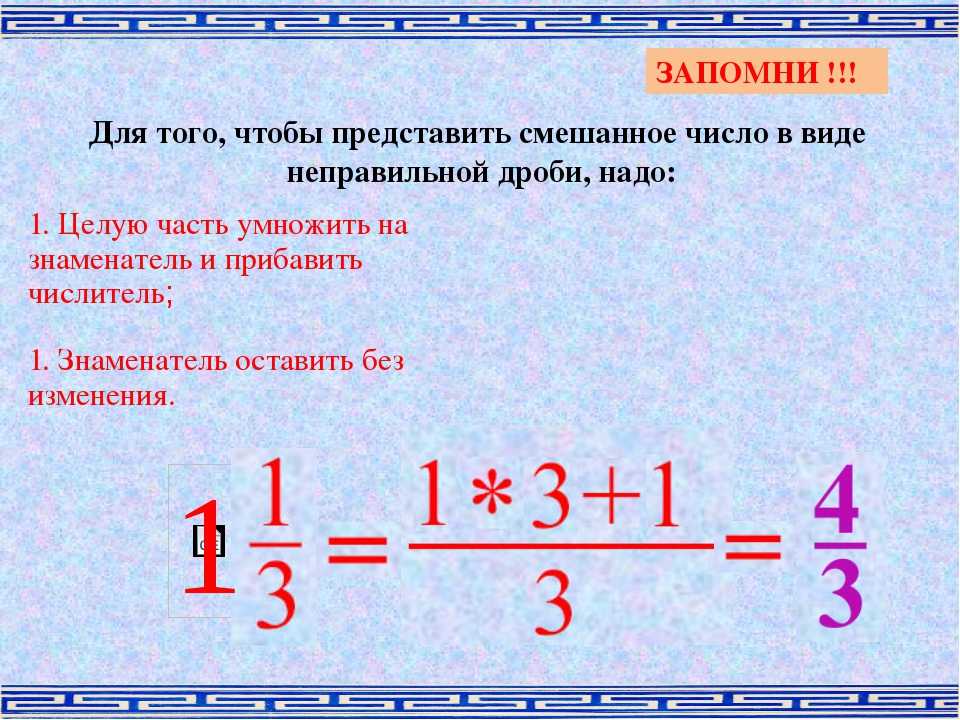
Пожалуйста, добавьте нас в исключения блокировщика.
Скрыть меню
На главную страницу
Войти при помощи
Темы уроков
Начальная школа
- Геометрия: начальная школа
- Действия в столбик
- Деление с остатком
- Законы арифметики
- Периметр
- Порядок действий
- Разряды и классы. Разрядные слагаемые
- Счет в пределах 10 и 20
Математика 5 класс
- Взаимно обратные числа и дроби
- Десятичные дроби
- Натуральные числа
- Нахождение НОД и НОК
- Обыкновенные дроби
- Округление чисел
- Перевод обыкновенной дроби в десятичную
- Площадь
- Проценты
- Свойства сложения, вычитания, умножения и деления
- Среднее арифметическое
- Упрощение выражений
- Уравнения 5 класс
- Числовые и буквенные выражения
Математика 6 класс
- Масштаб
- Модуль числа
- Окружность.
 Площадь круга
Площадь круга - Отношение чисел
- Отрицательные и положительные числа
- Периодическая дробь
- Признаки делимости
- Пропорции
- Рациональные числа
- Система координат
- Целые числа
Алгебра 7 класс
- Алгебраические дроби
- Как применять формулы сокращённого умножения
- Многочлены
- Одночлены
- Системы уравнений
- Степени
- Уравнения
- Формулы сокращённого умножения
- Функция в математике
Геометрия 7 класс
- Точка, прямая и отрезок
- Что такое аксиома и теорема
Алгебра 8 класс
- Квадратичная функция. Парабола
- Квадратные неравенства
- Квадратные уравнения
- Квадратный корень
- Неравенства
- Системы неравенств
- Стандартный вид числа
- Теорема Виета
Алгебра 9 класс
- Возрастание и убывание функции
- Нули функции
- Область определения функции
- Отрицательная степень
- Среднее
геометрическое - Чётные и нечётные функции
Алгебра 10 класс
- Иррациональные числа
Алгебра 11 класс
- Факториал
Надо учиться в школе, но ещё больше надо учиться по выходе из школы. Д.И. Писарев
Д.И. Писарев
на главную
Введите тему
Поддержать сайт
Дроби. Числитель и знаменатель Сокращение дробей Сравнение дробей Смешанные числа. Выделить целую часть Сложение дробей. Общий знаменатель Вычитание дробей Умножение дробей Деление дробей Нахождение дроби от числа Нахождение целого по известной дроби
Среди обыкновенных дробей различают два разных вида.
Правильные и неправильные дроби
Рассмотрим дроби.
Обратите внимание, что в двух первых дробях (
и
) числители меньше знаменателей. Такие дроби называют правильными.
Запомните!
У правильной дроби числитель меньше знаменателя. Поэтому правильная дробь всегда меньше единицы.
Рассмотрим две оставшиеся дроби.
Дробь
имеет числитель равный знаменателю (такие дроби равны единицы), а дробь
имеет числитель больший знаменателя. Такие дроби называют неправильными.
Запомните!
У неправильной дроби числитель равен или больше знаменателя. Поэтому неправильная дробь или равна единице или больше единицы.
Любая неправильная дробь всегда больше правильной.
Как выделить целую часть
У неправильной дроби можно выделить целую часть. Рассмотрим, как это можно сделать.
Чтобы из неправильной дроби выделить целую часть надо:
- разделить с остатком числитель на знаменатель;
- полученное неполное частное записываем в целую часть дроби;
- остаток записываем в числитель дроби;
- делитель записываем в знаменатель дроби.
Пример. Выделим целую часть из неправильной дроби
Выделим целую часть из неправильной дроби
.
- Разделим в столбик числитель на знаменатель.
- Теперь запишем ответ.
Запомните!
Полученное число выше, содержащее целую и дробную часть, называют смешанным числом.
Мы получили смешанное число из неправильной дроби, но можно
выполнить и обратное действие, то есть
Чтобы представить смешанное число в виде неправильной дроби надо:
- умножить его целую часть на знаменатель дробной части;
- к полученному произведению прибавить числитель дробной части;
- записать полученную сумму из пункта 2 в числитель дроби, а знаменатель дробной части оставить прежним.
Пример. Представим смешанное число в виде неправильной дроби.
- Умножаем целую часть на знаменатель.
3 · 5 = 15
- Прибавляем числитель.

15 + 2 = 17
- Записываем полученную сумму в числитель новой дроби, а знаменатель оставляем прежним.
Любое смешанное число можно представить как сумму целой и дробной части.
Запомните!Любое натуральное число можно записать дробью с любым натуральным знаменателем.
Частное от деления числителя на знаменатель такой дроби будет равно данному натуральному числу.
Примеры.
Дроби. Числитель и знаменатель Сокращение дробей Сравнение дробей Смешанные числа. Выделить целую часть Сложение дробей. Общий знаменатель Вычитание дробей Умножение дробей Деление дробей Нахождение дроби от числа Нахождение целого по известной дроби
Сложение дробей с целыми числами (примеры вопросов)
Смешанное число — это число, состоящее из целой части и дробной части.
Сложение дробей с целыми числами Примеры вопросов
Вот визуальное представление смешанного числа.
В этой модели показаны два полностью заштрихованных прямоугольника, которые представляют целые числа, и один частично заштрихованный прямоугольник, представляющий дроби.
Эта дробная модель представляет собой смешанное число \(2\frac{3}{8}\).
При сложении смешанного числа с целым числом мы сначала складываем целые числа, а затем добавляем дробь.
Пример:Чему равна сумма \(11\frac{2}{3}\) и \(19\)?
Мы начнем со сложения целых чисел, то есть \(11+19=30\). Затем добавляем дробную часть в конец.
Следовательно, сумма \(11\frac{2}{3}\) и \(19\) равна \(30\frac{2}{3}\).
Вот пример того, где это можно использовать в реальной жизни:Моника выбирает два пакета персиков, чтобы купить их на фермерском рынке. Она кладет каждую сумку на весы, и первая сумка весит \(5\) фунтов. а второй мешок весит \(6\frac{2}{3}\) фунтов. Сколько фунтов персиков покупает Моника?
При сложении целого числа и дроби мы сначала складываем целые числа, затем добавляем дробь.
\(5+6=11\), теперь мы включаем \(\frac{2}{3}\), следовательно, Моника покупает всего \(11\frac{2}{3}\) фунтов. персиков.
Примеры вопросов о сложении дробей с целыми числамиВот несколько примеров вопросов о сложении дробей с целыми числами.
Вопрос №1:
Вычислите сумму \(14\frac{5}{6}\) и \(38\).
\(54\)
\(52\frac{5}{6}\)
\(56\frac{2}{5}\)
\(55\)
Показать ответ
Ответ:
При сложении дробей и целых чисел сначала вычислите целое число плюс целое число, а затем включите в ответ оставшуюся дробь. Например, \(14+38=52\), поэтому ответом будет \(52\frac{5}{6}\).
Скрыть ответ
Вопрос №2:
Вычислите сумму \(45\) и \(2\frac{1}{3}\).
\(47\frac{2}{3}\)
\(45\frac{2}{3}\)
\(46\frac{3}{5}\)
\(47 \frac{1}{3}\)
Показать ответ
Ответ:
Еще раз, при сложении дробей и целых чисел сначала вычисляйте целое число плюс целое число, а затем включайте оставшуюся дробь в отвечать. Например, \(45+2=47\), поэтому ответом будет \(47\frac{1}{3}\).
Скрыть ответ
Вопрос №3:
Добавить \(4\frac{3}{2}+5\).
\(10\frac{1}{5}\)
\(11\frac{3}{5}\)
\(9\frac{1}{5}\)
\(10 \frac{1}{2}\)
Показать ответ
Ответ:
Первым шагом является рассмотрение неправильной дроби в смешанном числе \(4\frac{3}{2}\). Дробь \(\frac{3}{2}\) — это то же самое, что и \(1\frac{1}{2}\), поэтому перепишите \(4\frac{3}{2}\) как \ (5\разрыв{1}{2}\). Теперь просто объедините \(5\frac{1}{2}\) и \(5\), чтобы получить \(10\frac{1}{2}\).
Теперь просто объедините \(5\frac{1}{2}\) и \(5\), чтобы получить \(10\frac{1}{2}\).
Скрыть ответ
Вопрос № 4:
Добавить \(3+3\frac{5}{4}\).
\(6\frac{1}{4}\)
\(7\frac{1}{4}\)
\(6\frac{3}{4}\)
\(7 \frac{3}{4}\)
Показать ответ
Ответ:
Первым шагом является рассмотрение неправильной дроби в смешанном числе \(3\frac{5}{4}\). Дробь \(\frac{5}{4}\) — это то же самое, что и \(1\frac{1}{4}\), поэтому перепишите \(3\frac{5}{4}\) как \ (4 \ гидроразрыва {1} {4} \). Теперь просто объедините \(3\) и \(4\frac{1}{4}\), чтобы получить \(7\frac{1}{4}\).
Скрыть ответ
Вопрос № 5:
Вставьте пропущенное значение, чтобы уравнение было верным.
\(3\frac{4}{5}+\) ______\(=18\frac{4}{5}\)
\(13\)
\(14\frac{1}{5} \)
\(15\)
\(16\frac{1}{5}\)
Показать ответ
Ответ:
Чтобы составить сбалансированное уравнение, смешанное число \(18 \frac{4}{5}\) должны быть с каждой стороны. Если добавить \(3\frac{4}{5}+15=18\frac{4}{5}\), то \(15\) будет пропущенным значением.
Скрыть ответ
Вернуться к примерам вопросов по математике
Добавление дробей
PGSG8gJWt1g
Дробь типа 3 4 говорит, что у нас есть 3 из 4 частей, на которые делится целое.
Чтобы сложить дроби, нужно выполнить три простых шага:
- Шаг 1: Убедитесь, что нижние числа ( знаменатели ) совпадают
- Шаг 2: Добавьте верхние числа ( числители ), поместите этот ответ над знаменателем
- Шаг 3.

Пример:
1 4 + 1 4
Шаг 1 . Нижние числа (знаменатели) уже одинаковы. Сразу переходите к шагу 2.
Шаг 2 . Сложите верхние числа и поставьте ответ над тем же знаменателем:
1 4 + 1 4 «=» 1 + 1 4 «=» 2 4
Шаг 3 . Упростите дробь:
2 4 «=» 1 2
На картинке это выглядит так:
| 1 4 | + | 1 4 | = | 2 4 | = | 1 2 |
. .. и вы видите, как 2 4 проще, как 1 2 ? (см. Эквивалентные дроби.)
.. и вы видите, как 2 4 проще, как 1 2 ? (см. Эквивалентные дроби.)
Пример:
1 3 + 1 6
Шаг 1 : Нижние числа разные. Видите, как кусочки разного размера?
| 1 3 | + | 1 6 | = | ? | ||
Нам нужно сделать их одинаковыми, прежде чем мы сможем продолжить, потому что мы не может добавить их вот так.
Число «6» в два раза больше, чем «3», поэтому, чтобы сделать нижние числа одинаковыми, мы можем умножить верхнюю и нижнюю часть первой дроби на 2 , например:
| × 2 |
| 1 3 | = | 2 6 |
| × 2 |
Важно: вы умножаете как верхние, так и нижние на одну и ту же сумму,
, чтобы значение дроби осталось прежним
Теперь дроби имеют одинаковое нижнее число («6»), и наш вопрос выглядит так:
| 2 6 | + | 1 6 | ||||
Нижние числа теперь одинаковы, поэтому мы можем перейти к шагу 2.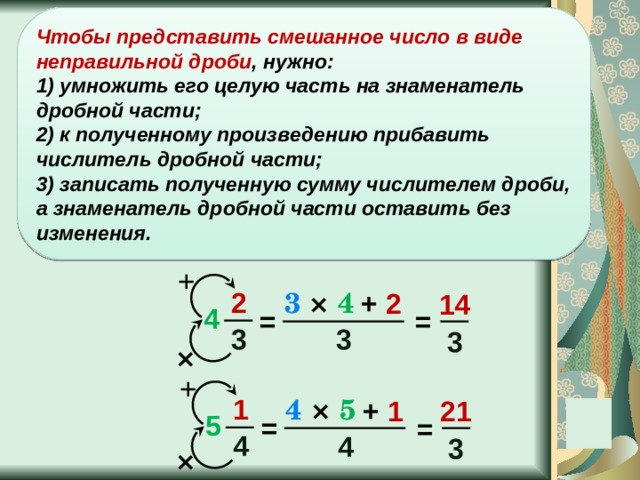
Шаг 2 : Сложите верхние числа и поместите их над одним знаменателем:
2 6 + 1 6 «=» 2 + 1 6 «=» 3 6
На картинке это выглядит так:
| 2 6 | + | 1 6 | = | 3 6 | ||
Шаг 3 : Упростить дробь:
3 6 «=» 1 2
В графической форме весь ответ выглядит так:
| 2 6 | + | 1 6 | = | 3 6 | = | 1 2 |
С ручкой и бумагой
А вот как это сделать ручкой и бумагой (нажмите кнопку воспроизведения):
Играй! Попробуйте сложить дроби. |
Стихотворение, которое поможет вам вспомнить
♫ «Если вашей целью является сложение или вычитание,
Нижние числа должны быть одинаковыми!
♫ «Измените низ, используя умножение или деление,
Но то же самое нужно применить к верху,
♫ » И не забудьте упростить,
Пока не пришло время прощаться»
Пример:
1 3 + 1 5
Опять же, нижние цифры разные (ломтики разного размера)!
| 1 3 | + | 1 5 | = | ? | ||
Но давайте попробуем разделить их на более мелкие, чтобы были одинаковыми :
| 5 15 | + | 3 15 | ||||
Первая дробь: умножив верх и низ на 5, мы получили 5 15 :
| × 5 |
| 1 3 | = | 5 15 |
| × 5 |
Вторая дробь: умножив верх и низ на 3, мы получили 3 15 :
| × 3 |
| 1 5 | = | 3 15 |
| × 3 |
Нижние числа теперь одинаковы, поэтому мы можем добавить верхние числа:
| 5 15 | + | 3 15 | = | 8 15 | ||
Результат уже настолько прост, насколько это возможно, поэтому ответ:
1 3 + 1 5 «=» 8 15
Уравнивание знаменателей
Откуда в предыдущем примере мы узнали, что нужно разрезать их на 1 / 15 тысяч, чтобы знаменатели совпадали? Мы просто перемножили два знаменателя (3 × 5 = 15).
Прочтите о двух основных способах приведения знаменателей в соответствие здесь:
- Метод общего знаменателя или
- Метод наименьшего общего знаменателя
Они оба работают, используйте тот, который вам больше нравится!
Пример: Кексы
Вы хотите испечь и продать кексы:
- Друг может предоставить ингредиенты, если вы им дадите 1 / 3 продаж
- Прилавок на рынке стоит 1 / 4 продаж
Сколько это вообще?
нам нужно добавить 1 / 3 и 1 / 4
1 3 + 1 9000? 4 = = = = = = = . ?
Сначала сделайте нижние числа (знаменатели) одинаковыми.
Умножить верх и низ 1 / 3 на 4 :
1×4 3×4 + 4 4 90 ?
и умноженное верхнее и дно 1 / 4 на 3 :
1 × 4 3 × 4 + 1 × 3 40006? ?
Now do the calculations:
4 12 + 3 12 = 4+3 12 = 7 12
Answer: 7 12 сбываний идут в ингридиентах и ценах рынка.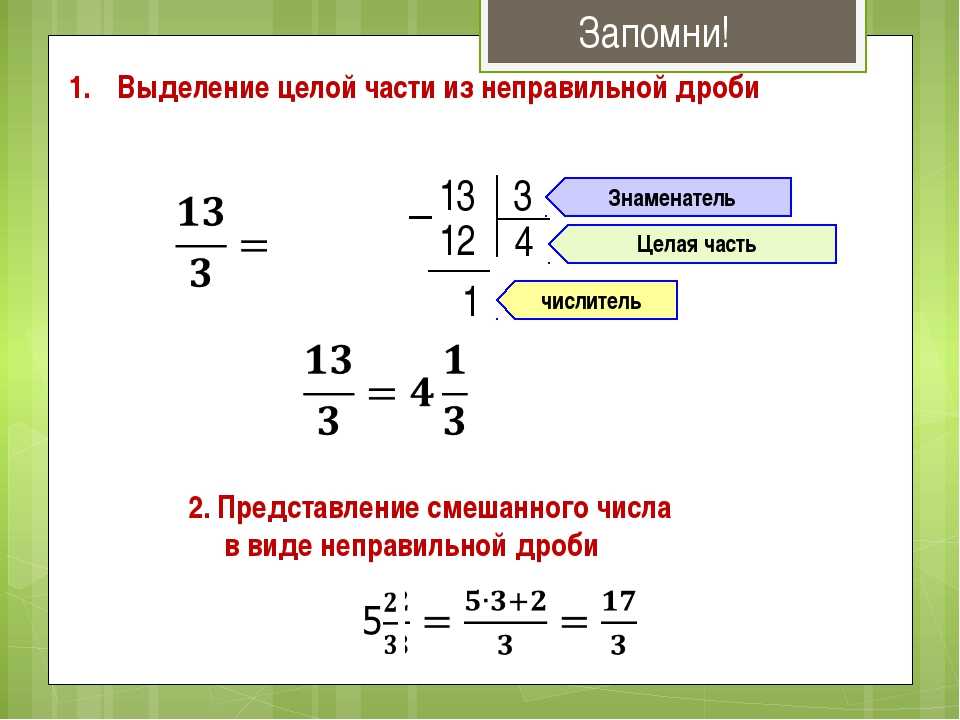


 Площадь круга
Площадь круга

