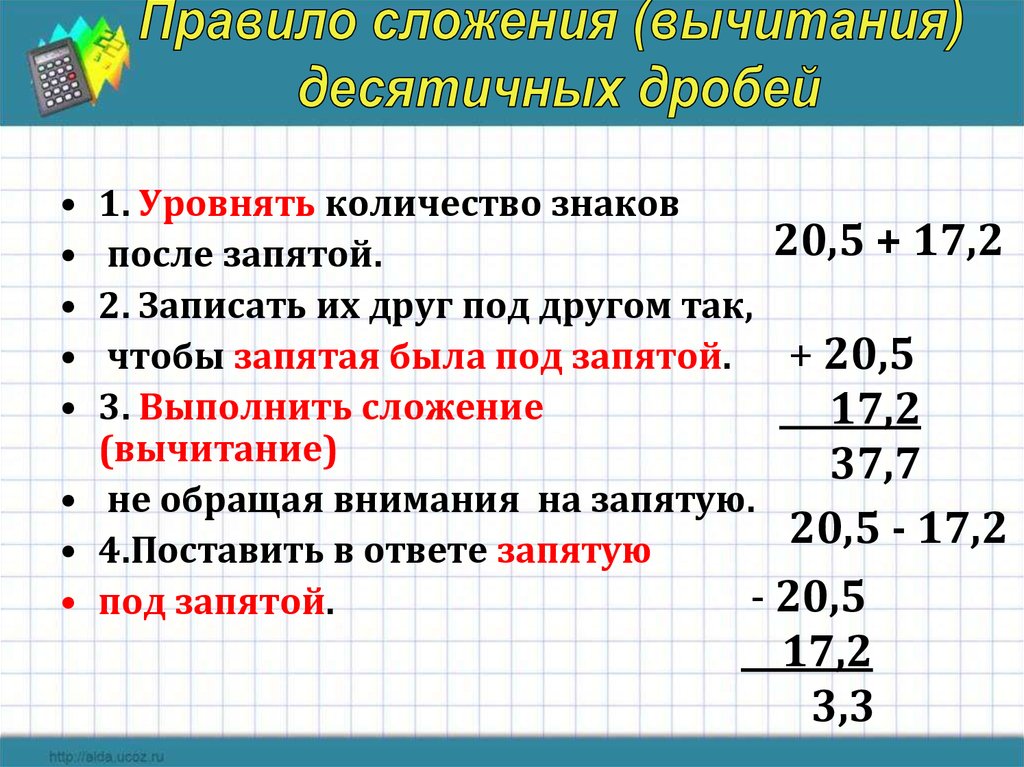
§ Сложение десятичных дробей
Похоже, вы используете блокировщик рекламы. Наш сайт существует и развивается только за счет дохода от рекламы.
Пожалуйста, добавьте нас в исключения блокировщика.
Скрыть меню
На главную страницу
Войти при помощи
Темы уроков
Начальная школа
- Геометрия: начальная школа
- Действия в столбик
- Деление с остатком
- Законы арифметики
- Периметр
- Порядок действий
- Разряды и классы. Разрядные слагаемые
- Счет в пределах 10 и 20
Математика 5 класс
- Взаимно обратные числа и дроби
- Десятичные дроби
- Натуральные числа
- Нахождение НОД и НОК
- Обыкновенные дроби
- Округление чисел
- Перевод обыкновенной дроби в десятичную
- Площадь
- Проценты
- Свойства сложения, вычитания, умножения и деления
- Среднее арифметическое
- Упрощение выражений
- Уравнения 5 класс
- Числовые и буквенные выражения
Математика 6 класс
- Масштаб
- Модуль числа
- Окружность.
 Площадь круга
Площадь круга - Отношение чисел
- Отрицательные и положительные числа
- Периодическая дробь
- Признаки делимости
- Пропорции
- Рациональные числа
- Система координат
- Целые числа
Алгебра 7 класс
- Алгебраические дроби
- Как применять формулы сокращённого умножения
- Многочлены
- Одночлены
- Системы уравнений
- Степени
- Уравнения
- Формулы сокращённого умножения
- Функция в математике
Геометрия 7 класс
- Точка, прямая и отрезок
- Что такое аксиома и теорема
Алгебра 8 класс
- Квадратичная функция. Парабола
- Квадратные неравенства
- Квадратные уравнения
- Квадратный корень
- Неравенства
- Системы неравенств
- Стандартный вид числа
- Теорема Виета
Алгебра 9 класс
- Возрастание и убывание функции
- Нули функции
- Область определения функции
- Отрицательная степень
- Среднее
геометрическое - Чётные и нечётные функции
Алгебра 10 класс
- Иррациональные числа
Алгебра 11 класс
- Факториал
Математику нельзя изучать, наблюдая, как это делает сосед.
на главную
Введите тему
Русский язык Поддержать сайт
Десятичные дроби Как читать десятичные дроби Сложение десятичных дробей Вычитание десятичных дробей Умножение десятичных дробей Деление десятичных дробей Как сравнивать десятичные дроби
Сложение десятичных дробей выполняется по правилам сложения в столбик.
При сложении десятичные дроби записываются «столбиком», так чтобы одноимённые разряды находились друг под другом без смещения. При этом запятые должны стоять чётко друг под другом.
Неправильная запись
Правильная запись
Складывают десятичные дроби в столбик как натуральные числа, не обращая внимания на запятые.
В ответе запятую ставим под запятыми в исходных дробях.
Запомните!
Если исходные десятичные дроби имеют разное
количество знаков (цифр) после запятой, то к дроби с меньшим количеством
десятичных знаков нужно приписать необходимое число нулей, чтобы уравнять
в дробях количество знаков после запятой.
Разберёмся на примере. Найдём сумму десятичных дробей.
0,678 + 13,7 =
Уравняем количество знаков после запятой в десятичных дробях. Допишем два нуля справа к десятичной дроби 13,7 .
0,678 + 13,700 =
Запишем ответ.
0,678 + 13,7 = 14,378
Если сложение десятичных дробей вами усвоено уже хорошо, то недостающие нули можно приписывать мысленно.
Итак, ещё раз коротко основные правила сложения:
- уравниваем количество знаков после запятой;
- выполняем сложение десятичных дробей, не обращая внимания на запятые, по правилам сложения в столбик натуральных чисел;
- ставим в ответ запятую под запятыми.
Десятичные дроби Как читать десятичные дроби Сложение десятичных дробей Вычитание десятичных дробей Умножение десятичных дробей Деление десятичных дробей Как сравнивать десятичные дроби
Сложение и вычитание десятичных дробей.
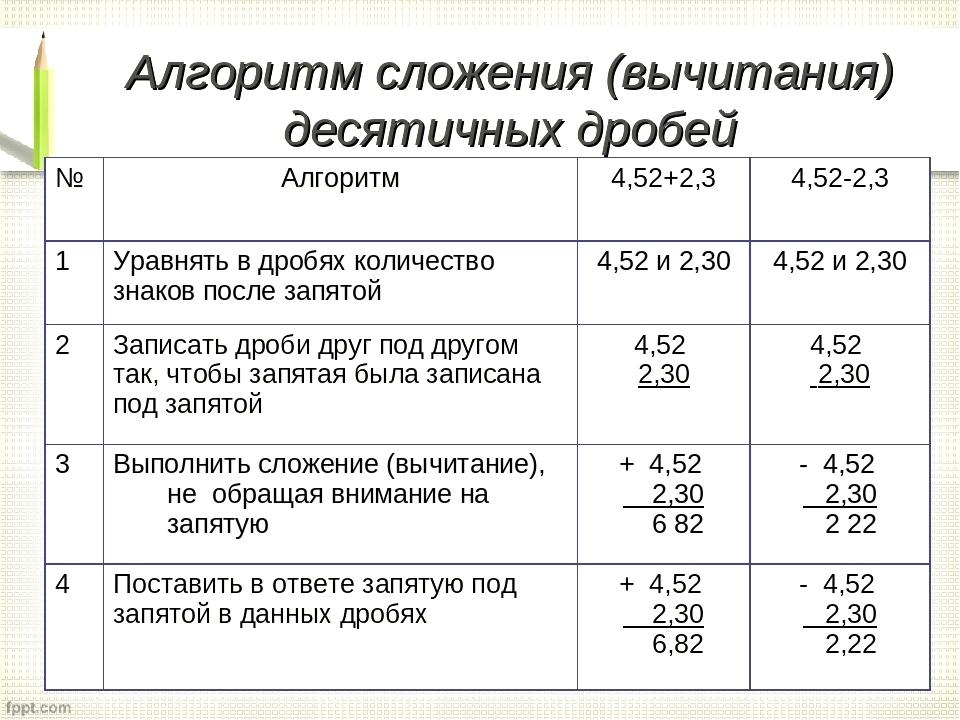 Решение задач на сложение и вычитание десятичных дробей.
Решение задач на сложение и вычитание десятичных дробей.- Альфашкола
- Статьи
- Сложение и вычитание десятичных дробей
Для того чтобы сложить или вычесть две и более десятичных дроби воспользуемся правилом столбика. Запишем десятичные запятые так, чтобы они находились одна под другой, то есть были в одном столбике. Сотни должны находиться под сотнями, десятки под десятками. Двадцать пять сотых – это ноль целых, две десятых и 5 сотых. Девять десятых – 0 целых и девять десятых. Ниже расписаны классы целых, десятых и сотых.
\(0,25=0+0,2+0,05\)
\(0,9=0+0,9\)
\(2,25=2+0,2+0,05\)
\(3,102=3+0,1+0,002\)
Разобрались с этим, двигаемся дальше.
Задача 1. Сложить две дроби \(0.25\) и \(0,9\).
Решение. Запишем запятые в один столбик, затем складываем по отдельности каждую цифру.
Ответ: \(1,15\).
Распространенная ошибка, заключается в том, что \(5\) прибавляется к \(9\). Сотые приравниваются с десятками, а так делать нельзя, \(5\) – сотые части, \(9\) – десятые. Позиция значения места в столбике должна быть строгой, и основываться на десятичной запятой.
Бывают случаи, когда у десятичных чисел не одинаковое количество цифр после запятой, тогда можно добавить ноль справа.
Задача 2. Вычесть две дроби 0,92 и 0,7.
Решение. Добавим один ноль справа у дроби 0,7 для удобства вычисления:
Ответ: \(0,22\).
Когда мы прибавляем десятичную дробь к натуральному числу, то в конце числа ставим запятую и столько нулей, сколько нам необходимо, чтобы приравнять цифры.
Выводы. При сложении и вычитании десятичных дробей в столбик существуют следующие правила:
- запятая располагается строго под запятой;
- если нужно приравнять цифры, то справа добавляются нули у десятичного числа, а у натурального числа ставится в конце запятая и добавляется необходимое количество нулей.
- в ответ записывается запятая под запятой;
Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!
Запишитесь на бесплатное тестирование знаний!
Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности
Наши преподаватели
Камо Аркадьевич Филипосян
Репетитор по математике
Стаж (лет)
Образование:
Самаркандский государственный университет
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Анастасия Александровна Чернова
Репетитор по математике
Стаж (лет)
Образование:
Национальный исследовательский ядерный университет
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Ирина Владимировна Милёшина
Репетитор по математике
Стаж (лет)
Образование:
Куйбышевский государственный педагогический институт
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Предметы
- Математика
- Репетитор по химии
- Репетитор по русскому языку
- Репетитор по английскому языку
- Репетитор по обществознанию
- Репетитор по истории России
- Репетитор по биологии
- Репетитор по географии
- Репетитор по информатике
Специализации
- Подготовка к ОГЭ по математике
- Репетитор по олимпиадной математике
- Подготовка к ЕГЭ по математике (профильный уровень)
- Репетитор для подготовки к ЕГЭ по физике
- Репетитор по русскому языку для подготовки к ЕГЭ
- Репетитор для подготовки к сочинению ЕГЭ по русскому
- Репетитор по английскому для взрослых
- Репетитор для подготовки к ВПР по русскому языку
- ВПР по обществознанию
- Подготовка к ЕГЭ по информатике
Похожие статьи
- Пропорция в математике
- Параллелограмм
- ГМУ: Финансовый Университет при Правительстве Российской Федерации
- ЕГЭ по математике, профильный уровень.
 Задачи на оптимальный выбор
Задачи на оптимальный выбор - Решаем задачи на движение по окружности
- Задачи на вычисление степенных выражений
- Обучение старшеклассников: как найти общий язык с учениками, если разница в возрасте небольшая?
- Как организовать режим школьника на каникулах, чтобы потом было легче снова идти в школу
Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности
Текст с ошибкой:
Расскажите, что не так
Сложение и вычитание десятичных дробей
Сложение и вычитание десятичных дробейСложение и вычитание десятичных дробей
Назад на страницу с десятичными дробями Назад к математике 187A страница Назад к математике Страница отдела электронная почта Вопросы и предложения
|
Сложение и вычитание десятичных дробей. Обзор математики (видео) часто появляются в нашей повседневной жизни.
Например, товар в магазине может стоить 2,75 доллара, а ваш любимый баскетболист может стоить в среднем 19 долларов.0,7 очка за игру. Вы можете взять кредит под 4,45% годовых, или победитель эстафеты на 100 метров может завершить гонку за 12,67 секунды.
Чтобы эффективно использовать десятичные дроби, важно уметь использовать десятичные дроби и манипулировать ими в математических выражениях.
Сегодня мы рассмотрим основы — сложение и вычитание.
Сложение десятичных знаков
Мы начнем с простого примера сложения десятичных знаков, так что давайте попробуем:
\(32.61+11.54\)
The first step, like you can see, is to line up the two decimals like so:
| \(32.61\) | |
| \ (+\) | \(11,54\) |
Обратите внимание, что из-за коммутативного свойства сложения не имеет значения, какой десятичный знак ставится первым (однако это будет иметь значение при вычитании).
Убедитесь, что десятичные точки в каждом числе выровнены точно. Если ваши десятичные дроби выстроены неправильно, вы получите неправильный ответ.
Как только вы выстроите два десятичных знака в ряд, вы начнете решать задачу так же, как и любую задачу на сложение.
Сначала мы складываем два числа в сотых , \(1\) и \(4\), что дает нам \(5\) в сотых. Затем мы добавляем \(6\) и \(5\), которые находятся в десятых разрядах, и это дает нам 11, поэтому мы переносим 1. Уменьшаем нашу десятичную дробь, и теперь у нас есть \(2+1+ \) этот другой \(1\), так что это \(3\), \(4\). А теперь складываем \(3\) и \(1\) и получаем \(4\). Итак, наш окончательный ответ: \(44,15\).
Затем мы добавляем \(6\) и \(5\), которые находятся в десятых разрядах, и это дает нам 11, поэтому мы переносим 1. Уменьшаем нашу десятичную дробь, и теперь у нас есть \(2+1+ \) этот другой \(1\), так что это \(3\), \(4\). А теперь складываем \(3\) и \(1\) и получаем \(4\). Итак, наш окончательный ответ: \(44,15\).
| \(32.61\) | |
| \(+\) | \(11.54\) |
| \(44.15\) |
Subtracting Decimals
Let’s move к вычитанию. Начнем с простой задачи:
\(7,5-2,8\)
Как и в случае сложения, первым шагом является выстраивание чисел с запятой в одном месте. Ваше выражение должно выглядеть так:
| \(7,5\) | |
| \(–\) | \(2,8\) |
9002. Начиная с десятого столбца, вам нужно сначала заимствовать из нашего столбца, потому что \(5-8\) не получается. Итак, возьмите \(1\), сделайте это \(6\), а затем перенесите его. Итак, теперь у нас есть \(8\), вычитаемое из \(15\), что дает нам \(7\). Сократите нашу десятичную дробь, и теперь у нас есть \(2\), вычитаемое из \(6\), что дает нам \(4\). Итак, наш окончательный ответ: \(4.7\).
Итак, возьмите \(1\), сделайте это \(6\), а затем перенесите его. Итак, теперь у нас есть \(8\), вычитаемое из \(15\), что дает нам \(7\). Сократите нашу десятичную дробь, и теперь у нас есть \(2\), вычитаемое из \(6\), что дает нам \(4\). Итак, наш окончательный ответ: \(4.7\).
| \ (7,5 \) | |
| \ ( — \) | \ (2.8 \) |
| \ (4,7 \) | \ (4,7 \) | 39.9039.9039.9039.9039.23\ (4,7 \) | 9039. \. задача:
Еще раз выстраиваем два наших числа, убедившись, что наши десятичные точки находятся в одном положении. Ваше выражение должно выглядеть так:
|
 Площадь круга
Площадь круга Задачи на оптимальный выбор
Задачи на оптимальный выбор Напомним, что десятичные дроби
просто дроби. Мы складываем дроби, складывая целые части числа и
дробные части отдельно, перенося 1 из дробной части, если
необходимо для целой части числа. Для десятичных дробей мы выстраиваем
десятичных знаков так, чтобы целые части числа совпадали, а десятичные части
расстановка. Затем добавьте каждый.
Напомним, что десятичные дроби
просто дроби. Мы складываем дроби, складывая целые части числа и
дробные части отдельно, перенося 1 из дробной части, если
необходимо для целой части числа. Для десятичных дробей мы выстраиваем
десятичных знаков так, чтобы целые части числа совпадали, а десятичные части
расстановка. Затем добавьте каждый.
 Мы линии
поднимите десятичные дроби по вертикали, прикрепите лишние нули справа и вычтите
вниз. В частности, выполните следующие действия:
Мы линии
поднимите десятичные дроби по вертикали, прикрепите лишние нули справа и вычтите
вниз. В частности, выполните следующие действия:  2 1 4
2 1 4 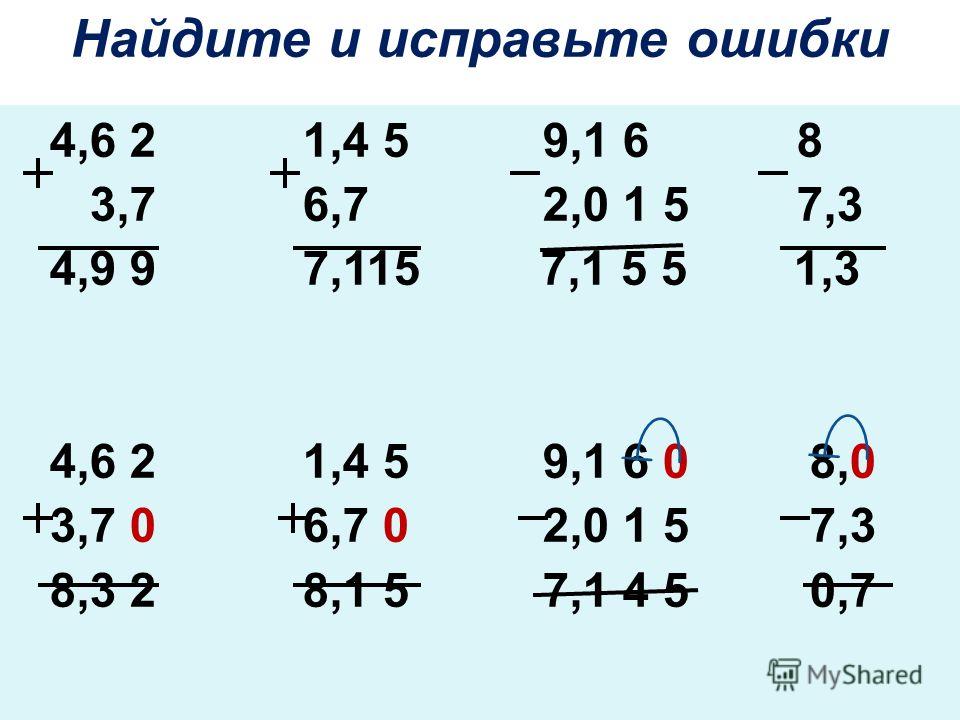 12 3 1 0
12 3 1 0 
 Их можно не добавлять, и это тоже нормально.
Их можно не добавлять, и это тоже нормально. Не забывайте всегда выстраивать числа и следить за тем, чтобы десятичные дроби каждого числа стояли на одном месте!
Не забывайте всегда выстраивать числа и следить за тем, чтобы десятичные дроби каждого числа стояли на одном месте!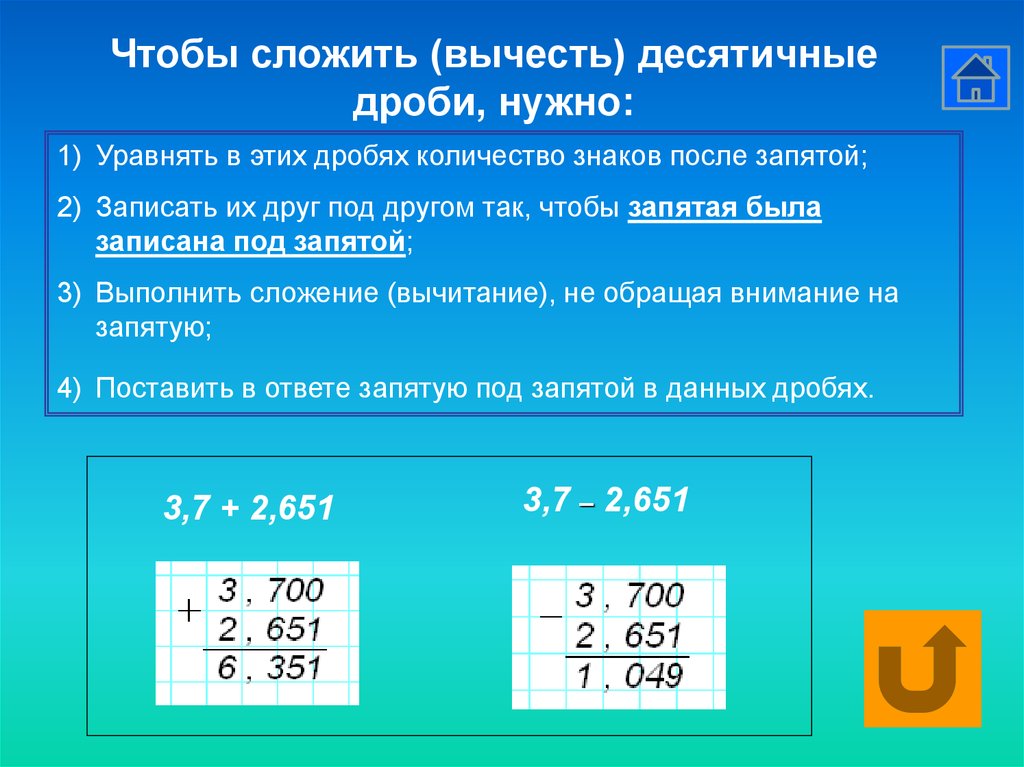 3,97 и близко не соответствует этому значению, поэтому вы понимаете, что где-то допустили ошибку. Вы возвращаетесь к исходной работе и замечаете, что забыли выровнять десятичные точки. Теперь вы можете исправить свою проблему и получить правильный ответ 15.13.
3,97 и близко не соответствует этому значению, поэтому вы понимаете, что где-то допустили ошибку. Вы возвращаетесь к исходной работе и замечаете, что забыли выровнять десятичные точки. Теперь вы можете исправить свою проблему и получить правильный ответ 15.13.
 Помните, если десятичной точки нет, она стоит в конце числа.
Помните, если десятичной точки нет, она стоит в конце числа.  Чтобы вычесть десятичные дроби, выровняйте десятичные точки друг над другом, добавьте 0, где необходимо, в качестве заполнителей и вычтите как обычно.
Чтобы вычесть десятичные дроби, выровняйте десятичные точки друг над другом, добавьте 0, где необходимо, в качестве заполнителей и вычтите как обычно.  Сколько денег у него осталось?
Сколько денег у него осталось?