Урок математики в 4-м классе по теме «Как умножать многозначные числа столбиком»
- Бодрягина Надежда Анатольевна, учитель начальных классов
Разделы: Математика, Начальная школа, Общепедагогические технологии
Цели урока:
- Образовательные: уточнить алгоритм умножения многозначных чисел и применить его на практике;
- Развивающие: развивать умение сравнивать, обобщать, делать выводы, выдвигать разные версии, формировать самоконтроль и самооценку, способствовать развитию математической речи, внимания, логического мышления.
- Воспитательные: воспитывать интерес к предмету, умение работать индивидуально и в группе.

Вопрос цикла | Место урока и его вопрос | Вид диалога на уроке | «Схема организации действия» по итогам урока |
«Как умножать на многозначные числа?» | Конкретизация модели «Как умножать на многозначные числа? По какому алгоритму решаются любые примеры на умножение в столбик?» (Алгоритм) | Диалог продуктивного действия. | Чтобы умножить многозначные числа в столбик, нужно: 2. Умножить единицы 2-го мн-ля на каждое разрядное слагаемое 1-го мн-ля, начиная с единиц. 3. Каждую разрядную единицу произведения записать в свой разряд. 4. Умножить 1-й мн-ль на число десятков 2-го мн-ля. 5. Каждую разрядную единицу произведения записать в свой разряд. 6. Сложить эти неполные произведения. |
Ход урока
2.1. Первый и второй этапы дискуссииТриада заданий: | Сценарий исследующей дискуссии | |||
Конкурирующие средства поиска детей | Запрос помощи учителем (фиксация ее получения) | Определенные детьми средства поиска | ||
I. | I. Проблема — Почему не удалось быстро и правильно вычислить произведения двух последних примеров? В чём их особенность?
| II. Вопрос | ||
Реши и объясни, как ты это делал. 2132х4 2400х7 136х700 312х12 705х14 |
|
— Итак, вы договорились, каким способом вычислить произведение при умножении многозначного числа на многозначное, чтобы получился одинаковый результат: (Согласна, что не договорились.) (Действительно, не помогло.) — А что помогло решить точно и быстро первые три примера? (Согласна, алгоритм.) — Значит, алгоритм – для быстрого и точного решения-хорошо, но другой, в котором можно объяснить, как умножить многозначные числа вам еще не известен? | ||
II. При определении вопроса поиска | ||||
— Как умножать на многозначные числа? По какому алгоритму решаются любые примеры на умножение в столбик? | — Тогда как будете двигаться дальше: повторно вычислять пример, или сначала разбираться в чем-то? (Действительно, надо разобраться.) | |||
Организация | Индивидуально (принцип индивидуальных вкладов), учитель-класс (обмен позициями) | |||
Триада заданий: | Сценарий исследующей дискуссии | |||
Конкурирующие средства поиска детей | Запрос помощи учителем (фиксация ее получения) | Определенные детьми средства поиска | ||
III. | III. Гипотеза | IV. Результат Чтобы умножить многозначные числаможно: | ||
Поработайте в группе. 312х12= | Гипотезы про: 1) 312х12=312х3х4=396х4=3744; 2)312х12=312х6х2=1872х2=3744; 3)312х12=312х10+312х2= | — На доске разные версии решения примера в строку. — Теперь есть ясность, как находятся произведения многозначных чисел? (Хорошо.) | ||
IV. При определении результата поиска | ||||
Чтобы умножить многозначные числа можно: | — Теперь скажите, пользуясь этим открытием, как действовать, чтобы найти произведения многозначных чисел. 312х12= — И какой порядок нахождения произведения получается, в итоге? (Теперь не ошибусь!) | |||
Организация | По группам (обмен позициями), учитель-группы-класс (обмен позициями). | |||
Триада заданий: | Сценарий исследующей дискуссии | ||
Конкурирующие средства поиска детей | Запрос помощи учителем (фиксация ее получения) | ||
V. | V. Вывод (на «схеме организации действия» знаками + и –) Чтобы умножить многозначные числа можно: Использовать решение в строку, где 2-й мн-ль разложен на разрядные слагаемые. аbc х ке=аbc х k0 + аbc х e 2. Грамотно вычислить и записать результат. — Cначала я разложил 2-й мн-ль на разрядные слагаемые. Затем умножил 1-й мн-ль на разрядное слагаемое. Получил неполные произведения. Сложил неполные произведения. | ||
1) Запиши и реши пример в столбик, используя заданные выражения. | (на доске без обсуждения фиксируются только разногласия): 1) не смог (не понял) | — Каждый узнал новый способ умножения многозначных чисел. — Кому наш порядок действий сразу помог найти произведение, и каждый шаг пройден успешно? (Спасибо, вижу, отмечаю ваш ход работы знаками +). — А у кого не получилось? (Спасибо, есть такие). Кто покажет на нашем «порядке действия», чему ему еще надо научиться? (Спасибо, если причина ясна, отредактируйте свои решения) — Я вижу, что наш порядок действий теперь всем помог найти произведение. | |
Организация | Индивидуально (принцип индивидуальных вкладов), учитель-класс (обмен позициями). | ||
Литература
- Выготский Л.С. Мышление и речь.
 М.: Лабиринт, 1996.
М.: Лабиринт, 1996. - Выготский Л.С. Педагогическая психология/ Лев Выготский; под ред. В.В.Давыдова. М.: АСТ: Астрель: Люкс, 2005.
- Выготский Л.С. Развитие личности и мировоззрение ребенка // Психология личности/ под ред. Ю.Б.Гиппенрейтер, А.А.Пузырея, В.В.Архангельской. М. АСТ: Астрель, 2009. С.329-333.
- Давыдов В.В. Деятельностная теория мышления. М.: Научный мир, 2005.
- Каминская М.В. Диагностическая программа исследования позиции взрослого как одной из детерминант развития в обучении. М.: АПК и ППРО, 2010.
- Педагогический дизайн в школе компетенций: идеи, конструкторы и дидактические материалы нового поколения. Сборник проектных разработок для руководителей школ и педагогов (по материалам Окружной инновационной площадки «Интерактивные дидактические материалы учителя как необходимое инновационное оснащение школы компетенций»)./ под ред. Каминской М.В. – М.: МЦ ВОУО ДО, 2013.
- Мониторинг учебно-предметных компетенций в начальной школе / под ред.
 П.Г.Нежнова, Б.И.Хасана, Б.Д.Эльконина. М.: Университетская книга, 2007.
П.Г.Нежнова, Б.И.Хасана, Б.Д.Эльконина. М.: Университетская книга, 2007. - Станиславский К.С. Мое гражданское служение России. Воспоминания. Статьи. Очерки. Речи. Беседы. Из записных книжек / сост. М.Н. Любомудрова. М.: Правда, 1990.
- Эльконин Б.Д. Опосредствование. Действие. Развитие. Ижевск: ERGO, 2010.
- Эльконин Д.Б. Выдержки из научных дневников (1960-1962) // Вопросы психологии. 2004. №1. С.9 – 22.
ПНШ 4 класс. Математика. Учебник № 1, с. 22
Алгоритм умножения столбикомОтветы к с. 2253. Выполни умножение столбиком многозначного числа на однозначное число и ответь на следующие вопросы.
×2052
3
С какого разряда первого множителя нужно начинать умножение на однозначное число столбиком и к какому разряду следует переходить далее?
Какое число нужно записывать в соответствующий разряд результата, если при умножении в этом разряде получается однозначное число, а какое — если двузначное?
Какое число при умножении в данном разряде должно получиться, чтобы не было перехода через разряд?
В каких случаях имеет место переход через разряд и как его нужно учитывать при дальнейших вычислениях?
×2052
3
6156
Умножение нужно начинать с разряда единиц первого множителя, а затем переходить к разряду десятков, сотен и тысяч. То сеть, сначала умножаются единицы, затем десятки, потом сотни и тысячи. Это позволяет учесть те единицы, которые образовались, если при умножении единиц предыдущего разряда произошёл переход через разряд.
То сеть, сначала умножаются единицы, затем десятки, потом сотни и тысячи. Это позволяет учесть те единицы, которые образовались, если при умножении единиц предыдущего разряда произошёл переход через разряд.
Если при умножении в данном разряде получается однозначное число, то оно и записывается в соотвествующий разряд результата. Если получается двузначное число, то в соотвествующий разряд результата записываетя число разряда единиц, а число разряда десятков переходит в следующий разряд результата — оно суммируется с произведение в этом разряде.
Должно получится однозначное число.
В случае, если при умножении в данном разряде получается двузначное число, то имеет место переход через разряд: число разряда десятков полученного двузначного числа переходит в следующий разряд — оно суммируется с результатом произведения в этом разряде.
54. Рассмотри, как выполнено умножение столбиком многозначного числа на двузначное число, и ответь на следующие вопросы.
×2052
23
+ 6156
41040
47196
На какое разрядное слагаемое второго множителя сначала умножаем первый множитель? На какое число нужно умножать далее? Чем отличается расположение записи результата умножения числа 2052 на 3 единицы от результата умножения этого же числа на 2 десятка?
С какого разряда начинаем записывать результат умножения числа 2052 на 2 десятка? Какая цифра стоит в этом случае в разряде единиц этого результата? Обязательно ли её записывать или можно оставить это место свободным?
Какое действие нужно выполнить над двумя полученными результатами умножения? Можно ли для выполнения этого действия применить алгоритм сложения столбиком? Можно ли использовать для сложения столбиком уже имеющуюся запись полученных чисел или нужно делать отдельную запись?
Сначала первый множитель умножается на число разряда единиц второго множителя, затем на число разряда десятков. При умножении числа 2052 на 3 единицы результат умножения записывается под соответствующим разрядом начиная с разряда единиц, а при умножении на 2 десятка — начиная с разряда десятков, то есть умножаем все разряды первого множителя на десятки второго множителя.
При умножении числа 2052 на 2 десятка записывать результат умножения начинаем под разрядом десятков. В разряде единиц этого результата будет цифра 0. Её можно не записывать и оставить место пустым.
Действие сложения. Алгоритм сложения столбиком применим. Рациональнее будет использовать для сложения столбиком уже имеющуюся запись полученных чисел.
Ответы к заданиям. Математика. Учебник. Часть 1. Чекин А.Л. 2012 г.
Математика. 4 класс. Чекин А.Л.
27.09.2018
Умножение многозначных чисел | Как?, Определение, Примеры, Метод
ВведениеУмножение — одна из четырех основных математических операций, а остальные три — это сложение, вычитание и деление. Прежде чем мы перейдем к изучению того, как умножать многозначные числа, давайте вспомним, что мы подразумеваем под умножением.
Как определить умножение? Умножение определяется как процесс нахождения произведения двух или более чисел. Полученный таким образом результат называется продукт . Предположим, вы купили 6 ручек в один день и 6 ручек на следующий день. Всего ручек, которые вы купили, теперь 2 умножить на 6 или 6 + 6 = 12.
Полученный таким образом результат называется продукт . Предположим, вы купили 6 ручек в один день и 6 ручек на следующий день. Всего ручек, которые вы купили, теперь 2 умножить на 6 или 6 + 6 = 12.
Это также можно записать как 2 x 6 = 12
Не тот символ, который используется для умножения. Символ (x) обычно используется для обозначения умножения. Другими распространенными символами, которые используются для умножения, являются звездочка (*) и точка (.)
Символ умноженияОбратите внимание на символ, используемый в приведенном выше примере для умножения. Символ (x) обычно используется для обозначения умножения. Другими распространенными символами, которые используются для умножения, являются звездочка (*) и точка (.)
Теперь давайте рассмотрим некоторые важные термины, которые используются при умножении двух чисел.
Важные термины при умноженииНекоторые важные термины, используемые при умножении: –
Множимое – Число, которое нужно умножить, называется множимым.
Множитель — Число, на которое мы умножаем, называется множителем.
Произведение – Результат, полученный после умножения множителя на множимое, называется произведением.
Связь между множителем, множимым и произведением может быть выражена как –
Множитель × Множитель = Произведение
Давайте разберемся с этим на примере.
Предположим, у нас есть два числа 9 и 5. Мы хотим умножить 9 на 5.
Итак, мы выражаем это как 9 x 5, что дает нам 45.
Следовательно, 9 x 5 = 45
Здесь 9 равно множимое, 5 — множитель, 45 — произведение.
Теперь, когда мы поняли, что мы подразумеваем под умножением и терминами, связанными с ним, давайте перейдем к изучению умножения однозначных чисел.
Теперь давайте разберемся, как выполнять умножение, когда у нас есть многозначные числа.
Как умножать многозначные числа?Прежде чем мы приступим к пониманию умножения многозначных чисел, важно вспомнить, что подразумевается под многозначными числами?
Напомним, что каждая цифра числа имеет разрядное значение. Например, число 5 — это однозначное число, где 5 стоит на месте единицы. Точно так же в числе 27 цифра 2 стоит на месте десятков, а цифра 7 — на месте единиц. Итак, как мы определяем многозначные числа? Многозначные числа — это числа, состоящие из более чем 1 цифры. Например, числа 535 и 678 являются многозначными числами.
Например, число 5 — это однозначное число, где 5 стоит на месте единицы. Точно так же в числе 27 цифра 2 стоит на месте десятков, а цифра 7 — на месте единиц. Итак, как мы определяем многозначные числа? Многозначные числа — это числа, состоящие из более чем 1 цифры. Например, числа 535 и 678 являются многозначными числами.
Теперь давайте перейдем к изучению умножения многозначных чисел. Когда дело доходит до умножения многозначных чисел, есть два метода умножения чисел. Этими методами являются метод расширенной записи и метод столбца. Давайте разберемся в обоих методах.
Метод расширенной записиВ методе расширенной записи мы расширяем множимое по разрядным значениям, а затем умножаем каждое число на множитель. Затем мы суммируем все полученные результаты, чтобы получить окончательный ответ. Давайте разберемся на примере.
Например, умножьте 1235 на 40
Решение
Мы решим это шаг за шагом.
Шаг 1 – Запишите число (множимое) в развернутом виде. Получаем,
Получаем,
1235 = 1000 + 200 + 30 + 5
Шаг 2 — Умножаем каждое число на заданное число (множитель) по одному. Получаем,
1000 х 40 + 200 х 40 + 30 х 40 + 5 х 40
= 40000 + 8000 + 1200 + 200
Шаг 3 – Складываем полученные результаты. Получаем,
40000 + 8000 + 1200 + 200 = 49400
Следовательно, 1235 x 40 = 49400
Этот метод, хотя и прост, может не подходить для больших чисел. Но он используется для понимания основных понятий умножения.
Метод столбцаВ этом методе мы разбиваем числа на столбцы и умножаем числа на множимое одно за другим. Есть два сценария использования этого метода.
Разберем их по порядку
Умножение без перегруппировкиЭтот метод вступает в силу, когда у нас есть меньшие числа, которые не требуют переноса каких-либо чисел к цифре на следующем разряде. Давайте разберемся на примере.
Например, умножьте 1021 на 32
Решение
Чтобы получить результат, выполните следующие действия.
Шаг 1. Сначала мы записываем множимое и множитель в столбцах. Здесь у нас есть 1021 как множимое и 32 как множитель.
Шаг 2. Теперь умножаем число, стоящее на месте множимого, т. е. 1, на число, стоящее на месте множителя, которое в данном случае равно 2. Получаем
. Шаг 3. Теперь умножаем число в десятом разряде множимого на 2. Получаем
Шаг 4 – Далее умножаем число в сотенном разряде множимого на 2. Получаем
Шаг 5 – Наконец, умножаем число в тысячный разряд множимого на 2. Получаем
Шаг 6. Теперь нам нужно поместить 0 на место единиц в следующей строке в качестве заполнителя. Мы получим
. Шаг 7. Так как мы завершили умножение множимого на первую цифру множителя, мы выполняем те же действия, что и выше для умножения множимого на следующее число множителя, а затем пишем результатом будет строка напротив 0, которую мы поместили в качестве заполнителя на предыдущем шаге. Получим –
Шаг 8 Теперь, когда мы перемножили все цифры множителя с множимым, сложим полученные цифры по вертикали. Получим –
Получим –
Полученный результат и есть наш ответ. Следовательно, 1021 x 32 = 32672
Умножение с перегруппировкойВ приведенном выше случае мы имеем небольшие умножения, которые ни на одном шаге не требуют двузначных результатов. Но в случае больших чисел потребуется перенести число на число со следующим значением разряда. Это называется умножением с перегруппировкой. Давайте разберемся на примере.
Например, умножить 1025 на 34
Решение
Мы будем использовать следующие шаги, чтобы получить наш результат.
Шаг 1. Сначала мы записываем множимое и множитель в столбцах.
Шаг 2. Умножьте цифру единицы множимого на 4. У нас 4 x 5 = 20. Запишите 0 в столбце единиц и перенесите 2 в столбец десятков.
Шаг 3 – Умножаем десятый разряд множимого на 4. Получаем 2 x 4 = 8. Прибавляем к нему перенесенные 2, получаем 8 + 2 = 10. Теперь запишем 0 в столбце десятков и перенесем 1 в сто столбик.
Шаг 4. Умножаем стозначную цифру множимого на 4. Получаем 0 x 4 = 0. Добавляем к ней перенесенную 1, чтобы получить 0 + 1 = 1. Теперь запишем 5 в столбце сотен.
Шаг 5. Умножьте цифры тысячного разряда множимого на 4. Получаем 4 x 1 = 4. Запишите 4 в столбце тысяч, чтобы получить –
Шаг 6. Теперь нам нужно поставить 0 вместо единиц. поместите в следующую строку в качестве заполнителя. Мы получим
. Шаг 7 — Далее мы повторяем описанные выше шаги, чтобы умножить все цифры множимого на цифру в десятом разряде множителя. мы получим
Шаг 8 Теперь, когда мы перемножили все цифры множителя с множимым, сложим полученные цифры по вертикали. Мы получим –
Следовательно, 1025 x 34 = 34850
Вышеприведенные шаги можно обобщить для определения умножения, которое обычно известно как длинное умножение. Определим эти шаги.
Длинное умножение Длинное умножение похоже на метод столбца, за исключением того факта, что здесь мы умножаем большие числа. Этот метод используется, когда множимое больше 9, то есть множимое больше однозначного числа. Этот метод включает следующие шаги:
Этот метод используется, когда множимое больше 9, то есть множимое больше однозначного числа. Этот метод включает следующие шаги:
- Сначала мы записываем множимое и множитель в столбцах.
- Сначала умножьте число, стоящее на месте единицы множителя, на все числа множимого и запишите их горизонтально.
- Убедитесь, что вы записываете числа справа налево и каждое число находится под соответствующим разрядом множимого.
- Теперь перейдите к следующей строке.
- Поставьте 0 на месте единицы в этой строке.
- Теперь найдите цифру в разряде десятков множителя. Умножьте число, стоящее в десятом разряде множителя, на все числа множимого и запишите их горизонтально в той строке, где вы отметили 0.
- Снова переходите на следующую строку.
- Поставьте 0 на месте единиц и десятков в этой строке.
- Теперь найдите цифру в разряде сотен множителя. Умножьте число, стоящее в сотенном разряде множителя, на все числа множимого и запишите их горизонтально в той строке, где вы отметили два нуля.

- Продолжайте в том же духе, добавляя дополнительный ноль в каждую строку, пока не дойдете до конца множителя
- Сложите числа по вертикали в соответствии с их разрядами.
- Полученное таким образом число и есть ваш результат.
Давайте разберемся на примере
Например, Умножьте 132 на 13
Решение
- Сначала мы запишем множимое и множитель в столбцах.
2. Сначала умножьте число, стоящее на месте единицы множителя, на все числа множимого и запишите их горизонтально.
3. Поставьте 0 на месте единицы следующей строки
4. Теперь найдите цифру на месте десятков множителя. Умножьте число, стоящее в десятом разряде множителя, на все числа множимого и запишите их горизонтально в строке, где вы отметили 0.
5. В множимом больше нет числа. Теперь сложите числа по вертикали в соответствии с их разрядностью.
6. Окончательный ответ: 1716. Следовательно, 132 x 13 = 1716
Давайте посмотрим на другой пример, где мы 3 цифры в множимом.
Например, Умножить 364 на 123
Решение
1. Сначала запишем множимое и множитель в столбцы
2. все числа множимого и запишем их горизонтально.
3. Поставьте 0 на месте единиц следующей строки
4. Теперь найдите цифру на десятом месте множителя. Умножьте число, стоящее в десятом разряде множителя, на все числа множимого и запишите их горизонтально в той строке, где вы отметили 0,9.0007
5. Поставьте 0 вместо единиц и десятков в следующей строке.
6. Теперь найдите цифру в разряде сотен множителя. Умножьте число, стоящее в сотенном разряде множителя, на все числа множимого и запишите их горизонтально в той строке, где вы отметили два нуля.
7. В множимом больше нет числа. Теперь сложите числа по вертикали в соответствии с их разрядностью.
8. Следовательно, конечный продукт равен 44 772. Мы можем сказать, что 364 х 123 = 44772
Умножение на 100 и 1000- Чтобы умножить число на 100, нужно поставить два нуля справа от числа.
 Например, 435 х 100 = 43500
Например, 435 х 100 = 43500 - Чтобы умножить число на 1000, поставьте справа от числа три нуля. Например, 435 x 1000 = 435000
- Чтобы умножить число на произведение 100 и 1000 на счетные числа, умножьте числа на ненулевые числа, а затем добавьте к результату количество нулей. Например, умножьте 45 на 200. Чтобы решить это, мы сначала умножим 45 на 200. Получаем 45 х 2 = 90. Теперь прибавляем 2 нуля (поскольку у 200 было 2 нуля) справа от 90. Получаем 9000. Следовательно, 45 x 200 = 9000
Пример 1 Шинный завод производит
6348 шин в день. Сколько шин произведет завод за 460 дней?
Решение Нам известно, что шинный завод производит 6348 шин в день. Нам нужно найти, сколько шин завод произведет за 460 дней. Обобщим эту информацию как –
Шины, произведенные заводом за один день = 6348
Количество шин, которые завод произведет за 460 дней = ?
Чтобы получить это значение, нам нужно будет умножить 6348 на 460. Мы будем использовать длинные шаги умножения, определенные выше, чтобы найти значение. Получим –
Мы будем использовать длинные шаги умножения, определенные выше, чтобы найти значение. Получим –
Следовательно, количество шин, которые будут произведены за 460 дней, будет 2920080.
Пример 2 World Tour Travels берет 80563 фунтов стерлингов за 7-дневную поездку в США на одного пассажира. Если 790 пассажиров совершили эту поездку за год, сколько туристическое агентство заработало за этот год? Кроме того, за год эту поездку совершают 790 пассажиров. Нам необходимо найти доходы от World Tour Travels в этом году. Подытожим имеющуюся у нас информацию.
Общая сумма, взимаемая World Tour Travels за 7-дневную поездку в США на одного пассажира = £80563
Количество пассажиров, совершающих эту поездку в год = 790
Общий доход от поездок в рамках мирового турне в этом году = ?
Чтобы найти общий доход от World Tour Travels в этом году, мы должны найти, умножив 80563 на 790. Мы получим
Следовательно, доход от World Tour Travels в год, когда он стоил 80563 фунтов стерлингов за 7-дневная поездка в США на одного пассажира и 790 пассажиров, совершающих эту поездку за год, составила 6 364 4770 фунтов стерлингов.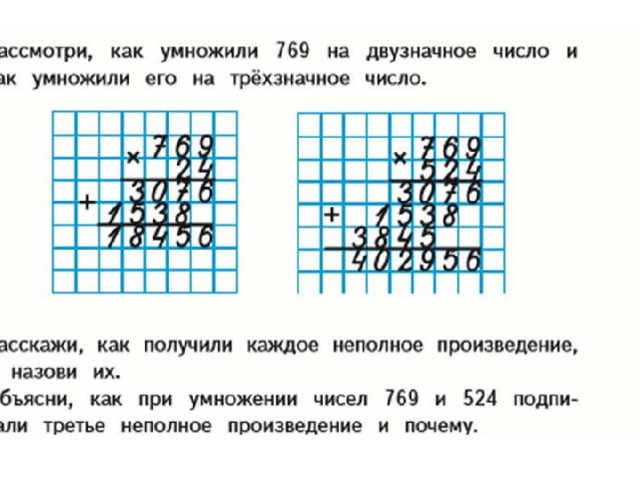
- Умножение определяется как процесс нахождения произведения двух или более чисел.
- Число, которое нужно умножить, называется множимым.
- Число, на которое мы умножаем, называется множителем.
- Результат, полученный после умножения множителя и множимого, называется произведением.
- Многозначные числа — это числа, состоящие из более чем 1 цифры.
- В методе расширенной записи мы расширяем множимое по разрядным значениям, а затем умножаем каждое число на множитель. Затем мы суммируем все полученные результаты, чтобы получить окончательный ответ.
- В методе столбца мы разбиваем числа на столбцы и умножаем числа на множимое одно за другим.
Умножение двузначных чисел (на тему путешествий и туров) Рабочие листы
Свойства умножения (на тему недвижимости) Рабочие листы
Умножение смешанных чисел (на тему Дня отца) Рабочие листы
Мы тратим много времени на изучение и сбор информации на этом сайте. Если вы сочтете это полезным в своем исследовании, используйте приведенный ниже инструмент, чтобы правильно указать ссылку Helping with Math в качестве источника. Мы ценим вашу поддержку!
Если вы сочтете это полезным в своем исследовании, используйте приведенный ниже инструмент, чтобы правильно указать ссылку Helping with Math в качестве источника. Мы ценим вашу поддержку!
Что такое Умножение многозначных чисел на однозначное число?
Содержание
- Как умножить трехзначное число на однозначное?
- Как умножить четырехзначное число на однозначное?
- Решенные примеры
- Часто задаваемые вопросы
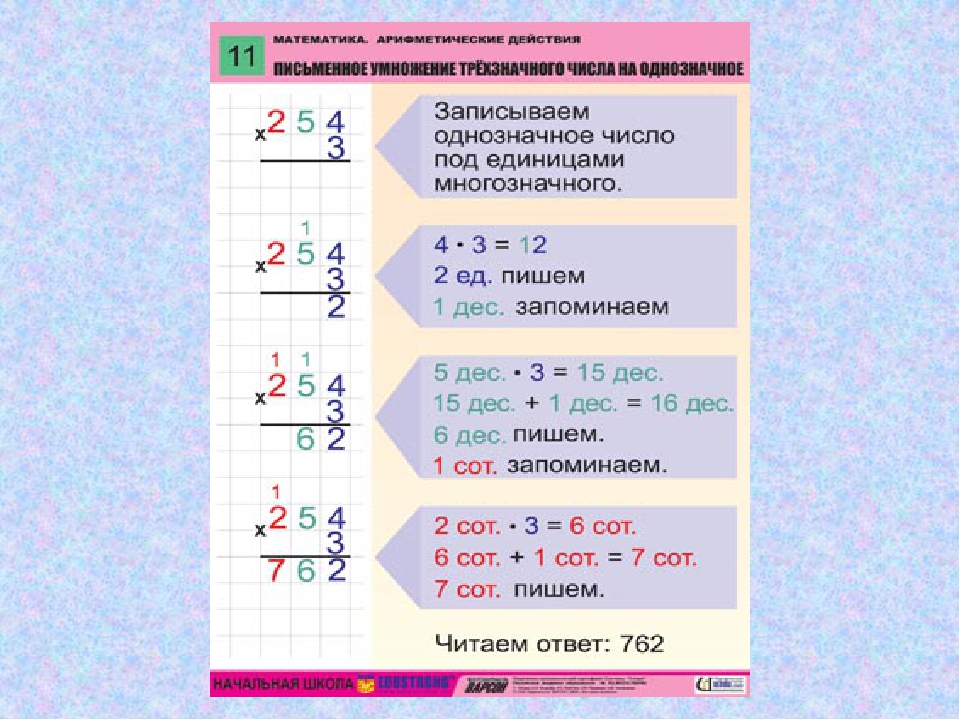
Как умножить трехзначное число на однозначное?
Когда мы умножаем многозначное число на однозначное, мы выполняем небольшие шаги умножения, чтобы получить ответ. Однозначное число стоит на месте единицы. Итак, сначала мы помещаем однозначное число под разряд единиц многозначного числа вместе с символом умножения, например:
Мы умножаем младшую цифру на цифру в разряде единиц, 7. Мы всегда начинаем умножение с крайнего правого угла, а затем продвигаемся влево.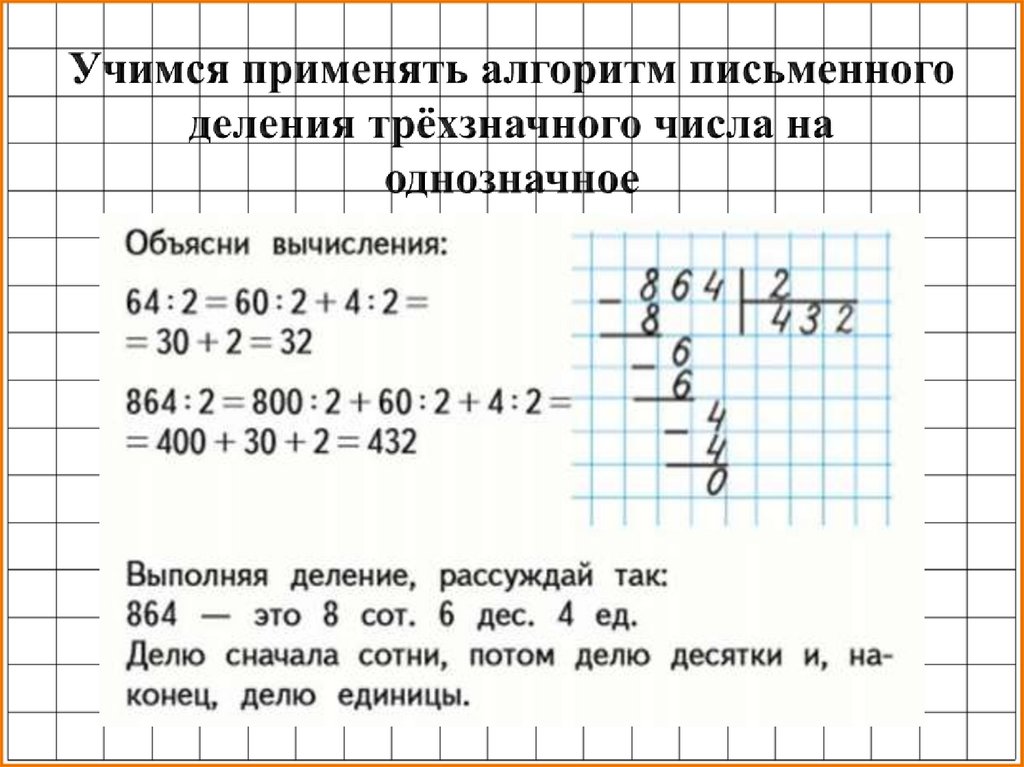 Теперь 5 умножить на 7 дает нам 35.
Теперь 5 умножить на 7 дает нам 35.
Аналогично сложению, мы перегруппируем 35 как 3 десятка и 5 единиц. Мы должны перенести первую цифру «35» в начало следующего столбца, десятки. Итак, 5 остается внизу на разряде единиц, а 3 переносится вверх на разряде десятков.
Теперь переходим к следующему столбцу десятков и умножаем 5 на 3 в разряде десятков. 5 умножить на 3 дает нам 15 десятков, и вместе с этим мы добавим 3 десятка сверху. Это дает нам 18 десятков. Опять же, мы перегруппируем 18 как 1 сотню и 8 десятков. Затем мы перенесем 1 из «18» в верхнюю часть столбца сотен, оставив 8 в месте ответа. Теперь переходим к последнему шагу умножения.
Умножим 5 на 1 в разряде сотен, и получим 5 сотен. Но в столбце сотен есть цифра, и мы должны добавить ее вместе со значением, которое мы получили на третьем шаге умножения. Итак, это дает нам 5 + 1 = 6 в разряде сотен. Ставим его рядом с двумя другими цифрами в месте ответа. Итак, окончательный ответ приходит к 685.
Итак, окончательный ответ приходит к 685.
Теперь применим метод частичного произведения для решения той же задачи. В этом методе мы не будем переносить цифры, а будем рассматривать цифры в их единицах, десятках и сотнях.
Здесь мы принимаем цифры слева как 1 как 100, 3 как 30 и 7 как 7. Если мы сложим их, мы получим 137, как указано в примере. Теперь давайте начнем с умножения. Сначала мы умножим 5 на 7, что даст нам 35. Мы запишем это.
Теперь мы переходим к следующему шагу умножения, 5 умножить на 3. Но вместо 5 умножить на 3 мы будем умножать 5 на 30 по правилу частичных произведений. Это даст нам 150.
На последнем шаге умножения мы должны умножить 5 на 1, но вместо этого мы умножим 5 на 100. Это даст нам 500, которые мы запишем в нашей таблице.
Теперь мы добавим все эти три значения, которые мы получили в результате умножения. Это даст нам 685, аналогично ответу, который мы получили от традиционного метода.
Как мы можем умножить четырехзначное число на однозначное число?
Подобно умножению трехзначных чисел, умножение четырехзначных чисел включает небольшие шаги умножения. Мы можем использовать как метод частичного произведения, так и метод перегруппировки. Давайте посмотрим на них обоих на следующем примере.
Мы можем использовать как метод частичного произведения, так и метод перегруппировки. Давайте посмотрим на них обоих на следующем примере.
Мы всегда начинаем с умножения справа, с разряда единиц. 3 раза по 5 даст нам 15. Мы перегруппируем это как 1 десяток и 5 единиц и, таким образом, перенесем «1» в столбец десятков, написав 5 в месте ответа.
Теперь умножим 3 на 4 в разряде десятков. Это даст нам 12 десятков. Мы должны добавить к нему 1 десяток, что дает нам 13 десятков. Теперь перегруппируем 13 как 1 сотню и 3 десятка и запишем их соответствующим образом.
Теперь перейдем к умножению 3 на 3, что дает нам 9 сотен. Вместе с этим мы добавим 1 сотню, что даст нам 10 сотен. Мы перегруппируем 10 как 1 тысячу и 0 сотен.
Последний шаг умножения 3 на 2, что даст нам 6 тысяч. Добавим к нему 1 тысячу, и получится 7 тысяч. Таким образом, ответ равен 7035.
Теперь воспользуемся методом частичных произведений для умножения четырехзначных чисел. В этом методе мы расширяем цифры числа в соответствии со значением разряда, а затем выполняем умножение. Давайте посмотрим на пример.
Начнем с разряда единиц. 3 раза по 5 даст нам 15, и мы запишем это соответственно.
Теперь переходим к разряду десятков. Умножим 3 на 4. Но вместо этого умножим 3 на 40 по правилу частичных произведений. Это даст нам 120.
Теперь давайте умножим 3 на 3 в разряде сотен. Но вместо 3 мы умножим его на 300. Это даст нам 900.
На последнем шаге умножения мы умножим 3 на 2 в разряде тысяч. Но вместо 2 умножим на 2000. Это даст нам 6000.
Теперь мы сложим эти столбцы в частичном произведении, чтобы получить окончательный ответ. Это даст нам 7035 в качестве ответа, что похоже на то, что мы получили в методе перегруппировки.
Решенное умножение многозначных чисел Примеры
Пример 1 : Найдите произведение: 2453 x 4
Сначала мы начнем с разряда единиц и будем двигаться справа налево. 4 раза по 3 даст нам 12, которые мы можем перегруппировать как 1 десяток и 2 единицы. Итак, мы переносим «1» в верхнюю часть столбца десятков и ставим «2» в ячейку ответа.
4 раза по 3 даст нам 12, которые мы можем перегруппировать как 1 десяток и 2 единицы. Итак, мы переносим «1» в верхнюю часть столбца десятков и ставим «2» в ячейку ответа.
Теперь умножаем 4 на 5 в разряде десятков. Это даст нам 20 десятков. Теперь мы добавляем 1 десяток вместе с 20 десятками, чтобы получить 21 десяток. Теперь мы можем перегруппировать его как 2 сотни и 1 десяток.
Перейдем к разряду сотен, 4 раза по 4 получим 16 сотен. Мы добавляем 2 сотни вместе с ним, чтобы получить 18 сотен. Теперь перегруппируем 18 как 1 тысяча и 8 сотен и перенесем «1» в столбец «тысячи» и поставим 8 в поле ответа.
Теперь умножаем 4 на 2 в разряде тысяч. 4 умножить на 2 даст нам 8 тысяч. Мы добавим 1 тысячу вместе с ним. Это даст нам 9тысяч, которые мы поместим в поле для ответов.
Следовательно, ответ равен 9812.
Пример 2 : Найдите 422 x 4 и проверьте, является ли оно разумным или нет.
Ответ:
Мы можем оценить эту задачу как 400 x 4 = 1600. Таким образом, если реальная стоимость продукта близка к расчетному продукту, то ответ будет разумным.
Таким образом, если реальная стоимость продукта близка к расчетному продукту, то ответ будет разумным.
Давайте воспользуемся методом перегруппировки, чтобы найти ответ.
422
x 4
———–
Мы начинаем с правого, где умножаем 4 на 2 на месте. Это даст нам 8. Поскольку у нас нет цифр для переноса, мы переходим к следующему шагу умножения, где мы умножаем 4 на 2 в разряде десятков. Это снова даст нам 8 десятков. У нас нет цифр для переноса, поэтому мы переходим к следующему шагу умножения. 4 умножить на 4 даст нам 16 сотен. Ответ 1688.
Если вы сверитесь с предполагаемым продуктом, ответ будет довольно близким и, следовательно, разумным.
Часто задаваемые вопросы
Какие существуют способы умножения многозначных чисел на однозначные?
Существует несколько способов умножения многозначных чисел на однозначные. Мы можем использовать традиционный метод вместе с перегруппировкой.


 При выполнении задания и определении проблемы поиска
При выполнении задания и определении проблемы поиска
 вопросы
вопросы При выдвижении гипотез об «открытии»
При выдвижении гипотез об «открытии» И какая же из них точно рассказывает о 1-м неполном произведении, о 2-м? (Поняла, тогда отредактируйте свои открытия те группы, у которых данные сравнения были не точными).
И какая же из них точно рассказывает о 1-м неполном произведении, о 2-м? (Поняла, тогда отредактируйте свои открытия те группы, у которых данные сравнения были не точными). (Спасибо, все ваши предложения про порядок вычисления я записала на доске. Попробую так действовать)
(Спасибо, все ваши предложения про порядок вычисления я записала на доске. Попробую так действовать)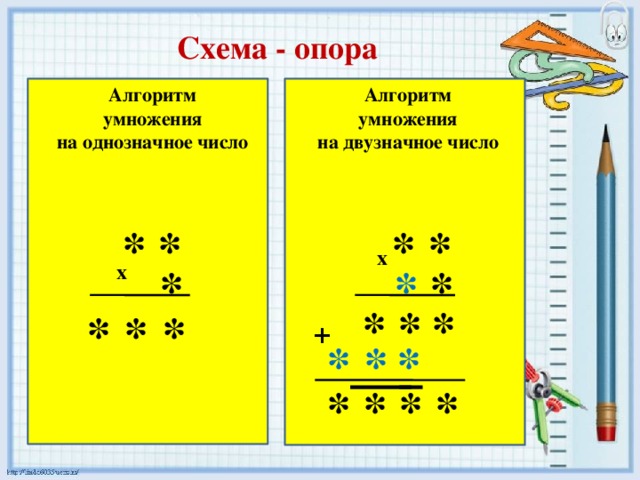 При формулировке вывода как руководства к собственному действию
При формулировке вывода как руководства к собственному действию Но у кого-то получилось, а кто-то пока не смог умножить в столбик. Как же надо было действовать, чтобы выполнить это задание? (Спасибо, убедили, по-нашему порядку действий).
Но у кого-то получилось, а кто-то пока не смог умножить в столбик. Как же надо было действовать, чтобы выполнить это задание? (Спасибо, убедили, по-нашему порядку действий). М.: Лабиринт, 1996.
М.: Лабиринт, 1996. П.Г.Нежнова, Б.И.Хасана, Б.Д.Эльконина. М.: Университетская книга, 2007.
П.Г.Нежнова, Б.И.Хасана, Б.Д.Эльконина. М.: Университетская книга, 2007.
 Например, 435 х 100 = 43500
Например, 435 х 100 = 43500