| Табличка на двери |
Правила умножения дробей с разными знаменателями, примеры
Обыкновенные дробные числа впервые встречают школьников в 5 классе и сопровождают их на протяжении всей жизни, так как в быту зачастую требуется рассматривать или использовать какой-то объект не целиком, а отдельными кусками. Начало изучения этой темы — доли. Доли — это равные части, на которые разделен тот или иной предмет. Ведь не всегда получается выразить, допустим, длину или цену товара целым числом, следует принять во внимание части или доли какой-либо меры. Образованное от глагола «дробить» — разделять на части, и имея арабские корни, в VIII веке возникло само слово «дробь» в русском языке.
Оглавление:
- Умножение дробей с разными знаменателями
- Как происходит перемножение
- Простейшие действия с дробями онлайн
Дробные выражения продолжительное время считали самым сложным разделом математики. В XVII веке, при появлении первоучебников по математике, их называли «ломаные числа», что очень сложно отображалось в понимании людей.
В XVII веке, при появлении первоучебников по математике, их называли «ломаные числа», что очень сложно отображалось в понимании людей.
Это интересно: Как найти разность чисел в математике?
Современному виду простых дробных остатков, части которых разделены именно горизонтальной чертой, впервые поспособствовал Фибоначчи — Леонардо Пизанский. Его труды датированы в 1202 году. Но цель этой статьи — просто и понятно объяснить читателю, как происходит умножение смешанных дробей с разными знаменателями.
Содержание
Умножение дробей с разными знаменателями
Изначально стоит определить разновидности дробей:
- правильные,
- неправильные,
- смешанные.
Далее нужно вспомнить, как происходит умножение дробных чисел с одинаковыми знаменателями. Само правило этого процесса несложно сформулировать самостоятельно: результатом умножения простых дробей с одинаковыми знаменателями является дробное выражение, числитель которой есть произведение числителей, а знаменатель — произведение знаменателей данных дробей. То есть, по сути, новый знаменатель есть квадрат одного из существующих изначально.
То есть, по сути, новый знаменатель есть квадрат одного из существующих изначально.
Это интересно: как обозначается площадь, примеры для вычисления.
При умножении простых дробей с разными знаменателями для двух и более множителей правило не меняется:
a/b * c/d = a*c / b*d.
Единственное отличие в том, что образованное число под дробной чертой будет произведением разных чисел и, естественно, квадратом одного числового выражения его назвать невозможно.
Это интересно: что такое модуль числа?
Стоит рассмотреть умножение дробей с разными знаменателями на примерах:
- 8/9 * 6/7 = 8*6 / 9*7 = 48/63 = 16/21,
- 4/6 * 3/7 = 2/3 * 3/7<,>, 2*3 / 3*7 = 6/21.
В примерах применяются способы сокращения дробных выражений. Можно сокращать только числа числителя с числами знаменателя, рядом стоящие множители над дробной чертой или под ней сокращать нельзя.
Наряду с простыми дробными числами, существует понятие смешанных дробей. Смешанное число состоит из целого числа и дробной части, то есть является суммой этих чисел:
1 4/11 =1 + 4/11.
Как происходит перемножение
Предлагается несколько примеров для рассмотрения.
Пример 1.
2 1/2 * 7 3/5 = 2 + 1/2 * 7 + 3/5 = 2*7 + 2* 3/5 + 1/2 * 7 + 1/2 * 3/5 = 14 + 6/5 + 7/2 + 3/10 = 14 + 12/10 + 35/10 + 3/10 = 14 + 50/10 = 14 + 5=19.
В примере используется умножение числа на обыкновенную дробную часть, записать правило для этого действия можно формулой:
a * b/c = a*b / c.
По сути, такое произведение есть сумма одинаковых дробных остатков, а количество слагаемых указывает это натуральное число. Частный случай:
4 * 12/15 = 12/15 + 12/15 + 12/15 + 12/15 = 48/15 = 3 1/5.
Существует еще один вариант решения умножения числа на дробный остаток. Стоит просто разделить знаменатель на это число:
Стоит просто разделить знаменатель на это число:
d * e/f = e/f: d.
Этим приемом полезно пользоваться, когда знаменатель делится на натуральное число без остатка или, как говорится, нацело.
Пример 2.
Перевести смешанные числа в неправильные дроби и получить произведение ранее описанным способом:
1 2/3 * 4 1/5 = 5/3 * 21/5 = 5*21 / 3*5 =7.
В этом примере участвует способ представления смешанной дроби в неправильную, его также можно представить в виде общей формулы:
a b c = a * b + c / c, где знаменатель новой дроби образуется при умножении целой части со знаменателем и при сложении его с числителем исходного дробного остатка, а знаменатель остается прежним.
Этот процесс работает и в обратную сторону. Для выделения целой части и дробного остатка нужно поделить числитель неправильной дроби на ее знаменатель «уголком».
Умножение неправильных дробей производят общепринятым способом. Когда запись идет под единой дробной чертой, по мере необходимости нужно сделать сокращение дробей, чтобы уменьшить таким методом числа и проще посчитать результат.
Когда запись идет под единой дробной чертой, по мере необходимости нужно сделать сокращение дробей, чтобы уменьшить таким методом числа и проще посчитать результат.
Простейшие действия с дробями онлайн
В интернете существует множество помощников, чтобы решать даже сложные математические задачи в различных вариациях программ. Достаточное количество таких сервисов предлагают свою помощь при счете умножения дробей с разными числами в знаменателях — так называемые онлайн-калькуляторы для расчета дробей. Они способны не только умножить, но и произвести все остальные простейшие арифметические операции с обыкновенными дробями и смешанными числами. Работать с ним несложно, на странице сайта заполняются соответствующие поля, выбирается знак математического действия и нажимается «вычислить». Программа считает автоматически.
Тема арифметических действий с дробными числами актуальна на всем протяжении обучения школьников среднего и старшего звена. В старших классах рассматривают уже не простейшие виды, а целые дробные выражения, но знания правил по преобразованию и расчетам, полученные ранее, применяются в первозданном виде. Хорошо усвоенные базовые знания дают полную уверенность в удачном решении наиболее сложных задач.
В старших классах рассматривают уже не простейшие виды, а целые дробные выражения, но знания правил по преобразованию и расчетам, полученные ранее, применяются в первозданном виде. Хорошо усвоенные базовые знания дают полную уверенность в удачном решении наиболее сложных задач.
В заключение имеет смысл привести слова Льва Николаевича Толстого, который писал: «Человек есть дробь. Увеличить своего числителя — свои достоинства, — не во власти человека, но всякий может уменьшить своего знаменателя — своё мнение о самом себе, и этим уменьшением приблизиться к своему совершенству».
| Табличка на двери |
правила, примеры, решения, умножение дробей с разными знаменателями
Еще одно действие, которое можно выполнять с обыкновенными дробями, – умножение. Мы попробуем разъяснить его основные правила при решении задач, покажем, как умножается обыкновенная дробь на натуральное число и как правильно выполнить умножение трех обыкновенных дробей и больше.
Как умножить одну обыкновенную дробь на другую
Запишем сначала основное правило:
Определение 1Если мы умножим одну обыкновенную дробь, то числитель дроби, полученной в результате, будет равен произведению числителей исходных дробей, а знаменатель – произведению их знаменателей. В буквенном виде для двух дробей a/b и c/d это можно выразить как ab·cd=a·cb·d.
Посмотрим на примере, как правильно применить это правило. Допустим, у нас есть квадрат, сторона которого равна одной числовой единице. Тогда площадь фигуры составит 1 кв. единицу. Если разделить квадрат на равные прямоугольники со сторонами, равными 14 и 18 числовой единицы, у нас получится, что он теперь состоит из 32 прямоугольников (потому что 8·4=32). Соответственно, площадь каждого из них будет равна 132 от площади всей фигуры, т.е. 132 кв. единицы.
Соответственно, площадь каждого из них будет равна 132 от площади всей фигуры, т.е. 132 кв. единицы.
Далее нам надо выделить цветом часть исходного квадрата так, как это сделано на рисунке:
У нас получился закрашенный фрагмент со сторонами, равными 58 числовой единицы и 34 числовой единицы. Соответственно, для вычисления его площади надо умножить первую дробь на вторую. Она будет равна 58·34 кв. единиц. Но мы можем просто подсчитать, сколько прямоугольников входит во фрагмент: их 15, значит, общая площадь составляет 1532 квадратных единиц.
Поскольку 5·3=15 и 8·4=32, мы можем записать следующее равенство:
58·34=5·38·4=1532
Оно является подтверждением сформулированного нами правила умножения обыкновенных дробей, которое выражается как ab·cd=a·cb·d. Оно действует одинаково как для правильных, так и для неправильных дробей; с помощью него можно умножить дроби и с разными, и с одинаковыми знаменателями.
Разберем решения нескольких задач на умножение обыкновенных дробей.
Умножьте 711 на 98.
Решение
Для начала подсчитаем произведение числителей указанных дробей, умножив 7 на 9. У нас получилось 63. Затем вычислим произведение знаменателей и получим: 11·8=88. Составим их двух чисел ответ: 6388.
Все решение можно записать так:
711·98=7·911·8=6388
Ответ: 711·98=6388.
Если в ответе у нас получилась сократимая дробь, нужно довести вычисление до конца и выполнить ее сокращение. Если же у нас получилась неправильная дробь, из нее надо выделить целую часть.
Пример 2Вычислите произведение дробей 415 и 556.
Решение
Cогласно изученному выше правилу, нам надо умножить числитель на числитель, а знаменатель на знаменатель. Запись решения будет выглядеть так:
415·556=4·5515·6=22090
Мы получили сократимую дробь, т.е. такую, у которой есть признак делимости на 10.
Выполним сокращение дроби: 22090 НОД (220, 90)=10, 22090=220:1090:10=229. В итоге у нас получилась неправильная дробь, из которой мы выделим целую часть и получим смешанное число: 229=249.
В итоге у нас получилась неправильная дробь, из которой мы выделим целую часть и получим смешанное число: 229=249.
Ответ: 415·556=249.
Для удобства вычисления мы можем сократить и исходные дроби перед выполнением действия умножения, для чего нам надо привести дробь к виду a·cb·d. Разложим значения переменных на простые множители и одинаковые из них сократим.
Поясним, как это выглядит, используя данные конкретной задачи.
Пример 3Вычислите произведение 415·556.
Решение
Запишем вычисления, исходя из правила умножения. У нас получится:
415·556=4·5515·6
Поскольку как 4=2·2, 55=5·11, 15=3·5 и 6=2·3, значит,4·5515·6=2·2·5·113·5·2·3.
Далее мы можем просто сократить некоторые множители и получить следующее: .
Нам осталось подсчитать несложные произведения в числителе и знаменателе и выделить целую часть из получившейся в итоге неправильной дроби:
2·113·3=229=249
Ответ: 415·556=249.
Числовое выражение, в котором имеет место умножение обыкновенных дробей, обладает переместительным свойством, то есть при необходимости мы можем изменить порядок следования множителей:
ab·cd=cd·ab=a·cb·d
Как перемножить обыкновенную дробь с натуральным числом
Запишем сразу основное правило, а потом попробуем объяснить его на практике.
Определение 2Чтобы умножить обыкновенную дробь на натуральное число, нужно умножить числитель этой дроби на это число. При этом знаменатель итоговой дроби будет равен знаменателю исходной обыкновенной дроби. Умножение некоторой дроби ab на натуральное число n можно записать в виде формулы ab·n=a·nb.
Понять эту формулу легко, если вспомнить, что любое натуральное число может быть представлено в виде обыкновенной дроби со знаменателем, равным единице, то есть:
ab·n=ab·n1=a·nb·1=a·nb
Поясним нашу мысль конкретными примерами.
Пример 4Вычислите произведение 227 на 5.
Решение
В результате умножения числителя исходной дроби на второй множитель получим 10. В силу правила, указанного выше, мы получим в результате 1027. Все решение приведено в этой записи:
В силу правила, указанного выше, мы получим в результате 1027. Все решение приведено в этой записи:
227·5=2·527=1027
Ответ: 227·5=1027
Когда мы перемножаем натуральное число с обыкновенной дробью, то часто приходится сокращать результат или представлять его как смешанное число.
Пример 5Условие: вычислите произведение 8 на 512.
Решение
По правилу выше мы умножаем натуральное число на числитель. В итоге получаем, что 512·8=5·812=4012. Итоговая дробь имеет признаки делимости на 2, поэтому нам нужно выполнить ее сокращение:
НОК(40, 12)=4, значит, 4012=40:412:4=103
Теперь нам осталось только выделить целую часть и записать готовый ответ: 103=313.
В этой записи можно видеть все решение целиком: 512·8=5·812=4012=103=313.
Также мы могли сократить дробь с помощью разложения числителя и знаменателя на простые множители, и результат получился бы точно таким же.
Ответ: 512·8=313.
Числовое выражение, в котором натуральное число умножается на дробь, также обладает свойством перемещения, то есть порядок расположения множителей не влияет на результат:
ab·n=n·ab=a·nb
Как выполнить умножение трех и более обыкновенных дробей
Мы можем распространить на действие умножения обыкновенных дробей те же свойства, которые характерны для умножения натуральных чисел. Это следует из самого определения данных понятий.
Это следует из самого определения данных понятий.
Благодаря знанию сочетательного и переместительного свойства можно перемножать три обыкновенные дроби и более. Допустимо переставлять множители местами для большего удобства или расставлять скобки так, как будет легче считать.
Покажем на примере, как это делается.
Пример 6Умножьте четыре обыкновенные дроби 120, 125, 37 и 58.
Решение: для начала сделаем запись произведения. У нас получится 120·125·37·58. Нам надо перемножить между собой все числители и все знаменатели: 120·125·37·58=1·12·3·520·5·7·8.
Перед тем, как начать умножение, мы можем немного облегчить себе задачу и разложить некоторые числа на простые множители для дальнейшего сокращения. Это будет проще, чем сокращать уже готовую дробь, получившуюся в результате.
1·12·3·520·5·7·8=1·(2·2·3)·3·52·2·5·5·7(2·2·2)=3·35·7·2·2·2=9280
Ответ: 1·12·3·520·5·7·8=9280.
Пример 7Перемножьте 5 чисел 78·12·8·536·10.
Решение
Для удобства мы можем сгруппировать дробь 78 с числом 8, а число 12 с дробью 536, поскольку при этом нам будут очевидны будущие сокращения. В итоге у нас получится:
В итоге у нас получится:
78·12·8·536·10=78·8·12·536·10=7·88·12·536·10=71·2·2·3·52·2·3·3·10==7·53·10=7·5·103=3503=11623
Ответ: 78·12·8·536·10=11623.
Решение задач
от 1 дня / от 150 р.
Курсовая работа
от 5 дней / от 1800 р.
Реферат
от 1 дня / от 700 р.
Действия с дробями
Дроби можно складывать, вычитать, умножать и делить. Также, дроби можно сравнивать между собой. В принципе всё что можно делать с обычными числами, можно делать и с дробями.
Сложение дробей с одинаковыми знаменателямиСложение дробей бывает двух видов:
- Сложение дробей с одинаковыми знаменателями;
- Сложение дробей с разными знаменателями.
Сначала изýчим сложение дробей с одинаковыми знаменателями. Тут всё просто. Чтобы сложить дроби с одинаковыми знаменателями, нужно сложить их числители, а знаменатель оставить без изменения.
Например, слóжим дроби и . Складываем числители, а знаменатель оставляем без изменения:
Этот пример можно легко понять, если вспомнить про пиццу, которая разделена на четыре части. Если к пиццы прибавить пиццы, то получится пиццы:
Пример 2. Сложить дроби и .
Сложить дроби и .
Опять же складываем числители, а знаменатель оставляем без изменения:
В ответе получилась неправильная дробь . Если наступает конец задачи, то от неправильных дробей принято избавляться. Чтобы избавится от неправильной дроби, нужно выделить в ней целую часть. В нашем случае целая часть выделяется легко — два разделить на два будет один:
Этот пример можно легко понять, если вспомнить про пиццу, которая разделена на две части. Если к пиццы прибавить еще пиццы, то получится одна целая пицца:
Пример 3. Сложить дроби и .
Опять же складываем числители, а знаменатель оставляем без изменения:
Этот пример можно легко понять, если вспомнить про пиццу, которая разделена на три части. Если к пиццы прибавить ещё пиццы, то получится пиццы:
Пример 4. Найти значение выражения
Этот пример решается точно также, как и предыдущие. Числители необходимо сложить, а знаменатель оставить без изменения:
Попробуем изобразить наше решение с помощью рисунка. Если к пиццы прибавить пиццы и ещё прибавить пиццы, то получится 1 целая и ещё пиццы.
Если к пиццы прибавить пиццы и ещё прибавить пиццы, то получится 1 целая и ещё пиццы.
Как видите в сложении дробей с одинаковыми знаменателями нет ничего сложного. Достаточно понимать следующие правила:
- Чтобы сложить дроби с одинаковыми знаменателями, нужно сложить их числители, а знаменатель оставить без изменения;
- Если в ответе получилась неправильная дробь, то нужно выделить в ней целую часть.
Сложение дробей с разными знаменателями
Теперь научимся складывать дроби с разными знаменателями. Когда складывают дроби, знаменатели этих дробей должны быть одинаковыми. Но одинаковыми они бывают не всегда.
Например, дроби и сложить можно, поскольку у них одинаковые знаменатели.
А вот дроби и сразу сложить нельзя, поскольку у этих дробей разные знаменатели. В таких случаях дроби нужно приводить к одинаковому (общему) знаменателю.
Существует несколько способов приведения дробей к одинаковому знаменателю. Сегодня мы рассмотрим только один из них, поскольку остальные способы могут показаться сложными для начинающего.
Сегодня мы рассмотрим только один из них, поскольку остальные способы могут показаться сложными для начинающего.
Суть этого способа заключается в том, что сначала ищется наименьшее общее кратное (НОК) знаменателей обеих дробей. Затем НОК делят на знаменатель первой дроби и получают первый дополнительный множитель. Аналогично поступают и со второй дробью — НОК делят на знаменатель второй дроби и получают второй дополнительный множитель.
Затем числители и знаменатели дробей умножаются на свои дополнительные множители. В результате этих действий, дроби у которых были разные знаменатели, обращаются в дроби, у которых одинаковые знаменатели. А как складывать такие дроби мы уже знаем.
Пример 1. Сложим дроби и
У этих дробей разные знаменатели, поэтому нужно привести их к одинаковому (общему) знаменателю.
В первую очередь находим наименьшее общее кратное знаменателей обеих дробей. Знаменатель первой дроби это число 3, а знаменатель второй дроби — число 2. Наименьшее общее кратное этих чисел равно 6
Наименьшее общее кратное этих чисел равно 6
НОК (2 и 3) = 6
Теперь возвращаемся к дробям и . Сначала разделим НОК на знаменатель первой дроби и получим первый дополнительный множитель. НОК это число 6, а знаменатель первой дроби это число 3. Делим 6 на 3, получаем 2.
Полученное число 2 это первый дополнительный множитель. Записываем его к первой дроби. Для этого делаем небольшую косую линию над дробью и записываем над ней найденный дополнительный множитель:
Аналогично поступаем и со второй дробью. Делим НОК на знаменатель второй дроби и получаем второй дополнительный множитель. НОК это число 6, а знаменатель второй дроби — число 2. Делим 6 на 2, получаем 3.
Полученное число 3 это второй дополнительный множитель. Записываем его ко второй дроби. Опять же делаем небольшую косую линию над второй дробью и записываем над ней найденный дополнительный множитель:
Теперь у нас всё готово для сложения. Осталось умножить числители и знаменатели дробей на свои дополнительные множители:
Посмотрите внимательно к чему мы пришли. Мы пришли к тому, что дроби у которых были разные знаменатели, превратились в дроби у которых одинаковые знаменатели. А как складывать такие дроби мы уже знаем. Давайте дорешаем этот пример до конца:
Мы пришли к тому, что дроби у которых были разные знаменатели, превратились в дроби у которых одинаковые знаменатели. А как складывать такие дроби мы уже знаем. Давайте дорешаем этот пример до конца:
Таким образом, пример завершается. К прибавить получается .
Попробуем изобразить наше решение с помощью рисунка. Если к пиццы прибавить пиццы, то получится одна целая пицца и еще одна шестая пиццы:
Приведение дробей к одинаковому (общему) знаменателю также можно изобразить с помощью рисунка. Приведя дроби и к общему знаменателю, мы получили дроби и . Эти две дроби будут изображаться теми же кусками пицц. Различие будет лишь в том, что в этот раз они будут разделены на одинаковые доли (приведены к одинаковому знаменателю).
Первый рисунок изображает дробь (четыре кусочка из шести), а второй рисунок изображает дробь (три кусочка из шести). Сложив эти кусочки мы получаем (семь кусочков из шести). Эта дробь неправильная, поэтому мы выделили в ней целую часть. В результате получили (одну целую пиццу и еще одну шестую пиццы).
В результате получили (одну целую пиццу и еще одну шестую пиццы).
Отметим, что мы с вами расписали данный пример слишком подробно. В учебных заведениях не принято писать так развёрнуто. Нужно уметь быстро находить НОК обоих знаменателей и дополнительные множители к ним, а также быстро умножать найденные дополнительные множители на свои числители и знаменатели. Находясь в школе, данный пример нам пришлось бы записать следующим образом:
Но есть и обратная сторона медали. Если на первых этапах изучения математики не делать подробных записей, то начинают появляться вопросы рода «а откуда вон та цифра?», «почему дроби вдруг превращаются совсем в другие дроби?«.
Поэтому на первых этапах советуем записывать каждую мелочь. Хвастаться можно лишь в будущем, когда будут усвоены азы.
Чтобы легче было складывать дроби с разными знаменателями, можно воспользоваться следующей пошаговой инструкцией:
- Найти НОК знаменателей дробей;
- Разделить НОК на знаменатель каждой дроби и получить дополнительный множитель для каждой дроби;
- Умножить числители и знаменатели дробей на свои дополнительные множители;
- Сложить дроби, у которых одинаковые знаменатели;
- Если в ответе получилась неправильная дробь, то выделить её целую часть;
Пример 2. Найти значение выражения .
Найти значение выражения .
Воспользуемся инструкцией, которая приведена выше.
Шаг 1. Найти НОК знаменателей дробей
Находим НОК знаменателей обеих дробей. Знаменатели дробей это числа 2, 3 и 4
Шаг 2. Разделить НОК на знаменатель каждой дроби и получить дополнительный множитель для каждой дроби
Делим НОК на знаменатель первой дроби. НОК это число 12, а знаменатель первой дроби это число 2. Делим 12 на 2, получаем 6. Получили первый дополнительный множитель 6. Записываем его над первой дробью:
Теперь делим НОК на знаменатель второй дроби. НОК это число 12, а знаменатель второй дроби это число 3. Делим 12 на 3, получаем 4. Получили второй дополнительный множитель 4. Записываем его над второй дробью:
Теперь делим НОК на знаменатель третьей дроби. НОК это число 12, а знаменатель третьей дроби это число 4. Делим 12 на 4, получаем 3. Получили третий дополнительный множитель 3. Записываем его над третьей дробью:
Шаг 3. Умножить числители и знаменатели дробей на свои дополнительные множители
Умножить числители и знаменатели дробей на свои дополнительные множители
Умножаем числители и знаменатели на свои дополнительные множители:
Шаг 4. Сложить дроби у которых одинаковые знаменатели
Мы пришли к тому, что дроби у которых были разные знаменатели, превратились в дроби, у которых одинаковые (общие) знаменатели. Осталось сложить эти дроби. Складываем:
Сложение не поместилось на одной строке, поэтому мы перенесли оставшееся выражение на следующую строку. Это допускается в математике. Когда выражение не помещается на одну строку, его переносят на следующую строку, при этом надо обязательно поставить знак равенства (=) на конце первой строки и в начале новой строки. Знак равенства на второй строке говорит о том, что это продолжение выражения, которое было на первой строке.
Шаг 5. Если в ответе получилась неправильная дробь, то выделить в ней целую часть
У нас в ответе получилась неправильная дробь. Мы должны выделить у неё целую часть. Выделяем:
Мы должны выделить у неё целую часть. Выделяем:
Получили ответ
Вычитание дробей с одинаковыми знаменателями
Вычитание дробей бывает двух видов:
- Вычитание дробей с одинаковыми знаменателями
- Вычитание дробей с разными знаменателями
Сначала изучим вычитание дробей с одинаковыми знаменателями.
Чтобы вычесть из одной дроби другую, нужно из числителя первой дроби вычесть числитель второй дроби, а знаменатель оставить без изменения.
Например, найдём значение выражения . Чтобы решить этот пример, надо из числителя первой дроби вычесть числитель второй дроби, а знаменатель оставить без изменения. Так и сделаем:
Этот пример можно легко понять, если вспомнить про пиццу, которая разделена на четыре части. Если от пиццы отрезать пиццы, то получится пиццы:
Пример 2. Найти значение выражения .
Опять же из числителя первой дроби вычитаем числитель второй дроби, а знаменатель оставляем без изменения:
Этот пример можно легко понять, если вспомнить про пиццу, которая разделена на три части. Если от пиццы отрезать пиццы, то получится пиццы:
Если от пиццы отрезать пиццы, то получится пиццы:
Пример 3. Найти значение выражения
Этот пример решается точно также, как и предыдущие. Из числителя первой дроби нужно вычесть числители остальных дробей:
В ответе получилась неправильная дробь. Выделим в ней целую часть:
Как видите в вычитании дробей с одинаковыми знаменателями ничего сложного нет. Достаточно понимать следующие правила:
- Чтобы вычесть из одной дроби другую, нужно из числителя первой дроби вычесть числитель второй дроби, а знаменатель оставить без изменения;
- Если в ответе получилась неправильная дробь, то нужно выделить в ней целую часть.
Вычитание дробей с разными знаменателями
Теперь научимся вычитать дроби у которых разные знаменатели. Когда вычитают дроби их знаменатели должны быть одинаковыми. Но одинаковыми они бывают не всегда.
Например, от дроби можно вычесть дробь , поскольку у этих дробей одинаковые знаменатели. А вот от дроби нельзя вычесть дробь , поскольку у этих дробей разные знаменатели. В таких случаях дроби нужно приводить к одинаковому (общему) знаменателю.
А вот от дроби нельзя вычесть дробь , поскольку у этих дробей разные знаменатели. В таких случаях дроби нужно приводить к одинаковому (общему) знаменателю.
Общий знаменатель находят по тому же принципу, которым мы пользовались при сложении дробей с разными знаменателями. В первую очередь находят НОК знаменателей обеих дробей. Затем НОК делят на знаменатель первой дроби и получают первый дополнительный множитель, который записывается над первой дробью. Аналогично НОК делят на знаменатель второй дроби и получают второй дополнительный множитель, который записывается над второй дробью.
Затем дроби умножаются на свои дополнительные множители. В результате этих операций, дроби у которых были разные знаменатели, обращаются в дроби, у которых одинаковые знаменатели. А как вычитать такие дроби мы уже знаем.
Пример 1. Найти значение выражения:
У этих дробей разные знаменатели, поэтому нужно привести их к одинаковому (общему) знаменателю.
Сначала находим НОК знаменателей обеих дробей. Знаменатель первой дроби это число 3, а знаменатель второй дроби — число 4. Наименьшее общее кратное этих чисел равно 12
Знаменатель первой дроби это число 3, а знаменатель второй дроби — число 4. Наименьшее общее кратное этих чисел равно 12
НОК (3 и 4) = 12
Теперь возвращаемся к дробям и
Найдём дополнительный множитель для первой дроби. Для этого разделим НОК на знаменатель первой дроби. НОК это число 12, а знаменатель первой дроби — число 3. Делим 12 на 3, получаем 4. Записываем четвёрку над первой дробью:
Аналогично поступаем и со второй дробью. Делим НОК на знаменатель второй дроби. НОК это число 12, а знаменатель второй дроби — число 4. Делим 12 на 4, получаем 3. Записываем тройку над второй дробью:
Теперь у нас всё готово для вычитания. Осталось умножить дроби на свои дополнительные множители:
Мы пришли к тому, что дроби у которых были разные знаменатели, превратились в дроби у которых одинаковые знаменатели. А как вычитать такие дроби мы уже знаем. Давайте дорешаем этот пример до конца:
Получили ответ
Попробуем изобразить наше решение с помощью рисунка. Если от пиццы отрезать пиццы, то получится пиццы
Если от пиццы отрезать пиццы, то получится пиццы
Это подробная версия решения. Находясь в школе, нам пришлось бы решить этот пример покороче. Выглядело бы такое решение следующим образом:
Приведение дробей и к общему знаменателю также может быть изображено с помощью рисунка. Приведя эти дроби к общему знаменателю, мы получили дроби и . Эти дроби будут изображаться теми же кусочками пицц, но в этот раз они будут разделены на одинаковые доли (приведены к одинаковому знаменателю):
Первый рисунок изображает дробь (восемь кусочков из двенадцати), а второй рисунок — дробь (три кусочка из двенадцати). Отрезав от восьми кусочков три кусочка мы получаем пять кусочков из двенадцати. Дробь и описывает эти пять кусочков.
Пример 2. Найти значение выражения
У этих дробей разные знаменатели, поэтому сначала нужно привести их к одинаковому (общему) знаменателю.
Найдём НОК знаменателей этих дробей.
Знаменатели дробей это числа 10, 3 и 5. Наименьшее общее кратное этих чисел равно 30
Наименьшее общее кратное этих чисел равно 30
НОК (10, 3, 5) = 30
Теперь находим дополнительные множители для каждой дроби. Для этого разделим НОК на знаменатель каждой дроби.
Найдём дополнительный множитель для первой дроби. НОК это число 30, а знаменатель первой дроби — число 10. Делим 30 на 10, получаем первый дополнительный множитель 3. Записываем его над первой дробью:
Теперь находим дополнительный множитель для второй дроби. Разделим НОК на знаменатель второй дроби. НОК это число 30, а знаменатель второй дроби — число 3. Делим 30 на 3, получаем второй дополнительный множитель 10. Записываем его над второй дробью:
Теперь находим дополнительный множитель для третьей дроби. Разделим НОК на знаменатель третьей дроби. НОК это число 30, а знаменатель третьей дроби — число 5. Делим 30 на 5, получаем третий дополнительный множитель 6. Записываем его над третьей дробью:
Теперь всё готово для вычитания. Осталось умножить дроби на свои дополнительные множители:
Мы пришли к тому, что дроби у которых были разные знаменатели, превратились в дроби у которых одинаковые (общие) знаменатели. А как вычитать такие дроби мы уже знаем. Давайте дорешаем этот пример.
А как вычитать такие дроби мы уже знаем. Давайте дорешаем этот пример.
Продолжение примера не поместится на одной строке, поэтому переносим продолжение на следующую строку. Не забываем про знак равенства (=) на новой строке:
В ответе получилась правильная дробь, и вроде бы нас всё устраивает, но она слишком громоздка и некрасива. Надо бы сделать её проще. А что можно сделать? Можно сократить эту дробь.
Чтобы сократить дробь , нужно разделить её числитель и знаменатель на наибольший общий делитель (НОД) чисел 20 и 30.
Итак, находим НОД чисел 20 и 30:
Теперь возвращаемся к нашему примеру и делим числитель и знаменатель дроби на найденный НОД, то есть на 10
Получили ответ
Умножение дроби на число
Чтобы умножить дробь на число, нужно числитель данной дроби умножить на это число, а знаменатель оставить без изменений.
Пример 1. Умножить дробь на число 1.
Умножим числитель дроби на число 1
Запись можно понимать, как взять половину 1 раз. К примеру, если пиццы взять 1 раз, то получится пиццы
К примеру, если пиццы взять 1 раз, то получится пиццы
Из законов умножения мы знаем, что если множимое и множитель поменять местами, то произведение не изменится. Если выражение , записать как , то произведение по прежнему будет равно . Опять же срабатывает правило перемножения целого числа и дроби:
Эту запись можно понимать, как взятие половины от единицы. К примеру, если имеется 1 целая пицца и мы возьмем от неё половину, то у нас окажется пиццы:
Пример 2. Найти значение выражения
Умножим числитель дроби на 4
В ответе получилась неправильная дробь. Выделим в ней целую часть:
Выражение можно понимать, как взятие двух четвертей 4 раза. К примеру, если пиццы взять 4 раза, то получится две целые пиццы
А если поменять множимое и множитель местами, то получим выражение . Оно тоже будет равно 2. Это выражение можно понимать, как взятие двух пицц от четырех целых пицц:
Число, которое умножается на дробь, и знаменатель дроби разрешается сокращать, если они имеют общий делитель, бóльший единицы.
Например, выражение можно вычислить двумя способами.
Первый способ. Умножить число 4 на числитель дроби, а знаменатель дроби оставить без изменений:
Второй способ. Умножаемую четвёрку и четвёрку, находящуюся в знаменателе дроби , можно сократить. Сократить эти четвёрки можно на 4, поскольку наибольший общий делитель для двух четвёрок есть сама четвёрка:
Получился тот же результат 3. После сокращения четвёрок, на их месте образуются новые числа: две единицы. Но перемножение единицы с тройкой, и далее деление на единицу ничего не меняет. Поэтому решение можно записать покороче:
Сокращение может быть выполнено даже тогда, когда мы решили воспользоваться первым способом, но на этапе перемножения числа 4 и числителя 3 решили воспользоваться сокращением:
А вот к примеру выражение можно вычислить только первым способом — умножить число 7 на числитель дроби , а знаменатель оставить без изменений:
Связано это с тем, что число 7 и знаменатель дроби не имеют общего делителя, бóльшего единицы, и соответственно не сокращаются.
Некоторые ученики по ошибке сокращают умножаемое число и числитель дроби. Делать этого нельзя. Например, следующая запись не является правильной:
Сокращение дроби подразумевает, что и числитель и знаменатель будет разделён на одно и тоже число. В ситуации с выражением деление выполнено только в числителе, поскольку записать это всё равно, что записать . Видим, что деление выполнено только в числителе, а в знаменателе никакого деления не происходит.
Умножение дробей
Чтобы перемножить дроби, нужно перемножить их числители и знаменатели. Если в ответе получится неправильная дробь, нужно выделить в ней целую часть.
Пример 1. Найти значение выражения .
Умножаем числитель первой дроби на числитель второй дроби, а знаменатель первой дроби на знаменатель второй дроби:
Получили ответ . Желательно сократить данную дробь. Дробь можно сократить на 2. Тогда окончательное решение примет следующий вид:
Выражение можно понимать, как взятие пиццы от половины пиццы. Допустим, у нас есть половина пиццы:
Допустим, у нас есть половина пиццы:
Как взять от этой половины две третьих? Сначала нужно поделить эту половину на три равные части:
И взять от этих трех кусочков два:
У нас получится пиццы. Вспомните, как выглядит пицца, разделенная на три части:
Один кусок от этой пиццы и взятые нами два кусочка будут иметь одинаковые размеры:
Другими словами, речь идет об одном и том же размере пиццы. Поэтому значение выражения равно
Пример 2. Найти значение выражения
Умножаем числитель первой дроби на числитель второй дроби, а знаменатель первой дроби на знаменатель второй дроби:
В ответе получилась неправильная дробь. Выделим в ней целую часть:
Пример 3. Найти значение выражения
Умножаем числитель первой дроби на числитель второй дроби, а знаменатель первой дроби на знаменатель второй дроби:
В ответе получилась правильная дробь, но будет хорошо, если её сократить. Чтобы сократить эту дробь, нужно числитель и знаменатель данной дроби разделить на наибольший общий делитель (НОД) чисел 105 и 450.
Чтобы сократить эту дробь, нужно числитель и знаменатель данной дроби разделить на наибольший общий делитель (НОД) чисел 105 и 450.
Итак, найдём НОД чисел 105 и 450:
Теперь делим числитель и знаменатель нашего ответа на НОД, который мы сейчас нашли, то есть на 15
Представление целого числа в виде дроби
Любое целое число можно представить в виде дроби. Например, число 5 можно представить как . От этого пятёрка своего значения не поменяет, поскольку выражение означает «число пять разделить на единицу», а это, как известно равно пятёрке:
Обратные числа
Сейчас мы познакомимся с очень интересной темой в математике. Она называется «обратные числа».
Определение. Обратным к числу a называется число, которое при умножении на a даёт единицу.
Давайте подставим в это определение вместо переменной a число 5 и попробуем прочитать определение:
Обратным к числу 5 называется число, которое при умножении на 5 даёт единицу.
Можно ли найти такое число, которое при умножении на 5, даёт единицу? Оказывается можно. Представим пятёрку в виде дроби:
Затем умножить эту дробь на саму себя, только поменяем местами числитель и знаменатель. Другими словами, умножим дробь на саму себя, только перевёрнутую:
Что получится в результате этого? Если мы продолжим решать этот пример, то получим единицу:
Значит обратным к числу 5, является число , поскольку при умножении 5 на получается единица.
Обратное число можно найти также для любого другого целого числа.
Примеры:
- обратным числа 2 является дробь
- обратным числа 3 является дробь
- обратным числа 4 является дробь
Найти обратное число можно также для любой другой дроби. Для этого достаточно перевернуть её.
Примеры:
- для дроби обратной дробью является дробь
- для для дроби обратной дробью является дробь
- для дроби обратной дробью является дробь
Деление дроби на число
Допустим, у нас имеется половина пиццы:
Разделим её поровну на двоих. Сколько пиццы достанется каждому?
Сколько пиццы достанется каждому?
Видно, что после разделения половины пиццы получилось два равных кусочка, каждый из которых составляет пиццы. Значит каждому достанется по пиццы.
Деление дробей выполняется с помощью обратных чисел. Обратные числа позволяют заменить деление умножением.
Чтобы разделить дробь на число, нужно эту дробь умножить на число, обратное делителю.
Пользуясь этим правилом, запишем деление нашей половины пиццы на две части.
Итак, требуется разделить дробь на число 2. Здесь делимым является дробь , а делителем число 2.
Чтобы разделить дробь на число 2, нужно эту дробь умножить на число, обратное делителю 2. Обратное делителю 2 это дробь . Значит нужно умножить на
Получили ответ . Значит при делении половины на две части получается четверть.
Попробуем понять механизм этого правила. Для этого рассмотрим следующий простейший пример. Пусть у нас имеется одна целая пицца:
Умножим её на 2. То есть повторим её два раза (или возьмём два раза). В результате будем иметь две пиццы:
То есть повторим её два раза (или возьмём два раза). В результате будем иметь две пиццы:
Теперь угостим этими пиццами двоих друзей. То есть разделим две пиццы на 2. Тогда каждому достанется по одной пицце:
Разделить две пиццы на 2 это всё равно, что взять половину от этих пицц, то есть умножить число 2 на дробь
В обоих случаях получился один и тот же результат.
Тоже самое происходило, когда мы делили половину пиццы на две части. Чтобы разделить на 2, мы умножили эту дробь на число, обратное делителю 2. А обратное делителю 2 это дробь
Пример 2. Найти значение выражения
Умножим первую дробь на число, обратное делителю:
Допустим, имеется четверть пиццы и нужно разделить её на двоих:
Если разделить эту четверть на две части, то каждая получившаяся часть будет одной восьмой частью целой пиццы:
Заменять деление умножением можно не только при работе с дробями, но и с обычными числами. Например, все мы знаем, что 10 разделить на 2 будет 5
Например, все мы знаем, что 10 разделить на 2 будет 5
10 : 2 = 5
Заменим в этом примере деление умножением. Чтобы разделить число 10 на число 2, можно умножить число 10 на число, обратное числу 2. А обратное числу 2 это дробь
Как видно результат не изменился. Мы снова получили ответ 5.
Можно сделать вывод, что деление можно заменять умножением при условии, что вместо делителя будет подставлено обратное ему число.
Пример 3. Найти значение выражения
Умножим первую дробь на число, обратное делителю. Обратное делителю число это дробь
Допустим, имелось пиццы:
Как разделить такую пиццу на шестерых? Если каждый из трех кусков разделить пополам, то можно получить 6 равных кусков
Эти шесть кусков являются шестью кусками из двенадцати. А один из этих кусков составляет . Поэтому при делении на 6 получается
Деление числа на дробь
Правило деления числа на дробь такое же, как и правило деления дроби на число.
Чтобы разделить число на дробь, нужно умножить это число на дробь, обратную делителю.
Например, разделим число 1 на .
Чтобы разделить число 1 на , нужно это число 1 умножить на дробь, обратную дроби . А обратная дроби это дробь
Выражение можно понимать, как определение количества половин в одной целой пицце. Допустим, имеется одна целая пицца:
Если зададим вопрос «сколько раз половина содержится в этой пицце», то ответом будет 2. Действительно, половина содержится в одной целой пицце два раза
Пример 2. Найти значение выражения
Умножим число 2 на дробь, обратную делителю. А обратная делителю дробь это дробь
Допустим, у нас имеются две целые пиццы:
Если зададим вопрос «сколько раз половина содержится в двух пиццах», то ответом будет 4. Действительно, половина содержится в двух пиццах четыре раза:
Деление дробей
Чтобы разделить дробь на дробь, нужно первую дробь умножить на дробь, обратную второй.
Например, разделим на
Чтобы разделить на , нужно умножить на дробь, обратную дроби . А обратная дроби это дробь
Допустим, имеется половина пиццы:
Если зададим вопрос «сколько раз четверть пиццы содержится в этой половине», то ответом будет 2. Действительно, четверть пиццы содержится в половине пиццы два раза:
Пример 1. Найти значение выражения
Умножаем первую дробь на дробь, обратную второй. Грубо говоря, умножаем первую дробь на перевёрнутую вторую:
Пример 2. Найти значение выражения
Умножаем первую дробь на дробь обратную второй:
Здесь советуем остановиться и потренироваться. Решите несколько примеров, приведенных ниже. Можете использовать материалы сайта, как справочник. Это позволит вам научиться работать с литературой.
Каждая следующая тема будет более сложной, поэтому нужно тренироваться.
Задания для самостоятельного решения:
Задание 1. Найдите значение выражения:
Найдите значение выражения:
Решение:
Показать решение
Задание 2. Найдите значение выражения:
Решение:
Показать решение
Задание 3. Найдите значение выражения:
Решение:
Показать решение
Задание 4. Найдите значение выражения:
Решение:
Показать решение
Задание 5. Найдите значение выражения:
Решение:
Показать решение
Задание 6. Найдите значение выражения:
Решение:
Показать решение
Задание 7. Найдите значение выражения:
Решение:
Показать решение
Задание 8. Найдите значение выражения:
Решение:
Показать решение
Задание 9. Найдите значение выражения:
Решение:
Показать решение
Задание 10. Найдите значение выражения:
Решение:
Показать решение
Задание 11. Найдите значение выражения:
Решение:
Показать решение
Задание 12. Найдите значение выражения:
Решение:
Показать решение
Задание 13. Найдите значение выражения:
Решение:
Показать решение
Задание 14. Найдите значение выражения:
Найдите значение выражения:
Решение:
Показать решение
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже
Чтобы умножить смешанные числа надо. Дроби
Чтобы правильно умножить дробь на дробь или дробь на число, нужно знать простые правила. Эти правила сейчас разберем подробно.
Умножение обыкновенной дроби на дробь.
Чтобы умножить дробь на дробь необходимо посчитать произведение числителей и произведение знаменателей этих дробей.
\(\bf \frac{a}{b} \times \frac{c}{d} = \frac{a \times c}{b \times d}\\\)
Рассмотрим пример:
Мы числитель первой дроби умножаем с числителем второй дроби, также и знаменатель первой дроби умножаем со знаменателем второй дроби.
\(\frac{6}{7} \times \frac{2}{3} = \frac{6 \times 2}{7 \times 3} = \frac{12}{21} = \frac{4 \times 3}{7 \times 3} = \frac{4}{7}\\\)
Дробь \(\frac{12}{21} = \frac{4 \times 3}{7 \times 3} = \frac{4}{7}\\\) сократили на 3.
Умножение дроби на число.
Для начала вспомним правило, любое число можно представить в виде дроби \(\bf n = \frac{n}{1}\) .
Воспользуемся этим правилом при умножении.
\(5 \times \frac{4}{7} = \frac{5}{1} \times \frac{4}{7} = \frac{5 \times 4}{1 \times 7} = \frac{20}{7} = 2\frac{6}{7}\\\)
Неправильную дробь \(\frac{20}{7} = \frac{14 + 6}{7} = \frac{14}{7} + \frac{6}{7} = 2 + \frac{6}{7}= 2\frac{6}{7}\\\) перевели в смешанную дробь.
Другими словами, при умножении числа на дробь, число умножаем на числитель, а знаменатель оставляем без изменения. Пример:
\(\frac{2}{5} \times 3 = \frac{2 \times 3}{5} = \frac{6}{5} = 1\frac{1}{5}\\\\\) \(\bf \frac{a}{b} \times c = \frac{a \times c}{b}\\\)
Умножение смешанных дробей.

Чтобы перемножить смешанные дроби, нужно сначала каждую смешанную дробь представить в виде неправильно дроби, а потом воспользоваться правилом умножения. Числитель умножаем с числителем, знаменатель умножаем со знаменателем.
Пример:
\(2\frac{1}{4} \times 3\frac{5}{6} = \frac{9}{4} \times \frac{23}{6} = \frac{9 \times 23}{4 \times 6} = \frac{3 \times \color{red} {3} \times 23}{4 \times 2 \times \color{red} {3}} = \frac{69}{8} = 8\frac{5}{8}\\\)
Умножение взаимно обратных дробей и чисел.
Дробь \(\bf \frac{a}{b}\) является обратной для дроби \(\bf \frac{b}{a}\), при условии a≠0,b≠0.
Дроби \(\bf \frac{a}{b}\) и \(\bf \frac{b}{a}\) называются взаимно обратными дробями. Произведение взаимно обратных дробей равно 1.
\(\bf \frac{a}{b} \times \frac{b}{a} = 1 \\\)
Пример:
\(\frac{5}{9} \times \frac{9}{5} = \frac{45}{45} = 1\\\)
Вопросы по теме:
Как умножить дробь на дробь?
Ответ: произведение обыкновенных дробей является умножение числитель с числителем, знаменатель со знаменателем. Чтобы получить произведение смешанных дробей нужно перевести их в неправильную дробь и перемножить по правилам.
Чтобы получить произведение смешанных дробей нужно перевести их в неправильную дробь и перемножить по правилам.
Как выполнить умножение дробей с разными знаменателями?
Ответ: не важно одинаковые или разные знаменатели у дробей, умножение происходит по правилу нахождения произведения числитель с числителем, знаменатель со знаменателем.
Как умножать смешанные дроби?
Ответ: в первую очередь надо перевести смешанную дробь в неправильную дробь и далее находить произведение по правилам умножения.
Как умножить число на дробь?
Ответ: число умножаем с числителем, а знаменатель оставляем тот же.
Пример №1:
Вычислите произведение: а) \(\frac{8}{9} \times \frac{7}{11}\) б) \(\frac{2}{15} \times \frac{10}{13}\)
Решение:
а) \(\frac{8}{9} \times \frac{7}{11} = \frac{8 \times 7}{9 \times 11} = \frac{56}{99}\\\\\)
б) \(\frac{2}{15} \times \frac{10}{13} = \frac{2 \times 10}{15 \times 13} = \frac{2 \times 2 \times \color{red} {5}}{3 \times \color{red} {5} \times 13} = \frac{4}{39}\)
Пример №2:
Вычислите произведения числа и дроби: а) \(3 \times \frac{17}{23}\) б) \(\frac{2}{3} \times 11\)
Решение:
а) \(3 \times \frac{17}{23} = \frac{3}{1} \times \frac{17}{23} = \frac{3 \times 17}{1 \times 23} = \frac{51}{23} = 2\frac{5}{23}\\\\\)
б) \(\frac{2}{3} \times 11 = \frac{2}{3} \times \frac{11}{1} = \frac{2 \times 11}{3 \times 1} = \frac{22}{3} = 7\frac{1}{3}\)
Пример №3:
Напишите число обратное дроби \(\frac{1}{3}\)?
Ответ: \(\frac{3}{1} = 3\)
Пример №4:
Вычислите произведение двух взаимно обратных дробей: а) \(\frac{104}{215} \times \frac{215}{104}\)
Решение:
а) \(\frac{104}{215} \times \frac{215}{104} = 1\)
Пример №5:
Могут ли взаимно обратные дроби быть:
а) одновременно правильными дробями;
б) одновременно неправильными дробями;
в) одновременно натуральными числами?
Решение:
а) чтобы ответить на первый вопрос приведем пример. Дробь \(\frac{2}{3}\) правильная, обратная ей дробь будет равна \(\frac{3}{2}\) – неправильная дробь. Ответ: нет.
Дробь \(\frac{2}{3}\) правильная, обратная ей дробь будет равна \(\frac{3}{2}\) – неправильная дробь. Ответ: нет.
б) практически при всех переборах дробей это условие не выполняется, но существуют некоторые числа, которые выполняют условие быть одновременно неправильной дробью. Например неправильная дробь \(\frac{3}{3}\) , обратная ей дробь равна \(\frac{3}{3}\). Получаем две неправильные дроби. Ответ: не всегда при определённых условиях, когда числитель и знаменатель равны.
в) натуральные числа – это числа которые мы используем при счете, например, 1, 2, 3, …. Если возьмем число \(3 = \frac{3}{1}\), то обратная ей дробь будет \(\frac{1}{3}\). Дробь \(\frac{1}{3}\) не является натуральным числом. Если мы переберем все числа, получать обратное число всегда дробь, кроме 1. Если возьмем число 1, то обратная ей дробь будет \(\frac{1}{1} = \frac{1}{1} = 1\). Число 1 натуральное число. Ответ: могут быть одновременно натуральными числами только в одном случае, если это число 1.
Пример №6:
Выполните произведение смешанных дробей: а) \(4 \times 2\frac{4}{5}\) б) \(1\frac{1}{4} \times 3\frac{2}{7}\)
Решение:
а) \(4 \times 2\frac{4}{5} = \frac{4}{1} \times \frac{14}{5} = \frac{56}{5} = 11\frac{1}{5}\\\\ \)
б) \(1\frac{1}{4} \times 3\frac{2}{7} = \frac{5}{4} \times \frac{23}{7} = \frac{115}{28} = 4\frac{3}{7}\)
Пример №7:
Могут ли два взаимно обратных числа быть одновременно смешанными числами?
Рассмотрим на примере. Возьмем смешанную дробь \(1\frac{1}{2}\), найдем для нее обратную дробь, для этого переведем ее в неправильную дробь \(1\frac{1}{2} = \frac{3}{2}\) . Обратная ей дробь будет равна \(\frac{2}{3}\) . Дробь \(\frac{2}{3}\) является правильной дробью. Ответ: взаимно обратные две дроби одновременно смешанными числами быть не могут.
Возьмем смешанную дробь \(1\frac{1}{2}\), найдем для нее обратную дробь, для этого переведем ее в неправильную дробь \(1\frac{1}{2} = \frac{3}{2}\) . Обратная ей дробь будет равна \(\frac{2}{3}\) . Дробь \(\frac{2}{3}\) является правильной дробью. Ответ: взаимно обратные две дроби одновременно смешанными числами быть не могут.
В курсе средней и старшей школы учащиеся проходили тему «Дроби». Однако это понятие гораздо шире, чем дается в процессе обучения. Сегодня понятие дроби встречается достаточно часто, и не каждый может провести вычисления какого-либо выражения, к примеру, умножение дробей.
Что такое дробь?
Так исторически сложилось, что дробные числа появились из-за необходимости измерять. Как показывает практика, часто встречаются примеры на определение длины отрезка, объема прямоугольного прямоугольника.
Первоначально ученики знакомятся с таким понятием, как доля. К примеру, если разделить арбуз на 8 частей, то каждому достанется по одной восьмой арбуза. Вот эта одна часть из восьми и называется долей.
Вот эта одна часть из восьми и называется долей.
Доля, равная ½ от какой-либо величины, называется половиной; ⅓ — третью; ¼ — четвертью. Записи вида 5 / 8 , 4 / 5 , 2 / 4 называют обыкновенными дробями. Обыкновенная дробь разделяется на числитель и знаменатель. Между ними находится черта дроби, или дробная черта. Дробную черту можно нарисовать в виде как горизонтальной, так и наклонной линии. В данном случае она обозначает знак деления.
Знаменатель представляет, на сколько одинаковых долей разделяют величину, предмет; а числитель — сколько одинаковых долей взято. Числитель пишется над дробной чертой, знаменатель — под ней.
Удобнее всего показать обыкновенные дроби на координатном луче. Если единичный отрезок разделить на 4 равные доли, обозначить каждую долю латинской буквой, то в результате можно получить отличное наглядное пособие. Так, точка А показывает долю, равную 1 / 4 от всего единичного отрезка, а точка В отмечает 2 / 8 от данного отрезка.
Разновидности дробей
Дроби бывают обыкновенные, десятичные, а также смешанные числа. Кроме того, дроби можно разделить на правильные и неправильные. Эта классификация больше подходит для обыкновенных дробей.
Кроме того, дроби можно разделить на правильные и неправильные. Эта классификация больше подходит для обыкновенных дробей.
Под правильной дробью понимают число, у которого числитель меньше знаменателя. Соответственно, неправильная дробь — число, у которого числитель больше знаменателя. Второй вид обычно записывают в виде смешанного числа. Такое выражение состоит из целой и дробной части. Например, 1½. 1 — целая часть, ½ — дробная. Однако если нужно провести какие-то манипуляции с выражением (деление или умножение дробей, их сокращение или преобразование), смешанное число переводится в неправильную дробь.
Правильное дробное выражение всегда меньше единицы, а неправильное — больше либо равно 1.
Что касается то под этим выражением понимают запись, в которой представлено любое число, знаменатель дробного выражения которого можно выразить через единицу с несколькими нулями. Если дробь правильная, то целая часть в десятичной записи будет равна нулю.
Чтобы записать десятичную дробь, нужно сначала написать целую часть, отделить ее от дробной с помощью запятой и потом уже записать дробное выражение. Необходимо помнить, что после запятой числитель должен содержать столько же цифровых символов, сколько нулей в знаменателе.
Необходимо помнить, что после запятой числитель должен содержать столько же цифровых символов, сколько нулей в знаменателе.
Пример . Представить дробь 7 21 / 1000 в десятичной записи.
Алгоритм перевода неправильной дроби в смешанное число и наоборот
Записывать в ответе задачи неправильную дробь некорректно, поэтому ее нужно перевести в смешанное число:
- разделить числитель на имеющийся знаменатель;
- в конкретном примере неполное частное — целое;
- и остаток — числитель дробной части, причем знаменатель остается неизменным.
Пример . Перевести неправильную дробь в смешанное число: 47 / 5 .
Решение . 47: 5. Неполное частное равняется 9, остаток = 2. Значит, 47 / 5 = 9 2 / 5 .
Иногда нужно представить смешанное число в качестве неправильной дроби. Тогда нужно воспользоваться следующим алгоритмом:
- целая часть умножается на знаменатель дробного выражения;
- полученное произведение прибавляется к числителю;
- результат записывается в числителе, знаменатель остается неизменным.

Пример . Представить число в смешанном виде в качестве неправильной дроби: 9 8 / 10 .
Решение . 9 х 10 + 8 = 90 + 8 = 98 — числитель.
Ответ : 98 / 10.
Умножение дробей обыкновенных
Над обыкновенными дробями можно совершать различные алгебраические операции. Чтобы перемножить два числа, нужно числитель перемножить с числителем, а знаменатель со знаменателем. Причем умножение дробей с разными знаменателямине отличается от произведения дробных чисел с одинаковыми знаменателями.
Случается, что после нахождения результата нужно сократить дробь. В обязательном порядке нужно максимально упростить получившееся выражение. Конечно, нельзя сказать, что неправильная дробь в ответе — это ошибка, но и назвать верным ответом ее тоже затруднительно.
Пример . Найти произведение двух обыкновенных дробей: ½ и 20 / 18 .
Как видно из примера, после нахождения произведения получилась сократимая дробная запись. И числитель, и знаменатель в данном случае делится на 4, и результатом выступает ответ 5 / 9 .
И числитель, и знаменатель в данном случае делится на 4, и результатом выступает ответ 5 / 9 .
Умножение дробей десятичных
Произведение десятичных дробей довольно сильно отличается от произведения обыкновенных по своему принципу. Итак, умножение дробей заключается в следующем:
- две десятичные дроби нужно записать друг под другом так, чтобы крайние правые цифры оказались одна под другой;
- нужно перемножить записанные числа, несмотря на запятые, то есть как натуральные;
- подсчитать количество цифр после знака запятой в каждом из чисел;
- в получившемся после перемножения результате нужно отсчитать справа столько цифровых символов, сколько содержится в сумме в обоих множителях после запятой, и поставить отделяющий знак;
- если цифр в произведении оказалось меньше, тогда перед ними нужно написать столько нулей, чтобы покрыть это количество, поставить запятую и приписать целую часть, равную нулю.
Пример . Вычислить произведение двух десятичных дробей: 2,25 и 3,6.
Решение .
Умножение смешанных дробей
Чтобы вычислить произведение двух смешанных дробей, нужно использовать правило умножения дробей:
- перевести числа в смешанном виде в неправильные дроби;
- найти произведение числителей;
- найти произведение знаменателей;
- записать получившийся результат;
- максимально упростить выражение.
Пример . Найти произведение 4½ и 6 2 / 5.
Умножение числа на дробь (дроби на число)
Помимо нахождения произведения двух дробей, смешанных чисел, встречаются задания, где нужно помножить на дробь.
Итак, чтобы найти произведение десятичной дроби и натурального числа, нужно:
- записать число под дробью так, чтобы крайние правые цифры оказались одна над другой;
- найти произведение, несмотря на запятую;
- в полученном результате отделить целую часть от дробной с помощью запятой, отсчитав справа то количество знаков, которое находится после запятой в дроби.

Чтобы умножить обыкновенную дробь на число, следует найти произведение числителя и натурального множителя. Если в ответе получается сократимая дробь, ее следует преобразовать.
Пример . Вычислить произведение 5 / 8 и 12.
Решение . 5 / 8 * 12 = (5*12) / 8 = 60 / 8 = 30 / 4 = 15 / 2 = 7 1 / 2.
Ответ : 7 1 / 2.
Как видно из предыдущего примера, необходимо было сократить получившийся результат и преобразовать неправильное дробное выражение в смешанное число.
Также умножение дробей касается и нахождения произведения числа в смешанном виде и натурального множителя. Чтобы перемножить эти два числа, следует целую часть смешанного множителя умножить на число, числитель помножить на это же значение, а знаменатель оставить неизменным. Если требуется, нужно максимально упростить получившийся результат.
Пример . Найти произведение 9 5 / 6 и 9.
Решение . 9 5 / 6 х 9 = 9 х 9 + (5 х 9) / 6 = 81 + 45 / 6 = 81 + 7 3 / 6 = 88 1 / 2.
Ответ : 88 1 / 2.
Умножение на множители 10, 100, 1000 или 0,1; 0,01; 0,001
Из предыдущего пункта вытекает следующее правило. Для умножения дроби десятичной на 10, 100, 1000, 10000 и т. д. нужно передвинуть запятую вправо на столько символов цифр, сколько нулей во множителе после единицы.
Пример 1 . Найти произведение 0,065 и 1000.
Решение . 0,065 х 1000 = 0065 = 65.
Ответ : 65.
Пример 2 . Найти произведение 3,9 и 1000.
Решение . 3,9 х 1000 = 3,900 х 1000 = 3900.
Ответ : 3900.
Если нужно перемножить натуральное число и 0,1; 0,01; 0,001; 0,0001 и т. д., следует передвинуть влево запятую в получившемся произведении на столько символов цифр, сколько нулей находится до единицы. Если необходимо, перед натуральным числом записываются нули в достаточном количестве.
Пример 1 . Найти произведение 56 и 0,01.
Решение . 56 х 0,01 = 0056 = 0,56.
Ответ : 0,56.
Пример 2 . Найти произведение 4 и 0,001.
Решение . 4 х 0,001 = 0004 = 0,004.
Ответ : 0,004.
Итак, нахождение произведения различных дробей не должно вызывать затруднений, разве что подсчет результата; в таком случае без калькулятора просто не обойтись.
Обыкновенные дробные числа впервые встречают школьников в 5 классе и сопровождают их на протяжении всей жизни, так как в быту зачастую требуется рассматривать или использовать какой-то объект не целиком, а отдельными кусками. Начало изучения этой темы — доли. Доли — это равные части , на которые разделен тот или иной предмет. Ведь не всегда получается выразить, допустим, длину или цену товара целым числом, следует принять во внимание части или доли какой-либо меры. Образованное от глагола «дробить» — разделять на части, и имея арабские корни, в VIII веке возникло само слово «дробь» в русском языке.
Дробные выражения продолжительное время считали самым сложным разделом математики. В XVII веке, при появлении первоучебников по математике, их называли «ломаные числа», что очень сложно отображалось в понимании людей.
В XVII веке, при появлении первоучебников по математике, их называли «ломаные числа», что очень сложно отображалось в понимании людей.
Современному виду простых дробных остатков, части которых разделены именно горизонтальной чертой, впервые поспособствовал Фибоначчи — Леонардо Пизанский. Его труды датированы в 1202 году. Но цель этой статьи — просто и понятно объяснить читателю, как происходит умножение смешанных дробей с разными знаменателями.
Умножение дробей с разными знаменателями
Изначально стоит определить разновидности дробей :
- правильные;
- неправильные;
- смешанные.
Далее нужно вспомнить, как происходит умножение дробных чисел с одинаковыми знаменателями. Само правило этого процесса несложно сформулировать самостоятельно: результатом умножения простых дробей с одинаковыми знаменателями является дробное выражение, числитель которой есть произведение числителей, а знаменатель — произведение знаменателей данных дробей. То есть, по сути, новый знаменатель есть квадрат одного из существующих изначально.
То есть, по сути, новый знаменатель есть квадрат одного из существующих изначально.
При умножении простых дробей с разными знаменателями для двух и более множителей правило не меняется:
a/ b * c/ d = a*c / b*d.
Единственное отличие в том, что образованное число под дробной чертой будет произведением разных чисел и, естественно, квадратом одного числового выражения его назвать невозможно.
Стоит рассмотреть умножение дробей с разными знаменателями на примерах:
- 8/ 9 * 6/ 7 = 8*6 / 9*7 = 48/ 63 = 16/2 1 ;
- 4/ 6 * 3/ 7 = 2/ 3 * 3/7 2*3 / 3*7 = 6/ 21 .
В примерах применяются способы сокращения дробных выражений. Можно сокращать только числа числителя с числами знаменателя, рядом стоящие множители над дробной чертой или под ней сокращать нельзя.
Наряду с простыми дробными числами, существует понятие смешанных дробей. Смешанное число состоит из целого числа и дробной части, то есть является суммой этих чисел:
1 4/ 11 =1 + 4/ 11.
Как происходит перемножение
Предлагается несколько примеров для рассмотрения.
2 1/ 2 * 7 3/ 5 = 2 + 1/ 2 * 7 + 3/ 5 = 2*7 + 2* 3/ 5 + 1/ 2 * 7 + 1/ 2 * 3/ 5 = 14 + 6/5 + 7/ 2 + 3/ 10 = 14 + 12/ 10 + 35/ 10 + 3/ 10 = 14 + 50/ 10 = 14 + 5=19.
В примере используется умножение числа на обыкновенную дробную часть , записать правило для этого действия можно формулой:
a * b/ c = a*b / c.
По сути, такое произведение есть сумма одинаковых дробных остатков, а количество слагаемых указывает это натуральное число. Частный случай:
4 * 12/ 15 = 12/ 15 + 12/ 15 + 12/ 15 + 12/ 15 = 48/ 15 = 3 1/ 5.
Существует еще один вариант решения умножения числа на дробный остаток. Стоит просто разделить знаменатель на это число:
d * e/ f = e/ f: d.
Этим приемом полезно пользоваться, когда знаменатель делится на натуральное число без остатка или, как говорится, нацело.
Перевести смешанные числа в неправильные дроби и получить произведение ранее описанным способом:
1 2/ 3 * 4 1/ 5 = 5/ 3 * 21/ 5 = 5*21 / 3*5 =7.
В этом примере участвует способ представления смешанной дроби в неправильную, его также можно представить в виде общей формулы:
a b c = a * b + c / c, где знаменатель новой дроби образуется при умножении целой части со знаменателем и при сложении его с числителем исходного дробного остатка, а знаменатель остается прежним.
Этот процесс работает и в обратную сторону. Для выделения целой части и дробного остатка нужно поделить числитель неправильной дроби на ее знаменатель «уголком».
Умножение неправильных дробей производят общепринятым способом. Когда запись идет под единой дробной чертой, по мере необходимости нужно сделать сокращение дробей, чтобы уменьшить таким методом числа и проще посчитать результат.
В интернете существует множество помощников, чтобы решать даже сложные математические задачи в различных вариациях программ. Достаточное количество таких сервисов предлагают свою помощь при счете умножения дробей с разными числами в знаменателях — так называемые онлайн-калькуляторы для расчета дробей. Они способны не только умножить, но и произвести все остальные простейшие арифметические операции с обыкновенными дробями и смешанными числами. Работать с ним несложно, на странице сайта заполняются соответствующие поля, выбирается знак математического действия и нажимается «вычислить». Программа считает автоматически.
Они способны не только умножить, но и произвести все остальные простейшие арифметические операции с обыкновенными дробями и смешанными числами. Работать с ним несложно, на странице сайта заполняются соответствующие поля, выбирается знак математического действия и нажимается «вычислить». Программа считает автоматически.
Тема арифметических действий с дробными числами актуальна на всем протяжении обучения школьников среднего и старшего звена. В старших классах рассматривают уже не простейшие виды, а целые дробные выражения , но знания правил по преобразованию и расчетам, полученные ранее, применяются в первозданном виде. Хорошо усвоенные базовые знания дают полную уверенность в удачном решении наиболее сложных задач.
В заключение имеет смысл привести слова Льва Николаевича Толстого, который писал: «Человек есть дробь. Увеличить своего числителя — свои достоинства, — не во власти человека, но всякий может уменьшить своего знаменателя — своё мнение о самом себе, и этим уменьшением приблизиться к своему совершенству».
) и знаменатель на знаменатель (получим знаменатель произведения).
Формула умножения дробей:
Например:
Перед тем, как приступить к умножению числителей и знаменателей, необходимо проверить на возможность сокращения дроби . Если получится сократить дробь, то вам легче будет дальше производить расчеты.
Деление обыкновенной дроби на дробь.
Деление дробей с участием натурального числа.
Это не так страшно, как кажется. Как и в случае со сложением , переводим целое число в дробь с единицей в знаменателе. Например:
Умножение смешанных дробей.
Правила умножения дробей (смешанных):
- преобразовываем смешанные дроби в неправильные;
- перемножаем числители и знаменатели дробей;
- сокращаем дробь;
- если получили неправильную дробь, то преобразовываем неправильную дробь в смешанную.
Обратите внимание! Чтобы умножить смешанную дробь на другую смешанную дробь, нужно, для начала, привести их к виду неправильных дробей, а далее умножить по правилу умножения обыкновенных дробей.
Второй способ умножения дроби на натуральное число.
Бывает более удобно использовать второй способ умножения обыкновенной дроби на число.
Обратите внимание! Для умножения дроби на натуральное число необходимо знаменатель дроби разделить на это число, а числитель оставить без изменения.
Из, приведенного выше, примера понятно, что этот вариант удобней для использования, когда знаменатель дроби делится без остатка на натуральное число.
Многоэтажные дроби.
В старших классах зачастую встречаются трехэтажные (или больше) дроби. Пример:
Чтобы привести такую дробь к привычному виду, используют деление через 2 точки:
Обратите внимание! В делении дробей очень важен порядок деления. Будьте внимательны, здесь легко запутаться.
Обратите внимание, например:
При делении единицы на любую дробь, результатом будет таже самая дробь, только перевернутая:
Практические советы при умножении и делении дробей:
1. Самым важным в работе с дробными выражениями является аккуратность и внимательность. Все вычисления делайте внимательно и аккуратно, сосредоточенно и чётко. Лучше запишите несколько лишних строчек в черновике, чем запутаться в расчетах в уме.
Самым важным в работе с дробными выражениями является аккуратность и внимательность. Все вычисления делайте внимательно и аккуратно, сосредоточенно и чётко. Лучше запишите несколько лишних строчек в черновике, чем запутаться в расчетах в уме.
2. В заданиях с разными видами дробей — переходите к виду обыкновенных дробей.
3. Все дроби сокращаем до тех пор, пока сокращать уже будет невозможно.
4. Многоэтажные дробные выражения приводим в вид обыкновенных, пользуясь делением через 2 точки.
5. Единицу на дробь делим в уме, просто переворачивая дробь.
Как складывать дроби с разными знаменателями
Если дроби, которые вы хотите сложить, имеют разные знаменатели, это можно сделать несколькими способами.Простое сложение дробей
В какой-то момент вашей жизни какой-то учитель где-то сказал вам эти золотые слова мудрости: «Нельзя складывать две дроби с разными знаменателями». Ваш учитель ошибся! Вы можете использовать простой способ, когда числители и знаменатели малы (скажем, 15 или меньше).
Вот как это сделать:
Перемножьте две дроби и сложите результаты вместе, чтобы получить числитель ответа.
Предположим, вы хотите сложить дроби 1/3 и 2/5. Чтобы получить числитель ответа, перемножьте. Другими словами, умножьте числитель одной дроби на знаменатель другой:
1*5 = 5
2*3 = 6
Сложите результаты, чтобы получить числитель ответа:
5 + 6 = 11
Перемножьте два знаменателя, чтобы получить знаменатель ответа.
Чтобы получить знаменатель, просто перемножьте знаменатели двух дробей:
3*5 = 15
Знаменатель ответа равен 15.
Запишите свой ответ в виде дроби.
Поскольку и числитель, и знаменатель — четные числа, вы знаете, что дробь можно уменьшить. Итак, попробуйте разделить оба числа на 2:
Эту дробь нельзя уменьшить, поэтому 37/40 — окончательный ответ.
В некоторых случаях может потребоваться добавить более одной дроби. Метод аналогичен, с одной небольшой поправкой.
Начните с умножения числителя первой дроби на знаменателя всех остальных дробей.
(1*5*7) = 35
Проделайте то же самое со второй дробью и прибавьте это значение к первой.
35 + (3*2*7) = 35 + 42
Проделайте то же самое с оставшимися фракциями.
35 + 42 + (4*2*5) = 35 + 42 + 40 = 117
Когда вы закончите, у вас будет числитель ответа.
Чтобы получить знаменатель, просто умножьте все знаменатели вместе:
Возможно, вам потребуется уменьшить или заменить неправильную дробь смешанным числом. В этом примере вам просто нужно изменить номер на смешанный:
Сложение дробей с помощью быстрого метода
Вы не всегда можете использовать этот метод, но вы можете использовать его, когда один знаменатель кратен другому. Посмотрите на следующую задачу:
Посмотрите на следующую задачу:Сначала решите ее простым способом:
Это несколько больших чисел, и вы еще не справились, потому что числитель больше знаменателя. Ответ — неправильная дробь. Что еще хуже, числитель и знаменатель являются четными числами, поэтому ответ все равно нужно сократить.
При некоторых проблемах со сложением дробей существует более разумный способ работы. Хитрость заключается в том, чтобы превратить задачу с разными знаменателями в более простую задачу с тем же знаменателем.
Прежде чем сложить две дроби с разными знаменателями, проверьте знаменатели, чтобы узнать, кратен ли один из них другому. Если это так, вы можете использовать быстрый трюк:
Увеличьте члены дроби с меньшим знаменателем, чтобы она имела больший знаменатель.
Взгляните на предыдущую задачу по-новому:
Как видите, 12 делится на 24 без остатка. В этом случае вы хотите возвести члены 11/12 так, чтобы в знаменателе было 24:
Чтобы заполнить вопросительный знак, трюк состоит в том, чтобы разделить 24 на 12, чтобы узнать, как связаны знаменатели; затем умножьте результат на 11:
? = (24 ÷ 12) 11 = 22
Перепишите задачу, подставив эту увеличенную версию дроби, и дополните.

Теперь вы можете переписать задачу так:
Как видите, числа в этом случае гораздо меньше и с ними проще работать. Ответ здесь — неправильная дробь; превратить его в смешанное число легко:
Сложение дробей традиционным способом
Используйте традиционный способ только тогда, когда вы не можете использовать ни один из других методов (или когда вы знаете наименьшее общее кратное [НОК], просто взглянув на знаменатели).Вот традиционный способ сложения дробей с двумя разными знаменателями:
Найдите НОК двух знаменателей.
Предположим, вы хотите сложить дроби 3/4 + 7/10. Сначала найдите НОК двух знаменателей, 4 и 10. Вот как найти НОК, используя метод таблицы умножения:
Кратность 10: 10, 20, 30, 40
Кратность 4: 4, 8, 12, 16, 20
Таким образом, НОК 4 и 10 равно 20.
Увеличьте члены каждой дроби так, чтобы знаменатель каждой равнялся НОК.

Увеличьте каждую дробь до большего члена так, чтобы знаменатель каждой был равен 20.
Замените эти две новые дроби исходными и сложите.
На данный момент у вас есть две дроби с одинаковым знаменателем:
Когда ответ представляет собой неправильную дробь, вам все равно нужно изменить ее на смешанное число:
Об этой статье
Эта статья можно найти в категории:
- Pre-Algebra,
Как добавить, вычитать, умножить и разделить фракции
. Чтобы освоить более сложные понятия алгебры и геометрии, вам необходимо сначала освоить все математические функции, относящиеся к дробям. В этой статье мы рассмотрим, как складывать, вычитать, умножать и делить две дроби, а также дробь и целое число. Мы также введем сложные дроби вместе с методами их упрощения.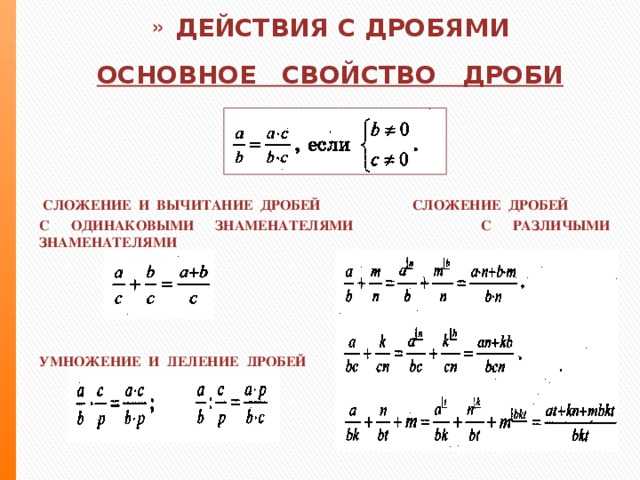 Прежде чем продолжить, убедитесь, что вы полностью понимаете четыре основных математических операции: сложение, вычитание, умножение и деление.
Прежде чем продолжить, убедитесь, что вы полностью понимаете четыре основных математических операции: сложение, вычитание, умножение и деление.
Ключевые термины
o Общий знаменатель
o Взаимные
o Комплексная фракция
Цели
O Изучите
o Понимание фракций, которые включают в себя негативные номера
4.Теперь, когда мы разработали прочную основу относительно того, что такое дроби, а также некоторые их типы, мы можем теперь перейти к применению основных арифметических операций (сложение, вычитание, умножение и деление) к дробям.
Сложение и вычитание
В случаях, когда речь идет о простых числах, сложение и вычитание дробей выполняется достаточно просто. Например, добавление одной трети и одной трети, очевидно, дает нам две трети. Точно так же три пятых минус две пятых — это одна пятая. Первый случай проиллюстрирован ниже.
А как быть с такими случаями, как половина плюс одна треть?
Обратите внимание, что складывать (вычитать) дроби с одинаковым знаменателем очень просто — мы просто складываем (вычитаем) числители и делим на тот же знаменатель. Мы уже должны знать, что можем написать эквивалентные дроби, которые имеют разные числители и знаменатели. Таким образом, если мы просто преобразуем одну или обе дроби, которые мы складываем или вычитаем, в эквивалентные дроби с тем же знаменателем, то мы можем складывать дроби простым способом, описанным выше. Затем, при необходимости, мы можем уменьшить результат до минимальных значений.
Мы уже должны знать, что можем написать эквивалентные дроби, которые имеют разные числители и знаменатели. Таким образом, если мы просто преобразуем одну или обе дроби, которые мы складываем или вычитаем, в эквивалентные дроби с тем же знаменателем, то мы можем складывать дроби простым способом, описанным выше. Затем, при необходимости, мы можем уменьшить результат до минимальных значений.
Задача при сложении и вычитании дробей состоит в том, чтобы найти общий знаменатель. Самый простой способ найти общий знаменатель — просто перемножить два существующих знаменателя, а затем соответствующим образом преобразовать числители, чтобы получить эквивалентные дроби. Хотя этот подход концептуально прост, он может быть математически сложным, когда знаменатели велики. Тем не менее, давайте попробуем этот подход для иллюстрации. Обратите внимание на упомянутое выше дополнение.
Общий знаменатель равен 6 (или 23), потому что мы можем умножить числитель и знаменатель на 3, чтобы получить , и мы можем умножить числитель и знаменатель на 2, чтобы получить . Добавление тогда просто.
Добавление тогда просто.
Практическая задача: Подсчитайте результат в каждом случае.
а. б. в.
Решение: В каждом случае найдите общий знаменатель и преобразуйте члены в эквивалентные дроби с этим знаменателем. Для каждого случая дается один возможный общий знаменатель. Сумма (разность) дробей есть сумма (разность) числителей над общим знаменателем. Если применимо, уменьшите результат до самых низких значений.
а. Общий знаменатель: 21
б. Общий знаменатель: 8
Хотите узнать больше? Почему бы не пройти онлайн-курс Pre-Algebra?
в. Общий знаменатель: 45
Умножение и деление
Умножение и деление дробей в некоторых отношениях проще, чем их сложение и вычитание. Допустим, мы хотим умножить на . Интуитивно ответ довольно очевиден: половина половины — это четверть (или одна четвертая). Например, если у вас есть 50 центов (полдоллара) и вы хотите умножить их на половину, то вы получите 25 центов (четверть доллара).
Чтобы умножить две дроби, просто умножьте числители и умножьте знаменатели, чтобы получить произведение. В некоторых случаях товар уже будет в наименьших условиях; в других вам может потребоваться уменьшить его до самых низких значений. Например, произведение и будет следующим:
При умножении дроби на целое число обратите внимание, что любое целое число — это просто дробь с целым числом в числителе и 1 в знаменателе. Например,
Практическая задача : Рассчитайте следующие произведения.
а. б. в.
Решение : В каждом случае произведение равно произведению числителей на произведение знаменателей. Если один из множителей является целым числом, рассматривайте его как дробь, имеющую целое число в числителе и 1 в знаменателе. Сократите продукт до самых низких условий, если это применимо.
а.
б.
в.
Теперь рассмотрим случай деления. Допустим, мы хотим разделить на . Интуитивно ответ равен 2. Например, 25 центов (четверть доллара) могут дважды превратиться в 50 центов (полдоллара).
Обратите внимание, что если бы мы перевернули второй множитель так, чтобы числитель стал знаменателем, а знаменатель стал числителем, а также изменили операцию деления на умножение, мы получили бы тот же результат.
На самом деле это удобный способ деления дробей. Деление на дробь равносильно умножению на 9.0156 обратное этой дроби. Обратное — это просто «перевернутая» дробь. Так, например, обратная величина равна (или ).
Как и при умножении дробей, помните, что целое число также можно записать в виде дроби. Так, например, обратное число 6 равно . Поэтому мы можем делить дроби на целые числа так же, как и на другие дроби. Кроме того, обратите внимание, что произведение дроби и ее обратной всегда равно 1. Рассмотрим пример ниже.
Рассмотрим пример ниже.
В свете того, как мы определили деление и умножение, мы можем дать более строгое обоснование нашего метода вычисления эквивалентных дробей. Обратите внимание, что число 1 можно записать как любое другое число, разделенное само на себя. Например,
Таким образом, процесс нахождения эквивалентных дробей есть не что иное, как умножение данной дроби на 1! Рассмотрим пример ниже.
Практическая задача : Вычислите следующие частные.
а. б. в.
Решение : В каждом случае умножьте делимое на обратную величину делителя. Сократите продукт до самых низких условий, если это применимо.
а.
б.
г.
Дроби и отрицательные числа
Поскольку дроби — это не что иное, как представление деления, у нас уже есть инструменты, необходимые для понимания роли отрицательных чисел в дробях. Напомним, что произведение (или частное) двух отрицательных или двух положительных чисел положительно, а произведение (или частное) одного отрицательного числа и одного положительного числа отрицательно. Итак, рассмотрим на примере дроби ; мы рассмотрим каждый возможный случай.
Напомним, что произведение (или частное) двух отрицательных или двух положительных чисел положительно, а произведение (или частное) одного отрицательного числа и одного положительного числа отрицательно. Итак, рассмотрим на примере дроби ; мы рассмотрим каждый возможный случай.
В первом случае (числитель и знаменатель имеют одинаковый знак) результатом является положительное число. Во втором случае (числитель и знаменатель имеют противоположные знаки) результатом является отрицательное число. Таким образом, во втором случае мы можем иногда просто ставить знак минус рядом со всей дробью, а не рядом с числителем или знаменателем. Тем не менее, обратите внимание, что все три представления равны, и в некоторых ситуациях одно может быть более полезным, чем другое.
Сложные дроби
Напомним, что дробь — это просто способ выражения деления двух чисел (где числитель — это делимое, а знаменатель — делитель). Поскольку мы можем делить дроби, мы также можем выразить это деление как «долю дробей» или сложную дробь . Ниже приведен пример сложной дроби. Обратите внимание, что для ясности дроби в числителе и знаменателе сложной дроби показаны «наклонными» — однако это изменение не означает никакой математической разницы.
Поскольку мы можем делить дроби, мы также можем выразить это деление как «долю дробей» или сложную дробь . Ниже приведен пример сложной дроби. Обратите внимание, что для ясности дроби в числителе и знаменателе сложной дроби показаны «наклонными» — однако это изменение не означает никакой математической разницы.
Такие дроби можно и часто нужно упрощать. Для этого мы можем воспользоваться одним из нескольких подходов. Напомним, что мы можем найти эквивалентную дробь, умножив числитель и знаменатель на одно и то же число. Таким образом, один из подходов состоит в том, чтобы умножить как числитель, так и знаменатель сложной дроби на произведение знаменателей простых дробей, как показано ниже.
В качестве альтернативы мы можем умножить и числитель, и знаменатель сложной дроби на обратную величину ее знаменателя. Поскольку знаменатель становится равным 1, результатом является просто значение числителя.
Другой способ взглянуть на этот последний подход состоит в том, что мы просто выполняем деление:
В зависимости от конкретной ситуации один подход может быть проще другого; однако все они одинаково приемлемы.
Практическая задача : Упростите следующие сложные дроби.
а. б. в.
Решение : Одним из возможных способов упрощения сложных дробей является умножение дроби в числителе на обратную дробь в знаменателе. Если применимо, уменьшите результат до самых низких значений. В случае части c обратите внимание, что обратная величина 5 равна и что частное (или произведение) положительного числа, деленного (умноженного) на отрицательное число, является отрицательным числом.
а.
б.
г.
Если у вас все еще возникают проблемы с дробями, вы также можете прочитать эту статью здесь: Как сделать дроби простым способом.
Дроби | Начальный курс алгебры
Цели обучения
- Сложение и вычитание дробей
- Найдите общий знаменатель двух или более дробей
- Используйте общий знаменатель для сложения или вычитания дробей
- Упростить дробь до минимума
- Умножение дробей
- Умножение двух или более дробей
- Умножить дробь на целое число
- Разделить дроби
- Найдите обратное число
- Разделить дробь на целое число
- Разделить дробь на дробь
Введение
Прежде чем мы начнем, вот несколько важных терминов, которые помогут вам понять принципы работы с дробями в этом разделе.
- произведение: результат умножения
- фактор: что-то умножается — для [latex]3 \cdot 2 = 6[/latex] , и 3, и 2 являются множителями 6
- числитель: верхняя часть дроби – числитель дроби [latex]\frac{2}{3}[/latex] равен 2
- знаменатель: нижняя часть дроби – знаменатель дроби [латекс]\фракция{2}{3}[/латекс] равен 3
Примечание к инструкциям
Учебники по математике и учителя используют много разных слов, чтобы дать учащимся инструкции о том, что они должны делать с данной задачей. Например, вы можете увидеть такие инструкции, как «Найти» или «Упростить» в примере в этом модуле. Важно понимать, что означают эти слова, чтобы вы могли успешно решать задачи этого курса. Вот краткий список слов, которые вы можете встретить и которые помогут вам понять, как работать с проблемами в этом модуле.
| Инструкция | Интерпретация |
|---|---|
| Найти | Выполните указанные математические действия, которые могут включать сложение, вычитание, умножение, деление. |
| Упрощение | 1) Выполнять указанные математические операции, включая сложение, вычитание, умножение, деление 2) Запишите математическую формулировку в наименьших терминах, чтобы не было других математических операций, которые можно было бы выполнить — часто встречается в задачах, связанных с дробями и порядком операций |
| Оценка | Выполнение указанных математических операций, включая сложение, вычитание, умножение, деление |
| Уменьшить | Напишите математическое выражение в наименьшем или минимальном выражении, чтобы не было других математических операций, которые можно было бы выполнить — часто встречается в задачах, связанных с дробями или делением |
Сложение и вычитание дробей
Сложение дробей
Когда вам нужно складывать или вычитать дроби, сначала нужно убедиться, что дроби имеют одинаковый знаменатель. Знаменатель говорит вам, на сколько частей разбито целое, а числитель говорит вам, сколько из этих частей вы используете.
Концепция «части целого» может быть смоделирована с помощью пиццы и кусочков пиццы. Например, представьте, что пиццу разрезают на 4 части, и кто-то берет 1 часть. Теперь [latex]\frac{1}{4}[/latex] из пиццы исчез, а [latex]\frac{3}{4}[/latex] остался. Обратите внимание, что обе эти дроби имеют знаменатель 4, который относится к количеству ломтиков, на которые была разрезана вся пицца. Что, если у вас есть еще одна пицца, разрезанная на 8 равных частей, и 3 из этих частей исчезли, оставив [латекс]\frac{5}{8}[/latex]?
Как описать общее количество оставшейся пиццы одним числом, а не двумя разными дробями? Вам нужен общий знаменатель, технически называемый наименьшим общим кратным 90 156. Помните, что если число кратно другому, вы можете разделить их и не получить остатка.
Один из способов найти наименьшее общее кратное двух или более чисел – сначала умножить каждое из них на 1, 2, 3, 4 и т. д. Например, найти наименьшее общее кратное 2 и 5.
| Сначала перечислите все числа, кратные 2: | Затем перечислите все числа, кратные 5: |
| [латекс]2\cdot 1 = 2[/латекс] | [латекс]5\cdot 1 = 5[/латекс] |
| [латекс]2\cdot 2 = 4[/латекс] | [латекс]5\cdot 2 = 10[/латекс] |
| [латекс]2\cdot 3 = 6[/латекс] | [латекс]5\cdot 3 = 15[/латекс] |
| [латекс]2\cdot 4 = 8[/латекс] | [латекс]5\cdot 4 = 20[/латекс] |
| [латекс]2\cdot 5 = 10[/латекс] | [латекс]5\cdot 5 = 25[/латекс] |
Наименьшее их общее кратное будет общим знаменателем для них двоих!
Чтобы сложить дроби с разными знаменателями, сначала перепишите их с одинаковыми знаменателями. Тогда вы знаете, что делать! Шаги показаны ниже.
Тогда вы знаете, что делать! Шаги показаны ниже.
Сложение дробей с разными знаменателями
- Найдите общий знаменатель.
- Перепишите каждую дробь, используя общий знаменатель.
- Теперь, когда дроби имеют общий знаменатель, можно сложить числители.
- Упростите, убрав все общие множители в числителе и знаменателе.
Упрощение дроби
Часто, если ответом на задачу является дробь, вас попросят записать ее в наименьших выражениях. Это общепринятое соглашение, используемое в математике, аналогично тому, как предложение начинается с заглавной буквы и заканчивается точкой. В этом курсе мы не будем вдаваться в подробности методов сокращения дробей, потому что их много. Процесс упрощения дроби часто называют уменьшение дроби . Мы можем упростить, сократив (разделив) общие множители в числителе и знаменателе дроби. Мы можем это сделать, потому что дробь представляет собой деление.
Например, чтобы упростить [латекс]\frac{6}{9}[/latex], вы можете переписать 6 и 9, используя наименьшие возможные коэффициенты, следующим образом:
[латекс]\frac{6}{9}= \frac{2\cdot3}{3\cdot3}[/latex]
Поскольку 3 есть и в числителе, и в знаменателе, а дроби можно считать делением, мы можем разделить 3 в верхней части на 3 в нижней снизу уменьшить до 1.
[латекс]\frac{6}{9}=\frac{2\cdot\cancel{3}}{3\cdot\cancel{3}}=\frac{2\cdot1}{3}=\frac {2}{3}[/latex]
Переписывание дробей с наименьшими возможными множителями часто называется простой факторизацией.
В следующем примере показано, как сложить две дроби с разными знаменателями, а затем упростить ответ.
Вы можете найти общий знаменатель, найдя общие кратные знаменателей. Наименьшее общее кратное является самым простым в использовании.
В следующем видео вы увидите пример сложения двух дробей с разными знаменателями.
Вы также можете сложить более двух дробей, если сначала найдете для них общий знаменатель. Пример суммы трех дробей показан ниже. В этом примере вы будете использовать метод простой факторизации, чтобы найти LCM.
Подумай об этом
Добавить [латекс] \frac{3}{4}+\frac{1}{6}+\frac{5}{8}[/latex]. Упростите ответ и запишите в виде смешанного числа.
Упростите ответ и запишите в виде смешанного числа.
Чем этот пример отличается от предыдущих? Используйте поле ниже, чтобы записать несколько мыслей о том, как бы вы сложили вместе три дроби с разными знаменателями.
Показать решение
Вычитание дробей
Когда вы вычитаете дроби, вы должны думать о том, есть ли у них общий знаменатель, как и при сложении дробей. Ниже приведены примеры вычитания дробей, знаменатели которых не совпадают.
В приведенном ниже примере показано, как использовать кратные для нахождения наименьшего общего кратного, которое будет являться наименьшим общим знаменателем.
В следующем видео вы увидите пример вычитания дробей с разными знаменателями.
Умножение дробей
Так же, как сложение, вычитание, умножение и деление при работе с целыми числами, вы также используете эти операции при работе с дробями. Есть много случаев, когда необходимо умножить дроби. Модель может помочь вам понять умножение дробей.
Есть много случаев, когда необходимо умножить дроби. Модель может помочь вам понять умножение дробей.
Когда вы умножаете дробь на дробь, вы получаете «долю дроби». Предположим, у вас есть [latex]\frac{3}{4}[/latex] конфеты, и вы хотите найти [latex]\frac{1}{2}[/latex] [latex]\frac{ 3}{4}[/латекс]:
Разделив каждую четвертую пополам, вы можете разделить шоколадный батончик на восьмые части.
Затем выберите половину из них, чтобы получить [латекс]\фрак{3}{8}[/латекс].
В обоих вышеперечисленных случаях, чтобы найти ответ, вы можете перемножить числители вместе и знаменатели вместе.
Умножение двух дробей
[латекс] \frac{a}{b}\cdot \frac{c}{d}=\frac{a\cdot c}{b\cdot d}=\frac{\text{ произведение числителей}}{\text{произведение знаменателей}}[/latex]
Умножение более двух дробей
[латекс] \frac{a}{b}\cdot \frac{c}{d}\cdot \frac{e}{f}=\frac{a\cdot c\cdot e}{b\cdot d\cdot f}[/latex]
Повторим: если дробь имеет общие делители в числителе и знаменателе, мы можем привести дробь к упрощенной форме, удалив общие делители.
Например,
- Учитывая [латекс] \frac{8}{15}[/latex], множители 8: 1, 2, 4, 8, а множители 15: 1, 3, 5 , 15. [latex] \frac{8}{15}[/latex] упрощено, поскольку нет общих делителей 8 и 15.
- Учитывая [латекс] \frac{10}{15}[/latex], множители 10: 1, 2, 5, 10, а множители 15: 1, 3, 5, 15. [латекс] \frac {10}{15}[/latex] не является упрощенным, поскольку 5 – общий делитель 10 и 15.
Прежде чем умножать две дроби, вы можете упростить, чтобы облегчить себе работу. Это позволяет вам работать с меньшими числами при умножении.
В следующем видео вы увидите пример как умножить две дроби, а затем упростить ответ.
Подумайте об этом
Умножьте [латекс] \frac{2}{3}\cdot \frac{1}{4}\cdot\frac{3}{5}[/latex]. Упростите ответ.
Чем этот пример отличается от предыдущих? Используйте поле ниже, чтобы записать несколько мыслей о том, как бы вы умножили три дроби.
Показать решение
Разделить дроби
Бывают случаи, когда вам нужно использовать деление для решения проблемы. Например, если для нанесения одного слоя краски на стены комнаты требуется 3 литра краски, а у вас есть ведро с 6 литрами краски, сколько слоев краски вы можете нанести на стены? Вы делите 6 на 3 для ответа 2 пальто. Также будут случаи, когда вам нужно разделить на дробь. Предположим, что для покраски шкафа в один слой требуется всего [латекс] \frac{1}{2}[/латекс] кварта краски. Сколько слоев можно нанести 6 литрами краски? Чтобы найти ответ, вам нужно разделить 6 на дробь [латекс] \фракция{1}{2}[/латекс].
Прежде чем мы начнем делить дроби, давайте рассмотрим некоторые важные термины.
- обратное: две дроби являются обратными, если их произведение равно 1 (не волнуйтесь, мы покажем вам примеры того, что это означает.)
- частное: результат деления
Для деления дробей необходимо использовать обратное число или дробь. Если вы умножаете два числа вместе и в результате получаете 1, то эти два числа являются обратными. Вот несколько примеров взаимного обмена:
Если вы умножаете два числа вместе и в результате получаете 1, то эти два числа являются обратными. Вот несколько примеров взаимного обмена:
| Исходный номер | Взаимный | Продукт |
|---|---|---|
| [латекс] \frac{3}{4}[/латекс] | [латекс] \frac{4}{3}[/латекс] | [латекс] \frac{3}{4}\cdot \frac{4}{3}=\frac{3\cdot 4}{4\cdot 3}=\frac{12}{12}=1[/ латекс] |
| [латекс] \frac{1}{2}[/латекс] | [латекс] \frac{2}{1}[/латекс] | [латекс]\frac{1}{2}\cdot\frac{2}{1}=\frac{1\cdot}{2\cdot1}=\frac{2}{2}=1[/latex] |
| [латекс] 3=\frac{3}{1}[/латекс] | [латекс] \frac{1}{3}[/латекс] | [латекс] \frac{3}{1}\cdot \frac{1}{3}=\frac{3\cdot 1}{1\cdot 3}=\frac{3}{3}=1[/ латекс] |
| [латекс]2\фракция{1}{3}=\фракция{7}{3}[/латекс] | [латекс] \frac{3}{7}[/латекс] | [латекс]\frac{7}{3}\cdot\frac{3}{7}=\frac{7\cdot3}{3\cdot7}=\frac{21}{21}=1[/latex] |
Иногда мы называем обратное число «переворотом» другого числа: переверните [латекс] \frac{2}{5}[/latex], чтобы получить обратное [латекс]\frac{5}{2}[ /латекс].
Деление на ноль
Вы знаете, что значит делить на 2 или делить на 10, но что значит делить количество на 0? Это вообще возможно? Можно ли разделить 0 на число? Рассмотрим дробь
[латекс]\фракция{0}{8}[/латекс]
. Мы можем прочитать это как «ноль разделить на восемь». Поскольку умножение обратно делению, мы могли бы переписать это как задачу на умножение.
[латекс]\текст{?}\cdot{8}=0[/латекс].
Мы можем сделать вывод, что неизвестное должно быть равно 0, так как это единственное число, которое дает 0 при умножении на 8.
Теперь давайте рассмотрим обратное значение [латекс]\фракция{0}{8}[/латекс], которое будет [латекс]\фракция{8}{0}[/латекс]. Если мы перепишем это как задачу на умножение, то получим
[латекс]\текст{?}\cdot{0}=8[/латекс].
Это не имеет никакого смысла. Не существует чисел, которые можно умножить на ноль, чтобы получить результат 8. Обратная величина [латекс]\фракция{8}{0}[/латекс] не определена, и фактически любое деление на ноль не определено.
Внимание! Деление на ноль не определено, как и обратная величина любой дроби с нулем в числителе. Для любого действительного числа а [латекс]\фракция{а}{0}[/латекс] не определена. Кроме того, обратная величина [latex]\frac{0}{a}[/latex] всегда будет неопределенной.
Деление дроби на целое число
Когда вы делите целое число, вы умножаете его на обратное. В примере покраски, где вам нужно 3 литра краски для слоя и у вас есть 6 литров краски, вы можете найти общее количество слоев, которые можно покрасить, разделив 6 на 3, [латекс]6\div3=2[/латекс ]. Вы также можете умножить 6 на обратную величину 3, то есть [латекс] \frac{1}{3}[/latex], поэтому задача умножения будет выглядеть так:
[латекс] \frac{6}{1}\cdot \ frac{1}{3}=\frac{6}{3}=2[/latex].
Деление – это умножение на обратное число
Для любого деления вы можете превратить операцию в умножение, используя обратное число. Деление равносильно умножению на обратное.
Та же идея будет работать, когда делитель (вещь, которую делят) является дробью. Если у вас есть [латекс] \frac{3}{4}[/latex] шоколадного батончика и вам нужно разделить его между 5 людьми, каждый получит [латекс] \frac{1}{5}[/latex] доступные конфеты:
[латекс] \frac{1}{5}\text{ of }\frac{3}{4}=\frac{1}{5}\cdot \frac{3}{4}= \frac{3}{20}[/латекс]
Каждый человек получает [латекс]\фрак{3}{20}[/латекс] целого шоколадного батончика.
Если у вас есть рецепт, который нужно разделить пополам, вы можете разделить каждый ингредиент на 2 или умножить каждый ингредиент на [латекс]\frac{1}{2}[/latex] , чтобы найти новое количество .
Например, деление на 6 равносильно умножению на обратную величину 6, то есть [латекс]\frac{1}{6}[/латекс]. Посмотрите на схему двух пицц ниже. Как можно справедливо разделить то, что осталось (область, заштрихованная красным), между 6 людьми?
Каждый человек получает один кусок, поэтому каждый человек получает [латекс] \frac{1}{4}[/latex] пиццы.
Деление дроби на целое — это то же самое, что и умножение на обратную, поэтому вы всегда можете использовать умножение дробей для решения задач на деление.
Разделить дробь на дробь
Иногда вам нужно решить задачу, требующую деления на дробь. Предположим, у вас есть пицца, которая уже разрезана на 4 куска. Сколько существует фрагментов [latex]\frac{1}{2}[/latex]?
Есть 8 ломтиков. Вы видите, что деление 4 на [latex] \frac{1}{2}[/latex] дает тот же результат, что и умножение 4 на 2.
Что произойдет, если вам нужно разделить каждый срез на трети?
У вас получится 12 частей, что равносильно умножению 4 на 3.
Деление дробями
- Найдите обратную величину числа, следующего за символом деления.
- Умножить первое число (то, что перед знаком деления) на величину, обратную второму числу (после знака деления).
Самый простой способ запомнить, как делить дроби, — это фраза «сохранить, изменить, перевернуть». Это означает СОХРАНИТЬ первое число, ЗАМЕНИТЬ знак деления на умножение, а затем ПЕРЕВЕРНУТЬ (использовать обратное) второго числа.
Это означает СОХРАНИТЬ первое число, ЗАМЕНИТЬ знак деления на умножение, а затем ПЕРЕВЕРНУТЬ (использовать обратное) второго числа.
Зачем повторять темы из предыдущих уроков математики?
Опять объедки?
Вы были в классе весь день, бегали, забирали своих детей из детского сада, и после долгой, жестокой дороги вы возвращаетесь домой и понимаете, что не подумали о том, что приготовить на ужин. Вы подходите к холодильнику, и все, что вы видите, это остатки, беспорядочные кусочки прошлых блюд. Несмотря на усталость, вам удается приготовить еду, которую все охотно съедят, и продолжить свой вечер.
В этом разделе вам может показаться, что темы представляют собой смесь объедков. Цель состоит в том, чтобы напомнить вам о некоторых навыках и темах из предыдущих уроков математики, которые, как и коробка с остатками в задней части вашего холодильника, легко забываются большинством людей. Потому что иногда мы просто забываем, как работают эти понятия. . . пока они нам снова не понадобятся.
. . пока они нам снова не понадобятся.
Результаты обучения
Свойства действительных чисел
- Определение действительных чисел и подмножеств действительных чисел
- Определить свойства действительных чисел и использовать их для вычисления алгебраических выражений
Многошаговые уравнения
- Использование свойств действительных чисел для решения многошаговых линейных уравнений
- Определение и использование распределительного свойства для решения линейных уравнений
- Классифицировать решения уравнений
Решение проблем
- Составление уравнений из описаний задач
- Использование формул для решения прикладных задач
Работая с остальными разделами этого курса, возвращайтесь к этому обзору, если считаете, что вам нужно напоминание о затронутых темах. Эти темы были выбраны потому, что о них часто забывают и они широко используются на протяжении всего курса. Не волнуйтесь, как и кетчуп, у этих концепций долгий срок годности. 92+4x+3)}}
\cssId{s25}{\cdot}
\cssId{s26}{\frac{x+1}{x+4}}$
Не волнуйтесь, как и кетчуп, у этих концепций долгий срок годности. 92+4x+3)}}
\cssId{s25}{\cdot}
\cssId{s26}{\frac{x+1}{x+4}}$
Интересно сравнить исходное выражение (до упрощения),
и упрощенное выражение (после отмены).
Хотя они равны
почти для всех значений $\,x\,$,
они немного отличаются,
из-за отмены:
| ЗНАЧЕНИЯ ИЗ $\,х\,$ | 92+20х+15}
\cdot
\фракция{х+1}{х+4}}
$ в факторизованной форме: $\displaystyle \cssId{s49}{\frac{\hphantom{5}(x+1)(x+3)(x-3)}{5(x+1)(x+3)(x+4)}}$ | УПРОЩЕННОЕ ВЫРАЖЕНИЕ: $\displaystyle \cssId{s51}{\frac{(x-3)}{5(x+4)}}$ | СРАВНЕНИЕ |
| $х = -4$ | не определено (деление на ноль) | не определено (деление на ноль) | ведут себя одинаково: оба не определены |
| $х = -1$ | не определено (деление на ноль) | $\displaystyle \cssId{s60}{\frac{-1-3}{5(-1+4)} = -\frac{4}{15}}$ | Наличие
$\,\фракция{х+1}{х+1}\,$
вызывает точку прокола в $\,х = -1\,$; см.  первый график ниже первый график ниже |
| $х = -3$ | не определено (деление на ноль) | $\displaystyle \frac{-3-3}{5(-3+4)} = -\frac{6}{5}$ | Наличие
$\,\фракция{х+3}{х+3}\,$
вызывает точку прокола в $\,х = -3\,$; см. первый график ниже |
| все остальные значений $\,х\,$ | оба определены; значений равны | ведут себя одинаково: значений равны | |
ГРАФИК: $\displaystyle \cssId{s72}{\frac{\hphantom{5}(x+1)(x+3)(x-3)}{5(x+1)(x+3)(x+4)}}$ | ГРАФИК: $\displaystyle \cssId{s74}{\frac{(x-3)}{5(x+4)}}$ |
Как умножать дроби с помощью простых шагов и 7 увлекательных заданий
Вы уже преуспели в обучении умножению, но теперь предстоит, казалось бы, непростая задача научить их умножать дроби.
Глубокие вдохи.
Как учителя, так и ученики могут утверждать, что эта концепция более сложна, чем переход от вычитания и сложения к умножению.
К счастью, существуют стратегии, которые значительно облегчат понимание процесса умножения дробей, и мы собрали их для вас в четком руководстве.
Простой способ умножить фракции
Существует три простых шага, которые должны следовать вашим ученикам, чтобы следовать, как умножить фракции:
- Умножьте числители ( Верхние числа )
- Умножение деноминаторов (7
- . нижние числа
) - Если необходимо, упростите или сократите дробь
0155 может умножить две дроби с различными знаменателями.
Давайте рассмотрим пример вместе!
Пример умножения дробей
Понимание трех типов дробей и способов их умножения
Прежде чем мы углубимся в эту концепцию и объясним умножение дробей, мы подумали, что имеет смысл понять различные типы дробей.
Хорошо бы начать с простой терминологии, касающейся того, как состоит дробь:
- Числитель — верхнее число, которое указывает, сколько частей (целого) у вас есть.
- Знаменатель — нижнее число, которое относится к общему количеству частей, составляющих целое.
Авторы и права: Бретт Берри
Теперь мы рассмотрим три типа дробей и способы их умножения.
1. Умножение правильных дробей
У правильной дроби числитель на меньше знаменателя . Это самое простое место для начала умножения дробей. Пример, который мы использовали выше, идеально подходит для умножения этого типа дроби.
Например: ½, ⅔, ¾, ⅘, ⅚
2. Умножение неправильных дробей
Неправильная дробь похожа по структуре, но имеет числитель больше знаменателя на .
Примечание : Когда числитель равен знаменателю, это считается «неправильным», потому что вы можете преобразовать его в целое число. То же правило применяется к неправильным дробям, таким как ²⁶⁄₁₃, которые при уменьшении становятся целыми (т. Е. Двойками).
То же правило применяется к неправильным дробям, таким как ²⁶⁄₁₃, которые при уменьшении становятся целыми (т. Е. Двойками).
Например: ³⁄₂, ⁵⁄₃, ⁷⁄₆, ¹¹⁄₁₀, ⁸⁄₈
Кредит: Миранда Венуск
Неправильные дроби умножаются точно так же, как и правильные. Однако иногда учащиеся могут столкнуться с неправильными дробями.
Возьмите эту проблему в качестве примера:
Решение : ⁵⁄₃ × ⁷⁄₆ Умножаемые числовые числиторы : 5 × 7 = 35 Умноженные знаменатели : 3 × 6 = 18 Новая фракция : ◦ ⁵ ⁵
Если учащиеся знакомы со смешанными дробями, они могут заменить неправильную дробь на смешанную. В этом случае это смешанное число будет 1 ¹⁷⁄₁₈.
Но вы можете узнать больше о смешанных числах ниже!
3. Умножение смешанных дробей
Прежде чем учить учащихся умножать дроби со смешанными числами, они должны знать три шага:
- Преобразование любых смешанных дробей в неправильные дроби
- Умножение неправильных дробей
- Преобразование конечного произведения обратно в смешанное число
Чтобы выполнить первый шаг, научите своих учеников составлять смешанное число «Безумно» .
Кредит: Fabulous Finch Facts
Помните: смешанное число состоит из целого числа и правильной дроби. Чтобы выполнить первый шаг и преобразовать смешанную дробь в неправильную, вам необходимо:
- Найти новый числитель — Умножить целое число на знаменатель, а затем прибавить к нему исходный числитель.
- Сохранить тот же знаменатель — Знаменатель остается неизменным.
Отсюда и полезная аббревиатура:
M умножить A дд D знаменатель
Шаг второй: умножьте неправильные дроби, как мы показали в этом разделе.
Шаг третий, превратите эту неправильную дробь обратно в смешанное число. Вот небольшой стишок, который поможет вашим учащимся запомнить, как это делать:
С неправильной дробью деление — это действие!
Кредит: Хизер «Покажи и расскажи»
Давайте воспользуемся показанным ранее примером: ¹⁶⁄₅.
Если деление — это действие, то нужно разделить числитель (16) на знаменатель (5) и посмотреть, есть ли остаток.
Пять входит в число 16 три раза равномерно , всего 15. Это означает, что целая часть смешанного числа будет три .
Но он не разделился идеально, что вы можете видеть по остатку один . Итак, дробная часть смешанного числа — это остаток от знаменателя исходной дроби (⅕).
В виде смешанной дроби это выглядит так: 3 ⅕ .
Чтобы получить более наглядное представление о том, как умножать смешанные числа, посмотрите этот четырехминутный видеоролик от Академии Хана:
И это то, что вам нужно знать при умножении дробей и смешанных чисел.
Как насчет умножения дробей на целые числа?
Кредит: Эрика Наджера
Умножение целых чисел и дробей может поставить ваших учеников в тупик. Почему? Потому что кажется, что дробь одна, а не две.
Но, изучая, как умножать дроби на целые числа, учащиеся могут переписать их как дроби. Вместо 4, например, превратите его в дробь ⁴⁄₁.
Вместо 4, например, превратите его в дробь ⁴⁄₁.
Теперь умножать стало проще и понятнее. Например, они могут переписать 2 × ⁵⁄₁₃:
Решение : 2 × ⁵⁄₁₃ Переписать целое число в виде фракции : ²⁄₁ × ⁵⁄₁₃ . Умножить знаменатели : 1 × 13 = 13 Новая дробь : ¹⁰⁄₁₃
Примечание . Если учащиеся испытывают затруднения с целыми числами, объясните, что они могут думать о целом числе как о верхнем числе, при этом нижнее число всегда равно единице.
Модели площадей для умножения дробей
Идеально подходит для визуалов в вашем классе, модель площади эффективно иллюстрирует, как одна дробь умножается на другую.
Как видно из рисунка ниже, создать модель площади при умножении дробей очень просто:
- Нарисуйте дроби, которые вы умножаете, в отдельных коробках, используя разные цвета
- Объедините рисунки в одну рамку, используя новый цвет для перекрывающихся частей
- Чтобы написать произведение, задайте себе два вопроса:
Сколько коробок имеют оба цвета? Это будет ваш числитель
Сколько всего коробок? Это будет ваш знаменатель
Кредит: миссис Коггинс
Броское напоминание
О! А если ваши ученики когда-нибудь забудут шаги, просто напомните им спеть эту песенку:
Умножение дробей? Это не большая проблема. Делайте верхние разы верхние над нижним временами нижние. И прежде чем попрощаться, не забудьте упростить!
Делайте верхние разы верхние над нижним временами нижние. И прежде чем попрощаться, не забудьте упростить!
2 Основные ошибки, которые учащиеся допускают при умножении дробей
Хотя некоторые ученики быстро усвоят ваши уроки умножения дробей, другие могут испытывать трудности с этими новыми понятиями.
Чем раньше учителя уловят эти заблуждения, тем быстрее ученики смогут извлечь уроки из своих ошибок и исправить их.
Согласно практическому руководству What Works Clearinghouse Института педагогических наук «Разработка эффективных инструкций по дробям для детского сада до 8-го класса», это одни из наиболее распространенных заблуждений в отношении обучения тому, как умножать дроби.
1. Вера в то, что целые числа имеют тот же знаменатель, что и дробь в задаче
Группа из восьми экспертов признала, что это заблуждение может привести к тому, что учащиеся возьмут такую задачу, как 4 – ⅜, и перепишут ее как ⁴⁄₈ – ⅜, для неверный ответ ⅛.
При представлении смешанного числа учащиеся с таким неправильным представлением могут добавить целое число к числителю, как в ³¹⁄₃ × ⁶⁄₇ = (³⁄₃ + ⅓) × ⁶⁄₇ = ⁴⁄₃ × ⁶ ⁄₇ = ²⁴⁄₂₁.
Помочь учащимся понять взаимосвязь между смешанными числами и неправильными дробями, а также то, как перевести одно в другое, крайне важно для работы с дробями.
Как помочь своим ученикам
Не поддавайтесь искушению взорвать основные уроки.
Уделите время своим ученикам, чтобы помочь им понять взаимосвязь между неправильными дробями и смешанными числами, а также способы их преобразования из одних в другие.
Кредит: Once Upon a Creative Classroom
2. Оставить знаменатель без изменений
Учащиеся могут совершить ошибку, забыв умножить равные знаменатели. Вероятно, это связано с тем, что вам не нужно касаться равных знаменателей при сложении дробей.
Например, они могут увидеть ⅔ × ⅓ и неправильно ответить ⅔ вместо ²⁄₉.
Как помочь учащимся
В практическом руководстве эксперты-эксперты предлагают «объяснить концептуальную основу умножения дробей с помощью единичных дробей (например, ½ × ½ = половина половины = ¼)».
В частности, учителя могут показать, что задача ½ × ½ на самом деле спрашивает, чему равно ½ от ½, а это означает, что произведение должно быть меньше, чем умножаемая дробь.
Вербализация этого заблуждения полезна, но особенно эффективна его визуализация. Войдите в стену фракции !
Дробные стены — отличный способ помочь учащимся увидеть, как в данном случае выглядит абстрактная половина одной половины (т. е. одна четверть).
Теперь вы знаете о болевых точках многих студентов, изучающих умножение дробей, что дальше? Давайте рассмотрим, как закрепить уроки дробей и почему рабочие листы могут быть не лучшей стратегией.
Помогают ли рабочие листы умножать дроби?
Доктор Стивен Камарата, специалист по детскому развитию и отклонениям в развитии, считает, что естественное детское любопытство рушится.
В эссе для Psychology Today он выразил недовольство предположением, что заполнение рабочих листов напрямую связано с улучшением обучения.
Но данные о количестве достижений в США по сравнению с остальным миром говорят об обратном. По иронии судьбы, по мере того, как все больше и больше рабочих листов выдвигают в более ранние классы и все больше механических и скучных домашних заданий навязывают развивающимся умам, успеваемость учащихся в США продолжает снижаться.
Источник: Источник: Исследователь данных NAEP, Национальный центр статистики образования
В отчете Центра исследований Пью отмечается снижение и без того удручающих показателей успеваемости в США. Д-р Камарата подчеркнул:
В 2011 г. только 34% четвероклассников и 27% восьмиклассников были оценены как хорошо владеющие математикой, и этот показатель снизился до 33% среди четвероклассников и 25% среди восьмиклассников в 2015 г. данные доступны). Невозможно оценить эти результаты положительно: в настоящее время 9 0156 более двух третей четвероклассников и трое из четырех восьмиклассников не владеют математикой . Это 38-е место в мире.
Означает ли это, что школы должны отказаться от рабочих листов? Не обязательно.
Корреляция не является причинно-следственной связью. На самом деле, многие учителя и ученики добились успеха с рабочими листами.
Однако преподаватели должны осознавать, что образование быстро меняется, начиная с рабочих листов и заканчивая классными технологиями.
Итак, вот несколько творческих способов научить умножению дробей — без рабочих листов!
7 Увлекательные занятия по обучению учащихся умножению дробей
1. Prodigy
Prodigy — это математическая онлайн-игра, адаптированная к учебной программе, которая предлагает материалы по всем основным математическим темам с 1 по 8 класс.
Наряду со многими другими навыками и стандартами Prodigy может помочь учащимся научиться:
- Умножать две дроби
- Умножать дробь на целое число
- Умножать две дроби с помощью текстовых задач
- Умножение целого числа на недостающую дробь
И еще!
Играя в Prodigy, вы можете отправить своих учеников в увлекательное и познавательное путешествие, вдохновленное фэнтези. Кроме того, вы получите данные об их успехах, чтобы использовать их в своих повседневных стратегиях обучения.
Кроме того, вы получите данные об их успехах, чтобы использовать их в своих повседневных стратегиях обучения.
Готовы начать?
Зарегистрируйтесь сейчас!2. Переверните дроби
Кредит: MathFileFolderGames
Для этого задания разделите учащихся на группы по четыре человека. Затем они делятся на команды по два человека, одна из которых является игроком А, а другая — игроком Б.
Дайте каждой группе по колоде перетасованных карт (тузы = 1, валеты = 10, дамы = 11 и короли = 12).
Как показано на рисунке выше, каждый учащийся вытягивает карту числителя (над карандашом) и карту знаменателя (под карандашом).
Оба игрока А перепишут и умножат дроби на бумаге, а затем, если возможно, упростят произведение. Как только они ответят, игрок Б сделает то же самое.
В зависимости от вашего расписания вы можете назначить всю колоду или дать учащимся таймер, чтобы заполнить столько, сколько они могут.
Предложите учащимся сдать листы для ответов после выполнения упражнения, чтобы вы могли их отметить, или вместе ответьте на 10+ вопросов всем классом.
Примечание : Вы также можете назвать эту игру «Slam-it дроби», заменив карты и карандаши на домино.
3. Умножение дробей БИНГО
Кредит: jimmiehomeschoolmom
Каждый ученик получает карточку бинго с заполненными дробями вместе с небольшими листами бумаги (или «фишками бинго»), на которых находятся соответствующие задачи на умножение дробей.
Когда вы говорите «ВПЕРЕД», они могут начать решать каждую задачу одну за другой, кладя фишку поверх правильной дроби.
Вам решать, хотите ли вы, чтобы они завершили линию или всю карту бинго. Вы также можете выбрать, будут ли упрощены ответы на карты бинго.
Для простоты вы можете дать всем одну и ту же карточку бинго с одинаковыми вопросами. Таким образом, вы сможете потом пройтись по каждой проблеме и вместе решить, как их решить.
Примечание : Вы можете использовать этот и последующие примеры в качестве формативного оценивания для оценки знаний учащихся и выявления неверных представлений на раннем этапе
4.
 Словесные задачи
Словесные задачиСловесные задачи — прекрасный способ сделать уроки математики актуальными для ваших учеников ‘ жизни.
Умение умножать дроби может показаться им чуждым, но простая история может полностью изменить их представление не только о дробях, но и о математике в целом.
Вот пример словесной задачи:
У вас есть ½ пакета чипсов в шкафу, но вы съели ½ после ужина. Сколько всего пакета ты съел? (Не сокращайте свой ответ до минимума.)
Конечно, это простой пример. Но секунду назад эта дробь была просто числом над и под короткой чертой. Однако теперь эта «повседневная» проблема со словами сделала умножение дробей применимым к реальной жизни.
5. Война фракций
Кредит: Шерри Фишер
Это занятие для двух человек взято из карточной игры «Война».
Примечание : Многие учителя отказываются от быстрого решения задач, потому что это не обязательно демонстрирует понимание учеником. У вас также могут быть дети в вашем классе, которые беспокоятся из-за необходимости быстро решать математику и поэтому не успевают. Поэтому лучше всего оценить свой класс, прежде чем играть в эту версию.
У вас также могут быть дети в вашем классе, которые беспокоятся из-за необходимости быстро решать математику и поэтому не успевают. Поэтому лучше всего оценить свой класс, прежде чем играть в эту версию.
У каждого ученика, сидящего рядом, будет половина колоды карт фракций (которую вы можете скачать здесь).
Положив стопку карт лицевой стороной вниз, каждый учащийся вытянет карту одновременно .
Первый учащийся, правильно умноживший две дроби, добавит эти карты в свою колоду.
Учащийся выигрывает, если у него на руках оказывается вся колода карт фракций или у него больше карт по истечении, например, 20 минут.
Более того, быстрый и немедленный характер этого дробного задания может помочь улучшить навыки ментальной математики ваших учеников.
Кроме того, вы можете запустить версию этой игры, позволяющую всем играть против вас.
Кто не любит шанс перехитрить своего учителя!?
Разделите свой класс на пять групп.
Вы попадете в первую группу и ответите на один вопрос, прежде чем перейти во вторую группу и так далее. Помните: цель этой версии не в том, чтобы ответить перед вашими учениками, а в том, чтобы помочь улучшить их математические способности в уме.
Это позволяет учащимся отвечать коллективно, чтобы не выделять детей, у которых могут возникнуть трудности с ментальной арифметикой.
6. Пищевые фракции
Дети любят поесть – это не секрет! Так почему бы не включить его в свой план урока?
Учитель в твиттере выше заставил своих детей попрактиковаться в умножении дробей путем преобразования рецептов вкусных блюд.
Каждый ученик может выбрать свою любимую еду и увеличить количество ингредиентов, чтобы накормить весь класс.
Поощрение тоже может помочь! Например, после того, как все переделают свою любимую еду, выберите безопасную закуску, которая понравится классу.
Откройте исходный рецепт. Теперь пусть ваши ученики поработают вместе, чтобы умножить ингредиенты, и, если они сделают это правильно, весь класс получит домашнюю (или купленную в магазине) выпечку!
7.
 Вымпел с умноженной дробью
Вымпел с умноженной дробьюКредит: Scaffolded Math
Вырежьте листы бумаги в форме ленты или треугольника для каждого учащегося. Вверху напишите «Я могу умножать…»
Ниже вы включите:
- Модель площади, иллюстрирующая дроби, которые они умножают
- Сама задача на умножение (с местом для демонстрации своей работы)
- Место внизу с надписью «Мой продукт сводится к…»
После того, как каждый учащийся заполнит и украсит свой вымпел на умножение дроби, клей или лента их в нитку!
Эта активная учебная деятельность не только поможет усвоить, как умножать дроби, но и придаст уверенности вашим ученикам. Это их работают на стене, проблема они решил, а каждый может его увидеть.
Хотите научить своих учеников умножать дроби прямо сейчас?
Надеемся!
Умножение дробей может оказаться непростой задачей — выучить и научить.
Надеемся, что подробный анализ различных типов дробей, способов их умножения и того, как сделать их изучение увлекательным, поможет вам и вашим ученикам обогатить опыт преподавания и обучения.
Читать далее: Как разделить дробь за 3 простых шага
Как умножать дроби?
Одной из самых важных операций в изучении дробей является знание того, как умножать дроби. Умножение дробей дает либо другую дробь, либо целое число. Действительно, умножать дроби очень просто. Прежде чем мы углубимся в умножение дробей, давайте изучим несколько терминов, связанных с дробями.
Что такое дробь? Дробь — это любое число, которое можно представить в виде m/n. Число над знаком «/» называется числителем, а число под знаком «/» — знаменателем. В приведенном выше случае «m» — это числитель, а «n» — знаменатель. Фракции далее делятся на 3 типа:
Правильные дроби: Дроби, в которых числитель всегда меньше знаменателя, называются правильными дробями.
Пример: 1/2, 3/4, 7/21 и т. д.
Неправильные дроби: Дроби, у которых числитель всегда больше знаменателя, называются неправильными дробями.
Пример: 21/3, 99/4, 5/2 и т. д.
Смешанные дроби: Дроби, состоящие из комбинации целого числа и дробного числа, известны как смешанные дроби.
Пример: 3
4
Мы видим, что неправильные дроби можно записать в виде смешанных дробей и наоборот.
В этой статье мы узнаем много нового об умножении дробей и умножении дробей на целые числа.
Как умножать дроби? Умножение дробей сильно отличается от сложения и вычитания. При суммировании или вычитании двух или более дробей знаменатель должен быть одинаковым, но при умножении дробей знаменатель не обязательно должен совпадать. Любые две дроби с разными знаменателями удобно перемножать таким образом. Главное помнить, что смешанные дроби нельзя умножать; вместо этого дроби должны быть либо правильными, либо неправильными, чтобы их можно было умножить.
Умножить две дроби так же просто, как умножить два целых числа. Следуйте инструкциям ниже, чтобы научиться умножать две дроби.
- Шаг 1: Сначала умножьте числитель данных дробей.
- Шаг 2: Теперь перемножьте знаменатели.
- Шаг 3: Запишите их в виде м/н.
- Шаг 4: Если вы обнаружите, что дроби можно еще уменьшить до меньших чисел, сделайте это.
Давайте рассмотрим пример, чтобы понять шаги, упомянутые выше:
Пример: Умножьте 2/7 и 3/4.
Решение: Пошаговое решение:
- Умножьте 2 и 3 = 2 x 3 = 6
- Умножьте 7 и 4 = 4 x 7 = 28
- Запишите их в дробной форме = 6/20 7 9000 Если возможно, уменьшите значение дроби. Здесь мы видим, что дробь является коэффициентом 2. Таким образом, мы можем разделить дробь на два; следовательно, 6/28 = 3/14.
Следовательно, результат умножения 2/7 и 3/4 равен 3/14.
При умножении дробей всегда помните о следующих правилах:
- Правило 1: Если есть смешанные дроби, превратите их в неправильные дроби. Затем следует умножить числители данных дробей.
- Правило 2: Разделите числители на знаменатели по отдельности.
- Правило 3: Приведите полученное значение к его простейшей форме.
Эти три принципа можно использовать для получения произведения любых двух фракций. Давайте теперь посмотрим на множество дробей умножения с различными дробями.
Умножение дробей с одинаковым знаменателем Подобные дроби — это дроби с одинаковыми знаменателями. Например, 5/7, 1/7 и 3/7 похожи на дроби, а 5/7 и 4/3 не похожи на дроби. Хотя сложение и вычитание одинаковых дробей отличается от сложения и вычитания разнородных дробей, подход к умножению и делению одинаков. На правило умножения дробей не влияет умножение дробей с одинаковым знаменателем. Давайте возьмем пример, чтобы понять это:
Давайте возьмем пример, чтобы понять это:
Пример: Умножить 11/4 × 5/4
Решение: Давайте вспомним шаги, изученные в предыдущем разделе, чтобы решить это
- Шаг 1: Умножить 11 и 5, 11 × 5 = 55.
- Шаг 2: Умножить 4 на 4, 4 × 4 = 16.
- Шаг 3: Представить результат в виде дроби, получится 55/16. Поскольку результат не является множителем любого числа, результирующая дробь равна 55/16.
Умножение дробей с разными знаменателями аналогично умножению дробей с одинаковыми знаменателями. Давайте посмотрим на пример, чтобы понять это лучше.
Пример: Умножить 2/7 × 9/11
Решение: Повторим те же шаги, что и в предыдущем примере
- Шаг 1: Умножим 2 и 9, 18 × 9 =
- Шаг 2: Умножить 7 и 11, 7 × 11 = 77.

- Шаг 3: Представить результат в дробной форме, получится 18/77. Поскольку результат не является множителем любого числа, результирующая дробь равна 18/77.
Мы даже можем использовать альтернативный метод для решения задач, связанных с умножением дробей.
Альтернативный метод:
Этот метод включает запись данных нам дробей вместе с использованием знака умножения «x». Затем мы проверяем, являются ли числа, находящиеся напротив друг друга, делителями друг друга или какого-то другого числа или нет. Затем мы упрощаем уравнение и умножаем числитель и знаменатель соответственно, чтобы получить результат. Вы можете обратиться к приведенному ниже примеру, чтобы упростить понимание этого метода.
Пример: Умножьте 8/6 × 3/24.
Решение: Запишите дроби как 8/6 x 3/24. Мы видим, что 24 можно разделить на 8 три раза, а 6 можно разделить на 3 два раза. Следовательно, дробь становится равной 12 x 13. Теперь мы упростили уравнение и можем легко перемножить их, чтобы получить ответ в виде ⅙.
Теперь мы упростили уравнение и можем легко перемножить их, чтобы получить ответ в виде ⅙.
Разве это не было легко? Этот метод был разработан, чтобы упростить решение, потому что люди путаются при работе с большими числами.
Умножение дробей на целые числаПрежде чем углубиться в концепцию умножения дробей на целые числа. Давайте разберемся с очень маленькой концепцией, но чрезвычайно важной для этого раздела. как мы все знаем, что целые числа 0, 1, 2, 3,………, бесконечность. Но знаете ли вы, как мы можем записать целое число в дробную форму? Мы можем легко записать любое целое число в дроби, сделав целое число числителем, а затем приняв знаменатель за 1. Таким образом, мы получим 0 как 0/1, 1 как 1/1, 2 и 2/1, и так далее. на.
Теперь, когда мы знаем это понятие, стало удобно решать задачи на умножение на целые числа. Из приведенного ниже примера вы легко поймете этот раздел.
Пример: Умножение: 13 × 2/9.
Решение: Выполните шаги, указанные ниже:
- Шаг 1: Запишите 13 в дробной форме как 13/1
- Шаг 2: Шаг 5 9000
3: Поскольку мы не можем просто уменьшить это выражение, умножьте 13 и 2 = 13 x 2 = 26
- Шаг 4: Теперь умножьте 1 на 9.
 1 x 9 = 9
1 x 9 = 9 - Шаг 5: Результат умножения данного коэффициента равен 26/9, что является неправильной дробью.
Мы знаем, что дробь, представляющая собой комбинацию целого числа и дроби, называется смешанной дробью. Нельзя умножать дроби, если они в смешанной форме. Таким образом, мы должны сначала преобразовать смешанные дроби в форму неправильной дроби. Это можно сделать, умножив знаменатель на целое число и прибавив результат к числителю.
Например, замените 6
на неправильную дробь.
Решение: Умножьте 6 на 5 = 6 x 5 = 30.
Добавьте результат к числителю. 30 + 2 = 32.
Поэтому неправильная дробь = 32/5
Остальные шаги при умножении дробей остаются такими же, как обсуждалось много раз в этой статье.
Пример: Умножить 4
и 7
- Шаг 1: Преобразуйте все смешанные дроби в неправильные дроби.


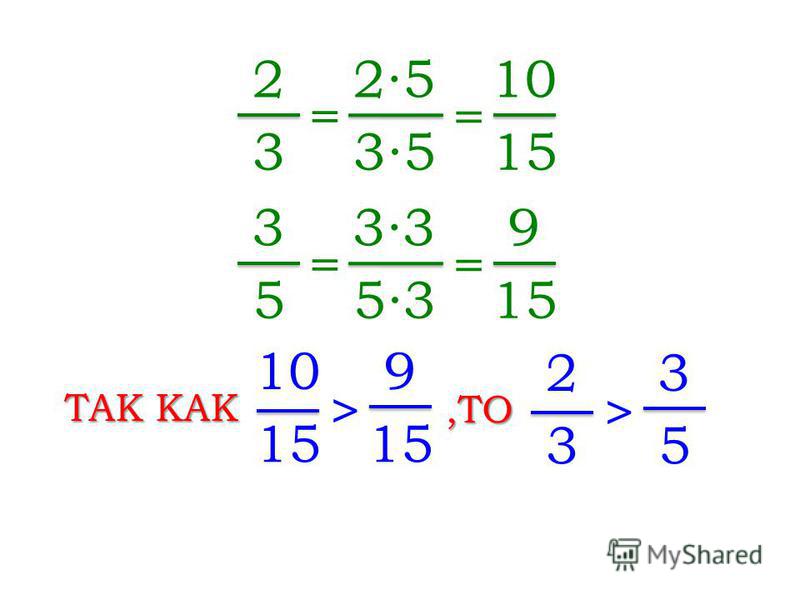
 Когда складывают дроби, знаменатели этих дробей должны быть одинаковыми. Но одинаковыми они бывают не всегда.
Когда складывают дроби, знаменатели этих дробей должны быть одинаковыми. Но одинаковыми они бывают не всегда. А как складывать такие дроби мы уже знаем.
А как складывать такие дроби мы уже знаем. Записываем его ко второй дроби. Опять же делаем небольшую косую линию над второй дробью и записываем над ней найденный дополнительный множитель:
Записываем его ко второй дроби. Опять же делаем небольшую косую линию над второй дробью и записываем над ней найденный дополнительный множитель:
 Найти значение выражения .
Найти значение выражения . Умножить числители и знаменатели дробей на свои дополнительные множители
Умножить числители и знаменатели дробей на свои дополнительные множители  Выделяем:
Выделяем: Если от пиццы отрезать пиццы, то получится пиццы:
Если от пиццы отрезать пиццы, то получится пиццы: В первую очередь находят НОК знаменателей обеих дробей. Затем НОК делят на знаменатель первой дроби и получают первый дополнительный множитель, который записывается над первой дробью. Аналогично НОК делят на знаменатель второй дроби и получают второй дополнительный множитель, который записывается над второй дробью.
В первую очередь находят НОК знаменателей обеих дробей. Затем НОК делят на знаменатель первой дроби и получают первый дополнительный множитель, который записывается над первой дробью. Аналогично НОК делят на знаменатель второй дроби и получают второй дополнительный множитель, который записывается над второй дробью. НОК это число 12, а знаменатель первой дроби — число 3. Делим 12 на 3, получаем 4. Записываем четвёрку над первой дробью:
НОК это число 12, а знаменатель первой дроби — число 3. Делим 12 на 3, получаем 4. Записываем четвёрку над первой дробью: Приведя эти дроби к общему знаменателю, мы получили дроби и . Эти дроби будут изображаться теми же кусочками пицц, но в этот раз они будут разделены на одинаковые доли (приведены к одинаковому знаменателю):
Приведя эти дроби к общему знаменателю, мы получили дроби и . Эти дроби будут изображаться теми же кусочками пицц, но в этот раз они будут разделены на одинаковые доли (приведены к одинаковому знаменателю):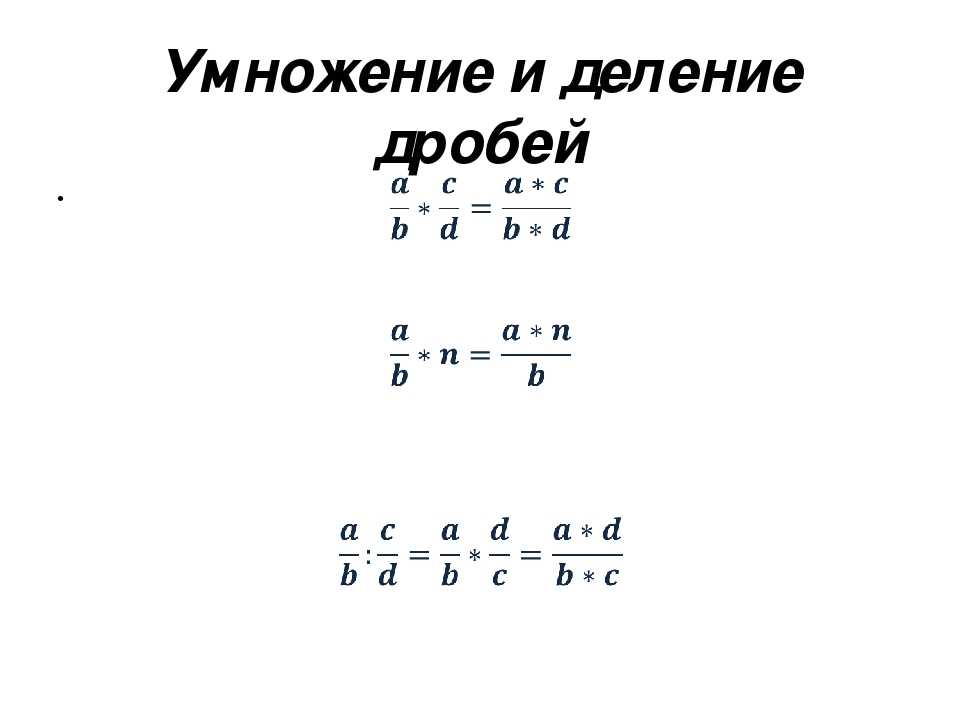 Делим 30 на 10, получаем первый дополнительный множитель 3. Записываем его над первой дробью:
Делим 30 на 10, получаем первый дополнительный множитель 3. Записываем его над первой дробью: Не забываем про знак равенства (=) на новой строке:
Не забываем про знак равенства (=) на новой строке: Если выражение , записать как , то произведение по прежнему будет равно . Опять же срабатывает правило перемножения целого числа и дроби:
Если выражение , записать как , то произведение по прежнему будет равно . Опять же срабатывает правило перемножения целого числа и дроби: Найти значение выражения .
Найти значение выражения . Найти значение выражения
Найти значение выражения
 Сколько пиццы достанется каждому?
Сколько пиццы достанется каждому? Если получится сократить дробь, то вам легче будет дальше производить расчеты.
Если получится сократить дробь, то вам легче будет дальше производить расчеты.
 Лучше запишите несколько лишних строчек в черновике, чем запутаться в расчетах в уме.
Лучше запишите несколько лишних строчек в черновике, чем запутаться в расчетах в уме.
 Мы, по инерции мышления, применяем постоянные единицы измерения времени к обратной величине. С физической точки зрения это выглядит, как замедление времени до его полной остановки в момент, когда Ахиллес поравняется с черепахой. Если время останавливается, Ахиллес уже не может перегнать черепаху.
Мы, по инерции мышления, применяем постоянные единицы измерения времени к обратной величине. С физической точки зрения это выглядит, как замедление времени до его полной остановки в момент, когда Ахиллес поравняется с черепахой. Если время останавливается, Ахиллес уже не может перегнать черепаху. Теперь Ахиллес на восемьсот шагов опережает черепаху.
Теперь Ахиллес на восемьсот шагов опережает черепаху.  Для определения факта движения автомобиля нужны две фотографии, сделанные из одной точки в разные моменты времени, но по ним нельзя определить расстояние. Для определения расстояния до автомобиля нужны две фотографии, сделанные из разных точек пространства в один момент времени, но по ним нельзя определить факт движения (естественно, ещё нужны дополнительные данные для расчетов, тригонометрия вам в помощь). На что я хочу обратить особое внимание, так это на то, что две точки во времени и две точки в пространстве — это разные вещи, которые не стоит путать, ведь они предоставляют разные возможности для исследования.
Для определения факта движения автомобиля нужны две фотографии, сделанные из одной точки в разные моменты времени, но по ним нельзя определить расстояние. Для определения расстояния до автомобиля нужны две фотографии, сделанные из разных точек пространства в один момент времени, но по ним нельзя определить факт движения (естественно, ещё нужны дополнительные данные для расчетов, тригонометрия вам в помощь). На что я хочу обратить особое внимание, так это на то, что две точки во времени и две точки в пространстве — это разные вещи, которые не стоит путать, ведь они предоставляют разные возможности для исследования. Математики выступают в роли обычных дрессировщиков, проповедуя нам свои абсурдные идеи.
Математики выступают в роли обычных дрессировщиков, проповедуя нам свои абсурдные идеи. Вот здесь начнется самое интересное.
Вот здесь начнется самое интересное.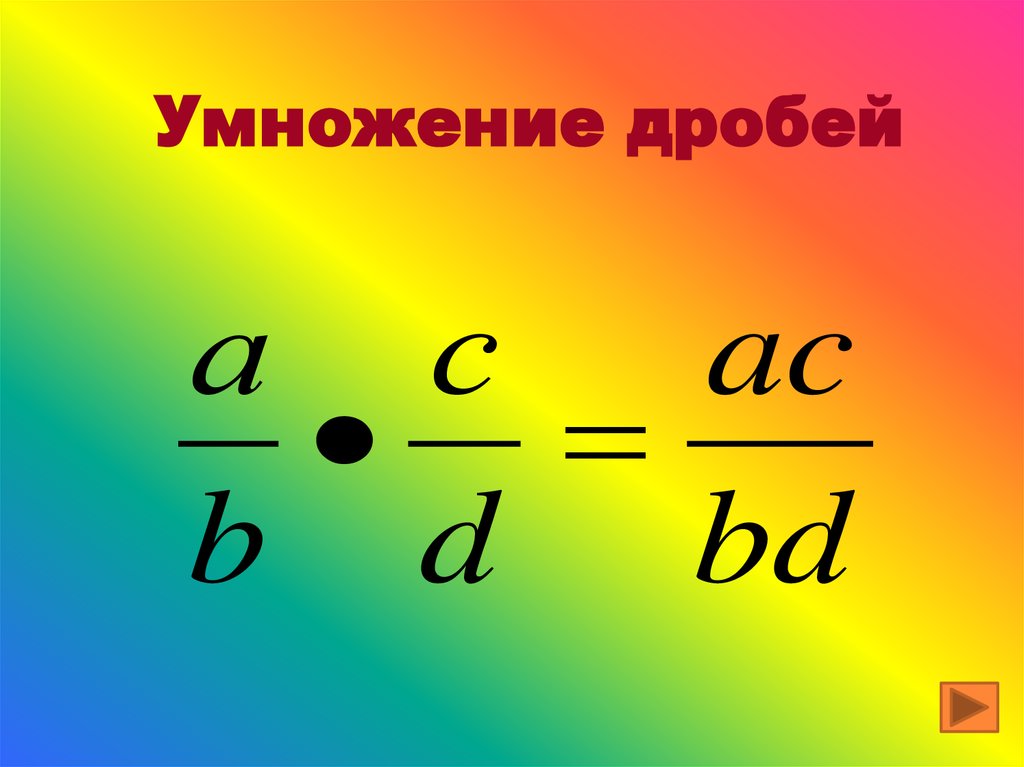 Как видите, один и тот же набор элементов одновременно является и множеством, и мультимножеством. Как правильно? А вот здесь математик-шаман-шуллер достает из рукава козырный туз и начинает нам рассказывать либо о множестве, либо о мультимножестве. В любом случае он убедит нас в своей правоте.
Как видите, один и тот же набор элементов одновременно является и множеством, и мультимножеством. Как правильно? А вот здесь математик-шаман-шуллер достает из рукава козырный туз и начинает нам рассказывать либо о множестве, либо о мультимножестве. В любом случае он убедит нас в своей правоте. Её не существует. Нет в математике формулы, по которой можно найти сумму цифр любого числа. Ведь цифры — это графические символы, при помощи которых мы записываем числа и на языке математики задача звучит так: «Найти сумму графических символов, изображающих любое число». Математики эту задачу решить не могут, а вот шаманы — элементарно.
Её не существует. Нет в математике формулы, по которой можно найти сумму цифр любого числа. Ведь цифры — это графические символы, при помощи которых мы записываем числа и на языке математики задача звучит так: «Найти сумму графических символов, изображающих любое число». Математики эту задачу решить не могут, а вот шаманы — элементарно.
 Это ещё один аргумент в пользу того, что . Вопрос к математикам: как в математике обозначается то, что не является числом? Что, для математиков ничего, кроме чисел, не существует? Для шаманов я могу такое допустить, но для ученых — нет. Реальность состоит не только из чисел.
Это ещё один аргумент в пользу того, что . Вопрос к математикам: как в математике обозначается то, что не является числом? Что, для математиков ничего, кроме чисел, не существует? Для шаманов я могу такое допустить, но для ученых — нет. Реальность состоит не только из чисел. Какой еще туалет?
Какой еще туалет? Наиболее сложным моментом в тех действиях было приведение дробей к общему знаменателю.
Наиболее сложным моментом в тех действиях было приведение дробей к общему знаменателю. Но чего точно не будет при умножении, так это приведения к общему знаменателю: никаких методов «крест-накрест», наибольших множителей и наименьших общих кратных.
Но чего точно не будет при умножении, так это приведения к общему знаменателю: никаких методов «крест-накрест», наибольших множителей и наименьших общих кратных. Если же последний минус не зачеркнут, поскольку ему не нашлось пары, выносим его за пределы умножения. Получится отрицательная дробь.
Если же последний минус не зачеркнут, поскольку ему не нашлось пары, выносим его за пределы умножения. Получится отрицательная дробь. Взгляните на примеры:
Взгляните на примеры: В общем, будьте внимательны.
В общем, будьте внимательны.

 Если наступает конец задачи, то от неправильных дробей принято избавляться. Чтобы избавится от неправильной дроби, нужно выделить в ней целую часть. В нашем случае целая часть выделяется легко — два разделить на два равно единице:
Если наступает конец задачи, то от неправильных дробей принято избавляться. Чтобы избавится от неправильной дроби, нужно выделить в ней целую часть. В нашем случае целая часть выделяется легко — два разделить на два равно единице: Достаточно понимать следующие правила:
Достаточно понимать следующие правила: Затем НОК делят на знаменатель первой дроби и получают первый дополнительный множитель. Аналогично поступают и со второй дробью — НОК делят на знаменатель второй дроби и получают второй дополнительный множитель.
Затем НОК делят на знаменатель первой дроби и получают первый дополнительный множитель. Аналогично поступают и со второй дробью — НОК делят на знаменатель второй дроби и получают второй дополнительный множитель. Делим 6 на 3, получаем 2.
Делим 6 на 3, получаем 2. К прибавить получается .
К прибавить получается .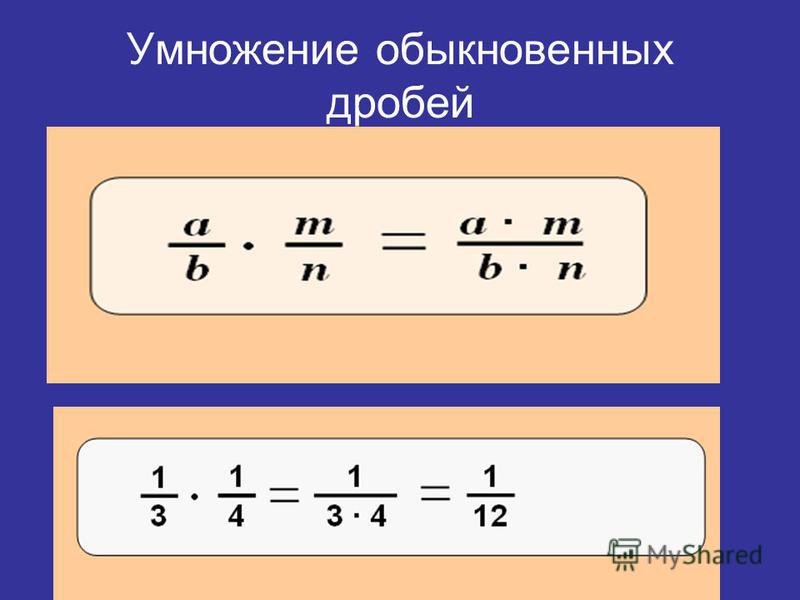 Находясь в школе, данный пример нам пришлось бы записать следующим образом:
Находясь в школе, данный пример нам пришлось бы записать следующим образом: Знаменатели дробей это числа 2, 3 и 4. Нужно найти НОК для этих чисел:
Знаменатели дробей это числа 2, 3 и 4. Нужно найти НОК для этих чисел: Сложить дроби у которых одинаковые знаменатели
Сложить дроби у которых одинаковые знаменатели  Тут всё просто. Чтобы вычесть из одной дроби другую, нужно из числителя первой дроби вычесть числитель второй дроби, а знаменатель оставить прежним.
Тут всё просто. Чтобы вычесть из одной дроби другую, нужно из числителя первой дроби вычесть числитель второй дроби, а знаменатель оставить прежним. Если пример завершен, то от неправильной дроби принято избавляться. Давайте и мы избавимся от неправильной дроби в ответе. Для этого выделим ее целую часть:
Если пример завершен, то от неправильной дроби принято избавляться. Давайте и мы избавимся от неправильной дроби в ответе. Для этого выделим ее целую часть: Аналогично НОК делят на знаменатель второй дроби и получают второй дополнительный множитель, который записывается над второй дробью.
Аналогично НОК делят на знаменатель второй дроби и получают второй дополнительный множитель, который записывается над второй дробью. Делим 12 на 4, получаем 3. Записываем тройку над второй дробью:
Делим 12 на 4, получаем 3. Записываем тройку над второй дробью: Отрезав от восьми кусочков три кусочка мы получаем пять кусочков из двенадцати. Дробь и описывает эти пять кусочков.
Отрезав от восьми кусочков три кусочка мы получаем пять кусочков из двенадцати. Дробь и описывает эти пять кусочков. Разделим НОК на знаменатель третьей дроби. НОК это число 30, а знаменатель третьей дроби — число 5. Делим 30 на 5, получаем третий дополнительный множитель 6. Записываем его над третьей дробью:
Разделим НОК на знаменатель третьей дроби. НОК это число 30, а знаменатель третьей дроби — число 5. Делим 30 на 5, получаем третий дополнительный множитель 6. Записываем его над третьей дробью:
 Если выражение , записать как , то произведение по прежнему будет равно . Опять же срабатывает правило перемножения целого числа и дроби:
Если выражение , записать как , то произведение по прежнему будет равно . Опять же срабатывает правило перемножения целого числа и дроби: Дробь можно сократить на 2. Тогда окончательное решение примет следующий вид:
Дробь можно сократить на 2. Тогда окончательное решение примет следующий вид: Чтобы сократить эту дробь, её нужно разделить на НОД числителя и знаменателя. Итак, найдём НОД чисел 105 и 450:
Чтобы сократить эту дробь, её нужно разделить на НОД числителя и знаменателя. Итак, найдём НОД чисел 105 и 450: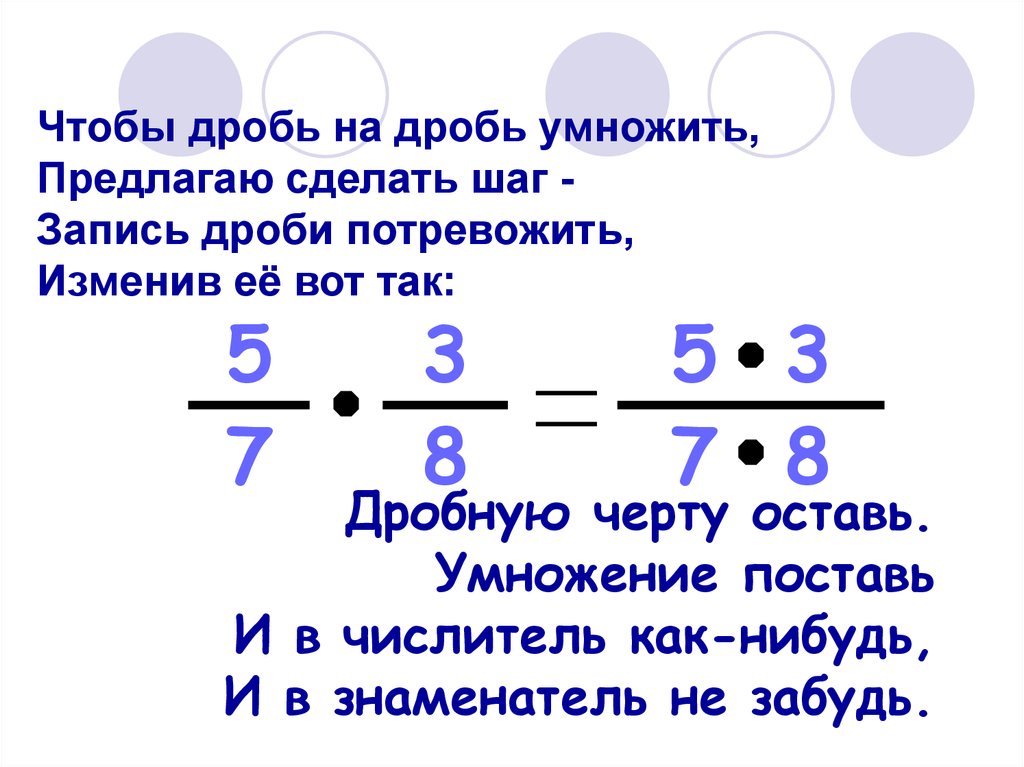
 Когда Ахиллес пробежит сто шагов, черепаха проползёт ещё десять шагов, и так далее. Процесс будет продолжаться до бесконечности, Ахиллес так никогда и не догонит черепаху.
Когда Ахиллес пробежит сто шагов, черепаха проползёт ещё десять шагов, и так далее. Процесс будет продолжаться до бесконечности, Ахиллес так никогда и не догонит черепаху.  Применение же нашей обычной логики приводит нас в ловушку. Мы, по инерции мышления, применяем постоянные единицы измерения времени к обратной величине. С физической точки зрения это выглядит, как замедление времени до его полной остановки в момент, когда Ахиллес поравняется с черепахой. Если время останавливается, Ахиллес уже не может перегнать черепаху.
Применение же нашей обычной логики приводит нас в ловушку. Мы, по инерции мышления, применяем постоянные единицы измерения времени к обратной величине. С физической точки зрения это выглядит, как замедление времени до его полной остановки в момент, когда Ахиллес поравняется с черепахой. Если время останавливается, Ахиллес уже не может перегнать черепаху. За следующий интервал времени, равный первому, Ахиллес пробежит ещё тысячу шагов, а черепаха проползет сто шагов. Теперь Ахиллес на восемьсот шагов опережает черепаху.
За следующий интервал времени, равный первому, Ахиллес пробежит ещё тысячу шагов, а черепаха проползет сто шагов. Теперь Ахиллес на восемьсот шагов опережает черепаху.  По одной фотографии автомобиля на дороге невозможно определить ни факт его движения, ни расстояние до него. Для определения факта движения автомобиля нужны две фотографии, сделанные из одной точки в разные моменты времени, но по ним нельзя определить расстояние. Для определения расстояния до автомобиля нужны две фотографии, сделанные из разных точек пространства в один момент времени, но по ним нельзя определить факт движения (естественно, ещё нужны дополнительные данные для расчетов, тригонометрия вам в помощь). На что я хочу обратить особое внимание, так это на то, что две точки во времени и две точки в пространстве — это разные вещи, которые не стоит путать, ведь они предоставляют разные возможности для исследования.
По одной фотографии автомобиля на дороге невозможно определить ни факт его движения, ни расстояние до него. Для определения факта движения автомобиля нужны две фотографии, сделанные из одной точки в разные моменты времени, но по ним нельзя определить расстояние. Для определения расстояния до автомобиля нужны две фотографии, сделанные из разных точек пространства в один момент времени, но по ним нельзя определить факт движения (естественно, ещё нужны дополнительные данные для расчетов, тригонометрия вам в помощь). На что я хочу обратить особое внимание, так это на то, что две точки во времени и две точки в пространстве — это разные вещи, которые не стоит путать, ведь они предоставляют разные возможности для исследования. Подобную логику абсурда разумным существам не понять никогда. Это уровень говорящих попугаев и дрессированных обезьян, у которых разум отсутствует от слова «совсем». Математики выступают в роли обычных дрессировщиков, проповедуя нам свои абсурдные идеи.
Подобную логику абсурда разумным существам не понять никогда. Это уровень говорящих попугаев и дрессированных обезьян, у которых разум отсутствует от слова «совсем». Математики выступают в роли обычных дрессировщиков, проповедуя нам свои абсурдные идеи. Затем берем с каждой стопки по одной купюре и вручаем математику его «математическое множество зарплаты». Поясняем математику, что остальные купюры он получит только тогда, когда докажет, что множество без одинаковых элементов не равно множеству с одинаковыми элементами. Вот здесь начнется самое интересное.
Затем берем с каждой стопки по одной купюре и вручаем математику его «математическое множество зарплаты». Поясняем математику, что остальные купюры он получит только тогда, когда докажет, что множество без одинаковых элементов не равно множеству с одинаковыми элементами. Вот здесь начнется самое интересное.

 Это не математическое действие.
Это не математическое действие.
 Какой еще туалет?
Какой еще туалет?
 А вот в трёхэтажной дроби легко ошибиться. Обратите внимание, например:
А вот в трёхэтажной дроби легко ошибиться. Обратите внимание, например: Лучше написать две лишние строчки в черновике, чем накосячить при расчёте в уме.
Лучше написать две лишние строчки в черновике, чем накосячить при расчёте в уме. Я специально их в беспорядке записал, подальше от соблазна, так сказать. Вот они, ответы, через точку с запятой записаны.
Я специально их в беспорядке записал, подальше от соблазна, так сказать. Вот они, ответы, через точку с запятой записаны. ru. Там в опции «Попробовать» есть 10 примеров для всех желающих. С мгновенной проверкой. Для зарегистрированных пользователей — 34 примера от простых до суровых. Это только по дробям.
ru. Там в опции «Попробовать» есть 10 примеров для всех желающих. С мгновенной проверкой. Для зарегистрированных пользователей — 34 примера от простых до суровых. Это только по дробям.
 Сокращение дробей при расчётах значительно облегчит ваши вычисления.
Сокращение дробей при расчётах значительно облегчит ваши вычисления.
 Сокращаем 16 и 24 на 8.
Сокращаем 16 и 24 на 8.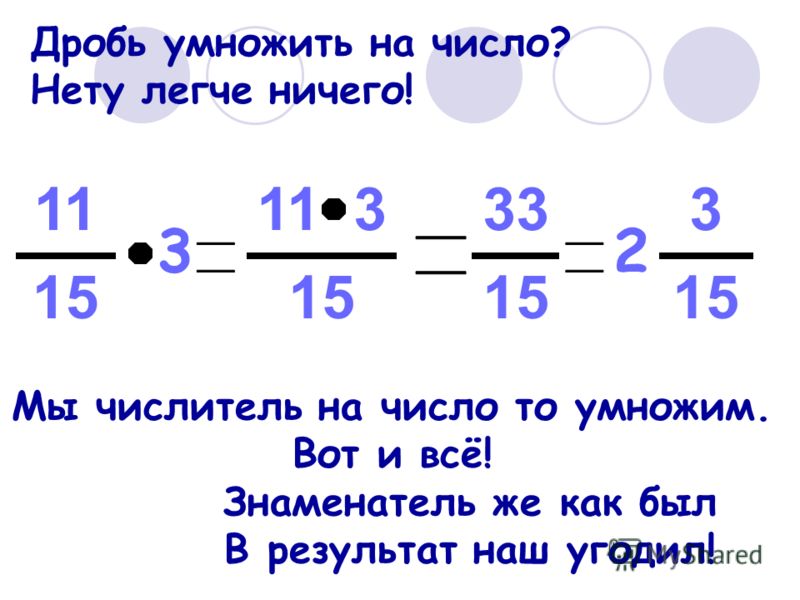 Поэтому весь урок мы будем рассматривать в основном умножение.
Поэтому весь урок мы будем рассматривать в основном умножение. Для произведения их можно обобщить, чтобы «сжигать» сразу несколько минусов:
Для произведения их можно обобщить, чтобы «сжигать» сразу несколько минусов: Числа здесь получаются довольно большие, и чтобы упростить задачу, можно попробовать сократить дробь еще до умножения . Ведь по существу, числители и знаменатели дробей — это обычные множители, и, следовательно, их можно сокращать, используя основное свойство дроби. Взгляните на примеры:
Числа здесь получаются довольно большие, и чтобы упростить задачу, можно попробовать сократить дробь еще до умножения . Ведь по существу, числители и знаменатели дробей — это обычные множители, и, следовательно, их можно сокращать, используя основное свойство дроби. Взгляните на примеры:



 Самым важным в работе с дробными выражениями является аккуратность и внимательность. Все вычисления делайте внимательно и аккуратно, сосредоточенно и чётко. Лучше запишите несколько лишних строчек в черновике, чем запутаться в расчетах в уме.
Самым важным в работе с дробными выражениями является аккуратность и внимательность. Все вычисления делайте внимательно и аккуратно, сосредоточенно и чётко. Лучше запишите несколько лишних строчек в черновике, чем запутаться в расчетах в уме. 12.2008 N 6-ФКЗ, от 30.12.2008 N 7-ФКЗ,от […]
12.2008 N 6-ФКЗ, от 30.12.2008 N 7-ФКЗ,от […] Допустим, у нас есть квадрат, сторона которого равна одной числовой единице. Тогда площадь фигуры составит 1 кв. единицу. Если разделить квадрат на равные прямоугольники со сторонами, равными 1 4 и 1 8 числовой единицы, у нас получится, что он теперь состоит из 32 прямоугольников (потому что 8 · 4 = 32). Соответственно, площадь каждого из них будет равна 1 32 от площади всей фигуры, т.е. 1 32 кв. единицы.
Допустим, у нас есть квадрат, сторона которого равна одной числовой единице. Тогда площадь фигуры составит 1 кв. единицу. Если разделить квадрат на равные прямоугольники со сторонами, равными 1 4 и 1 8 числовой единицы, у нас получится, что он теперь состоит из 32 прямоугольников (потому что 8 · 4 = 32). Соответственно, площадь каждого из них будет равна 1 32 от площади всей фигуры, т.е. 1 32 кв. единицы. Оно действует одинаково как для правильных, так и для неправильных дробей; с помощью него можно умножить дроби и с разными, и с одинаковыми знаменателями.
Оно действует одинаково как для правильных, так и для неправильных дробей; с помощью него можно умножить дроби и с разными, и с одинаковыми знаменателями. Запись решения будет выглядеть так:
Запись решения будет выглядеть так:









