другую дробь, целое натуральное число
Sign in
Password recovery
Восстановите свой пароль
Ваш адрес электронной почты
MicroExcel.ru Математика Алгебра Вычитание десятичных дробей: правила, примеры
В данной публикации мы рассмотрим, каким образом из десятичной дроби можно вычесть другую дробь (десятичную и обыкновенную) или целое натуральное число (и наоборот). Также разберем примеры для лучшего понимания представленного материала.
- Правило вычитания десятичных дробей
- Примеры
Правило вычитания десятичных дробей
Разность десятичных дробей находится путем их вычитания столбиком. Алгоритм приведен ниже:
1. Располагаем дроби так, чтобы их запятые были строго друг под другом. Таким образом, друг под другом окажутся и одноименные разряды: десятые под десятыми, сотые под сотыми, тысячные под тысячными и т.
д.
Примечание: Если число знаков после запятой у дробей разное, в конце дроби с меньшим количеством цифр в дробной части добавляем нули, чтобы уравнять ее по длине с другой. Согласно основному свойству десятичной дроби, это никак не повлияет на ее величину.
Примеры неправильной записи разности:
Примеры правильной записи разности:
2. Не обращая внимания на запятые вычитаем из одной дроби другую (т.е. условно принимаем их за целые числа).
3. В полученном результате добавляем запятую в том же месте, где расположены запятые дробей выше.
Разность десятичной дроби и целого натурального числа
Если требуется найти разность десятичной дроби и целого натурального числа, в конце последнего ставим запятую, после которой дописываем столько нулей, сколько знаков содержится после запятой в десятичной дроби. Далее выполняем требуемое действие, т.е. вычитание.
Разность десятичной и обыкновенной дробей
Чтобы найти разность десятичной и простой дробей, последнюю переводим в десятичную.
Далее выполняем вычитание.
Альтернативный вариант – наоборот, десятичную дробь преобразовать в обыкновенную. Здесь мы уже будем вычитать простые дроби.
Примеры
Вычислим разности десятичных дробей, которые рассмотрели выше:
А теперь давайте посмотрим примеры вычитания из десятичной дроби целого натурального числа и наоборот.
ЧАЩЕ ВСЕГО ЗАПРАШИВАЮТ
Таблица знаков зодиака
Нахождение площади трапеции: формула и примеры
Нахождение длины окружности: формула и задачи
Римские цифры: таблицы
Таблица синусов
Тригонометрическая функция: Тангенс угла (tg)
Нахождение площади ромба: формула и примеры
Нахождение объема цилиндра: формула и задачи
Тригонометрическая функция: Синус угла (sin)
Геометрическая фигура: треугольник
Нахождение объема шара: формула и задачи
Тригонометрическая функция: Косинус угла (cos)
Нахождение объема конуса: формула и задачи
Таблица сложения чисел
Нахождение площади квадрата: формула и примеры
Что такое тетраэдр: определение, виды, формулы площади и объема
Нахождение объема пирамиды: формула и задачи
Признаки подобия треугольников
Нахождение периметра прямоугольника: формула и задачи
Формула Герона для треугольника
Что такое средняя линия треугольника
Нахождение площади треугольника: формула и примеры
Нахождение площади поверхности конуса: формула и задачи
Что такое прямоугольник: определение, свойства, признаки, формулы
Разность кубов: формула и примеры
Степени натуральных чисел
Нахождение площади правильного шестиугольника: формула и примеры
Тригонометрические значения углов: sin, cos, tg, ctg
Нахождение периметра квадрата: формула и задачи
Теорема Фалеса: формулировка и пример решения задачи
Сумма кубов: формула и примеры
Нахождение объема куба: формула и задачи
Куб разности: формула и примеры
Нахождение площади шарового сегмента
Что такое окружность: определение, свойства, формулы
Вычитание десятичных дробей | Математика
Как и сложение, вычитание десятичных дробей зависит от правильной записи чисел.
Правило вычитания десятичных дробей
1) ЗАПЯТАЯ ПОД ЗАПЯТОЙ!
Эта часть правила самая важная. При вычитании десятичных дробей их следует записать так, чтобы запятые уменьшаемого и вычитаемого находились строго одна под другой.
2) Уравниваем количество цифр после запятой. Для этого в том числе, где количество цифр после запятой меньше, дописываем после запятой в конце нули.
3) Вычитаем числа, не обращая внимания на запятую.
4) Сносим запятую под запятыми.
Примеры на вычитание десятичных дробей.
1) 9,7-3,5
Чтобы найти разность десятичных дробей 9,7 и 3,5, запишем их так, чтобы запятые в обоих числах находились строго одна под другой. Затем вычитаем, не обращая внимания на запятую. В полученном результате запятую сносим, то есть записываем под запятыми уменьшаемого и вычитаемого:
9,7-3,5=6,2.
2) 23,45 — 1,5
Чтобы из одной десятичной дроби вычесть другую, надо записать их так, чтобы запятые располагались точно одна под другой.
23,45 — 1,5=21,95.
3) 63,5-8,921
Вычитание десятичных дробей начинаем с их записи так, чтобы запятые были расположены ровно одна под одной. В первом числе после запятой одна цифра, во втором — три, поэтому на место недостающих двух цифр в первом числе записываем нули. Затем вычитаем числа, не обращая внимания на запятую. В полученном результате сносим запятую под запятыми:
63,5-8,921=54,579.
4) 2,8703 — 0,507
Чтобы вычесть эти десятичные дроби, записываем их так, чтобы запятая второго числа расположилась точно под запятой первого. В первом числе после запятой четыре цифры, во втором — три, поэтому второе число дополняем после запятой нулем в конце. После этого вычитаем эти числа, как обычные натуральные, не учитывая запятую. В полученном результате записываем запятую под запятыми :
2,8703 — 0,507 = 2,3663.
5) 35,46 — 7,372
Вычитание десятичных дробей начинаем с записи чисел таким образом, чтобы запятые находились одна под другой. Дополняем нулем после запятой первое число, чтобы в обоих дробях после запятой было по три цифры. Затем вычитаем, не обращая внимания на запятую. В ответе сносим запятую под запятыми:
35,46 — 7,372 = 28,088.
6) 45 — 7,303
Чтобы из натурального числа вычесть десятичную дробь, в его записи в конце ставим запятую и приписываем необходимое количество нулей после запятой. Зачем вычитаем, не беря во внимание запятую. В ответ сносим запятую ровно под запятыми:
45 — 7,303 = 37,698.
7) 17,256 — 4,756
Этот пример на вычитание десятичных дробей выполняем аналогично. В результате получили число с нулями после запятой в конце. Их в ответе не пишем: 17,256 — 4,756 =12,5.
Что такое вычитание десятичных дробей? Определение, правила, примеры, факты
Бен покупает продукты на $\$$155,50. Он передает продавцу $\$$500 и, в свою очередь, получает обратно $\$$344,50.
Без знания десятичных дробей узнать точную сумму, которую он должен был заплатить за продукты, было бы невозможно.
Десятичные числа — это числа, в которых есть десятичная точка. Они состоят из двух частей: первая — целое число (слева от запятой), а вторая — дробная часть (справа от запятой).
Например, Сэм покупает апельсины за $\$$3,50. Здесь
- $\$$3,50 — десятичное число (цена апельсинов)
- 3 — целое число (слева от запятой)
- 50 — дробная часть (справа от запятой) )
Десятичные числа повышают точность счета и часто используются в повседневной деятельности.
Десятичные числа можно складывать, вычитать, умножать или делить в зависимости от конкретного сценария. Сегодня мы обсудим вычитание десятичных дробей , их правила и несколько примеров.
Как вычитать десятичные дроби
Вычитать десятичные дроби так же просто, как найти разницу между большим целым числом и меньшим целым числом.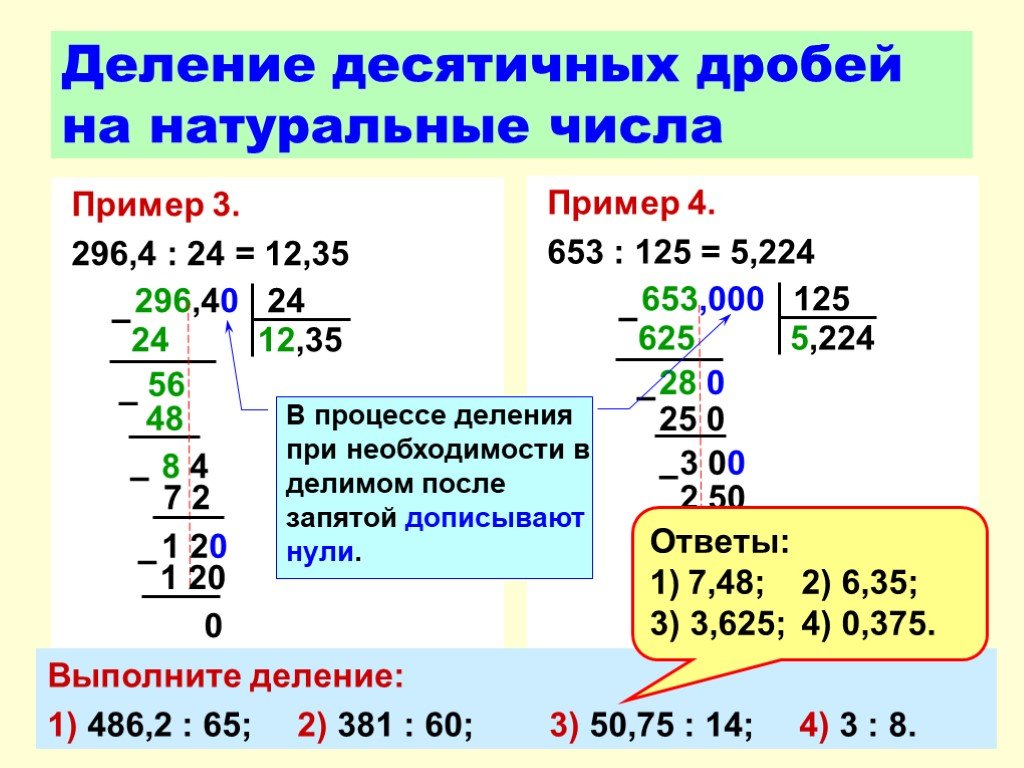
Возьмем первый пример, где цена на продукты составляла $\$$155,50. В этом сценарии 155 — это целое число, а 0,50 — его дробная часть.
В зависимости от разрядности десятичные числа должны располагаться одно под другим, не забывая при вычитании десятичной точки. Однако, если два десятичных числа различны, вычитание может быть немного сложным.
Следовательно, чтобы избежать такой путаницы, десятичные числа можно изменить на , как и десятичные числа , добавив необходимое количество нулей.
Количество знаков после запятой будет одинаковым в одинаковых десятичных дробях. Например, 5,23 и 7,89 похожи на десятичные дроби, тогда как 4,53 и 2,753 не похожи на десятичные дроби.
Рекомендуемые рабочие листы для детей:
Вычитание десятичных дробей без перегруппировки
Допустим, нам нужно вычесть 14,2 из 25,83. Вот как это сделать.
Шаг 1 : 25,83 и 14,2 не являются десятичными. Итак, сначала нам нужно преобразовать их в одинаковые десятичные дроби, добавив ноль в крайний правый угол числа 14,2, чтобы получилось 14,20.
Шаг 2 : Расположите меньшее число под большим таким образом, чтобы десятичные запятые совпадали.
Шаг 3: Вычтите каждый столбец справа налево, как если бы вычитали целое число.
Шаг 4 : Разместите десятичную точку на одной линии с другими десятичными точками.
Вычитание десятичных дробей с перегруппировкой
Перегруппировка при вычитании десятичных чисел очень похожа на перегруппировку, выполняемую при вычитании целых чисел. Давайте разберемся с помощью примера.
Рассмотрим пример вычитания десятичного числа 2,37 из 5,10. Вот как это сделать.
Шаг 1 : Десятичные дроби похожи на десятичные дроби. Итак, давайте перейдем к шагу 2.
Шаг 2: Расположите меньшее число под большим числом. Убедитесь, что цифры размещены в соответствии с их разрядами, а десятичные запятые точно выровнены.
Шаг 3: Вычтите каждый столбец отдельно, начиная справа и постепенно сдвигаясь влево.
- Если число в верхней строке меньше, чем в нижней, то из левой цифры следует заимствовать 1, добавляя к соответствующей цифре 10. Это называется перегруппировка.
- После заимствования 1 из левой цифры она уменьшается на 1. Следовательно, вычитание можно продолжить с уменьшенным числом.
Вычитание десятичных дробей из целых чисел
Допустим, мы вычитаем десятичное число 0,569 (десятичное число) из 3 (целое число). Вот как это сделать:
Шаг 1 : Первым шагом является преобразование целого числа в десятичное число. Для этого мы добавляем десятичную точку и необходимое количество нулей справа от целого числа.
Помните, что количество добавляемых нулей должно совпадать с длиной другого заданного десятичного числа.
Здесь мы добавим три нуля после 3, чтобы получить 0,569.. Таким образом, 3 станет 3.000.
Шаг 2: Расположите меньшее число под большим так, чтобы десятичные запятые совпадали.
Шаг 3: Вычтите числа, следуя обычному методу вычитания десятичных чисел.
Использование вычитания десятичных дробей в реальной жизни
Вычитание десятичных дробей используется в различных повседневных действиях, некоторые из которых следующие:
- Денежные операции: дюжина яиц стоит заплатите $\$$10 продавцу магазина. Затем, чтобы вернуть оставшуюся сумму, продавец возвращает нам $\$$4,50.
- Покупка топлива: Вы платите $\$$13,8 за 10 литров бензина для своего автомобиля.
- Научные расчеты. Ученые используют десятичные числа для получения точных показаний в своих экспериментах.
- Медицинские показания: при использовании термометра для измерения температуры тела он покажет вам показания в десятичных числах, например 98,6° F.
- Строительные измерения: Строительные проекты требуют измерения длины, ширины и высоты различных предметов , которые представлены десятичными числами.
- Здоровье и фитнес: различное оборудование для фитнеса, используемое в тренажерных залах, такое как гантели, штанги и т. д., имеет определенный предел веса, например, 8 фунтов или 10 фунтов, чтобы вы могли заниматься фитнесом в соответствии со своими возможностями. Беговая дорожка покажет вам мили, которые вы прошли или пробежали, с помощью десятичных чисел. Весы также отображают вес в десятичных дробях.
- Одометры: Вы можете рассчитать расстояние, пройденное на автомобиле или велосипеде, с помощью одометра, который использует десятичные точки для отображения точных показаний.
Решенные примеры
Пример 1. Вычтите 0,30 из 0,70.
Решение:
Пример 2: Вычтите 0,25 из 5,22.
Решение:
Пример 3: Вычтите 86,9 из 635,78.
Решение:
Практические задачи
1
Вычтите 8,20 из 9,57 и выберите правильный вариант.
1,37
3,25
0,96
1,55
Правильный ответ: 1,37
9,57 $ − 8,20 = 1,37 $
2
Вычитание десятичного числа 6 из числа 1.3 даст ответ 6.
1,37
6,05
8
7,15
Правильный ответ: 1,37
Чтобы найти ответ, вы можете добавить к результату второе десятичное число.
Следовательно, пропущенное десятичное число равно 8.
3
Вычитание десятичного числа 790,98 из 298,20 дает ответ 216,30. Является ли утверждение истинным или ложным? Объяснять.
Верно
Ложно
Правильный ответ: Ложно
Вычитая десятичное число 79,98 из 298,20, мы получаем 218,22, а не 216,30
16,2
24,861
21,6
18,22
Правильный ответ: 24,861
Во-первых, нам нужно заменить десятичные числа на подобные десятичные, добавив нули.
Итак, 36,1 будет переписано как 36,100
Тогда:
Часто задаваемые вопросы
Может ли вычитание десятичных чисел дать целое число?
Да, вычитая десятичные числа, можно получить в результате целое число. Однако цифры после запятой должны быть одинаковыми для обоих десятичных чисел.
Например, если из 4,25 вычесть 1,25, получится 3, то есть целое число.
Как проверить правильность вычитания двух десятичных чисел?
Чтобы проверить правильность вашего ответа после вычитания десятичных чисел, вы можете добавить результат с меньшим десятичным числом. Если ответ правильный, в результате вы получите большее десятичное число.
Например, если из 9,01 вычесть 2,33, получится 6,68. Теперь, если вы хотите проверить свой ответ, прибавьте 6,68 к 2,33. В результате вы получите 9,01, что означает, что ответ правильный.
Можно ли вычесть целое число из десятичного числа?
Да, целое число можно преобразовать в десятичное число, добавив нули после запятой.
Затем процесс аналогичен вычитанию десятичных чисел.
| Забавные факты – Китайцы были первыми людьми, которые использовали и разработали дроби или десятичные числа. |
Вычитание десятичных дробей — определение, правила, факты, примеры
Вычитание десятичных дробей означает нахождение разницы между десятичными числами и другими числами. Другое число может быть целым числом, десятичным числом или натуральным числом. Существуют определенные правила и шаги, которые необходимо учитывать при вычитании десятичных знаков. На этой странице мы узнаем больше о вычитании десятичных дробей, их правилах и примерах.
| 1. | Что такое вычитание десятичных дробей? |
| 2. | Правила вычитания десятичных дробей |
| 3. | Вычитание десятичных дробей с перегруппировкой |
4. | Вычитание десятичных дробей из целых чисел |
| 5. | Часто задаваемые вопросы о вычитании десятичных знаков |
Что такое вычитание десятичных дробей?
Вычитание десятичных дробей аналогично обычному вычитанию целых чисел. Нам просто нужно разместить десятичные числа, одно под другим, в соответствии с их разрядностью вместе с десятичной точкой. В некоторых случаях два заданных числа различны. При необходимости мы меняем данные десятичные дроби на , как десятичные дроби , чтобы упростить вычитание. Два десятичных знака называются , как и десятичные дроби 9.0303, если они имеют одинаковое количество знаков после запятой. Например, 0,23 и 0,65 похожи на десятичные дроби, тогда как 7,5 и 7,58 не похожи на десятичные дроби. После того, как десятичные числа преобразуются в подобно десятичным дробям , путем добавления необходимого количества нулей, два заданных числа вычитаются так же, как мы вычитаем обычные числа.
Например, вычтем данные числа:
Пример: Вычтем: 0,56 — 0,42.
Решение:
Так как это как десятичные дроби , мы расположим их по порядку и выполним обычное вычитание.
0,56
-0,42
0,14
Правила вычитания десятичных дробей
Существуют определенные правила и шаги, которые следует помнить при вычитании десятичных знаков.
- Измените данные десятичные дроби на как десятичные дроби .
- Запишите меньшее число под большим так, чтобы цифры располагались на соответствующих местах, а десятичные запятые располагались на одной вертикальной линии.
- Затем вычтите числа так же, как и в случае с целыми числами.
- После вычитания поместите десятичную точку на одной линии с другими десятичными точками.
Вычитание десятичных дробей с перегруппировкой
Вычитание десятичных дробей с перегруппировкой аналогично перегруппировке целых чисел.
Следующие шаги объясняют способ вычитания десятичных дробей путем перегруппировки.
- Шаг 1: После изменения цифр на как десятичные числа , и поместив меньшее число под большим числом, убедитесь, что десятичные точки выровнены, а цифры размещены в соответствующем столбце разряда.
- Шаг 2: Вычтите цифры в каждом столбце отдельно, начиная справа и двигаясь влево.
- Шаг 3: Если число в верхней строке меньше числа в нижней строке, мы заимствуем 1 из цифры слева и добавляем 10 к текущей цифре. Этот шаг известен как перегруппировка.
- Шаг 4: Поскольку 1 был заимствован, это число уменьшается на 1. Соответственно измените число и продолжите вычитание.
Например, давайте вычтем данные числа.
Пример: Вычтите 0,84 из 0,93.
Решение:
В приведенных выше числах 0,93 и 0,84 цифра 3 меньше 4 в столбце сотых, поэтому нам нужно заимствовать 1 из 9, чтобы выполнить вычитание. Нам нужно уменьшить 1 из 9, так как он дал 1 к числу слева от него.
Итак, 9станет 8, а 3 станет 13. Теперь вычтем 13 — 4 = 9 и 8 — 8 = 0
Наконец, мы помещаем десятичную точку в ответ, чтобы получить 0,09
Вычитание десятичных знаков с одинаковым количеством знаков после запятой
Вычитание десятичных знаков с одинаковым количеством знаков после запятой очень просто. Нам просто нужно выполнить простой процесс вычитания, а затем расставить десятичные точки в соответствии с заданными числами.
Например, давайте вычтем 3,67 из 4,98
Мы видим, что числа имеют одинаковые десятичные разряды. Итак, мы будем вычитать их обычным способом.
4,98
-3,67
1,31
Вычитание десятичных знаков с разными десятичными разрядами В этом случае мы подсчитываем количество знаков после запятой в обоих числах и определяем в них большее. Затем мы добавляем необходимое количество нулей к меньшему десятичному числу, чтобы сделать его такой же длины, как и другое число. После этого мы вычитаем десятичные числа.
Например, давайте вычтем 7,483 из 237,8
Мы видим, что оба числа имеют разные десятичные разряды. Поскольку 7,483 имеет 3 цифры после запятой, мы добавим два нуля к 237,8, чтобы привести его к той же длине. Это составит 237.800, после чего мы вычтем числа.
237,800
— 7,483
230,317
Вычитание десятичных дробей из 1
Для вычитания десятичных дробей из 1 мы используем ту же процедуру, что и для других десятичных чисел. Десятичные числа в пределах 1 означают, что данные числа меньше 1.
Например, вычтем 0,56 из 0,98.
Мы видим, что числа находятся в пределах единицы. Итак, чтобы решить эту проблему, мы расставим числа по порядку и сделаем обычное вычитание.
-0,56
0,42
Вычитание десятичных дробей из целых чисел
Чтобы вычесть десятичные числа из целых чисел, мы помещаем десятичную точку в целое число в соответствии с количеством цифр (после запятой) в другом числе.
Затем добавляем необходимое количество нулей, чтобы оба числа имели одинаковую длину.
Например, давайте вычтем 0,999 из 6.
Решение: Поскольку после запятой в числе 0,999 три цифры, мы поставим десятичную запятую после 6 и добавим три нуля после нее.
Статьи по теме
Ознакомьтесь со следующими темами, связанными с вычитанием десятичных дробей.
- Вычитание
- Двоичное вычитание
- Калькулятор вычитания десятичных дробей
Часто задаваемые вопросы о вычитании десятичных знаков
Как вычитать десятичные дроби, если верхнее число меньше?
При вычитании десятичных знаков, если число в верхней строке меньше числа в нижней строке, мы заимствуем 1 из цифры слева и добавляем 10 к текущей цифре. Этот процесс также называется перегруппировкой или заимствованием. После этого соответствующим образом меняем число и продолжаем вычитание. Поскольку 1 присваивается следующему числу, это число уменьшается на 1.
Давайте поймем это, вычитая данные числа.
3,52
-0,45
3,07
В этом случае, если мы посмотрим на цифры в столбце сотых, мы увидим, что 2 меньше 5, поэтому мы заимствуем 1 из предыдущего столбца (столбца десятых) и перегруппируем это число, то есть 2 станет 12. Из 12 вычтем 5 и получим 7. Теперь, так как из десятого столбца дана 1, 5 сводится к 4, а 4 — 4 = 0. После этого вычитание продолжается в обычным способом, и ответ, который мы получаем после вычитания, равен 3,07.
Какие советы по вычитанию десятичных дробей?
Для вычитания десятичных дробей нам нужно помнить несколько полезных советов.
- Запишите числа в таком порядке, чтобы большее число располагалось над меньшим, а десятичные запятые совпадали.
- Добавьте нули к нужному числу так, чтобы оба числа были одинаковой длины.
- Затем вычтите числа так же, как и в случае с целыми числами, и соответствующим образом поставьте десятичную точку.
Как брать взаймы при вычитании десятичных дробей?
При вычитании десятичных дробей могут быть случаи, когда число в первой строке меньше числа во второй строке. В этом случае мы заимствуем 1 из цифры слева и добавляем 10 к текущей цифре. Этот процесс также называется перегруппировкой или заимствованием. Например, если нам нужно вычесть 3,58 из 5,4, мы увидим, что в столбце сотых 0 меньше 8.
5,40
-3,58
1.82
Итак, заимствуем 1 из десятого столбца и перегруппируем число 0 как 10 + 0 = 10. Вычтем 8 из 10 и получим 2. Теперь, поскольку 1 была дана из десятого столбца, 4 сводится к 3 что снова приводит к заимствованию числа из столбца единиц. Итак, 3 становится 13, и мы вычитаем 5 из 13, чтобы получить 8. Переходя к следующему столбцу (столбец единиц), пересекая десятичные дроби, 5 уменьшается до 4 и 4 — 3 = 1. Это дает окончательный ответ как 1,82.
Как вычитать десятичные дроби из целых чисел?
Чтобы вычесть десятичные числа из целых чисел, мы помещаем десятичную точку в целое число в соответствии с количеством цифр (после запятой) в другом числе.
Затем добавляем необходимое количество нулей, чтобы оба числа имели одинаковую длину. Например, чтобы решить эти числа, 4 — 0,67, мы можем записать это как 4,00 — 0,67. Теперь мы можем легко вычитать числа. (4,00 — 0,67 = 3,33)
Каково правило сложения и вычитания десятичных дробей?
Основные правила сложения и вычитания десятичных знаков следующие:
- Изменить данные десятичные дроби на как десятичные дроби .
- Выровняйте числа таким образом, чтобы цифры располагались на соответствующих местах в соответствии с их разрядными значениями, а десятичные запятые располагались на одной вертикальной линии.
- Затем вычтите числа так же, как и в случае с целыми числами, и соответствующим образом поставьте десятичную точку.
Чем сложение десятичных знаков похоже на вычитание десятичных?
Сложение десятичных знаков аналогично вычитанию десятичных знаков, поскольку в обоих случаях используются одни и те же правила.